 Open Journal of Applied Sciences, 2013, 3, 490-513 Published Online December 2013 (http://www.scirp.org/journal/ojapps) http://dx.doi.org/10.4236/ojapps.2013.38059 Open Access OJAppS Numerical Analysis of the Analytical Relationships between Angstrom Coefficients of Aerosols and Their Optical Properties for Four Types of Aerosols Bello Idrith Tijjani1, Sha’aibu Uba2, Fatima Salman Koki1 1Department of Physics, Bayero University, Kano, Nigeria 2Department of Physics, Ahmadu Bello University, Zaria, Nigeria Email: idrith@yahoo.com, idrithtijjani@gmail.com, shuba356@yahoo.com, shuba356@yahoo.com, FatimaSK2775@gmail.com Received September 30, 2013; revised November 2, 2013; accepted November 10, 2013 Copyright © 2013 Bello Idrith Tijjani et al. This is an open access article distributed under the Creative Commons Attribution Li- cense, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intel- lectual property Bello Idrith Tijjani et al. All Copyright © 2013 are guarded by law and by SCIRP as a guardian. ABSTRACT In this paper, the authors numerically analyzed the analytical relationships between angstrom coefficients and optical properties of aerosols to the existing data extracted from OPAC at the spectral length of 0.25 μm to 2.5 μm at eight rela- tive humidity for desert, urban, marine clean and continental clean aerosols. That is apart from their relationships with the wavelength that was determined, in this paper their relation with respect to aerosols’ type and RHs are determined. The properties extracted are scattering, absorption, and extinction coefficients and single scattering albedo. The results showed that the extinction and single scattering albedo are correct for all the aerosols but single scattering co-albedo is satisfied for only sahara and continental clean. Keywords: Angstrom Coefficients; Analytical Relationships; Parameterize; Wavelength Dependence; Optical Properties 1. Introduction The Angstrom exponent (AC) is a parameter that is being widely used in atmospheric sciences to analyze the opti- cal properties of aerosol particles. Since the early publi- cations of Angstrom [1,2] and his later publications [3,4], where this parameter was mainly applied to the descrip- tion of the spectral behavior of the atmospheric extinc- tion and transmission, respectively, it is now being ap- plied to a variety of similar but slightly different optical properties, for instance to the atmospheric, optical depth, extinction coefficient, scattering or backscattering coef- ficients etc. It is very popular not only because of the simplicity of the equation, but because it enables ex- trapolation or interpolation of aerosols’ optical properties, because it is connected to particle microphysics (related with the mean size of aerosols) as it describes, approxi- mately for a certain radius range, and a spectral range, a power law (Junge) aerosol size distribution [5-8]. It was refined by O’Neill and Royer [9] who derived bimodal size distribution radii using these parameters. The Angstrom exponent being an indicator of the aero- sol spectral behaviour of aerosols [10], has been adopted by a number of authors in the literature to characterize biomass burning aerosols [11,12], urban and desert dust aerosol [13] and maritime aerosols [14]. In general, the aerosol optical depth (AOD) and AC parameters can be used to differentiate between coarse and fine particles [15]. Simple analytical relationships between extinction, scat- tering, and absorption coefficients and single scattering albedo (SSA) [16], and the corresponding relationships for ACs [17] exist. Such relationships are useful to com- pare ACs obtained from extinction, scattering, and ab- sorption, including the ground truthing of remote sensing and satellite measurements. For example, aerosol extinc- tion can be obtained from ground-based and satellite re- mote sensing at multiple wavelengths yielding extinction Angstrom coefficients (EACs). Simple analytical rela- tionships between EACs, scattering Angstrom coefficients (SACs), and absorption Angstrom coefficients (AACs)  B. I. TIJJANI ET AL. Open Access OJAppS 491 will help attribute the EACs to the underlying physical phenomena, namely scattering and absorption, and ana- lyzing closure between the different Angstrom coeffi- cients. In addition, SSA is the key parameter that nor- mally determines the sign and magnitude of aerosol ra- diativeforcing. SSA can be obtained at multiple wave- lengths from in-situ measurements [7,8,18], ground-based remote sensing measurements [19,20], and potentially from satellite measurements [21,22]. Relating the SSA Angstrom coefficient (SSAAC) to the underlying SAC, AAC, and EAC will help with data interpretation and closure and physical understanding. The SSAs are some of the most dominant input factors that determine the aero- sols type in radiative transfer models [23-26] and depend on the microphysical properties of the aerosols and there- fore their value can be used for the characterization of the aerosol type. SSA can be interpreted as the probability that light will be scattered, giving an extinction event or the ratio between the scattering coefficient and the ex- tinction coefficient while the Single scattering co-albedo (SSCA) can be considered as the probability of absorp- tion per extinction event or ratio between the absorption coefficient and the extinction coefficient. Therefore if SSAAC is less than 0 it indicates that SSA increases with wavelength, while if SSAAC is larger than 0, SSA de- creases with wavelength. This shows that SSAAC can be used to determine the increase or decrease in the radia- tive forcing and while for single scattering co-albedo Angstrom coefficient (SSCAAC) is the reverse. From the various plots we observed some spectral intervals where SSA decreases with the wavelength as well as some spec- tral intervals where SSA increases with the wavelength. In addition, ACs can be obtained from simple linear or nonlinear regression of data plotted on a log-log scale or more complicated non-linear fits of data that may also yield higher order terms which give additional informa- tion about the type of aerosols using the curvature [27]. Relationships between different ACs that include the SSA (ω) have only been derived by Moosmuller and Chakra- barty, [17]as for single- and two-wavelength ACs, while for ACs obtained from linear or non-linear fits the mathe- matics gets much more complicated due to the difficulty of appropriately attributing the influence of the SSA at different wavelengths. However, in most cases, the sin- gle-wavelength equations still give a good approximation depending on the type of aerosols and relative humidity. In aerosol optics, the ACs that are of most interest are scattering, absorption, and extinction coefficients and for the SSA (ω) and single scattering co-albedo (SSCA). The relationships between these ACs are analytically deter- mined by Moosmuller and Chakrabarty, [17] as: Extinction Angstrom coefficient EAC EACAACSAC AAC (1) Single Scattering Albedo (SSA) Angstrom coefficient (SSAAC) SSAACSAC EAC (2) Single Scattering Co-Albedo (SSCA) Angstrom coeffi- cient (SSCAAC) SSCAACAAC EAC (3) As suggested by Moosmuller and Chakrabarty [17], in this paper we are going to apply these relationships to the existing data extracted from OPAC at the spectral length of 0.25 μm to 2.5 μm and eight RHs (0%, 50%, 70%, 80%, 90%, 95%, 98%, and 99%) for desert, urban, ma- rine clean and continental clean to determine its accuracy and its dependence on the types of aerosols, the power of the polynomials and RHs (that is hygroscopic growth as a result of the change in RHs). 2. Methodology The models extracted from OPAC are given in Table 1. The spectral behavior of the aerosol’s optical parame- ter (X, say), with the wavelength of light (λ) is expressed as inverse power law [3]: Table 1. Compositions of aerosol types [28]. Aerosol model types Components Concentration Ni (cm−3) Urban WASO INSO SOOT Total 28000.0 1.5 130000.0 158001.5 Continental clean WASO INSO Total 2600.0 0.15 26000.15 Desert WASO MINM MIAM MICM Total 2000.0 269.5 30.5 0.142 2300.142 Maritime clean WASO SSAM SSCM Total 1500.0 20.0 0.0032 1520.0032 where: Ni is the mass concentration of the component, water soluble com- ponents (WASO, consists of scattering aerosols, that are hygroscopic in nature, such as sulfates and nitrates present in anthropogenic pollution), water insoluble (INSO), soot (SOOT, not soluble in water and therefore the particles are assumed not to grow with increasing relative humidity), min- eral nucleation mode (MINM), mineral accumulation mode(MIAM) , min- eral coarse mode (MICM), Sea salt accumulation mode (SSAM) and Sea salt coarse mode (SSCM). Urban aerosol represents strong pollution in urban areas. Continental clean aerosol represents remote continental areas without or with very low anthropogenic influences. Desert aerosol is used to describe aerosol over all deserts of the world, and no distinction with respect to the local properties is made. It consists of the mineral aerosol components in a combination that is representative for average turbidity, together with a certain part of the water-soluble component. Maritime aerosol types contain sea salt particles and Maritime clean is given to represent undisturbed re- mote maritime conditions with no soot, but with a certain amount of wa- ter-soluble aero-sol, which is used to represent the non-sea salt sulfate.  B. I. TIJJANI ET AL. Open Access OJAppS 492 X (4) where X(λ) can represent extinction, scattering, and ab- sorption coefficients, single scattering albedo and single scattering co-albedo while β is the turbidity and α is the Angstrom exponent (AC) [9,29]. The wavelength depend- ence of X(λ) can be characterized by the AC, which is a coefficient of the following regression: lnXln ln (5) However the Angstrom exponent itself varies with wavelength, and a more precise empirical relationship between aerosol extinction and wavelength is obtained with a 2nd-order polynomial [13,30-38] as: 2 21 lnXlnln ln (6) Here, the coefficient α2 accounts for a “curvature” of- ten observed in sunphotometry measurements. Eck et al. [12,13], Schuster et al., [27], O’ Neill et al., [34] and Kaskaoutis et al., [39,40] reported the existence of nega- tive curvatures for fine-mode aerosols and near zero or positive curvatures are characteristic of size distributions with a dominant coarse-mode or bimodal distributions with coarse-mode aerosols having a significant relative magnitude. Now differentiating Equation (5) with respect to lnλ we obtained dlnX dln (7) Also differentiating Equation (6) with respect to lnλ we obtained 12 dlnX 2ln dln (8) Assuming that Equations (7) and (8) are evaluated at a wavelength, this implies we can substitute Equation (7) into (8) to obtain 12 12ln (9) Equation (9) now shows the relationship between α and wavelength. We now also proposed a cubic relation of the form 23 12 3 lnXln lnlnln (10) to determine whether cubic relation can improve the ac- curacy of Equations (1)-(3). Also differentiating Equation (10) with respect to lnλ we obtained 2 12 3 dlnX 2ln3 ln dln (11) Assuming that Equations (7) and (11) are evaluated at a wavelength, this implies we can substitute Equation (7) into (11) to obtain 2 123 22ln3ln (12) In this paper we are going to determine the correlation of Equations (1)-(3) with Equations (7), (9) and (12) for all the four types of the aerosols with respect to wave- lengths and RHs. In Equation (1) since it involves prod- ucts, we determined the average, but in Equations (2) and (3), since they have linear relations, we compared the coefficients. 3. Results and Observations Figure 1(a) shows that power law is satisfied at 90%, 95%, 98% and 99% RH, but not satisfied at 0%, 50%, 70%, and 80%. Table 2(a) shows good correlations at 90%, 95%, 98% and 99% RH, but bad correlations 0%, 50%, 70%, and 80% RH for linear. The increase in the power of the polynomials and RHs caused increase in the correlations. Figure 1(b) shows that the plots can be approximated by the power law. Table 2(b) shows very good correlations, and the cor- relations increase with the increase in the power of the polynomials and RHs. Figure 1(c), spectral extinction coefficients decrease with wavelength and can be approximated with a power- law wavelength dependence and also a bi-modal type of particle size distributions [13]. The increase of the coef- ficients with RH has occurred because of the increase in mode size as a result of the increase in RHs. The increase of the extinction with RH at the deliquescence point (90 to 99) is that the growth increase substantially, making the process strongly nonlinear with RH [41,42]. Table 2(c) shows good correlations between extinc- tion and using Equations (5), (6) and (10). The correla- tions increase with the increase in the power of the poly- nomials and RHs. Observing Figures 1(a) and Table 2(a), it can be seen that at RHs 0% to 90% the scattering coefficients have not satisfied the power law, and within this range it can be observed that in Table 2(d), Equation (1) underesti- mated Equation (7) on the linear part but overestimated Equations (9) and (12) on the quadratic and cubic part respectively at all the RHs. The gaps decrease with the increase in RHs. Figure 1(d) shows that the plots can be barely ap- proximated by the power law. Table 2(e) shows that the correlations decrease with the increase in RH, but increase with the increase in the power of the polynomials. Comparing the coefficients at Tables 2(e) and (f) it 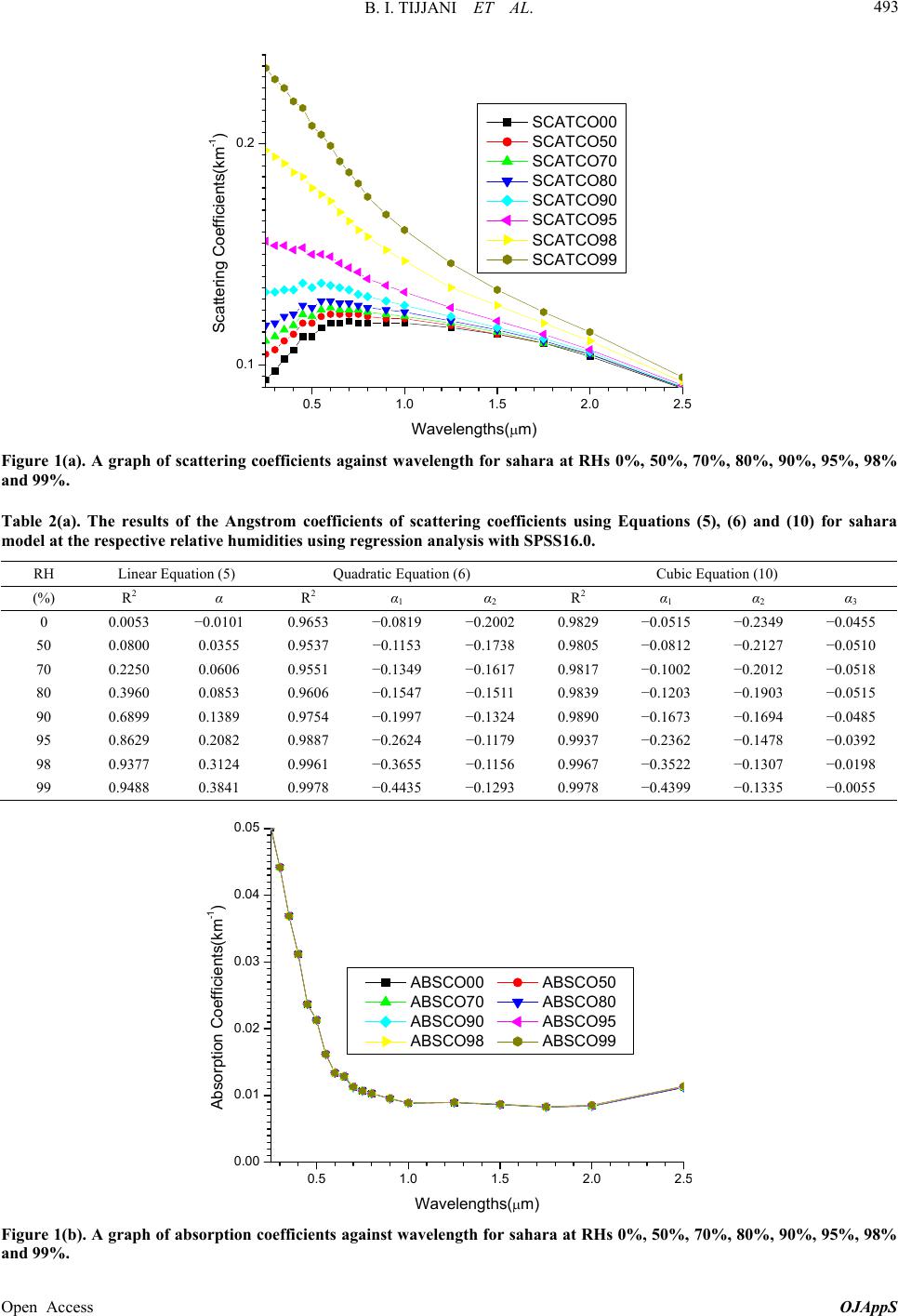 B. I. TIJJANI ET AL. Open Access OJAppS 493 0.5 1.0 1.5 2.0 2.5 0.1 0.2 Scattering Coefficients(km -1 ) Wavelengths( m) SCATCO00 SCATCO50 SCATCO70 SCATCO80 SCATCO90 SCATCO95 SCATCO98 SCATCO99 Figure 1(a). A graph of scattering coefficients against wavelength for sahara at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 2(a). The results of the Angstrom coefficients of scattering coefficients using Equations (5), (6) and (10) for sahara model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.0053 −0.0101 0.9653 −0.0819 −0.2002 0.9829 −0.0515 −0.2349 −0.0455 50 0.0800 0.0355 0.9537 −0.1153 −0.1738 0.9805 −0.0812 −0.2127 −0.0510 70 0.2250 0.0606 0.9551 −0.1349 −0.1617 0.9817 −0.1002 −0.2012 −0.0518 80 0.3960 0.0853 0.9606 −0.1547 −0.1511 0.9839 −0.1203 −0.1903 −0.0515 90 0.6899 0.1389 0.9754 −0.1997 −0.1324 0.9890 −0.1673 −0.1694 −0.0485 95 0.8629 0.2082 0.9887 −0.2624 −0.1179 0.9937 −0.2362 −0.1478 −0.0392 98 0.9377 0.3124 0.9961 −0.3655 −0.1156 0.9967 −0.3522 −0.1307 −0.0198 99 0.9488 0.3841 0.9978 −0.4435 −0.1293 0.9978 −0.4399 −0.1335 −0.0055 0.5 1.0 1.52.0 2. 0.00 0.01 0.02 0.03 0.04 0.05 Absorption Coefficients(km - ) Wavelengths( m) ABSCO00 ABSCO50 ABSCO70 ABSCO80 ABSCO90 ABSCO95 ABSCO98 ABSCO99 Figure 1(b). A graph of absorption coefficients against wavelength for sahara at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%.  B. I. TIJJANI ET AL. Open Access OJAppS 494 Table 2(b). The results of the Angstrom coefficients of absorption coefficients using Equations (5), (6) and (10) for sahara model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.7568 0.8058 0.9684 −0.5157 0.6315 0.9821 −0.6961 0.8374 0.2698 50 0.7562 0.8050 0.9686 −0.5144 0.6325 0.9821 −0.6932 0.8365 0.2673 70 0.7559 0.8047 0.9687 −0.5139 0.6329 0.9821 −0.6921 0.8362 0.2665 80 0.7557 0.8043 0.9688 −0.5134 0.6332 0.9822 −0.6912 0.8360 0.2659 90 0.7551 0.8036 0.9689 −0.5124 0.6340 0.9822 −0.6896 0.8361 0.2650 95 0.7541 0.8025 0.9690 −0.5108 0.6350 0.9822 −0.6875 0.8366 0.2643 98 0.7519 0.8003 0.9690 −0.5074 0.6375 0.9823 −0.6843 0.8392 0.2645 99 0.7497 0.7979 0.9689 −0.5040 0.6397 0.9824 −0.6816 0.8422 0.2655 0.5 1.0 1.5 2.0 2.5 0.10 0.12 0.14 0.16 0.18 0.20 0.22 0.24 0.26 0.28 0.30 Extinction Coefficients(km -1 ) Wavelengths( m) EXTCO00 EXTCO50 EXTCO70 EXTCO80 EXTCO90 EXTCO95 EXTCO98 EXTCO99 Figure 1(c). A graph of extinction coefficients against wavelength for sahara at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 2(c). The results of the Angstrom coefficients of extinction coefficients using Equations (5), (6) and (10) for sahara model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.8824 0.1225 0.9422 −0.1442 −0.0473 0.9880 −0.0979 −0.1001 −0.0693 50 0.9411 0.1552 0.9624 −0.1711 −0.0346 0.9911 −0.1261 −0.0859 −0.0673 70 0.9583 0.1733 0.9706 −0.1867 −0.0291 0.9922 −0.1435 −0.0784 −0.0646 80 0.9697 0.1918 0.9770 −0.2031 −0.0247 0.9932 −0.1620 −0.0716 −0.0615 90 0.9836 0.2320 0.9864 −0.2404 −0.0182 0.9948 −0.2047 −0.0588 −0.0533 95 0.9916 0.2855 0.9932 −0.2933 −0.0169 0.9963 −0.2670 −0.0469 −0.0393 98 0.9942 0.3684 0.9974 −0.3827 −0.0310 0.9977 −0.3722 −0.0430 −0.0156 99 0.9914 0.4272 0.9985 −0.4517 −0.0535 0.9985 −0.4520 −0.0532 0.0004  B. I. TIJJANI ET AL. Open Access OJAppS 495 Table 2(d). The results of the Angstrom coefficients of extinction coefficients using Equations (1), (7), (9) and (12) for sahara model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Quadratic Cubic (%) Equation (7) Equation (1) Equation (9) Equation (1) Equation (12) Equation (1) Α Α α1 (λ) α1 (λ) α2 (λ) α2 (λ) 0 0.122451 0.101199 0.115492 0.159794 0.139420 0.141914 50 0.155226 0.136194 0.150135 0.189424 0.173392 0.175070 70 0.173292 0.155676 0.169010 0.206057 0.191334 0.192991 80 0.191773 0.175054 0.188141 0.222690 0.209395 0.210576 90 0.231990 0.217366 0.229310 0.259265 0.247712 0.248438 95 0.285518 0.273175 0.283026 0.307763 0.296618 0.296840 98 0.368436 0.359011 0.363871 0.382144 0.369275 0.368879 99 0.427181 0.419607 0.419313 0.433753 0.419175 0.418214 0.5 1.0 1.5 2.0 2.5 0.65 0.70 0.75 0.80 0.85 0.90 0.95 Single Scattering Albedo Wavelengths( m) SSA00 SSA50 SSA70 SSA80 SSA90 SSA95 SSA98 SSA99 Figure 1(d). A graph of single scattering albedo against wavelength for sahara at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 2(e). The results of the Angstrom coefficients of single scattering albedo using Equations (5), (6) and (10) for sahara model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.6130 −0.1325 0.9840 0.0623 −0.1529 0.9873 0.0463 −0.1346 0.0239 50 0.6085 −0.1197 0.9840 0.0556 −0.1393 0.9859 0.0446 −0.1268 0.0165 70 0.6044 −0.1129 0.9838 0.0520 −0.1326 0.9851 0.0433 −0.1226 0.0130 80 0.5993 −0.1064 0.9835 0.0484 −0.1263 0.9844 0.0416 −0.1186 0.0102 90 0.5838 −0.0931 0.9828 0.0407 −0.1141 0.9830 0.0373 −0.1103 0.0051 95 0.5534 −0.0773 0.9814 0.0310 −0.1008 0.9814 0.0307 −0.1005 0.0001 98 0.4796 −0.0561 0.9787 0.0171 −0.0848 0.9791 0.0197 −0.0878 −0.0039 99 0.4041 −0.0430 0.9763 0.0082 −0.0758 0.9775 0.0121 −0.0803 −0.0059  B. I. TIJJANI ET AL. Open Access OJAppS 496 Table 2(f). The results of the Angstrom coefficients of single scattering albedo using Equation (2) for sahara model at the respective rela tive humid itie s RH Linear Quadratic Cubic (%) Α α1 α2 α1 α2 α3 0 −0.132502 0.062268 −0.15288 0.046363 −0.13473 0.023788 50 −0.119753 0.055814 −0.13917 0.044891 −0.12671 0.016337 70 −0.112727 0.051800 −0.13262 0.043217 −0.12283 0.012838 80 −0.106435 0.048374 −0.12638 0.041661 −0.11872 0.01004 90 −0.093124 0.040653 −0.11421 0.037474 −0.11059 0.004755 95 −0.077282 0.030909 −0.10094 0.030828 −0.10085 0.000121 98 −0.056080 0.017218 −0.08459 0.019982 −0.08774 −0.00413 99 −0.043050 0.008194 −0.07587 0.01212 −0.08035 −0.00587 can be observed that they are approximately the same with some to three places of decimal while some to four places of decimals. Figure 1(e) shows it is almost the opposite of Figure 1(d), and the plots can be barely approximated by power law and it decreases with the increase in RH. Table 2(g) shows that the correlations decrease with the increase in RH, but increase with the increase in the power of the polynomials. Comparing the coefficients in Tables 2(g) and (h) it can be observed that they are approximately the same, some to one place of decimals while some to two places of decimals. Figure 2(a) shows a steep but smooth decrease of the extinction coefficients with wavelengths and all the plots satisfy power law. Table 3(a) shows very good correlations for all the polynomials, and the correlations increase with the in- crease in the powers of the polynomials. Figure 2(b) shows a steep but smooth curves that de- crease with the increase in wavelength, but shows little effect with the increase in RH. They all satisfy power law. Table 3(b) shows very good correlations for all the polynomials, and the correlations increase with the in- crease in the powers of the polynomials. Figures 2(c) and (a) are almost similar. Table 3(c) shows very good correlations for all the equations, but the correlation increases with the increase in the power of the polynomials. From Table 3(d) it can be seen that they are approxi- mately the same, with some to one place of decimal while some to two places of decimals. Figure 2(d) shows that not all can satisfy power law. Table 3(e) shows that the correlations decrease with the increase in RH, but increase with the increase in the power of the polynomials. Comparing the coefficients in Tables 3(e) and (f) it can be observed that they are approximately the same with some to two places of decimals while some to four places of decimals. Figure 2(e) is almost the inverse of Figure 2(d). Table 3(g) shows very good correlations between, and the correlation increases with the increase in the power of the polynomials. Comparing Tables 3(g) and (h), the linear part shows that at 0%, 50% and 70% RH, they are the same to one place of decimal places. After that they are completely different. Comparing Figures 3(a) and 2(a) it can be observed that they are similar. Table 4(a) shows very good correlations for all the polynomials, and the correlations increase with the in- crease in the powers of the polynomials. From Figure 3(b), the plots barely obey power law. Table 4(b) shows that the correlations decrease with the increase in RH, but increase with the increase in the power of the polynomials. Comparing Figures 3(c) and 2(c) it can be observed that they are similar. Table 4(c) shows very good correlations, and the cor- relations increases with the increase in the power of the polynomials. From Table 4(d) it can be seen that the coefficients are approximately the same to one place of decimal and some to two places of decimals. Figure 3(d) shows that power law is not obeyed. Table 4(e) shows that there are poor correlations in the linear part, but the correlation improves with the increase in the power of the polynomials. Comparing the coefficients of Tables 4(e) and (f) it can be observed that they are all approximately the same within two places of decimals, while some to four places of decimals. Figure 3(e), is the inverse of Figure 3(d) and the power law is not obeyed. Table 4(g) shows that there are poor correlations in the linear part, but the correlation improves with the in- crease in the power of the polynomials. Comparing the coefficients of Tables 4(g) and (h) it  B. I. TIJJANI ET AL. Open Access OJAppS 497 0.5 1.0 1.5 2.0 2.5 0.05 0.10 0.15 0.20 0.25 0.30 0.35 Single Scattering Co-Albedo Wavelengths( m) SSCA00 SSCA50 SSCA70 SSCA80 SSCA90 SSCA95 SSCA98 SSCA99 Figure 1(e). A graph of single scattering co-albedo against wavelength for sahara at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 2(g). The results of the Angstrom coefficients of single scattering co-albedo using Equations (5), (6) and (10) for sahara model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.6604 0.6854 0.9563 −0.3730 0.6800 0.9820 −0.5976 0.9363 0.3359 50 0.6450 0.6510 0.9521 −0.3451 0.6658 0.9803 −0.5714 0.9240 0.3385 70 0.6342 0.6308 0.9511 −0.3271 0.6610 0.9795 −0.5488 0.9139 0.3315 80 0.6242 0.6101 0.9499 −0.3100 0.6532 0.9787 −0.5278 0.9018 0.3258 90 0.5946 0.5710 0.9481 −0.2711 0.6527 0.9774 −0.4818 0.8930 0.3151 95 0.5480 0.5172 0.9427 −0.2183 0.6507 0.9743 −0.4247 0.8863 0.3088 98 0.4483 0.4324 0.9379 −0.1246 0.6699 0.9695 −0.3150 0.8871 0.2848 99 0.3625 0.3721 0.9352 −0.0536 0.6932 0.9654 −0.2319 0.8966 0.2666 Table 2(h). The results of the Angstrom coefficients of single scattering co-albedo using Equation (3) for sahara model at the respective rela tive humid itie s. RH Linear Quadratic Cubic (%) α α1 α2 α1 α2 α3 0 0.68333 −0.37147 0.678817 −0.59818 0.937478 0.339073 50 0.64979 −0.3433 0.667123 −0.56704 0.922397 0.334632 70 0.631366 −0.32723 0.662004 −0.54863 0.914611 0.331136 80 0.61253 −0.3103 0.657862 −0.52921 0.907625 0.327408 90 0.571652 −0.27204 0.652168 −0.48483 0.894952 0.31826 95 0.51703 −0.21752 0.65193 −0.42055 0.883569 0.30365 98 0.431835 −0.12473 0.668464 −0.31204 0.882169 0.280141 99 0.370726 −0.0523 0.693104 −0.22958 0.895362 0.265135  B. I. TIJJANI ET AL. Open Access OJAppS 498 0.5 1.0 1.52.0 2.5 0.0 0.5 1.0 1.5 2.0 Scattering Coefficients(km -1 ) Wavelengths( m) SCATCO00 SCATCO50 SCATCO70 SCATCO80 SCATCO90 SCATCO95 SCATCO98 SCATCO99 Figure 2(a). A graph of scattering coefficients against wavelength for urban at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 3(a). The results of the Angstrom coefficients of scattering coefficients using Equations (5), (6) and (10) for urban model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.9906 1.5018 0.9961 −1.5781 −0.1661 0.9993 −1.7201 −0.0041 0.2124 50 0.9853 1.5793 0.9986 −1.7040 −0.2714 0.9997 −1.7925 −0.1704 0.1324 70 0.9816 1.5962 0.9992 −1.7416 −0.3165 0.9998 −1.8045 −0.2447 0.0941 80 0.9779 1.6022 0.9995 −1.7647 −0.3537 0.9998 −1.8060 −0.3065 0.0618 90 0.9698 1.5917 0.9997 −1.7820 −0.4143 0.9997 −1.7851 −0.4107 0.0047 95 0.9602 1.5506 0.9995 −1.7641 −0.4648 0.9996 −1.7325 −0.5008 −0.0473 98 0.9469 1.4597 0.9988 −1.6925 −0.5067 0.9995 −1.6291 −0.5791 −0.0948 99 0.9373 1.3840 0.9983 −1.6243 −0.5231 0.9993 −1.5473 −0.6109 −0.1151 0.25 0.50 0.75 1.00 1.25 1.50 1.75 2.00 2.25 2.50 0.00 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16 0.18 Absorption Coefficients (km -1 ) Wavelength( m) ABSCO00 ABSCO50 ABSCO70 ABSCO80 ABSCO90 ABSCO95 ABSCO98 ABSCO99 Figure 2(b). A graph of absorption coefficients against wavelength for urban at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. 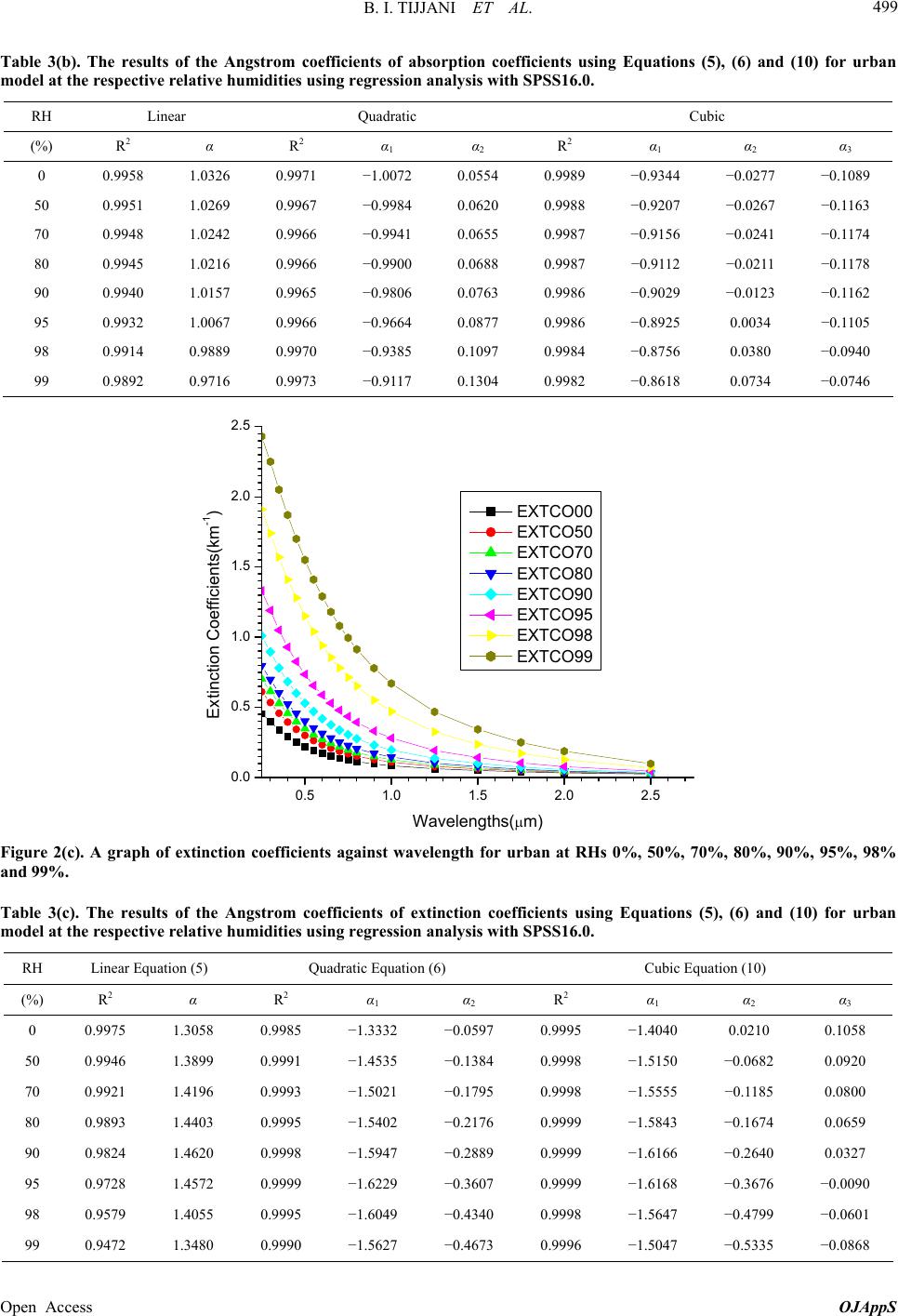 B. I. TIJJANI ET AL. Open Access OJAppS 499 Table 3(b). The results of the Angstrom coefficients of absorption coefficients using Equations (5), (6) and (10) for urban model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Quadratic Cubic (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.9958 1.0326 0.9971 −1.0072 0.0554 0.9989 −0.9344 −0.0277 −0.1089 50 0.9951 1.0269 0.9967 −0.9984 0.0620 0.9988 −0.9207 −0.0267 −0.1163 70 0.9948 1.0242 0.9966 −0.9941 0.0655 0.9987 −0.9156 −0.0241 −0.1174 80 0.9945 1.0216 0.9966 −0.9900 0.0688 0.9987 −0.9112 −0.0211 −0.1178 90 0.9940 1.0157 0.9965 −0.9806 0.0763 0.9986 −0.9029 −0.0123 −0.1162 95 0.9932 1.0067 0.9966 −0.9664 0.0877 0.9986 −0.8925 0.0034 −0.1105 98 0.9914 0.9889 0.9970 −0.9385 0.1097 0.9984 −0.8756 0.0380 −0.0940 99 0.9892 0.9716 0.9973 −0.9117 0.1304 0.9982 −0.8618 0.0734 −0.0746 0.51.01.52.02.5 0.0 0.5 1.0 1.5 2.0 2.5 Extinction Coefficients(km -1 ) Wavelengths( m) EXTCO00 EXTCO50 EXTCO70 EXTCO80 EXTCO90 EXTCO95 EXTCO98 EXTCO99 Figure 2(c). A graph of extinction coefficients against wavelength for urban at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 3(c). The results of the Angstrom coefficients of extinction coefficients using Equations (5), (6) and (10) for urban model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.9975 1.3058 0.9985 −1.3332 −0.0597 0.9995 −1.4040 0.0210 0.1058 50 0.9946 1.3899 0.9991 −1.4535 −0.1384 0.9998 −1.5150 −0.0682 0.0920 70 0.9921 1.4196 0.9993 −1.5021 −0.1795 0.9998 −1.5555 −0.1185 0.0800 80 0.9893 1.4403 0.9995 −1.5402 −0.2176 0.9999 −1.5843 −0.1674 0.0659 90 0.9824 1.4620 0.9998 −1.5947 −0.2889 0.9999 −1.6166 −0.2640 0.0327 95 0.9728 1.4572 0.9999 −1.6229 −0.3607 0.9999 −1.6168 −0.3676 −0.0090 98 0.9579 1.4055 0.9995 −1.6049 −0.4340 0.9998 −1.5647 −0.4799 −0.0601 99 0.9472 1.3480 0.9990 −1.5627 −0.4673 0.9996 −1.5047 −0.5335 −0.0868 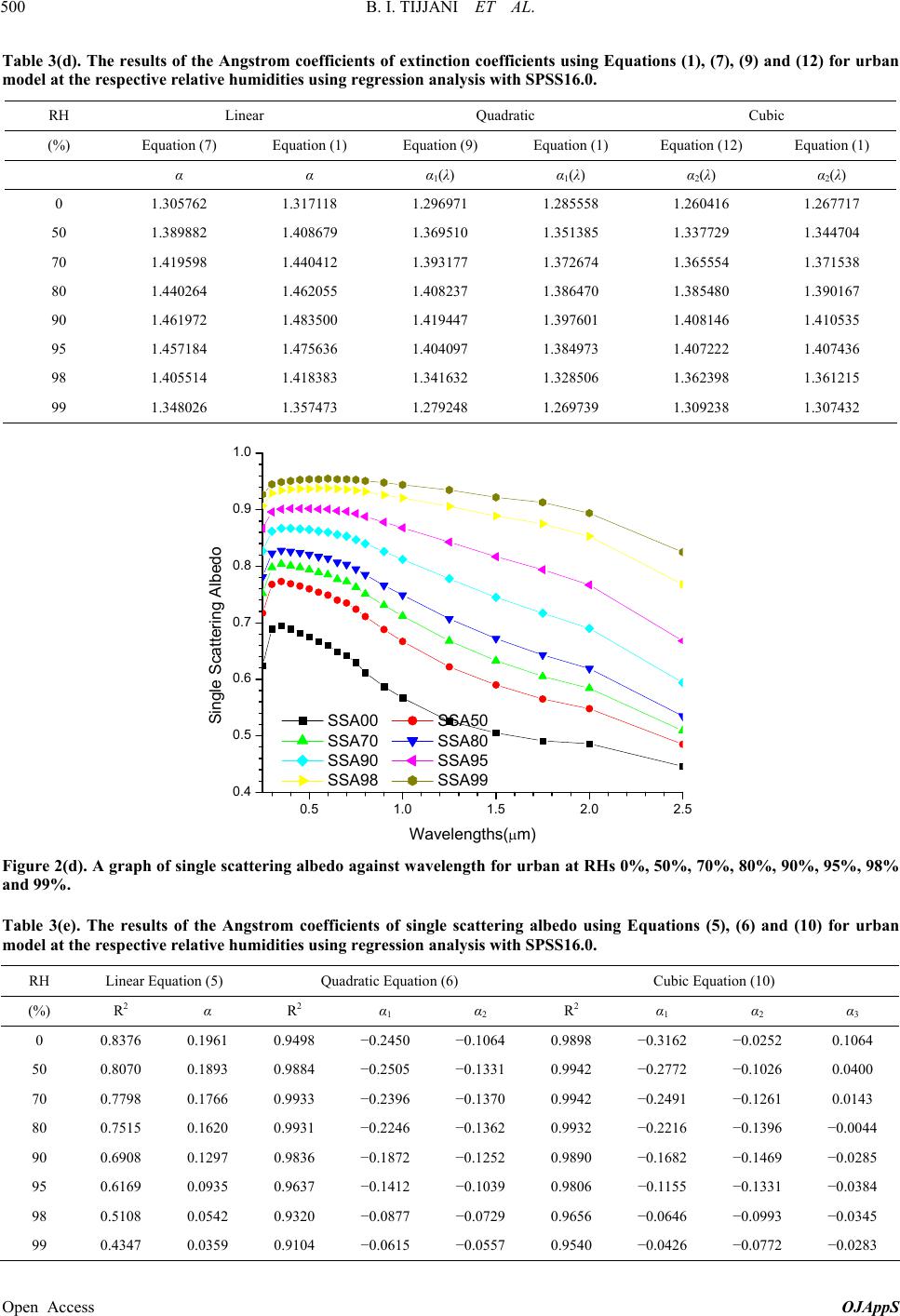 B. I. TIJJANI ET AL. Open Access OJAppS 500 Table 3(d). The results of the Angstrom coefficients of extinction coefficients using Equations (1), (7), (9) and (12) for urban model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Quadratic Cubic (%) Equation (7) Equation (1) Equation (9) Equation (1) Equation (12) Equation (1) α α α1(λ) α1(λ) α2(λ) α2(λ) 0 1.305762 1.317118 1.296971 1.285558 1.260416 1.267717 50 1.389882 1.408679 1.369510 1.351385 1.337729 1.344704 70 1.419598 1.440412 1.393177 1.372674 1.365554 1.371538 80 1.440264 1.462055 1.408237 1.386470 1.385480 1.390167 90 1.461972 1.483500 1.419447 1.397601 1.408146 1.410535 95 1.457184 1.475636 1.404097 1.384973 1.407222 1.407436 98 1.405514 1.418383 1.341632 1.328506 1.362398 1.361215 99 1.348026 1.357473 1.279248 1.269739 1.309238 1.307432 0.51.01.52.02.5 0.4 0.5 0.6 0.7 0.8 0.9 1.0 Single Scattering Albedo Wavelengths( m) SSA00 SSA50 SSA70 SSA80 SSA90 SSA95 SSA98 SSA99 Figure 2(d). A graph of single scattering albedo against wavelength for urban at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 3(e). The results of the Angstrom coefficients of single scattering albedo using Equations (5), (6) and (10) for urban model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.8376 0.1961 0.9498 −0.2450 −0.1064 0.9898 −0.3162 −0.0252 0.1064 50 0.8070 0.1893 0.9884 −0.2505 −0.1331 0.9942 −0.2772 −0.1026 0.0400 70 0.7798 0.1766 0.9933 −0.2396 −0.1370 0.9942 −0.2491 −0.1261 0.0143 80 0.7515 0.1620 0.9931 −0.2246 −0.1362 0.9932 −0.2216 −0.1396 −0.0044 90 0.6908 0.1297 0.9836 −0.1872 −0.1252 0.9890 −0.1682 −0.1469 −0.0285 95 0.6169 0.0935 0.9637 −0.1412 −0.1039 0.9806 −0.1155 −0.1331 −0.0384 98 0.5108 0.0542 0.9320 −0.0877 −0.0729 0.9656 −0.0646 −0.0993 −0.0345 99 0.4347 0.0359 0.9104 −0.0615 −0.0557 0.9540 −0.0426 −0.0772 −0.0283  B. I. TIJJANI ET AL. Open Access OJAppS 501 Table 3(f). The results of the Angstrom coefficients of single scattering albedo using Equation (2) for urban model at the re- spective relative humidities. RH Linear Quadratic Cubic (%) α α1 α2 α1 α2 α3 0 0.196057 −0.244939 −0.106400 −0.316179 −0.025120 0.106549 50 0.189424 −0.250513 −0.132973 −0.277519 −0.102162 0.040390 70 0.176572 −0.239505 −0.136985 −0.248942 −0.126217 0.014115 80 0.161910 −0.224417 −0.136057 −0.221713 −0.139142 −0.004044 90 0.129716 −0.187304 −0.125352 −0.168540 −0.146761 −0.028065 95 0.093392 −0.141213 −0.104091 −0.115660 −0.133245 −0.038218 98 0.054221 −0.087622 −0.072703 −0.064399 −0.099199 −0.034733 99 0.035931 −0.061562 −0.055790 −0.042615 −0.077408 −0.028338 0.5 1.0 1.5 2.02.5 0.1 0.2 0.3 0.4 0.5 0.6 Single Scattering Co-Albedo Wavelengths( m) SSCA00 SSCA50 SSCA70 SSCA80 SSCA90 SSCA95 SSCA98 SSCA99 Figure 2(e). A graph of single scattering co-albedo against wavelength for urban at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 3(g). The results of the Angstrom coefficients of single scattering co-albedo using Equations (5), (6) and (10) for urban model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.8636 −0.2906 0.8981 0.5267 −0.0928 0.9096 0.1643 0.2374 −0.0831 50 0.9171 −0.3964 0.9780 0.5457 −0.0587 0.9425 −0.0459 0.4805 −0.1357 70 0.9291 −0.4395 0.9313 0.5270 −0.0344 0.9508 −0.1609 0.5924 −0.1577 80 0.9327 −0.4714 0.9327 0.4762 −0.0019 0.9548 −0.3073 0.7121 −0.1796 90 0.9258 −0.5157 0.9320 0.3446 0.0673 0.9585 −0.5964 0.9248 −0.2158 95 0.8984 −0.5383 0.9292 0.1331 0.1593 0.9593 −0.9312 1.1292 −0.2440 98 0.8247 −0.5262 0.9197 0.1593 0.2855 0.9562 −1.3954 1.3749 −0.2741 99 0.7478 −0.4986 0.9077 0.2855 0.0695 0.9510 −1.7342 1.5489 −0.2970  B. I. TIJJANI ET AL. Open Access OJAppS 502 Table 3(h). The results of the Angstrom coefficients of single scattering co-albedo using Equation (3) for urban model at the respective rela tive humid itie s. RH Linear Quadratic Cubic (%) α α1 α2 α1 α2 α3 0 −0.273154 0.326035 0.115104 0.469589 −0.048684 −0.214705 50 −0.362993 0.455074 0.200432 0.594301 0.041582 −0.208233 70 −0.395439 0.508002 0.245014 0.639970 0.094445 −0.197376 80 −0.418647 0.550228 0.286412 0.673048 0.146282 −0.183694 90 −0.446297 0.614085 0.365224 0.713632 0.251647 −0.148885 95 −0.450505 0.656495 0.448377 0.724332 0.370979 −0.101459 98 −0.416653 0.666450 0.543730 0.689108 0.517878 −0.033888 99 −0.376471 0.651039 0.597649 0.642886 0.606951 0.012194 0.5 1.0 1.5 2.0 2.5 0.00 0.05 0.10 0.15 0.20 Scattering Coefficients(km -1 ) Wavelengths( m) SCATCO00 SCATCO50 SCATCO70 SCATCO80 SCATCO90 SCATCO95 SCATCO98 SCATCO99 Figure 3(a). A graph of scattering coefficients against wavelength for continental clean at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 4(a). The results of the Angstrom coefficients of scattering coefficients using Equations (5), (6) and (10) for continental clean model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.9887 1.3858 0.9956 −1.4647 −0.1718 0.9991 −1.6016 −0.0156 0.2048 50 0.9839 1.5029 0.9985 −1.6276 −0.2715 0.9997 −1.7142 −0.1727 0.1295 70 0.9802 1.5327 0.9992 −1.6781 −0.3164 0.9998 −1.7403 −0.2454 0.0931 80 0.9763 1.5483 0.9995 −1.7108 −0.3537 0.9998 −1.7522 −0.3065 0.0619 90 0.9682 1.5522 0.9998 −1.7429 −0.4151 0.9998 −1.7469 −0.4106 0.0060 95 0.9586 1.5227 0.9995 −1.7371 −0.4666 0.9997 −1.7067 −0.5013 −0.0455 98 0.9451 1.4423 0.9988 −1.6764 −0.5096 0.9995 −1.6141 −0.5807 −0.0933 99 0.9356 1.3710 0.9983 −1.6127 −0.5260 0.9993 −1.5366 −0.6129 −0.1138 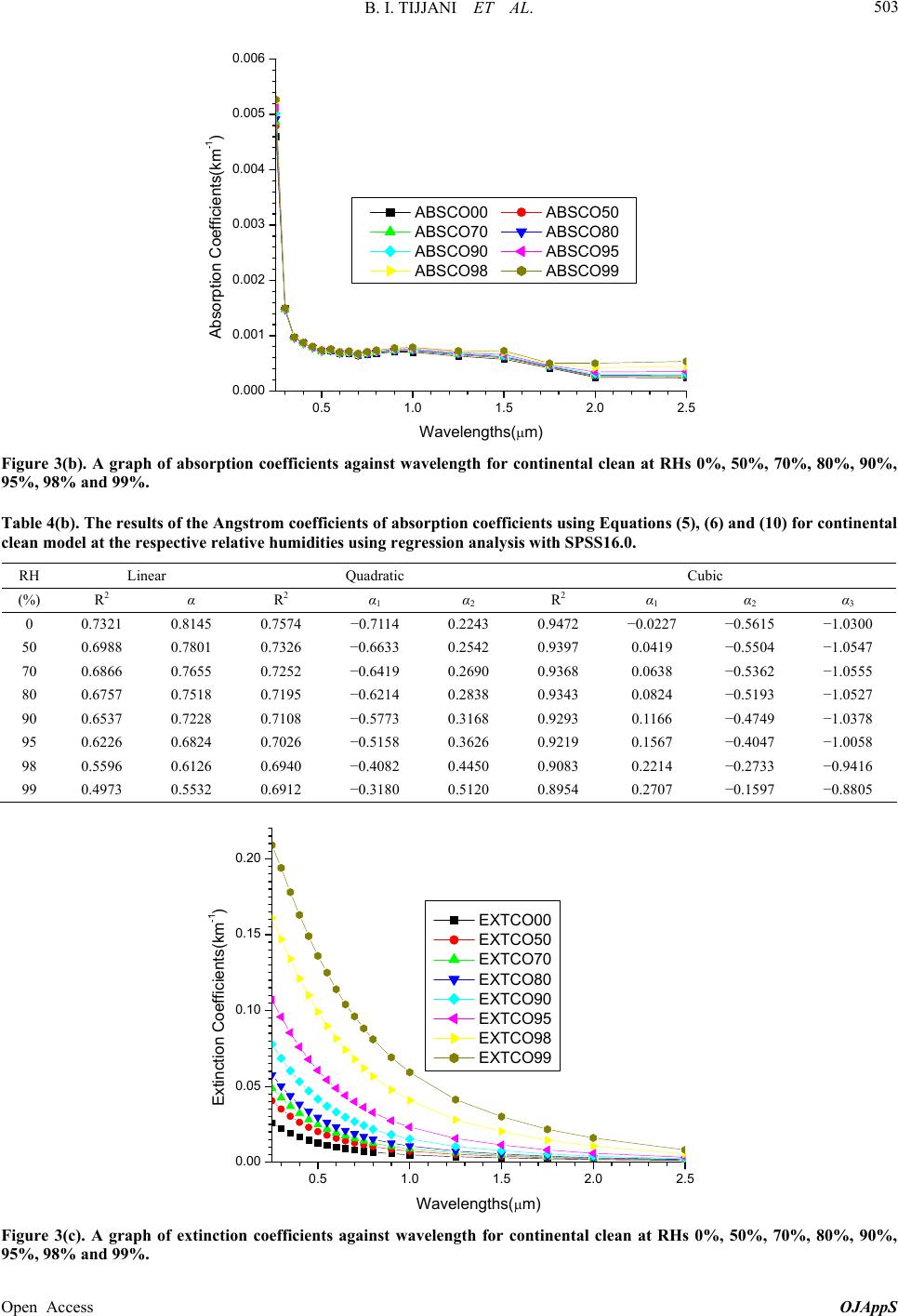 B. I. TIJJANI ET AL. Open Access OJAppS 503 0.5 1.0 1.52.0 2.5 0.000 0.001 0.002 0.003 0.004 0.005 0.006 Absorption Coefficients(km -1 ) Wavelengths( m) ABSCO00 ABSCO50 ABSCO70 ABSCO80 ABSCO90 ABSCO95 ABSCO98 ABSCO99 Figure 3(b). A graph of absorption coefficients against wavelength for continental clean at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 4(b). The results of the Angstrom coefficients of absorption coefficients using Equations (5), (6) and (10) for continental clean model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Quadratic Cubic (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.7321 0.8145 0.7574 −0.7114 0.2243 0.9472 −0.0227 −0.5615 −1.0300 50 0.6988 0.7801 0.7326 −0.6633 0.2542 0.9397 0.0419 −0.5504 −1.0547 70 0.6866 0.7655 0.7252 −0.6419 0.2690 0.9368 0.0638 −0.5362 −1.0555 80 0.6757 0.7518 0.7195 −0.6214 0.2838 0.9343 0.0824 −0.5193 −1.0527 90 0.6537 0.7228 0.7108 −0.5773 0.3168 0.9293 0.1166 −0.4749 −1.0378 95 0.6226 0.6824 0.7026 −0.5158 0.3626 0.9219 0.1567 −0.4047 −1.0058 98 0.5596 0.6126 0.6940 −0.4082 0.4450 0.9083 0.2214 −0.2733 −0.9416 99 0.4973 0.5532 0.6912 −0.3180 0.5120 0.8954 0.2707 −0.1597 −0.8805 0.5 1.0 1.5 2.0 2.5 0.00 0.05 0.10 0.15 0.20 Extinction Coefficients(km -1 ) Wavelengths( m) EXTCO00 EXTCO50 EXTCO70 EXTCO80 EXTCO90 EXTCO95 EXTCO98 EXTCO99 Figure 3(c). A graph of extinction coefficients against wavelength for continental clean at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. 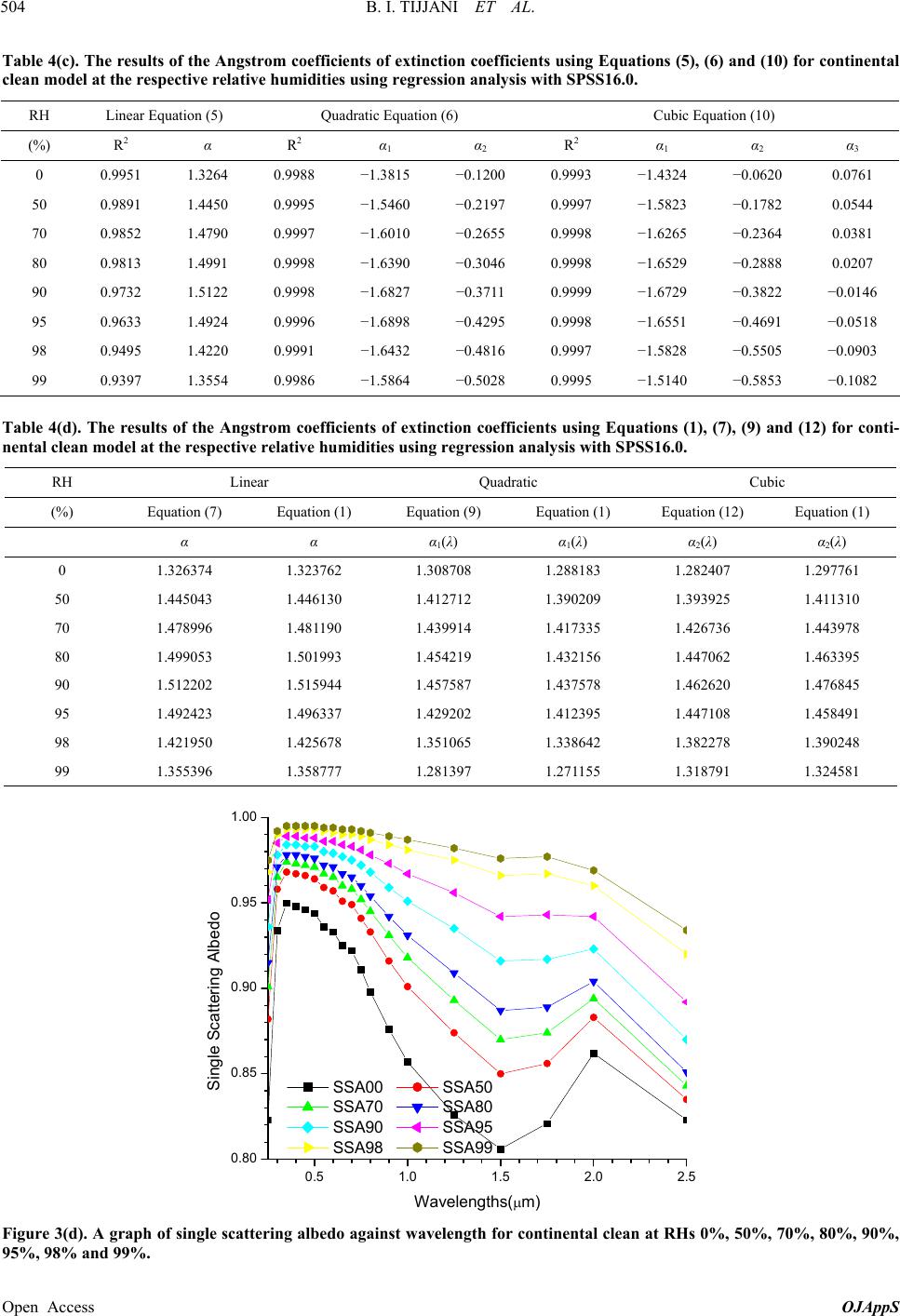 B. I. TIJJANI ET AL. Open Access OJAppS 504 Table 4(c). The results of the Angstrom coefficients of extinction coefficients using Equations (5), (6) and (10) for continental clean model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.9951 1.3264 0.9988 −1.3815 −0.1200 0.9993 −1.4324 −0.0620 0.0761 50 0.9891 1.4450 0.9995 −1.5460 −0.2197 0.9997 −1.5823 −0.1782 0.0544 70 0.9852 1.4790 0.9997 −1.6010 −0.2655 0.9998 −1.6265 −0.2364 0.0381 80 0.9813 1.4991 0.9998 −1.6390 −0.3046 0.9998 −1.6529 −0.2888 0.0207 90 0.9732 1.5122 0.9998 −1.6827 −0.3711 0.9999 −1.6729 −0.3822 −0.0146 95 0.9633 1.4924 0.9996 −1.6898 −0.4295 0.9998 −1.6551 −0.4691 −0.0518 98 0.9495 1.4220 0.9991 −1.6432 −0.4816 0.9997 −1.5828 −0.5505 −0.0903 99 0.9397 1.3554 0.9986 −1.5864 −0.5028 0.9995 −1.5140 −0.5853 −0.1082 Table 4(d). The results of the Angstrom coefficients of extinction coefficients using Equations (1), (7), (9) and (12) for conti- nental clean model at the respe c t ive relative humidities using regression analysis with SPSS16.0. RH Linear Quadratic Cubic (%) Equation (7) Equation (1) Equation (9) Equation (1) Equation (12) Equation (1) α α α1(λ) α1(λ) α2(λ) α2(λ) 0 1.326374 1.323762 1.308708 1.288183 1.282407 1.297761 50 1.445043 1.446130 1.412712 1.390209 1.393925 1.411310 70 1.478996 1.481190 1.439914 1.417335 1.426736 1.443978 80 1.499053 1.501993 1.454219 1.432156 1.447062 1.463395 90 1.512202 1.515944 1.457587 1.437578 1.462620 1.476845 95 1.492423 1.496337 1.429202 1.412395 1.447108 1.458491 98 1.421950 1.425678 1.351065 1.338642 1.382278 1.390248 99 1.355396 1.358777 1.281397 1.271155 1.318791 1.324581 0.51.01.52.02.5 0.80 0.85 0.90 0.95 1.00 Single Scattering Albedo Wavelengths( m) SSA00 SSA50 SSA70 SSA80 SSA90 SSA95 SSA98 SSA99 Figure 3(d). A graph of single scattering albedo against wavelength for continental clean at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%.  B. I. TIJJANI ET AL. Open Access OJAppS 505 Table 4(e). The results of the Angstrom coefficients of single scattering albedousing Equations (5), (6) and (10) for continental clean model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.4258 0.0592 0.5733 −0.0830 −0.0517 0.8994 −0.1691 0.0465 0.1288 50 0.5636 0.0578 0.7714 −0.0817 −0.0520 0.9251 −0.1318 0.0052 0.0749 70 0.5886 0.0537 0.8283 −0.0771 −0.0508 0.9299 −0.1142 −0.0085 0.0555 80 0.5963 0.0493 0.8647 −0.0718 −0.0490 0.9317 −0.0992 −0.0177 0.0410 90 0.5850 0.0400 0.9057 −0.0602 −0.0439 0.9300 −0.0737 −0.0285 0.0202 95 0.5456 0.0303 0.9168 −0.0472 −0.0370 0.9205 −0.0514 −0.0323 0.0062 98 0.4788 0.0202 0.9037 −0.0331 −0.0281 0.9053 −0.0311 −0.0303 −0.0029 99 0.4350 0.0155 0.8847 −0.0262 −0.0233 0.8939 −0.0224 −0.0276 −0.0056 Table 4(f). The results of the Angstrom coefficients of single scattering albedo using Equations (2) for continental clean model at the respective relative humidities. RH Linear Quadratic Cubic (%) α α1 α2 α1 α2 α3 0 0.059431 −0.083205 −0.051747 −0.169206 0.046376 0.128627 50 0.057803 −0.081609 −0.051818 −0.131833 0.005485 0.075117 70 0.053680 −0.077069 −0.050912 −0.113828 −0.008971 0.054979 80 0.049226 −0.071792 −0.049118 −0.099330 −0.017699 0.041187 90 0.039996 −0.060241 −0.044067 −0.073978 −0.028393 0.020547 95 0.030288 −0.047315 −0.037062 −0.051545 −0.032235 0.006327 98 0.020366 −0.033218 −0.027974 −0.031264 −0.030203 −0.002922 99 0.015601 −0.026296 −0.023278 −0.022555 −0.027546 −0.005594 0.51.01.52.02. 0.00 0.05 0.10 0.15 0.20 Single Scattering Co-Albedo Wavelengths( m) SSCA00 SSCA50 SSCA70 SSCA80 SSCA90 SSCA95 SSCA98 SSCA99 Figure 3(e). A graph of single scattering co-albedo against wavelength for continental clean at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. 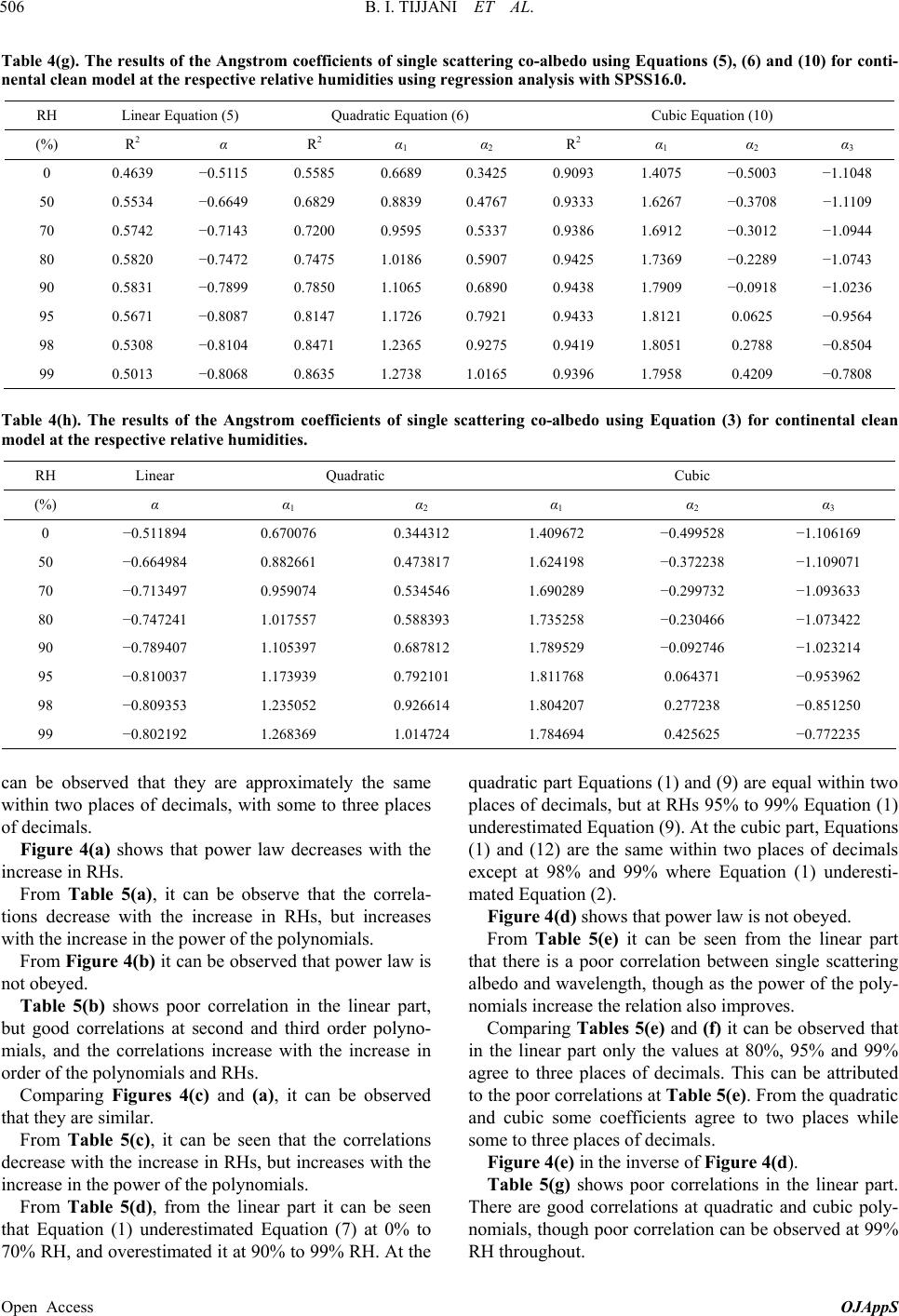 B. I. TIJJANI ET AL. Open Access OJAppS 506 Table 4(g). The results of the Angstrom coefficients of single scattering co-albedo using Equations (5), (6) and (10) for conti- nental clean model at the respect ive re lative humidities using regression anal ysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.4639 −0.5115 0.5585 0.6689 0.3425 0.9093 1.4075 −0.5003 −1.1048 50 0.5534 −0.6649 0.6829 0.8839 0.4767 0.9333 1.6267 −0.3708 −1.1109 70 0.5742 −0.7143 0.7200 0.9595 0.5337 0.9386 1.6912 −0.3012 −1.0944 80 0.5820 −0.7472 0.7475 1.0186 0.5907 0.9425 1.7369 −0.2289 −1.0743 90 0.5831 −0.7899 0.7850 1.1065 0.6890 0.9438 1.7909 −0.0918 −1.0236 95 0.5671 −0.8087 0.8147 1.1726 0.7921 0.9433 1.8121 0.0625 −0.9564 98 0.5308 −0.8104 0.8471 1.2365 0.9275 0.9419 1.8051 0.2788 −0.8504 99 0.5013 −0.8068 0.8635 1.2738 1.0165 0.9396 1.7958 0.4209 −0.7808 Table 4(h). The results of the Angstrom coefficients of single scattering co-albedo using Equation (3) for continental clean model at the respective relative humidities. RH Linear Quadratic Cubic (%) α α1 α2 α1 α2 α3 0 −0.511894 0.670076 0.344312 1.409672 −0.499528 −1.106169 50 −0.664984 0.882661 0.473817 1.624198 −0.372238 −1.109071 70 −0.713497 0.959074 0.534546 1.690289 −0.299732 −1.093633 80 −0.747241 1.017557 0.588393 1.735258 −0.230466 −1.073422 90 −0.789407 1.105397 0.687812 1.789529 −0.092746 −1.023214 95 −0.810037 1.173939 0.792101 1.811768 0.064371 −0.953962 98 −0.809353 1.235052 0.926614 1.804207 0.277238 −0.851250 99 −0.802192 1.268369 1.014724 1.784694 0.425625 −0.772235 can be observed that they are approximately the same within two places of decimals, with some to three places of decimals. Figure 4(a) shows that power law decreases with the increase in RHs. From Table 5(a), it can be observe that the correla- tions decrease with the increase in RHs, but increases with the increase in the power of the polynomials. From Figure 4(b) it can be observed that power law is not obeyed. Table 5(b) shows poor correlation in the linear part, but good correlations at second and third order polyno- mials, and the correlations increase with the increase in order of the polynomials and RHs. Comparing Figures 4(c) and (a), it can be observed that they are similar. From Table 5(c), it can be seen that the correlations decrease with the increase in RHs, but increases with the increase in the power of the polynomials. From Table 5(d), from the linear part it can be seen that Equation (1) underestimated Equation (7) at 0% to 70% RH, and overestimated it at 90% to 99% RH. At the quadratic part Equations (1) and (9) are equal within two places of decimals, but at RHs 95% to 99% Equation (1) underestimated Equation (9). At the cubic part, Equations (1) and (12) are the same within two places of decimals except at 98% and 99% where Equation (1) underesti- mated Equation (2). Figure 4(d) shows that power law is not obeyed. From Table 5(e) it can be seen from the linear part that there is a poor correlation between single scattering albedo and wavelength, though as the power of the poly- nomials increase the relation also improves. Comparing Tables 5(e) and (f) it can be observed that in the linear part only the values at 80%, 95% and 99% agree to three places of decimals. This can be attributed to the poor correlations at Table 5(e). From the quadratic and cubic some coefficients agree to two places while some to three places of decimals. Figure 4(e) in the inverse of Figure 4( d). Table 5(g) shows poor correlations in the linear part. There are good correlations at quadratic and cubic poly- nomials, though poor correlation can be observed at 99% RH throughout. 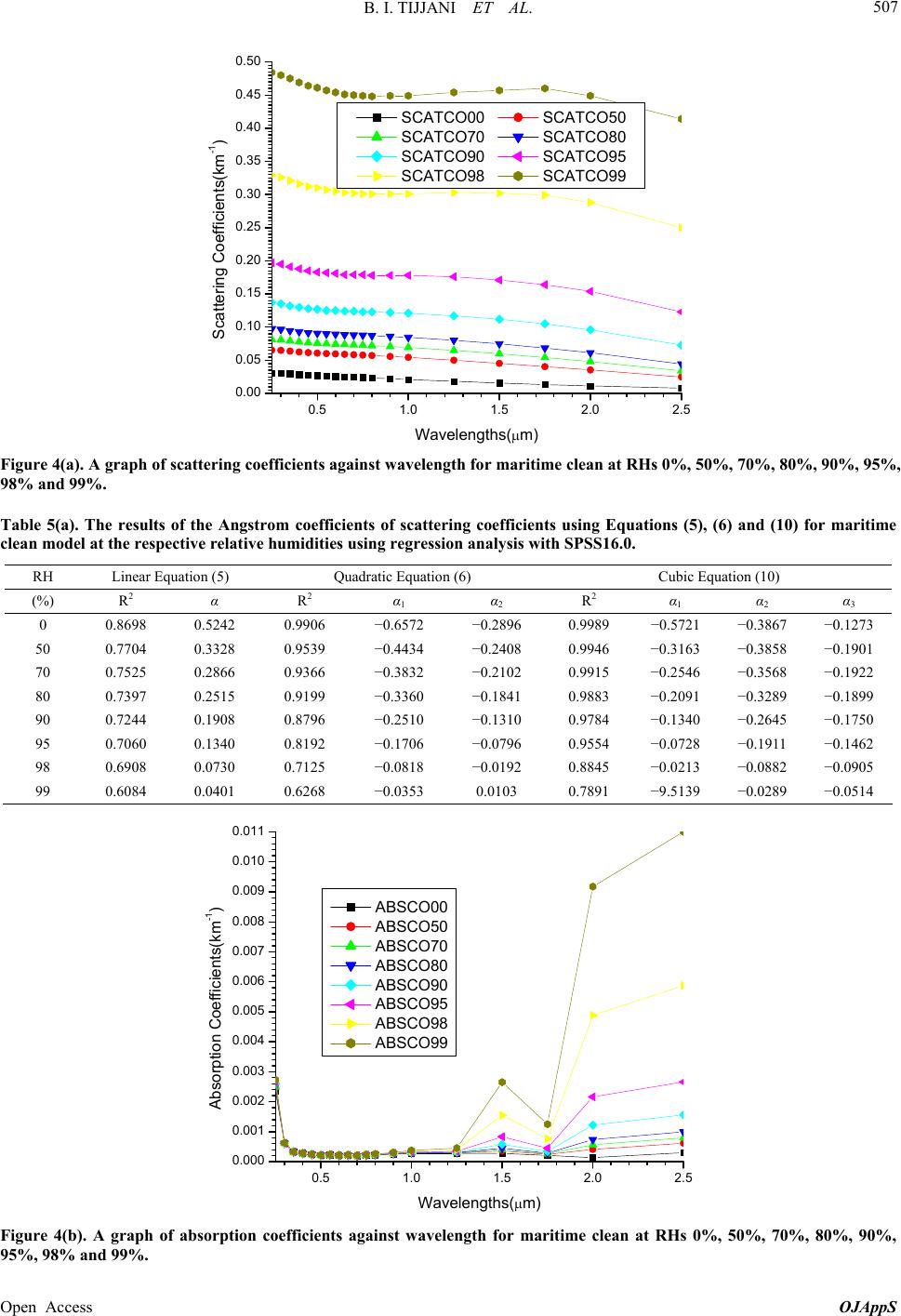 B. I. TIJJANI ET AL. Open Access OJAppS 507 0.51.01.52.02.5 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50 Scattering Coefficients(km -1 ) Wavelengths( m) SCATCO00 SCATCO50 SCATCO70 SCATCO80 SCATCO90 SCATCO95 SCATCO98 SCATCO99 Figure 4(a). A graph of scattering coefficients against wavelength for maritime clean at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 5(a). The results of the Angstrom coefficients of scattering coefficients using Equations (5), (6) and (10) for maritime clean model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.8698 0.5242 0.9906 −0.6572 −0.2896 0.9989 −0.5721 −0.3867 −0.1273 50 0.7704 0.3328 0.9539 −0.4434 −0.2408 0.9946 −0.3163 −0.3858 −0.1901 70 0.7525 0.2866 0.9366 −0.3832 −0.2102 0.9915 −0.2546 −0.3568 −0.1922 80 0.7397 0.2515 0.9199 −0.3360 −0.1841 0.9883 −0.2091 −0.3289 −0.1899 90 0.7244 0.1908 0.8796 −0.2510 −0.1310 0.9784 −0.1340 −0.2645 −0.1750 95 0.7060 0.1340 0.8192 −0.1706 −0.0796 0.9554 −0.0728 −0.1911 −0.1462 98 0.6908 0.0730 0.7125 −0.0818 −0.0192 0.8845 −0.0213 −0.0882 −0.0905 99 0.6084 0.0401 0.6268 −0.0353 0.0103 0.7891 −9.5139 −0.0289 −0.0514 0.51.01.52.02.5 0.000 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.010 0.011 Absorption Coefficients(km -1 ) Wavelengths( m) ABSCO00 ABSCO50 ABSCO70 ABSCO80 ABSCO90 ABSCO95 ABSCO98 ABSCO99 Figure 4(b). A graph of absorption coefficients against wavelength for maritime clean at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%.  B. I. TIJJANI ET AL. Open Access OJAppS 508 Table 5(b). The results of the Angstrom coefficients of absorption coefficients using Equations (5), (6) and (10) for maritime clean model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Quadratic Cubic (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.2846 0.4908 0.6576 −0.1081 0.8328 0.8516 0.5647 0.0652 −1.0063 50 0.0391 0.1833 0.7554 0.3512 1.1634 0.8894 0.9147 0.5204 −0.8429 70 0.0067 0.0799 0.7822 0.5037 1.2703 0.8899 1.0339 0.6653 −0.7930 80 0.0001 −0.0106 0.8041 0.6368 1.3629 0.8903 1.1369 0.7923 −0.7480 90 0.0277 −0.1927 0.8392 0.9028 1.5455 0.8943 1.3540 1.0307 −0.6748 95 0.0961 −0.4180 0.8720 1.2267 1.7603 0.9050 1.6339 1.2957 −0.6090 98 0.2118 −0.7747 0.9045 1.7287 2.0765 0.9230 2.1088 1.6428 −0.5686 99 0.2933 −1.0722 0.9205 2.1399 2.3242 0.9338 2.5189 1.8917 −0.5669 0.51.01.52.02.5 0.0 0.1 0.2 0.3 0.4 0.5 Extinction Coefficients(km -1 ) Wavelengths( m) EXTCO00 EXTCO50 EXTCO70 EXTCO80 EXTCO90 EXTCO95 EXTCO98 EXTCO99 Figure 4(c). A graph of extinction coefficients against wavelength for maritime clean at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 5(c). The results of the Angstrom coefficients of extinction coefficients using Equations (5), (6) and (10) for maritime clean model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Quadratic Cubic (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.8883 0.5272 0.9880 −0.6475 −0.2618 0.9998 −0.5464 −0.3772 −0.1512 50 0.7887 0.3333 0.9515 −0.4365 −0.2245 0.9966 −0.3041 −0.3755 −0.1980 70 0.7704 0.2863 0.9352 −0.3765 −0.1963 0.9942 −0.2449 −0.3464 −0.1968 80 0.7571 0.2501 0.9180 −0.3286 −0.1709 0.9910 −0.1997 −0.3180 −0.1928 90 0.7395 0.1877 0.8798 −0.2434 −0.1212 0.9817 −0.1277 −0.2533 −0.1731 95 0.7260 0.1300 0.8153 −0.1611 −0.0676 0.9608 −0.0644 −0.1778 −0.1445 98 0.7056 0.0686 0.7108 −0.0726 −0.0088 0.8872 −0.0157 −0.0737 −0.0852 99 0.5279 0.0332 0.6218 −0.0236 0.0207 0.7764 0.0062 −0.0133 −0.0446 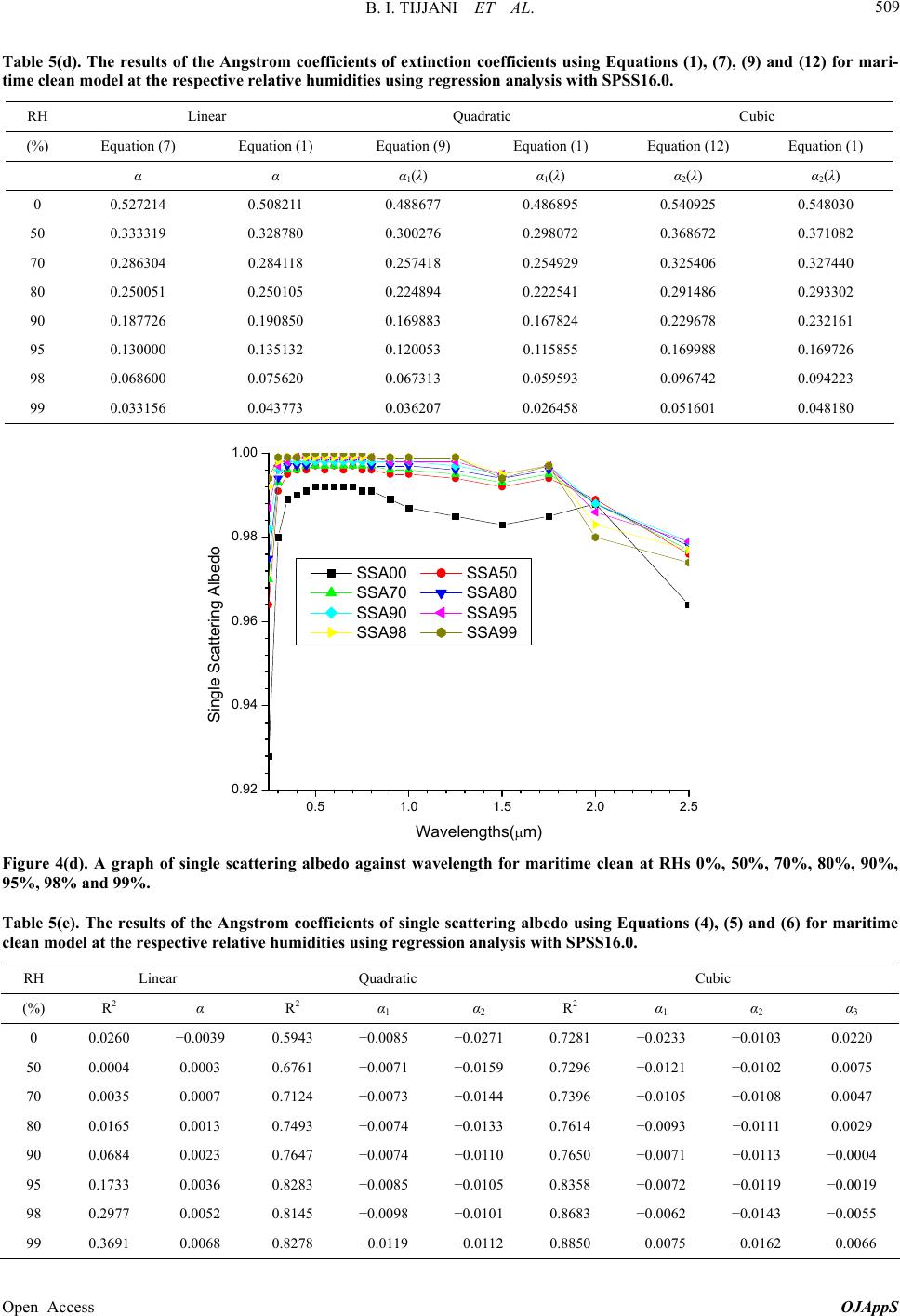 B. I. TIJJANI ET AL. Open Access OJAppS 509 Table 5(d). The results of the Angstrom coefficients of extinction coefficients using Equations (1), (7), (9) and (12) for mari- time clean model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Quadratic Cubic (%) Equation (7) Equation (1) Equation (9) Equation (1) Equation (12) Equation (1) α α α1(λ) α1(λ) α2(λ) α2(λ) 0 0.527214 0.508211 0.488677 0.486895 0.540925 0.548030 50 0.333319 0.328780 0.300276 0.298072 0.368672 0.371082 70 0.286304 0.284118 0.257418 0.254929 0.325406 0.327440 80 0.250051 0.250105 0.224894 0.222541 0.291486 0.293302 90 0.187726 0.190850 0.169883 0.167824 0.229678 0.232161 95 0.130000 0.135132 0.120053 0.115855 0.169988 0.169726 98 0.068600 0.075620 0.067313 0.059593 0.096742 0.094223 99 0.033156 0.043773 0.036207 0.026458 0.051601 0.048180 0.51.01.52.02.5 0.92 0.94 0.96 0.98 1.00 Single Scattering Albedo Wavelengths( m) SSA00 SSA50 SSA70 SSA80 SSA90 SSA95 SSA98 SSA99 Figure 4(d). A graph of single scattering albedo against wavelength for maritime clean at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 5(e). The results of the Angstrom coefficients of single scattering albedo using Equations (4), (5) and (6) for maritime clean model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Quadratic Cubic (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.0260 −0.0039 0.5943 −0.0085 −0.0271 0.7281 −0.0233 −0.0103 0.0220 50 0.0004 0.0003 0.6761 −0.0071 −0.0159 0.7296 −0.0121 −0.0102 0.0075 70 0.0035 0.0007 0.7124 −0.0073 −0.0144 0.7396 −0.0105 −0.0108 0.0047 80 0.0165 0.0013 0.7493 −0.0074 −0.0133 0.7614 −0.0093 −0.0111 0.0029 90 0.0684 0.0023 0.7647 −0.0074 −0.0110 0.7650 −0.0071 −0.0113 −0.0004 95 0.1733 0.0036 0.8283 −0.0085 −0.0105 0.8358 −0.0072 −0.0119 −0.0019 98 0.2977 0.0052 0.8145 −0.0098 −0.0101 0.8683 −0.0062 −0.0143 −0.0055 99 0.3691 0.0068 0.8278 −0.0119 −0.0112 0.8850 −0.0075 −0.0162 −0.0066 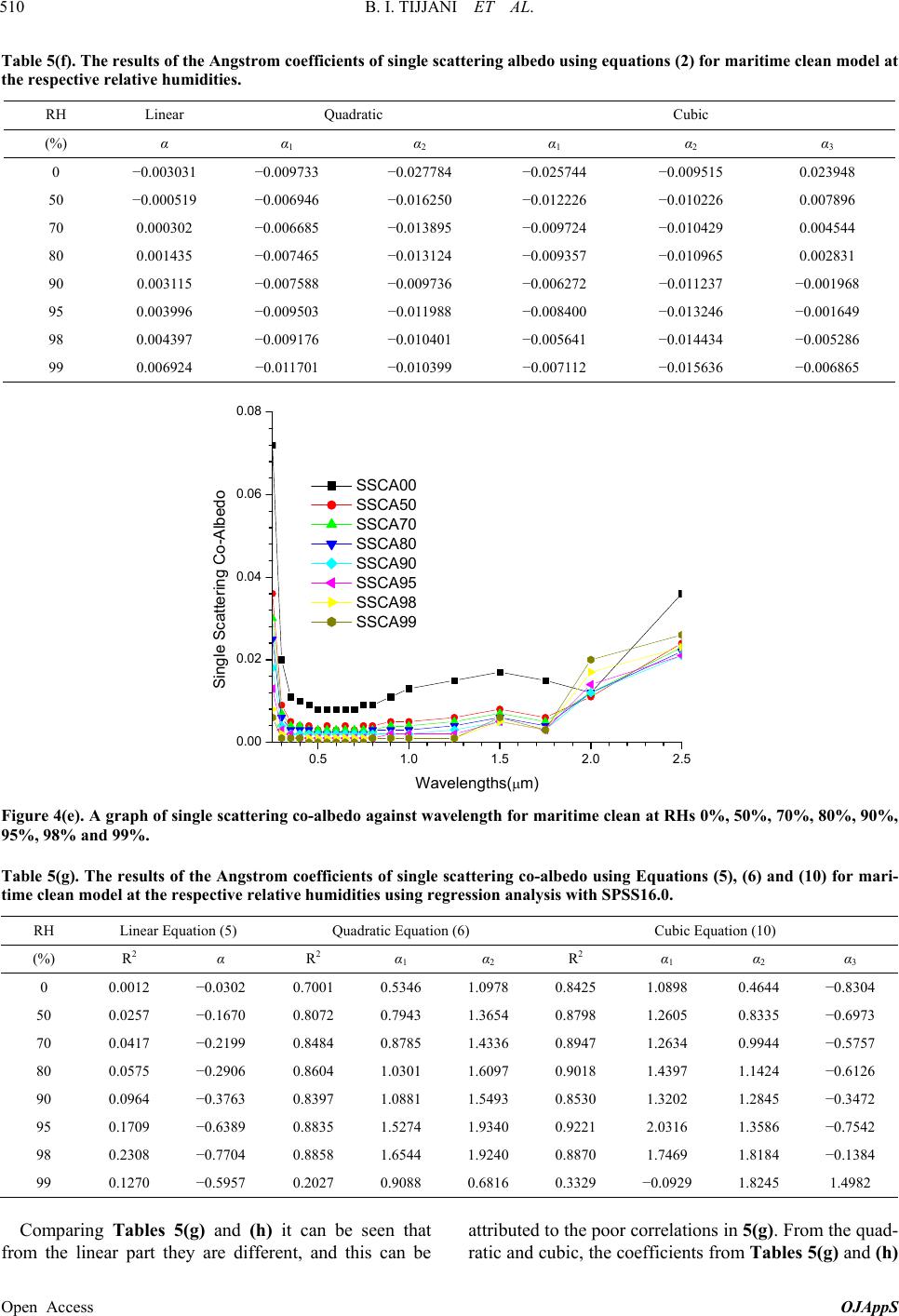 B. I. TIJJANI ET AL. Open Access OJAppS 510 Table 5(f). The results of the Angstrom coefficients of single scattering albedo using equations (2) for maritime clean model at the respective relative humidities. RH Linear Quadratic Cubic (%) α α1 α2 α1 α2 α3 0 −0.003031 −0.009733 −0.027784 −0.025744 −0.009515 0.023948 50 −0.000519 −0.006946 −0.016250 −0.012226 −0.010226 0.007896 70 0.000302 −0.006685 −0.013895 −0.009724 −0.010429 0.004544 80 0.001435 −0.007465 −0.013124 −0.009357 −0.010965 0.002831 90 0.003115 −0.007588 −0.009736 −0.006272 −0.011237 −0.001968 95 0.003996 −0.009503 −0.011988 −0.008400 −0.013246 −0.001649 98 0.004397 −0.009176 −0.010401 −0.005641 −0.014434 −0.005286 99 0.006924 −0.011701 −0.010399 −0.007112 −0.015636 −0.006865 0.5 1.0 1.5 2.0 2.5 0.00 0.02 0.04 0.06 0.08 Single Scattering Co-Albedo Wavelengths( m) SSCA00 SSCA50 SSCA70 SSCA80 SSCA90 SSCA95 SSCA98 SSCA99 Figure 4(e). A graph of single scattering co-albedo against wavelength for maritime clean at RHs 0%, 50%, 70%, 80%, 90%, 95%, 98% and 99%. Table 5(g). The results of the Angstrom coefficients of single scattering co-albedo using Equations (5), (6) and (10) for mari- time clean model at the respective relative humidities using regression analysis with SPSS16.0. RH Linear Equation (5) Quadratic Equation (6) Cubic Equation (10) (%) R2 α R 2 α1 α2 R 2 α1 α2 α3 0 0.0012 −0.0302 0.7001 0.5346 1.0978 0.8425 1.0898 0.4644 −0.8304 50 0.0257 −0.1670 0.8072 0.7943 1.3654 0.8798 1.2605 0.8335 −0.6973 70 0.0417 −0.2199 0.8484 0.8785 1.4336 0.8947 1.2634 0.9944 −0.5757 80 0.0575 −0.2906 0.8604 1.0301 1.6097 0.9018 1.4397 1.1424 −0.6126 90 0.0964 −0.3763 0.8397 1.0881 1.5493 0.8530 1.3202 1.2845 −0.3472 95 0.1709 −0.6389 0.8835 1.5274 1.9340 0.9221 2.0316 1.3586 −0.7542 98 0.2308 −0.7704 0.8858 1.6544 1.9240 0.8870 1.7469 1.8184 −0.1384 99 0.1270 −0.5957 0.2027 0.9088 0.6816 0.3329 −0.0929 1.8245 1.4982 Comparing Tables 5(g) and (h) it can be seen that from the linear part they are different, and this can be attributed to the poor correlations in 5(g). From the quad- ratic and cubic, the coefficients from Tables 5(g) and (h)  B. I. TIJJANI ET AL. Open Access OJAppS 511 Table 5(h). The results of the Angstrom coefficients of single scattering co-albedo using Equation (3) for maritime clean model at the respective relative humidities. RH Linear Quadratic Cubic (%) α α1 α2 α1 α2 α3 0 −0.036462 0.539358 1.094649 −0.018294 0.312034 1.157534 50 −0.150011 0.787625 1.387888 −0.610640 −0.144866 1.040860 70 −0.206397 0.880150 1.466550 −0.789011 −0.318965 0.989806 80 −0.260667 0.965345 1.533866 −0.937193 −0.474357 0.940760 90 −0.380442 1.146174 1.666761 −1.226255 −0.777471 0.847912 95 −0.548017 1.387765 1.827872 −1.569516 −1.117854 0.753569 98 −0.843281 1.801288 2.085286 −2.093174 −1.569053 0.653780 99 −1.105303 2.163529 2.303430 −2.525064 −1.878473 0.611415 are almost the same, but to only one place of decimals. 4. Conclusions From all the tables and graphs obtained, it can be seen that it is only urban aerosols that scattering, absorption and extinction coefficients that satisfy power laws excel- lently at this spectral range and can be seen that it is the only aerosols that show very good relations between the estimated Equations (1)-(3) and the linear Equation (5). Linear models are considered most important, because they are the values that are obtainable from remote sens- ing and ground truthing instruments. Another observation made is that Equations (1) and (2) are sufficient. This is because the information that can be obtained from equation is almost the same as that of Equation (3). Additional important observation made from the vari- ous graphs is that, at the spectral range of 0.4 to 1.5 power laws are obeyed by all the aerosols. Therefore, since 99% of sun’s radiation falls between 0.2 - 5.6 μm; and 80% falls between 0.4 - 1.5 μm (visible and near infrared) and the atmosphere is quite transparent to in- coming solar radiation with the maximum radiation at 0.48 μm (visible) and in the study of the earth’s surface, most of the remote sensing instruments are designed to operate within solar spectral window (0.4 - 0.7 μm) and near infrared (0.7 - 1.5 μm), where cloudless atmosphere will transmit sufficient radiation for detection, which also shows that these formulas can be useful in remote sens- ing. REFERENCES [1] A. Angstrom, “On the Atmospheric Transmission of Sun Radiation and on Dust in the Air,” Geografiska Annaler, Vol. 11, 1929, pp. 156-166. http://dx.doi.org/10.2307/519399 [2] A. Angstrom, “On the Atmospheric Transmission of Sun Radiation II,” Geografiska Annaler, Vol. 12, 1930, pp. 130-159. http://dx.doi.org/10.2307/519561 [3] A. Angstrom, “Techniques of Determining the Turbidity of the Atmosphere,” Tellus, Vol. 13, No. 2, 1961, pp. 214-223. http://dx.doi.org/10.1111/j.2153-3490.1961.tb00078.x [4] A. Angstrom, “The Parameters of Atmospheric Turbid- ity,” Tellus, Vol. 16, No. 1, 1964, pp. 64-75. http://dx.doi.org/10.1111/j.2153-3490.1964.tb00144.x [5] P. B. Russell, R. W. Bergstrom, Y. Shinozuka, A. D. Clarke, P. F. De-Carlo, J. L. Jimenez, J. M. Livingston, J. Redemann, O. Dubovik and A. Strawa, “Absorption Ang- strom Exponent in AERONET and Related Data as an In- dicator of Aerosol Composition,” Atmospheric Chemistry and Physics, Vol. 10, 2010, pp. 1155-1169. http://dx.doi.org/10.5194/acp-10-1155-2010 [6] E. V. Fischer, D. A. Jaffe, N. A. Marley, J. S. Gaffney and A. Marchany-Rivera, “Optical Properties of Aged Asian Aerosols Observed over the US Pacific North- west,” Journal of Geophysical Research, Vol. 115, No. D20, 2010. http://dx.doi.org/10.1029/2010JD013943 [7] A. Virkkula, N. C. Ahlquist, D. S. Covert, W. P. Arnott, P. J. Sheridan, P. K. Quinn and D. J. Coffman, “Modifica- tion, Calibration and a Field Test of an Instrument for Measuring Light Absorption by Particles,” Aerosol Sci- ence and Technology, Vol. 39, No. 1, 2005, pp. 68-83. [8] B. A. Flowers, M. K. Dubey, C. Mazzoleni, E. A. Stone, J. J. Schauer, S.-W. Kim and S. C. Yoon, “Optical-Chemi- cal-Microphysical Relationships and Closure Studies for Mixed Car-Bonaceous Aerosols Observed at Jeju Island; 3-Laser Photoa-Coustic Spectrometer, Particle Sizing, and Filter Analysis,” Atmospheric Chemistry and Physics, Vol. 10, 2010, pp. 10387-10398. http://dx.doi.org/10.5194/acp-10-10387-2010 [9] N. O’Neill and A. Royer, “Extraction of Bimodal Aero- sol-Size Distribution Radii from Spectral and Angular Slope (Angstrom) Coefficients,” Applied Optics, Vol. 32, No. 9, 1993, pp. 1642-1645. http://dx.doi.org/10.1364/AO.32.001642 [10] M. K. Latha and K. V. S. Badarinath, “Factors Influenc- ing Aerosol Characteristics over Urban Environment,” Environmental Monitoring and Assessment, Vol. 104, No. 1-3, 2005, pp. 269-280. http://dx.doi.org/10.1007/s10661-005-1615-7 [11] J. S. Reid, T. F. Eck, S. A. Christopher, P. V. Hobbs and B. Holben, “Use of the Angstrom Exponent to Estimate  B. I. TIJJANI ET AL. Open Access OJAppS 512 the Variability of Optical and Physical Properties of Ag- ing Smoke Particles in Brazil,” Journal of Geophysical Research, Vol. 104, No. D22, 1999, pp. 27473-27489. http://dx.doi.org/10.1029/1999JD900833 [12] T. F. Eck, B. N. Holben, D. E. Ward, M. M. Mukelabai, O. Dubovik, A. Smirnov, J. S. Schafer, N. C. Hsu, S. J. Piketh, A. Queface, J. Le Roux, R. J. Swap and I. Slutsker, “Variability of Biomass Burning Aerosol Optical Char- acteristics in Southern Africa during the SAFARI 2000 Dry Season Campaign and a Comparison of Single Scat- tering Albedo Estimates from Radiometric Measure- ments,” Journal of Geophysical Research, Vol. 108 No. D13, 2003, p. 8477. [13] T. F. Eck, B. N. Holben, J. S. Reid, O. Dubovic, A. Smir- nov, N. T. O’Neill, I. Slutsker and S. Kinne, “Wavelength Dependence of the Optical Depth of Biomass Burning, Urban, and Desert Dust Aerosols,” Journal of Geophysi- cal Research, Vol. 104, No. D24, 1999, pp. 31333-31349. http://dx.doi.org/10.1029/1999JD900923 [14] A. Smirnov, A. Royer, N. T. O’Neill and A. Tarussov, “A Study of the Link between Synoptic Air Mass Type and Atmospheric Optical Parameters,” Journal of Geophysi- cal Research, Vol. 99, No. D10, 1994, pp. 20967-20982. http://dx.doi.org/10.1029/94JD01719 [15] N. C. Hsu, S. C. Tsay, M. D. King and J. R. Herman, “Deep-Blue retrievals of Asian aerosol properties during ACE-Asia,” IEEE Transactions on Geoscience and Re- mote Sensing, Vol. 44, No. 11, 2006, pp. 3180-3195. http://dx.doi.org/10.1109/TGRS.2006.879540 [16] H. Moosmuller, R. K. Chakrabarty and W. P. Arnott, “Aerosol Light Absorption and Its Measurement: A Re- view,” Journal of Quantitative Spectroscopy and Radia- tive Transfer, Vol. 110, NO. 11, 2009, pp. 844-878. http://dx.doi.org/10.1016/j.jqsrt.2009.02.035 [17] H. Moosmuller and R. K. Chakrabarty, “Technical Note: Simple Analytical Relationships between Angstrom Co- efficients of Aerosol Extinction, Scattering, Absorption, and Single Scattering Albedo,” Atmospheric Chemistry and Physics, Vol. 11, 2011, pp. 10677-10680. http://dx.doi.org/10.5194/acp-11-10677-2011 [18] K. Lewis, W. P. Arnott, H. Moosmuller and C. E. Wold, “Strong Spectral Variation of Biomass Smoke Light Ab- sorption and Single Scattering Albedo Observed with a Novel Dual-Wavelength Photoacoustic Instrument,” Jour- nal of Geophysical Research, Vol. 113, No. D16, 2008. http://dx.doi.org/10.1029/2007JD009699 [19] O. Dubovik, B. N. Holben, Y. J. Kaufman, M. Yamasoe, A. Smirnov, D. Tanre and I. Slutsker, “Single-Scattering Albedo of Smoke Retrieved from the Sky Radiance and Solar Transmittance Measured from Ground,” Journal of Geophysical Research, Vol. 103, No. D24, 1998, pp. 31901-31923. http://dx.doi.org/10.1029/98JD02276 [20] O. Dubovik and M. D. King, “A Flexible Inversion Algo- rithm for Retrieval of Aerosol Optical Properties from Sun and Sky Radiance Measurements,” Journal of Geo- physical Research, Vol. 105, No. D16, 2000, pp. 20673- 20696. http://dx.doi.org/10.1029/2000JD900282 [21] M. I. Mishchenko, B. Cairns, G. Kopp, C. F. Schueler, B. A. Fafaul, J. E. Hansen, R. J. Hooker, T. Itchkawich, H. B. Maring and L. D. Travis, “Accurate Monitoring of Ter- restrial Aerosols and Total Solar Irradiance—Introducing the Glory Mission,” Bulletin of the American Meteoro- logical Society, Vol. 88, No. 5, 2007, pp. 677-691. http://dx.doi.org/10.1175/BAMS-88-5-677 [22] L. Zhu, J. V. Martins and L. A. Remer, “Biomass Burning Aerosol Absorption Measurements with MODIS Using the Critical Reflectance Method,” Journal of Geophysical Research, Vol. 116, No. D7, 2011. http://dx.doi.org/10.1029/2010JD015187 [23] A. Sanchez, T. F. Smith and W. F. Krajewski, “A Three- Dimensional Atmospheric Radiative Transfer Model Based on the Discrete-Ordinates Method,” Atmospheric Research, Vol. 33, No. 1-4, 1994, pp. 283-308. http://dx.doi.org/10.1016/0169-8095(94)90024-8 [24] Z. Li, P. Goloub, C. Devaux, X. Gu, Y. Qiao, F. Zhao and H. Chen, “Aerosol Polarized Phase Function and Single- Scattering Albedo Retrieved from Ground-Based Meas- urements,” Atmospheric Research, Vol. 71, No. 4, 2004, pp. 233-241. http://dx.doi.org/10.1016/j.atmosres.2004.06.001 [25] K. N. Liou and Y. Takano, “Light Scattering by Non- spherical Particles: Remote Sensing and Climatic Impli- cations,” Atmospheric Research, Vol. 31, No. 4, 1994, pp. 271-298. http://dx.doi.org/10.1016/0169-8095(94)90004-3 [26] A. Kylling, A.F. Bais, M. Blumthaler, J. Shreder and C. S. Zerefos, “UV Irradiances during the PAUR Campaign: Comparison between Measurement and Model Simula- tions,” Journal of Geophysical Research, Vol. 103 No. D20, 1998, pp. 26051-26060. [27] G. L. Schuster, O. Dubovik and B. N. Holben, “Angstrom Exponent and Bimodal Aerosol Size Distributions,” Jour- nal of Geophysical Research, Vol. 111, No. D7, 2006. http://dx.doi.org/10.1029/2005JD006328 [28] M. Hess, P. Koepke and I. Schult, “Optical Properties of Aerosols and Clouds: The Software Package OPAC,” Bulletin of the American Meteorological Society, Vol. 79, No. 5, 1998, pp. 831-844. [29] K. N. Liou, “An Introduction to Atmospheric Radiation,” 2nd Edition, Academic Press, San Diego, 2002, p. 583. [30] M. D. King and D. M. Byrne, “A Method for Inferring Total Ozone Content from Spectral Variation of Total Optical Depth Obtained with a Solar Radiometer,” Jour- nal of the Atmospheric Sciences, Vol. 33, No. 11, 1976, pp. 2242-2251. http://dx.doi.org/10.1175/1520-0469(1976)033<2242:AM FITO>2.0.CO;2 [31] T. F. Eck, B. N. Holben, O. Dubovic, A. Smirnov, I. Slutsker, J. M. Lobert and V. Ramanathan, “Column-In- tegrated Aerosol Optical Properties over the Maldives During the Northeast Mon-Soon for 1998-2000,” Journal of Geophysical Research, Vol. 106, No. D22, 2001, pp. 28555-28566. [32] T. F. Eck, B. N. Holben, D. E. Ward, O. Dubovic, J. S. Reid, A. Smirnov, M. M. Mukelabai, N. C. Hsu, N. T. O’ Neil and I. Slutsker, “Characterization of the Optical Properties of Biomass Burning Aerosols in Zambia dur- ing the 1997 ZIBBEE Field Campaign,” Journal of Geo- physical Research, Vol. 106, No. D4, 2001, pp. 3425-  B. I. TIJJANI ET AL. Open Access OJAppS 513 3448. http://dx.doi.org/10.1029/2000JD900555 [33] Y. J. Kaufman, “Aerosol Optical Thickness and Atmos- pheric Path Radiance,” Journal of Geophysical Research, Vol. 98, No. D2, 1993, pp. 2677-2992. http://dx.doi.org/10.1029/92JD02427 [34] N. T. O’Neill, T. F. Eck, B. N. Holben, A. Smirnov, O. Dubovik and A. Royer, “Bimodal Size Distribution Influ- ences on the Variation of Angstrom Derivatives in Spec- tral and Optical Depth Space,” Journal of Geophysical Research, Vol. 106, No. D9, 2001, pp. 9787-9806. http://dx.doi.org/10.1029/2000JD900245 [35] N. T. O’Neill, T. F. Eck, A. Smirnov, B. N. Holben and S. Thulasiraman, “Spectral Discrimination of Coarse and Fine Mode Optical Depth,” Journal of Geophysical Re- search, Vol. 198, No. D17, 2003, p. 4559. [36] D. G. Kaskaoutis and H. D. Kambezidis, “Investigation into the Wavelength Dependence of the Aerosol Optical Depth in the Athens Area,” Journal of the Royal Meteoro- logical Society, Vol. 132, No. 620, 2006, pp. 2217-2234. http://dx.doi.org/10.1256/qj.05.183 [37] B. Schmid, D. A. Hegg, J. Wang, D. Bates, J. Redemann, P. B. Russell, J. M. Livingston, H. H. Jonsson, E. J. Wel- ton, J. H. Seinfeld, R. C. Flagan, D. S. Covert, O. Dubo- vik, A. Jefferson, “Column Closure Studies of Lower Tropospheric Aerosol and Water Vapor During ACE- Asia Using Airborne Sun Photometer and Airborne in Situ and Ship-Based Lidar Measurements,” Journal of Geophysical Research, Vol. 108 No. D23, 2003, p. 8656. http://dx.doi.org/10.1029/2002JD003361 [38] J. A. Martinez-Lozano, M. P. Utrillas, F. Tena, Pedros, R., J. Canada, J. V. Bosca and J. Lorente, “Aerosol Optical Characteristics from Summer Campaign in an Urban Coastal Mediterranean Area,” IEEE Transactions on Geoscience and Remote Sensing, Vol. 39, No. 7, 2001, pp. 1573-1585. http://dx.doi.org/10.1109/36.934089 [39] D. G. Kaskaoutis, H. D. Kambezidis, N. Hatzianastassiou, P. G. Kosmopoulos and K. V. S. Badarinath, “Aerosol Climatology: Dependence of the Angstrom Exponent on Wavelength over Four AERONET Sites,” Atmospheric Chemistry and Physics, Vol. 7, 2007, pp. 7347-7397. http://dx.doi.org/10.5194/acpd-7-7347-2007 [40] D. G. Kaskaoutis, H. D. Kambezidis, , N. Hatzianastas- siou, P. G. Kosmopoulos and K. V. S. Badarinath, “Aero- sol Climatology: On the Discrimination of Aerosol Types over Four AERONET Sites,” Atmospheric Chemistry and Physics Discussion, Vol. 7, No. 3, 2007, pp. 6357-6411. [41] J. W. Fitzgerald, “Approximation Formulas for the Equi- librium Size of an Aerosol Particle as a Function of Its Dry Size and Composition and Ambient Relative Humid- ity,” Journal of Applied Meteorology, Vol. 14, No. 6, 1975, pp. 1044-1049. http://dx.doi.org/10.1175/1520-0450(1975)014<1044:AF FTES>2.0.CO;2 [42] I. N. Tang, “Chemical and Size Effects of Hygroscopic Aerosols on Light Scattering Coefficients,” Journal of Geophysical Research, Vol. 101, No. D14, 1996, pp. 19245-19250. http://dx.doi.org/10.1029/96JD03003
|