Vol.3, No.2, 154-164 (2011) Natural Science
http://dx.doi.org/10.4236/ns.2011.32022
Thermal dependence of the properties of cubic boron
nitride crystal
Zainelabideen Y. Mijbil1, Mudar A. Abdulsattar2, Ahmed M. Abdul-Lettif3
1Basic Science Department, Veterinary Medicine College, University of Babylon, Hilla, Iraq
2Ministry of Sciences and Technology, Baghdad, Iraq
3Department of Physics, College of Science, University of Babylon, Hilla, Iraq; *Corresponding author:
Received 20 November 2010; revised 23 December 2010; accepted 26 December 2010.
ABSTRACT
Lattice constant, total energy, cohesive energy,
bulk modulus, speed of sound (υ), plasmon en-
ergy (Epl), valence charge distribution and en-
ergy bands of cubic boron nitride crystal have
been calculated and studied as a function of
temperature using self-consistent field tight
binding method with complete neglect of dif-
ferential overlap version 2 using 8-atom large
unit cell approach. Our results illustrate that the
increase of temperature leads to an increase of
lattice constant, cohesive energy, and valence
charge distribution at the atoms, whereas a de-
crease is obtained for bulk modulus, energy
band widths, valence charge distribution in the
intratomic distance, speed of sound, and the
plasmon energy. The comparison with experi-
mental and other theoretical results has showed
an excellent agreement for the lattice constant,
bulk modulus, cohesive energy, speed of sound,
plasmon energy value and the valence band,
whereas remarkable differences in charge dis-
tribution values, and the band gap are found.
These differences are common in the results
that depend on this type of calculation. Values
for conduction band and speed of sound have
not been found for comparison. Our relation for
Epl-T fails but the υ-T relation is successful.
Keywords: Electronic Structure; Temperature
Dependence; Boron Nitride
1. INTRODUCTION
The high account of hardness [1], melting point [2],
high thermal conductivity [3] and band gap [4], resis-
tance for oxidation as temperature increases[5] with inert
state [6] low electrical conductivity [7], and no iron re-
action [8]are all for sp3 [9] cubic boron nitride. So it has
amazing aspects [10] of multiuse [11,12] such as in pol-
ishing, cutting [13] and protection [14], and it has been
the core for many studies [15-18] since its discovery in
1957 [19].
Methods of semiempirical calculations give a privi-
lege of reasonable computer execution time for getting
the results due to the approximations which are involved
[20,21], accordingly they are used in many studies
[22-25]. In this paper we have used linear combination
of atomic orbitals (LCAO) approach as a starting point
[26] which includes both 1) the CNDO, as one of the
primary semiempirical methods, that is presented by
Popel et al. [27] in which many electron-electron inter-
actions had been neglected. CNDO focused on both va-
lence electrons and nuclei as a core of the atom (with the
other electrons) [21], and 2) LUC (Large Unit Cell) ap-
proximation or (Supercell) [28] is used in order to mini-
mize the size of Brillion Zone (BZ) and so to reduce the
number of the wave vector (k) points in which the as-
pects of the crystal such as band structure could be cal-
culated [29,30].
The aim of this project is to study the c-BN by
CNDO/2. CNDO/2 is an old fashion method but here we
try to see its merits and drawbacks through works and
results due to the trend to couple between ab initio cal-
culations with semiempirical methods, specially if we
know that the ab initio method is used for small systems,
in comparison with the semiempirical calculations which
were applied for large systems, so it is a competition
between the accuracy of the former and the high speed
of the later [31].
2. METHODOLOGY
According to LCAO-LUC with eight atoms, and STO
(Slater Type Orbital), the atomic orbital is of the form:
 
*1
,,exp ,
n
rGr rY
 



  (1)
where Ψ(r, θ,φ) is Slater type orbital. r, θ,φ are the polar
spherical coordinates of the atom. G is the normalization

Z. Y. Mijbil et al. / Natural Science 3 (2011) 154-164
155
constant. n* is the effective principal quantum number,
and Y(θ,φ) is the spherical harmonics [32]. The Fock-
matrix element (Fμμ) and the total energy (E) can be cal-
culated as [21]:


10.5 1
2AAA BAB
BA
FIAPQ Q
 




 


(2)
0.5
AB AB
FSP
 

 (3)

1
0.5 ABAB
AB
EPHFZZR
 







(4)
where μ and ν represent atomic orbitals and here they are
used either as s or p orbitals, the quantity –0.5 (Iμ +Aμ) is
either EES or EEP for μ ≡ s or p respectively, Iμ and Aμ
represent the ionization potential and the atomic electron
affinity respectively, βAB is the bonding parameter, Pμμ is
the density matrix, QB and QA are the net charge on atom
A and B respectively, and γAB is the average electrostatic
repulsion between any electron on atom A and any elec-
tron on atom B.
The final expressions with LUC approaches [20] are:
  
 
,
1
00.50
2
0.5 0
oo oz
AA BAB
Bz
oz oz
AB ozvAA
zo z
FIA Q
SPfx
 





 


 (5)
 
,
00.50
oz oz
AB o zvAB
zv
F
SP fx
 
 

(6)
 
1
0.5 000
0.5 ABAB
AB
EPFH
ZZR
 







 (7)
where f(x) it is Szymanski enhancement function, o is
the central LUC and z is the other LUCs [33].
We have firstly studied how CNDO/2 parameters: the
orbital exponent (ξ), bonding parameter (β), s-shell elec-
tronigativity (EES) and p-shell electronegativity (EEP)
could be changed and how this change may affect the
results. Our suggested parameters are shown in Table 1,
and secondly we have calculated the lattice constant,
cohesive energy, valence band width, conduction band
width, direct band gap, according to these parameters as
shown later.
Table 1.The parameters of CNDO/2.
Property -β (eV) ξ (a.u.) EES (eV) EEP (eV)
Reference B N B N B N B N
[33] 7.452 13.95 1.531 1.9575 9.158 4.128 7.511
[21] 17 25 1.3 1.959.549 19.316 4.0017.375
Pres. 8.455 11.95 1.53 1.9528.416 34.766 14.666 22.728
The procedure of the present work can be summarized
as follows:
1) We change the four parameters of the CNDO
method ξ, βAB, EES and EEP in arbitrary way until we
get a value of the lattice that is very close to the ex-
perimental value with the minimum value of the total
energy of the crystal.
2) Then we measure the values of the cohesive energy
and all the energies of the electronic band.
3) If the values of energies are in agreement with the
experiments then the iterations are ended and we fix
the parameters.
4) If the values of the energies are incorrect the pa-
rameters are changed until getting the closest values to
the experiments.
3. CALCULATIONS
3.1. The Total Energy
The total energy (E) is calculated when the difference
between two successive iterations from the program is
less than (0.0136 eV) and our result is fitted to Birch-
Murnaghan equation [34] as below:

/1
11
o
B
o
ooo
o
oo o
VV
BV BV
EE BB B



 





(8)
where Eo, Vo, and Bo are the total energy, volume of the
unit cell and the bulk modulus at the equilibrium point,
zero temperature-pressure point, respectively, V is the
volume at any temperature, and B’
o is the pressure de-
rivative of bulk modulus with a value of (3.79) [35].
3.2. Cohesive Energy
The cohesive energy (Ecoh) is calculated from the LUC
total energy according to the equation [36]:
8
cohfree zp
E
EEE (9)
Efree is the energy of (sp) orbitals for the free atom and
equals to 169.164 eV [37], and Ezp is the zero point en-
ergy and equals to 0.165 eV [38].
3.3. Volume
For tetrahedral structure it is found that [39]:
0.021
m
T


 (10)
α is the linear thermal expansion and Tm is the melting
temperature [39] which equals to 3000 K [40]. We have
also from [40] that:
1
o
a
aT


 (11)

Z. Y. Mijbil et al. / Natural Science 3 (2011) 154-164
156
T is the temperature, a is the lattice constant at any tem-
perature and ao is the lattice constant at zero temperature.
If we take the initial temperature equals to (0 K), and
combine Eq.10 to Eq.11 we get a relation for tetrahedral
structure:
1 0.021
o
m
T
aa T




(12)
Let [1 + 0.021 T/Tm] ≡ X, and we have V = a3 then we
will get:
3
o
VVX (13)
3.4. Bulk Modulus
The bulk modulus has been calculated from the Cohen
empirical formula [41]:
3.5
1970200 C
o
I
Bd

 (14)
IC is the Cohen ionicity factor (= 0, 1 and 2 for IV, III-V
and II-V groups respectively) [35], and it is used instead
of Pauling ionicity factor (IP) (Eq.15 [42]), d (= 0.433 a)
is the intratomic distance [43].

2
1exp 4
AB P
I



  


(15)
where χA and χB are the atom A and B electronigativity
respectively.
Now by substituting Eq.13 in Eq.14 with some sim-
ple mathematical treatment, we get a general relation for
tetrahedral structure:
3.5
o
BBX

 (16)
3.5. Plasmon Energy and the Speed of
Sound
According to (Kumar and Sastry) [40] the plasmon
energy (Epl) is defined as:
2
3
15.3
p
l
dE

 (17)
From the above relations we have d = do X, so the
general relation for tetrahedral structure is:
3
2
15.3
o
pl
d
EX




(18)
For the speed of sound (υ) we have [44]:
B


 (19)
ρ represents the density at any temperature and relates to
ρo (= 3.47 g/cm according to [45]) the density at zero
temperature with the relation:
o
o
V
V
  (20)
So by gathering Eqs.13,16,19,20 we get:
0.25
oX


 (21)
o
o
o
B


 (22)
3.6. Energy Bands
They are found by calculating the energy difference
between the symmetric points where (Γ25V-Γ1V) deter-
mines the valence band [46,47], (X1C -Γ25V) for indirect
band gap, (Γ15C -Γ25V) for direct band gap [1,33], while
(X5C-X1C) for conduction band [48].
3.7. Valence Charge Density
The electronic charge distribution ρ(r) can be calcu-
lated at any point from the equation:


()rPrr
 

 

(23)
Pμν is the density matrix, and both øμ(r) and øν(r) are the
basis functions.
4. RESULTS AND DISCUSSION
The calculated properties of c-BN at 300 K and 0 GPa
are illustrated in Table 2.
Table 2. The structural and electronic properties of c-BN at
300 K and 0 GPa.
Prop-
erty Pres. Exp. [33] [1] [49] [38][43]
ao (A)3.6192 3.617 [50] 3.6 3.606 3.623 3.633.582
Bo
(GPa) 367.73 368 [50]1132 367 365.3 360392.3
B’o 4.848 3.94 3.763
Ecoh
(eV) 13.21 13.2 [1]8.131 14.3 6.711713.9
DBG
(eV) 23.929 14.5 [51]16.01 8.6
VBW
(eV) 20.121 20.6 [51]21.78 20.3
CBW
(eV) 14.05
η 5.019
υ (m/s)10326.813
Epl (eV)30.5036616722.758 [52] 24.53
[52]
30.55
[40]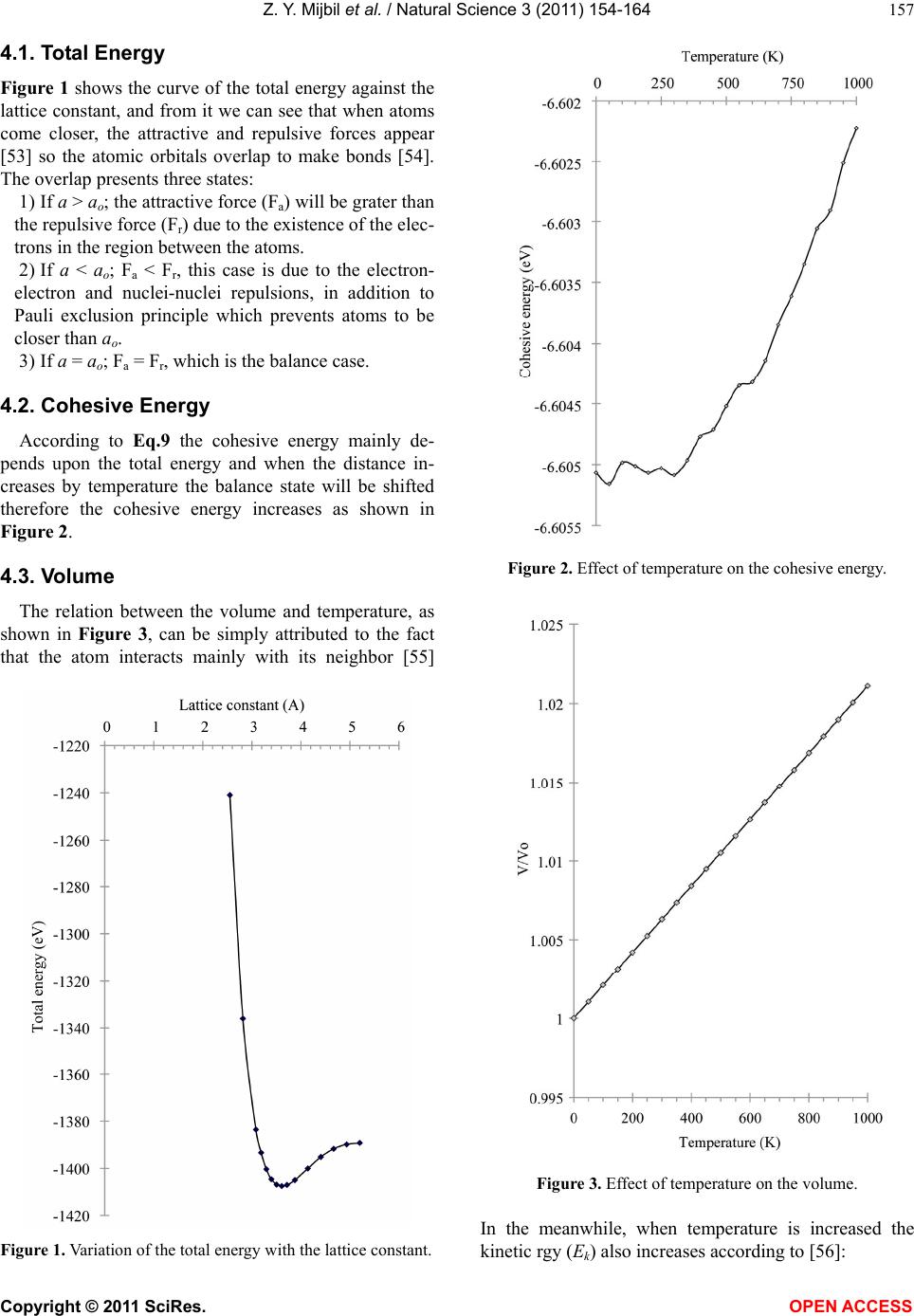

Z. Y. Mijbil et al. / Natural Science 3 (2011) 154-164
157
4.1. Total Energy
Figure 1 shows the curve of the total energy against the
lattice constant, and from it we can see that when atoms
come closer, the attractive and repulsive forces appear
[53] so the atomic orbitals overlap to make bonds [54].
The overlap presents three states:
1) If a > ao; the attractive force (Fa) will be grater than
the repulsive force (Fr) due to the existence of the elec-
trons in the region between the atoms.
2) If a < ao; Fa < Fr, this case is due to the electron-
electron and nuclei-nuclei repulsions, in addition to
Pauli exclusion principle which prevents atoms to be
closer than ao.
3) If a = ao; Fa = Fr, which is the balance case.
4.2. Cohesive Energy
According to Eq.9 the cohesive energy mainly de-
pends upon the total energy and when the distance in-
creases by temperature the balance state will be shifted
therefore the cohesive energy increases as shown in
Figure 2.
4.3. Volume
The relation between the volume and temperature, as
shown in Figure 3, can be simply attributed to the fact
that the atom interacts mainly with its neighbor [55]
Figure 1. Variation of the total energy with the lattice constant.
Figure 2. Effect of temperature on the cohesive energy.
Figure 3. Effect of temperature on the volume.
In the meanwhile, when temperature is increased the
kinetic rgy (Ek) also increases according to [56]: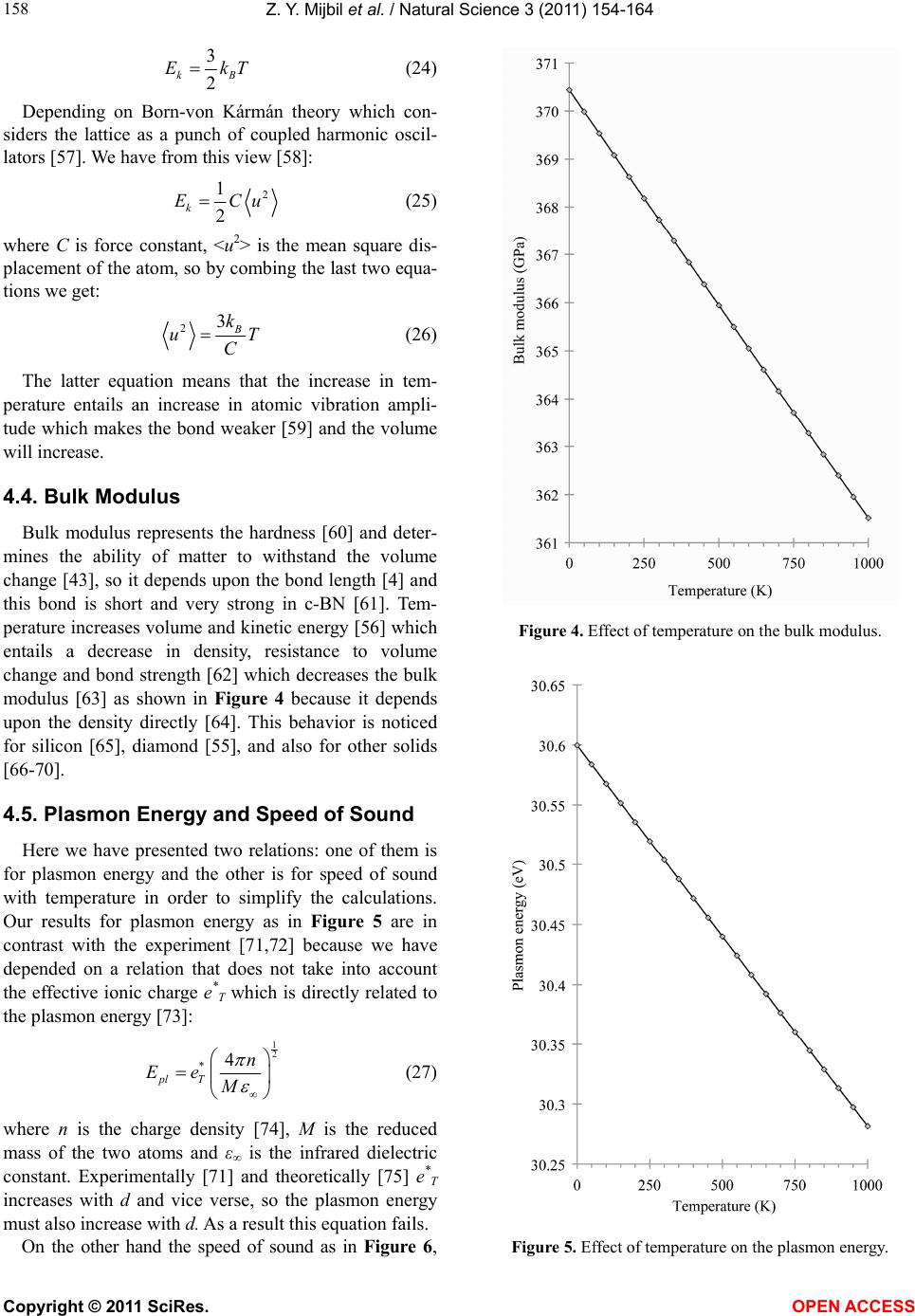

Z. Y. Mijbil et al. / Natural Science 3 (2011) 154-164
158
3
2
kB
EkT (24)
Depending on Born-von Kármán theory which con-
siders the lattice as a punch of coupled harmonic oscil-
lators [57]. We have from this view [58]:
2
1
2
k
ECu (25)
where C is force constant, <u2> is the mean square dis-
placement of the atom, so by combing the last two equa-
tions we get:
23B
k
uT
C
 (26)
The latter equation means that the increase in tem-
perature entails an increase in atomic vibration ampli-
tude which makes the bond weaker [59] and the volume
will increase.
4.4. Bulk Modulus
Bulk modulus represents the hardness [60] and deter-
mines the ability of matter to withstand the volume
change [43], so it depends upon the bond length [4] and
this bond is short and very strong in c-BN [61]. Tem-
perature increases volume and kinetic energy [56] which
entails a decrease in density, resistance to volume
change and bond strength [62] which decreases the bulk
modulus [63] as shown in Figure 4 because it depends
upon the density directly [64]. This behavior is noticed
for silicon [65], diamond [55], and also for other solids
[66-70].
4.5. Plasmon Energy and Speed of Sound
Here we have presented two relations: one of them is
for plasmon energy and the other is for speed of sound
with temperature in order to simplify the calculations.
Our results for plasmon energy as in Figure 5 are in
contrast with the experiment [71,72] because we have
depended on a relation that does not take into account
the effective ionic charge e*
T which is directly related to
the plasmon energy [73]:
1
2
*4
pl T
n
Ee
M






(27)
where n is the charge density [74], M is the reduced
mass of the two atoms and ε∞ is the infrared dielectric
constant. Experimentally [71] and theoretically [75] e*
T
increases with d and vice verse, so the plasmon energy
must also increase with d. As a result this equation fails.
On the other hand the speed of sound as in Figure 6,
Figure 4. Effect of temperature on the bulk modulus.
Figure 5. Effect of temperature on the plasmon energy.

Z. Y. Mijbil et al. / Natural Science 3 (2011) 154-164
159
Figure 6. Effect of temperature on the speed of sound.
which also represents the average of phonon velocity [76]
and is related to the average energy of phonon Ēph by Eq.
28, behaves consistently with other experimental calcu-
lations [71] for III-V compounds and theoretical calcula-
tions for InP [44,72], Si and Diamond [77]
1
3
6
ph
N
EV





 (28)
4.6. Energy Bands
The energy bands show the following points:
1) The value of direct band gap is greater than the ex-
perimental value as shown in Table 3. This behavior is
also noticed in most calculations that use Hartree-Fock
method [78-80] due to its approximations which are:
• The minimal basis sets include (s and p) orbitals
only, these orbitals determine the valence and the
conduction band accurately, while the outer orbi-
tals that have not been taken into account decrease
the value of the band gap [81].
• We have not considered the correlation corrections
which decrease the value of the indirect band gap
[79].
• Both s and p orbitals are given the same value of ξ
and β and the latter parameter determines the bon-
ding and the antibonding states.
• Neglecting of core states which affect the outer va-
lence electrons distribution [36].
2) All bands decrease with temperature as shown in
Figures 7 and 8.
Figure 7. Effect of temperature on the direct and indirect band
gaps.
Figure 8. Effect of temperature on valence and conduction
bands.

Z. Y. Mijbil et al. / Natural Science 3 (2011) 154-164
160
Table 3. The symmetry points value with their approximate
structure in (eV).
Points Approximate
structure Pres. [33] Exp. [33]
Γ1V
Nitrogen bonding s
orbitals −20.1218 −21.78 −20.06
Γ1C
Boron antibonding
s orbitals 35.792 16.38
Γ15V
Nitrogen bonding
p orbitals 0 0 0
Γ15C
Boron antibonding
p orbitals 23.932 16.06 8.19
X1V
Nitrogen bonding s
orbitals −13.0319 −10.88
X1C
Boron antibonding
s orbitals 21.951 12.34 6
Symmetric points are a combination of atomic orbitals
to produce either bonding or antibonding orbitals [82].
Our calculations of the main points with their relativistic
corrections are illustrated in Table 3 and compared with
(Zunger and Freeman) [10] and Ferhat et al. [42] who
both explained the structure of these points.
Valence band is nearly determined by (2s and 2p) ni-
trogen bonding orbitals [82], while the conduction band
is determined by (2s and 2p) boron antibonding orbitals
[79,40]. Therefore, when the difference between these
points increases, the energy bands will be wider. Our
results are consistent with [1,10,83] for c-BN.
The effect of temperature is similar to the effect of
tension pressure but it is thermal [84], while it directly
affects the band gaps [85]. Due to the increase in tem-
perature which leads to increase in distance, the orbitals
overlap will be decreased and the repulsion will also
decrease, and the energy difference between bonding
and antibonding states will be decreased accordingly.
This means that the widths become narrower. Our results
are consistent with Pässler’s results for semicoductors
[86], and with measurements for band gab as reported by
Olguín et al. [87] and Fan [88].
4.7. Valence Charge Distribution
First of all we need to mention the approximations
used in CNDO method because this kind of results is
sensitive to them, and they are:
1) Zero differential overlap which neglects the repul-
sion integrals and the electron-electron overlap on the
same atom, and these change the Coulomb potentials
that affect the distribution [89].
2) The values of EES and EEP are very high, “two of
the semiempirical method parameters used to get the
results”, and both of them represent the electronigativ-
ity of the atom and determine the bond polarity [90].
3) Correlation corrections have not been taken into
account.
Figures 9-11 and the high anharmonicity parameter (η)
[91] in Table 2 show that the density of the charge is
higher around nitrogen’s atoms than boron’s atoms, be-
cause the electrons can stay near one of them more than
the another which leads to transfer of charge which is
called charge transfer factor (ci). This dimensionless
parameter reflects the ability of atom to lose electrons
either for another atom or for the intratomic distance.
(a) (b)
Figure 9. Valence charge distribution of the plane (110): a - at (0K) and b - at (1000K).

Z. Y. Mijbil et al. / Natural Science 3 (2011) 154-164
161
(a) (b)
Figure 10. Valence charge distribution of the plane (001): a - at (0K) and b - at (1000K).
(a) (b)
Figure 11. Valence charge distribution of the plane (400): a - at (0K) and b - at (1000K).
This case is obvious in polar compounds such as c-BN
which has (ci = 0.8) [92]. On the other hand, nitrogen
pulls the electrons from boron [93] due to its high elec-
tronigativity with respect to boron [94], but as tempera-
ture increases the atoms try to separate and return to
their original state, as free atoms [95].
5. CONCLUSIONS
1) TB-LUC-CNDO/2 method is preferred for wide
range of calculations such as the lattice constant,
cohesive energy and valence band etc..
2) In this method the energy bands can not be accu-
rately calculated all together.
3) The correlation corrections have remarkable ef-
fects upon the band gaps’ width and charge distri-
bution.
4) The c-BN tends to be more conductive with tem-
perature increase.
5) Even with high temperature, c-BN can withstand
corrosions and abrasives.
6) The infrared absorption of c-BN increases with the
increase of temperature.

Z. Y. Mijbil et al. / Natural Science 3 (2011) 154-164
162
REFERENCES
[1] Wentzcovitch, R.M., Chang, K.J. and Cohen, M.L. (1986)
Physical Review B, 34, 1071-1079.
doi:10.1103/PhysRevB.34.1071
[2] Sun, H., Jhi, S.H., Roundy, D., Cohen, M.L., Louie, S.G.
(2001) Physical Review B, 64, 094108/1-6.
[3] Kádas, K., Kern, G. and Hafner, J. (2000) Surface Sci-
ence, 494-497. doi:10.1016/S0039-6028(00)00254-5
[4] Mattesini, M. and Matar, S.F. (2001) Computational
Materials Science, 20, 107-119.
doi:10.1016/S0927-0256(00)00132-4
[5] Major, B., Mróz, W., Jelinek, M., Kosydar, R., Kot, M.,
Major, Ł., Burdyńska, S. and Kustosz, R. (2006) Bulletin
of the Polish Academy of Sciences: Technical Sciences,
54, pp. 181-188.
[6] Knittle, E., Kaner, R.B. Jeanloz, R. and Cohen, M. L.
(1995) Physical Review B, 51, 12149-12156.
doi:10.1103/PhysRevB.51.12149
[7] Lambrecht, W.R.L. and Segall, B. (1989) Physical Re-
view B, 40, 9909-9919.
[8] Watanabe, S., Wheeler, D.R., Abel, P.B., Murakawa, M.
and Miyake, S. (1998) Surface chemistry, microstructure,
and tribological properties of cubic boron nitride films.
NASA Lewis Research Center.
[9] Mãrlid, B. (2001) Theoretical modling of thin film
growth in the B-N system. Acta Universitais.
[10] Zunger, A. and Freeman, A.J. (1978) Physical Review B,
17, 2030-2042. doi:10.1103/PhysRevB.17.2030
[11] Meng, Y., Mao, H., Eng, P.J., Trainor, T.P., Newville, M.,
Hu, M.Y., Kao, C., Shu, J., Hausermann, D. and Hemley,
R. J. (2004) Nature Materials, 3, 111-114.
doi:10.1038/nmat1060
[12] Karlsson, J. and Larsson, K. (2010) Journal of Physical
Chemistry C, 114, 3516-3521. doi:10.1021/jp907186a
[13] Horiuchi, S., Huang, J.Y., He, L.L., Mao, J.F. (1998)
Philosophical Magazine A, 78, 1065-1072.
doi:10.1080/01418619808239974
[14] Huang, J.Y. and Zhu, Y.T. (2002) Chemistry of Materials,
14, 1873-1878. doi:10.1021/cm0109645
[15] Hang-Sheng, Y., Fa-Min, Q. and An-Min, N. (2010)
Journal of Inorganic Materials, 25, 748-752.
doi:10.3724/SP.J.1077.2010.00748
[16] Khavryuchenko, O.V., Alekseev, S.A., Beobide, A.S.,
Kandilioti, G., Voyiatzis, G.A., Lisnyak, V.V. (2010) The
Journal of Physical Chemistry C, 114, 1102-1109.
doi:10.1021/jp908711x
[17] Zhao, Y. and Wang, M. (2009) Journal of Materials
Processing Technology, 209, 355-359.
doi:10.1016/j.jmatprotec.2008.02.005
[18] Yallese, M.A., Chaoui, K., Zeghib, N., Boulanouar, L.,
Rigal, J.F., (2009) Journal of Materials Processing
Technology, 209, 1092-1104.
doi:10.1016/j.jmatprotec.2008.03.014
[19] Wentorf, R.H., Jr. (1962) Journal of Chemical Physics,
34, 809-812. doi:10.1063/1.1731679
[20] Harker, A.H. and Larkins, F.P. (1979) Journal of Physics
C: Solid State Physics, 12, 2487-2495.
doi:10.1088/0022-3719/12/13/013
[21] Pople, J.A. and Beveridge, D.L. (1970) Approximate
molecular orbital theory. McGraw-Hill.
[22] Harker, A.H. and Larkins, F.P. (1979) Journal of Physics
C: Solid State Physics, 12, 2497-2507.
doi:10.1088/0022-3719/12/13/014
[23] Freund, H. and Hohlneicher, G. (1979) Theoretica
chimica acta, 51, 145-162. doi:10.1007/BF00554098
[24] Schmid, E. and Brodbe, E. (1985) Canadian Journal of
Chemistry, 63, 1365-1371. doi:10.1139/v85-233
[25] Vogl, P., Hjalmarsons, H.P. and Dow, J.d. (1983) Journal
of Physics and Chemistry of Solids, 44, 365-378.
doi:10.1016/0022-3697(83)90064-1
[26] Slater, J.C. and Koster, G.F. (1954) Physical Review, 94,
1498-1529. doi:10.1103/PhysRev.94.1498
[27] Pople, J.A. Santry, D.P. and Segal, G.A. (1965) Journal of
Chemical Physics, 43, 129-S135. doi:10.1063/1.1701475
[28] Bredow, T., Evarestov, R.A. and Jug, K. (2000) Physica
Status Solidi B, 222, 495-514.
doi:10.1002/1521-3951(200011)222:2<495::AID-PSSB4
95>3.0.CO;2-5
[29] Rogan, J. and Lagos, M. (2001) Philosophical Magazine
B, 81, 551-559. doi:10.1080/13642810108225450
[30] Chadi, D.J. and Cohen, M.L. (1973) Physical Review B,
8, 5747-5753. doi:10.1103/PhysRevB.8.5747
[31] Janesko, B.G. and Yaron, D. (2004) Journal of Chemical
Physics, 121, 5635-5645. doi:10.1063/1.1785771
[32] Daudal, R., Leroy, G., Peeters, D. and Sana, M. (1983)
Quantum chemistry. John Wiley and Sons.
[33] Hassan, I.Z. (2001) Semiempirical self-consistent field
calculations of III-V zinc-blende semiconductors. Ph. D.
thesis. University of Al-Nahrain.
[34] Murnaghan, F.D. (1944) Proceedings of the National
Academy of Science, 30, 244. doi:10.1073/pnas.30.9.244
[35] Zheng, J.C., Huan, C.H.A., Wee, A.T.S., Wang, R.Z. and
Zheng, Y.M. (1999) Journal of Physics: Condensed Mat-
ter, 11, 927-935. doi:10.1088/0953-8984/11/3/030
[36] Abdulsattar, M.A. (1997) Self consistent field calcula-
tions of covalent semiconductors. Ph.D. Thesis, Univer-
sity of Baghdad.
[37] Allen, C. (1976) Astrophysical quantities. Athlone Press.
[38] Lee, S.H., Kang, J.H. and Kang, M.H.J. (1997) The Ko-
rean Physical Society, 31, 811-814.
[39] Omer, M.S. (2007) Materials Research Bulletin, 42,
319-326. doi:10.1016/j.materresbull.2006.05.031
[40] Kumar, V. and Sastry, B.S.R. (2001) Crystal Research
and Technology, 36, 565-569.
doi:10.1002/1521-4079(200107)36:6<565::AID-CRAT5
65>3.0.CO;2-F
[41] Lam, P.K., Cohen, M.L. and Martinez, G. (1987) Physi-
cal Review B, 35, 9190-9194.
doi:10.1103/PhysRevB.35.9190
[42] Ferhat, M., Bouhafs, B., Zaoui, A. and Aourag, H. (1998)
Journal of Physics: Condensed Matter, 10, 7995-8006.
doi:10.1088/0953-8984/10/36/010
[43] Wang, S.Q. and Ye, H.Q. (2002) Physical Review B, 66,
235111/1-7.
[44] Schlosser, H. and Ferrante, J. (1988) Physical Review B,
Condensed Matter, 37, 4351-4357.
[45] Soma, T., Sawaoka, S. and Saito, S. (1974) Materials
Research Bulletin, 9, 755.
doi:10.1016/0025-5408(74)90110-X
[46] Calzaferri, G. and Rytz, R. (1996) Journal of Physical
Chemistry, 100, 11122-11124. doi:10.1021/jp960840t
[47] Levitas, V.I. and Shvedov, L.K. (2002) Physical Review

Z. Y. Mijbil et al. / Natural Science 3 (2011) 154-164
163
B, 65, 104109/1-6.
[48] Merdan, M.G. (2005) Self-consistent field calculations of
the effect of pressure and temperature on some properties
of grey tin crystal. Master’s Thesis, Babylon University.
[49] Sekkal, W., Bouhaf, B., Aourag, H. and Certier, M. (1998)
Journal of Physics: Condensed Matter, 10, 4975-4984.
doi:10.1021/jp960840t
[50] Mujica, A., Rubio, A., Munoz, A. and Need, R.J. (2003)
Reviews of Modern Physics, 75, 863.
doi:10.1103/RevModPhys.75.863
[51] Jayawardane, D.N., Pickard, C.J., Brown, L.M. and
Payne, M.C. (2001) Physical Review B, 64, 11517/1-4.
[52] Reddy, R.R., Ahammed, Y.N., Abdul Azeem, P., Gopal,
K.R., Devi, B.S. and Rao, T.V.R. (2003) Defence Science
Journal, 53, 239-248.
[53] Murrel, J.N., Kettle, S.F.A. and Tedder, J.M. (1982) The
chemical bond. 2nd Edition, Translated to Arabic by M.
N. Al-Zakum, University of Basrah.
[54] Ladd, M.F.C. (1983) Structure and bonding in solid state
chemistry. Translated to Arabic by I. J. Selomi, Univer-
sity of Mosul.
[55] Adamska, C.M., Sloma, P. and Tomaszeewski, J. (2006)
Journal of Physics: Condensed Matter, 18, 751-758.
doi:10.1088/0953-8984/18/2/028
[56] Sibona, G.J. Schreiber, S., Hoppe, R.H.W., Strizker, B.
and Revńic, A. (2003) Materials Science in Semicon-
ductor Processing, 6, 71-76.
doi:10.1016/S1369-8001(03)00073-8
[57] Phillips, J.C. (1956) Physical Review, 104, 1263-1277.
[58] Kittel, C. (1996) Introduction to solid state physics. 7th
Edition, John Wiley and Sons.
doi:10.1103/PhysRev.104.1263
[59] Glazov, V.M. and Shchelikov, O.D. (1998) Semiconduc-
tor Equipment and Materials International, 32, 382-384.
[60] Olguín, D., Cantarero, A., Ulrich, C. and Syassen, K.
(2003) Physica Status Solidi B, 235, 456-463.
doi:10.1002/pssb.200301602
[61] Audronis, M., Valiulis, A.V. and Silickas, P. (2004) Jour-
nal of Materials Science, 10, 152-156.
[62] Jiang, J.Z., Lindelov, H., Gerward, L., Ståhl, K., Recio, J.
M., Mori-Sanchez, P., Carlson, S., Mezouar, M., Doory-
hee, E., Fitch, A. and Frost, D.J. (2002) Physical Review
B, 65, 161202/1-4.
[63] D’Evelyn, M.P. and Taniguchi, T. (1998) Elastic proper-
ties of translucent polycrystalline cubic boron nitride as
characterized by the dynamic resonance method. GE Re-
search & Development Center, General Electric Com-
pany.
[64] Wang, B.T., Zhang, P., Shi, H.L., Sun, B. and Li, W.D.
(2010) The European Physical Journal B, 74, 303-308.
doi:10.1140/epjb/e2010-00081-x
[65] Hung, V.V., Jindo, K.M. and Haun, P.T.M. (2006) Jour-
nal of Physics: Condensed Matter, 18, 283-293.
doi:10.1088/0953-8984/18/1/021
[66] Mijbil, Z.Y. (2011) Journal of Bab. University, 19, Under
Publishing.
[67] Garai, J. and Laugier, A. (2007) Journal of Applied
Physics, 101, 023514/1-4.
[68] Anderson, O.L. (1966) Physical Review, 144, 553-557.
doi:10.1103/PhysRev.144.553
[69] Nandanpawar, M.L. and Rajagopalan, S. (1978) Journal
of Applied Physics, 49, 3976-3979.
doi:10.1063/1.325408
[70] Wachtman, J.B. Jr., Tefft, W.E., Lam, D.G., Jr., and Ap-
stein, C.S. (1961) Physical Review, 122, 1754-1759.
doi:10.1103/PhysRev.122.1754
[71] Sanjurjo, J.A., López-Cruz, E., Vogl, P. and Cardona, M.
(1983) Physical Review B, 28, 4579-4584.
doi:10.1103/PhysRevB.28.4579
[72] Trommer, R., Müller, H., Cardona, M. and Vogl, P. (1980)
Physical Review B, 21, 4869-4878.
doi:10.1103/PhysRevB.21.4869
[73] Burstein, E., Perkowitz, S. and Brodsky, M.H. (1968)
Journal de Physique, 29, C4/78-83.
[74] Miranda, L.C.M. and Haar, ter D. (1972) Revista Bra-
sileira de Ensino de Física, 2, 77-86.
[75] Molinàs-Mata, P.A., Shields, J. and Cardona, M. (1993)
Physical Review B, 47, 1866-1875.
doi:10.1103/PhysRevB.47.1866
[76] Raj, G.D. (2004) Solid state physics. 1st Edition, Anmol
Pub. Pvt. Ltd..
[77] Xu, C.H., Wang, C.Z., Chan, C.T. and Ho, K.M. (1991)
Physical Review B, 43, 5024-5027.
doi:10.1103/PhysRevB.43.5024
[78] Kleinman, L. and Phillips, J.C. (1960) Physical Review,
117, 460-464. doi:10.1103/PhysRev.117.460
[79] Yang, D., Su, Z., Du, Y., Ji, X., Yang, X., Gong, X. and
Zhang, T. (2006) Chinese Physics Letters, 23, 1324-
1326. doi:10.1088/0256-307X/23/5/072
[80] Dovesi, R., Pisani, C., Roetti, C. and Dellarole, P. (1981)
Physical Review B, 24, 4170-4176.
doi:10.1103/PhysRevB.24.4170
[81] Chadi, D.J. (1977) Physical Review B, 16, 3572-3578.
doi:10.1103/PhysRevB.16.3572
[82] Mori, Y., Ikai, T., Teranishi, R. and Takarabe, K. (2003)
Physica Status Solidi B, 235, 302-306.
doi:10.1002/pssb.200301573
[83] Kim, K., Lambrecht, W.R.L. and Segall, B. (1996)
Physical Review B, 53, 16310-16326.
doi:10.1103/PhysRevB.53.16310
[84] Jain, S.C., Willander, M. and Maes, H. (1996) Semicon-
ductor Science and Technology, 11, 641-671.
doi:10.1088/0268-1242/11/5/004
[85] Vurgaftmana, I., Meyer, J.R. and Mohan, L.R.R. (2001)
Journal of Applied Physics, 89, 5815-5875.
doi:10.1063/1.1368156
[86] Pässler, R. (1999) Physica Status Solidi B, 216, 975-1007.
doi:10.1002/(SICI)1521-3951(199912)216:2<975::AID-
PSSB975>3.0.CO;2-N
[87] Olguín, D., Cantarero, A. and Cardona, M. (2000)
Physica Status Solidi B, 220, 33-39.
doi:10.1002/1521-3951(200007)220:1<33::AID-PSSB33
>3.0.CO;2-J
[88] Fan, H.Y. (1951) Physical Review, 82, 900-905.
doi:10.1103/PhysRev.82.900
[89] Raczkowski, D., Canning, A. and Wang, L.W. (2001)
Physical Review B, 46, 121101/1-4.
[90] Cotton, F.A. and Wilkinson, G. (1976) Basic inorganic
chemistry. John Wiley & Sons.
[91] Rose, J., Smith, J.R., Guinea, F. and Ferrante, J. (1984)
Physical Review B, 29, 2963-2969.
doi:10.1103/PhysRevB.29.2963
[92] Sánchez, P.M., Pendás, A.M. and Luaña, V. (2002) Jour-
nal of the American Chemical Society, 124, 14721-

Z. Y. Mijbil et al. / Natural Science 3 (2011) 154-164
164
14723. doi:10.1021/ja027708t
[93] Bouhafs, B., Aourag, H. and Certier, M. (2000) Journal
of Physics: Condensed Matter, 12, 5655-5668.
doi:10.1088/0953-8984/12/26/312
[94] Wu, R.Q., Peng, G.W., Lui, L. and Feng, Y.P. (2006)
Journal of Physics: Condensed Matter, 18, 569-575.
doi:10.1088/0953-8984/18/2/015
[95] Al-Jelawy, I.O.R. (2005) Effect of pressure and tempera-
ture on some properties of diamond crystal using har-
tree-fock method. Master Thesis, University of Babylon.