 Vol.3, No.2, 145-153 (2011) Natural Science http://dx.doi.org/10.4236/ns.2011.32021 Copyright © 2011 SciRes. OPEN ACCESS Two solutions for the BVP of a rotating variable-thickness solid disk Ashraf M. Zenkour1,2, Suzan A. Al-Ahmadi1 1Department of Mathematics, Faculty of Science, King AbdulAziz University, Jeddah, Saudi Arabia; Coresponding Author: zenkour@kau.edu.sa 2Department of Mathematics, Faculty of Science, Kafr El-Sheikh University, Kafr El-Sheikh, Egypt; zenkour@sci.kfs.edu.eg Received 23 November 2010; revised 25 December 2010; accepted 28 December 2010. ABSTRACT This paper presents the analytical and numeri- cal solutions for a rotating variable-thickness solid disk. The outer edge of the solid disk is considered to have free boundary conditions. The governing equation is derived from the ba- sic equations of the rotating solid disk and it is solved analytically or numerically using finite difference algorithm. Both analytical and nu- merical results for the distributions of stress function and stresses of variable-thickness solid disks are obtained. Finally, the distributions of stress function and stresses are presented and the appropriate comparisons and discussions are made at the same angular velocity. Keywords: Rotating, Solid Disk, Variable Thickness, Analytical Method, Finite Difference Method 1. INTRODUCTION The theoretical and experimental investigations on the rotating solid disks have been widespread attention due to the great practical importance in mechanical engi- neering. Rotating disks have received a great deal of attention because of their widely used in many me- chanical and electronic devices. They have extensive practical engineering application such as in steam and gas turbines, turbo generators, flywheel of internal com- bustion engines, turbojet engines, reciprocating engines, centrifugal compressors and brake disks. The problems of rotating solid disks have been performed under vari- ous interesting assumptions and the topic can be easily found in most of the standard elasticity books [1,2]. For a better utilization of the material, it is necessary to al- low variation of the effective material or thickness prop- erties in one direction of the solid disk. The problems of rotating variable-thickness solid disks are rare in the literature. Most of the research works are concentrated on the analytical solutions of rotating iso- tropic disks with simple cross-section geometries of uniform thickness and specifically variable thickness. The solution of a rotating solid disk with constant thick- ness is obtained by Gamer [3,4] taking into account the linear strain hardening material behavior. The inelastic and viscoelastic deformations of rotating variable- thickness solid disks have been presented in the litera- ture [5-8]. Eraslan [5], and Eraslan and Orcan [6] have analytically studied rotating disks of exponentially varying thickness and of linearly strain hardening mate- rial. Eraslan [7] has presented the stress distributions in elastic-plastic rotating disks with elliptical thickness pro- files using Tresca and von Mises criteria. Zenkour and Allam [8] have developed analytical solution for the analysis of deformation and stresses in elastic rotating viscoelastic solid and annular disks with arbitrary cross- sections of continuously variable thickness. As many rotating components in use have complex cross-sectional geometries, they cannot be dealt with using the existing analytical methods. Numerical meth- ods, such as the finite element method [9], the boundary element method [10] and Runge-Kutta’s algorithm [11], can be applied to cope with these rotating components. You et al. [11] have numerically studied rotating solid disks of uniform thickness and constant density as well as annular disks of variable thickness and variable den- sity. In a recent paper, Zenkour and Mashat [12] have presented both analytical and numerical solutions for the analysis of deformation and stresses in elastic rotating disks with arbitrary cross-sections of continuously vari- able thickness. In this article, a unified governing equation is firstly derived from the basic equations of the rotating variable- thickness solid disk and the proposed stress-strain rela- tionship. The analytical solution for rotating solid disk with arbitrary cross-section of continuously variable thickness is presented. Next, the finite difference method  A. M. Zenkour et al. / Natural Science 3 (2011) 145-153 Copyright © 2011 SciRes. OPEN ACCESS 146 (FDM) is also introduced to solve the governing equa- tion. A comparison between both analytical and numeri- cal solutions is made. Finally, a number of application examples are given to demonstrate the validity of the proposed method. 2. BASIC EQUATIONS As the effect of thickness variation of rotating solid disks can be taken into account in their equation of mo- tion, the theory of the variable-thickness solid disks can give good results as that of uniform-thickness disks as long as they meet the assumption of plane stress. The present solid disk is considered as a single layer of vari- able thickness. After considering this effect, the equation of motion of rotating disks with variable thickness can be written as 22 d0, dr hrhh r r (1) where r and are the radial and circumferential stresses, h is the variable thickness of the disk, r is the radial coordinate, is the material density of the ro- tating solid disk and is the constant angular velocity. The relations between the radial displacement u and the strain components are irrespective of the thickness of the rotating solid disk. They can be written as d,, d r uu rr (2) where r and are the radial and circumferential strains, respectively. The above geometric relations lead to the following condition of deformation harmony: d0. dr r r (3) For the elastic deformation, the constitutive equations for the variable-thickness solid disk can be described with Hooke’s law ,, rr rEE (4) where E is Young’s modulus and is Poisson’s ratio. Introducing the stress function and assuming that the following relations hold between the stresses and the stress function 22 1d ,. d rr hrh r (5) Substituting Eq.5 into Eq.4 , one obtains 22 22 11 d, d 11d . d rr Ehrhr r Ehrhr (6) 3. FORMULATION AND ANALYTIC ELASTIC SOLUTION The substitution of Eq.6 into Eq.3 produces the fol- lowing confluent hypergeometric differential equation for the stress function ():r 2 2 2 23 ddd 1dd d d 13 0. d rh rr hr r r rh hr hr (7) The boundary conditions for the rotating solid disk are at 0, 0at . r r r rb (8) The thickness of the solid disk is assumed to vary nonlinearly through the radial direction. It is assumed to be in terms of a simple exponential power law distribu- tion according to the following case: 0e, k r nb hrh (9) where 0 h is the thickness at the middle of the disk, n and k are geometric parameters and b is the outer radius of the disk (see Figure 1). The value of n equal to zero represents a uniform-thickness solid disk while the value of k equal to unity represents a linearly decreasing vari- able-thickness solid disk. For small k and large n (k = 0.7 or 1.5 and n = 2) the profile of the solid disk is concave while it is convex for large k and small n (k = 2.5 and n = 0.5). It is to be noted that the parameter n determines the thickness at the outer edge of the solid disk relative to 0 h while the parameter k determine the shape of the profile. Introducing the following dimensionless forms: 2 0 12 2 12 2 / 3, 1, ,,, 1 ,,. r r Rrb b Rr bh E (10) Then, Eq.7 may be written in the following simple form 2 2 3 2 dd 11e0. d d k kknR RknRRknRR R R (11) The general solution of the above equation can be 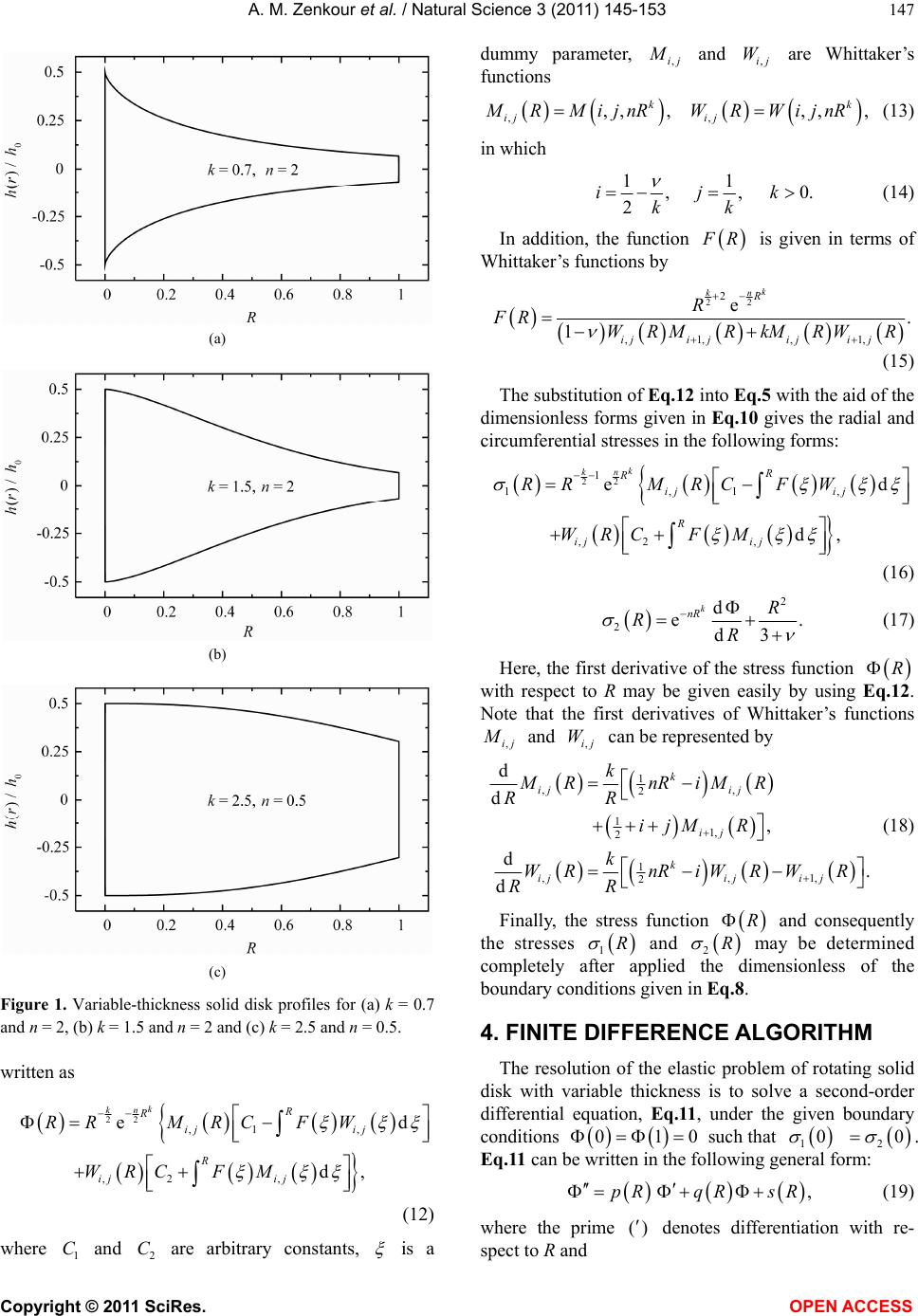 A. M. Zenkour et al. / Natural Science 3 (2011) 145-153 Copyright © 2011 SciRes. OPEN ACCESS 147 (a) (b) (c) Figure 1. Variable-thickness solid disk profiles for (a) k = 0.7 and n = 2, (b) k = 1.5 and n = 2 and (c) k = 2.5 and n = 0.5. written as 22 ,1 , ,2 , ed d, k kn R R ij ij R ij ij RRMRC FW WRCF M (12) where 1 C and 2 C are arbitrary constants, is a dummy parameter, ,ij and ,ij W are Whittaker’s functions ,, ,, ,,, , kk ij ij MRMijnRWRWijnR (13) in which 11 ,,0. 2 ijk kk (14) In addition, the function R is given in terms of Whittaker’s functions by 22 2 ,1,,1, e. 1 k kn R ijijij ij R FR WRMRkM RWR (15) The substitution of Eq.12 into Eq.5 with the aid of the dimensionless forms given in Eq.10 gives the radial and circumferential stresses in the following forms: 22 1 1,1, ,2 , ed d, k kn R R ijij R ijij RRMRC FW WRCFM (16) 2 2 d e. d3 k nR R RR (17) Here, the first derivative of the stress function R with respect to R may be given easily by using Eq.12. Note that the first derivatives of Whittaker’s functions ,ij and ,ij W can be represented by 1 ,, 2 1 1, 2 1 ,,1, 2 d d , d. d k ij ij ij k ijiji j k MR nRiMR RR ijM R k WRnRiWRWR RR (18) Finally, the stress function R and consequently the stresses 1R and 2R may be determined completely after applied the dimensionless of the boundary conditions given in Eq.8. 4. FINITE DIFFERENCE ALGORITHM The resolution of the elastic problem of rotating solid disk with variable thickness is to solve a second-order differential equation, Eq.11, under the given boundary conditions 010 such that 10 20 . Eq.11 can be written in the following general form: ,pRqR sR (19) where the prime () denotes differentiation with re- spect to R and  A. M. Zenkour et al. / Natural Science 3 (2011) 145-153 Copyright © 2011 SciRes. OPEN ACCESS 148 2 1, 1, e. k k k nR knR pR R kn R qR R sR R (20) It is clear that the above problem has a unique solution because ,,pRqR and R are continuous on [0,1] and 0qR on [0,1]. The linear second-order boundary value problem given in Eq.19 requires that difference-quotient approximations be used for ap- proximating and . First we select an integer 0N and divided the interval [0,1] into 1N equal subintervals, whose end points are the mesh points , i RiR for 0,1,..., 1,iN where 1/ 1RN . At the interior mesh points, , i R 1, 2,...,,iN the dif- ferential equation to the approximated is . iiiiii RpRRqR RsR (21) If we apply the centered difference approximations of i R and i R to Eq.21, we arrive at the system (see Eq.22): for each 1, 2,...,.iN The N equations, together with the boundary conditions 0 1 0, 0, N (23) are sufficient to determine the unknowns , i 0,1, 2,...,1iN . The resulting system of Eq.22 is ex- presses in the tri-diagonal NN -matrix form: , B (24) where 2 , ,1 ,1 ,, 2 2()(),1,2,...,, 1(),1, 2,...,1, 2 1(),2,3,..., , 2 0,1, 2,...,2,3, 4,...,,2, ()(),1,2,...,. ii i ii i ii i ij ji ii ARqRiN R ApRiN R ApRiN AAiN jNji BRsRiN (25) The solution of the finite difference discretization of the two-point linear boundary value problem can there- fore be found easily even for very small mesh sizes. 5. NUMERICAL EXAMPLES AND DISCUSSION Some numerical examples for the rotating variable- thickness solid disks will be given according the ana- lytical and numerical solutions 0.3 . According to Eq.10, the stress function , the radial stress 1 and the circumferential stress 2 determined as per the analytical solution are compared with those obtained by the numerical FDM solution. The results of the present investigations for the stress function are reported in Table 1 for rotating vari- able-thickness solid disk with k = 2.5 and n = 0.5. For this example, N = 9, 19, 39 and 79, so R has the cor- responding values 0.1, 0.05, 0.025 and 0.0125, respec- tively. The FDM gives results compared well with the exact solution, especially for small values of R . The relative error between the exact method and the FDM with 0.0125,R may be less than 4 1.3 10 . Richardson’s extrapolation method is applied here with 0.1,0.05,0.025,R and 0.0125 and the obtained results are listed in Table 2. These extrapolations are given, respectively by 1 4 0.050.1 Ext , 3 ii i RR (26a) 2 4 0.0250.05 Ext , 3 ii i RR (26b) 3 4 0.01250.025 Ext , 3 ii i RR (26c) 21 4 16 ExtExt Ext , 15 ii i (26d) Table 2 shows that all extrapolations results are cor- rect to the decimal places listed. In fact, if sufficient dig- its are maintained, the approximation of 4 Ext i gives results those agree with the exact solution with maxi- mum difference error of 9 1.0 10 at some of the mesh points. Additional results for the stress function are reported for rotating variable-thickness solid disk with k = 0.7 and n = 2 in Table 3 and with k = 1.5 and n = 2 in Table 4. Once again, the FDM gives results compared well with the exact analytical solution, especially for small values of R . Now the least square method and curve fitting are used for the discrete results of the stress function . So, one can get easily the radial and circumferential stresses 22 11 12 1, 22 iiii iii RR pRR qRpRR sR (22)  A. M. Zenkour et al. / Natural Science 3 (2011) 145-153 Copyright © 2011 SciRes. OPEN ACCESS 149 Table 1. Dimensionless stress function of a rotating variable-thickness solid disk (k = 2.5, n = 0.5). FDM i 0.1R 0.05R 0.025R 0.0125R Analytical 0 0 0 0 0 0 0.0125 0.0250 0.0375 0.0500 0.0625 0.0750 0.0875 0.1000 --- --- --- --- --- --- --- 0.010333909 --- --- --- 0.005341761 --- --- --- 0.010398523 --- 0.002632275 --- 0.005253982 --- 0.007852303 --- 0.010414946 0.001317819 0.002634312 0.003947918 0.005270818 0.006560297 0.007856045 0.009142869 0.010419072 0.001318247 0.002635012 0.003948803 0.005258119 0.006561453 0.007857295 0.009144132 0.010420449 0.1125 0.1250 0.1375 0.1500 0.1625 0.1750 0.1875 0.2000 --- --- --- --- --- --- --- 0.019984044 --- --- --- 0.015367662 --- --- --- 0.020049282 --- 0.012929711 --- 0.015384444 --- 0.017767073 --- 0.020065635 0.011683316 0.012934026 0.014169696 0.015388799 0.016589850 0.017771346 0.018931799 0.020069727 0.011684731 0.012935466 0.014171142 0.015390252 0.016591293 0.017772771 0.018933196 0.020071091 0.2125 0.2250 0.2375 0.2500 0.2625 0.2750 0.2875 0.3000 --- --- --- --- --- --- --- 0.028132394 --- --- --- 0.024349525 --- --- --- 0.028175489 --- 0.022268320 --- 0.024363514 --- 0.026339842 --- 0.028186218 0.021183663 0.022272149 0.023333741 0.024367011 0.025370546 0.026342953 0.027282855 0.028188899 0.021184986 0.022273424 0.023334964 0.024368176 0.025371649 0.026343989 0.027283820 0.028189791 0.3125 0.3250 0.3375 0.3500 0.3625 0.3750 0.3875 0.4000 --- --- --- --- --- --- --- 0.034048816 --- --- --- 0.031439588 --- --- --- 0.034060453 --- 0.029891894 --- 0.031446504 --- 0.032840118 --- 0.034063288 0.029059753 0.029894109 0.030690687 0.031448230 0.032165512 0.032841338 0.033474542 0.034063994 0.029060568 0.029894846 0.030691343 0.031448803 0.032166002 0.032841742 0.033474861 0.034064227 0.4125 0.4250 0.4375 0.4500 0.4625 0.4750 0.4875 0.5000 --- --- --- --- --- --- --- 0.037107585 --- --- --- 0.035964469 --- --- --- 0.037087271 --- 0.035107098 --- 0.035963207 --- 0.036623899 --- 0.037082122 0.034608596 0.035107288 0.035559047 0.035962888 0.036317868 0.036623085 0.036877677 0.037080832 0.034608743 0.035107349 0.035559023 0.035962780 0.036317677 0.036622811 0.036877324 0.037080400 0.5125 0.5250 0.5375 0.5500 0.5625 0.5750 0.5875 --- --- --- --- --- --- --- --- --- --- 0.037375156 --- --- --- --- 0.037331532 --- 0.037366529 --- 0.037182291 --- 0.037231777 0.037329791 0.037374198 0.037364369 0.037299729 0.037179570 0.037003958 0.037231269 0.037329209 0.037373544 0.037363648 0.037298942 0.037178902 0.037003051  A. M. Zenkour et al. / Natural Science 3 (2011) 145-153 Copyright © 2011 SciRes. OPEN ACCESS 150 0.6000 0.036832186 0.036786324 0.036774810 0.036771929 0.036770967 0.6125 0.6250 0.6375 0.6500 0.6625 0.6750 0.6875 0.7000 --- --- --- --- --- --- --- 0.032936503 --- --- --- 0.035291940 --- --- --- 0.032876919 --- 0.036140911 --- 0.035278284 --- 0.034185494 --- 0.032862001 0.036483294 0.036137738 0.035734998 0.035274868 0.034757198 0.034181892 0.033548911 0.032858271 0.036482282 0.036136679 0.035733896 0.035273729 0.034756025 0.034180690 0.033547685 0.032857027 0.7125 0.7250 0.7375 0.7500 0.7625 0.7750 0.7875 0.8000 --- --- --- --- --- --- --- 0.025353741 --- --- --- 0.029540441 --- --- --- 0.025296129 --- 0.031308165 --- 0.029525248 --- 0.027515416 --- 0.025281728 0.032110047 0.031304368 0.030441421 0.029521449 0.028544751 0.027511682 0.026422653 0.025278128 0.032108789 0.031303102 0.030440152 0.029520183 0.028543493 0.027510437 0.026421427 0.025276927 0.8125 0.8250 0.8375 0.8500 0.8625 0.8750 0.8875 0.9000 --- --- --- --- --- --- --- 0.014247568 --- --- --- 0.020171897 --- --- --- 0.014209433 --- 0.022828123 --- 0.020159404 --- 0.017281209 --- 0.014199988 0.024078628 0.022824727 0.021517051 0.020156281 0.018743148 0.017278432 0.015762966 0.014197627 0.024077458 0.022823594 0.021515961 0.020155240 0.018742161 0.017277507 0.015762106 0.014196841 0.9125 0.9250 0.9375 0.9500 0.9625 0.9750 0.9875 1.0000 --- --- --- --- --- --- --- 0 --- --- --- 0.007463350 --- --- --- 0 --- 0.010922960 --- 0.007458083 --- 0.003814000 --- 0 0.012583344 0.010921087 0.009211874 0.007456766 0.005656864 0.003813309 0.001927282 0 0.012582635 0.010920462 0.009211340 0.007456327 0.005656526 0.003813078 0.001927164 0 Table 2. Dimensionless stress function of a rotating variable-thickness solid disk using Richardson’s extrapolation method with different values of ΔR (k = 2.5, n = 0.5). i 1 Ext i 2 Ext i 3 Ext i 4 Ext i Analytical 0.0 0 0 0 0 0 0.1 0.010420061 0.010420421 0.010420447 0.010420444 0.010420449 0.2 0.020071028 0.020071086 0.020071091 0.020071090 0.020071091 0.3 0.028189855 0.028189794 0.028189792 0.028189790 0.028189791 0.4 0.034064332 0.034064233 0.034064229 0.034064227 0.034064227 0.5 0.037080500 0.037080406 0.037080401 0.037080400 0.037080400 0.6 0.036771037 0.036770972 0.036770969 0.036770967 0.036770967 0.7 0.032857058 0.032857029 0.032857028 0.032857028 0.032857027 0.8 0.025276926 0.025276927 0.025276928 0.025276927 0.025276927 0.9 0.014196825 0.014196839 0.014196840 0.014196840 0.014196841 1.0 0 0 0 0 0  A. M. Zenkour et al. / Natural Science 3 (2011) 145-153 Copyright © 2011 SciRes. OPEN ACCESS 151 Table 3. Dimensionless stress function of a rotating variable-thickness solid disk (k = 0.7, n = 2). FDM Analytical 0.0125R 0.025R 0.05R 0.1R i 0 0 0 0 0 0.0 0.003891568 0.003891627 0.003891774 0.003892229 0.003893631 0.1 0.006897877 0.006898133 0.006898890 0.006901872 0.006913732 0.2 0.008971625 0.008972022 0.008973209 0.008977938 0.008996897 0.3 0.010102762 0.010103227 0.010104619 0.010110178 0.010132490 0.4 0.010321685 0.010322155 0.010323563 0.010329193 0.010351793 0.5 0.009683519 0.009683947 0.009685228 0.009690352 0.009710919 0.6 0.008256930 0.008257280 0.008258329 0.008262527 0.008279371 0.7 0.006116796 0.006117044 0.006117787 0.006120761 0.006132695 0.8 0.003339509 0.003339638 0.003340026 0.003341577 0.003347797 0.9 0 0 0 0 0 1.0 Table 4. Dimensionless stress function of a rotating variable-thickness solid disk (k = 1.5, n = 2). FDM Analytical 0.0125R 0.025R 0.05R 0.1R i 0 0 0 0 0 0.0 0.005416705 0.005416605 0.005416315 0.005415269 0.005412300 0.1 0.009932747 0.009933554 0.009935982 0.009945759 0.009985706 0.2 0.013033300 0.013034871 0.013039590 0.013058534 0.013135277 0.3 0.014512487 0.014514484 0.014520482 0.014544543 0.014641868 0.4 0.014415043 0.014417117 0.014423346 0.014448330 0.014549332 0.5 0.012959495 0.012961364 0.012966973 0.012989467 0.013080378 0.6 0.010460010 0.010461482 0.010465900 0.010483617 0.010555201 0.7 0.007259771 0.007260750 0.007263688 0.007275470 0.007323059 0.8 0.003682061 0.003682530 0.003683938 0.003689581 0.003712369 0.9 0 0 0 0 0 1.0 since we have as a continuous function of R. The distributions of the stress function, radial and circum- ferential stresses are presented in Figure 2. The numeri- cal FDM solution is compared with the exact analytical solution for the rotating variable-thickness solid disk with k = 2.5 and n = 0.5. It can be seen that the FDM can describe the stress function and stresses through the thickness of the rotating solid disk very well enough. For the sake of completeness and accuracy, additional results for the stress function and stresses are presented in Figures 3-5 for different values of the geometric pa- rameters k and n. Figure 3 shows the stress function through the radial direction of the rotating solid disk with k = 2.5, n = 0.5; k = 0.7, n = 2 and k = 1.5, n = 2. Similar results for the radial 1 and the circumferential 2 stresses are plotted in Figures 4 and 5. Figure 3 shows that the stress function increases as k in- creases and this irrespective of the value of n (see also Tables 3 and 4). Figures 4 and 5 show that k = 2.5, n = 0.5 gives the largest stresses. The intersection of the two cases k = 0.7, n = 2 and k = 1.5, n = 2 may be occurred at R = 0.1 for the radial stress and at R = 0.15 for the circumferential stress. It is clear that, the FDM gives stress function and, 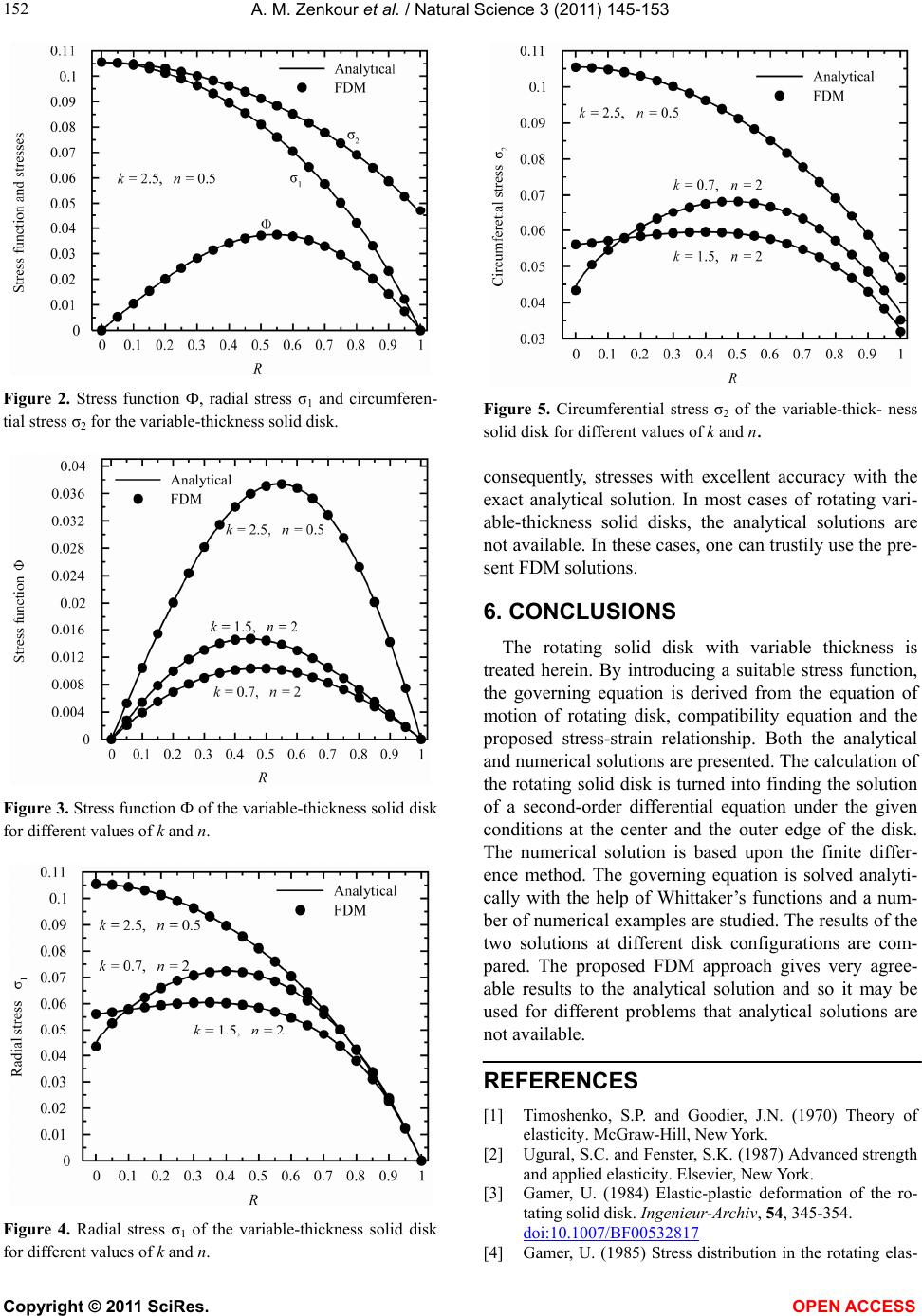 A. M. Zenkour et al. / Natural Science 3 (2011) 145-153 Copyright © 2011 SciRes. OPEN ACCESS 152 Figure 2. Stress function Ф, radial stress σ1 and circumferen- tial stress σ2 for the variable-thickness solid disk. Figure 3. Stress function Ф of the variable-thickness solid disk for different values of k and n. Figure 4. Radial stress σ1 of the variable-thickness solid disk for different values of k and n. Figure 5. Circumferential stress σ2 of the variable-thick- ness solid disk for different values of k and n. consequently, stresses with excellent accuracy with the exact analytical solution. In most cases of rotating vari- able-thickness solid disks, the analytical solutions are not available. In these cases, one can trustily use the pre- sent FDM solutions. 6. CONCLUSIONS The rotating solid disk with variable thickness is treated herein. By introducing a suitable stress function, the governing equation is derived from the equation of motion of rotating disk, compatibility equation and the proposed stress-strain relationship. Both the analytical and numerical solutions are presented. The calculation of the rotating solid disk is turned into finding the solution of a second-order differential equation under the given conditions at the center and the outer edge of the disk. The numerical solution is based upon the finite differ- ence method. The governing equation is solved analyti- cally with the help of Whittaker’s functions and a num- ber of numerical examples are studied. The results of the two solutions at different disk configurations are com- pared. The proposed FDM approach gives very agree- able results to the analytical solution and so it may be used for different problems that analytical solutions are not available. REFERENCES [1] Timoshenko, S.P. and Goodier, J.N. (1970) Theory of elasticity. McGraw-Hill, New York. [2] Ugural, S.C. and Fenster, S.K. (1987) Advanced strength and applied elasticity. Elsevier, New York. [3] Gamer, U. (1984) Elastic-plastic deformation of the ro- tating solid disk. Ingenieur-Archiv, 54, 345-354. doi:10.1007/BF00532817 [4] Gamer, U. (1985) Stress distribution in the rotating elas-  A. M. Zenkour et al. / Natural Science 3 (2011) 145-153 Copyright © 2011 SciRes. OPEN ACCESS 153 tic-plastic disk. ZAMM, 65, T136-137. [5] Eraslan, A.N. (2000) Inelastic deformation of rotating variable thickness solid disks by Tresca and Von Mises criteria. International Journal of Computational Engi- neering Science, 3, 89-101. doi:10.1142/S1465876302000563 [6] Eraslan, A.N. and Orcan, Y. (2002) On the rotating elas- tic-plastic solid disks of variable thickness having con- cave profiles. International Journal of Mechanical Sci- ences, 44, 1445-1466. doi:10.1016/S0020-7403(02)00038-3 [7] Eraslan, A.N. (2005) Stress distributions in elastic-plastic rotating disks with elliptical thickness profiles using Tresca and von Mises criteria. ZAAM, 85, 252-266. [8] Zenkour, A.M. and Allam, M.N.M. (2006) On the rotat- ing fiber-reinforced viscoelastic composite solid and an- nular disks of variable thickness. International Journal for Computational Methods in Engineering Science, 7, 21-31. doi:10.1080/155022891009639 [9] Zienkiewicz, O.C. (1971) The finite element method in engineering science. McGraw-Hill, London. [10] Banerjee, P.K. and Butterfield, R. (1981) Boundary ele- ment methods in engineering science. McGraw-Hill, New York. [11] You, L.H., Tang, Y.Y., Zhang, J.J. and Zheng, C.Y. (2000) Numerical analysis of with elastic-plastic rotating disks arbitrary variable thickness and density. The Interna- tional Journal of Solids and Structures, 37, 7809-7820. doi:10.1016/S0020-7683(99)00308-X [12] Zenkour, A.M. and Mashat, D.S. (2010), Analytical and numerical solutions for a rotating disk of variable thick- ness. Applied Mathematics, 1, 430-437. doi:10.4236/am.2010.15057
|