Theoretical Economics Letters, 2013, 3, 322-327
Published Online December 2013 (http://www.scirp.org/journal/tel)
http://dx.doi.org/10.4236/tel.[phone]
Open Access TEL
Why Does the US Prevent Parallel Imports?
Yih-Ming Lin
Department of Applied Economics, National Chiayi University, Chiayi, Taiwan
Received November 1, 2013; revised December 1, 2013; accepted December 8, 2013
Copyright © 2013 Yih-Ming Lin. This is an open access article distributed under the Creative Commons Attribution License, which
permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of
the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property
Yih-Ming Lin. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
ABSTRACT
Most studies on parallel trade conclude that parallel imports, in general, benefit the importing country because it lowers
the price of parallel imports and benefits to the consumers in the importing country. Richardson [1] explicitly indicates
that there is no importing country not to permit parallel imports because they are discriminated against in its absence.
However, an obvious counter example is observed in the US. In this paper, we propose a two-country model of parallel
trade with innovation to explain why some countries, such as the US would like to prevent parallel imports. We show
that the elasticity of innovation is crucial to the welfare of importing country and global welfare.
Keywords: Parallel Imports; Welfare; Innovation
1. Introduction
Most of the previous literatures, such as Malueg and Sch-
wartz [2], Richardson [1], Maskus and Chen [3,4], and
Chen and Maskus [5], on parallel trade conclude that pa-
rallel imports, in general, benefit the importing country
because it lowers the price of parallel imported goods
and benefits to the consumers. Among them, Richardson
[1] explicitly indicates that there is no importing country
not to permit parallel imports because they are discrimi-
nated against in its absence. However, an obvious coun-
ter example is observed in the US. For instance, the mes-
sage “This International Edition is not for sale in the
United States of America, its dependencies or Canada.”
is common to be found in a copyright page or cover of
the International Edition textbook, which indicates that
the US does not allow new or used international edition
textbooks to be circulated within the country. Therefore,
this phenomenon raises the question: If parallel import is
always in favor of the importing country, then why
would the US government prevent parallel import?
Previous discussion on whether parallel trade should
be prevented includes Maskus [6,7], Malueg and Schwartz
[2], and so on. Maskus [6] summarizes the arguments
which are in favor of preventing parallel trade. Among
them, the most well-known explanation is that third-de-
gree price discrimination may be beneficial to the global
welfare, which will not necessarily happen but depend
on whether the global output increases or not under each
case (Varian [8]). Another argument opposing to parallel
trade proposed by Malueg and Schwartz [2] is that some
markets will become unserved due to a uniform price, the
direct consequence of parallel trade. However, the above
arguments seem hard to explain why a country is willing
to block parallel import if its government concerns its
own welfare, instead of the global welfare. In particular,
the above discussions are concentrated on the benefits of
the entire world, instead of that of an individual country.
In this paper, we build in a two-country model with in-
novation to analyze the welfare effects of parallel im-
ports from the viewpoint of an importing country. The
welfare effects of parallel trade on the importing country
and global welfare are also investigated by a simulation
approach. We investigates the welfare effects and how
parallel trade relates to the incentive of product innova-
tion by employing a differentiated-goods model, which
extends the models of Li and Maskus [9], Li and Robles
[10], and Li [11,12]. It distinguishes from the previous
studies, while only a single product model is used to de-
monstrate how parallel trade affects the welfare in most
of existing literatures. See Malueg and Schwartz [2],
Maskus and Chen [3,4], and Chen and Maskus [5] for
examples.
The remainder of this paper is organized as follows. In
Section 2, we demonstrate a conventional two-country

Y.-M. LIN 323
model with linear demand. Following Section 2, we set
up a two-country model of parallel trade incorporated
with innovation to explain why a country would like to
prevent parallel imports in Section 3. Section 4 gives
conclusions.
2. The Single Product Case
In this section, we describe a simple, conventional, two-
country model of parallel trade with a single product.
Consider an economy with two countries, North and
South, denoted by n and s, and a monopolistic manufac-
turer. The monopolist manufacturer produces and sells
identical products in both countries. Further, we follow
Malueg and Schwartz [2] to assume that the demand
function is linear such that he inverse demand function of
the market i has the form
 
1, ,
ii ii
pqaqi ns , (1)
where pi and q
i represent the price and consumption in
country i, respectively. Both countries have horizontal
intercepts at 1, but different vertical intercepts at ai.
Without of loss of generality, we may assume that an = 1
+ x and as = 1 − x, where x < 1.
The monopolist determines the price in both markets
to maximize its profits. Suppose that the markets are
segmented so that the producer can set different prices
according to the demand elasticity in both countries in
order to make its profit maximized, which is a standard
case of third degree price discrimination. Moreover,
suppose that the marginal production cost is constant and
the same in the two countries. Without loss of generality,
we may assume that marginal production cost is zero and
there is no transaction cost for simplicity. Therefore, the
monopoly price in the North, 1
2
m
n
x
p , is higher than
the price in the South’s market, 1
m
s2
x
p, which im-
plies that the North is the importing country if parallel
trade is exhibited.
As long as there exists a price difference, there are in-
centives for arbitrage. If parallel trade is allowed, the
optimization problem of the monopolist is

Max π11
11
pp
pp
x
x


 












,
where p is the uniform price,

11px

 and

11px are the quantities consumed in the North
and the South, respectively. Taking derivative with re-
spect to p, we obtain
  
22 12 1
ppxpx
p
  
.
and the optimal price is

2
12px
 .
Note that p* is greater than m
s
p, but less than .
m
n
p
Next, we investigate the welfare effects of parallel
trade. First, assume that the two markets are segmented,
and let Wi represent the welfare of country i (i = n, s),
which is equivalent to the sum of consumers’ and pro-
ducer’s surplus of the country. Then Wn = 3 (1 + x)/8 and
Ws = 3 (1 − x)/8 and the global welfare Wn + Ws = 3/4.
Next, let’s consider the case where parallel trade is al-
lowed. solving the firm’s problem gives the optimal price
p* = (1 − x2)/2 and Wn = (1 + x)2 (3 − x)/8 and Ws = (1 −
x)2 (3 + x)/8, respectively. The global welfare Wn + Ws =
3/4 + x2/4 in this case. Consequently, we can conclude
that the global welfare in the case of parallel trade is
greater than in the case of segmented markets. In par-
ticular, global welfare is increasing in x.
Furthermore, if the monopolistic manufacturer is from
the North, the welfare of the South decreases once paral-
lel trade is allowed which makes the price of goods
higher in the South. Thus, the welfare of the North im-
proves. Moreover, if the monopolist is from the South, it
is easy to show that the welfare of the North improves
because the price in the North decreases. Therefore, we
can conclude that global welfare and the welfare of the
North improve if parallel trade is allowed. Consequently,
we may generalize the above linear demand model to
different market size and can still conclude the same for
importing country. In particular, the above conclusion for
importing country holds under the model of Varian [8] as
well as the multi-country model of Malueg and Schwartz
[2]. However, for simplicity, we shall still focus on the
case of a two-country model with the same market size
but generalize our analysis to a multiple-products setting.
3. The Welfare Effects of Parallel Trade
Incorporated with Innovation
In this section, we develop a two-country model with
innovation. Similar to the previous setting, we consider
an economy with two countries, named South (s) and
North (n), and a firm that develops new products in the
North. But, here we assume that there are two sectors in a
firm, including a homogenous good sector and a differ-
entiated products sector. Following Deardorff [13] and
Scotchmer [14], innovation is incorporated in to the
model through a two-stage model; i.e., the firm chooses
the number of differentiated products to be produced in
the first stage and then sells the products in both coun-
tries in the next stage.
Consumers in the same country are assumed to have
identical preferences but consumers in different countries
may have different preferences. Consumer i chooses z
and x(j) to maximize his utility function ui(·), where


i
u


> 0 and


i
u



< 0 and i = n, s. The problem can
be written as
Open Access TEL

Y.-M. LIN 324
 
0
Max N
ii j
ux jdj z
, (2)
Subject to
 
0
N
ii
pjxj j djz Y
i


,
where j is the index of differentiated goods, N is a meas-
ure of differentiated products in the North, xi(j) is the
consumption of a differentiated good j in country i, zi is
the consumption of the homogenous good, and Yi repre-
sents the income of an individual in country i.
Solving the first order condition of the consumer’s
problem yields xi(j) = xi(p(j)), where xi = (ui’)−1, which
suggests that the demand for the numeraire good is zi =
Yi − Furthermore, the indirect
 
0
N
ii
pjxjdj
j
i
z
utility function can be written as
 
0,
N
ii
USpjdjY

where si(pi(j)) = ui(xi(pi(j))) − p
i(j)xi(p(j)), is the con-
sumer surplus associated with a representative differenti-
ated product.
The equilibrium of the two-stage model can be thought
of as that representing the steady state of an infinite ho-
rizon general equilibrium model in which a firms inno-
vates in every period and products have an exogenously
given useful life, as has been shown by Grossman and
Lai [15]. In order to make a comparison, we assume that
the demand function for each differentiated product is the
same as that in Equation (1) for a different country.
For the monopolistic manufacturer, we may, without
loss of generality, assume that the production of one unit
of all varieties of differentiated products has the same
constant marginal cost c, where c is set to be 0, similar to
the assumption imposed in the previous section. Fur-
thermore, we follow Grossman and Lai [15] and assume
that the innovation cost function is specified as

CN N

, (3)
where α > 1. Note that we rule out the caseα ≤ 1, where
both the marginal and average innovation cost are nonin-
creasing in N. Equation (3) implies that the innovation
cost is convex in N. Next, we define
 


C' NNCN 


to be the elasticity of innovation with respect to an in-
crease in the profit from innovation. Our specification of
innovation cost function has a constant elasticity of in-
novation, which has the same properties as the innova-
tion cost function in Grossman and Lai [15].
The firm’s problem is to choose the number of the new
differentiated products, N, and the price in both markets
to maximize its profit. Since the ps and pn are determined
as in Section 2, the optimal N* is determined by marginal
profit and the marginal innovation cost of innovating a
new differentiated good. Thus,




π
ss
p,

where the right hand side is the marginal profit generated
ition of the profit
of
π
nn
C' Np

by an additional differentiated product.
The welfare of the North is a compos
the firm in the North and the South, the consumers’
surplus in the North, and the innovation cost.








CN. ππ
nnnssnn
WN Nppsp
Moreover, since the firm is in the North, the welfa of
th
re
e South includes only the consumers’ surplus generated
in the South.

 
s
ss
WNNs p.
Furthermore, the global welfare is the sum of two
co
a simulation approach to investigate
th
untries welfare.
Next, we utilize
e welfare effects of parallel trade for the North and the
global welfare effects. The welfare effects of parallel
trade is examined by numerical simulation for x

[0, 0.5]
under different innovation cost functions. Here,e con-
centrate on the cases only when x[0, 0.5], because no
parallel trade will happen when x 0.5. Similar results
for different cases of the innovation cost function are
obtained, therefore, we use two representative cases of γ
in Figures 1 and 2 to illustrate the results. In Figures 1
and 2, the x-axis is defined as x and the y-a xis is defined
as the relative welfare of the North and relative global
welfare.
Two c
w
>
ases of elasticity of innovation, γ = 5 and γ =
10
are concave in x.
Th
/11 are illustrated in Figures 1 and 2, respectively. The
former represents the cases of high elasticity of innova-
tion and the latter represents the cases of low elasticity of
innovation. We define the “Wn ratio” as the North wel-
fare with the occurrence of parallel trade divided by that
of the North without the occurrence of parallel trade.
Then “Wn ratio” > 1 means that the North welfare is im-
proved when parallel trade exists. Analogously, we can
also define the global welfare ratio, denoted by “GW
ratio” and the global welfare with an occurrence parallel
trade improves when “GW ratio” > 1.
Figure 1 shows that the two ratios
ey are increasing in x first, and then decreasing in x.
We can find that there exists a x = 0.117, which makes
the North obtain the maximal Wn ratio, i.e., the maximal
welfare improvement for the North from parallel imports.
For x

[0.117, 0.5], Wn ratio is decreasing in x. In addi-
tion, when x = 0.231, we have Wn ratio = 1, i.e. the North
welfare of parallel trade is equal to that without parallel
trade. It suggests that if x is big enough, parallel importa-
tion is not beneficial to the importing country. Further-
more, it also shows that GW ratio is no greater than 1,
and is decreasing in x for all x when γ = 5. It suggests that
when the elasticity of innovation is relatively high then
the global welfare will decrease due to parallel import-
Open Access TEL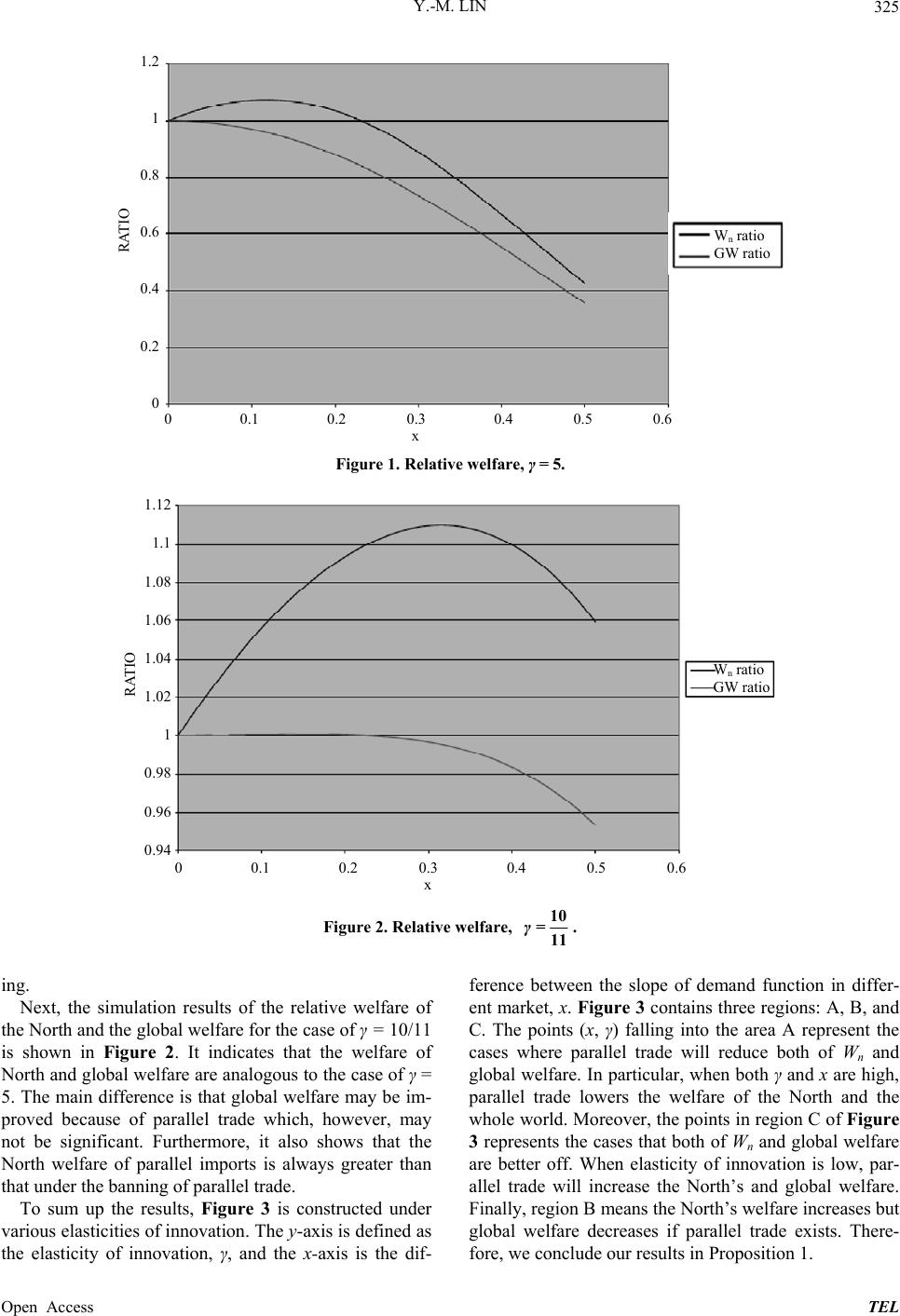

Y.-M. LIN
Open Access TEL
325
W
n
ratio
GW ratio
1.2
1
0.8
0.6
0.4
0.2
0
0 0.1 0.2 0.3 0.4 0.5 0.6
RATIO
x
Figure 1. Relative welfare, γ = 5.
Wn ratio
GW ratio
1.12
1.1
1.08
1.06
1.04
1.02
1
0.98
0.96
0.94
0 0.1 0.2 0.3 0.4 0.5 0.6
RATIO
x
10
=11 γ.
Figure 2. Relative welfare,
ing.
Next, the simulation results of the relative welfare of
orth and the global welfare for the case of γ = 10/11
is
xis is defined as
th
between the slope of demand function in differ-
ent market, x. Figure 3 contains three regions: A, B, and
ference
the N
shown in Figure 2. It indicates that the welfare of
North and global welfare are analogous to the case of γ =
5. The main difference is that global welfare may be im-
proved because of parallel trade which, however, may
not be significant. Furthermore, it also shows that the
North welfare of parallel imports is always greater than
that under the banning of parallel trade.
To sum up the results, Figure 3 is constructed under
various elasticities of innovation. The y-a
e elasticity of innovation, γ, and the x-axis is the dif-
C. The points (x, γ) falling into the area A represent the
cases where parallel trade will reduce both of Wn and
global welfare. In particular, when both γ and x are high,
parallel trade lowers the welfare of the North and the
whole world. Moreover, the points in region C of Figure
3 represents the cases that both of Wn and global welfare
are better off. When elasticity of innovation is low, par-
allel trade will increase the North’s and global welfare.
Finally, region B means the North’s welfare increases but
global welfare decreases if parallel trade exists. There-
fore, we conclude our results in Proposition 1.

Y.-M. LIN 326
B
2
1
0
C
0.5 x
A
Figure 3. The relation between elasticity of innovation, γ
and x.
Proposition 1:
ntry welfare increases in x first, and it decreases
in when x is getting large. Global welfare decreases in
x.
When elasticity of innovation and x are high, paral-
le
parallel trade
w
nd, if the difference between the two markets
is
global welfare always increases under a
si
cies
the real world. One reasonable inter-
llowing parallel imports may reduce
ardson, “An Elementary Proposition Concerning
Parallel Imports,” Journal of International Economics,
Vol. 56, No. 1, 2
http://dx.doi.org/10.1016/S0022-1996(01)00110-6
1) When elasticity of innovation is high, the innovat-
ing cou
x
2) When elasticity of innovation is low, the innovating
country welfare and global welfare increase in x first, and
they decrease in x when x is getting large.
3)
l trade decreases the innovating country welfare as well
as global welfare.
4) When elasticity of innovation is low,
ill improve the innovating country welfare as well as
global welfare. However, the increase in global welfare
is limited.
Proposition 1 indicates that parallel imports can usu-
ally make the North’s welfare improve whenever the
difference between the North and the South is small. On
the other ha
significant, parallel imports will make the North worse.
Thus, Proposition 1 provides a reasonable interpretation
of why some countries permit parallel importing, but
some do not.
Another finding is that global welfare decreases under
the case of high elasticity of innovation at any given val-
ues of x, which is quite different from the results in sec-
tion 2, where
ngle product model with linear demand function. It is
mainly resulted from the reduced number of innovations
which is accompanied with the reduced profit. For the
case of low elasticity of innovation, global welfare is
improved if the difference between the two markets is
not significant. The profit of monopolist is reduced which
is a direct consequence of parallel trade reduces. There-
fore, parallel trade reduces the incentives for innovation,
which results in a decreasing number of innovations.
Although parallel trade in a single product case improves
the welfare of the importing country and global welfare
concluded in Section 2, the welfare effects of parallel
trade become ambiguous in the more general model.
4. Conclusion
We introduce a model of parallel trade with innovation to
explain the phenomena why there exist various poli
on parallel trade in
pretation is that a
producers’ incentives for innovation, and thus reduce the
number of new innovation. We show that the welfare
effect is not only related to the difference between the
two markets, but also related to the elasticity of innova-
tion. Parallel trade improves the welfare of importing
country, which, however, also reduces the incentives to
innovate new products. Overall, the welfare effects of
parallel imports are ambiguous. It provides an interpreta-
tion for why some countries allow parallel import but
some do not. Furthermore, when elasticity of innovation
and x is high, parallel trade decreases the innovating
country welfare as well as global welfare. When elastic-
ity of innovation is low, allowing parallel trade improves
the welfare of the innovating country as well as global
welfare. However, the increase in global welfare is not
significant.
REFERENCES
[1] M. Rich
002, pp. 233-245.
[2] D. A. Malueg and M. Schwartz, “Parallel Imports, De-
mand Dispersion, and International Price Discrimina-
tion,” Journal of International Economics, Vol. 37, No.
3-4, 1994, pp. 167-195.
http://dx.doi.org/10.1016/0022-1996(94)90044-2
[3] K. E. Maskus and Y. Chen, “Parallel Imports in a Model
of Vertical Distribution: Theory and Evidence and Pol-
icy,” Pacific Economic Review, Vol. 7, No. 2, 2002, pp.
319-334. http://dx.doi.org/10.1111/1468-0106.00167
[4] K. E. Maskus and Y. Chen, “Vertical Price Control and
Parallel Imports: Theory and Evidence,” Review of Inter-
national Economic, Vol. 12, No. 4, 2004, pp. 551-570.
http://dx.doi.org/10.1111/j.1467-9396.2004.00467.x
[5] Y. Chen and K. E. Maskus, “Vertical Pricing and Parallel
Imports,” Journal of International Trade and Economic
Development, Vol. 14, No. 1, 2005, pp. 1-18.
Open Access TEL

Y.-M. LIN
Open Access TEL
327
http://dx.doi.org/10.1080/0963819042000333225
[6] K. E. Maskus, “Intellectual Property Rights in the Global
Economy,” Institute for International Economics, Wash-
ington DC, 2000.
[7] K. E. Maskus, “Parallel Imports,” The World Economy
Vol. 23, No. 9, 2002, pp. 1269-1284.
,
http://dx.doi.org/10.1111/1467-9701.00329
[8] H. Varian, “Price Discrimination and Social Welfare,”
American Economic Review, Vol. 75, 1985, pp. 870-875.
h and Devel-
ics, Vol. 68,
[9] C. Li and K. E. Maskus, “The Impact of Parallel Imports
on Investments in Cost-Reducing Researc
opment,” Journal of International Econom
No. 2, 2006, pp. 443-455.
http://dx.doi.org/10.1016/j.jinteco.2005.07.006
[10] C. Li and J. Robles, “Product Innovation and Parallel
Trade,” International Journal of Industrial Organization,
Vol. 25, No. 2, 2007. pp. 417-429.
http://dx.doi.org/10.1016/j.ijindorg.2006.03.007
nd Parallel Imports,”
005, pp.
[11] C. Li, “Vertical Product Innovation a
Singapore Economic Review, Vol. 50, No. 1, 2
35-46. http://dx.doi.org/10.1142/S0217590805001822
[12] C. Li, “Competition, Parallel Imports and Cost-Reducing
Innovation,” Scottish Journal of Political Economy, Vol.
53, No. 3, 2006, pp. 377-397.
http://dx.doi.org/10.1111/j.1467-9485.2006.00385.x
[13] A. V. Deardorff, “Welfare Effects of Global P
tection,” Economica, Vol. 59, No. 233, 1992, pp. 35-5
atent Pro-
1.
http://dx.doi.org/10.2307/2555064
[14] S. Scotchmer, “The Political Economy of Intellectual
Property Treaties,” Journal of Law, Economics, and Or-
ganizations, Vol. 20, No. 2, 2004, pp. 415-437.
http://dx.doi.org/10.1093/jleo/ewh040
[15] G. M. Grossman and E. L. C. Lai, “Internationa
tion of Intellectual Property,” American
l Protec-
Economic Review,
Vol. 94, No. 5, 2004, pp. 1635-1653.
http://dx.doi.org/10.1257/0002828043052312