Vol.3, No.2, 109-119 (2011) Natural Science
http://dx.doi.org/10.4236/ns.2011.32016
Seismic activity of the earth, the cosmological vectorial
potential and method of a short-term earthquakes
forecasting
Baurov Yury Alexeevich*, Baurov Alexey Yur’evich, Baurov Alexandr Yur’evich (Jr.), Spitalnaya
Alexandra Alfredovna, Abramyan Ara Arshavirovich, Solodovnikov Vladimir Alexandrovich
Closed Joint Stock Company Research Institute of Cosmic Physics, Korolev, Russia; *Corresponding Author:
Received 10 October 2010; revised 12 November 2010; accepted 15 November 2010.
ABSTRACT
To the foundation of a principally new short-term
forecasting method there has been laid down a
theory of surrounding us world’s creation and of
physical vacuum as a result of interaction of
byuons-discrete objects. The definition of the
byuon contains the cosmological vector-potential
Ag - a novel fundamental vector constant. This
theory predicts a new anisotropic interaction of
nature objects with the physical vacuum. A pe-
culiar “tap” to gain new energy (giving rise to an
earthquake) are elementary particles because
their masses are proportional to the modulus of
some summary potential A that contains po-
tentials of all known fields. The value of A
cannot be larger than the modulus of Ag. In ac-
cordance with the experimental results a new
force associated with A ejects substance from
the area of the weakened A along a conical
formation with the opening of 100о ± 10о and the
axis directed along the vector A. This vector
has the following coordinates in the second
equatorial coordinate system: right ascension  
293 ± 10, declination   36 ± 10. The 100%
probability of an earthquake (earthquakes of 6
points strong and more by the Richter scale)
arises when in the process of the earth rotation
the zenith vector of a seismically dangerous
region and/or the vectorial potential of Earth’s
magnetic fields are in a certain way oriented
relative to the vector Ag. In the work, basic
models and standard mechanisms of earth-
quakes are briefly considered, results of proc-
essing of information on the earthquakes in the
context of global spatial anisotropy caused by
the existence of the vector Ag, are presented,
and an analysis of them is given.
Keywords: Earthquake; New Anisotropic Interaction
1. INTRODUCTION
In References [1-3] theory of surrounding us world’s
creation and of physical space (vacuum) as a result of
interaction of byuons-discrete objects, is given. The
definition of the byuon contains the cosmological vec-
tor-potential Ag - a novel fundamental vector constant.
This theory predicts a new anisotropic interaction of
nature objects with physical vacuum.
Peculiar “tap” to gain new energy (giving rise to an
earthquake) are elementary particles because their masses
are proportional to the modulus of some summary po-
tential A
 that contains potentials of all known fields.
The value of A cannot be larger than the modulus of Ag.
In accordance with the experimental results shown in
[1-9], this force ejects substance from the area of the
weakened A along a conical formation with the open-
ing of 100о  10о and the axis directed along the vector
A. This vector has the following coor- dinates in the
second equatorial coordinate system: right ascension  
293  10, declination   36  10 [3,4].
In the present paper, the hypothesis for connection of
the Earth’s seismic activity with fluctuations in the
structure of physical space (vacuum) is considered. That
is, our planet, the Earth, will be treated as a peculiar
large-scale probe in the physical space the seismic activ-
ity of which allows to judge the fluctuations of physical
space itself and in so doing to refine its structure and
direction of the vector Ag. And vice versa, with a
knowledge of space structure and of its fluctuations one
would be able to predict more accurately the most dan-
gerous day time for Earth’s inhabitants at one or another
place of our planet. The urgency of this problem has no
need of much to talk because earthquakes lead to many-
thousand victims and catastrophic destructions.

Y. A. Baurov et al. / Natural Science 3 (2011) 109-119
110
In the work, basic models and standard mechanisms
of earthquakes are briefly considered, results of proc-
essing of information on the earthquakes in the context
of global spatial anisotropy caused by the existence of
the vector Ag, are presented, and an analysis of them is
given. A method of short-term earthquakes forecasting
(1-2 days in advance) is advanced.
2. EARTHQUAKES AND THEIR
MECHANISMS OF GENERATION
An earthquake is the sudden release of potential en-
ergy of bowels of the earth in the form of shock waves
and elastic vibrations propagating every which way from
the center (hypocenter), as well as in the form of shifts
of the Earth’s surface such as warpings of crust, dis-
placements along fault lines, compactions of granular or
not grouted precipitations, soil slips and mudflows, soil
dilution, snow avalanches, new fracture formation in
rocks [10].
The mechanism of release of potential energy is not
yet sufficiently studied for earthquakes at depths from 60
km to 720 km [11].
The Earth is never quiescent. Sensible seismographs
constantly detect weak oscillations, microseisms, with
periods from 4 to 6 seconds and variable amplitudes. Even
“microseismic storms” take place, they are connected
mainly with sharp changes in weather. During powerful
earthquakes almost total seismic energy is released.
An energy characteristic of earthquakes is the magni-
tude. A scale of magnitudes was elaborated by Karl
Richter, a professor of Californian Technological Insti-
tute. The magnitude of an earthquake is a measure of the
total energy quantity released in the form of elastic
waves, and that is not equal to the total energy of earth-
quake. Part of elastic energy accumulated in the center
of earthquake is turned into heat.
The magnitude is characterized by the maximum am-
plitude of record by a seismograph of standard type at a
fixed distance from the hypocenter of earthquake. The
most potent disastrous earthquakes have amplitude M =
9. As an example of earthquakes with M = 9, that in
Lissabon at November 1, 1755, may be considered.
Any earthquake with M  7 is the great disaster, par-
ticularly if that happens in the neighbourhood of popu-
lated area. The energy released during such earthquakes
ranges from 2.1̣·1022 to 1.6·1025 erg.
Very strong earthquakes lead to torsion and spheroidal
oscillations of the Earth as a whole. For very weak
shocks, negative values of the magnitude are used [10].
As to depth of occurrence (h) of earthquake centers,
those are classified into three categories: crustal (0  h 
70 km), middle focal (intermediate) (70 < h  300 km),
and deep focal h > 300 km earthquakes.
The most deep focal shocks were recorded only in the
southern hemisphere of the Earth:
1) in the vicinity of Kermadec runner (10047 m in
depth, interval of latitudes 35S    25S):
2) in the neighbourhood of Tonga runner (10882 m in
depth, interval of latitudes 25S    15S) (both run-
ners are located to the north-west from New Zealand);
3) in the latitude   6 to the south from Sulawesi is-
land (Indonesia).
The centers of those earthquakes were up to 720 km
deep from the surface.
In Table 1 are listed distributions of earthquakes of all
types (from deep focal to crustal ones) registered at a
period from 1904 till 19881 and having magnitudes M =
7 and more except for the deep focal earthquakes for
which, to magnify the sample, we had to use those be-
ginning with М  5.9. The data were chosen from cata-
logues [10-15].
It follows from Table 1 that great majority of earth-
quakes of all type occurs at latitudes 35-45 north as
well as in southern latitudes of equatorial region and at
25S. Therewith the crustal earthquakes are prevalent in
the northern hemisphere, whereas deep focal earth-
quakes are in the southern one as evidenced by confi-
dence intervals L obtained with the use of Student t-test
for random values of the average with the level of sig-
nificance of 0.01 and 0.001 (see Figure 1).
The first fact was known as early as the beginning of
20-th century [16-19] and even earlier [20] in the context
of the question of how and where the stresses accumu-
late in the Earth’s crust.
The question of a particular role of 35-th parallel in
the tectonic life of the Earth was repeatedly posed by
geographers and geologists as in the Russian so in for-
eign literature. The first work along this line was proba-
bly that by A. A. Tillo [20] which has pointed out all the
most high peaks and mountain chains as well as the most
great depths in the northern hemisphere to gravitate to-
wards the latitudes of 30-40. All researches of this sort
persued prior 1962 (with voluminous list of literature)
may be acquainted with in the articles of M. V. Stovas,
an astronomer-geodesist [16,17], and V. A. Tsaregradsky,
an astrogeologist [18]. One of important conclusions of
those studies was that all processes connected with the
most potent earthquakes have a common mechanism for
the whole Globe.
Following German geologists, the authors of Refs.
[16-18] considered the periodic variation of the Earth’s
rotation velocity due to tide influence of Moon and Sun
as one of the sources of energy for tectonic processes.
The smaller is the angular velocity of rotation, the more
1In Precisely this period of time will be analyzed further without refer-
ence to dates.

Y. A. Baurov et al. / Natural Science 3 (2011) 109-119
111
Table 1. The dependence of number of earthquakes (ni) from the latitude (or declination) of their epicenters
and hypocenters.
h > 300 км 70 < h  300 км 0  h  70 км Все
 = 
ni ni/n ni ni/n ni ni/n ni ni/n
+85 0 0,00 0 0,00 0 0,00 0 0,00
+75 0 0,00 0 0,00 1 0,02 1 0,01
+65 0 0,00 2 0,12 14 0,25 16 0,15
+55 26 0,78 17 1,05 92 1,64 135 1,28
+45 69 2,06 20 1,23 120 2,14 209 1,98
+35 70 2,09 30 1,85 122 2,18 222 2,10
+25 45 1,34 16 0,99 75 1,34 136 1,29
+15 13 0,39 33 2,04 92 1,64 138 1,31
+5 23 0,69 19 1,17 85 1,52 127 1,20
−5 −99 2,96 42 2,59 137 2,45 278 2,63
−15 70 2,09 49 3,02 99 1,77 218 2,06
−25 168 5,01 48 2,96 68 1,22 284 2,69
−35 20 0,60 9 0,56 42 0,75 71 0,67
−45 0 0,00 1 0,06 25 0,45 26 0,25
−55 0 0,00 5 0,31 20 0,36 25 0,24
−65 0 0,00 0 0,00 15 0,27 15 0,14
−75 0 0,00 0 0,00 0 0,00 0 0,00
−85 0 0,00 0 0,00 0 0,00 0 0,00
 603 291 1007 1901
n 33,5 16,2 55,9 105,6
nS
nN
357
246


 4,5  154
137


  406
601


 −6,1 917
984


 1,5
– is the total number of earthquakes with M  7 over the period from 1904 till 1988; n
–is the average number of earthquakes in
10-interval of latitudes; –is the standard deviation characterizing the anisotropy of Northern and Southern hemispheres relative to
the number of the most strong earthquakes; ns–is the number of earthquakes in the southern hemisphere; nN–is that in the Northern
hemisphere.
globe-shaped becomes the form of the Earth. And vice
versa, with the growth of angular velocity the planet
becomes more ellipsoid-shaped. The reconstruction of
superficial form of the Earth will be the most considera-
bly reflected in the regions of 35-th parallels of north-
ern and southern hemispheres. Those regions are named
critical. Said parallels are also associated with compres-
sive and tensile strains originated under the action of
precession (slow motion of the Earth’s axis of rotation
over a circular cone around an axis orthogonal to the
plane of ecliptic. Many epicenters of earthquakes con-
centrate near the critical parallels, too.
To explain large number of meridionally extending
structures, supporters of rotational hypothesis admitted
the possibility of time variations of the Earth’s axis of
rotation.
As the form of the Earth changes, all tectonic proc-
esses are to be symmetric about the equator. But from
Figure 1, it is clearly seen that at southern latitudes of
30-40S the number of the strongest earthquakes is
lesser than the average, and there is no symmetry in their
distribution about the equator.

Y. A. Baurov et al. / Natural Science 3 (2011) 109-119
112
Figure 1. The distribution of earthquakes (in relative units ni/n) in dependence from latitude (φ) and depth (h) of earthquakes hypo-
center. n–average numbers of earthquakes (n= 1); L–confidence interval at significance level 0,01-0,001.
In the summary curve of latitude distribution of
earthquakes, the maximums are the sames as in the
curves of their depth-distribution, i.e.  = 25S and  =
5 on the south,  = (45-35) N on the north.
A substantial predominance of crustal earthquakes in
the Northern hemisphere (6.1) and deep focal earth-
quakes in the Southern one (4.5) as well as their statis-
tics equality (1) for the middle focal earthquakes, are
also important facts.
In this regard it is interesting to note that the irregular-
ity of distribution of oceans and continents over the
Earth’s surface has first drawn attention of Ch. Layel
who has established an idea of evolution and principles
of actualism in geology. In the first edition of his book
“Basic principles of geology” published in the years
1830-1833, he gives a projection of Earth’s hemispheres
which is displaced in such a manner that one of them is
mainly continental whereas the other is oceanic. There-
with the “northern pole” is represented by a district of
London ( ~ 51N) and the “southern pole” is located
close to New Zealand. The plane of “equator” forms at
that an angle of 39with that of geographic equator.
When investigating the planetary jointing of the Earth,
it was elucidated [21,22] that the modern global relief
presented mainly by lineaments (i.e. by extended straight
lines manifested as contours of continental coasts,
mountain chains, river valleys, and divides) is consid-
erably a summary effect of manifestation of crustal
jointing associated with epicenters of earthquakes.
Hence the lineaments are very much to do with the most
new tectonic displacements of the Earth’s crust. The
statistic distribution of lineamental azimuths reveals the
existence of two quadrupole (cruciform) systems with
dominant orientation along the “meridian-parallel” di-
rections as well as diagonally to those [21,22]. The Sun’s
“zones of instability” (regions of predominant origin of
spot groups and flare activity) manifest similar systems
of preferable directions. The filaments arranged in par-
allel with such a zone, are more stable as compared with
those of orthogonal orientation, i.e. the filaments them-
selves also form quadrupole systems of two types. The
similarity of orientation of Sun’s “instable zones” asso-
ciated with the most potent non-stationary processes, and
of lineaments connected with the present tectonic active-
ity on the Earth, has raised a question of the possibility
of existence of some energy factors external to the Solar
system and manifesting themselves in the form of the
solar activity and tectonic actions on planets and their
satellites [23,24]. The results of a number of works
[23-30] dedicated to analyse of cosmic factors in the
geotectonics and above all to elucidation of the relation
between the solar activity (SA) and the seismicity of the
Earth, have led to the conclusion that such relation does
exist, that the earthquakes occur the most often in a
phases of increase and decrease of solar cycle, and that
the frequency of earthquake events depends more likely
on SA-fluctuations than on its level itself.
Several mechanisms for this relation were proposed:
1) According to References [25-27], it can be accom-
plished through general atmospheric processes on planet.
The intensification of corpuscular radiation of the Sun
when an active region passes through the central merid-
ian, increases the potential energy of the atmosphere, de-
presses zonal circulation, and leads to local accumula-
tion of energy. Redistribution of atmospheric masses
over the Globe disturbs the balance of the Earth’s shape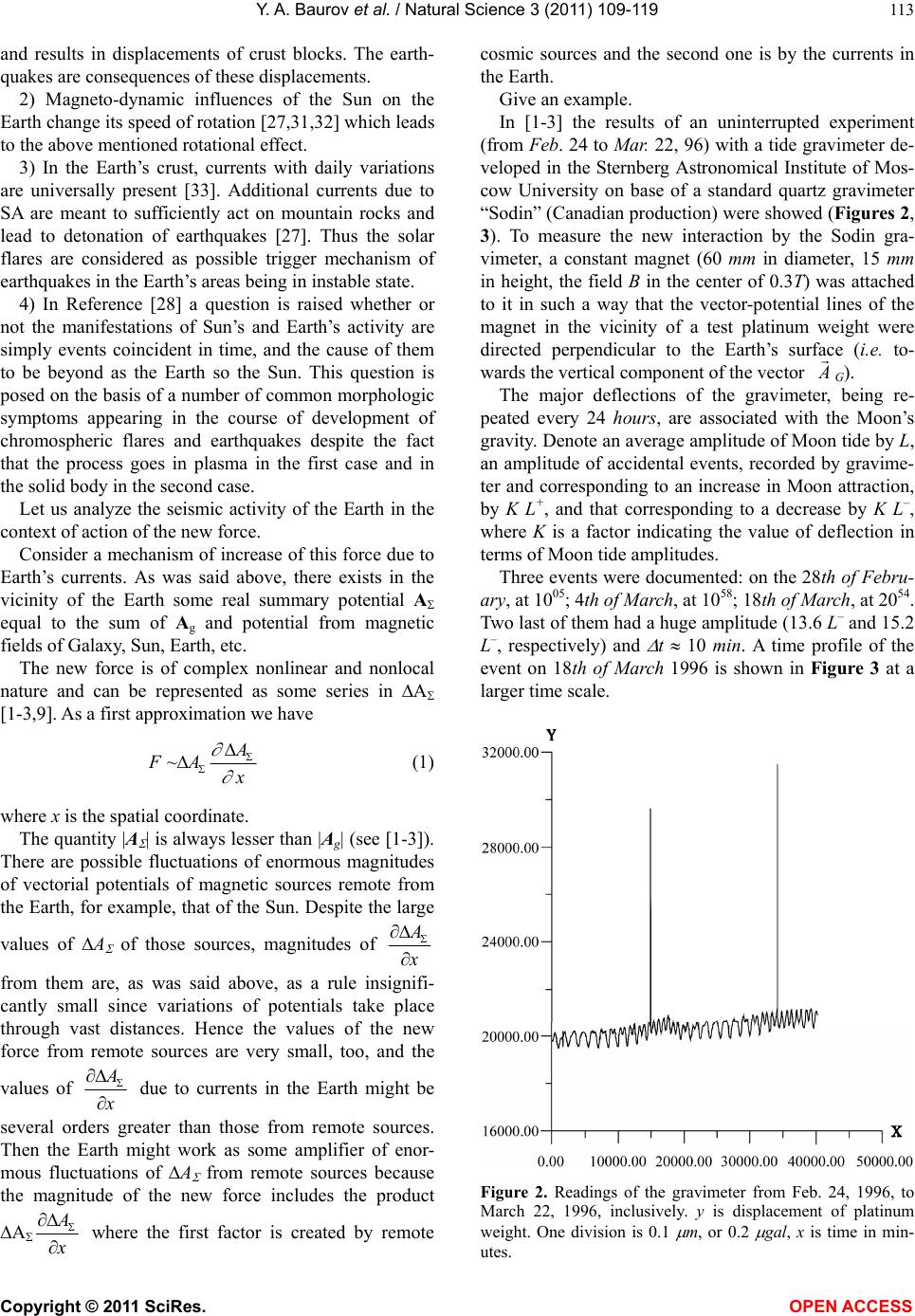

Y. A. Baurov et al. / Natural Science 3 (2011) 109-119
113
and results in displacements of crust blocks. The earth-
quakes are consequences of these displacements.
2) Magneto-dynamic influences of the Sun on the
Earth change its speed of rotation [27,31,32] which leads
to the above mentioned rotational effect.
3) In the Earth’s crust, currents with daily variations
are universally present [33]. Additional currents due to
SA are meant to sufficiently act on mountain rocks and
lead to detonation of earthquakes [27]. Thus the solar
flares are considered as possible trigger mechanism of
earthquakes in the Earth’s areas being in instable state.
4) In Reference [28] a question is raised whether or
not the manifestations of Sun’s and Earth’s activity are
simply events coincident in time, and the cause of them
to be beyond as the Earth so the Sun. This question is
posed on the basis of a number of common morphologic
symptoms appearing in the course of development of
chromospheric flares and earthquakes despite the fact
that the process goes in plasma in the first case and in
the solid body in the second case.
Let us analyze the seismic activity of the Earth in the
context of action of the new force.
Consider a mechanism of increase of this force due to
Earth’s currents. As was said above, there exists in the
vicinity of the Earth some real summary potential A
equal to the sum of Ag and potential from magnetic
fields of Galaxy, Sun, Earth, etc.
The new force is of complex nonlinear and nonlocal
nature and can be represented as some series in A
[1-3,9]. As a first approximation we have
~
A
FA
x





 (1)
where x is the spatial coordinate.
The quantity |A

| is always lesser than |Ag| (see [1-3]).
There are possible fluctuations of enormous magnitudes
of vectorial potentials of magnetic sources remote from
the Earth, for example, that of the Sun. Despite the large
values of А

of those sources, magnitudes of
А
x




from them are, as was said above, as a rule insignifi-
cantly small since variations of potentials take place
through vast distances. Hence the values of the new
force from remote sources are very small, too, and the
values of
А
x


 due to currents in the Earth might be
several orders greater than those from remote sources.
Then the Earth might work as some amplifier of enor-
mous fluctuations of А

from remote sources because
the magnitude of the new force includes the product
А
А
x


 where the first factor is created by remote
cosmic sources and the second one is by the currents in
the Earth.
Give an example.
In [1-3] the results of an uninterrupted experiment
(from Feb. 24 to Mar. 22, 96) with a tide gravimeter de-
veloped in the Sternberg Astronomical Institute of Mos-
cow University on base of a standard quartz gravimeter
“Sodin” (Canadian production) were showed (Figures 2,
3). To measure the new interaction by the Sodin gra-
vimeter, a constant magnet (60 mm in diameter, 15 mm
in height, the field B in the center of 0.3T) was attached
to it in such a way that the vector-potential lines of the
magnet in the vicinity of a test platinum weight were
directed perpendicular to the Earth’s surface (i.e. to-
wards the vertical component of the vector
A

G).
The major deflections of the gravimeter, being re-
peated every 24 hours, are associated with the Moon’s
gravity. Denote an average amplitude of Moon tide by L,
an amplitude of accidental events, recorded by gravime-
ter and corresponding to an increase in Moon attraction,
by K L+, and that corresponding to a decrease by K L–,
where K is a factor indicating the value of deflection in
terms of Moon tide amplitudes.
Three events were documented: on the 28th of Febru-
ary, at 1005; 4th of March, at 1058; 18th of March, at 2054.
Two last of them had a huge amplitude (13.6 L– and 15.2
L–, respectively) and  t  10 min. A time profile of the
event on 18th of March 1996 is shown in Figure 3 at a
larger time scale.
Figure 2. Readings of the gravimeter from Feb. 24, 1996, to
March 22, 1996, inclusively. y is displacement of platinum
weight. One division is 0.1  m, or 0.2  gal, x is time in min-
utes.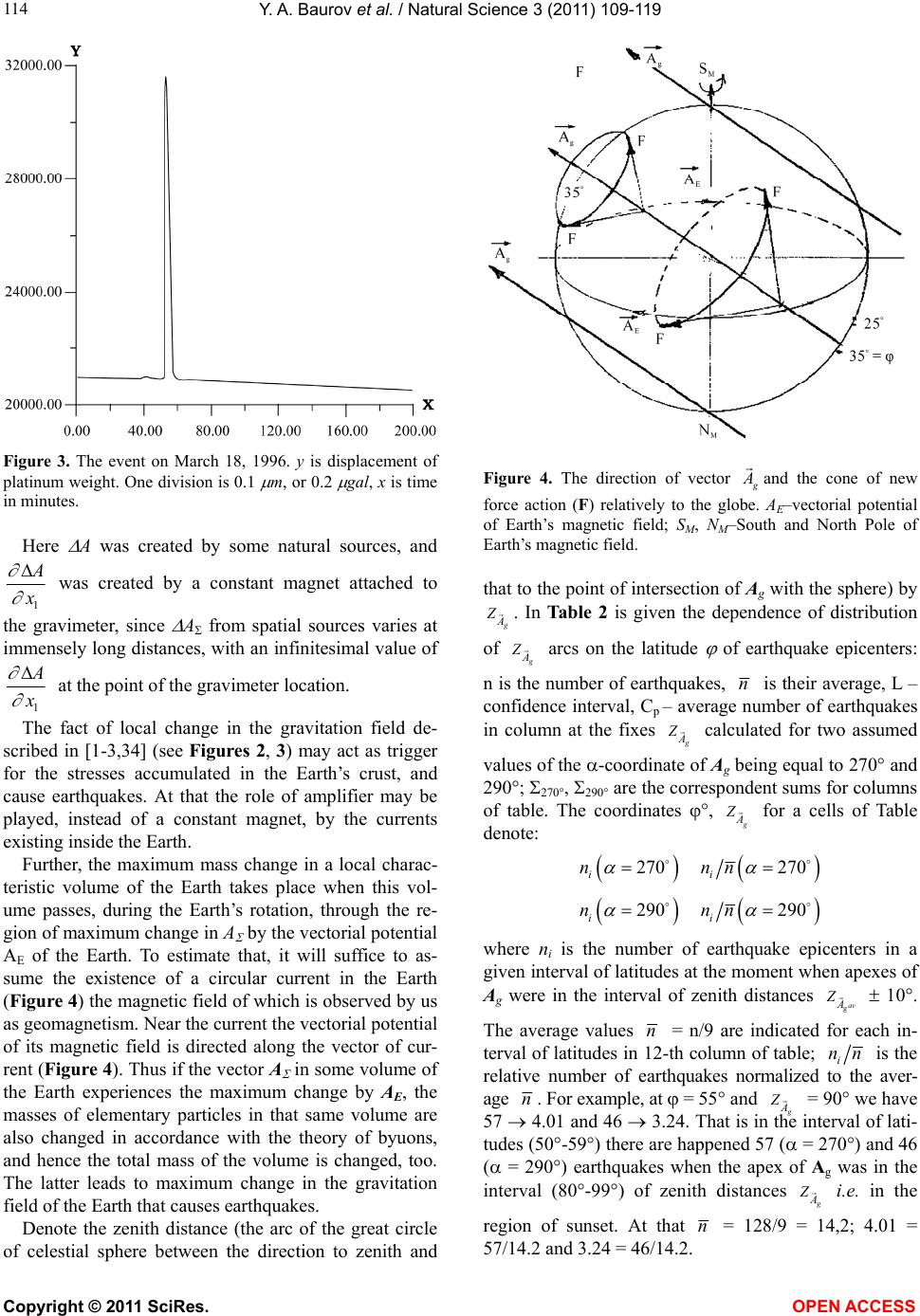

Y. A. Baurov et al. / Natural Science 3 (2011) 109-119
114
Figure 3. The event on March 18, 1996. y is displacement of
platinum weight. One division is 0.1  m, or 0.2  gal, x is time
in minutes.
Here
 A was created by some natural sources, and
1
A
x


 was created by a constant magnet attached to
the gravimeter, since
 A from spatial sources varies at
immensely long distances, with an infinitesimal value of
1
A
x


 at the point of the gravimeter location.
The fact of local change in the gravitation field de-
scribed in [1-3,34] (see Figures 2, 3) may act as trigger
for the stresses accumulated in the Earth’s crust, and
cause earthquakes. At that the role of amplifier may be
played, instead of a constant magnet, by the currents
existing inside the Earth.
Further, the maximum mass change in a local charac-
teristic volume of the Earth takes place when this vol-
ume passes, during the Earth’s rotation, through the re-
gion of maximum change in A

by the vectorial potential
AE of the Earth. To estimate that, it will suffice to as-
sume the existence of a circular current in the Earth
(Figure 4) the magnetic field of which is observed by us
as geomagnetism. Near the current the vectorial potential
of its magnetic field is directed along the vector of cur-
rent (Figure 4). Thus if the vector A

in some volume of
the Earth experiences the maximum change by AE, the
masses of elementary particles in that same volume are
also changed in accordance with the theory of byuons,
and hence the total mass of the volume is changed, too.
The latter leads to maximum change in the gravitation
field of the Earth that causes earthquakes.
Denote the zenith distance (the arc of the great circle
of celestial sphere between the direction to zenith and
Figure 4. The direction of vector
g
A

and the cone of new
force action (F) relatively to the globe. AE–vectorial potential
of Earth’s magnetic field; SM, NM–South and North Pole of
Earth’s magnetic field.
that to the point of intersection of Ag with the sphere) by
g
А
Z

. In Table 2 is given the dependence of distribution
of
g
А
Z

arcs on the latitude  of earthquake epicenters:
n is the number of earthquakes, n is their average, L –
confidence interval, Cp – average number of earthquakes
in column at the fixes
g
А
Z

calculated for two assumed
values of the -coordinate of Ag being equal to 270 and
290; 270, 290 are the correspondent sums for columns
of table. The coordinates ,
g
А
Z
 for a cells of Table
denote:


270 270
ii
nnn  



290 290
ii
nnn  

where ni is the number of earthquake epicenters in a
given interval of latitudes at the moment when apexes of
Ag were in the interval of zenith distances
gavА
Z

 10.
The average values n = n/9 are indicated for each in-
terval of latitudes in 12-th column of table; i
nn is the
relative number of earthquakes normalized to the aver-
age n. For example, at  = 55 and
g
А
Z
 = 90 we have
57  4.01 and 46  3.24. That is in the interval of lati-
tudes (50-59) there are happened 57 ( = 270) and 46
( = 290) earthquakes when the apex of Ag was in the
interval (80-99) of zenith distances
g
А
Z
 i.e. in the
region of sunset. At that n = 128/9 = 14,2; 4.01 =
57/14.2 and 3.24 = 46/14.2.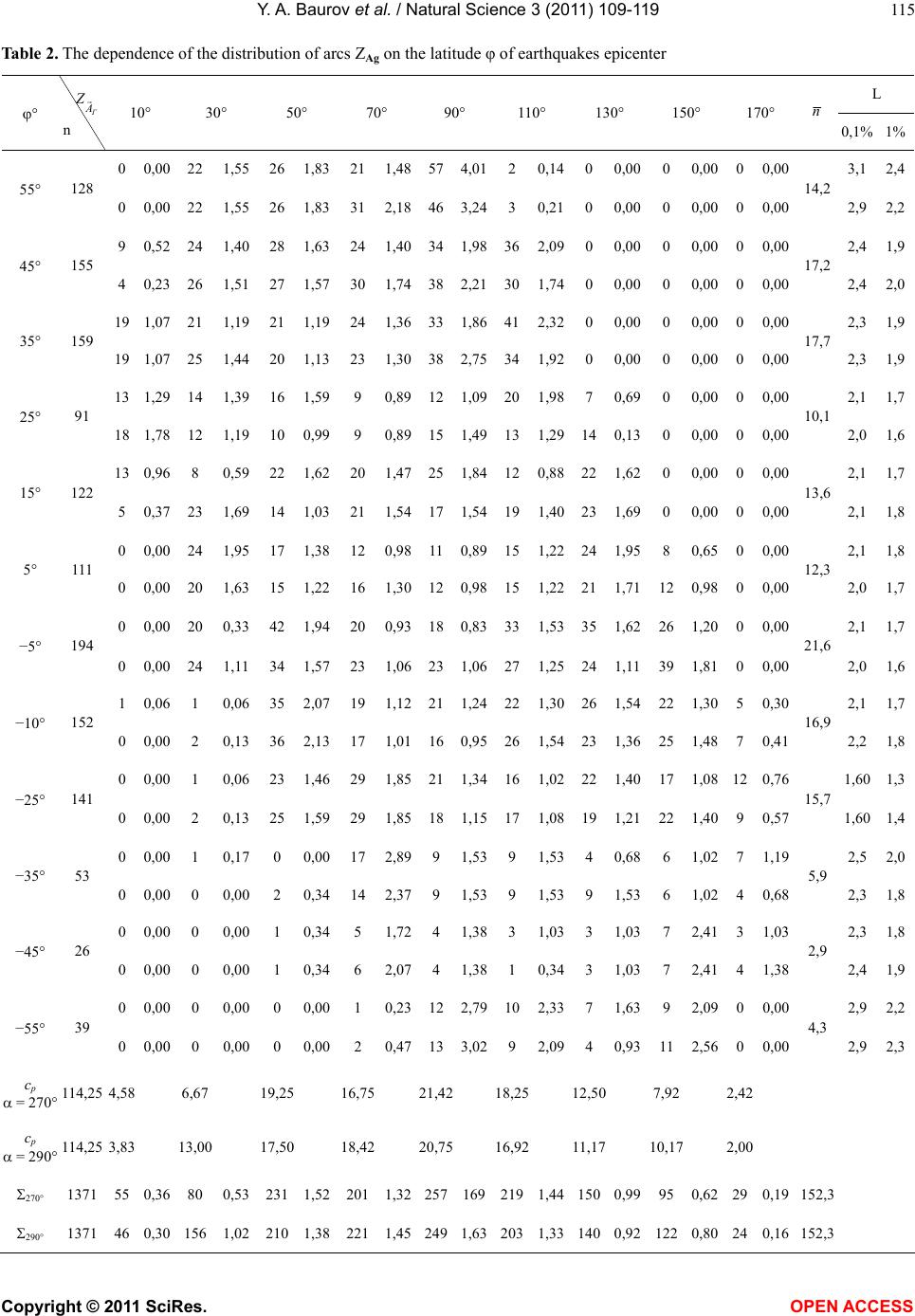

Y. A. Baurov et al. / Natural Science 3 (2011) 109-119
115
Table 2. The dependence of the distribution of arcs ZAg on the latitude φ of earthquakes epicenter
L

Г
А
Z

n
10 30 50 70 90 110 130 150 170 n
0,1% 1%
0 0,00 22 1,55 26 1,83 211,48574,0120,1400,0000,00 0 0,00 3,12,4
55 128
0 0,00 22 1,55 26 1,83 312,18463,2430,2100,0000,00 0 0,00
14,2
2,9 2,2
9 0,52 24 1,40 28 1,63 241,40341,98362,0900,0000,00 0 0,00 2,41,9
45 155
4 0,23 26 1,51 27 1,57 301,74382,21301,7400,0000,00 0 0,00
17,2
2,4 2,0
19 1,07 21 1,19 21 1,19 241,36331,86412,3200,0000,00 0 0,00 2,31,9
35 159
19 1,07 25 1,44 20 1,13 231,30382,75341,9200,0000,00 0 0,00
17,7
2,3 1,9
13 1,29 14 1,39 16 1,59 9 0,89121,09201,9870,6900,00 0 0,00 2,11,7
25 91
18 1,78 12 1,19 10 0,99 9 0,89151,49131,29140,1300,00 0 0,00
10,1
2,0 1,6
13 0,96 8 0,59 22 1,62 201,47251,84120,88221,6200,00 0 0,00 2,11,7
15 122
5 0,37 23 1,69 14 1,03 211,54171,54191,4023 1,6900,00 0 0,00
13,6
2,1 1,8
0 0,00 24 1,95 17 1,38 120,98110,89151,2224 1,9580,65 0 0,00 2,11,8
5 111
0 0,00 20 1,63 15 1,22 161,30120,98151,2221 1,71 120,98 0 0,00
12,3
2,0 1,7
0 0,00 20 0,33 42 1,94 200,93180,83331,5335 1,62 261,20 0 0,00 2,11,7
−5 194
0 0,00 24 1,11 34 1,57 231,06231,06271,25241,11391,81 0 0,00
21,6
2,0 1,6
1 0,06 1 0,06 35 2,07 191,12211,2422 1,3026 1,54 22 1,30 5 0,30 2,11,7
−10 152
0 0,00 2 0,13 36 2,13 171,01160,9526 1,5423 1,36 25 1,48 7 0,41
16,9
2,2 1,8
0 0,00 1 0,06 23 1,46 291,85211,3416 1,0222 1,40 17 1,08 12 0,76 1,601,3
−25 141
0 0,00 2 0,13 25 1,59 291,85181,1517 1,0819 1,21 22 1,40 9 0,57
15,7
1,60 1,4
0 0,00 1 0,17 0 0,00 172,8991,5391,5340,6861,02 7 1,19 2,52,0
−35 53
0 0,00 0 0,00 2 0,34 142,3791,5391,5391,5361,02 4 0,68
5,9
2,3 1,8
0 0,00 0 0,00 1 0,34 5 1,7241,3831,0331,0372,41 3 1,03 2,31,8
−45 26
0 0,00 0 0,00 1 0,34 6 2,0741,3810,3431,0372,41 4 1,38
2,9
2,4 1,9
0 0,00 0 0,00 0 0,00 1 0,23122,7910 2,3371,6392,09 0 0,00 2,92,2
−55 39
0 0,00 0 0,00 0 0,00 2 0,47133,0292,0940,93 11 2,56 0 0,00
4,3
2,9 2,3
cp
 = 270
114,25 4,58 6,67 19,25 16,75 21,42 18,25 12,50 7,92 2,42
cp
 = 290 114,25 3,83 13,00 17,50 18,42 20,75 16,92 11,17 10,17 2,00
270 1371 55 0,36 80 0,53 231 1,52 2011,32257 169219 1,441500,99950,62 29 0,19 152,3
290 1371 46 0,30 156 1,02 210 1,38 2211,452491,632031,331400,921220,80 24 0,16 152,3

Y. A. Baurov et al. / Natural Science 3 (2011) 109-119
116
It is seen from Table 2 that this theoretical statement
is in total consistency with experiment. i.e. the maxi-
mum of earthquakes is observed at an angle of 90 be-
tween the direction to zenith and the vector Ag.
As was above said, the local increase in the Earth’s
currents gives effects similar to those shown in Figures
2, 3 (i.e. currents in the Earth are playing part of magnet
attached to the gravimeter), since in that case a consid-
erable enhancement of
А
x


 may occur and, as the
result, of the magnitude of new force functioning as
trigger for earthquakes.
As was shown in experiments with the plasma gen-
erator in gimbal suspension [3,4], the energy of the
plasma jet increases up to 40% when the vectorial poten-
tial A of current of the plasma generator has an angle of
~ 135 relative to the vector Ag.
On the basis of experiments with plasma generator
and those on investigating the action of the new force on
the -decay rate of radioactive elements [1-3,5], in Fig-
ure 4 a cone of directions of action of the new force on
the Earth’s substance is shown (in the case that there are
currents there flowing antiparallel to Ag). As is seen from
this figure, in the Northern hemisphere the maxi- mum
of new force will fall into latitudes between 30– 40
due to the current system of the Earth’s magnetic field
and the known direction of vector Ag.
The substance at those latitudes should “bulge” from
the Earth.
As was said above, in those latitudes we have maxi-
mum number of earthquakes of substantionally superfi-
cial character. The mountain rocks themselves are of
lesser hardness there than in the Southern hemisphere
where the new force compresses the substance and re-
jects the epicenters of earthquakes deeper into the Earth.
At that the epicenters become closer to the plane of
equator as is shown in Figure 1. The maximum number
of earthquakes occurs in southern latitudes, at 25S and
more close to the equator.
The long-term investigations of the influence of the
new force on the rate of -decay of radioactive elements
[1-3,5] as well as experiments with plasma devices on
energy generation with the aid of that force [1-4] allow
to conclude that in the bowels of the earth similar mani-
festations of new force might take place which lead to
local earth heating up, origination of various stresses in
its deep layers, and hence to accumulation of potential
energy liberated during earthquakes. The interaction of
current systems with the physical space through the new
force is possibly the main contribution of energy to
maintain energy balance of celestial bodies: stars and
planets. Such statement is naturally only a hypothesis
requiring thorough and long verification.
Thus the following factors point to the fact of influ-
ence of new interaction and the global anisotropy caused
by the vector Ag, on earth’s tectonic processes and par-
ticularly on earthquakes:
1) Predominance of crustal earthquakes in Northern
hemisphere and of deep focal ones in the Southern
hemisphere.
2) Maximum probability of initiation of earthquakes
when a local Earth’s volume passes the direction drawn
from the center of the Earth perpendicularly to the vector
Ag (the region of maximum change in the gravitational
field in the result of decreased |А| under the action of
vectorial potential of the Earth’s magnetic field). A re-
verse estimation of direction of Ag gives therewith its
coordinates:   270-290,   30 (from the distribu-
tion of earthquakes).
3) Existence of an “oceanic” and a “continental”
hemispheres of the Earth.
4) Absence of symmetry in the number of the most
potent earthquakes at 35 north and 35 south. The
southern hemisphere is formed by stronger mountain
rocks than the northern one.
5) Stresses in the earth’s crust experience daily varia-
tion along parallels of latitude and meridians (depend-
ence of
g
А
Z

on latitude  and on hour angle t). That
creates not only a system of parallel and meridional
stresses but also a diagonal quadrupole system. The ac-
tion of those stresses during long periods of time leads to
structural rearrangements in the earth’s crust. The influ-
ence of new interaction on the Earth has to have a near-
yearly variation, too, which probably manifests itself in
the Chandler’s motion of poles and, precisely, in
on-earth experiments as well [1,2].
6) The higher is the latitude , the lesser is the prob-
ability of potent earthquakes. In the Antarctic there are
mountains and fractures but no very strong earthquake
was on record in the entire period of observation on that
territory.
3. METHOD OF A SHORT-TERM
EARTHQUAKES FORECASTING
The analysis of collected data about strong earth-
quakes (see above) shows that practically all of them
happened at the moments when a seismically dangerous
region was in a certain manner oriented in space relative
to the stars.
To clarify the regularity observed, consider the dia-
gram in Figure 5 that conventionally represents the po-
sitions of the Earth and the earthquake zone at the mo-
ment of the event (see Table 3). For simplicity, the dia-
gram is brought to the plane of the ecliptic. The Earth 1
(globe) moves relative to the Sun 2 in an orbit 3 lying in

Y. A. Baurov et al. / Natural Science 3 (2011) 109-119
117
Table 3. Greatest earthquakes in the world in the second part of the XX century and in XXI century.
№ Place, coordinates Date, UTC time (Greenwich time)Magnitude by Richter scale α β
1 Kamchatka
52.76N 160.06E 1952 November 04 16:58:26.0 9.0 1° -
2 Andreanof Islands, Alaska
51.56N 175.39W 1957 March 09 8.6 90° -
3 Chile
38.24S 73.05W 1960 May 22 19:11:14 9.5 12° -
4 Prince William Sound, Alaska
61.02N 147.65E 1964 March 28 03:36:14 9.2 14° -
5 Armenia
41.0 N 44.2 E
1988, December 7,
07:41 6,9 - 41°
6 West Coast of Northern Sumatra
3.295 N 95.982 E
2004, December 26
00:58 9.0 90° -
7 Sakhalin Island
52.63 N 142.83 E 1995, May 27 13:03 6,7 - 40°
8 Pakistan
34.53 N 73.58E
2005 October 08
19:46 7.6 90° -
9 Haiti
19.0 N 72.0 W 2010 January 13 81° 3°
α–Angle between projection of the vector Zenith and projection of the vector Ag on the plane of the ecliptic; β–Angle between projection of
the vector V and projection of the vector Ag on the plane of the ecliptic.
Figure 5. Directions of vectors: Ag, V and R (radius vector
from Earth center or vector Zenith) for greatest earthquakes in
the world in the second part of the XX century and in XXI
century (Table 3).
the ecliptic plane. The latter is inclined to the equatorial
plane at an angle of
 = 2326’ (in the diagram the plane
of the ecliptic and the rotation of the Earth around its
axis are shown as circles). Eight positions of the Earth
are given at the moments of earthquakes (Positions: 1-8;
(Table 3)).
The Earth rotates around its axis, and the regions of
earthquakes also move along circular trajectories 4 rela-
tive to this axis. At the moments of earthquakes their
regions were in positions 1-8. The vectors V (Positions:
1-8) of linear velocities of daily rotation of earthquake’s
regions as well as the vector Ag take certain positions
relative to each other. (Vectors V are antiparallel with the
vector potential A from the magnetic field of the Earth).
Namely, if one brings the vector Ag and vector V of lin-
ear velocities, by a parallel transfer, to the point of the
earthquake epicenter, then in the moment of earthquake
the vectors V of circular velocities of the earthquake
regions fall into the limits of a zone restricted by two
conic surfaces circumscribed about the vector Ag, and
are directed along the generatrices of the family of conic
surfaces inside the zone in consideration. The openings
of the cones forming that zone are, respectively, 90 and
110.
The analysis of additional factors accompanying the
earthquakes has shown that the seismic activity in-
creased when the earthquakes were preceded by severe
changes in the total activity of the Sun (i.e. changes in
A

).
From the above reasoning one can indicate, with an
accuracy of  1 hour, the time points when a seismically
dangerous region will go through the most hazardous
spatial directions. Will an earthquake happen or not at a
given timepoint, show special devices measuring
changes in A

/t.
The detected regularities are used as the basis for a
method of short-term forecast of earthquakes with the
probability close to 100%.

Y. A. Baurov et al. / Natural Science 3 (2011) 109-119
118
The invention [35] has received a recognition in the
form of three gold medals in International Exhibitions in
Brussels, Geneva, and Seoul.
4. CONCLUSIONS
In this paper we have considered our planet as a pecu-
liar large-scale probe in the physical space the seismic
activity of which allows to judge the fluctuations of
physical space itself and so doing to refine its structure
from scales (10-33 cm-10-17 cm) [1-3,5,36,] up to 1028 cm
[1-3,37], (“probe in dark matter and dark energy” [38])
and as a peculiar large-scale probe and analogy of phys-
ics of seismic activity other astrophysical objects, for
example, pulsar [39,40].
As distinct from all earlier models of earthquakes
[16-33], the theory of byuon allows to establish the
deep-seated nature of physics of earthquakes, and there-
fore to predict place and time of an earthquake with the
probability close to 100%.
REFERENCES
[1] Baurov, Y.A. (1998) Structure of physical space and new
method of obtaining energy (theory, experiment, applica-
tions). Krechet, Moscow (in Russian).
[2] Baurov, Y.A. (2000) On the structure of physical vacuum
and a new interaction in Nature (theory, experiment and
applications). Nova Science, New York.
[3] Baurov, Y.A. (2004) Global anisotropy of physical space:
Experimental and theoretical basis. Nova Science, New
York.
[4] Baurov, Y.A., Timofeev, I.B., Chernikov, V.A., Chalkin,
S.F. and Konradov, A.A. (2003) Experimental investiga-
tion of the distribution of pulsed-plasma-generator at its
various spatial orientation and global anisotropy of space.
Physics Letters A, 311, 512.
doi:10.1016/S0375-9601(03)00567-X
[5] Baurov, Y.A., Konradov, A.A., Kuznetsov, E.A., Kush-
niruk, V.F., Ryabov, Y.B., Senkevich, A.P., Sobolev, Y.G.
and Zadorozsny, S. (2001) Modern Physics Letters A,
16(32), 2089.
doi:10.1142/S0217732301005187
[6] Baurov, Yu.A., Klimenko, E.Yu., and Novikov, S.I.,
(1990), Doklady Akademii Nauk, 315, 1116, (in Rus-
sian).
[7] Baurov, Y.A., Klimenko, E.Y. and Novikov, S.I. (1992)
Physics Lettets A, 162, 32.
doi:10.1016/0375-9601(92)90954-K
[8] Baurov, Yu.A. and Ryabov P.M., (1992), Doklady
Akademii Nauk, 326, 73 (in Russian).
[9] Baurov, Y.A. (1993) Physics Letters A, 181, 283.
doi:10.1016/0375-9601(93)90609-4
[10] Aiby, J.A. (1978) Earthquakes, M, Progress, 1978 (in
Russian).
[11] Thomaas, C.N., Jr. (1974) Global summary of human
response to natural hazards: Earthquakes. In: White, G.F.,
College Work: Natural Hazards Local, National, Global,
University of Colorado, New York, London, Toronto,
274-284.
[12] Golubeva, N.V. (1972) Catalogue of strong earthquakes
of the Globe, 1953 to 1967 with M  6. Academy of
Science USSR, Institute of the Earth’s Physics (in Rus-
sian).
[13] Regional Catalague of Earthquakes, Berkshire, United
Kingdom (1972-1981).
[14] Catalogue of epicentres in the international seismological
summary.
[15] Seismic bulletin of the network of reference seismic
stations of USSR (in Russian).
[16] Stovas, M.V. (1963) On stressed state of crustal layer in
region between 30 and 40. In: Gosgeoltechizdat, M.,
College Work: Problems of Planetary Geology, 275-284
(in Russian).
[17] Stovas, M.V. (1963) Several questions of tektogenesis. In:
Gosgeoltechizdat, M., College Work: Problems of Plane-
tary Geology, 222-274 (in Russian).
[18] Tsaregradsky, V.A. (1963) To question on deformations
of the earth’s crust. In: Gosgeoltechizdat, M., College
Work: Problems of Planetary Geology, 149-221 (in Rus-
sian).
[19] Veronnet Al. La forme de la Terre et sa constitution
interne. Paris, 1914.
[20] Tillo, A.A. (1889) Average height of land and average
depth of sea in Northern and Southern Hemispheres.
Dependence of Average Depths of Seas on Geographic
Latitude, Izvestiya Russkogo Geograficheskogo ob-
shchestva, 25 (in Russian).
[21] Schulz, S.S. (1965) In: Gosgeoltechizdat, M., College
Work: Basic Problems of Study of Quaternary Period,
1965, 147-150. (in Russian).
[22] Voronov, P.S. (1965) Essays on morphometry laws of
global relief of earth. Nauka, (in Russian).
[23] Shpitalnaya, A.A. (1978) On importance of choice of
reference system during investigation of non-stationary
cosmic processes. In: College Work: Problems of Inves-
tigation of Universe, 7 (in Russian).
[24] Shpitalnaya, A.A. (1971) To the question of destruction
of filaments by flares. Solar Data, 2, (in Russian).
[25] Sytinsky, A.D. (1966) Geomagnetisdm and aeronomy. 3
(in Russian).
[26] Sytinsky, A.D. (1973) Uspekhy Phyzicheskikh Nauk
(UFN), 3, 367 (in Russian).
[27] Simpson, J.F. (1968) Science Letters, 3, 418.
[28] Shpitalnaya, A.A., Vasilieva, G.Y. and Pystina, N.S.
(1975) On possibility of action of gravitation waves on
activity of earth and sun. In: College Work: Problems of
Investigation of Universe, 4, 129-137 (in Russian).
[29] Yakovlev, B.A. (1960) Astronomical collective work of
Lvov State University. 3, 152 (in Russian).
[30] Afanassieva, V.N. (1963) Geomagnetism and aeronomy.
3, 561 (in Russian).
[31] Danjon, A., (1962) CR Academy Science. Paris, 254,
3058.
[32] Gribbin, J. and Plagemaun, S. (1973) Nature, 243, 26.
doi:10.1038/243026a0
[33] Hessler, V.P. and Wescott, E.M. (1959) Nature, 184
(Suppl. 9), 627.
doi:10.1038/184627a0
[34] Baurov, Y.A. and Kopaev, A.V. (2002) Experimental
investigation of signals of a new nature with the aid of

Y. A. Baurov et al. / Natural Science 3 (2011) 109-119
119
two high precision stationary quartz gravimeters. Had-
ronic Journal, 25, 697.
[35] Baurov, Y.A., Baurov, A.Y., Baurov, A.Y., Shpitalnaya,
A.A., Abramyan, A.A. and Solodovnikov, V.A. (2006)
Method of short-term forecasting heightened seismic
danger of seismically dangerous regions. Invention,
2006110310 RF.
[36] Baurov, Y.A., et al. (2007) Physics of atomic nuclei. 70,
1825; Yadernaya fizika, 70, 1875.
[37] Baurov, Y.A. (2009) La Trama Svelata, La Teoria Byuon:
dall’origine dell’ Universo alla tecnlogia del futuro, pas-
sando per I’Uomo. Edizioni Polistampa.
[38] Baurov, Y.A. and Malov, I.F. (2010) Journal of Modern
Physics, 1, 17.
doi:10.4236/jmp.2010.11003
[39] Baurov, Y.A., Shpitalnaya, A.A. and Malov, I.F. (2005)
International Journal of Pure & applied Physics, 1, 71.
[40] Malov, I.F. and Baurov Y.A. (2007) Astronomy Reports,
51, 830.
doi:10.1134/S1063772907100071