J. Biomedical Science and Engineering, 2013, 6, 29-37 JBiSE
http://dx.doi.org/10.4236/jbise.2013.612A005 Published Online December 2013 (http://www.scirp.org/journal/jbise/)
Finite element modeling of the viscoelastic responses of the
eye during microvolumetric changes
Benjamin Cruz Perez1, Hugh J. Morris1, Richard T. Hart1, Jun Liu1,2*
1Department of Biomedical Engineering, The Ohio State University, Columbus, USA
2Department of Ophthalmology, The Ohio State University, Columbus, USA
Received 14 September 2013; revised 16 October 2013; accepted 1 November 2013
Copyright © 2013 Benjamin Cruz Perez et al. This is an open access article distributed under the Creative Commons Attribution
License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
A linear viscoelastic finite element model was built to
investigate factors that influenced the intraocular pres-
sure (IOP) elevations due to micro-volumetric changes
in the eye at three different rates. The viscoelastic
properties of the cornea and the sclera, including the
instantaneous modulus, equilibrium modulus, and
relaxation time constants, parametrically varied to
examine their effects on IOP elevations at different
rates of volumetric changes. The simulated responses
were in good agreement with the previously reported
experimental results obtained from porcine globes,
showing the general trend of higher IOP elevations at
faster rates. The simulations showed that all viscoe-
lastic properties influenced the profile of the dynamic
IOP due to volumetric changes, and the relative sig-
nificance of a specific parameter was highly depend-
ent on the rate of change.
Keywords: Viscoelasticity; Finite Element Modeling;
Intraocular Pressure; Cornea; Sclera
1. INTRODUCTION
Glaucoma is one of the leading causes of blindness
worldwide [1]. It is known to be associated with elevated
intraocular pressure (IOP), although the mechanisms of
IOP-induced optic nerve damages are not well under-
stood. The longstanding focus in the glaucoma field has
been on the steady-state IOP [2], but it is also known that
the IOP fluctuates during the day [3], as well as during
normal physiological activities such as postural change
[4,5], valsalva maneuver [6,7], water drinking [8], and
eye movement [9]. Previous studies have shown that
these short-term IOP fluctuations may be linked to glau-
coma risk [8,10,11].
Because it has been very difficult to characterize the
IOP-associated mechanical effects on ocular structures in
vivo, computational modeling has been a helpful tool to
describe and predict the biomechanical responses to IOP.
Using finite element modeling of the posterior portion of
the eye, Sigal et al. found that the material properties
(i.e., the elastic modulus) of the peripapilary sclera play-
ed an important role in determining the deformation and
stress states of the optic nerve head (ONH) [12], which
was the primary site for early glaucomatous damages.
These findings have led to a growing interest in study-
ing the biomechanical properties of the ocular shell and
the association with glaucoma progression. Characteriza-
tion of the mechanical properties of the cornea and sclera
has been conducted, including uniaxial [13-16], biaxial
[17], and inflation testing [18-22]. These studies showed
that cornea and sclera exhibit the typical nonlinear, ani-
sotropic, and viscoelastic mechanical behavior seen in
many other biological tissues [23-27].
Very little has been done to understand the response of
the eye to the short-term changes of volume and pressure.
Recently, our group examined IOP elevations in porcine
globes due to short-term micro-volumetric infusions. We
found a strong rate-dependent response showing that a
fast volumetric change induced a significantly higher
IOP change in the same eye compared to slow volumet-
ric changes [28]. The current study aims to build a finite
element model of the whole corneoscleral shell (omitting
the optic nerve head) to investigate how cornea and
sclera viscoelastic properties influence the eye’s response
to microvolumetric changes and how each factor con-
tributes to the rate-dependent response.
The whole eye models have been developed in the past
for understanding ocular physiology. Srodka [29] utilized
an axisymmetric finite element of the whole eye model
to evaluate the accuracy of the standard clinical method
for IOP measurement, the Goldmann applanation tono-
metry. Anderson et al. [30] utilized a 3D hyperelastic
*Corresponding author.

B. Cruz Perez et al. / J. Biomedical Science and Engineering 6 (2013) 29-37 30
whole eye model to investigate the influence of the
boundary conditions at the cornea and sclera conjunction
on the apical rise of the cornea during inflation. Our cur-
rent study incorporated the general formulation of these
previous whole eye models such as using an axisymmet-
ric geometry and omitting the ONH.
2. METHODS
2.1. Finite Element Modeling
An axisymmetric model of the corneoscleral shell of a
porcine eye was constructed in COMSOL (v4.3, Bur-
lington, MA, USA) using a series of ellipses assuming
symmetry along the optic axis. The ellipsoidal building
blocks allowed for realistic representation of the thick-
ness variations in the corneoscleral shell. The central
cornea thickness (CCT) was set to 0.96 mm [31], with a
radius of curvature of 7.5 mm, an assumed eccentricity
of 0.5, and a white-to-white (WTW) diameter of 13.5
mm. The scleral radius of curvature was set to 12.8 mm,
the anterior thickness to 0.89 mm, the equatorial thick-
ness to 0.58 mm, and the posterior thickness to 1.12 mm.
Because of the oblate spheroidal shape of the porcine
sclera, the ratio between the posterior radius and the
equatorial radius was set to 0.86. These dimensions were
the average measurements in porcine eyes (SiouxPreme
Packing Co, Sioux City, IA) acquired for other studies in
our laboratory.
The cornea and sclera were divided by a radial line
going through the center of the sclera ellipse. A small
transition zone at the cornea-sclera junction was imple-
mented with a finer mesh to avoid convergence difficult-
ties at the boundary of material property change. A filling
material was used to fill the inner space of the ocular
shell and to couple the intraocular volumetric change to
the mechanical responses of the shell (as described sub-
sequently). Figure 1(a) shows the constructed geometry
of the whole eye as described above, and Figure 1(b)
illustrates the typical finite element mesh.
The mesh was constructed using quadratic triangular
elements. A displacement mesh convergence test was
performed with five different mesh densities that moni-
tored five different locations to ensure mesh accuracy.
The mesh density chosen for this study had approxima-
tely 11,900 elements for a total of 54,000 degrees of
freedom (Figure 1(b)). A time-dependent solver in
COMSOL was utilized for solving the constitutive equa-
tions.
2.2. Simulated Infusions
Our laboratory has previously reported an experimental
infusion study on porcine whole globes at three different
rates (the details of the experiments are provided in the
referenced article) [28]. In the present study, the simula-
tions were performed following the design of the infu-
sion experiments. Specifically, three different infusion
rates (as shown in Ta b l e 1 ) were implemented to repre-
sent the typical time scales seen in short-term IOP fluc-
tuations (seconds to minutes) [28]. The total volume
change was set to 15 µL.
2.3. Using Thermal Expansion to Simulate
Intraocular Volumetric Change
In order to simulate intraocular volume increments, it
was computationally convenient to use a thermal expan-
sion model although in reality there is no temperature
dependence being studied. However, by assuming that
the tissue and fluids inside the ocular shell are income-
pressible, the volume change can be modeled as a simple
uniform volumetric thermal expansion of an intraocular
filling material, which can be implemented in the
COMSOL software to conveniently provide mechanical
coupling between the shell and the intraocular material.
The thermal expansion model assumed that all mesh
points within the enclosed filling material had a heat
source and the total power (P) was computed by the fol-
lowing relation:
d
d
p
V
V
Pt
C


 (1)
where dV/dt is the volumetric change rate, Cp is the spe-
cific heat, ρ is the density and αV is the coefficient of
thermal expansion for the filling material. The parame-
ters for low density polyethylene (LDPE) was used to
simulate the filling material because of its high coeffi-
cient of thermal expansion (αV = 4 × 10−4 1/˚C) [32]. The
volumetric change rate (dV/dt) resulted from the thermal
(a) (b)
Figure 1. (a) General geometry of the porcine eye; and (b)
Typical finite element mesh.
Table 1. The infusion rates and total duration used in the ex-
periments and simulations.
Fast Intermediate Slow
Rate 15 L/s 1 L/s 0.1 L/s
Duration 1 s 15 s 150 s

B. Cruz Perez et al. / J. Biomedical Science and Engineering 6 (2013) 29-37 31
expansion was set equal to the experimental infusion rate
assuming no leakage. A fixed point was placed at the
center of the filling material to ensure that it expands
equally in all directions. The filling material was ther-
mally insulated at the outer boundary to ensure conserva-
tion of energy.
To the best of our knowledge, experimental measure-
ments of the viscoelastic properties of the porcine cornea
and sclera including the instantaneous modulus, equilib-
rium modulus, and time constants have not been reported.
The selected baseline values were estimated from ap-
proximating the model predictions with the average re-
sults obtained from the infusion experiments in porcine
eyes [28]. 2.4. Constitutive Model
The cornea and sclera were modeled using a nearly in-
compressible linear viscoelastic generalized Maxwell
model. The stress-strain relationship is defined as follows
[32]:
3. RESULTS
A comparison of the simulated IOP/infusion volume re-
sponse (solid lines) and the average experimental re-
sponses in the porcine eyes (individual markers) is pre-
sented in Figure 2. All viscoelastic properties were set at
the baseline values. Selected volume levels (11 levels
evenly distributed between 0 to 15 µL) were used for
plotting the experimental response for visual clarity.
Most of the markers fell on the corresponding curves,
suggesting a good agreement between the model simula-
tion and the experimental results could be simultaneously
achieved at all three rates.
 
1
1i
t
m
equi i
i
tE t Ee

 



  




(2)
where Eequ is the equilibrium modulus, Ei is the relaxa-
tion modulus of the i-th branch, τi is the time constant of
the i-th branch, ε is the strain, and

 is the strain rate. A
two-branch model (i.e., m = 2) was adopted [16]. The
time constants (τ1 and τ2) are denoted as the short term
time constant (τs) and the long term time constant (τl) in
the later discussions for clear differentiation. The instant-
taneous (Einst) is defined as [14]:
Figure 3 presents the effects of instantaneous modulus
and equilibrium modulus on IOP elevations during mi-
cro-volumetric changes in the eye at different rates. The
instantaneous moduli of the cornea and the sclera were
varied proportionally (i.e., 1:5) while all other parame-
ters were kept at their baseline. In general, IOP eleva-
tions were higher at higher modulus regardless of the
infusion rates. Figure 3(a) shows that the IOP elevations
increased almost linearly with the instantaneous moduli
of the cornea and sclera at all rates. The slope however
was different for different rates with a larger slope at the
higher infusion rate. Figure 3(b) shows the effects of the
equilibrium modulus. The response was less linear for
the fast and intermediate infusion rates, particularly at
the lower modulus range.
0
inst
t
E



. (3)
The branch relaxation moduli were set to be equal (i.e.,
E1 = E2). Therefore, the branch relaxation moduli can be
found as:
12 2
inst equ
EE
EE   . (4)
The instantaneous and equilibration moduli of the
sclera were set to be 5 times of those of the cornea to
ensure a stiffer response of the sclera commonly reported
in experimental results and simulation studies [28,34,35].
All other parameters were allowed to vary independently. Treating each data point in Figure 3(a) as an individ-
ual eye, the data points form a group of simulated eyes
that only differ in instantaneous modulus. The relation-
ships of the IOP elevations at different infusion rates in
the group of eyes are plotted in Figure 4(a), showing
that the IOP elevations at different infusion rates are pre-
dicted to be linearly correlated in a group of eyes that
only differ in the instantaneous modulus. A similar plot
2.5. Parametric Study
The values of the material parameters of ocular shell
were varied within a range of the plausible values for the
porcine eye (as shown in Table 2) to evaluate the effects
that each parameter has on the short-term IOP elevations.
Table 2. Material parameters used in the model simulations.
Sclera Cornea
Material properties Baseline Range Baseline Range
Instantaneous modulus 5.5 MPa 3.1 - 7.9 MPa 1.1 MPa 0.62 - 1.6 MPa
Equilibrium modulus 1.325 MPa 0.325 - 2.325 MPa 0.265 MPa 0.065 - 0.465 MPa
Short term time constant 0.35 sec 0.05 - 0.65 sec 0.35 sec 0.05 - 0.65 sec
Long term time constant 68 sec 18 - 128 sec 68 sec 18 - 128 sec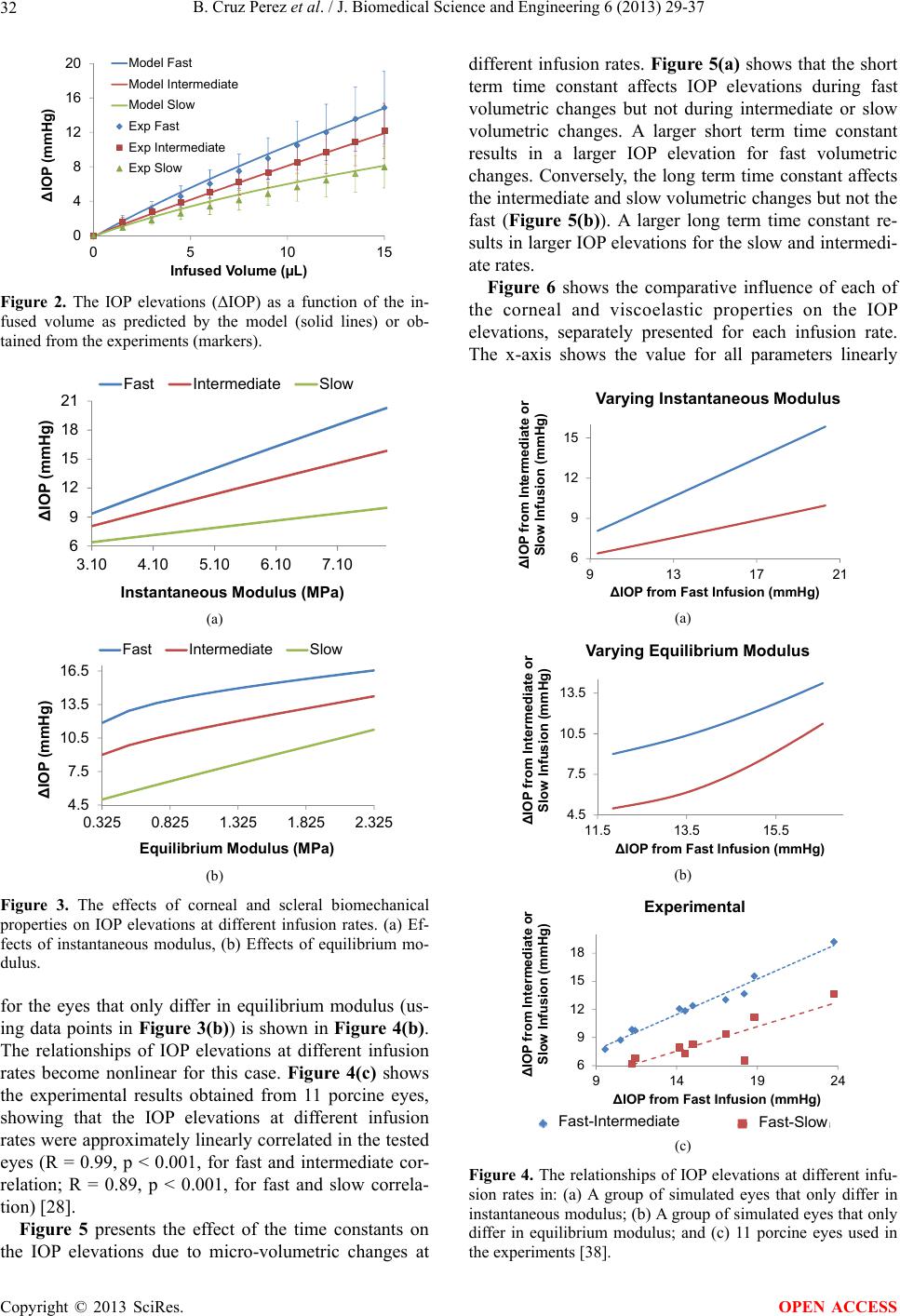

B. Cruz Perez et al. / J. Biomedical Science and Engineering 6 (2013) 29-37 32
0
4
8
12
16
20
0510 15
∆IOP (mmHg)
Infused Volume (µL)
Model Fast
Model Intermediate
Model Slow
Exp Fast
Exp Intermediate
Exp Slow
Figure 2. The IOP elevations (ΔIOP) as a function of the in-
fused volume as predicted by the model (solid lines) or ob-
tained from the experiments (markers).
6
9
12
15
18
21
3.10 4.10 5.10 6.10 7.10
∆IOP (mmHg)
Instantaneous Modulus (MPa)
Fast Intermediate Slow
a
.
(a)
4.5
7.5
10.5
13.5
16.5
0.325 0.825 1.325 1.825 2.325
∆IOP (mmHg)
Equilibrium Modulus (MPa)
Fast IntermediateSlow b.
(b)
Figure 3. The effects of corneal and scleral biomechanical
properties on IOP elevations at different infusion rates. (a) Ef-
fects of instantaneous modulus, (b) Effects of equilibrium mo-
dulus.
for the eyes that only differ in equilibrium modulus (us-
ing data points in Figure 3(b)) is shown in Figure 4(b).
The relationships of IOP elevations at different infusion
rates become nonlinear for this case. Figure 4(c) shows
the experimental results obtained from 11 porcine eyes,
showing that the IOP elevations at different infusion
rates were approximately linearly correlated in the tested
eyes (R = 0.99, p < 0.001, for fast and intermediate cor-
relation; R = 0.89, p < 0.001, for fast and slow correla-
tion) [28].
Figure 5 presents the effect of the time constants on
the IOP elevations due to micro-volumetric changes at
different infusion rates. Figure 5(a) shows that the short
term time constant affects IOP elevations during fast
volumetric changes but not during intermediate or slow
volumetric changes. A larger short term time constant
results in a larger IOP elevation for fast volumetric
changes. Conversely, the long term time constant affects
the intermediate and slow volumetric changes but not the
fast (Figure 5(b)). A larger long term time constant re-
sults in larger IOP elevations for the slow and intermedi-
ate rates.
Figure 6 shows the comparative influence of each of
the corneal and viscoelastic properties on the IOP
elevations, separately presented for each infusion rate.
The x-axis shows the value for all parameters linearly
6
9
12
15
9 13172
∆IOP from Intermediate or
Slow Infusion (mmHg)
∆IOP from Fast Infusion (mmHg)
a. Varying Instantaneous Modulus
1
(a)
4.5
7.5
10.5
13.5
11.5 13.5 15.5
∆IOP from Intermediate or
Slow Infusion (mmHg)
∆IOP from Fast Infusion (mmHg)
b. Varying Equilibrium Modulus
(b)
6
9
12
15
18
91419
∆IOP from Intermediate or
Slow Infusion (mmHg)
∆IOP from Fast Infusion (mmHg)
c. Experimental
24
Fast-Intermediate Fast-Slow
(c)
Figure 4. The relationships of IOP elevations at different infu-
sion rates in: (a) A group of simulated eyes that only differ in
instantaneous modulus; (b) A group of simulated eyes that only
differ in equilibrium modulus; and (c) 11 porcine eyes used in
the experiments [38].

B. Cruz Perez et al. / J. Biomedical Science and Engineering 6 (2013) 29-37 33
7
10
13
16
0.05 0.2 0.35 0.5 0.65
∆IOP (mmHg)
Short Term Time Constant (sec)
Fast Intermediate Slow
a.
(a)
5.5
8.5
11.5
14.5
18 43 68 93118
∆IOP (mmHg)
Long Term Time Constant (sec)
Fast Intermediate Slow
b.
(b)
Figure 5. The effects of (a) the short term time constant and (b)
the long term time constant on IOP elevations at different infu-
sion rates.
scaled from its minimum value (−1) to maximum value
(+1). It is found that the instantaneous modulus has the
largest influence for the fast and intermediate rates, but
its influence diminishes for the slow infusion rate, for
which the equilibrium modulus takes the dominant role.
The time constants generally have smaller effects than
the moduli, but their influence could be comparable to
one of the two types of moduli depending on the rates.
Figure 7 shows the distribution of the von Mises
stresses and principal strains in the cornea and the sclera
at the end of the fast infusion. The stresses and strains
were apparently different in the cornea as compared to
those in the sclera, due to the discrepancy in the material
properties. The stresses and strains also showed varia-
tions through the thickness as contrasted to what a thin-
shell model would predict [22].
4. DISCUSSION
In this work, we have built a finite element model of the
whole ocular shell to investigate factors influencing the
short-term volume/pressure changes in the eye. We found
that a simple linear viscoelastic model with two branches
simulating the short-term and long-term relaxation proc-
esses could adequately reproduce the experimental data
obtained from the infusion experiments performed in
porcine eyes (Figure 2). Although the three different
infusion rates used in this study are all within the time
scale of short-term IOP fluctuations seen in the eye (i.e.,
a time scale shorter than a few minutes), there was a
9
12
15
18
21
-1-0.50 0.5 1
∆IOP (mmHg)
Scaled Factor
a. fast
(a)
8
11
14
17
-1 -0.500.51
∆IOP (mmHg)
Scaled Factor
b. intermediate
(b)
4.5
6.5
8.5
10.5
-1 -0.500.51
∆IOP (mmHg)
Scaled Factor
c. slow
Instantaneous ModulusEquilibrium ModulusShort Term T ime ConstLong T erm Time Const
(c)
Figure 6. Effects of all corneal scleral factors on IOP eleva-
tions due to micro-volumetric changes at the (a) fast, (b) inter-
mediate, and (c) slow rate.
clear rate-dependent response suggesting that the eye
responds differently to micro-volumetric changes that
occur within seconds, 10’s of seconds, or minutes. The
larger the rate of change within this time scale, the higher
the IOP elevations observed in both experiments and
simulations. This rate-dependence confirmed the viscoe-
lastic responses of the ocular shell, as well as the relevant
range for the time constants of the relaxation processes in
the ocular shell (i.e., seconds to minutes), which were
found using stress relaxation tests on tissue strips [16].
Both experiments and simulations reported a linear
ΔIOP/volume relationship, which was also experimen-
tally observed by Pierscionek et al. in fresh porcine eye
[36].
Based on the finite element model, a higher instanta-
neous modulus, i.e., a stiffer response to a step load,
would result in a larger final ∆IOP for a given infusion
volume regardless of the rate of change (Figure 3(a)). A
similar positive relationship between ∆IOP and equilib-
rium modulus was also shown (Figure 3(b)). The rela-
tionship between instantaneous modulus and ∆IOP

B. Cruz Perez et al. / J. Biomedical Science and Engineering 6 (2013) 29-37 34
(A)
2.4229 × 10
4
×10
4
2.4
2.2
2
1.8
1.6
1.4
1.2
1
0.8
0.6
0.4
2978.7
(a)
(B)
2.5612 × 10
−3
1.9321 × 10
−3
0.0027
0.0026
0.0025
0.0024
0.0023
0.0022
0.0021
0.002
0.0019
(b)
Figure 7. Color maps of von Mises stress (a) and first principal
strain (b) in the cornea and the sclera at the end of the fast infu-
sion (15 µL/s for 1 second).
relationship was linear (i.e., a constant slope) while there
was a degree of nonlinearity in the relationship between
equilibrium modulus and ∆IOP, although that was mostly
seen in the fast rate response.
In our previous experimental study, we found a strong
correlation between the IOP elevations measured at dif-
ferent rates across different eyes (Figure 4(c)), that is, an
eye that had a larger ΔIOP at the fast rate would also
have a larger ΔIOP at the slower rates. Interestingly, this
correlation was strongly linear (R = 0.99 or 0.89) ac-
cording to the experimental data. This linear correlation
could be better predicted by the variance in instantaneous
modulus (Figure 4(a)) rather than the variance in the
equilibrium modulus which corresponded to a more
nonlinear response (Figure 4(b)).
The short term time constant had a positive relation-
ship with ΔIOP during fast infusions, but a flat response
for intermediate and slow infusions (Figure 5(a)). This
time constant represents the time scale of the fast relaxa-
tion processes in the tissue. Because of the selected range
of this constant in the present study (0.05 to 0.65 sec), it
is expected that it does not influence the intermediate and
slow rates whose time scales were far beyond this range.
The long term time constant represents the slower re-
laxation process. As shown in Figure 5(b), the ΔIOP in
the intermediate and slow infusions were noticeably af-
fected by this time constant, but the ΔIOP in the fast in-
fusion had a flat response because its short duration.
As discussed above, all viscoelastic properties affected
the volume/pressure response, and the relative signifi-
cance of each specific parameter was rate-dependent. For
example, at the faster rates (e.g., the fast and intermedi-
ate infusion rates used in the present study), the instant-
taneous modulus had the largest influence on the magni-
tude of ΔIOP (Figures 6(a) and (b)). As the rate decreas-
ed, the equilibrium modulus started to dominate (Figure
6(c)). In addition, the short-term time constant had mini-
mal effect on intermediate and slow infusions, but sig-
nificant effect on fast infusion; while the long-term time
constant showed the opposite trend.
Previous computational work has shown that the pos-
terior sclera is a major biomechanical structure that
strongly influences the mechanical states of the optic
nerve head where the glaucomatous injuries occur [12].
The results from the present study showed that the vis-
coelastic properties of the corneoscleral shell could also
influence the dynamic profile of IOP. For example, a
larger instantaneous modulus or equilibrium modulus
(i.e., a stiffer corneoscleral shell) would result in higher
IOP fluctuations due to micro-volumetric changes in the
eye during daily activities. Although the pathophysiolgi-
cal consequences of IOP fluctuations are not fully under-
stood, it is generally believed that they are detrimental to
the delicate tissue structures in the eye, especially when
they are at high magnitudes and fast acting [37,38]. It is
therefore important to understand and characterize the
viscoelastic properties of the ocular shell and their rela-
tionship to the dynamic IOP.
This work has several limitations. First, the eye is ac-
tually a “leaky” shell with a pressure-dependent outflow
[39]. For simplicity, this pressure-dependent outflow was
not implemented in the current model. Instead, a net flow
rate was used as the infusion rate. This could have intro-
duced certain inaccuracy in the calculations of the ΔIOP;
however, this error was likely small due to the short time
duration of the simulated experiments. Second, the re-
laxation moduli for the branches in the Maxwell model
were set to the same values. Although this assumption
has been used in the past [14], future experimental stud-
ies as well as modeling work are needed to verify this
assumption and investigate its implications. Third, a lin-
ear viscoelastic model was used and the reported nonlin-

B. Cruz Perez et al. / J. Biomedical Science and Engineering 6 (2013) 29-37 35
earity in the stress-strain relationship of the cornea and
sclera was neglected. Because the corneoscleral shell is
primarily a collagenous tissue, mechanical nonlinearity is
expected and has been confirmed in the past. Constitu-
tive modeling that accounts for the nonlinear responses
would thus be more desirable [40-44]. However, in the
present study, the IOP was always above the baseline of
15 mmHg during the simulated infusion studies, which
likely positioned the eye close to or beyond the toe re-
gion of the corneoscleral response [28]. Therefore, the
linear approximation, which simplifies the model, is
likely sufficient in the present study. Fourth, previous
studies have shown the importance of collagen micro-
structure (for example, anisotropic collagen fiber align-
ment) in affecting the stress and strain distributions in the
cornea and sclera [20,45-48]. Future work should invest-
tigate how heterogeneous microstructural and material
properties could affect the eye’s response to dynamic
micro-volumetric changes.
5. CONCLUSION
In conclusion, this study utilized finite element models of
a porcine corneoscleral shell to investigate the effects of
the shell’s viscoelastic properties on the IOP elevations
due to volumetric changes in the eye. The major finding
was that the instantaneous and equilibrium moduli, as
well as the short-term and long-term time constants, had
an effect on IOP elevations, and the relative significance
of the specific parameters was highly dependent on the
rate of change.
6. ACKNOWLEDGEMENTS
This project was funded by NIH grants RO1EY020929 and RO1EY-
020929-S1. The authors greatly acknowledge Xueliang Pan (PhD),
Paul A Weber (MD), Junhua Tang (PhD), and Joel Palko for their valu-
able input to this work.
REFERENCES
[1] Quigley, H.A. (1999) Neuronal death in glaucoma. Pro-
gress in Retinal and Eye Research, 18, 39-57.
http://dx.doi.org/10.1016/S1350-9462(98)00014-7
[2] Musch, D.C., Gillespie, B.W., Niziol, L.M., Lichter, P.R.
and Varma, R. (2011) Intraocular pressure control and
long-term visual field loss in the collaborative initial
glaucoma treatment study. Ophthalmology, 118, 1766-
1773. http://dx.doi.org/10.1016/j.ophtha.2011.01.047
[3] Liu, J.H.K., Zhang, X., Kripke, D.F. and Weinreb, R.N.
(2003) Twenty-four-hour intraocular pressure pattern as-
sociated with early glaucomatous changes. Investigative
Ophthalmology & Visual Science, 44, 1586-1590.
http://dx.doi.org/10.1167/iovs.02-0666
[4] Parsley, J., Powell, R.G., Keightley, S.J. and Elkington,
A.R. (1987) Postural response of intraocular pressure in
chronic open-angle glaucoma following trabeculectomy.
British Journal of Ophthalmology, 71, 494-496.
http://dx.doi.org/10.1136/bjo.71.7.494
[5] Weinreb, R.N., Cook, J. and Friberg, T.R. (1984) Effect
of inverted body position on intraocular pressure. Ameri-
can Journal of Ophthalmology, 98, 784-787.
[6] Rafuse, P.E., Mills, D.W., Hooper, P.L., Chang, T.S. and
Wolf, R. (1994) Effects of Valsalva’s manoeuvre on in-
traocular pressure. Canadian Journal of Ophthalmology,
29, 73-76.
[7] Vieira, G.M., Oliveira, H.B., de Andrade, D.T., Bottaro,
M. and Ritch, R. (2006) Intraocular pressure variation dur-
ing weight lifting. Archives of Ophthalmology, 124, 1251-
1254. http://dx.doi.org/10.1001/archopht.124.9.1251
[8] Susanna Jr., R., Vessani, R.M., Sakata, L., Zacarias, L.C.
and Hatanaka, M. (2005) The relation between intraocu-
lar pressure peak in the water drinking test and visual
field progression in glaucoma. British Journal of Oph-
thalmology, 89, 1298-1301.
http://dx.doi.org/10.1136/bjo.2005.070649
[9] Coleman, D.J. and Trokel, S. (1969) Direct-recorded in-
traocular pressure variations in a human subject. Archives
of Ophthalmology, 82, 637-640.
http://dx.doi.org/10.1001/archopht.1969.00990020633011
[10] Kiuchi, T., Motoyama, Y. and Oshika, T. (2006) Rela-
tionship of progression of visual field damage to postural
changes in intraocular pressure in patients with normal-
tension glaucoma. Ophthalmology, 113, 2150-2155.
http://dx.doi.org/10.1016/j.ophtha.2006.06.014
[11] Schuman, J.S., et al. (2000) Increased intraocular pres-
sure and visual field defects in high resistance wind in-
strument players. Ophthalmology, 107, 127-133.
http://dx.doi.org/10.1016/S0161-6420(99)00015-9
[12] Sigal, I.A., Flanagan, J.G. and Ethier, C.R. (2005) Factors
influencing optic nerve head biomechanics. Investigative
Ophthalmology & Visual Science, 46, 4189-4199.
http://dx.doi.org/10.1167/iovs.05-0541
[13] Palko, J.R., Pan, X. and Liu, J. (2011) Dynamic testing of
regional viscoelastic behavior of canine sclera. Experi-
mental Eye Research, 93, 825-832.
http://dx.doi.org/10.1016/j.exer.2011.09.018
[14] Downs, J.C., et al. (2005) Viscoelastic material properties
of the peripapillary sclera in normal and early-glaucoma
monkey eyes. Investigative Ophthalmology & Visual Sci-
ence, 46, 540-546. http://dx.doi.org/10.1167/iovs.04-0114
[15] Girard, M., Suh, J.-K.F., Hart, R.T., Burgoyne, C.F. and
Downs, J.C. (2007) Effects of storage time on the mecha-
nical properties of rabbit peripapillary sclera after enucle-
ation. Current Eye Research, 32, 465-470.
http://dx.doi.org/10.1080/02713680701273792
[16] Downs, J.C., et al. (2003) Viscoelastic characterization of
peripapillary sclera: Material properties by quadrant in
rabbit and monkey eyes. Journal of Biomechanical Engi-
neering, 125, 124-131.
http://dx.doi.org/10.1115/1.1536930
[17] Eilaghi, A., et al. (2010) Biaxial mechanical testing of
human sclera. Journal of Biomechanics, 43, 1696-1701.
http://dx.doi.org/10.1016/j.jbiomech.2010.02.031

B. Cruz Perez et al. / J. Biomedical Science and Engineering 6 (2013) 29-37 36
[18] Fazio, M.A., et al. (2012) Regional variations in mecha-
nical strain in the posterior human sclera. Investigative
Ophthalmology & Visual Science, 53, 5326-5333.
http://dx.doi.org/10.1167/iovs.12-9668
[19] Coudrillier, B., et al. (2012) Biomechanics of the human
posterior sclera: Age- and glaucoma-related changes
measured using inflation testing. Investigative Ophthal-
mology & Visual Science, 53, 1714-1728.
http://dx.doi.org/10.1167/iovs.11-8009
[20] Girard, M.J.A., Downs, J.C., Bottlang, M., Burgoyne, C.F.
and Suh, J.K.F. (2009) Peripapillary and posterior scleral
mechanics—Part II: Experimental and inverse finite ele-
ment characterization. Journal of Biomechanical Engi-
neering, 131, Article ID: 051012.
http://dx.doi.org/10.1115/1.3113683
[21] Girard, M.J.A., Downs, J.C., Burgoyne, C.F. and Suh,
J.K.F. (2008) Experimental surface strain mapping of
porcine peripapillary sclera due to elevations of intraocu-
lar pressure. Journal of Biomechanical Engineering, 130,
Article ID: 041017. http://dx.doi.org/10.1115/1.2948416
[22] Tang, J. and Liu, J. (2012) Ultrasonic measurement of
scleral cross-sectional strains during elevations of intra-
ocular pressure: Method validation and initial results in
posterior porcine sclera. Journal of Biomechanical Engi-
neering, 134, Article ID: 091007.
http://dx.doi.org/10.1115/1.4007365
[23] Nguyen, T. and Boyce, B. (2011) An inverse finite ele-
ment method for determining the anisotropic properties of
the cornea. Biomechanics and Modeling in Mechanobi-
ology, 10, 323-337.
http://dx.doi.org/10.1007/s10237-010-0237-3
[24] Nguyen, T.D., Jones, R.E. and Boyce, B.L. (2008) A
nonlinear anisotropic viscoelastic model for the tensile
behavior of the corneal stroma. Journal of Biomechanical
Engineering, 130, Article ID: 041020.
http://dx.doi.org/10.1115/1.2947399
[25] Elsheikh, A. and Anderson, K. (2005) Comparative study
of corneal strip extensometry and inflation tests. Journal
of the Royal Society Interface, 2, 177-185.
http://dx.doi.org/10.1098/rsif.2005.0034
[26] He, X. and Liu, J. (2009) A quantitative ultrasonic spec-
troscopy method for noninvasive determination of cor-
neal biomechanical properties. Investigative Ophthalmo-
logy & Visual Science, 50, 5148-5154.
http://dx.doi.org/10.1167/iovs.09-3439
[27] Liu, J. and He, X. (2009) Corneal stiffness affects IOP
elevation during rapid volume change in the eye. Investi-
gative Ophthalmology & Visual Science, 50, 2224-2229.
http://dx.doi.org/10.1167/iovs.08-2365
[28] Morris, H.J., et al. (2013) Correlation between biomecha-
nical responses of posterior sclera and IOP elevations
during micro intraocular volume change. IOVS, Under
Review.
[29] Sródka, W. (2010) Goldmann applanation tonometry—
Not as good as gold. Acta of Bioengineering and Biome-
chanics/Wrocław University of Technology, 12, 39-47.
[30] Anderson, K., El-Sheikh, A. and Newson, T. (2004) Ap-
plication of structural analysis to the mechanical behav-
iour of the cornea. Journal of the Royal Society Interface,
1, 3-15. http://dx.doi.org/10.1098/rsif.2004.0002
[31] Asejczyk-Widlicka, M., Schachar, R.A. and Pierscionek,
B.K. (2008) Optical coherence tomography measure-
ments of the fresh porcine eye and response of the outer
coats of the eye to volume increase. Journal of Biomedi-
cal Optics, 13, Article ID: 024002.
http://dx.doi.org/10.1117/1.2907453
[32] Callister, W.D. (2003) Materials science and engineering
an introduction. John Wiley & Sons, New York.
[33] Mase, G.T. and Mase, G.E. (2010) Continuum mechanics
for engineers. 3rd Edition, Taylor & Francis, London.
[34] Ethier, C.R., Johnson, M. and Ruberti, J. (2004) Ocular
biomechanics and biotransport. Annual Review of Biome-
dical Engineering, 6, 249-273.
http://dx.doi.org/10.1146/annurev.bioeng.6.040803.14005
5
[35] Woo, S.L.Y., Kobayashi, A.S., Schlegel, W.A. and Law-
rence, C. (1972) Nonlinear material properties of intact
cornea and sclera. Experimental Eye Research, 14, 29-39.
http://dx.doi.org/10.1016/0014-4835(72)90139-X
[36] Pierscionek, B.K., Asejczyk-Widlicka, M. and Schachar,
R.A. (2007) The effect of changing intraocular pressure
on the corneal and scleral curvatures in the fresh porcine
eye. The British Journal of Ophthalmology, 91, 801-803.
http://dx.doi.org/10.1136/bjo.2006.110221
[37] Caprioli, J. and Coleman, A.L. (2008) Intraocular pres-
sure fluctuation: A risk factor for visual field progression
at low intraocular pressures in the advanced glaucoma
intervention study. Ophthalmology, 115, 1123-1129.e3.
http://dx.doi.org/10.1016/j.ophtha.2007.10.031
[38] Resta, V., Novelli, E., Vozzi, G., Scarpa, C., Caleo, M.,
Ahluwalia, A., Solini, A., Santini, E., Parisi, V., Di Vir-
gilio, F. and Galli-Resta, L. (2007) Acute retinal ganglion
cell injury caused by intraocular pressure spikes is medi-
ated by endogenous extracellular ATP. European Journal
of Neuroscience, 25, 2741-2754.
http://dx.doi.org/10.1111/j.1460-9568.2007.05528.x
[39] Epstein, D.L., Rowlette, L.L. and Roberts, B.C. (1999)
Acto-myosin drug effects and aqueous outflow function.
Investigative Ophthalmology & Visual Science, 40, 74-81.
[40] Tang, H., Buehler, M.J. and Moran, B. (2009) A constitu-
tive model of soft tissue: From nanoscale collagen to tis-
sue continuum. Annals of Biomedical Engineering, 37, 1117-
1130. http://dx.doi.org/10.1007/s10439-009-9679-0
[41] Comninou, M. and Yannas, I.V. (1976) Dependence of
stress-strain nonlinearity of connective tissues on the geo-
metry of collagen fibers. Journal of Biomechanics, 9, 427-
433. http://dx.doi.org/10.1016/0021-9290(76)90084-1
[42] Maceri, F., Marino, M. and Vairo, G. (2012) An insight
on multiscale tendon modeling in muscle-tendon integra-
ted behavior. Biomechanics and Modeling in Mechanobi-
ology, 11, 505-517.
http://dx.doi.org/10.1007/s10237-011-0329-8
[43] Maceri, F., Marino, M. and Vairo, G. (2010) A unified
multiscale mechanical model for soft collagenous tissues
with regular fiber arrangement. Journal of Biomechanics,
43, 355-363.
http://dx.doi.org/10.1016/j.jbiomech.2009.07.040

B. Cruz Perez et al. / J. Biomedical Science and Engineering 6 (2013) 29-37 37
[44] Marino, M. and Vairo, G. (2012) Stress and strain locali-
zation in stretched collagenous tissues via a multiscale
modelling approach. Computer Methods in Biomechanics
and Biomedical Engineering, 2012, 1-20.
http://dx.doi.org/10.1080/10255842.2012.658043
[45] Pinsky, P.M., van der Heide, D. and Chernyak, D. (2005)
Computational modeling of mechanical anisotropy in the
cornea and sclera. Journal of Cataract & Refractive Sur-
gery, 31, 136-145.
http://dx.doi.org/10.1016/j.jcrs.2004.10.048
[46] Girard, M.J.A., Downs, J.C., Burgoyne, C.F. and Suh, J.K.F.
(2009) Peripapillary and posterior scleral mechanics—Part I:
Development of an anisotropic hyperelastic constitutive
model. Journal of Biomechanical Engineering, 131, Ar-
ticle ID: 051011. http://dx.doi.org/10.1115/1.3113682
[47] Grytz, R., Sigal, I.A., Ruberti, J.W., Meschke, G. and
Downs, J.C. (2012) Lamina cribrosa thickening in early
glaucoma predicted by a microstructure motivated growth
and remodeling approach. Mechanics of Materials, 44,
99-109. http://dx.doi.org/10.1016/j.mechmat.2011.07.004
[48] Grytz, R., Meschke, G. and Jonas, J. (2011) The collagen
fibril architecture in the lamina cribrosa and peripapillary
sclera predicted by a computational remodeling approach.
Biomechanics and Modeling in Mechanobiology, 10, 371-
382. http://dx.doi.org/10.1007/s10237-010-0240-8