 Engineering, 2013, 5, 386-390 http://dx.doi.org/10.4236/eng.2013.510B078 Published Online October 2013 (http://www.scirp.org/journal/eng) Copyright © 2013 SciRes. ENG Using the Support Vector Machine Algorithm to Predict β-Turn Types in Proteins Xiaobo Shi, Xiuzhen Hu College of Sciences Inner Mongolia University of Technology, Hohhot, China Email: hh_xx_zz@yahoo.com.cn Received ********* 2013 ABSTRACT The structure and function of proteins are closely related, and protein structure decid es its function, ther efore protein structure pr ediction is quite important. β-turns are important components of protein secondary structure. So develop- ment of an accurate prediction method of β-turn types is very necessary. In this paper, we used the composite vector with position conservation scoring function, increment of diversity and predictive secondary structure information as the input parameter of support vector machine algorithm for predicting the β-turn types in the database of 426 protein chains, obtained the overall prediction accuracy of 95.6%, 97.8%, 97.0%, 98.9%, 99.2%, 91.8%, 99.4% and 83.9% with the Matthews Correlation Coefficient values of 0.74, 0.68, 0.20, 0.49, 0.23, 0.47, 0.49 and 0.53 for types I, II, VIII, I’, II’, IV, VI and nonturn respectively, which is better than other predictio n. Keywords: Support Vector Machine Algorithm; Increment of Diversity Value; Position Conservation Scoring Function Value; Secondary Structure Information 1. Introduction Protein secondary structure prediction is an intermediate step in overall tertiary structure prediction. The second- ary structure of a protein consists of regular, local regular and non-regular secondary structure. Local regular sec- ondary structure contains tight turns and Ω loops. Tight turns can be divided into δ-, γ-, β-, α- and π-turns ac- cording to the number of residues involved [1,2]. β-turns are the most common and largest number turns, which constitute about 25% of the res idues in proteins [1,3-5]. β-turn is a fo ur-residue reversal in a protein chain that the distance between the residues i and i + 3 is less than 7Å and the two central residues (i + 1 and i + 2) must not be helical. According to the ψ/ ϕ values of the central resi- dues i + 1 and i + 2, β-turns are classified into nine types: I, II, VIII, I’, II’, VIa1, VIa2, VIb and IV [3-7]. Mostly, β-turn types VIa1, VIa2 and VIb are merged into one type, called type VI [3 ,5]. β-turn plays a vital role in protein, such as folding sta- bility, recognition and structure assembly [2,8] and can provide templates information for drug molecule design, such as anesthetic, pesticide and antigen, etc. [1]. Ac- cording to the ψ/ ϕ values of β-turn residues we can build up a complete three-dimensional structure for a given primary sequence. Thus, it is important to develop a me- thod, which can predict β-turn types with high accuracy [4]. Some methods have been developed for prediction of β-turn types, such as propensities [5,6,9], sequence-cou- pled model [3], neural networks (NN) algorithm [4,7,8] and support vector machine (SVM) algorithm [10]. In 2008, Kirschner and Frishman [7] using NN algorithm to predicting the β-turn types, obtained the best prediction performance among above works, the Qtotal for types I, II, VIII, IV, I’ and II’ are 85.4%, 96.2%, 93.0%, 85.2%, 98.8% and 98.6%, and the MCC are 0.31, 0.34, 0.08, 0.19, 0.36 and 0.14, respectively. In this work, we improved the input parameters of the SVM and used the seven-fold cross-validation to predict- ing the β-turn types in the widely used database which contained 426 protein chains, achieved better prediction result than previous studies. Furthermore, to test the ef- fect of the database size, we also predicted β-turn types in other two databases contained 547 and 823 protein chains, respectively. 2. Materials and Methods 1) Database In this paper, we used the database contained 426 pro- tein chains, called SET426. The SET426 described by Guruprasad and Rajkumar [11] that has been widely used in β-turn type prediction [4,5,7]. And we also used other two databases contained 547 and 823 protein chains, call- ed SET547 and SET823, respectively. The SET547 and  X. B. SHI, X. Z. HU Copyright © 2013 SciRes. ENG 387 SET823 described by Fuchs and Alix [5]. The databases contain chains solved by X-ray crystallogr aphy with a re- solution better than 2.0 Å, and no two protein chains have >25% identity. The numbers of β-turn types and nonturn are shown in Table 1. There are one hundred and nin e ty one proteins in the SET426 are contained in the SET547, ninety proteins in the SET426 are contained in the SET823 and two hun- dred and ten proteins in the SET547 are contained in the SET823. 2) Extracted Segments According to the Fu chs and Alix’s [5] work, the pre- diction of the β-turn types on a given window which con- tained L amino acids, that the center amino acid is a β- turn (residues i to i + 3) with m flanking residues on the left (i-m to i-1) and n flanking residues on the right (i + 4 to i + 3 + n). In Fuchs and Alix’s [5] work, they selected the window which contained 12 amino acids. In our work, we found that the optimal window size is 10 residues long (m = n = 3). So we selected the window which con- tained 10 amino acids to predict the β-turn types in pro- teins. 3) The Position Conservation Scoring Function (DF) The position conservation scoring function algorithm is a simple but effective forecast model. In this work, we only calculate the scores of β-turn types, the score of seg- ment S can be defined as [2]. 20 ,min 120 ,max ,min 1 () () i iji i ii i i Cp p SCp p = = − = − ∑ ∑ (1) (2 ) 20 1 100 (log log20) log20 iij ij j C Pp = = + ∑ (3) Where j is the 20 amino acids, Ni is the number of amino acids in the position i, nij is the number of amino acids j in the position i. Pi,min and Pi,max are the minimal and maximal values of amino acid probabilities at posi- tion i, respectively. Pij is the observed probability of ami- no acid j at position i, Ci is the conservation index vector at position i. The frequencies of 20 amino acids at each position are selected as the basic parameters. Using the training set of Table 1. The numbers of β-turn types and nonturn extract- ed from the three databases. Type I I’ II II’ VIII IV IV Nonturn SET426 2457 302 924 168 672 2542 132 21371 SET547 2640 314 992 183 739 2672 144 25279 SET823 3808 500 1393 271 971 3794 226 35313 seven β-turn types and nonturn, arbitrary sequence seg- ments can obtain 8 DF values which be calculated by (1). 4) The Increment of Diversity (ID ) The increment of diversity algorithm is essentially a measure of the composition similarity level for two sys- tems which has been applied in the recognition of protein structural class [12] and the prediction of subcellular location of proteins [13]. In this work, we only calculate the increment of diversity values of β-turn types. In the state space of s dimension, the diversity measure for diversity sources S: {m1, m2,…, ms} is defined as [12,13]: (4 ) In the same state space, ID between the source of di- versity X: {n1, n2,…ns} and Y: {m1, m2,…, ms} is defined as: (5) Where . The frequencies of 20 amino acids at each position are selected as the basic parameters. Construct 8 diversity sources using the training sets of seven β-turn types and nonturn, arbitrary sequence segments can obtain 8 ID values which be calculated by (5). 5) Support Vector Machine (SVM) SVM is an extremely successful learning machine bas- ed on statistical learning theory and first proposed by Vapnik [14,15], which is a convex optimization problem, thus local optimal solution is the global optimal solution. The machine conceptually implements the following idea: input vector are non-linearly mapped to a very high-di- mension feature space. In this feature space a linear decision surface is con- structed [10,14]. In this paper, our work is a non-linearly problem, so we only introduce the linear non-separable case. In order to allow f or training errors, “soft margin” technique was introduced, which were slack variables i and the relax ed separation constraint: (i = 1,..., N) (6) The optimal separating hyperplane can be found by: (7) Here C is a regularization parameter used to decide a trade-off between the training error and the margin. The form of the decision function is: 1 ( )sgn(( ,)) N ii i i fxyaKx xb = = ⋅+ ∑ (8 ) Here, is the kernel function. In this paper, we select the radial basis kernel function  X. B. SHI, X. Z. HU Copyright © 2013 SciRes. ENG ( 2 ( ,)exp() iji j Kx xgxx=−− . Figure 1 is an example of a separable problem in a two dimensional space, which comes from [14]. The sup- port vectors, marked with grey squares, define the mar- gin of largest separation between the two classes. SVM has been compiled into the software packages, in this paper, we use the libsvm-2.89 software packages, which can be downloaded from http://www.csie.ntu.edu.tw/~cjlin/libsvm. The following steps were performed to predict β-turn types: first, select the input vector of the SVM; second, inputting the vector into SVM for training, we can obtain the optimal values of parameters C and g are all 0.5; third, a classifier is constructed, and then use this classifier to predict β-turn types. 6) Performance Measures In order to measure the performance of prediction me- thod, the four most frequently-used parameters [4,5,7] percentages of observed β-turn types that are correctly predicted (Qobs), percentages of correctly predicted β-turn types (Qpred), the Matthews Correlation Coefficient (MCC) and the overall prediction accuracies (Qtotal ) have been calculated by following equations. (9) (1 0) () ()()( )() iii i i iiiiiii ab cd MCC acadb cb d − =++ ++ (11) () [] 100 () ii total iii i ab Qabcd + = × +++ (12) Where ai is the number of correctly classified β-turn type i, bi is the number of correctly classified nonturns, ci is the number of β-turn type i incorrectly classified as nonturns or some other turn type, di is the number of nonturns incorrectly classified as β-turn type i. 3. Results and Discussion 1) Predictive Results of β-turn Types in the SET426 Figure 1. A se parable prob le m i n a two dimensional space. Widely believed, the prediction performance of β-turn types can be greatly improved by using the predictive se- condary structure information (PS I ) [4,5,7]. So in this pa- per, we selected the PSI as input parameter of SVM. The PSI from PSIPRED [16] is encoded as follows: helix→ (1, 0, 0), strand→ (0, 1, 0), coil→ (0, 0, 1). Because the prediction methods of β-turn types mostly used seven-fold cross-validation to assess the accuracy [4, 5,7], in this work we also employed seven-fold cross-va- lidation to evaluate the performance of our method. Using composite vector with 8 DF, 8 ID and 3 PSI as input parameter of SVM to predict the β-turn types in the SET426. The pr edictive result for seven-fold cross-vali- dation is shown in Table 2. In Table 2 the MCC for every β-turn types are highe r than 0.47 (except β-turn types VIII and II’). Particularly, the MCC for β-turn types I and II reach 0.74 and 0.68 respectively. The Qtotal for every β-turn types exceed 91.8%. The Qpred for every β-turn types exceed 83.6% (except β-turn types II’ and Ⅵ). In order to comparing with other methods, the predic- tive result of other methods [4,5,7] for seven-fold cross- validation in the SET426 are also shown in Table 2. Comparing with other methods, the prediction perfor- mance of our method is better than other methods. For example, in previous work, the MCC in Kirschner’s [7] work is the best among other works (except β-turn type IV), but the MCC in our method are better than Kirsch- ner’s [7] work. 2) Predictive Results of β-turn Types in the SET547 and SET823 To evaluate the predictive method, we selected the composite vector with 8 DF, 8 ID and 3 PSI as input pa- rameter of SVM to predic t the β-turn types in the SET547 and SET823, respectively. The seven-fold cr oss-valida- tion results were shown in Table 3. The prediction per- formance in the SET823 is better than in the SET547. For example, the MCC in the SET823 is better than in the SET547 (except β-turn typ e I’). Compared Tables 2 and 3, in the SET426, we obtained the best prediction performance among the three databases. The prediction results of our method in three datab ases are different, but the trend remained the same. The results are consistent with the Fuchs and Alix’s work [5]. It denoted our me- thod presented a strong stability whatev er the database size. 4. Conclusion In this work, we selected the frequencies of 20 amino acids at each position as basic parameters and in order to avoid ove rfitting, we used the position conservation scoring function and increment of diversity algorithms to reduce the dimension. The values of the DF, ID and PSI were used to construct the composite vector as input pa- 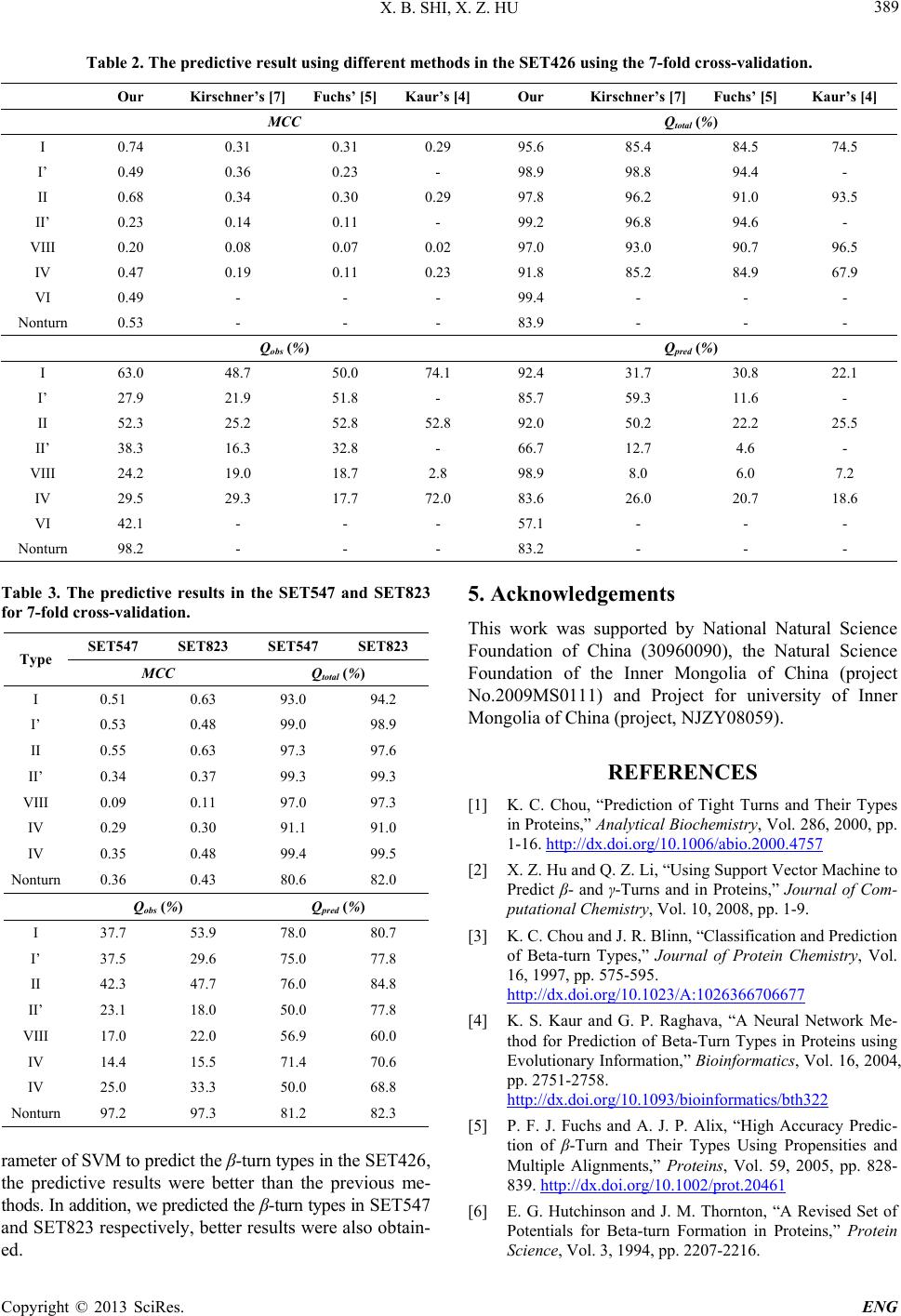 X. B. SHI, X. Z. HU Copyright © 2013 SciRes. ENG 389 Table 2. The predictive result using different methods in the SET426 using the 7-fold cross-validation. Our Kirschner’s [7] Fuchs’ [5] Kaur’s [4] Our Kirschner’s [7] Fuchs’ [5] Kaur’s [4] MCC Qtotal (%) I 0.74 0.31 0.31 0.29 95.6 85.4 84.5 74.5 I’ 0.49 0.36 0.23 - 98.9 98.8 94.4 - II 0.68 0.34 0.30 0.29 97.8 96.2 91.0 93.5 II’ 0.23 0.14 0.11 - 99.2 96.8 94.6 - VIII 0.20 0.08 0.07 0.02 97.0 93.0 90.7 96.5 IV 0.47 0.19 0.11 0.23 91.8 85.2 84.9 67.9 VI 0.49 - - - 99.4 - - - Nonturn 0.53 - - - 83.9 - - - Qobs (%) Qpred (%) I 63.0 48.7 50.0 74.1 92.4 31.7 30.8 22.1 I’ 27.9 21.9 51.8 - 85.7 59.3 11.6 - II 52.3 25.2 52.8 52.8 92.0 50.2 22.2 25.5 II’ 38.3 16.3 32.8 - 66.7 12.7 4.6 - VIII 24.2 19.0 18.7 2.8 98.9 8.0 6.0 7.2 IV 29.5 29.3 17.7 72.0 83.6 26.0 20.7 18.6 VI 42.1 - - - 57.1 - - - Nonturn 98.2 - - - 83.2 - - - Table 3. The predictive results in the SET547 and SET823 for 7-fold cross-validation. Type SET547 SET823 SET547 SET823 MCC Qtotal (%) I 0.51 0.63 93.0 94.2 I’ 0.53 0.48 99.0 98.9 II 0.55 0.63 97.3 97.6 II’ 0.34 0.37 99.3 99.3 VIII 0.09 0.11 97.0 97.3 IV 0.29 0.30 91.1 91.0 IV 0.35 0.48 99.4 99.5 Nonturn 0.36 0.43 80.6 82.0 Qobs (%) Qpred (%) I 37.7 53.9 78.0 80.7 I’ 37.5 29.6 75.0 77.8 II 42.3 47.7 76.0 84.8 II’ 23.1 18.0 50.0 77.8 VIII 17.0 22.0 56.9 60.0 IV 14.4 15.5 71.4 70.6 IV 25.0 33.3 50.0 68.8 Nonturn 97.2 97.3 81.2 82.3 rameter of SVM to predict the β-turn types in the SET426 , the predictive results were better than the previous me- thods. In addition, we predic ted the β-turn type s in SET547 and SET823 respectively, better results were also obtain- ed. 5. Acknowledgements This work was supported by National Natural Science Foundation of China (30960090), the Natural Science Foundation of the Inner Mongolia of China (project No.2009MS0111) and Project for university of Inner Mongolia of China (project, NJZY08059). REFERENCES [1] K. C. Chou, “Prediction of Tight Turns and Their Types in Proteins,” Analytical Biochemistry, Vol. 286, 2000, pp. 1-16. http://dx.doi.org/10.1006/abio.2000.4757 [2] X. Z. Hu and Q. Z. Li, “Using Support Vector Machine to Predict β- and γ-Turns and in Proteins,” Journal of Com- putational Chemistry, Vol. 10, 2008, pp. 1-9. [3] K. C. Chou and J. R. Blinn, “Classification and Prediction of Beta-turn Types,” Journal of Protein Chemistry, Vol. 16, 1997, pp. 575-595. http://dx.doi.org/10.1023/A:1026366706677 [4] K. S. Kaur and G. P. Raghava, “A Neural Network Me- thod for Prediction of Beta-Turn Types in Proteins using Evolutionary Information,” Bioinformatics, Vol. 16, 2004, pp. 2751-2758. http://dx.doi.org/10.1093/bioinformatics/bth322 [5] P. F. J. Fuchs and A. J. P. Alix, “High Accuracy Predic- tion of β-Turn and Their Types Using Propensities and Multiple Alignments,” Proteins, Vol. 59, 2005, pp. 828- 839. http://dx.doi.org/10.1002/prot.20461 [6] E. G. Hutchinson and J. M. Thornton, “A Revised Set of Potentials for Beta-turn Formation in Proteins,” Protein Science, Vol. 3, 1994, pp. 2207-2216.  X. B. SHI, X. Z. HU Copyright © 2013 SciRes. ENG http://dx.doi.org/10.1002/pro.5560031206 [7] A. Kirschner and D. Frishman, “Prediction of β-Turns and β-Turn Types by a Novel Bidirectional Elman-Type Recurrent Neural Network with Multiple Output Layers,” Gene, Vol. 422, 2008, pp. 22-29. http://dx.doi.org/10.1016/j.gene.2008.06.008 [8] A. J. Shepherd, D. Gorse and J. M. Thornton, “Prediction of the Location and Type of Beta-turns in Proteins using Neural Networks,” Protein Science, Vol. 8, 1999, pp. 1045-1055. http://dx.doi.org/10.1110/ps.8.5.1045 [9] C. M. Wilmot and J. M. Thornton, “Analysis and Predic- tion of the Different Types of Beta-turn in Proteins,” Journal of Molecular Biology, Vol. 203, 1988, pp. 221- 232. http://dx.doi.org/10.1016/0022-2836(88)90103-9 [10] Y. D. Cai, X. J. Liu, Y. X. Li, X. B. Xu and K. C. Chou, “Support Vector Machines for the Classification and Pre- diction of Beta-Turn Types,” Journal of Peptide Science, Vol. 8, 2002, pp. 297-301. http://dx.doi.org/10.1002/psc.401 [11] K. Guruprasad and S. Rajkumar, “B eta-and Ga mma -Turns in Proteins Revisited: A New Set of Amino Acid Turn- Type Dependent Positional Preferences and Potentials,” Journal of Bioscience, Vol. 25, 2000, pp. 143-156. [12] Q. Z. Li and Z. Q. Lu, “The Prediction of the Structural Class of Protein: Application of the Measure of Diversity,” Journal of Theoretical Biology, Vol. 213, 2001, pp. 493- 502. http://dx.doi.org/10.1006/jtbi.2001.2441 [13] Y. L. Chen and Q. Z. Li, “Prediction of the Subcellular Lo- cation of Apoptosis Proteins,” Journal of Theoretical Bi- ology, Vol. 245, 2007, pp. 775-783. http://dx.doi.org/10.1016/j.jtbi.2006.11.010 [14] C. Cortes and V. Vapnik, “Support Vector Network,” Ma- chine Learning, Vol. 20, 1995, pp. 273-293. http://dx.doi.org/10.1007/BF00994018 [15] V. Vapnik, “Statistical Learning Theory,” Wiley-Inter- Science, New York, 1998. [16] D. T. Jones, “Protein Secondary Structure Prediction Bas- ed on Position-Speck Scoring Matrices,” Journal of Mo- lecular Biology, Vol. 292, 1999, pp. 195-202. http://dx.doi.org/10.1006/jmbi.1999.3091
|