American Journal of Analytical Chemistry, 2013, 4, 749-755
Published Online December 2013 (http://www.scirp.org/journal/ajac)
http://dx.doi.org/10.4236/ajac.2013.412091
Open Access AJAC
Thermal Stability and Decomposition Kinetics of
Polysuccinimide
Li Zhang, Mingxing Huang, Cairong Zhou
1School of Chemical Engineering and Energy, Zhengzhou University, Zhengzhou, China
Received November 5, 2013; revised December 1, 2013; accepted December 9, 2013
Copyright © 2013 Li Zhang et al. This is an open access article distributed under the Creative Commons Attribution License, which
permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
The thermal stability and decomposition kinetics of polysuccinimide (PSI) were investigated using analyzer DTG-60
under high purity nitrogen atmosphere at different heating rates (3, 6, 9, 12 K/min). The thermal decomposition mecha-
nism of PSI was determined by Coats-Redfern method. The kinetic parameters such as activation energy (E), pre-ex-
ponential factor (A) and reaction order (n) were calculated by Flynn-Wall-Ozawa and Kissinger methods. The results
show that the thermal decomposition of PSI under nitrogen atmosphere mainly occurs in the temperature range of
619.15 - 693.15 K, the reaction order (n) was 3
4, the activation energy (E) and pre-exponential factor (A) were ob-
tained to be 106.585 kJ/mol and 4.644 × 109 min−1, the integral and differential forms of the thermal decomposition
mechanism of PSI were found to be

34
ln 1   

and
 
14
41ln1
3
 



, respectively. The results play an
important role in understanding the thermodynamic properties of polysuccinimide.
Keywords: Polysuccinimide; Thermal Gravimetric Analysis; Thermal Stability; Decomposition Kinetics
1. Introduction
Polyaspartic acid (PASP, CAS181828-06-8) has amino
and carboxyl groups, which belongs to the biological
macromolecule material and is a kind of polymer of
amino acids. Since it has the characteristics of good bio-
compatibility and biodegradability, PASP has been widely
used in industrial and medical fields as a new type of
green chemicals [1]. Polysuccinimide (PSI, CAS6899-
03-2) is the intermediate of PASP. The experimental
formula and relative molecular mass of its monomer are
C4H3O2N and 97.074 g/mol, respectively. The chemical
structure of the monomer can be written as:
H2NCH C
C
CH2
O
O
N
n
CH C
CH2C
O
O
NCHC
CH2C
O
O
OH
OH
In view of this, PSI is a kind of linear polyimide with
high activity and it is easy to open ring changing into
poly asparagine with side chains. With the special prop-
erty, many kinds of derivatives that were used as drug
carriers have been prepared [2].
The thermal stability and decomposition kinetics of
Polysuccinimide (PSI) were investigated by TG-DTA
method. Kinetic parameters such as activation energy (E)
and pre-exponential factor (A) were calculated by Flynn-
Wall-Ozawa (F-W-O) and Kissinger methods. The ki-
netic mechanism function of thermal decomposition of
PSI was established by Coats-Redfern method. Using
TG-DTA method to study the stability of drugs has the
advantages of less sample dose, short experimental pe-
riod and reliable results. These data not only play an ac-
tive role in understanding the thermodynamic properties
of PSI but also provide a theoretical basis for practical
application.
2. Experimental
2.1. Materials and Instruments
Polysuccinimide (the mass fraction was higher than 99.5%)
was purchased from Henan Xinlianxin Fertilizer Limited

L. ZHANG ET AL.
750
Co. α-Al2O3 (standard material, Shimadu Company in
Japan) was used as standard material in the process of
thermal analysis.
The TG-DTA analyzer (type DTG-60, Shimadzu Cor-
poration, Japan) was used to determine the TG-DTA
curves of the sample. SPN-500-type nitrogen generator
(Hewleet-Packard, Beijing Institute of Technology, China)
was used to provide a high purity nitrogen atmosphere
for the experimental system of thermal analysis. Fourier
Transform Infrared Spectrometer (type WQF, Beijing
Beifen-Ruili Analytical Instrument (Group) Co, Ltd) was
used to analyze PSI. Gel permeation chromatography
(type Agilent1100, Agilent Corporation, America) was
used to analyze PSI’s purity and the number-average
molecular weight (Mn) and polydispesity index (Mw/Mn).
2.2. Experiment Methods
The PSI sample was dried in the vacuum oven at 378.15
K before analysis. The thermogravimetric measurements
were carried out at different heating rates (3, 6, 9, 12
K/min) from room temperature to 873.15 K under high
purity nitrogen atmosphere (20 ml/min). Mass of each
powdered sample was about 4 - 5 mg.
2.3. Characterization of PSI
2.3.1. FTIR Analysis of PSI
FTIR spectra of PSI were recorded in the wave number
range of 4000 - 500 cm−1. The result is shown in Figure
1. From Figure 1, we can know that the carboxyl group
of branched chain in the opened ring appears at 1400
cm−1, the carbon-carbon bond appears at 1165 cm−1, the
coupled carbonyl group appears at 1720 cm−1 and the
carbonyl group in the ring obviously appears at 1797
cm−1.
2.3.2. Gel Per m eat ion Chromatography A nalysis of
PSI
The analysis diagram of PSI by gel permeation chroma-
tography is shown in Figure 2. The analysis results show
Figure 1. FTIR spectra of PSI.
Figure 2. The analysis diagram of PSI by gel permeation
chromatography.
that the number-average molecular weight (Mn) of PSI is
2.7941 × 104 g/mol, the polydispersity index of relative
molecular mass (Mw/Mn) of PSI is 21.644 and Polymeri-
zation degree of PSI is obtained to be 287.5.
2.4. Theoretical Analysis
There are two major categories to study the thermal de-
composition kinetics of polymer, which are differential
method and integral method. The differential method
contains Kissinger [3-5], Caroll-Freeman [6] and Fried-
man [7] methods while Coats-Redfern [8-12], Doyle [13]
and Flynn-Wall-Ozawa (F-W-O) [14-16] methods belong
to the integral method. Coats-Redfern, Flynn-Wall-Ozawa
(F-W-O) and Doyle methods are usually used for inves-
tigating thermal decomposition kinetics of polymers.
In general, the thermal decomposition of a solid poly-
mer under inert atmosphere can be summarized as: Bsolid
→ Csolid + Dgas. Polymer is finally decomposed into solid
residue (C) and gaseous matter (D).
The kinetic analysis of solid-state sample is usually
given by Equation (1) [17]
 
d
d
rKTf
t


 (1)
where d
dt

is the rates of conversion;

is the con-
version degree that can be defined as ot
of
mm
mm
 
 in
which m0 and mf are the initial and final masses of the
sample, respectively; mt is the mass of the sample at time
t (or temperature T) of the decomposition process, mg. In
Equation (1), is the temperature dependent rates
constant and is normally assumed to obey the Arrhenius
equation:
()kT

e
E
R
T
kT A  (2)
where A is the pre-exponential factor (min−1), E is the
Open Access AJAC

L. ZHANG ET AL.
Open Access AJAC
751
activation energy (kJ/mol) of the kinetic process, R is the
gas constant (8.314 J/(mol·K)) and T is the absolute tem-
perature (K).
is approximately constant when the values of α are the
same at the different heating rates βi, so it is easy to ob-
tain values of E by plotting lgβ against 1/T at the certain
conversion degree α.
Moreover, taking into account the heating rates β =
dT/dt under non-isothermal condition, d
dt

can be de- 2.4.3. Coats- R edfern Method
Coats-Redfern method can be described as Equation (7).
[8-10,12]:
scribed by Equation (3):
ddd d
ddd d
T
tTt T








(3)


2
lnln c
ii i
gc
A
RE
ERT T


 (7)
Equation (4) can be obtained by combing Equations
(1)-(3), which describes the thermal decomposition ki-
netics. Based on TGA data, the kinetic parameters can be
calculated from Equation (4). [18]:
where g(α) comes from one of 34 forms of integral for-
mula in the literature which are shown in Table 1 [11].
From Equation (7), the values of both Ec and Ac can be
obtained for any selected g(α) and fixed βi (i = 1, 2, 3, 4,
even more). The calculating steps in detail are: 1) choose
the same αj for each heating rates βi and calculate the
corresponding g(αij); 2) give the corresponding tempera-

de
d
E
RT
aA f
t



 (4)
ture Tij according to αij; 3) describe the sketch of


2
ln
i
g
T

2.4.1. Kiss i ng er Method
The formula of Kissinger method is given by Equation (5)
[3-5]: versus 1/Ti for each fixed βi, and calculate the values of
both Ec and ln(Ac) according to the slope and intercept of
the line, respectively; 4) determine the mechanism func-
tion of the thermal decomposition process. Generally, the
selected mechanism functions should meet all the condi-
tions, which are: 1) 0 < Ec < 400 kJ/mol; 2)
2
1
ln ln
ikk
kp pi
AR E
ERT T




 i
(5)
where i = 1, 2, 3, 4 (or even more); Tpi is the peak tem-
peratures of different DTA curve at different heating
rates. By plotting

2
ln ipi T 

versus 1/Tpi, the activation
energy Ek and pre-exponential factor Ak can be calculated
based on its slope (−Ek/R) and intercept ln(AkR/Ek), re-
spectively.


00
0.3
c
EEE where E0 come from F-W-O method
3)


ln lnln0.3
ckc
AAA in which ln(Ak) are ob-
tained from Kissinger method. If g(α) meet the require-
ments mentioned above, g(α) can be regarded as the
probable mechanism function for the thermal decomposi-
tion process.
2.4.2. Flynn-Wall-Ozawa (F-W-O) Method
F-W-O method can be used directly to calculate the acti-
vation energy E. The integral formula of F-W-O method
[14-16] is showed in Equation (6):

lglg2.315 0.4567
A
E
Rg RT

 

 
 

E


(6)
2.5. Determination of High Temperature
Heat-Resistance of PSI
In Equation (6), since the value of




lg AE Rg 

The activation energy data obtained by above-mentioned
methods can be used to evaluate the high temperature
heat-resistance of PSI. The relationship between activa-
Table 1. 34 types of thermal decomposition mechanism functions.
NO g(α) N
O g(α)
1 - 6 111 3
,,,1,2,
432 2
nn
  27

1
11 



7

1ln1

  28

12
1 


8

32
2
11
3




 29

2
1 


9 - 19 
111223 3
ln1, ,, , , ,1, ,2,3,4
2435342
nn
   
 30 - 31

12 1
11 ,2
2
n
n 

 

20 - 25 
111
11 ,,,2,3,4
432
nn
   32 - 33

13 1
11 ,2
2
n
n 



26 
1
1


 34

2
13
11 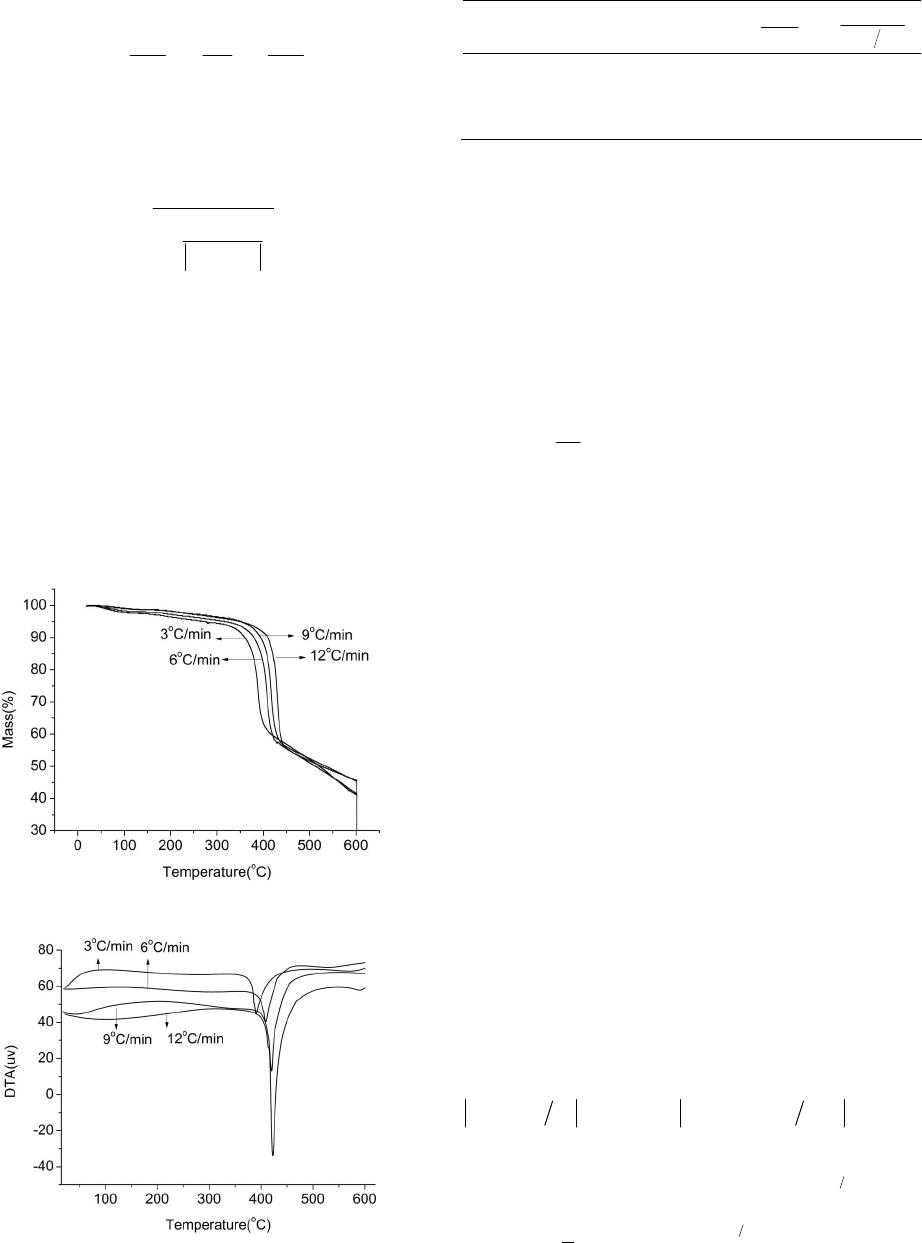






L. ZHANG ET AL.
752
tion energy and lifetime of polymer can be expressed by
Equation (8) [19]:
ln ln
f
f
EEE
tP
RTR RT



 




(8)
where tf is the lifetime of PSI at the temperature of Tf, Tα
is the temperature at the conversion degree α. Combined
Equations (4) and (8), Tf can be shown as:

1
ln ln 1
f
f
ER
TAt







(9)
3. Results and Discussion
3.1. Thermal Decomposition of PSI
TG and DTA curves of PSI sample are shown in Figures
3 and 4. The thermal analysis data are summarized in
Table 2. In Figure 3, the thermal decomposition tem-
perature at different heating rates increases with the in-
creasing of

. That indicates the decomposition tem-
perature is affected by the heating rate

. Besides, each
TG curve of PSI under nitrogen atmosphere has an ob-
vious mass loss process where percentage of mass loss
Figure 3. The TG curves of PSI in nitrogen atmosphere.
Figure 4. The DTA curves of PSI in nitrogen atmosphere.
Table 2. Basic data of kinetics of PSI from TG.
β/(K·min−1)Tp/K (1/Tp)/K−1 FWO
ln


2
Kissinger
ln p T 
3 663.94 0.001516 1.099 −11.898
6 682.76 0.001473 1.792 −11.261
9 693.17 0.001451 2.197 −10.885
12 696.97 0.001444 2.485 −10.609
increases gradually with the increasing of heating rates
and TG curve moves toward to the right.
From Figures 3 and 4, the thermal decomposition of
PSI under nitrogen atmosphere mainly occurs in the
temperature range of 619.15 to 693.15 K. Mass loss is
accompanied by heat absorption, so thermal decomposi-
tion process and solid rearrangement reaction may si-
multaneously happen in this process.
3.2. Non-Isothermal Kinetic of PSI
Plots of 2 ln
p
T

against 1/Tp of PSI by Kissinger method
is shown in Figure 5. The values of activation energy Ek
and exponential factor ln(Ak) calculated by Kissinger
method are 143.874 kJ/mol and 23.897 min1, respec-
tively. The linear correlation coefficient (R2) is 0.9852.
The activation energies calculated at different conver-
sion degree using Flynn-Wall-Ozawa method are shown
in Table 3 and the relationship between E0 and conver-
sion degree α are showed in Figure 6.
The results show that the correlation coefficients (R2)
of FWO method is better, the values of activation energy
is between 81.509 and 122.205 kJ/mol and increase with
the increasing of conversion degree. From Table 3 and
Figure 6, the average value of activation energy Eo is
104.202 kJ/mol and the pre-exponential factor lgAo is
9.967.
The kinetic parameters calculated by Coats-Redfern
method are listed in Table 4. The values of activation
energy and exponential factor calculated by Coats-Red-
fern method compare respectively with the average value
of activation energy calculated using FWO method and
the value of pre-exponential factor obtained by Kissinger
method, the results are listed in Table 5.
The thermal decomposition process of PSI in the tem-
perature stage of 619.15 to 693.15 K is consistent with
the sequence number 14 in Table 1, this is because Ec
and ln(Ac) meet better with the conditions of both


00
0.3
c
EEE and


ln lnln0.3
ckc
AAA
than others; besides, the relative coefficients (R2) are
much better. The integral and differential forms of the
mechanism function are
 
34
ln 1g   


and
 
14
41ln1
3
f    



, respectively. The
Open Access AJAC

L. ZHANG ET AL. 753
values of Ec and ln(Ac) are obtained to be 108.967 kJ/mol
and 16.802 min−1. So the activation energy and pre-ex-
ponential factor of thermal decomposition process of PSI
can be regarded as 106.585 kJ/mol and 4.644 × 109 min−1
(i.e. average values obtained by the Coats-Redfern and
FWO methods). The thermal decomposition kinetic equa-
tion of PSI can be described as:
Figure 5. Plots of
p
T2
ln

and 1/Tp of PSI of Kissinger
method.
Table 3. The activation energy Eo and exponential factor
lgAo of PSI.
α E
o(kJ/mol) lgAo(min−1) R2
0.15 81.509 8.134 0.9853
0.20 95.987 9.285 0.9895
0.25 106.373 10.131 0.9885
0.30 114.936 10.839 0.9902
0.35 122.205 11.447 0.9912
Mean* 104.202 9.967 0.9889
Figure 6. FWO curves of PSI at different conversion.
Table 4. Results of 34 ty pe s of kinetic equations of PSI calculate d with Coats-Redfern method.
β = 3 K/min β = 6 K/min β = 9 K/min β = 12 K/min
No Ec/(kJ·mol−1) lnAc R2 Ec/(kJ·mol−1) lnAc R2 Ec/(kJ·mol−1)lnAc R2 Ec/(kJ·mol−1) lnAc R2
1 12.759 −2.491 0.926 25.349 0.969 0.94826.880 1.676 0.95131.494 2.782 0.969
2 20.575 −0.678 0.948 37.511 3.417 0.95739.043 4.106 0.95945.789 5.520 0.976
3 36.204 2.558 0.961 61.836 8.030 0.96463.367 8.703 0.96574.378 10.733 0.982
4 83.094 11.400 0.970 134.812 21.146 0.970136.341 21.806 0.970160.144 25.684 0.986
5 176.872 28.178 0.973 280.755 46.555 0.972282.285 47.209 0.972331.679 54.781 0.987
6 129.981 19.859 0.972 207.783 33.917 0.971209.313 34.573 0.971245.912 40.298 0.987
7 185.510 29.230 0.971 294.174 48.401 0.970295.704 49.054 0.970347.600 56.992 0.986
8 71.090 8.701 0.977 116.155 17.352 0.977117.685 18.013 0.977138.012 21.381 0.990
9 43.011 4.068 0.954 72.413 10.150 0.95773.945 10.820 0.95886.931 13.140 0.976
10 16.162 −1.586 0.922 30.638 2.140 0.94132.169 2.837 0.94437.771 4.089 0.964
11 25.112 0.413 0.941 44.563 4.898 0.95046.094 5.581 0.95254.157 7.189 0.971
12 32.272 1.911 0.948 55.703 7.028 0.95457.234 7.704 0.95567.267 9.597 0.974
13 60.910 7.532 0.959 100.267 15.243 0.960101.797 15.907 0.960119.705 18.940 0.979
14 69.859 9.227 0.960 114.193 17.756 0.961115.723 18.418 0.961136.092 21.807 0.979
15 96.708 14.227 0.963 155.962 25.218 0.962157.492 25.876 0.963185.253 30.333 0.981
16 150.400 24.018 0.965 239.518 39.948 0.964241.048 40.603 0.964283.574 47.195 0.982
17 204.100 33.672 0.966 323.065 54.547 0.965324.595 55.201 0.965381.895 63.929 0.983
18 311.492 52.793 0.967 490.168 83.565 0.966491.698 84.218 0.966578.538 97.216 0.983
19 418.884 71.787 0.968 657.272 112.4600.966 658.801 113.1110.966 775.181 130.3780.983
20 93.175 12.110 0.965 150.483 22.778 0.964152.013 23.437 0.965178.743 27.744 0.982
21 92.019 12.158 0.965 148.679 22.720 0.965150.209 23.379 0.965176.606 27.637 0.983
22 89.733 12.089 0.966 145.129 22.442 0.966146.659 23.101 0.966172.383 27.261 0.983
23 70.820 9.515 0.977 115.731 18.140 0.977117.261 18.802 0.977137.522 22.161 0.990
24 59.848 7.583 0.983 98.679 15.209 0.983100.209 15.873 0.983117.319 18.771 0.994
25 50.119 5.764 0.989 83.547 12.505 0.98985.077 13.172 0.99099.419 15.665 0.997
26 17.893 −0.548 0.787 33.271 3.307 0.83334.802 4.001 0.84341.333 5.412 0.876
27 111.674 17.306 0.956 179.217 29.666 0.955180.746 30.323 0.956212.872 35.419 0.976
28 3.604 −4.956 0.378 11.067 −1.911 0.68912.597 −1.133 0.73514.972 −0.329 0.761
29 46.471 6.017 0.861 77.680 12.390 0.87179.211 13.059 0.87594.056 15.685 0.908
30 39.523 2.951 0.957 66.993 8.721 0.96168.525 9.392 0.96180.498 11.564 0.979
31 190.149 29.474 0.970 301.391 49.070 0.968302.921 49.724 0.969356.163 57.858 0.985
32 40.667 3.002 0.956 68.771 8.874 0.95970.302 9.545 0.96082.608 11.765 0.978
33 194.722 29.587 0.969 308.499 49.601 0.967310.029 50.256 0.967364.602 58.585 0.984
34 164.725 23.498 0.975 261.874 40.758 0.974263.404 41.414 0.974309.331 48.480 0.989
Open Access AJAC

L. ZHANG ET AL.
754
Table 5. Calculation of 6 types of kinetics equations for PSI with Coats-Redfern method.
Sequence number of mechanism function  g

β
K/mol
Ec
kJ/mol
lnAc
min−1 R2 oc
o
EE
E
 ln ln
ln
ck
k
A
A
A

4 3 83.094 11.400 0.970 0.203 0.523
4 6 134.812 21.146 0.970 0.294 0.115
4 9 136.341 21.806 0.970 0.308 0.088
4 12 160.144 25.684 0.986 0.537 0.075
8 3 71.090 8.701 0.977 0.318 0.636
8 6 116.155 17.352 0.977 0.115 0.274
8 9 117.685 18.013 0.977 0.129 0.246
8 12 138.012 21.381 0.990 0.324 0.105
13 3 60.91 7.532 0.959 0.415 0.685
13 6 100.267 15.243 0.960 0.038 0.362
13 9 101.797 15.907 0.960 0.023 0.334
13 12 119.705 18.940 0.979 0.149 0.207
14 3 69.859 9.227 0.960 0.330 0.614
14 6 114.193 17.756 0.961 0.096 0.257
14 9 115.723 18.418 0.961 0.111 0.229
14 12 136.092 21.807 0.979 0.306 0.087
23 3 70.82 9.515 0.977 0.320 0.602
23 6 115.731 18.140 0.977 0.111 0.241
23 9 117.261 18.802 0.977 0.125 0.213
23 12 137.522 22.161 0.990 0.320 0.073
24 3 59.848 7.583 0.983 0.426 0.683
24 6 98.679 15.209 0.983 0.053 0.364
24 9 100.209 15.873 0.983 0.038 0.336
24 12 117.319 18.771 0.994 0.126 0.215

334
9106.585 10
d4.64410 e1
d
RT
t


  (10)
3.3. High Temperature Heat-Resistance of PSI
Selecting tf = 60 s and α = 15% as the evaluation indexes
of the high temperature heat-resistance of the polymer.
According to Equation (12), value of Tf of PSI in nitro-
gen atmosphere is 259.27˚C. The result shows that the
high temperature heat-resistance of PSI is not very well.
4. Conclusion
The thermal behavior of polysuccinimide under non-
isothermal condition was investigated using TG-DTA
method at different heating rates in nitrogen atmosphere.
The results show that the thermal decomposition of PSI
under nitrogen atmosphere mainly occurs in the tem-
perature range of 619.15 - 693.15 K, the reaction order (n)
was 3/4, the activation energy (E) and pre-exponential
factor (A) were obtained to be 106.585 kJ/mol and 4.644
× 109 min−1, the integral and differential forms of the
thermal decomposition mechanism of PSI were found to
be

34
ln 1  


and

14 41ln1
3
 
 
, re-
spectively.
REFERENCES
[1] A. W. Yang, G. P. Cao and M. H. Zhang, “Synthesis of
Polysuccinimide and Determination of the Intrinsic Vis-
cosity,” Polymer Materials Science & Engineering, Vol.
26, 2010, pp. 4-7.
[2] J. H. Jeong, H. S. Kang, S. R. Yang and J. D. Kim,
“Polymer Micelle-Like Aggregates of Novel Amphiphilic
Biodegradable Poly(Asparagine) Grafted with Poly(Ca-
prolactone),” Polymer, Vol. 44, No. 3, 2003, pp. 583-591.
http://dx.doi.org/10.1016/S0032-3861(02)00816-9
[3] A. Rotaru, M. Anca, G. Popa, P. Rotaru and E. Segal,
“Non-Isothermal Kinetics of 2-Allyl-4-((4-(4-Methylben-
zyloxy)Phenyl) Diazenyl) Phenol in Air Flow,” Journal
of Thermal Analysis and Calorimetry, Vol. 97, No. 2,
2009, pp. 485-491.
http://dx.doi.org/10.1007/s10973-009-0214-1
[4] H. E. Kissinger, “Variation of Peak Temperature with
Heating Rate in Different Rate in Differential Thermal
Analysis,” Journal of Research of the National Bureau of
Standards, Vol. 57, No. 4, 1956, pp. 217-221.
http://dx.doi.org/10.6028/jres.057.026
[5] H. E. Kissinger, “Reaction Kinetic in Differential Ther-
mal Analysis,” Analytical Chemistry, Vol. 29, No. 11,
1957, pp. 1702-1706.
http://dx.doi.org/10.1021/ac60131a045
[6] E. S. Freeman and B. Carroll, “The Application of Ther-
moanalytical Technique to Reaction Kinetics,” Journal of
Physical Chemistry, Vol. 3, 1958, pp. 394-397.
[7] H. L. Friedman, “Kinetics and Gaseous Products of Ther-
mal Decomposition of Polymers,” Journal of Macromo-
lecular Science: Part A—Chemistry, Vol. 1, No. 1, 1967,
pp. 57-59. http://dx.doi.org/10.1080/10601326708053917
[8] A. W. Coats and J. P. Redfern, “Kinetic Parameters from
Thermogravimetric Data,” Nature, Vol. 201, 1964, pp.
68-69. http://dx.doi.org/10.1038/201068a0
Open Access AJAC

L. ZHANG ET AL. 755
[9] C. R. Zhou, Q. H. Li and H. F. Wang, “Thermal Analysis
for the Thermal Decomposition of Methylsulfonate Tin,”
Journal of Chemical Engineering of Chinese Universities,
Vol. 20, 2006, pp. 669-672.
[10] C. R. Zhou, X. H. Shi, H. F. Wang and D. G. Jiang,
“Thermal Decomposition and the Non-Isothermal De-
composition Kinetics of DL-2-Naproxen,” Journal of
Chemical Engineering of Chinese Universities, Vol. 25,
2011, pp. 442-446.
[11] L. G. Lu, Q. Zhang, X. N. Xu, X. L. Dong and D. W.
Wang, “Thermal Degradation Kinetics of Novel Intu-
mescent Flame Retardant Polypropylene,” China Plastics,
Vol. 23, 2009, pp. 53-60.
[12] C. Y. Ou, C. H. Zhang, S. D. Li, L. Yang and J. J. Dong,
“Thermal Degradation Kinetics of Chitosan-Cobalt Com-
plex as Studied by Thermogravimetric Analysis,” Car-
bohydrate Polymers, Vol. 82, No. 4, 2010, pp. 1284-1289.
http://dx.doi.org/10.1016/j.carbpol.2010.07.010
[13] C. D. Doyle, “Kinetic Analysis of Thermogravimetric
Data,” Journal of Applied Polymer Science, Vol. 5, No.
15, 1961, pp. 285-292.
http://dx.doi.org/10.1002/app.1961.070051506
[14] T. Ozawa, “Kinetic Analysis of Derivative Curves in
Thermal Analysis,” Journal of Thermal Analysis, Vol. 2,
No. 3, 1970, pp. 301-310.
http://dx.doi.org/10.1007/BF01911411
[15] F. X. Chen, C. R. Zhou and G. P. Li, “Study on Thermal
Decomposition and the Non-Isothermal Decomposition
Kinetics of Glyphosate,” Journal of Thermal Analysis
and Calorimetry, Vol. 109, No. 3, 2012, pp. 1457-1462.
[16] Q. F. Wang, L. Wang, X. W. Zhang and Z. T. Mi, “Ther-
mal Stability and Kinetic of Decomposition of Nitrated
HTPB,” Journal of Hazardous Materials, Vol. 172, No.
2-3, 2009, pp. 1659-1664.
http://dx.doi.org/10.1016/j.jhazmat.2009.08.040
[17] C. D. Gamlin, N. K. Dutta, N. R. Choudhury, D. Kehoe
and J. Matisons, “Evaluation of Kinetic Parameters of
Thermal and Oxidative Decomposition of Base Oils by
Conventional, Isothermal and Modulated TGA, and Pres-
sure DSC,” Thermochimica Acta, Vol. 392-393, 2002, pp.
357-369.
http://dx.doi.org/10.1016/S0040-6031(02)00121-1
[18] X. Y. Li, Y. Q. Wu, D. H. Gu and F. X. Gan, “Thermal
Decomposition Kinetics of Nickel(II) and Cobalt(II) Azo
Barbituric Acid Complexes,” Thermochimica Acta, Vol.
493, No. 1-2, 2009, pp. 85-89.
http://dx.doi.org/10.1016/j.tca.2009.04.010
[19] Z. W. Zhou and Q. X. Wu, “Studies on Thermal Proper-
ties of Poly(Phenylene Sulfide Amide),” Journal of Ap-
plied Polymer Science, Vol. 66, No. 7, 1997, pp. 1227-
1230.
http://dx.doi.org/10.1002/(SICI)1097-4628(19971114)66:
7<1227::AID-APP2>3.0.CO;2-I
Open Access AJAC