J. Software Engineering & Applications, 2009, 2:20-24
Published Online April 2009 in SciRes (www.SciRP.org/journal/jsea)
Data Hiding Method with Quality Control for Binary
Images
Ki-Hyun Jung
1
, Kee-Young Yoo
2
1
School of Computer Information, Yeungjin College, 218 Bokhyun-Dong, Buk-Gu, Daegu 702-721, Republic of Korea,
2
Department of Computer Engineering, Kyungpook National University, 1370 Sankyuk-Dong, Buk-Gu, Daegu 702-701, Republic of
Korea.
Received December 16
th
, 2008; revised January 21
st
, 2009; accepted February 24
th
, 2009.
ABSTRACT
Secret data hiding in binary images is more difficult than other formats since binary images require only one bit repre-
sentation to indicate black and white. This study proposes a new method for data hiding in binary images using opti-
mized bit position to replace a secret bit. This method manipulates blocks, which are sub-divided. The parity bit for a
specified block decides whether to change or not, to embed a secret bit. By finding the best position to insert a secret bit
for each divided block, the image quality of the resulting stego-image can be improved, while maintaining low compu-
tational complexity. The experimental results show that the proposed method has an improvement with respect to a pre-
vious work.
Keywords: Data Hiding, Quality Control, Binary Images
1. Introduction
Data hiding involves concealing information in a host
signal, such as text, image, audio, or video. Binary im-
ages are two-color images, with a 0 or 1 value for each
pixel, in which each pixel requires only one bit represen-
tation, to indicate black and white. The difficulty lies in
the fact that changing pixel values in a binary image can
cause irregularities that are visually very noticeable.
Hiding data in binary images is therefore more challeng-
ing than hiding it in other formats [1].
There are two primary methods of data hiding in these
images: sub-block modification and single pixel manipulation.
The first modifies the sub-block, which is divided into a
group of pixels. Matsui and Tanaka embedded secret data
in ‘dithered’ images by manipulating the dithering patterns;
they also embedded in fax images, by manipulating the
run lengths [2]. Low et al. changed line spacing and
character spacing to embed secret data in textual images,
for bulk electronic publications [3,4]. These methods are
used for some special types of binary images. The second
approach modifies single pixel from black to white or
vice versa: some special single pixels in the image are
changed to embed the secret data. Koch and Zhao pro-
posed a data hiding method by forcing the ratio of black
and white pixels in a block to be larger or smaller than
one [5]. However, there is a difficulty with this. Only a
limited number of bits can be embedded, since the en-
forcing method has trouble dealing with blocks that have
a significantly low or high percentage of black pixels.
Wu et al. embedded bits in image blocks, selected by
calculating a characteristic value and finding a pattern [6].
Lie et al. partitioned the binary image into blocks of 2x2
pixels and embedded a bit 0 or 1 in the block. This
method can hide one bit per block by modifying 0.5 pix-
els on average [7]. Wu and Liu manipulated flappable
pixels to enforce a specific block-based relationship in
order to embed a significant amount of data without
causing noticeable visual effects [8]. Venkatesan et al.
proposed using the parity of blocks. The cover image is
partitioned into small blocks, in which one bit informa-
tion is stored. Unfortunately, if all of the pixel values
belong to 0 or 1, a secret bit cannot be hidden [9].
This paper proposes a new data hiding method for bi-
nary images, using optimized bit position and parity bit
check with adopted block parity. This method manipulates
sub-divided blocks. The parity bit for a specified block
decides whether to change or not, to embed a secret bit.
By finding the best position to insert a secret bit for each
divided block, the image quality of the stego-image can
be maintained with relatively low computational complexity.
This paper is organized as follows. In Section 2, data
hiding scheme using block parity proposed by Venkate-
san et al. is reviewed. In Section 3, our proposed data
hiding method is described in more detail. In Section 4,
our experimental results are presented and discussed. Our
conclusions are presented in Section 5.
2. Related Work
Venkatesan et al. proposed data hiding method for binary
images to maintain the quality of cover image. To change
a bit close to the position which has the same value,

Data Hiding Method with Quality Control for Binary Images 21
neighbor matrix was adopted. For 3x3 sub-block B
m
, the
resulted sub-block B′′
m
is more difficult to be detected
than B′
m
. To find the location, Venkatesan et al. defined a
neighbor matrix.
Figure 1. Sub-block matrix of cover image
But there is a room to improve the capacity with less dis-
tortion to the human visual system. This paper proposes a
new data hiding method for binary images using opti-
mized bit position and parity bit check.
3. Proposed Method
In this section, we consider the position of data embed-
ding, and how the secret data is embedded and extracted.
The binary image is made up of black and white. There is
only one bit representation for each pixel, say 0 or 1.
Let C be the cover image of WxH pixels and S be the
n-bit secret data. For p(i,j) pixel value belonging to C
image, a new pixel value is defined as p′ (i,j).
3.1 Embedding Scheme
The following steps are executed to embed secret data.
Step 1: For a given cover image, calculate the matrix
which stores the position of the isolated pixel. Given a
specified pixel value p(i,j), the value of the neighboring
four pixels for the row and column direction is compared,
and the difference value is calculated for each 0 or 1.
Next, the difference of the neighboring eight pixels which
are surrounding the specified pixel is compared and cal-
culated. These are defined as NB
4
(i,j) and NB
8
(i,j) sepa-
rately, where Γ(·) is an indicator function which is taking
value from {0,1}.
(1)
For example, when a cover image is given as Figure
2, the difference of the neighboring pixels for p(2,1) are
calculated as NB
4
(2,1) = 2 and NB
8
(2,1) = 4 respec-
tively.
Step 2: The cover image is partitioned into MxN-size
blocks. For a specified sub-block B
m
, calculate the sum of
the block which is given by
(2)
Step 3: If S(B
m
) is not equal to 0 or MxN, embed 1-bit
of secret data into B
m
to the following three cases:
Case 1: If S(B
m
) mod 2 is equal to 0 and the embed-
ding bit is 1, then change the isolated pixel p(i,j) where
NB
4
(i,j) value is larger than any other pixel for p(i,j) = 0
pixel. When there exists another pixel which the value of
Figure 2. Difference of the neighboring pixels
the neighboring four pixels is equal, select a pixel that
NB
8
(i,j) value is larger.
Case 2: If S(B
m
) mod 2 is equal to 1 and the embed-
ding bit is 0, then change the isolated pixel p(i,j) where
NB
4
(i,j) value is larger than any other pixel for p(i,j) = 1
pixel. When there exists another pixel, for which the
value of the neighboring four pixels is equal, select a
pixel that NB
8
(i,j) value is larger than.
Case 3: If it does not belong to Case 1 and Case 2, any
other pixel values for the block remain unchanged.
Step 4: For the embedded block B′
m
which is a new
block for B
m
after embedding, calculate the sum of the
block. When the value belongs to 0 or MxN, discard this
block for embedding a secret bit.
For example, NB
4
(i,j) and NB
8
(i,j) values are calcu-
lated for the 4x4 sub-block shown in Figure 3. As a result,
NB
4
(0,3) = 3 and NB
8
(i,j) = 7 are largest value for a sub-
block, so pixel p(0,3) is selected to embed a secret bit.
3.2 Extracting Scheme
The following steps are executed to recover the secret data.
It can be directly extracted from the stego-image only.
Step 1: For a given stego-image, partition into
MxN-size blocks. For each block B′
m
, calculate the sum
of the block which is given by
S(B′m) = ∑ ∑ p′(k,l)
k=0 l=0
M-1 N-1
(3)
Step 2: If S(B′
m
) is not equal to 0 or MxN, extract 1-bit
from B′
m
to the following two cases:
Case 1: If S(B′
m
) mod 2 is equal to 0, the extracted bit
is 0.
Case 2: If S(B′
m
) mod 2 is equal to 1, the extracted bit
is 1.
Step 3: For all the embedded block B′
m
, stack an ex-
tracted bit.
41(3,3)
32(2,3)
63(1,2)
42(1,1)
73(0,3)
42(0,2)
30(0,1)
21(0,0)
41(3,3)
32(2,3)
63(1,2)
42(1,1)
73(0,3)
42(0,2)
30(0,1)
21(0,0)
Figure 3. Example of data embedding process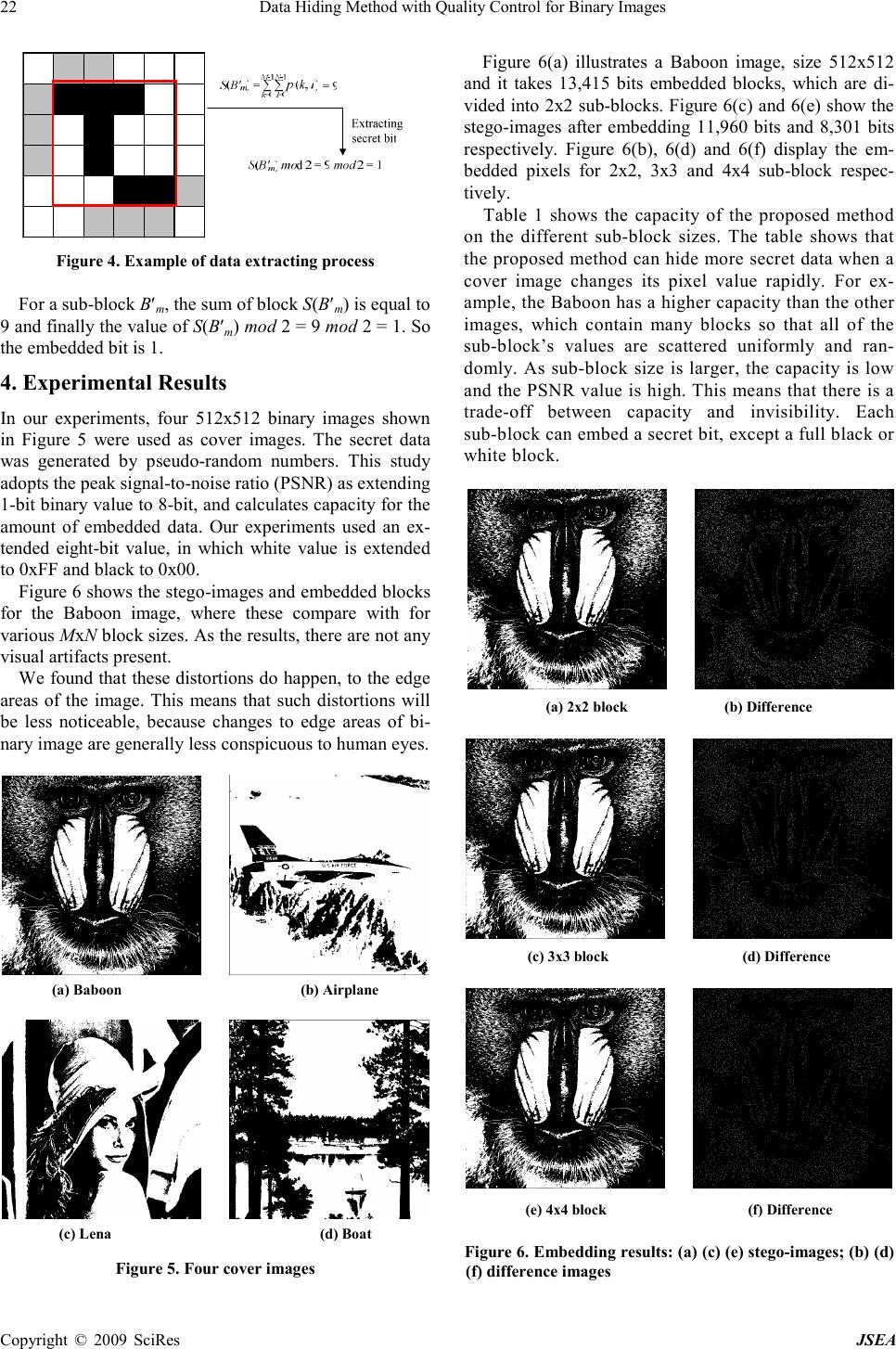

22 Data Hiding Method with Quality Control for Binary Images
Figure 4. Example of data extracting process
For a sub-block B′
m
, the sum of block S(B′
m
) is equal to
9 and finally the value of S(B′
m
) mod 2 = 9 mod 2 = 1. So
the embedded bit is 1.
4. Experimental Results
In our experiments, four 512x512 binary images shown
in Figure 5 were used as cover images. The secret data
was generated by pseudo-random numbers. This study
adopts the peak signal-to-noise ratio (PSNR) as extending
1-bit binary value to 8-bit, and calculates capacity for the
amount of embedded data. Our experiments used an ex-
tended eight-bit value, in which white value is extended
to 0xFF and black to 0x00.
Figure 6 shows the stego-images and embedded blocks
for the Baboon image, where these compare with for
various MxN block sizes. As the results, there are not any
visual artifacts present.
We found that these distortions do happen, to the edge
areas of the image. This means that such distortions will
be less noticeable, because changes to edge areas of bi-
nary image are generally less conspicuous to human eyes.
(a) Baboon (b) Airplane
(c) Lena (d) Boat
Figure 5. Four cover images
Figure 6(a) illustrates a Baboon image, size 512x512
and it takes 13,415 bits embedded blocks, which are di-
vided into 2x2 sub-blocks. Figure 6(c) and 6(e) show the
stego-images after embedding 11,960 bits and 8,301 bits
respectively. Figure 6(b), 6(d) and 6(f) display the em-
bedded pixels for 2x2, 3x3 and 4x4 sub-block respec-
tively.
Table 1 shows the capacity of the proposed method
on the different sub-block sizes. The table shows that
the proposed method can hide more secret data when a
cover image changes its pixel value rapidly. For ex-
ample, the Baboon has a higher capacity than the other
images, which contain many blocks so that all of the
sub-block’s values are scattered uniformly and ran-
domly. As sub-block size is larger, the capacity is low
and the PSNR value is high. This means that there is a
trade-off between capacity and invisibility. Each
sub-block can embed a secret bit, except a full black or
white block.
(a) 2x2 block (b) Difference
(c) 3x3 block (d) Difference
(e) 4x4 block (f) Difference
Figure 6. Embedding results: (a) (c) (e) stego-images; (b) (d)
(f) difference images

Data Hiding Method with Quality Control for Binary Images 23
Table 1 shows the comparison with other method. The
proposed method can hide more secret data than other
method although the PSNR value is similar for each image.
In here, the PSNR value is adopted for comparison with
other method.
Figure 7 shows the stego-images after embedding se-
cret data for each 3x3 sub-blcok. In these experiments,
the proposed method produces less distortion to the cover
image, in spite of its higher capacity. For the stego- im-
ages shown in Figure 7(a), 7(b), 7(c) and 7(d), it can be
embedded less than other two images since many
sub-blocks in these images have a full 0 or 1 value, where
discarded for embedding.
Figure 8 shows the detailed image for result. The
stego-images are shown in Figure 8(b), 8(c), 8(e) and 8(f)
for 170x170 cover images. As shown in Figure 8, the
proposed method has less distortion than the previous
method.
5. Conclusions
We have proposed a data hiding method using optimized
bit position and parity bit check for binary images. No
reference to the original cover image was required when
extracting the embedded secret data from the stego-image.
Table 1. Comparison of embedding for 3x3 block size
Venkatesan et al.’s The proposed method
Cover
Image
Capacity
(bits) PSNR (dB) Capacity (bits) PSNR (dB)
Baboon 9,441 16.36 11,960 16.32
Airplane
3,293 21.25 3,587 21.50
Lena 3,657 20.45 4,433 20.51
Boat
3,714 20.56 4,429 20.45
(a) capacity=11,960bits (b) capacity=3,587bits
(c) capacity=4,433bits (d) capacity=4,429bits
Figure 7. Stego-images of the proposed method
(a) Original Lena image (b) Venkatesan et al’s method
(c) Proposed method (d) Original Airplane image
(e) Venkatesan et al’s method (f) Proposed method
Figure 8. Detailed comparison for stego-images.
This method manipulated blocks which were sub-divided
into a small MxN-size block. The parity bit for a specified
block decided whether to change or not, to embed a se-
cret bit. By finding the best position to insert a secret bit
for each divided block, the image quality of the
stego-image could be improved, while retaining a low
computational complexity. Our experimental results have
shown that the proposed method provided a better way to
hide more secret data compared with other method with-
out making noticeable distortions.
REFERENCES
[1] H. Liang, W. Ran, and X. Nie, “A secure and high capac-
ity scheme for binary images,” Proceedings of the
ICWAPR, pp. 224-229, 2007.
[2] K. Matsui and K. Tanaka, “Video-steganography: How to
secretly embed a signature in a picture,” Proceedings IMA
Intellectual Property Project, pp. 187-206, 1994.
[3] S. H. Low, N. F. Maxemchuk, and A. M. Lapone,
“Document identification for copyright protection using

24 Data Hiding Method with Quality Control for Binary Images
centroid detection,” IEEE Transactions on Communications,
pp. 372-383, 1998.
[4] J. T. Brassil, S. H. Low, and N. F. Maxemchuk, “Copyright
protection for the electronic distribution of text docu-
ments,” Proceedings of IEEE, pp. 1181-1196, 1999.
[5] E. Koch and J. Zhao, “Embedding robust labels into im-
ages for copyright protection,” Proceedings of the Inter-
national Congress on Intellectual Property Rights for Spe-
cialized Information, Knowledge & New Technologies,
1995.
[6] M. Wu, E. Tang, and B. Liu, “Data hiding in digital binary
images,” IEEE International Conference on Multimedia &
Expo, 2000.
[7] C. Liu, Y. Dai, and Z. Wang, “A novel information hiding
method in binary images,” Journal of Southeast University,
2003.
[8] M. Wu and B. Liu, “Data hiding in binary image for au-
thentication and annotation,” IEEE Transations on Mul-
timedia, pp. 528-538, 2004.
[9] M. Venkatesan, P. Meenakshidevi, K. Duraiswamy, and
K. Thiagarajah, “A new data hiding scheme with quality
control for binary images using block parity,” 3rd Inter.
Symposium on Information Assurance and Security, pp.
468-471, 2007.
[10] H. Yang and A. C. Kot, “Pattern-based data hiding for
binary image authentication by connectivity-preserving,” IEEE
Transactions on Multimedia, Vol. 9, No. 3, pp. 475-486, 2007.
[11] J. Chen and T. S. Chen, “A new data hiding method in
binary images,” Proceedings of 4th International Symposium
on Multimedia Software Engineering, pp. 88-93, 2003.
[12] H. B. Zhang and L. Man, “Data hiding in binary line
drawing images,” Wavelet Analysis and Pattern Recognition,
ICWAPR, pp. 134-140, 2008.
[13] Y. J. Chang and J. C. Lin, “Data hiding using VQ index
file,” Intelligence and Security Informatics, ISI 2008, pp.
230-232, 2008.
[14] H. Gou and M. Wu, “Improving embedding payload in
binary images with super-pixels,” Image Processing, ICIP
2007, pp. 277-280, 2007.
[15] S. Huang and J. K. Wu, “Optical watermarking for printed
document authentication,” Information Forensics and Se-
curity, Vol. 2, pp. 164-173, 2007.
[16] K. H. Jung, K. S. Ha, and K. Y. Yoo, “Data hiding in binary
images by pixel-value weighting,” Convergence and Hybrid
Information Technology, ICHIT 2008. pp. 262-265, 2008.
[17] A. M. Attar, O. Taheri, S. Sadri, and A. F. Rasoul, “Data
hiding in halftone images using error diffusion halftoning
with adaptive thresholding,” Electrical and Computer
Engineering, CCECE 2006, pp. 2029-2032, 2006.