Journal of Software Engineering and Applications, 2011, 4, 81-85
doi:10.4236/jsea.2011.42009 Published Online February 2011 (http://www.SciRP.org/journal/jsea)
81
RPBTC: An Implementation Method for Robot
Planning
Shan Zhong, Qiuya Chen, Yunfei Zhou, Juan Yuan
Computer Science and Engineering College, Changshu Institute of Technology, Changshu, China.
Received January 4th, 2011; revised January 13th, 2011; accepted January 20th, 2011.
ABSTRACT
Aiming at the former formalized methods such as Strips, Situation Calculus and Fluent Calculus can not represent the
action time and get the action sequence automatically, a novel method based on timed color Petri net—RPBTC was
defined. The action time, the precondition and the post-condition of action are formalized in RPBTC based on the Flu-
ent Calculus reasoning rules. An algorism for constructing the RPBTC net system based on bidirectional search stra te-
gy is proposed, and through executing the RPBTC net system, the action sequence for reaching the goal can be gener-
ated dynamically and the time for the robot reaching the goal also can be obtained. The experiment has proved the me-
thod RPBTC as a feasible method for robot planning.
Keywords: Timed Petri Net, Robot Planning, Reasoning, Actio n, Goal
1. Introduction
Reasoning about action [1] of robot is one of the most
important areas of Artificial Intelligence. Reasoning about
action is mainly to construct the action sequence accord-
ing to t he spe cif ic pr ob lem, na mel y, give n the i nitial state,
the goal state and the actions robot can do, describing how
the robot constructs the action sequence to reach the goal.
Petri net has the strict math mode l, and it is special sui-
table for the rep resentation a nd simulation o f the systems
char acter istic o f sync hroni sm, concurr ency a nd d ynami cs
[2-3]. Vittorio [4] introduced a method for the robot plan-
ning based on Petri net, formally describing actions and
the relations between the actions, but it lacks the formal
description for the state including the environment state
and robot state. MA Bingxian [5] describes the inner ac-
tion and the external action, and using two algorisms to
reason the action sequence, but can not obtain the action
automatically in the constructed hierarchical Petri net sy-
ste m for so me give n go a l.
Therefore, a model for using the timed colored Petri
net to represent robot planning based on Fluent Calculus
[6-7] rules is introduced, the two axioms such as precon-
dition axiom and state update axiom are converted to the
corresponding timed transitions, the places and the arcs
between the timed transitions and the places, a bidirec-
tional search strategy is introduced applying to the con-
structing algorism of RPBTC net system, which is in or-
der to improve the efficiency for robot reasoning and
generating the action sequences automatically. Finally,
the simulation experi ment proves the RPBTC net system
is feasible method for robot to reason about action in dy-
namic envi ronment.
2. Fluent Calculus
As for the Fluent Calculus, all changes to the world can
be the result of named ac tions. A possible state histor y is
a sequence of actions to reach the goal called situation.
Fluent is for repr esentation of the ato mic prop ertie s of the
physical world. The function State(s) denotes the state in
situation s, which links the two key notions named state
and si tuation.
Precondition axioms are used to formally specify the
circumstances under which an action is possible in a state
in situation s, denoted by predicate Poss(a, state(s))
sho wed in Eq ua ti on ( 1 ) , whic h means at the state state (s),
the action A(x) can be executed. The
(,)
A
xzΠ
as a pure
state axiom about z is the conjunction of the conditions
under which the action can be happened.
( ) ( ) ( )
,
A
PossAxx z≡Π

(1)
State update axioms defines the effects of an action a
as the difference between the state prior to the action,
State(s), and the successor State(Do(a,s)), showed in Eq-
uation (2), in which
(,)xz∆
is the pure state axiom

RPBTC: An Implementation Method for Robot Planning
82
representing the current state, v+ (the positive effect)
represents the adding states, while v− (the negative ef-
fect) represents the removed states, and state(s) repre-
sent s the unchanged stat es and the unknown states.
( )
( )
( )
( )
( ) ( )
( )
( )
,,
,
PossAxsx States
State DoA xsState svv
+−
∧∆ ⊃
= −

 (2)
3. RPBTC Net System
Definition 1 A RPBTC net system is a 7-tuple system ∑
= (P, Tv; F, C, I-, I+, M0), which is a timed colored petri
net system has the followin g chara c te ristics:
1)The place i
pP
∈ represents the states including
both the state of robot and the environment state.
2)The timed transition v
tT
∈ represents the actions
which the robot has the ability to do. Any action has the
corresponding timed transition.
3) For any arc
fF
∈, the value on the arc such as
I-(f)and I+(f) defines the change rules between the
place and the transition, the specific value is decided by
the relations between the action and the precondition of
the action, and also the relations between the action and
the successor states of the action.
4) C is the colored set, defining the possible token col-
or in the place and the appearance color in the transition.
5) M0 as the initial state represents the initial state of
the agent and the environment.
Definition 2 The corresponding relations between the
precondition axiom of Fluent Calculus and the RPBTC
net is showed as follows: the preco nditions of actio n A(x)
are represented by places, the specific value of the state is
represented as the token in the place, the executing time
for the action is using the @ + t attached to the tra nsition.
Definition 3 The relation between state update axiom
and the RPBT C net is showed as follo ws: the representa-
tion of the action is showed in the definition 2, the suc-
cessor state of the actions such as
()State svv
+−
−
are
using the place to represent, the specific value in the
place is represented by specific token, v+ denotes the
add state, the specified value of v+ can be represented
by token fro m the transitio n to the plac e, v− denotes the
removed the state from the place to the transition. State(s)
represents the unchanged state, namely, the representa -
tion of the framework problem, the token from the place
goes back to the same place.
Definition 4 Given a action sequence
{ }
1,, n
tt σ =
for a robot to reach the goal, then the backward action
sequence can be represented as
{ }
1
,,
n
tt σ =
.
Definition 5 The bidirectional search strategy is the
combination of the forward search strategy and the
backward search strategy, the action sequence from the
initial state M0 to some midd le state M mid is
{ }
1,, i
tt σ =
,
and the action sequence from the goal state Mg to the
same middle state Mmid is
{ }
,,
ni
tt σ =
, then the for-
ward search action sequence
σ
is connected to the re-
versed backward search action sequence, finally, the re-
pea ted actio n seque nce for reac hing the s ame middl e state
is removed, then the action sequence for the bidirectional
search strategy is as:
{ }
1
,,
goal n
tt σ =
.
4. The Constructing Algorism for RPBTC
Net System
Given the initial state, the goal state of the syste m and the
actions robot can do, a bidirectional RPBTC net system
can be constructed using the bidirectional search strategy
in definition 5, in which a action in the RPBTC net sys-
tem has both the forward transition t and backward tran-
sition t_Reverse. As for the place representing robot state,
there are two places such as pi and pi_reverse, represen-
ting the forward search place and backward search place
respectively. As for the representation of the environment
state, there is only one place pk in the forward search and
backward search processes, finally, the RPBTC net sys-
tem can be constructed.
The input o f algoris m: the pla ce set Pre in the precon-
dition axiom and the place set Post of successor state
update axioms, the initial state and the goal state. The
output of algorism: the bidirectional RPBTC net system
for robot planning. Pre is used to represent the place set
of precondition axioms of specific planning instance, and
Post is used to repr esent the place set of successor states.
Step 1 Define P, Tv, F, C, I-, I+, M0 as set, P is t he col-
lection of places,
Action Sequences
pP∈
stores action se-
quence,
Goal
pP∈
stores the goal of agent, T is the col-
lection of timed transition, F is the collection of arc, I-
and I+ are the arc set, M0 is the initial marking converting
from initial state, for the co nv enient, the s ubset F1 of F is
define d.
Define i as a counter, the initia l value of i is 1
Action SequencesGoal
P=P pp∪∪
Step 2 Loop the implementation of the following part
until all the preconditions and successor states of the ac-
tion have already been constructed, and when the i-th
acti on is executing,
{ }
{ }
_ii Reverse
TT tt=∪∪
; //Action and its executing
time is represented by transition adding @+
( ) ( )( )
( )
( )()
() ()
( )
,
__
_
,,, ,,
,,,, ,,
1,,, ,
,
ikiiAction SequencesAction Sequencesi
iAction SequencesiGoalGoali
ikiReverseiReverseAction Sequences
Action SequencesiReverse
pt tppt
tptpp t
FF ptt p
pt




=∪





RPBTC: An Implementation Method for Robot Planning
83
if pik appears in the precondition place set Pre and not
in the successor state update place set Post
if pik is a environme nt state then
;
Action SequencesGoalik
P=P ppp∪ ∪∪
1F=F
;
else if pik is the state place of robot then
_
;
Action SequencesGoalikikReverse
P=P pppp∪∪ ∪∪
{ }
__
1 ,;
ikReverseiReverse
F=F pt∪
end if
if pik is an environment place then
if pik appears in the post co nditions set Post and not in
the precondition place set Pre
;
Action SequencesGoalik
P=P ppp∪ ∪∪
( )
{ }
( )
{ }
_ ,_
1, ;
i Reverseikik i Reverse
F=Ftpp t∪−
else if pik is the state plac e of robot then
_
;
Action SequencesGoalikikReverse
P=P pppp∪∪ ∪∪
( ) { } ( ) { }
( ) { }
_ __
,_
1, ,
;
i ReverseikikReverseiReverse
ik i Reverse
F=F tppt
pt
∪∪
−
end if
else if pik appears both in the precondition place set Pre
and in the successor state place set Post
if pik is t he enviro n ment state place then
;
Action SequencesGoalik
P=P ppp∪ ∪∪
( )
{ }
_
1 ,;
i Reverseik
F=F tp∪
else if pik is the state place of robot then
_
;
Action SequencesGoalikikReverse
P=P pppp∪∪ ∪∪
( )
{ }
( )
{ }
_ __
1 ,,;
i ReverseikikReverseiReverse
F=F tppt∪∪
end if
end if
Step 3 i: = i + l, if all the actions have been iterated for
once, then go to the step 4, else go the step 2
Step 4 After the precondition place set and the succes-
sor place set have been constructed, according to the ini-
tial states of system, the token is added to the relative
place then the initial marking M0 is obtained. In the fol-
lowing part, the RPBTC model of the entire system will
be constructed in the example.
4.1. Simulation Experiment
The robot example is showed as Figure 1. The round r e-
presents the robot. There are four rooms such as R401,
R402, R403, R404, and alley. Every neighbor room is
D34 D12
DA
4
2 D A1
Alley
R303
agent
DA3
DR302 R301 23
304R
DA
Figure 1 . Robo t pl anning i n office sce ne .
connected by a door, and the door also connects the nei-
ghbor room and alley, for example, D34 connects room
R304 and room R303, and DA3 connects Alley and room
R303. The goal of the robot is reaching the goal room
fro m the i nit ial ro om, a nd for r ea chin g t he g ive n go a l, t he
robot have some actions that he can do. The actions
whic h the robot can do are as follows:
1) The action Go(x) means robot goes to the door x.
The executing time for the action is 2 units. The precon-
dition axioms and the state update axioms will be de-
scribed showed in Equations (3) and (4)
( ) ( ) ( )()
,_,'',, _Poss GoxzPositionstartr xConnectsxr∧
(3)
( ) ( ) ( ) ( )
( ) ( )
( )
( )
( )()
,Holds ,', s
,',,_
_ ,,'
PossGoxsPositionr x
StateDo GoxsConnectsxr
Positionstartr xPositionrx
∧
⊃
−


(4)
2) The action Enter(r) represents the robot go to the
room r, the executing time for the action is 1 unit, The
precondition axiom and the state update axioms are
showed as Equation (5) and Equation (6):
( )
( )
( )
()( )
, ,,'
_',
Poss Enter rzConnects xrr
Positionstart rxClosedx
∧∧
 (5)
( ) ( ) ( ) ()
( ) ( )
( )
( )
( )()
( )
,Holds ',, s
, ,,'
_,
_ ',
Poss Enter rsPositionrx
StateDoEnterrsConnectsx r r
ClosedxPositionstartr x
Positionstart rx
∧
⊃
∧
−


(6)
3) The action Open(x) represents opening a door, and
the executi ng time for the action is 1 unit. T he precondi-
tion axiom and the state update axiom are showed as Eq-
uation (7) and Equation (8), respectively.
( )
( )
( )
()( )
,
_,
Poss OpenxzClosedx
Positionstartr xKeyx∧∧

(7)
( )
( )
( )
( )
( ) ( ) ( )
,Holds ,
, _,
()()()
Poss OpenxsClosedxs
StateDoOpen sPositionstartrx
KeyxClosed xClosed x
∧
⊃
∧−


(8)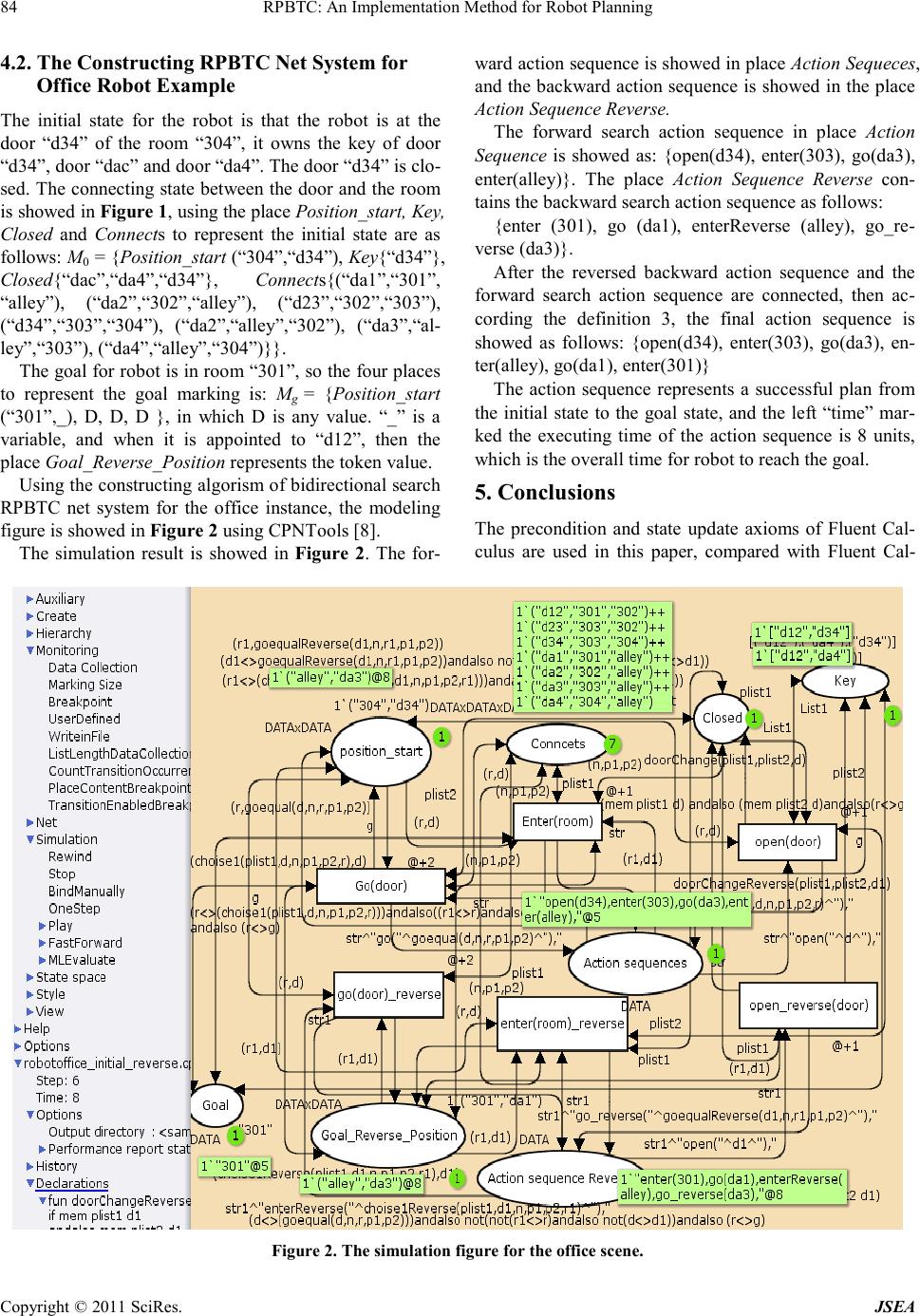

RPBTC: An Implementation Method for Robot Planning
84
4.2. The Constructing RPBTC Net System for
Office Robot Example
The initial state for the robot is that the robot is at the
door “d34” of the room “304”, it owns the key of door
“d34”, door “dac” and door “da4”. The door “d34” is clo -
sed. The connecting state between the door and the room
is sho we d in Fig ure 1, using the place Position_start, Key,
Closed and Connects to represent the initial state are as
follows: M0 = {Position_start (“304”,“d34”), Ke y { “d 34” },
Closed{“dac”,“da4”,“d34”}, Connects{(“da1”,“301”,
“alley”), (“da2”,“302”,“alley”), (“d23”,“302”,“303”),
(“d34”,“303”,“304”), (“da2”,“alley”,“302”), (“da3”,“al-
ley”,“303”), (“da4”,“alley”,“304”)}}.
The goal for robot is in room “301”, so the four places
to represent the goal marking is: Mg = {Position_start
(“301”,_), D, D, D }, in which D is any value. “_” is a
variable, and when it is appointed to “d12”, then the
place Goal_Reverse_Position represents the toke n val ue .
Using the constr ucting algorism of bid irectional search
RPBTC net system for the office instance, the modeling
figure is s howed in Figure 2 using CPNTools [8].
The simulation result is showed in Figure 2. The for-
ward action sequence is showed in place Action Sequeces,
and the backward action sequence is showed in the place
Action Sequence Reverse.
The forward search action sequence in place Action
Sequence is showed as: {open(d34), enter(303), go(da3),
enter(alley)}. The place Action Sequence Reverse con-
tains the backward search action sequence as follows:
{enter (301), go (da1), enterReverse (alley), go_re-
verse (da3)}.
After the reversed backward action sequence and the
forward search action sequence are connected, then ac-
cording the definition 3, the final action sequence is
showed as follows: {open(d34), enter(303), go(da3), en-
ter(alley), go(da1), enter(301)}
The action sequence represents a successful plan from
the initial state to the goal state, and the left “time” mar-
ked the executing time of the action sequence is 8 units,
which is the overa ll time for r obot to reach the goal.
5. Conclusions
The precondition and state update axioms of Fluent Cal-
culus are used in this paper, compared with Fluent Cal-
Figure 2. The simulation figure for the office scene.

RPBTC: An Implementation Method for Robot Planning
85
culus, RPBTC net system add the representation for the
action time, can satisfy the high demand for the real time,
secondly, Fluent Calculus using the directional search
strategy and backdate mechanism to reach the goal, but
RPBTC net system use the bidirectional strategy, so it
has t he hig her effic ie ncy. Fina ll y, RP BT C net s yste m ca n
dynamically and automatically simulate the action se-
quence reaching the goal, it also can according the time
demand to choose the best action sequence. The method
in thi s pap er has improved the efficiency and timing.
The next work is to use hierarchical petri net to repre-
sent and implement robot planning, to avoid the problem
of state explosion problem when the system scale and
state become larger.
REFERENCES
[1] J. McCart hy and P. J. Hayes, “Haves Some Philosophical
Problems from the Standpoint of Arti fi cial Intelligence,”
B. Meltzer and D. Michie, Eds., Machine Intelligence,
Vol. 4, 1969, pp. 463-502.
[2] K. Jensen, L. M. Kristensen and L. Wells. “Coloured Petri
Nets and CPN Tools for Modelling and Validation of
Concurrent Systems,” Software Tools for Technology
Transfer, Vol. 9, No. 3-4, 2007, pp. 213-254.
doi:10.1007/s10009-007-0038-x
[3] P. F. Pal amara, V. A. Zip aro, L. Iocch i, et a l., “A Robotic
Soccer P assing Task Using P etri Net Plans,” Proceedings
of 7th International Conference on Autonomous Agents
and Multiagent Systems, Estoril, 12-16 May 2008, pp.
1711-1712.
[4] V. A. Ziparo and L. Iocchi, “Petri Net Plans,” Fourth
International Workshop on Modelling of Objects, Com-
ponent s , an d A ge nts, Turku , 26 June 2006, pp. 267-290.
[5] B. X. Ma, Z. H. Wu and Y. L. Xu, “Research on Mul-
ti-Agent Planning with Petri Nets,” Computer Engineer-
ing, In Chinese, Vol. 32, No. 14, 2006, pp. 4-6.
[6] Y. Jin and M. Thielsch er , “Iterated Belief Revision, Re-
vised,” Artificial Intelligence, Vol. 171, No. 1, 2007, pp.
1-18. doi:10.1016/j.artint.2006.11.002
[7] S. S ardina, G. de Gia como, Y . Lesperance, et al., “O n the
Semantics of Deliberation in Indigolog-From Theory to
Implementation,” Annals of Mathematics and Artificial
Intelligence, Vol. 41, No. 2-4, 2004, pp. 259-299.
doi:10.1023/B:AMAI.0000031197.13122.aa
[8] CPN Tool s. http://www.daimi.au.dk/CPNTools/