J. Biomedical Science and Engineering, 2011, 4, 136-145
doi:10.4236/jbise.2011.42020 Published Online February 2011 (http://www.SciRP.org/journal/jbise/
JBiSE
).
Published Online February 2011 in SciRes. http://www.scirp.org/journal/JBiSE
Mathematical modeling of the biphasic dopaminergic
response to glucose
Matthias Chung1, Britta Göbel2, Achim Peters3, Kerstin M. Oltmanns4, Andr eas Moser5
1Department of Mathematics, Texas State University, San Marcos, USA;
2Institute of Mathematics and Image Computing, Graduate School for Computing in Medicine and Life Sciences, University of
Lübeck, Lübeck, Germany;
3Medical Clinic I, University of Lübeck, Lübeck, Germany;
4Department of Psychiatry and Psychotherapy, University of Lübeck, Lübeck, Germany;
5Department of Neurology, University of Lübeck, Lübeck, Germany.
Received 3 November 2010; revised 9 December 2010; accepted 12 January 2011.
ABSTRACT
In this work, we specify potential elements of the
brain to sense and regulate the energy metabolism
of the organism. Our numerical investigations base
on neurochemical experiments demonstrating a
biphasic association between brain glucose level
and neuronal activity. The dynamics of high and
low affine KATP channels are most likely to play a
decisive role in neuronal activity. We develop a
coupled Hodgkin-Huxley model describing the in-
teractive behavior of inhibitory GABAergic and
excitatory dopaminergic neurons projecting into
the caudate nucleus. The novelty in our approach is
that we include the synaptic coupling of GA BAergic
and dopaminergic neurons as well as the interac-
tion of high and low affine KATP channels. Both
are crucial mechanisms described by kinetic models.
Simulations demonstrate that our new model is co-
herent with neurochemical in vitro experiments.
Even experimental interventions with glibencla-
mide and glucosamine are reproduced by our new
model. Our results show that the considered dy-
namics of high and low affine KATP channels may
be a driving force in energy sensing and global reg-
ulation of the energy metabolism, which supports
central aspects of the new Selfish Brain Theory.
Moreover, our simulations suggest that firing fre-
quencies and patterns of GABAergic and dopa-
minergic neurons are correlated to their neuro-
chemical outflow.
Keywords: Neuronal Model; Coupled Neurons; Dopa-
mine; GABA; K-ATP Channels; Biphasic; Glibencla-
mide; Glucosamine
1. INTRODUCTION
Neurochemical experiments show that extracellular glu-
cose level influences the neurochemical activity of neu-
rons. More precisely, Steinkamp and colleagues showed
that decreasing glucose levels cause a neuronal biphasic
response [1]. In their study, slices of the rat caudate nu-
cleus are examined in vitro in a superfusion chamber
treated by artificial cerebrospinal fluid. The glucose lev-
el in the fluid varies from 0 to 10 mM while the dopa-
mine outflow is measured concomitantly. The effect of
different glucose concentrations on dopamine and GA-
BA (γ-aminobutyric acid) outflow is investigated by
means of high-performance liquid chromatography and
electrochemical detection. We will focus on the neuro-
chemical mechanisms in Section 2.1.
During glucose reduction from 10 to 0 mM, a biphasic
effect on dopamine outflow can be observed, Figure 1(a).
In the first phase (glucose concentration of 10 down to 7
mM in the incubation medium), an increase in dopamine
outflow is observed. This phase is followed by a decline
of dopamine outflow at glucose concentrations from 6
down to 0 mM. To investigate the modes of action,
Steinkamp et al. repeated this experiment with three dif-
ferent interventions.
First, they added glibenclamide in a concentration of 1
µM to the cerebrospinal fluid changing the dopaminergic
outflow, Figure 1(c). While dopamine outflow remains
unchanged at high glucose levels, its outflow is reversed in
the second phase (glucose levels lower than 4 mM). In a
second intervention, Steinkamp and colleagues increased
the glibenclamide concentration in the cerebrospinal fluid
to 10 µM. Here, the effects of glucose variation on dopa-
mine is completely antagonized, both phases are annihi-
lated, Figure 1(d). The third intervention adds glucosa-
mine to the cerebrospinal fluid (5 mM). Here, biphasic
dopamine outflow is completely abolished, Figure 1(b).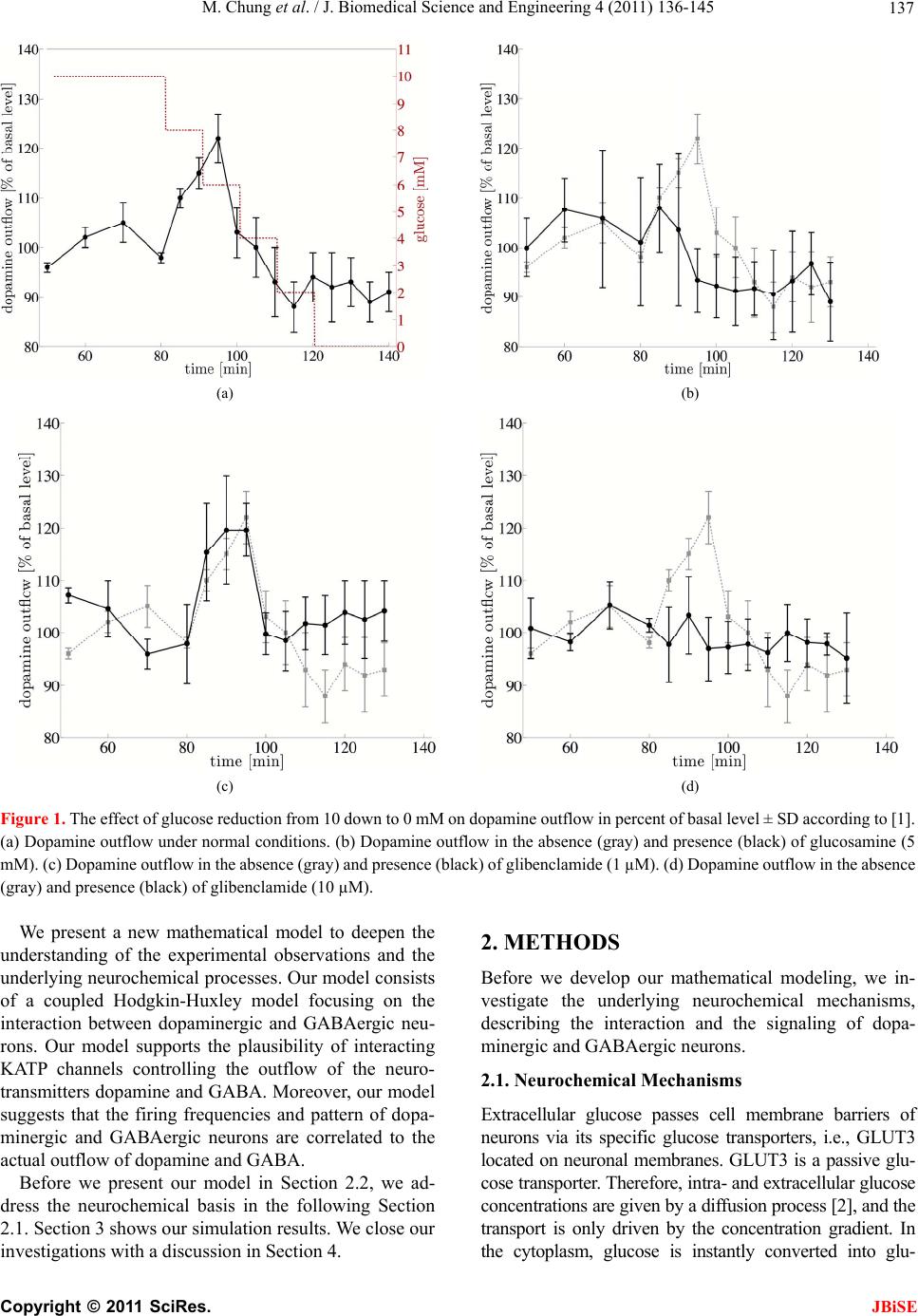

M. Chung et al. / J. Biomedical Science and Engineering 4 (2011) 136-145 137
(a) (b)
 
(c) (d)
Figure 1. The effect of glucose reduction from 10 down to 0 mM on dopamine outflow in percent of basal level ± SD according to [1].
(a) Dopamine outflow under normal conditions. (b) Dopamine outflow in the absence (gray) and presence (black) of glucosamine (5
mM). (c) Dopamine outflow in the absence (gray) and presence (black) of glibenclamide (1 µM). (d) Dopamine outflow in the absence
(gray) and presence (black) of glibenclamide (10 µM).
We present a new mathematical model to deepen the
understanding of the experimental observations and the
underlying neurochemical processes. Our model consists
of a coupled Hodgkin-Huxley model focusing on the
interaction between dopaminergic and GABAergic neu-
rons. Our model supports the plausibility of interacting
KATP channels controlling the outflow of the neuro-
transmitters dopamine and GABA. Moreover, our model
suggests that the firing frequencies and pattern of dopa-
minergic and GABAergic neurons are correlated to the
actual outflow of dopamine and GABA.
Before we present our model in Section 2.2, we ad-
dress the neurochemical basis in the following Section
2.1. Section 3 shows our simulation results. We close our
investigations with a discussion in Section 4.
2. METHODS
Before we develop our mathematical modeling, we in-
vestigate the underlying neurochemical mechanisms,
describing the interaction and the signaling of dopa-
minergic and GABAergic neurons.
2.1. Neuro ch emical Mechani sms
Extracellular glucose passes cell membrane barriers of
neurons via its specific glucose transporters, i.e., GLUT3
located on neuronal membranes. GLUT3 is a passive glu-
cose transporter. Therefore, intra- and extracellular glucose
concentrations are given by a diffusion process [2], and the
transport is only driven by the concentration gradient. In
the cytoplasm, glucose is instantly converted into glu-
C
opyright © 2011 SciRes. JBiSE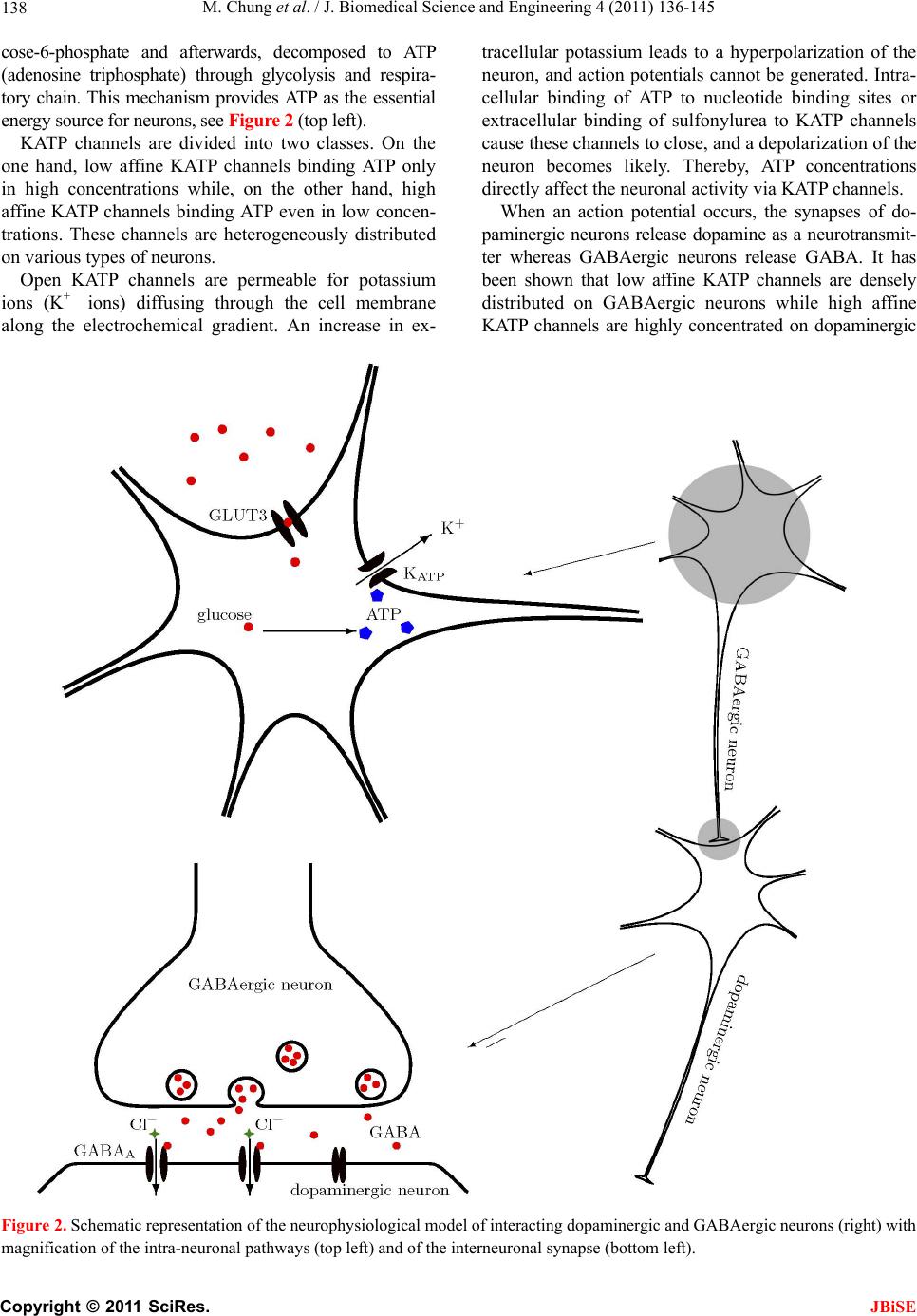

M. Chung et al. / J. Biomedical Science and Engineering 4 (2011) 136-145 138
cose-6-phosphate and afterwards, decomposed to ATP
(adenosine triphosphate) through glycolysis and respira-
tory chain. This mechanism provides ATP as the essential
energy source for neurons, see Figur e 2 (top left).
KATP channels are divided into two classes. On the
one hand, low affine KATP channels binding ATP only
in high concentrations while, on the other hand, high
affine KATP channels binding ATP even in low concen-
trations. These channels are heterogeneously distributed
on various types of neurons.
Open KATP channels are permeable for potassium
ions (K+ ions) diffusing through the cell membrane
along the electrochemical gradient. An increase in ex-
tracellular potassium leads to a hyperpolarization of the
neuron, and action potentials cannot be generated. Intra-
cellular binding of ATP to nucleotide binding sites or
extracellular binding of sulfonylurea to KATP channels
cause these channels to close, and a depolarization of the
neuron becomes likely. Thereby, ATP concentrations
directly affect the neuronal activity via KATP channels.
When an action potential occurs, the synapses of do-
paminergic neurons release dopamine as a neurotransmit-
ter whereas GABAergic neurons release GABA. It has
been shown that low affine KATP channels are densely
distributed on GABAergic neurons while high affine
KATP channels are highly concentrated on dopaminergic
Figure 2. Schematic representation of the neurophysiological model of interacting dopaminergic and GABAergic neurons (right) with
magnification of the intra-neuronal pathways (top left) and of the interneuronal synapse (bottom left).
C
opyright © 2011 SciRes. JBiSE

M. Chung et al. / J. Biomedical Science and Engineering 4 (2011) 136-145 139
neurons [3,4]. Hence, dopaminergic neurons are more
active at low ATP concentrations than GABAergic neu-
rons.
The neurotransmitter GABA binds ionotropic GABAA
receptors. Activated GABAA receptors lead to confor-
mation changes within the membrane, i.e., open pores
allow chloride ions (Cl− ions) to pass along the electro-
chemical gradient. Typically, an influx of Cl− ions into
the neuron occurs. Here, the neuron tends toward the
resting potential. GABAA receptors are densely distrib-
uted on the post-synaptic membrane of dopaminergic
neurons so that the GABAergic neurons modulate do-
pamine outflow by inhibition of dopaminergic activity.
Evidence exists that systemic signal propagation from
GABAergic onto dopaminergic neurons occurs in neu-
ronal networks, see Figur e 2 (bottom left) [5].
In case of high extracellular glucose concentrations,
low and high affine KATP channels bind ATP. Both
neuron types fire and release their neurotransmitter. This
implies a GABA mediated inhibition of dopamine out-
flow, which is regulated by extracellular glucose via
high and low affine KATP channels. When extracellular
glucose decreases, the ATP concentration in the cyto-
plasm drops and merely high affine KATP channels bind
ATP causing these channels to close. The dopaminergic
neurons release their neurotransmitter. Furthermore, the
dopamine release is increased by reduced GABAergic
activity. When the extracellular glucose concentration is
further reduced, a decline of the neurotransmitter dopa-
mine can be observed. In this phase, neither high nor low
affine KATP channels bind ATP, and the dopaminergic
and GABAergic neurons aspire towards their resting
potential. This interpretation leads to the biphasic ob-
servation shown in Figure 1(a).
Glibenclamide extracellularly binds to sulfonylurea
subunits of KATP channels resulting in a consecutive
inhibition of the channels [6,7]. Hence, glibenclamide
and intracellular ATP regulate the KATP channels in a
similar manner. Adding a low concentration of gliben-
clamide to the cerebrospinal fluid now leads to an eleva-
tion of the dopaminergic outflow at low glucose concen-
trations, see Figure 1(c). Since this intervention corre-
sponds to a slightly elevated intraneuronal ATP concen-
tration, the effect is predominant at low extracellular
glucose concentrations. Adding a high concentration of
glibenclamide leads to a permanent inhibition of the
KATP channels, and a constant dopaminergic outflow
can be observed, see Figure 1(d).
Glucosamine inhibits glucose phosphorylation by
hexokinases and therefore blocks ATP production
through glycolysis. Adding glucosamine leads to a re-
duction of the intracellular ATP concentration [8]. Hence,
the biphasic dopamine outflow is completely abolished
by adding glucosamine, see F igure 1(b) .
To systemically analyze the neurochemical interaction
between GABAergic and dopaminergic neurons and to
simulate the experiments, we now turn to a mathematical
model of a coupled neuronal system. Various mathe-
matical models of single dopaminergic and GABAergic
midbrain neurons have been investigated over the years.
They range from single to multiple compartment models
of single neurons, see [9,10,11,12]. A review on single
dopaminergic neuron models by Kuznetsov et al. can be
found online [13]. All of these detailed models base on a
Hodgkin-Huxley type model and incorporate various
currents and fluxes, such as T-, L-, and N-type calcium,
potassium, hyperpolarization activated, and NMDA in-
duced currents. Despite their detailed modeling ap-
proaches most of these models fail to mirror realistic
time series of synaptic stimulations [13,10]. These mod-
els aim to investigate electrophysiological behavior. We
do not aim to model the precise neurochemical behavior
and realistic time series of synaptic stimulations of mid-
brain dopaminergic and GABAergic neurons. Our focus
is on the functional mechanism of glucose dependent
neuronal activity and the synaptic coupling of GABAer-
gic and dopaminergic neurons rather than on a detailed
electrophysiological description. These features are not
covered and analyzed in previous dopaminergic and
GABAergic neuronal models. Hence, previous models
may not be considered to investigate functional mecha-
nism of glucose dependent neuronal activity. Here, we
investigate a rather simple Hodgkin-Huxley type model
to reduce ambiguity to massive number of parameters.
2.2. Coupled Neuronal Model
Based on the neurophysiologic mechanisms described in
the last section, we present a mathematical model, which
simulates the behavior of a neuronal network in the
midbrain. More precisely, we investigate a Hodgkin-
Huxley type model of synaptic coupledGABAergic-
dopaminergic neurons [14]. Hodgkin-Huxley type mod-
els describe how action potentials of a single neuron
proceed in time. The model can be specified by the sys-
tem of differential equations
Na K L P
1()
(1) ,
(1 ),
(1 )
mm
nn
hh
VIIII
C
mmm
nnn
hhh











,
with
3
Na NaNa
4
KK K
LL L
(),
(),
()
IgmhVV
IgnVV
IgVV



C
opyright © 2011 SciRes. JBiSE

M. Chung et al. / J. Biomedical Science and Engineering 4 (2011) 136-145 140
and the functions


75 13.5
40 75
1
mV
V
e





,
/42.248
1.2262 V
me


,
(95 )/11.8
95
1
V
nV
e





,
/22.222
0.025 V
ne


,
/24.186
0.0035V
he


,
( 51.25)/5.2
0.017 (51.25)
1
hV
V
e



.
Here, is the membrane potential and is its de-
rivative in time, is the capacitance, and
VV

C
N
a
I
,
K
I
are
the currents of sodium and potassium ion channels, re-
spectively. Furthermore,
L
I
is a leakage current while
P
I
is an externally applied current. The currents
N
a
I
,
K
I
and
L
I
can be described as a product of maximal
conductance
N
a
g
,
K
g
and
L
g
, voltage dependent gat-
ing variables m, n and h (with its derivatives , and
) and deviation between actual membrane potential and
its reversal potentials
m
n 
h

N
a
V,
K
V and
L
V. The gating
variables , and consist of functions m
mn h

, n

,
h

and m

, n

, h

reflecting the membrane potential
dependent rate constants of channel opening and closing,
respectively.
As for the constants, we choose typical values for
GABAergic neurons given by literature [15]: 55
Na
V

, mV 97m
V
K
V , , 70 mV
L
V 2 mScm112
Na
g


1μC, , ,
2
224mScm
K
g2 g0.1mScm
L
2 Fcm

 and
P representing the ion pumps and an ex-
ternally applied current (bias). The neuronal activity of a
GABAergic neuron can be described by the Hodgkin-
Huxley model (see equations above and compare Figure 3
top).
2
μAcm 10I
As previously discussed, some potassium channels are
ATP and therewith glucose dependent. In turn, KATP
channel kinetics depends on the extracellular glucose
concentration. We assume that the linear transformation
calculates the intra-neuronal ATP
concentration
0.0014 0.033AG
A
from the extracellular glucose concen-
tration (compare [16]). This transformation seems to
be arbitrary at first sight. However, the observed glucose
levels of 0 to 10 mM in the experimental superfusion
system lead to intra-neuronal ATP concentrations of 33 to
47 µM, the relevant range of KATP channel kinetics
(compare [17]). Note the neurochemical experiment in-
cludes hyperphysiological glucose levels (see Section 1).
In order to mathematically simulate the addition of glu-
cosamine, we modify the ATP production by glucose
utilization, i.e.,
G
0.0A0140.033G

 with 0.05


.
Furthermore, we introduce an ATP dependent mo-
notonously increasing function

;:
A
AK 


.
The constant A
K
illustrates the affinity of the KATP
channel. The kinetics of the KATP channels can be de-
scribed by
max
(; )
1·
A
H
A
v
AK K
A





,
where ma is the saturated closing rate of the KATP
channels, A
x
v
K
is the ATP concentration causing half-
maximal channel closing, and
H
is the Hill coefficient.
We choose max 0.1v

, for low affine
and for high affine KATP channels and
0.05mM
A
K
0.02mM
AK

1.8H

(compare [17]). The parameter

represents
the addition of the KATP channel blocker glibenclamide.
Without glibenclamide, we set 1

, 1.03

 models
a low glibenclamide concentration and 4

 reflects
adding a high glibenclamide concentration.
Since the closing probability of the KATP channels de-
pends on the ATP concentration, we receive the follow-
ing modification of n

for the GABAergic neuron
/22.222
(;)0.025 V
nA
AK e 

.
Here, we assume that KATP and voltage dependent po-
tassium channels interact. Hence, we model the closing
rate n

as product of ATP and voltage dependent
channels. The open probability is independent of ATP,
and n

does not need to be modified.
The same Hodgkin-Huxley model holds for the do-
paminergic neuron if we for once neglect the inhibitory
effect of the GABAergic neuron. Taking the effect of the
GABAA receptors on the dopaminergic neuron into ac-
count, we couple two Hodgkin-Huxley models. We in-
troduce the synaptic current GABA , which depends on the
membrane potential V of the GABAergic neuron (see
first equation of equations above). It describes the in-
hibitory chemical connection between GABAergic and
dopaminergic neuron. We use “~” to identify the specific
values of the dopaminergic neuron
I

NaKL GABA P
1
VIIII
C
 

 I
,
with the synaptic current
()
GABA synsyn
IgrVV

.
In neuronal models, synaptic events are often formal-
ized as stereotyped, time-varying conductance wave-
forms. The α-function is most commonly used [18]. Al-
ternatively, one can compute synaptic conductances using
a kinetic model [19]. This approach is consistent with the
formalism, which describes conductances of ion channels
in the Hodgkin-Huxley model. It allows a more realistic
C
opyright © 2011 SciRes. JBiSE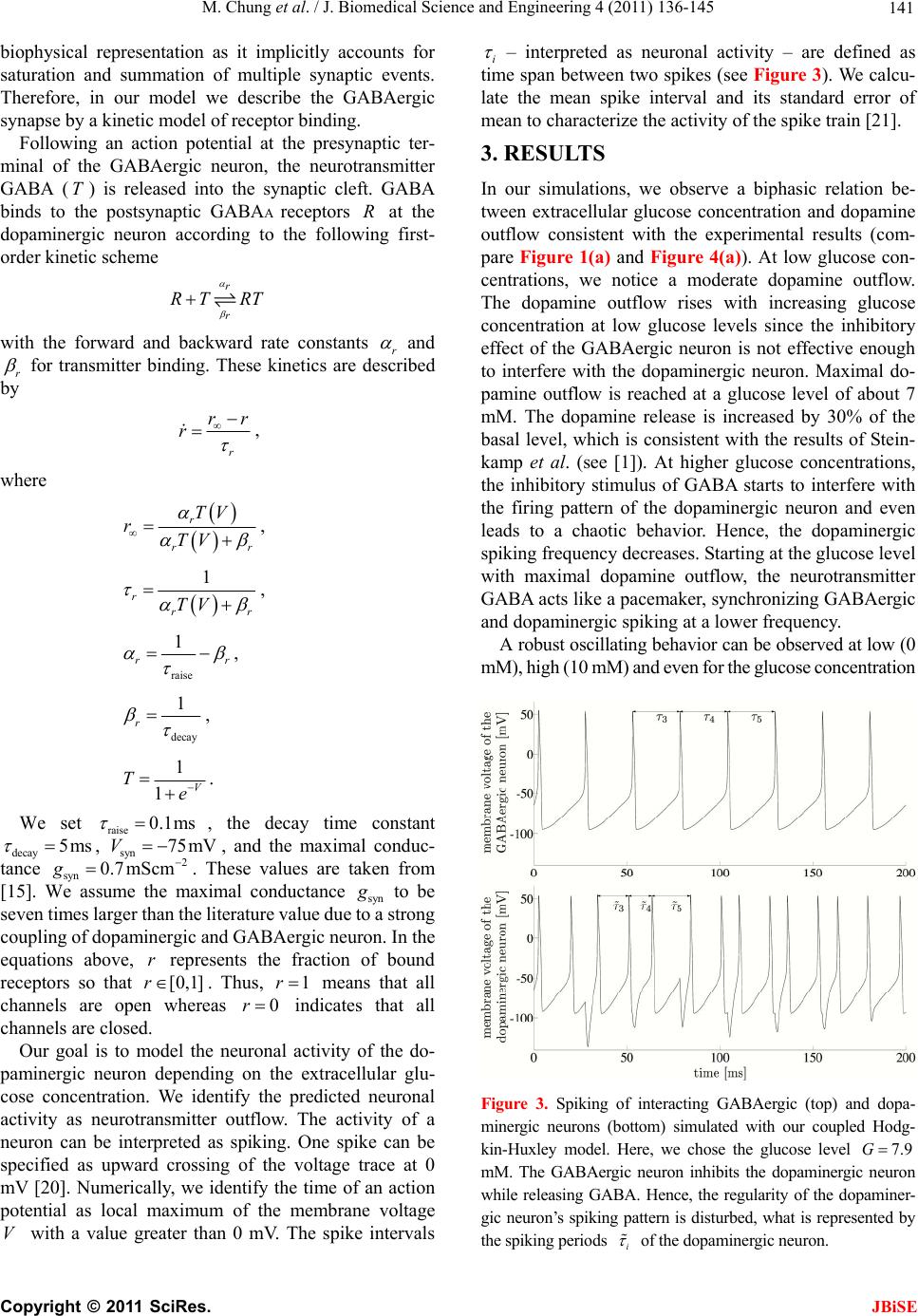

M. Chung et al. / J. Biomedical Science and Engineering 4 (2011) 136-145 141
biophysical representation as it implicitly accounts for
saturation and summation of multiple synaptic events.
Therefore, in our model we describe the GABAergic
synapse by a kinetic model of receptor binding.
JBiSE
Following an action potential at the presynaptic ter-
minal of the GABAergic neuron, the neurotransmitter
GABA () is released into the synaptic cleft. GABA
binds to the postsynaptic GABAA receptors at the
dopaminergic neuron according to the following first-
order kinetic scheme
TR
r
r
RT RT



with the forward and backward rate constants r

and
r

for transmitter binding. These kinetics are described
by
r
rr
r




,
where


r
rr
TV
rTV



,

1
rrr
TV


,
raise
1
rr




,
decay
1
r
 ,
1
1V
Te .
We set raise 0.1ms

, the decay time constant
decay5ms

g
, , and the maximal conduc-
tance syn. These values are taken from
[15]. We assume the maximal conductance syn
syn 75mV
2
0.7 mScmV
g
to be
seven times larger than the literature value due to a strong
coupling of dopaminergic and GABAergic neuron. In the
equations above, represents the fraction of bound
receptors so that . Thus, means that all
channels are open whereas indicates that all
channels are closed.
r
[0,1]r1r
0r
Our goal is to model the neuronal activity of the do-
paminergic neuron depending on the extracellular glu-
cose concentration. We identify the predicted neuronal
activity as neurotransmitter outflow. The activity of a
neuron can be interpreted as spiking. One spike can be
specified as upward crossing of the voltage trace at 0
mV [20]. Numerically, we identify the time of an action
potential as local maximum of the membrane volta
V with a value greater than 0 mV. The spike intervals
i
ge

– interpreted as neuronal activity – are defined as
time span between two spikes (see Figure 3). We calcu-
late the mean spike interval and its standard error of
mean to characterize the activity of the spike train [21].
3. RESULTS
In our simulations, we observe a biphasic relation be-
tween extracellular glucose concentration and dopamine
outflow consistent with the experimental results (com-
pare Figure 1(a) and Figure 4(a)). At low glucose con-
centrations, we notice a moderate dopamine outflow.
The dopamine outflow rises with increasing glucose
concentration at low glucose levels since the inhibitory
effect of the GABAergic neuron is not effective enough
to interfere with the dopaminergic neuron. Maximal do-
pamine outflow is reached at a glucose level of about 7
mM. The dopamine release is increased by 30% of the
basal level, which is consistent with the results of Stein-
kamp et al. (see [1]). At higher glucose concentrations,
the inhibitory stimulus of GABA starts to interfere with
the firing pattern of the dopaminergic neuron and even
leads to a chaotic behavior. Hence, the dopaminergic
spiking frequency decreases. Starting at the glucose level
with maximal dopamine outflow, the neurotransmitter
GABA acts like a pacemaker, synchronizing GABAergic
and dopaminergic spiking at a lower frequency.
A robust oscillating behavior can be observed at low (0
mM), high (10 mM) and even for the glucose concentration
Figure 3. Spiking of interacting GABAergic (top) and dopa-
minergic neurons (bottom) simulated with our coupled Hodg-
kin-Huxley model. Here, we chose the glucose level 7.9G

mM. The GABAergic neuron inhibits the dopaminergic neuron
while releasing GABA. Hence, the regularity of the dopaminer-
gic neuron’s spiking pattern is disturbed, what is represented by
the spiking periods i

 of the dopaminergic neuron.

M. Chung et al. / J. Biomedical Science and Engineering 4 (2011) 136-145 142
(a) (b)
(c) (d)
Figure 4. Dopaminergic spiking frequency interpreted as dopamine outflow with varying extracellular glucose concentration. Depicted
is the mean dopamine outflow in percent of basal level ± standard error of mean. (a) Dopamine outflow under normal conditions. (b)
Dopamine outflow in the absence (gray) and presence (black) of glucosamine. (c) Dopamine outflow in the absence (gray) and presence
(black) of a low glibenclamide concentration (1.03

). (d) Dopamine outflow in the absence (gray) and presence (black) of a high
glibenclamide concentration (4

).
with maximal dopamine outflow (7 mM). Figure 5(a)
illustrates this behavior. However, at glucose concentra-
tions between 7 and 9 mM, the neurotransmitter GABA
starts to interfere more powerful, compare Figure 5(c).
Then, the spiking pattern of the dopaminergic neuron
reaches a chaotic behavior; see Figure 5 (b) and 5(d). The
uniformity of the dopaminergic neuron spiking pattern is
disturbed since its firing is suppressed by excitation of the
GABAergic neuron. The rapid response of the GABAA
receptors to the neurotransmitter [22] and the immediate
influence on the dopaminergic neuron become dominant.
As the glucose level increases, the KATP channels are
inactivated resulting in increased inhibition to the dopa-
minergic neuron due to GABA. This leads to the overall
stable decrease of dopamine outflow.
In general, we observe a higher spiking frequency of
the dopaminergic neuron compared to the GABAergic
cell for a fixed glucose concentration (see Figure 3 ). This
is caused by the high affine KATP channels in the mem-
brane of dopaminergic neuron compared to the GABAer-
gic low affine KATP channels. This simulation result is
consistent with experimental measurements [5]. The ratio
of dopaminergic to GABAergic spiking frequency re-
mains almost constant (slightly increasing from 2 at 0
mM up to 2.1 at 7 mM). At high glucose concentrations,
the ratio steeply decreases to about 1.5 indicating the
inhibitory effect of GABA on dopamine outflow (data not
shown).
The effects of glibenclamide on neuronal activity can
be observed in our simulations. The addition of a low
glibenclamide concentration is represented by the pa-
rameter 1.03


in our model. At low glucose concen-
trations, characterized by an elevation of dopaminergic
activity, the spiking frequency of the dopaminergic neu-
ron is increased compared to values found without gliben-
clamide. However, maximum frequency as well as de-
creased dopaminergic activity at higher glucose concen-
trations remain unaffected. At glucose concentrations
higher than 8 mM, the spiking frequency of the dopa-
minergic neuron slightly increases compared to the values
C
opyright © 2011 SciRes. JBiSE

M. Chung et al. / J. Biomedical Science and Engineering 4 (2011) 136-145 143
(a) (b)
(c) (d)
Figure 5. (a) Phase diagrams for low (0 mM, dotted), medium (7 mM, dashed) and high (10 mM, solid) extracellular glucose con-
centration. (b) Chaotic behavior for the extracellular glucose concentration 8.2 mM. (c) Spiking times of the GABAergic neuron
depending on the extracellular glucose concentration. (d) Spiking times of the dopaminergic neuron depending on the extracellular
glucose concentration.
without glibenclamide (compare Figure 4(c)). At high
glibenclamide concentrations, the increasing glucose
concentration does not modulate the spiking frequency of
dopaminergic neurons. Consistently, our simulation re-
sults with 4

 show neither an increase nor a decrease
in the spiking frequency (Figure 4(d)).
As shown in Figure 4(b), glucosamine does not
change the activity of the dopaminergic neuron with 10
mM glucose. However, at 7 mM glucose, glucosamine
decreases the spiking frequency in comparison to the
control values without glucosamine. It is reduced to ap-
proximately 95% of the frequency at 10 mM glucose,
which coincides with the value at low glucose concen-
trations.
Our simulations are consistent with the experimental
observations shown in Section 1. Therefore, they give
evidence to the regulatory mechanisms of KATP chan-
nels.
4. DISCUSSION
The purpose of this study is to specify a potential regu-
latory element of the brain to sense and regulate the en-
ergy supply of the organism. Our presented results
demonstrate that a simple isolated coupled Hodgkin-

M. Chung et al. / J. Biomedical Science and Engineering 4 (2011) 136-145 144
Huxley model simulates the interactive behavior of
GABAergic and dopaminergic neurons accurately. The
simulations are consistent with the results of the in vitro
cell experiments [1]. The model reflects the observed
neuronal biphasic response. Furthermore, simulations on
interventions with glibenclamide and glucosamine show
consistent dynamics with experimental observations.
To our best knowledge, there do not exist any experi-
mental data on the frequency of firing in neuronal net-
works consisting of dopaminergic and GABAergic neu-
rons. The relation between spiking frequency and neuro-
transmitter outflow of neurons remains unknown. Our
model for the first time predicts the spiking behavior of
neuronal networks consisting of dopamine and GABA
neurons under varying glucose concentrations. Moreover,
our simulation results suggest that the dopamine outflow
of a dopaminergic neuron is congruent to its spiking
frequency.
One may argue that our developed coupled Hodg-
kin-Huxley model is too comprehensive to address the
observed biphasic dynamics. Apart from this model, there
exist several other mathematical models describing the
behavior of neurons, which give an even more simplified
representation. For example, one could mention the
Leaky-Integrate-and-Fire model or the FitzHugh-Na-
gumo model. Unlike these models, the Hodgkin-Huxley
model particularly describes ion channel gating resulting
in excitation of neurons. Since weinvestigate the KATP
channel dynamics that cause the associated changes in
neuronal activity, the Hodgkin-Huxley model is adequate
to model extracellular glucose dependent dopamine out-
flow.
Furthermore, one may argue that our model is over-
simplified since we only investigate an isolated two-
neuron model. But one has to take into account that sim-
ple and robust biological mechanisms are more likely to
evolutionary prevail. Therefore, the development of a
simple stable system is required. Here, we simply address
coupled dopaminergic and GABAergic neurons with
different KATP channels as essential regulatory mecha-
nism behind the dopamine outflow. Our future research
will investigate and simulate the behavior of larger neu-
ronal networks with coupled dopaminergic and GABAer-
gic neurons as basic subunits.
The principle of interacting excitatory and inhibitory
elements like high and low affine KATP channels can be
found in many other biological systems (see [23,24]). For
instance, almost all known ligands bind to at least two
receptor types. In most cases, the formed complexes have
opposing actions. Considered in closed loops these posi-
tive and negative feedbacks are shown to generate ho-
meostatic systems [25]. This gives additional evidence
for our presented concept and may reveal the potential
control mechanism of the biphasic dopamine response in
a global brain energy sensing concept.
How does the brain sense energy, and how does the
brain send control signals to the body? The answer to
these questions is fairly unknown. The Selfish Brain
Theory [26] specifies KATP channels to be involved in
sensing the energy supply in the brain so that the biphasic
dopamine release may be explained by the dynamic of
high and low affine KATP channels. Our neuronal model
supports the plausibility of interacting KATP channels
controlling dopamine and GABA outflow. Suppose the
maximal dopaminergic outflow as an energy resting state.
A deviation from this glucose resting state will result in a
dopaminergic response and might be identified as a brain
energy sensing mechanism.
In this way, the brain might be able to sense its energy
supply via the intra-neuronal ATP concentration and to
react accordingly. It has been demonstrated that the cau-
date nucleus is highly involved in learning, memory, and
feedback processes, in particular [27,28]. These proc-
esses play a decisive role in the energy metabolism of
the whole organism. This may be evidence that the brain
is the superior administrative instance and has the
strongest position in the competition for energy within
the body. Hence, consistent with the Selfish Brain The-
ory on a systemic scale the described mechanisms may
be a driving force for a global regulation in energy me-
tabolism.
5. ACKNOWLEDGEMENTS
The authors M. C., B. G., and K. M. O. thank the Graduate School for
Computing in Medicine and Life Sciences at the University of Lübeck
funded by the German Research Foundation [DFG GSC 235/1] for its
support.
REFERENCES
[1] Steinkamp, M., Li, T., Fuellgraf, H. and Moser, A. (2007)
K(ATP)-dependent neurotransmitter release in the neu-
ronal network of the rat caudate nucleus. Neurochemistry
international, 50, 159-163.
doi:10.1016/j.neuint.2006.07.011
[2] Baldwin, S.A. (1993) Mammalian passive glucose trans-
porters: members of an ubiquitous family of active and
passive transport proteins. Biochimica et Biophysica Acta,
1154, 17-49.
[3] Karschin, C., Ecke, C., Ashcroft, F.M. and Karschin, A.
(1997) Overlapping distribution of K(ATP) channel-
forming Kir6.2 subunit and the sulfonylurea receptor
SUR1 in rodent brain. FEBS Letters, 401, 59-64.
doi:10.1016/S0014-5793(96)01438-X
[4] During, M.J., Leone, P., Davis, K.E., Kerr, D. and Sher-
win, R.S. (1995) Glucose modulates rat substantia nigra
GABA release in vivo via ATP-sensitive potassium
channels. Journal of Clinical Investigation, 95,
2403-2408.

M. Chung et al. / J. Biomedical Science and Engineering 4 (2011) 136-145 145
JBiSE
doi:10.1172/JCI117935
[5] Ramrath, L., Levering, J., Conrad, M., Thuemen, A.,
Fuellgraf, H. and Moser, A. (2009) Mathematical identi-
fication of a neuronal network consisting of GABA and
DA in striatal slices of the rat brain. Computational and
Mathematical Methods in Medicine, 10, 273-285.
doi:10.1080/17486700802616526
[6] Conti, L.R., Radeke, C.M., Shyng, S.-L. and Vandenberg,
C.A. (2001) Transmembrane topology of the sulfonylurea
receptor SUR1. Journal of Biology and Chemistry, 276,
41270-41278. doi:10.1074/jbc.M106555200
[7] Ashcroft, F.M. and Gribble, F.M. (200) New windows on
the mechanism of action of K(ATP) channel openers.
Trends in Pharmacological Sciences, 21, 439-445.
doi:10.1016/S0165-6147(00)01563-7
[8] Levin, B.E., Routh, V.H., Kang, L., Sanders, N.M. and
Dunn-Meynell, A.A. (2004) Neuronal glucosensing: what
do we know after 50 years? Diabetes, 53, 2521-2528.
doi:10.2337/diabetes.53.10.2521
[9] Destexhe, A., Mainen, Z. and Sejnowski, T.J. (1998)
Methods in Neuronal Modeling, Chapter Kinetic models
of synaptic transmission. 2nd Edition, MIT Press, Cam-
bridge. doi:10.1152/jn.00422.2007
[10] Canavier, C., Oprisan, S., Callaway, J.C., Ji, H. and She-
pard, P. (2007) Computational model predicts a role for
ERG current in repolarizing plateau potentials in dopa-
mine neurons: implications for modulation of neuronal
activity. Journal of Neurophysiology, 98, 3006-3022.
[11] Amini, B., Clark, J.W. and Canavier, C.C. (1999) Calcium
dynamics underlying pacemaker- like and burst firing in
midbrain dopaminergic neurons: a computational study.
Journal of Neurophysiology, 82, 2249-2261.
[12] Komendantov, A. and Canavier, C. (2002) Electrical
coupling between model midbrain dopamine neurons:
effects on firing pattern and synchrony. Journal of Neu-
rophysiology, 87, 1526-1541.
[13] Kuznetsov, A.S. (2010) Models of midbrain dopaminer-
gic neurons. Scholarpedia.
http://www. schol a rpe di a. org/ a rtic le/ Mode l s_of_midbra i n
_dopaminergic_neurons,
doi:10.4249/scholarpedia.1812, 2(10), 1812.
[14] Hodgkin, A.L. and Huxley, A.F. (1952) A quantitative
description of membrane current and its application to
conduction and excitation in nerve. The Journal of Phy-
siology, 117, 500-544.
[15] Nomura, M., Fukai, T. and Aoyagi, T. (2003) Synchrony
of fast-spiking interneurons interconnected by GABAer-
gic and electrical synapses. Neural Computation, 15,
2179-2198. doi:10.1162/089976603322297340
[16] Ainscow, E.K., Mirshamsi, S., Tang, T., Ashford, M.L.J.
and Rutter, G.A. (2002) Dynamic imaging of free cyto-
solic ATP concentration during fuel sensing by rat hypo-
thalamic neurones: evidence for ATP-independent control
of ATP-sensitive K(+) channels. The Journal of Physi-
ology, 544, 429-445.
doi:10.1113/jphysiol.2002.022434
[17] Nichols, C.G., Lederer, W.J. and Cannell, M.B. (1991)
ATP dependence of K(ATP) channel kinetics in isolated
membrane patches from rat ventricle. Biophysical Journal,
60, 1164-1177. doi:10.1016/S0006-3495(91)82152-X
[18] Rall, W. (1967) Distinguishing theoretical synaptic po-
tentials computed for different soma-dendritic distribu-
tions of synaptic input. Journal of Neurophysiology, 30,
1138-1168.
[19] Destexhe, A., Mainen, Z. and Sejnowski, T.J. (1994) An
efficient method for computing synaptic conductances
based on a kinetic model of receptor binding. Neural
Computation, 6, 14-18.
doi:10.1016/S0006-3495(91)82152-X
[20] Lundstrom, B.N. and Fairhall, A.L. (2006) Decoding
stimulus variance from a distributional neural code of in-
ter-spike intervals. The Journal of Neuroscience Online,
26, 9030-9037.
[21] Wang, M., Hou, Z. and Xin, H. (2004) Double-system-
size resonance for spiking activity of coupled Hodgkin-
Huxley neurons. ChemPhysChem, 5, 1602-1605.
doi:10.1002/cphc.200400255
[22] Clements, J.D. (1996) Transmitter timecourse in the
synaptic cleft: its role in central synaptic function. Trends
in Neurosciences, 19, 163-171.
doi:10.1016/S0166-2236(96)10024-2
[23] Calabrese, E.J. (2004) Hormesis: a revolution in toxicol-
ogy, risk assessment and medicine. EMBO Reports, 5,
S37-S40. doi:10.1038/sj.embor.7400222
[24] Peters, A., Conrad, M., Hubold, C., Schweiger, U.,
Fischer, B. and Fehm, H.L. (2007) The principle of ho-
meostasis in the hypothalamus-pituitary-adrenal system:
new insight from positive feedback. American Journal of
Physiology: Regulatory, Integrative and Comparative
Physiology, 293, R83-98.
doi:10.1152/ajpregu.00907.2006
[25] Conrad M., Hubold, C., Fischer, B. and Peters A. (2009)
Modeling the hypothalamus–pituitary–adrenal system:
homeostasis by interacting positive and negative feedback.
Journal of Biological Physics, 35, 149-162.
doi:10.1007/s10867-009-9134-3
[26] Peters, A., Schweiger, U., Pellerin, L., Hubold, C., Olt-
manns, K.M., Conrad, M., Schultes, B., Born, J. and Fehm,
H.L. (2004) The selfish brain: competition for energy
resources. Neuroscience and Biobehavioral Reviews, 28,
143-180. doi:10.1016/j.neubiorev.2004.03.002
[27] Graybiel, A.M. (2005) The basal ganglia: learning new
tricks and loving it. Current Opinio n in Neurobiology, 15,
638-644. doi:10.1016/j.conb.2005.10.006
[28] Packard, M.G. and Knowlton, B.J. (2002) Learning and
memory functions of the basal ganglia. Annual Review of
Neuroscience, 25, 563-593.
doi:10.1146/annurev.neuro.25.112701.142937