J
ournal o
f
A
pp
Published Onli
n
http://dx.doi.or
g
Open Access
A
M
Squee
z
ABSTRA
C
In this study
w
effects prese
n
tioned device
s
fectly vacuu
m
strate, which
electro-static
a
To accurately
eling squeeze
p
late elasticit
y
solve the cou
p
coupled with
p
roblem at h
a
ments of whi
c
evaluated for
trostatic press
single step, u
s
and publishe
d
Keywords: S
q
1. Introdu
c
The wide sc
a
MEMS senso
to increasing
due to the thi
n
cally such d
e
b
rating norm
a
trapped in-
b
e
t
sions of the
height of the
spring and a
squeeze film
nant dissipati
o
operating in
*
Corresponding
a
p
lied Mathemat
i
n
e November 2
0
g
/10.4236/jamp
.
M
onolit
h
z
e Film
Anis
h
1
Depar
t
2
Center
C
T
w
e describe a
n
n
t in vibratory
s
often consis
t
m
packed. Thi
s
behaves like
a
a
lly, necessitat
i
model these
d
film effects f
o
y
often use a
p
p
led fluid elas
t
the 3D elasti
c
a
nd, using onl
y
c
h the lowest l
a
these nodes o
n
ure load on th
e
s
ing only one
e
d
experimental
q
ueeze Film
D
c
tion
a
le applicatio
n
rs, using par
a
interest in th
e
n
film of air t
r
e
vices consist
a
lly to a fixed
t
ween (see Fi
g
plate happen
air gap, the tr
a
viscous dam
p
effect. Squee
z
o
n mechanis
m
the aforeme
n
a
utho
r
.
i
cs and Ph
y
sics
,
0
13 (http://ww
w
.2013.16005
h
ic, FE
M
Proble
Usin
g
h
Roychowd
h
tment of Mech
a
for Nano Scien
c
n
FEM-
b
ased
m
MEMS devi
c
t
of a plate-li
k
s
results in a t
h
a
squeeze fil
m
i
ng the thin ai
r
d
evices the sq
u
o
r rigid motio
n
p
proximate m
o
t
icity proble
m
c
ity Equation
.
y
one type of
e
a
yer of nodes
n
ly. We also
a
e top surface
o
e
lement type.
data.
D
amping; Cou
p
n
of electro-
s
a
llel
p
late cap
a
e
study of en
e
r
apped in suc
h
of a plate li
k
substrate, wit
h
g
ure 1). If th
e
to be much
a
pped air beh
a
p
e
r
, a pheno
m
z
e fil
m
dampi
n
m
in Si based
n
tioned cond
i
,
2013, 1, 20-2
5
w
.scirp.org/jour
n
M
-Bas
e
m
of a
n
g
3D 2
7
h
ury
1,2*
, Aru
a
nical Engineeri
n
c
e and Enginee
r
*
anishr
o
Recei
v
m
ethodology
t
c
es, such as r
e
k
e structure th
a
h
in film of air
m
offering bot
h
r
gap for impr
o
u
eeze film eff
e
n
for both per
fo
o
de shapes as
m
, report iterati
v
.
In this work
e
lement (27 n
o
is also treated
a
pply an elect
r
o
f the structur
e
T
he FEM res
u
p
led Problem;
s
tatically driv
e
a
citors have l
e
e
rgy dissipati
o
h
devices. Ty
p
k
e structure,
v
h
a thin air fil
m
e
lateral dime
n
larger than t
h
a
ves both like
m
enon known
a
n
g is the do
m
MEMS devic
e
i
tions [1]. T
h
5
n
al
/
jamp )
e
d App
r
n
Oscill
7
-Node
p Nandy
1
,
C
n
g, Indian Insti
t
r
ing, Indian Inst
i
o
s
v
e
d
August 201
3
t
o solve the c
o
e
sonators, gyr
o
a
t vibrates no
r
being sandwi
c
h
stiffness an
d
o
ving the effi
c
e
ct must be in
c
fo
rated as well
input to the 2
D
v
e FEM-
b
ase
d
we present
a
o
de 3D brick)
.
as the fluid d
o
r
ostatic loadin
e
. Thus we sol
v
u
lts show goo
d
27-
N
ode Bric
k
e
n
e
d
o
n
p
i-
v
i-
m
n
-
h
e
a
a
s
m
i-
e
s
h
e
squeez
e
dynam
i
[2]. In
sary to
due to
tems i
n
structu
r
main e
Figure
brating
r
oach
fo
ating
E
Eleme
n
C
. S. Jog
1
, R
u
t
ute of Science,
i
tute of Science
,
s
c.ernet.in
3
o
upled flui
d
-st
r
o
scopes, and
a
r
mal to a fixe
d
c
hed between
d
damping. T
y
c
iency of actu
a
c
orporated. E
x
as non-
p
erfor
D
Reynolds
E
d
solution stra
t
a
FEM-
b
ased
s
.
The structur
e
o
main (2D) a
n
g to our mod
e
v
e the couple
d
d
agreement
w
k
; Micro-Plat
e
e
film offere
d
i
c characteris
t
order to corre
c
accurately d
e
the squeeze f
i
n
volves coupl
i
r
al and fluid.
ffect is mode
l
1. Schematic
o
elastic plate a
n
fo
r the
C
E
lastic
M
n
ts
u
dra Pratap
1
Bangalore, Indi
,
Bangalore, In
d
r
ucture probl
e
a
coustic trans
d
d
substrate, an
the moving p
l
y
pically, such
s
a
tion and the s
x
tensive literat
u
ated plates. St
u
E
quation. Rec
e
t
egies for the
2
s
ingle ste
p
so
l
e
is modeled
w
n
d the integral
s
e
l by consider
i
d
2D-fluid-3D
-
w
ith both existi
n
e
d
damping an
d
t
ics of the vi
b
c
tly model su
c
e
termine the
s
i
lm. Accurate
i
ng of three
d
Traditionally
l
ed using the
l
o
f an air film
n
d a fixed subs
t
C
ouple
d
M
icro-
P
1
,2
a
d
ia
e
m due to squ
e
d
ucers. The a
f
d is generally
l
ate and the fi
x
s
tructures are
ensitivity of
d
u
re is present
u
dies which
m
e
nt works whi
c
2
D Reynolds
E
l
ution for the
w
ith 27 node
b
s
over fluid do
m
i
ng an equival
-
structure pro
b
n
g analytical
s
d
stiffness cha
n
b
ratory MEM
S
c
h devices, it
i
s
tiffness and
d
modeling of
s
d
omains, elect
r
the squeeze
l
ubrication th
e
trapped betw
e
t
rate.
JAMP
d
P
late
e
eze film
f
oremen-
not pe
r
-
x
ed sub-
actuated
d
etection.
on mo
d
-
m
odel the
c
h try to
E
quation
coupled
b
rick ele-
m
ain are
ent elec-
b
lem in a
s
olutions
a
nges the
S
device
i
s neces-
d
amping
s
uch sys-
r
ostatics,
film do-
e
ory, via
e
en a vi-

A. ROYCHOWDHURY ET AL.
Open Access JAMP
21
the Reynolds Equation [3]. With rigid plate assumption
the Reynolds Equation can be decoupled from the elas-
ticity Equation and, further, on linearization can be
solved to obtain analytical expressions for stiffness and
damping. Blech [3] studied the effect of squeeze film
induced stiffness and damping for rigid plates with trivial
pressure boundary conditions. Darling et al. [4] presented
analytical solutions to the linearized Reynolds Equation
for various venting conditions, using a Greens function
approach. For flexible structures one has to account for
the variable air gap, and the elasticity Equation has to be
coupled with the Reynolds Equation for accurate model-
ing. Hung et al. [5] presented a reduced order macro
model based on basis functions generated from finite
difference simulations. They applied this technique to
model a pressure sensor as a clamped-clamped micro-
beam to study the pull-in dynamics of the system using a
1D Euler beam Equation and the non-linear Reynolds
Equation. McCarthy et al. [6] studied cantilever micro-
switches using a transient finite difference method ap-
proximating a parabolic pressure distribution along the
length and non variance along the width and obtained
good agreement with experimental measurements. You-
nis et al. [7] studied the effect of squeeze film damping
for an electrically actuated micro-plate, using the com-
pressible Reynolds Equation. They used perturbation me-
thods to derive analytical expressions for pressure distri-
butions in terms of the structural mode shape. Pandey et
al. [8] studied the effect of flexural mode shapes on the
squeeze film offered stiffness and damping for a canti-
lever resonator, they used Green’s function to solve the
linearized compressible Reynold’s Equation and used the
modal projection method available in ANSYS to solve
the coupled fluid structure problem for several flexural
modes of vibration. The analytical and numerical values
of damping obtained were in good agreement with expe-
rimental results. Li et al. [8] accounted for the static bias
deflection for a fixed- fixed micro-beam and a cantilever
under electrostatic actuation. They assumed a parabolic
function for the pressure along the beam width and a
cosine series along the beam length, and solved the
coupled Reynolds Equation and the Euler Bernoulli beam
Equation. Hannot et al. [9] presented an approach to
solve the coupled elasticity Equation and Reynolds’s
Equation for modeling a capacitive micro-switch. They
employed a non-linear Newmark time integration scheme
for the mechanical Equations and a trapezoidal rule for
the fluid Equations. The above mentioned models at-
tempt to solve the coupled problem, though not in a sin-
gle step. The geometry modeled is also limited to 1D
beam type structures.
These methods, though accurate, are cumbersome and
involve iterative or staggered approaches. We propose a
single step methodology to solve the coupled fluid-
structure squeeze film problem. We use the 3D elastic-
city Equation, thus not restricting ourselves to any par-
ticular geometry, and couple it with the 2D Reynolds
Equation for squeeze film. A single step “monolith” ap-
proach [10] is presented to solve the coupled problem.
The numerical results show good agreement with pub-
lished experimental data and existing analytical solutions.
2. Numerical Modeling
The problem at hand involves solving for pressure on the
vibrating plate due to the squeezed film, taking into ac-
count the elasticity of the plate. Thus the problem in-
volves solution of the Reynolds Equation for the fluid
domain coupled with the 3D elasticity Equation for the
structural domain. In our finite element model, the air
gap is treated as a 2D layer and the structural domain is
modeled in three dimensions. The element used for mod-
eling the structural domain is 3D, 27 node brick element.
The “wet” face of the 3D element is treated as the fluid
domain. Thus the relevant integrals for the fluid domain
are evaluated over the corresponding 9 noded “wet” sur-
face of the 3D, 27 node brick element.
2.1. Variational Formulation for the Fluid
Domain
The linearized Reynolds Equation is given as follows [2],
322
00
22
a
eff
,
12
hh
P
PPH
P
ttxy 
 





 (1)
where μeff is the effective viscosity, 0 h is the initial air
gap, a
P is the ambient air pressure, P is the fluid pres-
sure (perturbed about a
P) and H is the air gap (perturbed
about 0
h). The last term on the right hand side of the
above Equation couples the structure and the fluid do-
main. Substituting for harmonic solution
j
t
P
pe

 and
jt
z
Hue

 in Equation (1) and considering p

as varia-
tion of p  in a weighted integral sense we have,
3
2
00
eff a
0.
12
hhj
ppjupd
z
P










 (2)
For the fluid domain we have 0p
 on the open
borders and 0
ˆ
p
n



 on the closed borders. After doing
integration by parts and implementing the above boun-
dary conditions, we get the governing Equation for fluid
domain as,
3
00
eff a
.
12
0
z
hhj
p
pd ppd
P
jupd










 
 
 






(3)

A. ROYCHOWDHURY ET AL.
Open Access JAMP
22
2.2. FEM Formulation for the Fluid Domain
For the FEM formulation we use 9 noded quadrilateral
elements for 2D fluid domain. Pressure, its variation and
z
u
at any point are obtained from interpolation of the
corresponding nodal values using the following relation-
ships.

1
2
12 9
9
ˆ,
p
p
pNNN
p



 



p
Np (4)
ˆ,p p Np (5)

1
1
1
19
9
9
9
ˆ00 00.
z
u
v
w
uNN
u
v
w











z
u
Nu (6)
Pressure gradient can be expressed as
ˆ
p

p Bp, (7)
where
9 12
9 12
.
N NN
x
xx
N NN
yy y
 


 





 



p
B (8)
Similarly we have,
ˆ
p.

p B
p
(9)
where
p
N is (1 × 9), ˆ
p is (9 × 1), ˆδ
pis (9 × 1)
p
B
is (2 × 9),
z
u
Nis (1 × 27) and ˆ
u is (27 × 1).
Substituting Equations (4), (5), (6), (7) and (9) in Equ-
ation (3) and using arbitrariness of ˆδ
p
we get,
3
00
a
eff
0.
ˆ
12
ˆ
TT
T
hjh
dd
P
jd






 








z
ppp p
pu
BBNN p
NN u
(10)
2.3. FEM Formulation for the Structure
We have the variational statement for dynamic structural
problem without anybody force as:


:( ),
t
ddd 






uuuu u.t  (11)
where

is density, u is displacement,

u is its
variation,


τu is stress, t is prescribed traction over
the boundary t

and



εu is given by

1
() .
2
T






uuu 
Here,


:( ):( ),ij ij

uuu u  
with the summation convention over repeated indices.
For coupled squeeze film damping problem with
structural interaction, the wet surface (the surface which
constitutes the 2D fluid domain) is subjected to prescrib-
ed traction ˆ,
p

 tn then Equation (11) can be written
as


wet
t
ˆ
:( )
,
ddpd
d










 
uu uuu.n
u.t



(12)
where the last term on the left hand side signifies coupl-
ing effect of the fluid over the structural domain. The
standard FEM discretization for displacement and other
quantities are
ˆ, u uNu
ˆ,


u
uNu
ˆ () , u uCBu 
ˆ
() , u uBu 
ˆ
() .

u
uBu 
Substituting above relations in Equation (12) and using
arbitrariness of

u we have the discretized Equation for
the structural domain as

wet t
ˆˆ
ˆ.
TT
TT
dd
dd





 
 

 

 

 



 





uu uu
up u
uu
p
BCBN N
NnN Nt
(13)
2.4. Coupled FEM Formulation
For the coupled problem at hand the 2D fluid domain
corresponds to the “wet” surface of the structural domain.
Thus coupling the fluid and structure domains we have
(combining Equations (10) and (13))
ˆ
ˆ,






  

uu upu
pupp
KK uf
KK p0
(14)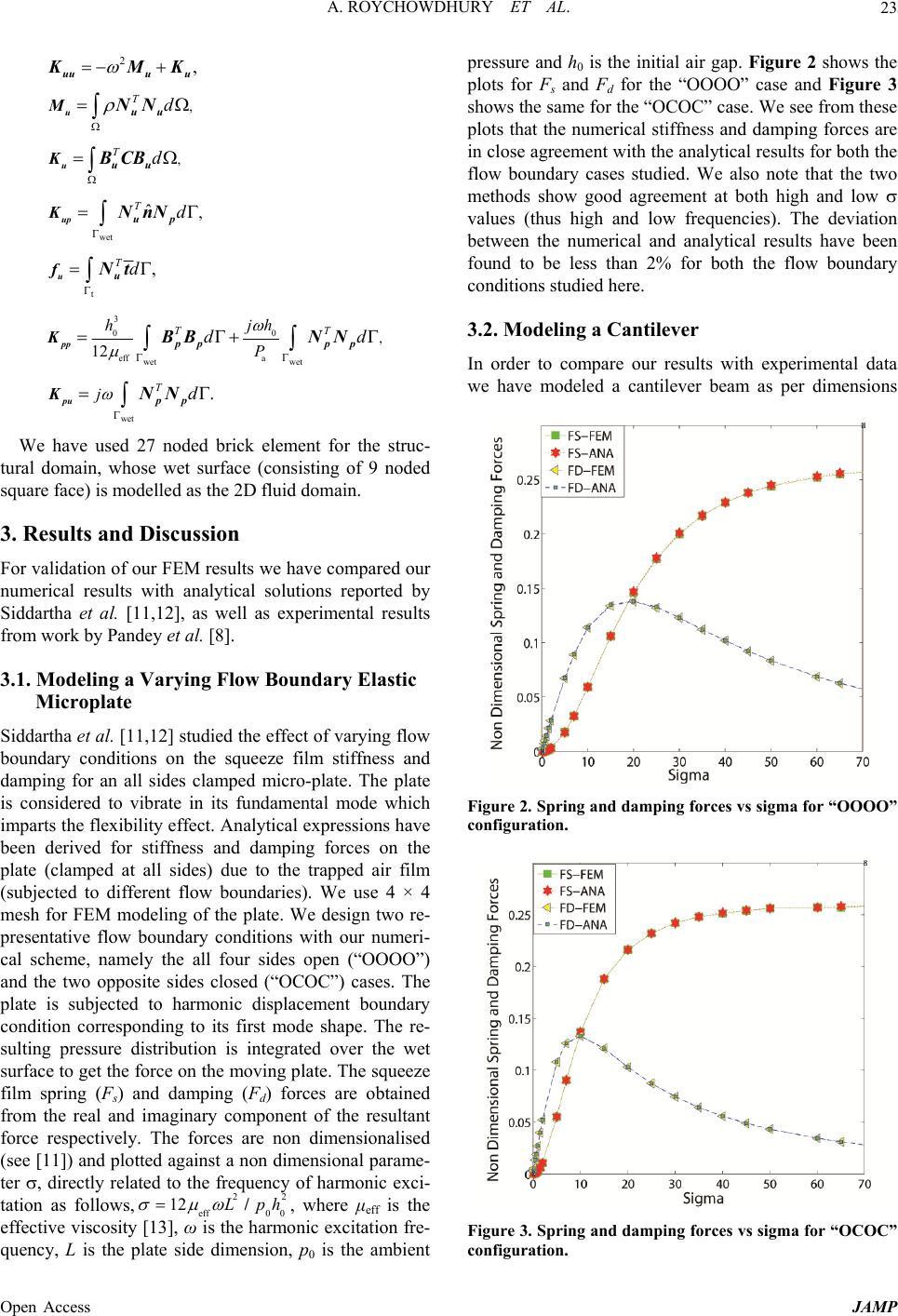

A. ROYCHOWDHURY ET AL.
Open Access JAMP
23
2,
  
uuu u
K
MK
,
Td




uuu
MNN
,
Td



uuu
KBCB
wet
,
ˆ
Td



up up
KNnN
t
,
Td



uu
fNt
3
00
eff a
wet wet
,
12
TT
hjh
P
dd





pp ppp p
KBBN N
wet
.
T
jd 



pu pp
KNN
We have used 27 noded brick element for the struc-
tural domain, whose wet surface (consisting of 9 noded
square face) is modelled as the 2D fluid domain.
3. Results and Discussion
For validation of our FEM results we have compared our
numerical results with analytical solutions reported by
Siddartha et al. [11,12], as well as experimental results
from work by Pandey et al. [8].
3.1. Modeling a Varying Flow Boundary Elastic
Microplate
Siddartha et al. [11,12] studied the effect of varying flow
boundary conditions on the squeeze film stiffness and
damping for an all sides clamped micro-plate. The plate
is considered to vibrate in its fundamental mode which
imparts the flexibility effect. Analytical expressions have
been derived for stiffness and damping forces on the
plate (clamped at all sides) due to the trapped air film
(subjected to different flow boundaries). We use 4 × 4
mesh for FEM modeling of the plate. We design two re-
presentative flow boundary conditions with our numeri-
cal scheme, namely the all four sides open (“OOOO”)
and the two opposite sides closed (“OCOC”) cases. The
plate is subjected to harmonic displacement boundary
condition corresponding to its first mode shape. The re-
sulting pressure distribution is integrated over the wet
surface to get the force on the moving plate. The squeeze
film spring (Fs) and damping (Fd) forces are obtained
from the real and imaginary component of the resultant
force respectively. The forces are non dimensionalised
(see [11]) and plotted against a non dimensional parame-
ter , directly related to the frequency of harmonic exci-
tation as follows,22
eff0 0
12
L
ph  /, where μeff is the
effective viscosity [13], ω is the harmonic excitation fre-
quency, L is the plate side dimension, p0 is the ambient
pressure and h0 is the initial air gap. Figure 2 shows the
plots for Fs and Fd for the “OOOO” case and Figure 3
shows the same for the “OCOC” case. We see from these
plots that the numerical stiffness and damping forces are
in close agreement with the analytical results for both the
flow boundary cases studied. We also note that the two
methods show good agreement at both high and low 
values (thus high and low frequencies). The deviation
between the numerical and analytical results have been
found to be less than 2% for both the flow boundary
conditions studied here.
3.2. Modeling a Cantilever
In order to compare our results with experimental data
we have modeled a cantilever beam as per dimensions
Figure 2. Spring and damping forces vs sigma for “OOOO”
configuration.
Figure 3. Spring and damping forces vs sigma for “OCOC”
configuration.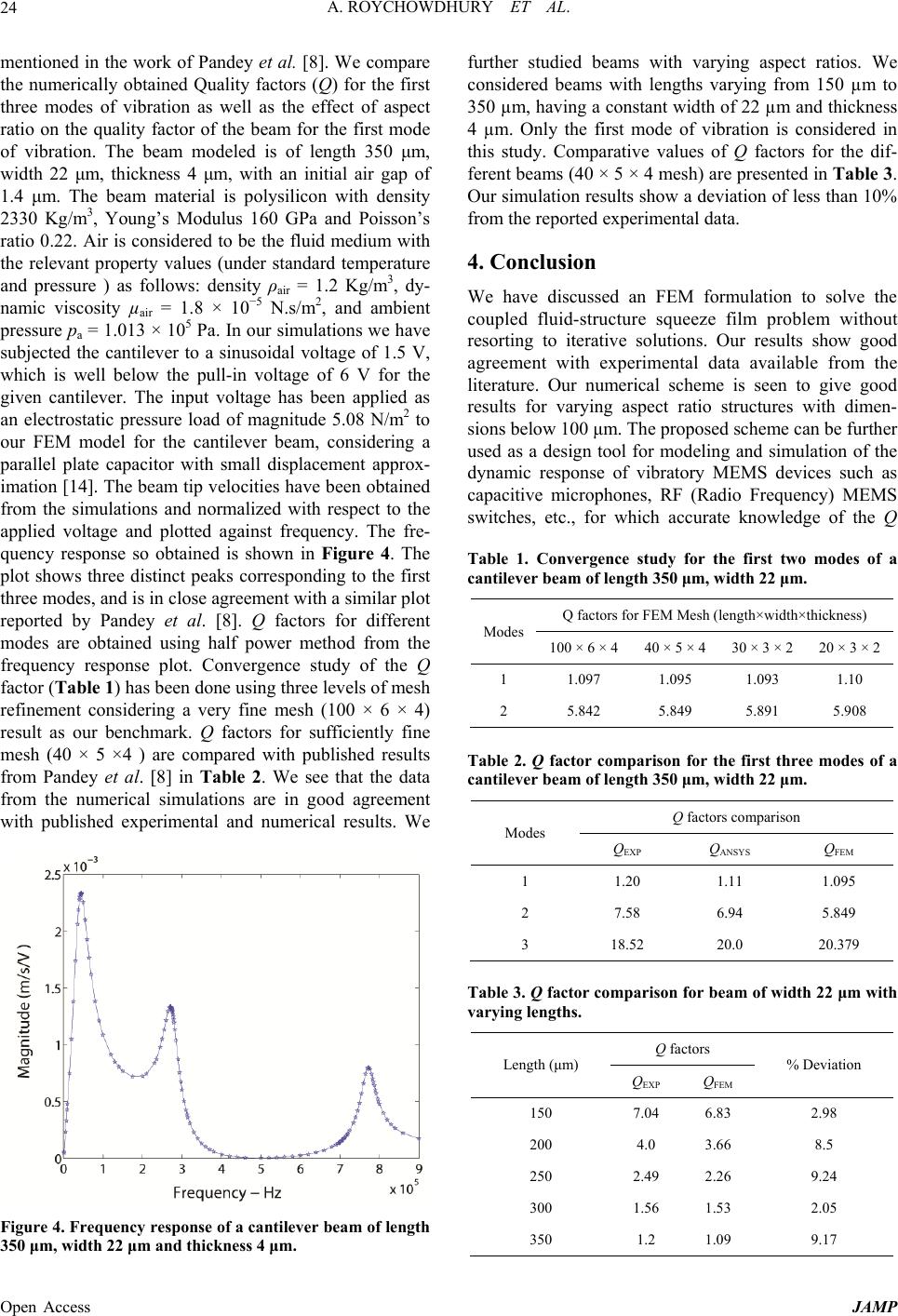

A. ROYCHOWDHURY ET AL.
Open Access JAMP
24
mentioned in the work of Pandey et al. [8]. We compare
the numerically obtained Quality factors (Q) for the first
three modes of vibration as well as the effect of aspect
ratio on the quality factor of the beam for the first mode
of vibration. The beam modeled is of length 350 μm,
width 22 μm, thickness 4 μm, with an initial air gap of
1.4 μm. The beam material is polysilicon with density
2330 Kg/m3, Young’s Modulus 160 GPa and Poisson’s
ratio 0.22. Air is considered to be the fluid medium with
the relevant property values (under standard temperature
and pressure ) as follows: density ρair = 1.2 Kg/m3, dy-
namic viscosity µair = 1.8 × 10−5 N.s/m2, and ambient
pressure pa = 1.013 × 105 Pa. In our simulations we have
subjected the cantilever to a sinusoidal voltage of 1.5 V,
which is well below the pull-in voltage of 6 V for the
given cantilever. The input voltage has been applied as
an electrostatic pressure load of magnitude 5.08 N/m2 to
our FEM model for the cantilever beam, considering a
parallel plate capacitor with small displacement approx-
imation [14]. The beam tip velocities have been obtained
from the simulations and normalized with respect to the
applied voltage and plotted against frequency. The fre-
quency response so obtained is shown in Figure 4. The
plot shows three distinct peaks corresponding to the first
three modes, and is in close agreement with a similar plot
reported by Pandey et al. [8]. Q factors for different
modes are obtained using half power method from the
frequency response plot. Convergence study of the Q
factor (Table 1) has been done using three levels of mesh
refinement considering a very fine mesh (100 × 6 × 4)
result as our benchmark. Q factors for sufficiently fine
mesh (40 × 5 ×4 ) are compared with published results
from Pandey et al. [8] in Table 2. We see that the data
from the numerical simulations are in good agreement
with published experimental and numerical results. We
Figure 4. Frequency response of a cantilever beam of length
350 μm, width 22 μm and thickness 4 μm.
further studied beams with varying aspect ratios. We
considered beams with lengths varying from 150 µm to
350 µm, having a constant width of 22 µm and thickness
4 µm. Only the first mode of vibration is considered in
this study. Comparative values of Q factors for the dif-
ferent beams (40 × 5 × 4 mesh) are presented in Table 3.
Our simulation results show a deviation of less than 10%
from the reported experimental data.
4. Conclusion
We have discussed an FEM formulation to solve the
coupled fluid-structure squeeze film problem without
resorting to iterative solutions. Our results show good
agreement with experimental data available from the
literature. Our numerical scheme is seen to give good
results for varying aspect ratio structures with dimen-
sions below 100 μm. The proposed scheme can be further
used as a design tool for modeling and simulation of the
dynamic response of vibratory MEMS devices such as
capacitive microphones, RF (Radio Frequency) MEMS
switches, etc., for which accurate knowledge of the Q
Table 1. Convergence study for the first two modes of a
cantilever beam of length 350 μm, width 22 μm.
Modes
Q factors for FEM Mesh (length×width×thickness)
100 × 6 × 440 × 5 × 4 30 × 3 × 2 20 × 3 × 2
1 1.097 1.095 1.093 1.10
2 5.842 5.849 5.891 5.908
Table 2. Q factor comparison for the first three modes of a
cantilever beam of length 350 μm, width 22 μm.
Modes
Q factors comparison
QEXP QANSYS QFEM
1 1.20 1.11 1.095
2 7.58 6.94 5.849
3 18.52 20.0 20.379
Table 3. Q factor comparison for beam of width 22 μm with
varying lengths.
Length (μm)
Q factors
% Deviation
QEXP QFEM
150 7.04 6.83 2.98
200 4.0 3.66 8.5
250 2.49 2.26 9.24
300 1.56 1.53 2.05
350 1.2 1.09 9.17

A. ROYCHOWDHURY ET AL.
Open Access JAMP
25
factor is critical for design. With this methodology one
can directly couple the elasticity effect of the structure
with the fluid flow and need not limit oneself to 1D
geometries.
5. Acknowledgements
This work is partially supported by NPMASS grant for
computational micro-systems. The authors acknowledge
the support from CoNE Lab of the Center for Nano
Science and Engineering at IISC.
REFERENCES
[1] M. Bao and H Yang, “Squeeze Film Air Damping in
MEMS,” Sensors and Actuators A, Vol. 136, No. 1, 2007,
pp. 3-27. http://dx.doi.org/10.10 16/j.sna.2007 .01.008
[2] R. Pratap, S. Mohite and A. K. Pandey, “Squeeze Film
Effects in MEMS Devices,” Journal of the Indian Insti-
tute of Science, Vol. 87, No. 1, 2007, pp. 75-94.
http://eprints.iisc.ernet.in/id/eprint/12328
[3] J. J. Blech, “On Isothermal Squeeze Films,” Journal of
Lubrication Technology, Vol. 105 No. 4, 1983, pp. 615-
620. http://dx.doi.org/10.1115/1.3254692
[4] R. B. Darling, C. Hivick and J. Xu, “Compact Analytical
Models for Squeeze Film Damping with Abitrary Venting
Conditions,” International Conference on Solid State Sen-
sors and Actuators, Vol. 2, 1997, pp. 1113-1116.
http://dx.doi.org/10.1109/SENSOR.1997.635397
[5] E. S. Hung and S. D. Senturia, “Generating Efficient Dy-
namical Models for Microelectromechanical Systems
from a Few Finite-Element Simulation Runs,” Journal of
Microelectromechanical Systems, Vol. 8, No. 3, 1999, pp.
280-289. http://dx.doi.o rg/10.1109 /84.788632
[6] B. McCarthy, G. G. Adams, N. E. McGruer and D. Potter,
“A Dynamic Model, Including Contact Bounce, of an
Electrostatically Actuated Microswitch,” Journal of Mi-
croelectromechanical Systems, Vol. 11, No. 3, 2002, pp.
276-283.
http://dx.do i.org/10.1109 /JMEMS.2002.1007406
[7] M. I. Younis and A. H. Nayfeh, “Simulation of Squeeze-
Film Damping of Microplates Actuated by Large Elec-
trostatic Load,” Journal of Computational and Nonlinear
Dynamics, Vol. 2, No. 3, 2007, pp. 232-240.
http://dx.doi.org/10.1115/1.2727491
[8] A. K. Pandey and R. Pratap, “Effect of Flexural Modes on
Squeeze Film Damping in MEMS Cantilever Resonators,”
Journal of Micromechanics and Microengineering, Vol.
17 No. 12, 2007, pp. 2475-2484.
ttp://dx.do i.org/10.10 88/0960-1317 /17/12/013
[9] S. D. A. Hannot and D. J. Rixen, “Coupling Plate Defor-
mation, Electrostatic Actuation and Squeeze Film Damp-
ing in a FEM Model of a Micro Switch,” International
Conference on Computational Methods for Coupled Pro-
blems in Science and Engineering, Barcelona, 2009.
[10] C. S. Jog, “An Outward-Wave-Favouring Finite Element-
Based Strategy for Exterior Acoustical Problems,” Inter-
national Journal of Acoustics and Vibration, Vol. 18, No.
1, 2013, pp. 27-38
http://eprints.iisc.ernet.in/id/eprint/46436
[11] S. Patra, A. Roychowdhury and R. Pratap, “Effect of
Fluid Flow Boundary Conditions on Squeeze Film Para-
meters of Planar MEMS Structures,” Applied Mathemat-
ics Modelling, AMM 14573, Unpublished.
[12] S. Patra, “Effect of Rarefaction, Flexibility and Restric-
tive Flow Boundary Conditions on Squeeze Film Flow of
MEMS Devices,” Master’s Thesis, Indian Institute of Sci-
ence, Bangalore, 2011.
[13] T. Veijola, H. Kuisma, J. Lahdenperä and T. Ryhänen,
“Equivalent-Circuit Model of the Squeezed Gas Film in a
Silicon Accelerometer,” Sensors and Actuators A: Phys-
ical, Vol. 48, No. 43, 1995, pp. 239-248,
http://dx.doi.org/10.1016/0924-4247(95)00995-7
[14] E. Saucedo-Flores, R. Ruelas, M. Florer and I. C. Chiao,
“Study of the Pull in Voltage for MEMS Parallel Plate
Capacitor Actuators,” Materials Research Society Fall
Meeting, Boston, 1-5 December 2003.