J
ournal o
f
A
pp
Published Onli
n
http://dx.doi.or
g
Open Access
Dete
c
ABSTRA
C
In view of ex
t
nization clust
e
tensity and s
e
can detect the
ess of extrem
e
Keywords: P
r
1. Introdu
c
With global
w
come increas
sessment rep
o
about extrem
e
p
articular ti
m
ability ones,
w
even more lo
w
tion curve of
events were
strictly extre
m
what damage
cause to soc
i
affected area
focus on the
p
the fall of e
x
searchers hav
these method
s
artificial judg
m
A. Hutt an
d
mutual phas
e
kind of thou
g
The data rec
o
to be split in
t
the one han
d
scales on the
considered to
p
resenting te
m
Here the ap
p
detect tempo
r
detail.
p
lied Mathemat
i
n
e November 2
0
g
/10.4236/jamp
.
c
tion o
f
Colle
g
C
T
t
reme values
e
e
ring method
e
quence lengt
h
temporal pro
c
e
weather eve
n
r
ocess; Phase
c
tion
w
arming extr
e
ingly commo
n
o
rts by the IP
C
e
weathe
r
eve
n
m
e, extreme w
e
w
hose occurri
n
w
e
r
[1]. Then
meteorologic
a
defined and
m
e values ev
e
every extrem
e
i
ety and econ
o
and duration
.
p
rocess, i.e.,
t
x
treme weath
e
e concerned
a
s
are not obj
e
m
ent.
d
co-workers
e
synchroniza
t
g
ht to detect t
h
o
rded in certai
n
t
o temporal s
e
d
and time w
i
other. The pa
r
be a state or
a
m
poral partiti
o
p
licability ab
o
r
al process of
i
cs and Ph
y
sics
,
0
13 (http://ww
w
.2013.16002
f
the Pr
Zhongh
u
g
e of Physical S
c
e
vents mathe
m
is introduced
h
. At last the
o
c
ess objective
l
n
ts.
Synchronizati
o
e
me weather
e
n
. The third
C
C both gave
a
n
ts: for a part
i
e
ather events
n
g probability
based on pro
b
a
l elements,
e
researche
d
[
2
e
nts mathem
a
e
weather eve
n
o
my depend
.
So it is ver
y
t
he rise, the d
e
e
r events. Re
c
a
bout this issu
e
e
ctive enough
proposed a
m
t
ion [12], w
h
h
e process of
n
open syste
m
e
quences of f
a
i
ndows of na
r
r
t of phase sy
n
a
cluster abou
t
o
n, i.e., the te
m
o
ut phase sy
n
weather eve
n
,
2013, 1, 6-10
w
.scirp.org/jour
n
ocess a
b
u
a Qian, Ze
n
c
ience & Techn
i
Recei
v
m
atically rathe
r
a
nd the appli
c
o
bserved data
l
y to a certain
o
n; Clustering
e
vents have b
and fourth
a
a
definite defi
n
i
cular place at
are small pro
b
is about 10%
o
b
ability distrib
u
e
xtreme weath
2
-9], which a
r
a
tically. In fa
c
n
t amount cou
l
on its streng
t
y
significant
t
e
velopment a
n
c
ently some r
e
e
[10,11], wh
i
and need so
m
m
ethod to det
e
h
ich provides
weather even
t
m
s is consider
e
a
st transients
o
r
row-
b
and ti
m
n
chronization
t
time windo
w
m
poral proce
s
n
chronization
t
n
ts is studied
i
n
al
/
jamp )
b
out E
x
n
gping Zha
n
n
ology, Yangzh
o
i
v
e
d
August 201
3
r
than the pro
c
c
ability of the
is applied. T
h
degree and it
h
e-
a
s-
n
e
a
b
-
o
r
u
-
er
r
e
c
t,
ld
t
h,
t
o
n
d
e-
i
le
m
e
e
ct
a
t
s.
e
d
o
n
m
e
is
w
s,
s
s.
t
o
in
2. Me
2.1. D
e
In phy
synchr
o
about
a
inform
a
phase
corres
p
(
)
H
t
where
the Ca
u
is the
p
2.2. P
h
M
In ord
e
p
hase
s
rithm
a
p
roper
about
t
approa
c
p
hase
d
ordere
d
x
treme
n
g, Guolin F
o
u University,
Y
.cn
3
c
ess about ext
r
method is dis
c
h
e results sho
w
h
as certain ap
p
thod of De
t
e
finition of
P
sics, phase r
e
o
nization ana
l
a
mplitude an
d
a
tion and ph
a
()t

of a re
a
p
onding analyt
i
()
s
t


)
is Hilbert t
r
()
1
Ht






() 1/ht t

,
t
u
chy principal
()
a
t 

p
hase of signal
h
ase Cluster
i
M
easure
e
r to detect te
m
s
equences are
a
nd cluster q
u
number of cl
u
t
he method o
f
c
hed by A.
H
d
ata represent
d
in time. The
r
Weath
e
eng
Y
angzhou, Chin
a
r
eme weather
e
c
ussed from t
h
w
that clusteri
n
p
lication to de
t
t
ectin
g
the
P
P
hase
e
flects the st
a
l
ysis is to se
p
d
phase from
s
a
se relativity
a
l signal s(t)
c
i
cal signal s˜(
t
() ()st iHt


r
ansform abou
t
() ()
()
stht
d
s
HV
d
t














t
he integral in
value. Then

a
rctan() /Ht
s
.
i
ng and Clu
s
m
poral proces
s
clustered by
K
u
ality measur
e
u
s
t
ers [12]. T
h
f
detection of
p
H
utt and co-
w
time series a
n
r
efore, cluster
s
e
r Eve
n
a
e
vents, phase
s
h
e aspects of
n
n
g measure d
i
t
ect the tempo
P
rocess
a
te of a sign
a
p
arate the inf
o
s
ignal and on
l
are conside
r
c
an be define
d
t
).
t
()
s
t,
d
d


Equation (2)

()
s
t
s
ter Quality
s
objectively,
t
K
-means clus
t
e
is used to
h
e following i
s
p
hase synchr
o
w
orkers. Bec
a
n
d all the data
s
can be cons
i
JAMP
n
ts
s
ynchro-
n
oise in-
i
fference
ral proc-
a
l. Phase
o
rmation
l
y phase
r
ed. The
d
via its
(1)
(2)
refers to
(3)
t
emporal
t
er algo-
give the
s
mainly
o
nization
a
use the
are well
i
dered as

Z.-H. QIAN ET AL.
Open Access JAMP
7
temporal segments as the K-means algorithm maps data
points to their nearest cluster centers. For every number
of clusters K, each data point i is associated with a clus-
ter measure ()
K
A
i,
()
[() ()]/
K
s
jnjK
ji
Ai
dC xdCxN


 (4)
where
1
()
T
KK
i
NAi

 is the normalized factor. n C and
s
C denote the nearest and the second-nearest cluster
center of data point i, respectively. i  represents a
subset of members of the cluster to which data point i
is associated. The dataset is partitioned into distinct sub-
sets i  reflecting consecutive time segments each. For
every number of clusters K the subsets i  represent
consecutive time segments. Usually the optimal number
of clusters is unknown resulting in an uncertainty about a
proper choice of K. To minimize this uncertainty a statis-
tical approach and average different cluster measures
with increasing K are used and yields the so so-called
cluster quality measure,
() ()/piAiA (5)
where
2
1
() ()
1
R
K
K
A
iAi
R
,
1
()
T
i
A
Ai

. R is the
maximum number of clusters. An increasing number of
clusters K yields an increasing number of subsets i

and subsequently, it diminishes the cluster measures
()
K
A
i. In general, an optimal value of the upper bound R
depends on the real number of clusters in the data but R
is usually in the range of tens.
In order to compare cluster qualities across different
datasets, a reference system is introduced by randomiz-
ing the examined dataset with respect to its temporal or-
der. Because the surrogates ()
()
s
pi
do not contain any
temporal structure they can be used to normalize the
original values ()pi [13]. An effective clustering mea-
sure eff
p is defined by means of
()
()max{0,()max[( )]}
s
eff
pipip j (6)
The difference
() ()
()max{0, (1)()
max[(1)()]}
ss
peffip ip i
p
jpj
 

(7)
reveals significant peaks at segment borders between
different clusters[13].
Based on the above analysis, the detection of phase
synchronization can classify the temporal phase se-
quences. A cluster means a temporal phase window, i.e.,
a state of some event, so the method provides a kind of
way to give the process of event.
3. Numerical Simulation of Phase
Synchronization
3.1. Detection of One-Dimensional Data
In order to compare with the result of A.Hutt and co-
workers’, the following stochastic dynamical system is
also discussed,
sinsin 22
k
kkk
dQ
dt
 

 
(8)
where 1, 2,,kN

, () 0
kt

,
()( ')2(')
kl kl
tt tt 

 
.
The values ()
kk
t



represent phases that evolve
along the gradient of a potential,
() cos/2cos2
kk k
V

 

 (9)
Considering the complexity of practically observed
meteorological elements data, N = 1 is chosen. Equation
(8) is simulated solution as a trial being obtained by de-
creasing

from −1 to 1 for Q = 0.001 in 500 equidis-
tant steps. At each step the system relaxes for 1000 inte-
grations and the final one is stored. The initial phase an-
gles were (0)



. Figure 1 shows the detection result.
The phase changes show that this system switches at
about

= 0.5 and about

= −0.5 which is in accord
with potential change of the system [14,15]. eff
p

val-
ues reveal significant peaks at corresponding

value,
which indicates eff
p

can distinguish different state
objectively.
3.2. Sensitive Numerical Simulation of Noise
Intensity Q
It can be known from Equation (8) that this system
shows various forms of phase locking and/or bifurcation
patterns depending on parameters

and Q for N = 1.
Here how noise intensity Q affects the result of detec-
tion is considering. Figure 2 is phase changing for Q =
0.001, 0.01, 0.05, 1 respectively and Figure 3 is the cor-
responding detection result. It indicates that enough
strong noise intensity makes phase distortion which leads
not to detect different clusters with phase synchroniza-
tion.
3.3. Sensitive Numerical Simulation of Sequence
Length
Because small noise intensity is better for the detection,
Q = 0.001 is chosen. Then the influence of sequence
length is considered. For the phase system, it is assumed
that phase changes as the same with the time changing.
Figure 4 is the clustering result for different sequence
length. It shows that with sequence length n increasing,
eff
p

reveals significant peaks at the borders of different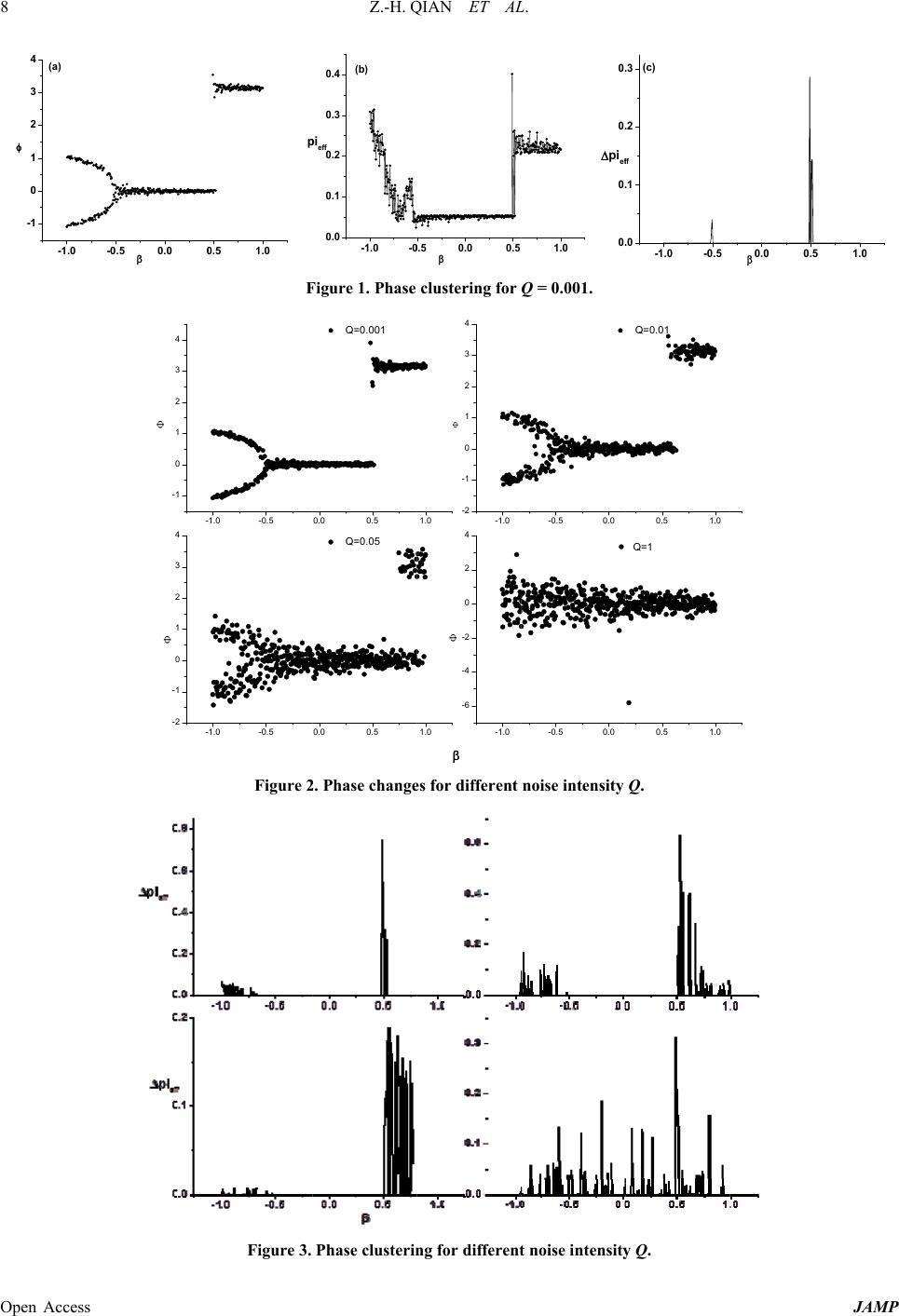

Open Access
8
-1.0
-1
0
1
2
3
4

(a)
-0.5 0.0
0

-
-1
0
1
2
3
4

-
-2
-1
0
1
2
3
4

F
Figure
2
Figure 3.
0
.5 1.0
p
-
1.0 -0.5
-
1.0 -0.5
Z.-H.
Q
F
igure 1. Phase
2
. Phase chang
e
Phase clusteri
n
-1.0 -
0
0.0
0.1
0.2
0.3
0.4
p
i
eff
(b)
0.0 0.5
Q=0.001
0.0 0.5
Q=0.05
Q
IAN ET A
L
clustering for
e
s for different
n
g for differen
t
0
.5 0.00.5

1.0

-1.0
-2
-1
0
1
2
3
4

1.0 -1.0
-6
-4
-2
0
2
4

L
.
Q = 0.001.
noise intensity
t
noise intensit
y
1.0
0
.
0
.
0
.
0
.
pi
e
f
-0.5 0.0
-0.5 0.0
Q.
y
Q.
-1.0 -0.5
.
0
.
1
.
2
.
3
f
f
(c)
0.5 1.0
Q=0.01
0.5 1.0
Q=1
0.0 0.5

JAMP
1.0

Open Access
states and

unchanged d
y
p
oints of se
g
eff
p value
m
b
le clusters,
h
which is in ac
4. Applica
t
For the sake
data to phas
e
dized Precipi
t
Figure 4
.
eff
p

value b
e
y
namic mech
a
g
ment border
s
m
eans the rati
o
h
ence its valu
e
cord with phy
s
t
ion of Pra
c
of the adapta
b
e
clustering,
M
t
ation Index)
.
Phase cluster
i
e
comes small
e
a
nisms of pha
s
s
are unchan
g
o
of some clu
s
e
should ge
t
s
m
s
ical meaning
s
c
ticall
y
Obs
b
ility of prac
t
M
SPI (Multi-
[16] January
2
i
ng for sequen
c
Z.-H.
Q
e
r. Because
o
s
e system, ti
m
g
ed too, wh
i
s
ter to all pos
s
m
aller over ti
m
s
of
eff
p.
erved Data
t
ically observ
e
scales Stand
a
2
009-Decemb
c
e length n.
Q
IAN ET A
L
o
f
m
e
i
le
s
i-
m
e
e
d
ar
-
e
r
2012
o
analyz
e
ure 5
Guizh
o
tion e
x
drough
t
getting
tempor
drough
t
getting
5. Su
m
In vie
w
than t
h
synchr
o
applic
a
of noi
s
served
measu
r
p
roces
s
applic
a
weathe
r
studie
d
search
w
6. Ac
k
Fundin
nology
Fi
g
MSPI

i
L
.
o
f 31 observa
t
e
d on Southw
e
shows the c
l
o
u province a
s
x
perienced to
t
t
, oscillating
moist. Phas
e
al process obj
t
event, som
e
drought from
m
mar
y
an
d
w
of extreme
v
h
e process ab
o
o
nization clus
t
a
bility of the
m
s
e intensity a
n
data is appli
e
r
e difference
s
objectively t
o
a
tion to detec
t
r
events. Fo
r
d
only, multi-
d
w
hich is our f
u
k
nowled
g
e
m
g was obtain
e
Support
p
rog
r
g
ure 5. Phase c
l
-4.2
-2.1
0.0
2.1
6
6
0
2
4
6
8
MSPI

p
i
eff
t
ion stations
i
e
st Drought E
v
l
ustering res
u
s
an example.
t
al three pro
c
continuous
d
e
clustering
m
ectively to a
c
e
station in s
o
January 2009
.
d
Discussio
n
v
alues events
o
ut extreme
w
t
ering method
m
ethod is disc
u
n
d sequence l
e
e
d. The result
s
eff
p can
o
a certain de
g
t
the tempor
a
r
simplicity
o
d
imensions d
a
u
ture research
m
ents
e
d from Natio
n
r
am under Gr
a
l
ustering detec
t
12 18
2
12 18
2
5770
7
i
n southwest
C
v
ent in fall 2
0
u
lt of Bijie s
t
It shows that
c
esses, i.e., i
n
d
rought and
g
m
ethod can d
e
c
ertain degree.
o
uthwest Chi
n
.
n
mathematical
l
w
eather even
t
is introduce
d
u
ssed from th
e
e
ngth. At las
t
s
show that c
l
detect the
t
g
ree and it ha
a
l process of
o
ne-dimension
a
ta deserve fu
r
would focus
o
n
al Science a
n
a
nt No. 2012C
B
t
ion in Bijie sta
2
43036
2
43036
7
JAMP
9
C
hina is
0
09. Fig-
t
ation in
this sta-
n
creasing
g
radually
e
tect the
For this
n
a began
l
y rather
t
s, phase
d
and the
e
aspects
t
the ob-
l
ustering
t
emporal
s certain
extreme
data is
rther re-
o
n.
n
d Tech-
B
955901
a
tion.

Z.-H. QIAN ET AL.
Open Access JAMP
10
and National Natural Science Foundation of China under
Grant No.41105033.
REFERENCES
[1] IPCC, “Summary for Policymakers of the Synthesis Re-
port of the IPCC Fourth Assessment Report,” Cambridge
University Press, Cambridge, 2007, pp. 1-15.
[2] P. Frich, L. V. Alexander and P. M. Della-Marta, “Obse-
vered Coherent Changes in Climatic Extremes during the
Second Half of the 20th Century,” Climate Researc h, Vol.
19, No. 3, 1993, pp. 193-212.
http://dx.doi.org/10.3354/cr019193
[3] M. J. Manton, P. M. Della-Martaand M. R. Haylock,
“Trend in Extrmeme Daily Rainfall and Temperature in
Southeast Asia and the South Pacific 1961-1998,” Inter-
national Journal of Climatology, Vol. 2, No. 3, 2001, pp.
269-284. ttp://dx.doi.org/10.1002/joc.610
[4] P. Zhai and X. H. Pan, “Change in Extreme Temperature
and Precipitation over Northern China during the Second
Half of the 20th,” Acta Geologica Sinica, Vol. 58, 2003,
pp. 1-9.
[5] X. H. Pan, “The Study of Extreme Temperature and Rain-
fall about 50 Years over China,” Chinese Academy of
Meteorological Sciences, Beijing, 2002, pp. 32-40.
[6] Y. F. Qian and D. Q. Huang, “The Definition of Daily
Mean Temperature Extreme over China and Its Trend,”
Acta Scientiarum Naturalium Universitatis Sunyatseni,
Vol. 47, 2008, pp. 112-116.
[7] Z. B. Sun and Z. Ning, “Change of Extreme Temperature
in China during 1955-2005,” Journal of Nanjing Institute
of Meteorology, Vol. 31, 2008, pp. 123-128.
[8] Y. Ping, W. D. Liu and Q. G. Wang, “The Climatic
Change Trend and Seasonal Characteristics of Daily
Temperature Extremes in China for the Latest 40 Years,”
Journal of Applied Meteorological Society, Vol. 21, 2010,
pp. 29-35.
[9] Z. Q. Gong, X. J. Wangand Z. Rong, “Regional Characte-
ristics of Temperature Changes in China during the Past
58 Years and Its Probable Correlation with Abrupt Tem-
perature Change,” Acta Physica Sinica, Vol. 58, 2009, pp.
4342-4353.
[10] D. Q. Zhang and G. L. Feng, “The Relationship between
Spatial Extent and Duration of Severe Droughts in China
over the Last 50 Years,” 2010 Second IITA Conference on
Geoscience and Remote Sensing, Vol. 2, 2010, pp. 345-
348.
[11] Z. J. Zhang and W. H. Qian, “Identifying Regional Pro-
longed Low Temperature Events in China,” Advance in
Atmosphere Science, Vol. 28, No. 2, 2011, pp. 338-351.
[12] H. A. Daffertshofer and U. Steinmetz, “Detection of Mu-
tual Phase Synchronization in Multivariate Signals and
Application to Phase Ensembles and Chaotic data,” Phy-
sical Review E, Vol. 68, 2003, Article ID: 036219.
http://dx.doi.org/10.1103/PhysRevE.68.036219
[13] A. Hutt and H. Riedel, “Analysis and Modeling of Quasi-
Stationary Multivariate Time Series and Their Applica-
tion to Middle Latency Auditory Evoked Potentials,”
Physica D, Vol. 177, No. 1-4, 2003, pp. 203-215.
http://dx.doi.org/10.1016/S0167-2789(02)00747-9
[14] G. Schner, H. Haken and J. Kelso, “A Stochastic Theory
of Phase Transitions in Human Hand Movement,” Bio-
logical Cybernetics, Vol. 53, No. 4, 1986, pp. 247-257.
http://dx.doi.org/10.1007/BF00336995
[15] H. Haken, J. A. S. Kelso and H. Bunz, “A Theoretical
Model of Phase Transitions in Human Hand Movements,”
Biological Cybernetics, Vol. 51, No. 5, 1985, pp. 347-356.
http://dx.doi.org/10.1007/BF00336922
[16] W. Hou, G. J. Zhang and G. Gao, “Research on the Me-
teorological Drought Index Based on the Hierarchy of
Climate System,” Meteorological Monthly, Vol. 38, No. 6,
2012, pp. 707-717.