World Journal of Condensed Matter Physics, 2013, 3, 216-220
Published Online November 2013 (http://www.scirp.org/journal/wjcmp)
http://dx.doi.org/10.4236/wjcmp.2013.34036
Open Access WJCMP
The Temperature Dependence of the Density of States in
Semiconductors
Gafur Gulyamov1, Nosir Yusupjanovich Sharibaev1,2, Ulugbek Inoyatillaevich Erkaboev1
1Namangan Engineering Pedagogical Institute, Namangan, Uzbekistan; 2Namangan Engineering Institute of Technology, Namangan,
Uzbekistan.
Received September 17th, 2013; revised October 21st, 2013; accepted November 10th, 2013
Copyright © 2013 Gafur Gulyamov et al. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
The temperature dependence of the density of energy states in semiconductors is considered. With the help of mathe-
matical modeling of the thermal broadening of the energy levels, the temperature dependence of the band gap of semi-
conductors is studied. In view of the non-parabolic and the temperature dependence of the effective mass of the density
of states in the allowed bands, graphs of temperature dependence of the band gap are obtained. The theoretical results of
mathematical modeling are compared with experimental data for Si, InAs and solid solutions of p-Bi2−xSbxTe3−ySey. The
theoretical results satisfactorily explain the experimental results for Si and InAs. The new approach is investigated by
the temperature dependence of the band gap of semiconductors.
Keywords: Band Gap; The Effective Mass Density of States; The Energy Spectrum; The Numerical Simulation and
Experiment
1. Introduction
Density of states determines thermal, optical, magnetic,
electric and other physical properties of semiconductors.
The change of the energy gaps with increasing tempera-
ture can be explained by the influence of lattice vibra-
tions on the energy levels in crystals. Statistical analysis
of the problem is carried out by analyzing the free energy
of the crystal as the sum of the energies of the electron
gas, lattice vibrations and electron-phonon interactions [1,
2]. On the other hand, one should take into account the
thermal broadening of the energy levels of the radiative
transitions [1,2]. In [3-8] the temperature dependence of
the density of states is determined by relaxation spec-
troscopy of energy levels in semiconductors. It is shown
that the density of surface states varies according to tem-
perature. Due to the thermal broadening of the levels, the
discrete spectrum with hanging temperature becomes a
continuous energy spectrum. With the expansion of the
energy spectrum of the density of states in the energy
derived from the probability required energy level, it was
shown that the amount of energy slits is dependent on
temperature. The temperature dependence of the band
gap is determined by the density of states of the conduc-
tion band and valence band of the semiconductor. Due to
the thermal broadening of the density of states near the
bottom of the conduction band, valence band reduces
band gap. In the calculation of the temperature depend-
ence of the forbidden assumed for simplicity, the density
of states in the areas of constant edge of the conduction
band and valence band is sharp and has a stepped shape.
In these works, the effective mass of the density of states
does not depend on the temperature. However, as shown
in experiments [9], the effective mass of the density of
states depends on the temperature. This change in the
effective mass changes the temperature dependence of
the band gap. However, in the real state of the semicon-
ductor, density is a function of speed and energy band
structure of the sample is determined. Moreover, the
density of states is so general that it can be used even
when there is no Brillouin zone and sharp boundaries of
permitted and prohibited zones [10,11].
Thus, the analysis of experimental results for compari-
son between theory and experiment is necessary to con-
sider the specific form of the band structure of the semi-
conductor and the dependence of the effective mass of
the charge carriers of the temperature.
The aim of this work is to study the temperature de-
pendence of the band gap semiconductor with the band

The Temperature Dependence of the Density of States in Semiconductors 217
structure and temperature dependence of the effective
mass of carriers and comparison of theory with experi-
ment.
2. The Dependence of the Energy Gap with
Temperature
As was shown in [3-8], the density of states can be de-
composed into a series of GN functions. The temperature
dependence of GN function will determine the statistical
thermal broadening of the discrete levels. The resulting
density of states is determined by the expansion of dis-
crete states by GN-function takes into account the ther-
mal broadening of each discrete level. We assume that
the density of states at absolute zero parabolic Ns(E). We
define a specific form of the electron dispersion. For ex-
ample, the electron dispersion parabola or according to
the Kane model. According to the procedure [3-8] we
expand the density of states in a series of GN-functions.
We will take into account nonparabolicity zones via the
temperature dependence of the effective mass of the
temperature:

 
1
,
n
ssiii
i
NEТNEGNEET

,,
(1)
where

 
,,
11 1
exp exp
i
ii
GNEE T
EE EE
kT kTkT



 






Ns(E)—the density of states at zero temperature [12,
13]

0
0
at
0at
at
nc
scv
pv v
NEEEE
NEEE E
NEE EE










c







(2)
where

32
*
023
2
2π
n
n
m
N,

32
*
023
2
2π
p
p
m
N and Ec, Ev—
The value of the energy of the conduction band and
valence band at T = 0.
Substituting (2) into (1) we obtain the density of states
at temperature T. In determining the width of the gap, we
use the density of states, which depends on temperature.
When modeling the process of measuring the width of
the band gap with increasing temperature, use the condi-
tion given in [8]. We assume that the density of states
corresponding to the energy band gap edges Ec and Ev is
Nk. Energy region where the density of states Ns(T) is less
than the critical Nk assume band gap. The energy range
where Ns(T) > Nk permission from the zones. The values
of the edges of the band gap position of the bottom of the
conduction band Ec(T) and valence bands Ev(T) is deter-
mined by the solution of the equation transcendent
 
1
,,
n
s
ii ik
i
NEGNЕЕТ N


 (3)
transcendent solution of Equation (3) with respect to E at
the specified temperature T, and the critical value of the
density of states Nk determines the position of the edges
of the gap Ec(Nk, T) and Ev(Nk, T). In Equation (3) Nk
included as a parameter. Nk value is determined by the
condition of the experiment and by the accuracy of meas-
urement techniques. Then the band gap is defined as the
difference between the values of Ec(T, Nk) and Ev(T, Nk):




,,

,
g
kc kv k
ETNETN ETN (4)
It follows that the method of determining the accuracy of
the experiment and the important factors in determining
the width of the gap. Indeed the band gap, determined by
optical methods, “optical width” of the band gap can not
match the value of the band gap, determined by the tem-
perature dependence of the resistance of the semicon-
ductor. One of the reasons is that different values for Nk
optical and electrical measuring techniques.
3. The Influence of the Effective Mass of the
Density of States at the Temperature
Dependence of the Band Gap in Solid
p-Bi2−xSbxTe3−ySey
In [9] found that in solid p-Bi2−xSbxTe3−ySey effective
density of states in the valence band is strongly depend-
ent on temperature. Figure 1 shows the temperature de-
pendence of the effective mass of the density of states in
solid p-Bi2−xSbxTe3−ySey from [9]. Using the data of Fig-
ure 1 calculated by the model bandgap variation with
temperature.
Figure 2 shows plots of the density of states at a tem-
perature T = 100 K and T = 300 K. As can be seen from
Figure 2 into account the change of the effective mass
density of states significantly affects the density of states
near the valence band.
Figure 3 shows the temperature dependence of the
graphics of the band gap for the solid solutions p-
Bi2−xSbxTe3−ySey to changing the effective mass density
of states taken from Figure 3 [9]. For example, for a
solid solution of p-Bi2−xSbxTe3−ySey change in the band
gap by changing the effective mass at T = 100 K is




**
100100, 0.93100, const
ggp gp
EEm Em

0.001эВ

. By increasing the temperature to T = 300 K,
changing the width of the band gap due to change in the
effective mass of the density of states is


300
g
E




**
300,1.35300,const 0.0165
gp gp
Em EmэВ
This shows that the reduction of the band gap by chang-
ing the effective mass with increasing temperature from
Open Access WJCMP

The Temperature Dependence of the Density of States in Semiconductors
218
Figure 1. The temperature dependence of the effective mass
of the density of states m/m0 in solid solutions
p-Bi2−xSbxTe3−ySey [14]. 1→ x = 1, y = 0.06; 2→ x = 1.1, y =
0.06; 3→ x = 1.2, y = 0.06; 4→ x = 1.2, y = 0.09; 5→ x = 1.3,
y = 0.09, 6→ x = 1.3, y = 0.07; 7→ x = 1.5, y = 0.09.
Figure 2. Graphic density of states at T = 100 K and 300 K.


*
p
mmT and


*
p
mmT. ______ ------
*
p
mсоnst*
p
m


mT.
100 K to 300 K can be increased more than tenfold. Fig-
ure 3 shows plots of the temperature dependence of the
band gap of the solid solutions p-Bi2−xSbxTe3−ySey for the
changes in the effective mass of the density of states
taken from Figure 1. Thus, changes in the effective mass
of the density of states with temperature can greatly af-
fect the temperature dependence of the band gap.
4. Comparison of Theory with Experiment
The temperature dependence of the width of the energy
gap depends on the density of states at the absolute tem-
perature. In the model used in [3-8] the temperature de-
pendence of the density of states is determined by the
temperature dependence of GN-functions and band struc-
ture of the allowed bands at the bottom of the conduction
Figure 3. Graphic Eg(T)—temperature dependence of the
band gap. и
*
p
mсоnst


*
p
mmT. _____ ; ----
*
p
mсоnst


*
p
mmT, p-Bi0.7Sb1.3Te2.93Se0.07; ......


*
p
mmT,
p-Bi0.6Sb1.2Te2.91Se0.09; ····


*
p
mmT ,
p-Bi0.5Sb1.5Te2.91Se0.09.
band and at the top of the valence band. Analysis of the
results of numerical modeling of changes in the density
of states at the temperature showed that the value of the
density of states near the band edges is determined by the
number of states of the band edges, a few tens of kT or
about 0.1 meV, the density of states in the depths of the
allowed zones does not affect the width of the gap. Since
the GN-function of deep area of the zone does not pene-
trate into the region band gap semiconductor, the main
contribution to the shift of the band edges give the states
lying close to the edges of the allowed bands. According
to this law of dispersion near the top of the valence band
and the conduction band edge is crucial in determining
the temperature dependence of the band gap Eg(T). Fig-
ures 4 and 5 are graphs of temperature dependence of the
band gap of InAs [14] and Si [15].
Using mathematical modeling of the temperature de-
pendence of Eg(T) for a parabolic band and Kane model
obtained plots of the band gap of the temperature. As can
be seen in the investigated temperature range of parabolic
dispersion and a model for the use of Kane’s model is in
good agreement with experimental data for InAs [14] and
Si [15]. Theoretical calculations of the theoretical given
for these materials is in good agreement with the experi-
mental data. It follows that the temperature dependence
of the band gap is satisfactorily described by a mathe-
matical model of expansion of the density of states in a
series of GN-functions, which describes the temperature
dependence of the thermal broadening of individual en-
ergy levels in the zones and in the forbidden zone.
5. Conclusion
The temperature dependence of the energy spectrum of
the density of states of solid solutions of
Open Access WJCMP

The Temperature Dependence of the Density of States in Semiconductors 219
1.050
1.070
1.090
1.110
1.130
1.150
1.170
1.190
0 50 100 150 200 250 300 350 400 450 500
Т, К
E
g
, eV
Experiment for Si [13]
calculations for the parabolic zone
calculation for the of Kane
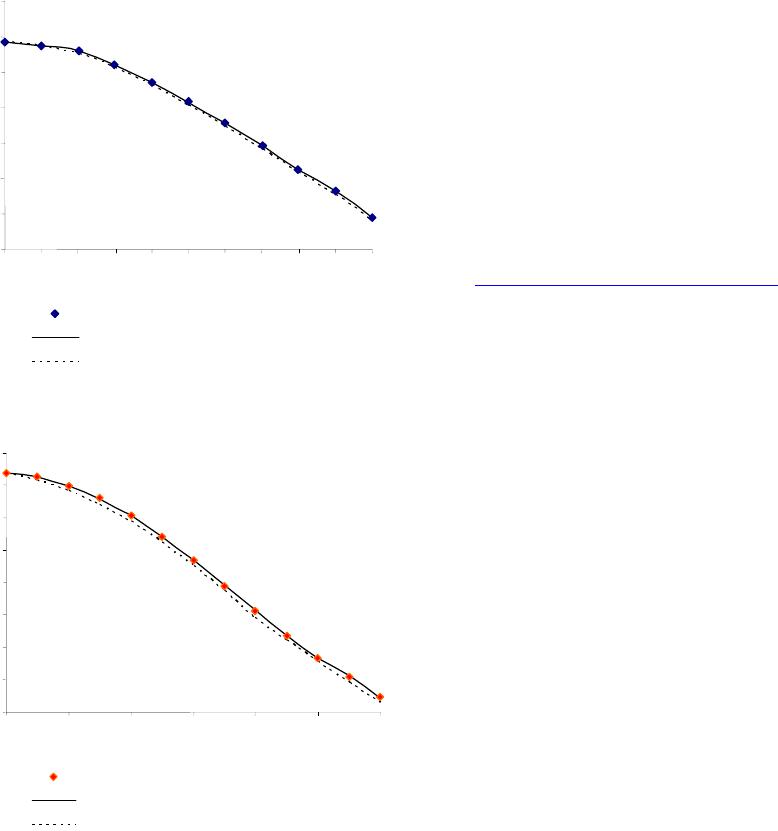
Figure 4. The temperature dependence of the band gap of
Si.
0.3400
0.3500
0.3600
0.3700
0.3800
0.3900
0.4000
0.4100
0 50 100 150 200250300
T, K
E
g
, eV
0.4200
Experiment for InAs [14]
calculations for paraboliс zony
calculation for the model of Kane
Figure 5. The temperature dependence of the band gap of
InAs.
p-Bi2−xSbxTe3−ySey takes into account of the temperature
dependence of the effective mass of the density of states
in the valence band. The temperature dependence of the
band gap for the changes in the effective mass of the
density of states is obtained. The numerical experiments
show that at temperatures T > 120 K, change in the effec-
tive mass of the density of states by increasing T has sig-
nificant effect on the temperature dependence of the band
gap.
In this temperature range ([0, 300 K], [0, 500 K]),
mathematical modeling of the temperature dependence of
the band gap is satisfactorily described by a parabolic
dispersion law and the Kane model. The experimental
results of changing the band gap of silicon [13] and InAs
[14] within the accuracy of measurement is consistent
with the results of theoretical calculations. Comparison
of theory and experiment shows that the thermal broad-
ening of the energy levels with the GN function satisfac-
torily describes the process of the temperature depend-
ence of the band gap of Si and InAs.
REFERENCES
[1] B. Ridley, “Quantum Processes in Semiconductors,” Clar-
endon Press, Oxford, 1982.
[2] R. Pässler, “Semi-Empirical Descriptions of Temperature
Dependences of Band Gaps in Semiconductors,” Physica
Status Solidi (b), Vol. 236, No. 3, 2003, pp. 710-728.
http://dx.doi.org/10.1002/pssb.200301752
[3] G. Gulyamov and N. Yu. Sharibaev, “Determination of
the Density of Surface States at the Semiconductor-Insu-
lator Interface in a Metal-Insulator-Semiconductor Struc-
ture,” FTP (Fizika Technika Poluprovodnikov), Vol. 45,
No. 2, 2011, pp. 178-182.
[4] G. Gulyamov and N. Yu. Sharibaev, “Determination of
the Discrete Spectrum of Surface State Density in MOS-
Structures Al-SiO2-Si Irradiated by Neutrons,” Poverkh-
nost’. Rentgenovskie, Sinkhrotronnye i Neitronnye Issle-
dovaniya, No. 9, 2012, pp. 13-17.
[5] G. Gulyamov, N. Yu. Sharibaev and U. I. Erkaboev,
“Thermal Broadening Density of States and Temperature
Dependence of the Band Gap Ge,” FIP (Fyzicheckaya
Injeneriya Poverkhnosti), Vol. 10, No. 4, 2012, pp. 366-
370.
[6] G. Gulyamov and N. Yu. Sharibaev, “Temperature De-
pendence of the Band Gap of Si and Due to the Thermal
Broadening of the Density of States of,” FIP (Fyzi-
checkaya Injeneriya Poverkhnosti), Vol. 10, No. 2, 2012,
pp. 4-8.
[7] G. Gulyamov, I. N. Karimov, N. Yu. Sharibaev and U. I.
Erkaboev, “Determination of the Density of Surface States
at the Semiconductor-Insulator Structures in Al-SiO2-Si
and Al-SiO2-n-Si <Ni> at Low Temperatures,” Uzbek
Journal of Physic, Vol. 12, No. 3, 2010, pp. 143-146.
[8] G. Gulyamov, N. Yu. Sharibaev and U. I. Erkaboev,
“Influence Effective Mass Density of States at Tem-
perature Dependence of Band Gap in Solid Solutions
p-Bi2−xSbxTe3−ySey,” FIP (Fyzicheckaya Injeneriya Po-
verkhnosti), Vol. 11, No. 2, 2013, pp. 195-198.
[9] L. N. Lukyanova, V. Kutasov and P. Konstantinov,
“Effective Mass and Mobility in Solid p-Bi2−xSbxTe3−ySey
for Temperatures <300K,” Solid State, Vol. 47, No. 2,
2005, pp. 224-228.
[10] N. Mott and E. Devis, “Electronic Processes in Non-Crys-
talline Materials,” 2nd Edition, Clarendon Press, Oxford,
1982.
[11] V. B. Bonch-Bruyevich, et al., “Electronic Theory of Non-
Crystalline Semiconductors,” Nauka, Moscow, 1981.
[12] A. I. Anselm, “Introduction to Semiconductor,” Nauka,
Moscow, 1978.
[13] K. V. Shalimova, “Physics of Semiconductors,” Energ-
oatomizdat, Moscow, 1985.
[14] A. M. R. Godenir, “Novel Dilute Nitride Semiconductor
Open Access WJCMP

The Temperature Dependence of the Density of States in Semiconductors
Open Access WJCMP
220
Materials for Mid-Infrared Applications,” University of
Lancaster, 2008.
[
15] A. Caiafa, X. Wang, J. L. Hudgins, E. Santi and P. R.
Palmer, “Cryogenic Study and Modeling of IGBTS,”
IEEE 34th Annual Power Electronics Specialist Confer-
ence, 15-19 June 2003, pp. 1897-1903.