J. Biomedical Science and Engineering, 2011, 4, 105-109
doi:10.4236/jbise.2011.42015 Published Online February 2011 (http://www.SciRP.org/journal/jbise/
JBiSE
).
Published Online February 2011 in SciRes. http://www.scirp.org/journal/JBiSE
Medical ultrasound image segmentation using genetic active
contour
Mohammad T alebi, Ahamd Ay atollahi, Ali Kermani
Department of Electrical Engineering, Iran University of Science and Technology, Tehran, Iran
Received 10 November 2010; 15 November 2010; 19 November 2010.
ABSTRACT
Image segmentation is one of the earliest and most
important stages of image processing and plays an
important role in both qualitative and quantitative
analysis of medical ultrasound images but ultrasound
images have low level of contrast and are corrupted
with strong speckle noise. Due to these effects, seg-
mentation of ultrasound images is very challenging
and traditional image segmentation methods may not
be leads to satisfactory results. The active contour
method has been one of the widely used techniques
for image segmentation; however, due to low quality
of ultrasound images, it has encountered difficulties.
In this paper, we presented a segmental method com-
bined genetic algorithm and active contour with an
energy minimization procedure based on genetic al-
gorithms. This method have been proposed to over-
come some limits of classical active contours, as con-
tour initialization and local minima (speckle noise),
and have been successfully applied on medical ultra-
sound images. Experimental result on medical ultra-
sound image show that our presented method only
can correctly segment the circular tissue’s on ultra-
sound images.
Keywords: Segmentation; Active Contour; Genetic Al-
gorithm; Ultrasound Images
1. INTRODUCTION
The ultrasound imaging method is used in medical prac-
tices, along with other imaging procedures such as X-
Ray, CT, etc., for producing images of live tissue and for
the purpose of clinical diagnosis. Since advantages of
ultrasound imaging method such as: being less costly,
portability of the device, safety of the imaging technique
to the patient, and the less amount of real time required
for imaging, it has been paid more attention than other
imaging techniques.
Despite all these advantages, ultrasound images, be-
cause of characteristic flaws such as speckle noises, and
artificial borders, have very low qualities that cause the
processing of such images to run into complications and
difficulties. Therefore, the implementation of many ex-
isting processing algorithms on these images yields no
favorable outcomes.
Meanwhile, segmentation is major part of medical
image processing. Accurate image segmentation and de-
tection of tissues provides great help to the physicians for
clinical diagnosis and tissue classification. So far, many
different image segmentation methods have been pre-
sented including: the clustering method [1], watershed
transform method [2,3], Markov’s random field method
[4], and methods based on statistical models [5].
The active contour is one of the methods used exten-
sively in recent decades for segmentation of medical
ultrasound images [6]. Kass [7] proposed the idea of us-
ing active contour for the first time. This method is based
on balancing the internal and external forces and mini-
mizing energy. Investigations show that this procedure
has produced acceptable results; although, it also has
several drawbacks and weak points. The first and the
most important drawback is the entrapment of the active
contour in the local points of minima, which causes the
deviation of the contour from its original path. This
problem is magnified in the processing of ultrasound
images that have higher noise levels.
To solve this problem, various methods have been
suggested, such as the Balloon model [8], the GVF
model [9], the distance potential model [10] and etc.
More recently, the use of the genetic model besides the
active contour has been suggested [11,12]. In this paper,
we have tried to utilize the genetic algorithm to solve
some of active contour problems.
In the section 2, the concept of active contour will be
discussed and its weak points delineated. Then, section 3,
presents a simple introduction of the genetic algorithm.
The proposed method will be explained in section 4 and
finally, the obtained results will be evaluated in section 5.

M. Talebi et al. / J. Biomedical Science and Engineering 4 (2011) 105-109 106
2. INTRODUCING THE ACTIVE
CONTOUR
The idea of using an active contour was first brought up
by Kass in 1988, which became known as the snake model
[9]. Active contour is a two-dimensional curve in the im-
age space whose deformation is based on energy minimi-
zation. In this method, first, a primary contour is defined
close to the edge of the object in mind and then, in order to
detect the edge, an energy function is specified for contour
through various arithmetic techniques, the edge detection
and segmentation process is completed. If x and y are the
position coordinates of the 2-D image 

,
I
xy , one can
use the curve
 

 
,Vsxs ys

, in which,


0,1s
for parametric representation of the contour on the image.
In general, the energy function of the active contour is
expressed as:
     
11
int
00
total ext
EEV sdsEV sEV sds



 

(1)
The defined energy function for the contour consists of
two components which respectively are Internal energy
, External energy . The former is
used to control the rate of stretch and to prevent discon-
tinuity in the contour the latter is generated by using the
image characteristic features or the limitations imposed
on the contour by the user, and it is used for contour dis-
placement.
 
int
EVs
   
ext
EVs
In order to control the contour deformation and dis-
placement, these energy components are converted into
two internal and external forces. During the process of
contour deformation, the force resulting from internal en-
ergy, keeps the contour smooth and prevents breaking and
discontinuity of the contour which are caused mainly by
the presence of irregularities and noise in the image. Also,
the external force has the task of displacing the contour
from its initial position and guiding it towards the subject’s
edge.
The internal energy component can be defined as fol-
low:
    
2
int
11
22
ss
EVssVs sVs 

2
s






(2)
The first term of the internal energy is related to the
contour’s bending ability. Weight factor α(s) is used to
control and adjust it. The second term in this relation
specifies the contour’s strength and resistance against
sudden changes and β(s) factor controls it. Equation (3)
represents a typical external energy defined for the con-
tour.
  
2
,,
ext
EVs GxyIxy

   
 
(3)
In this equation,

is the external energy weight factor,


,Gxy

is a two-dimensional Gaussian function with
the standard deviation σ, ∇ is the gradient operator and
* specifies the convolution operator for the 2-D image


,
I
xy .
When the energy function attains its minimum value,
in other words, when external and internal forces balance
out:
int 0 ext
FF

 (4)
Contour deformation stops and the edge detection proc-
ess reaches to the end. This indicates that the contour has
coincided with the edge. More details about the energy
minimization process have been fully described in refer-
ence [9]. The presented model has several deficiencies
which are:
 Sensitivity of the contour to defined initial curve
position.
 Formation of minimum energy points due to the
presence of noise in the image in which entrap
contour in these local points and deviate it from the
original path.
These weaknesses become more prominent when we
try to use the model for the segmentation of ultrasound
images. The existence of speckle noise in the image cre-
ates many local minima which cause the entrapment of
the contour in these points. As was mentioned before, so
far, many different methods have been submitted to solve
the active contour’s problem. Using the genetic algo-
rithm is one way of solving such a problem and obtain-
ing the optimum answer in the search space. In the fol-
lowing section, we will describe the generic algorithm.
3. GENETIC ALGORITHM
The genetic algorithm is an efficient, adaptive and stable
method of optimization which has caught the attention of
the researchers in the last several years. However, these
algorithms don’t guarantee the optimum solution for
problems. Using them for the optimization problems has
shown that these algorithms often find the closest solu-
tion to the optimum and in some cases; they obtain the
most optimum solution among the existing solutions in
the search space. The genetic algorithm uses a set of
population called chromosomes for optimization. These
chromosomes are in fact the solutions of the problem. In
a search process, the best of them are selected from the
solution set available in the search space. Each of these
chromosomes is made up of several genes, and these
genes represent the parameters that should be optimized.
These chromosomes are encoded by numbers. The man-
ner of encoding these genes and chromosomes depends
on the type of problem that needs to be solved. Usually, a
string of zeros and ones is used for encoding the chro-
mosomes. After determining the population size and the
manner of encoding, the appropriate solution should be
C
opyright © 2011 SciRes. JBiSE

M. Talebi et al. / J. Biomedical Science and Engineering 4 (2011) 105-109 107
evaluated. To do this, the fitness function is used. After
the fitness function is determined for each member of the
population, three genetic operators should be applied on
them to prevent premature convergence. These three ge-
netic operators are as follows [13]:
 Selection operator:
This operator is applied on the members of the popu-
lation and selects a number of individuals who possess
the best fitness function values to reproduce the new
generation. Different methods exist for the selection of
the bests of the society including: selection by the Rou-
lette wheel method, selection by the competition method
and the elitist selection method.
 Cross over operator:
After the best members of the society are selected for
reproduction, it is necessary for them to cross over and
produce the new generation. In this situation, from
among selected individuals, certain pairs are identified as
parents and by crossing those over two offspring are born.
To cross over the parent chromosomes, single point cross
over, double point cross over and the uniform cross over
methods can be used.
 Mutation operator:
Mutation, by changing the genes, can produce a new
chromosome. Applying the mutation operator in the ge-
netic algorithm saves valuable information of the chro-
mosomes which may otherwise be deleted during the
execution of the algorithm. In other hand, this act can
greatly enhance the algorithm operation and prevent its
quick convergence and falling in the trap of local minima.
The amount of mutation taking place in a chromosome is
determined by the mutation rate. At first, a random
number between zero and one is generated for each gene
to carry out the mutation operation. If the generated
number was smaller than the value of mutation probabil-
ity, the mutation takes place and the gene changes. Oth-
erwise, no change is carried out on the gene. To calculate
the mutation rate, usually, the relation 1
m
PL  is used,
where L is the chromosome length. The process of pro-
ducing a new generation and selecting the best member
is repeated continually until the algorithm’s termination
condition is satisfied.
4. GENETIC ACTIVE CONTOUR
Sensitivity to the initial position of contour and the en-
trapment within local minima are among the problems
inflicted on the active contour model used for image
segmentation. This problem is magnified when we try to
apply the model to the segmentation of low quality im-
ages like an ultrasound images. To resolve this issue, we
used the genetic active contour. The process of applying
this algorithm has several steps which will be described
below.
We first assumed that the tissue under examination is
confined within two circles with the radius Rmin and
Rmax (Figure 1). In this situation, the specific region
under study can be considered as concentric circles,
where each of these circles acts like a contour (Figure 2).
As the figure shows, each of these contours can contain
points from the tissue’s edge. So, if we are able to sepa-
rate these points from each contour and connect them
together, we can reveal the tissue’s edge. As a first step,
we consider a population of chromosomes as the initial
population to generate these circles. We then include two
genes for every chromosome. The first gene specifies the
circle’s radius and the second one, the angle of the start-
ing point (Figure 3). After the contours are produced, we
mark a number of equidistant points on every on. If N
denotes the number of points on the contour, the distance
of every point from the adjacent one would be
equal to360
N.
Once the initial contours are formed and the contour
points are determined, each of these points should be
evaluated and the best ones be selected. To do this, first
we should define a fitness function. Since the active
Figure 1. Space where the tissue is confined within two circles.
Figure 2. How the initial contours is positioned and the points
specified for each contour.
C
opyright © 2011 SciRes. JBiSE

M. Talebi et al. / J. Biomedical Science and Engineering 4 (2011) 105-109 108
Figure 3. The structure of chromosomes and the production of
initial chromosomes. RM represents radius of contours and

specifies the start angle.
contours are founded on the energy minimization princi-
ple, therefore the fitness function can be defined as:

int
1
1
fitness
ernal external
FEE 


1
1ContinuityCurvaure image EEE  
(5)
With respect to the defined function, by calculating the
energy of each contour point, its relevant fitness function
can be obtained. Those contour points which are situated
on the tissue’s edge or in the local minima possess the
least amount of energy. So, their fitness functions will
have the highest values. Therefore, we calculate the fit-
ness function for the overall contour points to remedy the
problem of local minima and to have a better evaluation
of all the points at every step, instead of using each sin-
gle point’s fitness function. The overall fitness function
for every contour is obtained from the sum of fitness
functions of individual contour points. After calculating
the overall fitness functions, we select the contours that
have the highest values of fitness functions as the best
solutions.
At this stage, considering the rate of selection, some of
the best individuals from the society are selected and put
into the reproduction pool. Then, the members of the
pool are paired up and allowed to reproduce. We used the
uniform cross over method. Next, to prevent quick con-
vergence and to have a better generation, mutation op-
eration is performed on the chromosome populations.
This process is repeated until a set of best contours is
finally acquired. After the algorithm runs its course,
some of the best individuals are separated and the best
points of each contour are selected from the generation
that remains. The final contour is obtained by connecting
those points.
5. EXPERIMENTAL RESULTS
To evaluate the proposed algorithm, it was first applied
on a simple image like that of Figure 4-a. As is observed,
this image consists of two sections of background and
tissue, with some added speckle noise. In this test, 40
points are considered for each contour and the contour
energy coefficients are: 0.2

, 0.35

, 0.13


.
This test is repeated for 10,000 times and 100 chromo-
somes. Figure 4-b illustrates the final result of image
segmentation. Figure 5-b shows segmentation result of
ultrasound breast lesion (Figure 5-a) for 40 contour
points and 10,000 iteration and 40 chromosomes. Energy
coefficients are equal to before examination. Figure 6
shows another medical ultrasound image segmentation
results by proposed algorithm. Due to initial contours
have circular structure, experimental results show that
using the mentioned algorithm for the segmentation of
circular tissue’s as breast tumor in ultrasound images
(a)
(b)
Figure 4. (a) Original image. (b) Segmented image by means
of proposed method
(a) (b)
Figure 5. (a) Anatomical structure from an ultrasound breast
lesion. (b) Final result of segmentation after the proposed algo-
rithm is applied.
C
opyright © 2011 SciRes. JBiSE

M. Talebi et al. / J. Biomedical Science and Engineering 4 (2011) 105-109 109
JBiSE
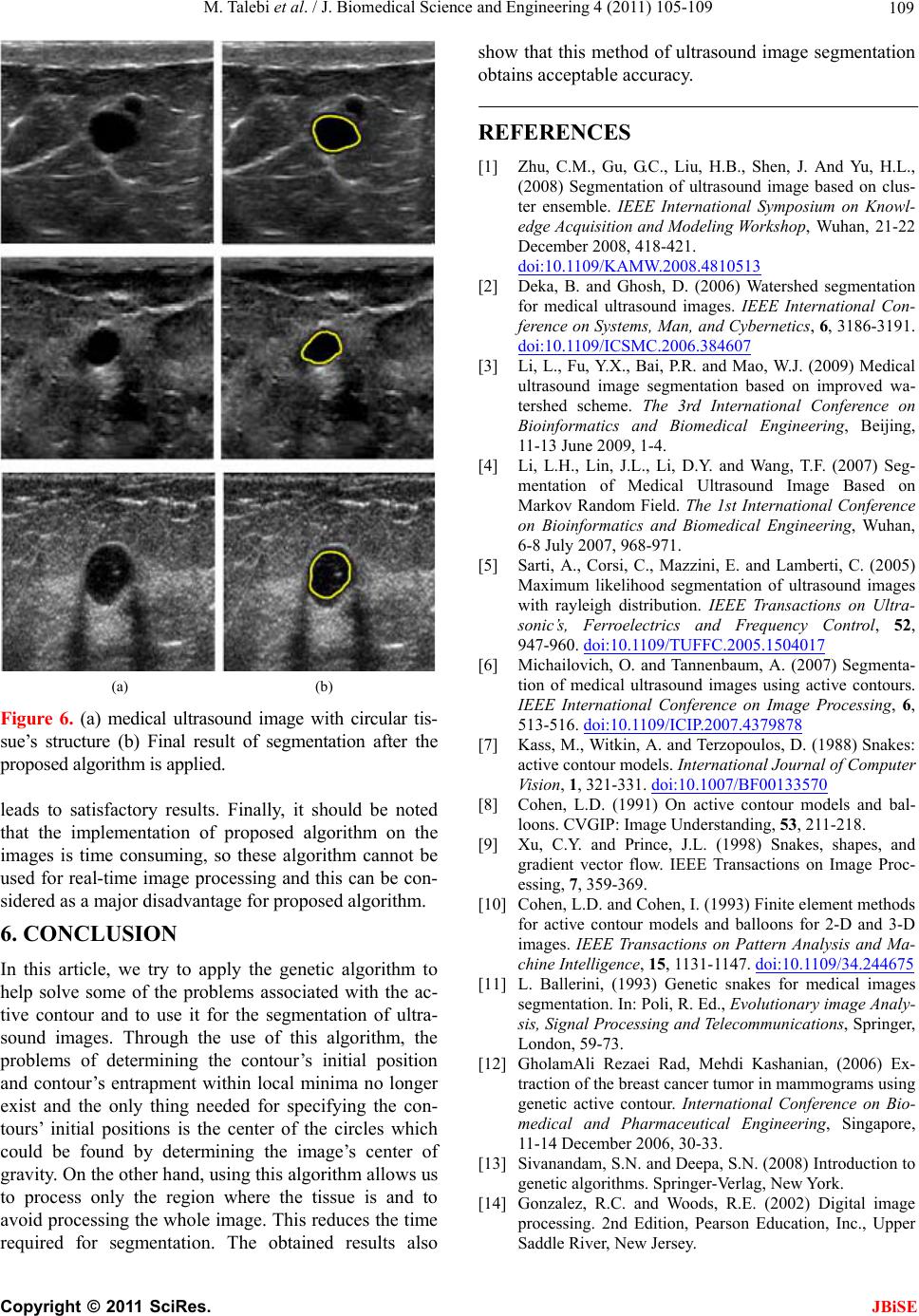
(a) (b)
Figure 6. (a) medical ultrasound image with circular tis-
sue’s structure (b) Final result of segmentation after the
proposed algorithm is applied.
leads to satisfactory results. Finally, it should be noted
that the implementation of proposed algorithm on the
images is time consuming, so these algorithm cannot be
used for real-time image processing and this can be con-
sidered as a major disadvantage for proposed algorithm.
6. CONCLUSION
In this article, we try to apply the genetic algorithm to
help solve some of the problems associated with the ac-
tive contour and to use it for the segmentation of ultra-
sound images. Through the use of this algorithm, the
problems of determining the contour’s initial position
and contour’s entrapment within local minima no longer
exist and the only thing needed for specifying the con-
tours’ initial positions is the center of the circles which
could be found by determining the image’s center of
gravity. On the other hand, using this algorithm allows us
to process only the region where the tissue is and to
avoid processing the whole image. This reduces the time
required for segmentation. The obtained results also
show that this method of ultrasound image segmentation
obtains acceptable accuracy.
REFERENCES
[1] Zhu, C.M., Gu, G.C., Liu, H.B., Shen, J. And Yu, H.L.,
(2008) Segmentation of ultrasound image based on clus-
ter ensemble. IEEE International Symposium on Knowl-
edge Acquisition and Modeling Workshop, Wuhan, 21-22
December 2008, 418-421.
doi:10.1109/KAMW.2008.4810513
[2] Deka, B. and Ghosh, D. (2006) Watershed segmentation
for medical ultrasound images. IEEE International Con-
ference on Systems, Man, and Cybernetics, 6, 3186-3191.
doi:10.1109/ICSMC.2006.384607
[3] Li, L., Fu, Y.X., Bai, P.R. and Mao, W.J. (2009) Medical
ultrasound image segmentation based on improved wa-
tershed scheme. The 3rd International Conference on
Bioinformatics and Biomedical Engineering, Beijing,
11-13 June 2009, 1-4.
[4] Li, L.H., Lin, J.L., Li, D.Y. and Wang, T.F. (2007) Seg-
mentation of Medical Ultrasound Image Based on
Markov Random Field. The 1st International Conference
on Bioinformatics and Biomedical Engineering, Wuhan,
6-8 July 2007, 968-971.
[5] Sarti, A., Corsi, C., Mazzini, E. and Lamberti, C. (2005)
Maximum likelihood segmentation of ultrasound images
with rayleigh distribution. IEEE Transactions on Ultra-
sonic’s, Ferroelectrics and Frequency Control, 52,
947-960. doi:10.1109/TUFFC.2005.1504017
[6] Michailovich, O. and Tannenbaum, A. (2007) Segmenta-
tion of medical ultrasound images using active contours.
IEEE International Conference on Image Processing, 6,
513-516. doi:10.1109/ICIP.2007.4379878
[7] Kass, M., Witkin, A. and Terzopoulos, D. (1988) Snakes:
active contour models. International Journal of Computer
Vision, 1, 321-331. doi:10.1007/BF00133570
[8] Cohen, L.D. (1991) On active contour models and bal-
loons. CVGIP: Image Understanding, 53, 211-218.
[9] Xu, C.Y. and Prince, J.L. (1998) Snakes, shapes, and
gradient vector flow. IEEE Transactions on Image Proc-
essing, 7, 359-369.
[10] Cohen, L.D. and Cohen, I. (1993) Finite element methods
for active contour models and balloons for 2-D and 3-D
images. IEEE Transactions on Pattern Analysis and Ma-
chine Intelligence, 15, 1131-1147. doi:10.1109/34.244675
[11] L. Ballerini, (1993) Genetic snakes for medical images
segmentation. In: Poli, R. Ed., Evolutionary image Analy-
sis, Signal Processing and Telecommunications, Springer,
London, 59-73.
[12] GholamAli Rezaei Rad, Mehdi Kashanian, (2006) Ex-
traction of the breast cancer tumor in mammograms using
genetic active contour. International Conference on Bio-
medical and Pharmaceutical Engineering, Singapore,
11-14 December 2006, 30-33.
[13] Sivanandam, S.N. and Deepa, S.N. (2008) Introduction to
genetic algorithms. Springer-Verlag, New York.
[14] Gonzalez, R.C. and Woods, R.E. (2002) Digital image
processing. 2nd Edition, Pearson Education, Inc., Upper
Saddle River, New Jersey.