Journal of Mathematical Finance, 2013, 3, 476-486
Published Online November 2013 (http://www.scirp.org/journal/jmf)
http://dx.doi.org/10.4236/jmf.2013.34050
Open Access JMF
Optimal Variational Portfolios with Inflation Protection
Strategy and Efficient Frontier of Expected Value of
Wealth for a Defined Contributory Pension Scheme
Joshua O. Okoro1, Charles I. Nkeki2
1Department of Physical Science, Faculty of Science and Engineering, Landmark University,
Omu-Aran, Nigeria
2Department of Mathematics, Faculty of Physical Sciences, University of Benin, Benin City, Nigeria
Received August 16, 2013; revised September 27, 2013; accepted October 26, 2013
Copyright © 2013 Joshua O. Okoro, Charles I. Nkeki. This is an open access article distributed under the Creative Commons Attri-
bution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly
cited.
ABSTRACT
This paper examines optimal variational Merton portfolios (OVMP) with inflation protection strategy for a defined con-
tribution (DC) Pension scheme. The mean and variance of the expected value of wealth for a pension plan member
(PPM) are also considered in this paper. The financial market is composed of a cash account, inflation-linked bond and
stock. The effective salary of the plan member is assumed to be stochastic. It was assumed that the growth rate of
PPM’s salary depends on some macroeconomic factors over time. The present value of PPM’s future contribution was
obtained. The sensitivity analysis of the present value of the contribution was established. The OVMP processes with
inter-temporal hedging terms and inflation protection that offset any shocks to the stochastic salary of a PPM were es-
tablished. The expected values of PPM’s terminal wealth, variance and efficient frontier of the three classes of assets
are obtained. The efficient frontier was found to be nonlinear and parabolic in shape. In this paper, we allow the stock
price to be correlated to inflation risk index, and the effective salary of the PPM is correlated to inflation and stock risks.
This will enable PPMs to determine extents of the stock market returns and risks, which can influence their contribu-
tions to the scheme.
Keywords: Optimal Variational Merton Portfolios; Mean-Variance; Expected Wealth, Defined Contribution; Pension
Scheme; Pension Plan Member; Inter-Temporal Hedging Terms; Stochastic Salary
1. Introduction
This paper considers the OVMP strategy under inflation
protection, expected wealth and its variance for a DC
pension scheme. It was assumed that the salary and risky
asset are driven by a standard geometric Brownian mo-
tion. The growth rate of salary of PPM is assumed to be a
linear function of time. In this paper, we focus on study-
ing the OVMP strategy under inflation protection for a DC
pension scheme. In related literature, [1] and [2], studied
optimal portfolio strategy based on the non-Gaussian
models. They constructed optimal portfolios of variance
swaps based on a variance gamma correlated model. The
portfolios of the variance swaps are optimized based on
the maximization of the distorted expectation given in
the index of acceptability. [3] examined the rationale,
nature and financial consequences of two alternative ap-
proaches to portfolio regulations for the long term insti-
tutional investor sectors of life insurance and pension
funds. [4] studied the deterministic life styling and grad-
ual switch from equities to bonds in accordance to preset
rules. This approach was a popular asset allocation strat-
egy during the accumulation phase of a defined contribu-
tion pension plan and was designed to protect the pen-
sion funds from a catastrophic fall in the stock market
just prior to retirement. They showed that this strategy,
although easy to understand and implement, can be
highly suboptimal. [5] developed a model for analyzing
the ex ante liquidity premium demanded by the holder of
an illiquid annuity. The annuity is an insurance product
that is similar to a pension savings account with both an
accumulation and decumulation phase. They computed
the yield needed to compensate for the utility welfare

J. O. OKORO, C. I. NKEKI 477
loss, which is induced by the inability to re-balance and
maintain an optimal portfolio when holding an annuity.
[6-8] considered the optimal design of the minimum
guarantee in a defined contribution pension fund scheme.
They studied the investment in the financial market by
assuring that the pension fund optimizes its retribution
which is a part of the surplus, which is the difference
between the pension fund value and the guarantee. [9]
studied optimal investment strategy for a defined con-
tributory pension plan. They adopted dynamic optimiza-
tion technique. [10] considered optimal portfolio strate-
gies with minimum guarantee and inflation protection for
a DC pension scheme. [11,12] studied the optimal port-
folio and strategic lifecycle consumption process in a
defined contributory pension plan. This work is an ex-
tension of [13]. [13] studied the OVMP process of a PPM.
In this paper, we introduce additional underlying asset,
which is the inflation-linked bond that will protect the
investment against inflation risks in the investment pro-
file. [14] considered optimal investment strategy with
discounted cash flows. In their work, the investment and
the portfolios processes were protected from inflation
risks by trading on the index bond asset that is linked to
inflation risk over time.
The remainder of this paper is organized as follows. In
Section 2, we present the financial market models and
wealth process of a PPM. Section 3 presents the expected
value of PPM’s future contribution, the present value of
the expected flow of future discounted contribution, sen-
sitivity analysis of the present value of expected future
discounted contribution and value of wealth process of a
PPM. In Section 4, we present the optimization process
and portfolio value of wealth of a PPM in pension
scheme. Also, in this section, some numerical illustra-
tions were made. Section 5 presents the expected wealth
and variance of expected wealth for a PPM up to termi-
nal period. Finally, Section 6 concludes the paper.
2. Problem Formulation
Let

,,

F
P be a probability space. Let






:0,
t,
F
Ft T 
where




:
t
F
Ws s t  
and the Brownian motion
 

,,
QS
WtWt Wt 
0tT is a 2-dimensional process, defined on a com-
plete probability space
 
,,, ,

F
FP T
 
where is
the real world probability measure and the terminal
time. The vectors S and
P

t 

zt
 are the volatility
vector for stock and inflation index with respect to
changes in


S
Wt and


Q
Wt , respectively.


t  is
the appreciation rate for stock. Moreover,


St
 and


zt
 are the volatilities for the stock and inflation in-
dex, respectively, referred to as the coefficients of the
market and are progressively measurable with respect to
the filtration .
F
We assume that the investor faces a
market that is characterized by a risk-free asset (cash
account), inflation-linked bond and stock, all of whom
are tradeable. In this paper, we allow the stock price to be
correlated to inflation risk index and the effective salary
of the PPM to be correlated to inflation and stock. This
will enables us to check how stock market risks can in-
fluence contribution into the scheme.
2.1. The Financial Model
The dynamics of the underlying assets are given by (1)
and (2)






t tC

d,tCdCt r01

 (1)








d

0
0
St S
Ss

dd
S
tt   ,ttWt (2)

 

   

 
,
0
Qz


d,
d,
z
d
,
Z
tQ tQt
Z
 t Z
tWt
t rt
z


t t

(3)
where,


rt


 is the nominal interest rate,


Ct is
the price of the riskless asset at time , t

 
,
Z
tQt is
the price of the inflation-linked bond at time , t


Qt is
the inflation index at time , and satisfies the dynamics t
 

  


dddqt tQ
Q
QtEt W  Qtt ,




Eqt is the expected rate of inflation which the dif-
ference between the nominal interest rate and the real
interest rate and


Q
 t is the volatility of inflation in-
dex,


St is the stock price process at time , t


zt


 is the inflation price of risk,


 is the
correlation coefficient and
 


2
 ,1 S 
SS
tt  t
,



,0 .t
zQ
 
The volatility matrice now become



 
2
0
1
Q
SS
t
ttt












The market is complete since

2
10
QS ,
  tt
therefore there exists a unique market price of risk vctor,


t 
2

 satisfying


 


  
2
1
z
z
S
t
t




 Sz
t

S
tr
t
t
t
t






t







Open Access JMF

J. O. OKORO, C. I. NKEKI 478
The effective salary of the PPM is assume to follow the
dynamics













0
ddd
00,
Y
YtYtt tt Wt
Yy
 

,
(4)
where, 12 ,
  
,
YYY
tt  

t


1Yt
 is the volati-
lity caused by the source of inflation,


Q
Wt and


2Yt

is the volatility caused by the source of uncer-
tainty arises from the stock market,


S
Wt . We assume
that the growth rate of the salary of PPM is linear and
satisfies


, 0, 0.tata  
a is seen as expected yearly growth of PPM’s salary
and

economic growth effect or welfare of the PPM.
(4) define the buying power of PPM’s salary at time .t
Suppose that (4) becomes
 
0, 0,
Yt
 








0
dd,0YttYt tYy  0, (5)
define the deterministic salary process of the PPM at
time In this paper, we assume that the salary process
of the PPM is stochastic. In the case of deterministic sal-
ary, we shall state it.
.t
Therefore, the flow of contributions of the PPM is
given by


,cY t where is a proportion of
PPM’s salary that he/she is contributing into the scheme.
We assume in this paper that ,
0c

rt


t  ,


t  ,
, ,

Yt


St



Qt
 ,


1Y, t



2Yt
 ,


t  ,


Zt
 ,


S
We now define the following exponential process
which we assume to be Martingale in
t  are constants in time.
:P
 
2
1
exp ,
2
Z
tWt 

  


t
which will be useful in the next section.
2.2. The Wealth Process of a PPM
Let

X
t

be the wealth process and







,
QS
ttt . The portfolio process,


Qt
represents the proportion of wealth invested in infla-
tion-linked bond and the proportion of wealth
invested in stock at time . Then,

t
t
S




01QS
tt

t
is the proportion wealth invested in the riskless asset at
time . We now have the following definition: t
Definition 1: The portfolio process is said to be
self-financing if the corresponding wealth process





, 0,,
X
tt T satisfies
 




    
0
dd
d, 0

,
zz r



.
,
X
tXtrtcYtt
XttWtXx








 


(6)
where
3. The Expected Value of PPM’s Future
Contribution
section, we considr the value of PPM’s expected
future contribution over the planning horizon. We now
scounted value of expected future
In this e
make the following definitions.
Definition 2: The di
contribution process is defined as
 
 
d
T
tt
s
tE cYss
t











where
, (7)






t
EEFt  is the conditional expectation
with respect to the Brownian filtration and
 
0t
Ft 






exptZtrt


is the s factor which adjusts for nomi-
nal interest rate and market price of risk.
Definition 3: A portfolio process is e admis-
tochastic discount
s
said to b
sible if the corresponding wealth process

X
t satisfies
 
 
01,
t
s
T
PXt EcYsds
tt




0, .tT

 
 


Theorem 1: Let




)(t

be the discounted value of
expected future contrin (PVFC) process of PPM,
then
butio a



 
 

0
1 ,0
0exp1,0
tTt
cY T



exp
cY t







 
(8)







2
0
2
2
2
πexp ,
422
0
02
2
πexp ,
422
0.
cY t
t
Tt
Erfi Erfi
cy
T
Erfi Erfi









 









 







  








 





 

 












(9)


0,T

 where, .
z
ar

 
See Nkeki and Nwozo (2012).
Remark 1: The present value of expected future con
tribution of a PPM is given by
In this paper, we consider te case of
Proof:
-
0
.
h0.

 For the
Open Access JMF

J. O. OKORO, C. I. NKEKI 479
0,

see [4case of ,7,10,11,12].
3. uti(PVPPMFC)
bution for
1. Sensitivity Analysis of Present Value of
PPM’s Future Contribon
In this subsection, we consider the sensitivity analysis of
PPM’s p value future contriresent 0


it
and
y of
a-
rame
for stochastic salary. We intend to find the elastic
PVPPMFC with respect to change in its dependent p
ters. In a sequel, we set

0.
0

 First, we fi
the partial derivative of 0
 with respect to .
nd



2
2
2
00
5
2
3
e
4π
cy





 


2
2
2
4
2
2
eπ2e
πe2
2
π() ;
2
T
T
Erfi
T
Erfi




  



 


 










 





(10)
The partial derivative of with respect to
0
 :c
2
00
22
πe;
22
Erfi Erfi

  


 


2
y
c
T




 





(11)
The partial derivative of with respect to
0
 0:y
2
0
0
22
πe;
22
Erfi Erfi

  


 


2
c
y
T




 





(12)
The partial derivative of with respect to
0
 :a

2
2
00
3
2
44
e
2π
2
eπeπ;
2
cy
a
T
Erfi







 








 





(13)
The partial derivative of with respect to
2
22
3T



 
 
0
 :T
22
4 0
0e
TT
cy
T



 
 
 (14)
The partial derivative of with respect to
0

12
,,,,
z
SY Y
r

  are respectively given as;

2
22
23
4
eπ
T
Erfi

 





 

00 2
32
2
24
1
1
2
2
ee π2
Y
S
cy
r
T










 











(15)

2
22
00 2
1
32
2
23
24 4
1
2
2
eee π
π2
Y
Y
z
T
cy
T
Erfi


 










 















(16)



2
2
2
2
00
3
12
2
32
3
244
e
2π1
2
1eπeπ
2
z
YS
T
S
cy
T
Erfi






 

 

 







 

 





(17)

2
22
2 00
3
22
23
44
e
2
2
eeπ.
π2
S
Y
T
cy
T
Erfi


 








 












(18)


2
2
2
2
002
3
22
2
2
3
244
e
21π
2
1e πeπ.
2
Y
S
T
S
cy
T
Erfi








 


 








 









2
22 2
00 2 2
2
2
2
424 2
1
21
ee πe2
.
π2
SY Yz
T
cy
T
Erfi

 
 
  




 














  







We set (to obtain the values in Table 1 by vary-
ing each of the parameters) , 0.0292a0.04,r

10.18 Y


, 20.20
Y


, 0.09
z

, 0.30
S


,
0.40


, 0.09


, 0.01


, 20T, 0.25
Q


,
Open Access JMF

J. O. OKORO, C. I. NKEKI
Open Access JMF
480
the values of the parameters and the
in PVPPMFC. It is observed that
sitively sensitive to all the parame-
that is constant overtime (or we
astic in and ). But,
nsitive in
00.8y,
Table 1
the PVPPMFC
ters exce
say that
PVPPMFC is ne
0.15.c
gives
corresponding change
is po
pt c and
PVPPMFC is inel
0
y
gatively se
c 0 y

. We observe
that as

increases by 0.1, the PVPcreases by
ve the otr. Fo
P
han
MFC de
about 15.192. We also observed that among the sensitive
parameters, some are more sensititsr
instance, a small change in
he

PPM
will lead to a veh
inFCf
ry hig
PV, , an se oproportionate changei.e. increa

by
PV
0.001 unit will
av
bt an ave if rinease og aboueragncr
PPMFC by 251 units. It is further observed that an
increase of T by one unit will lead to a very small
change in PVPPMFC. Increasing a by 0.001 will lead
to about anerage of 2.19 increases in PCPPMFC.
Similarly, an increase in r by 0.01 will lead to a pro-
portionate increase in PVPPMFC by 1.65. Similarly, an
increase in
z

by 0.01 will bring about 0.20 propor-
tionate increases in PVPPMFC. Again, an increase in
1Y

by 0.05 will lead to about 0.75 proportionate in-
creases in PVPPMFC. Finall , an increase in 2Y y

by
0.05 will lead to about 1.52 proportionate increases in
PPPMFC. When increase by 0.01, the PVPPMFC in-
creases alongside with 15.2. We therefore conclude that
PVPPMFC isastic with respect to change in the pa-
rameters. The elasticity of PVPPMFC with respect to
change in the above parameters will enable fund manag-
ers and investors to value assets, flow of contributions,
and investment flow that are to be receive some time in
future. From (14), we obtain the critical time horizon for
the present value of PPM’s future discounted contribu-
ti as follows:
V
on
el
22
*
e0
2
14log .
2
Tcy
 
 


 


 (19)
Lemma 1: The dynamics of the discounted value of
future contribution process is given by



  

dd
d,
z
ttttWt
cY tt
  

d
(20)
where,


π
2,
22
At
Tt
Erfi Erfi
 

























,,
atAtHt
tT
At


 t


 

22
2
exp2 exp.
44
Tt
Ht
 




 






Proof: See Nkeki and Nwozo (2012).
3.2 Value of PPM’s Wealth Process
Let the value of PPM’s wealth be


Vt at timeis
gi
t
ven by



 

,0,VtXtt tT .
(21)
s of Finding the differential of both side(21) and sub-
stituting in (6) and (20), we obtain
 


 
ddVtXtrtttt 





   


d.
Ytt
XtWt 
(22)




4. The Optimization Process and Portfolio
Value of a PPM
In this section, we consider the optimal portfolio process.
sit
Table 1. Simulation of the sen
T
ivity analysis of PVPPMFC.
0
T



0


 a
0
a

 r
0
r



z

0
z




1Y

0
1Y



2Y

0
2Y





0




0




1 0.1062 0.001 −2838.87 0.020 116.76 0.01 −42.830.05 −13.519 0.15 −12.903 0.20−19.52 0.01 −244.9 0.11.93
2 0.1035 0.002 −60.0597 0.021 118.84 0.02 −40.930.06 −13.310 0.20 −11.952 0.25−17.26 0.02 −220.9 0.21.60
3 0.1030 0.003 249.936 0.022 21 0.03 −198.8 0.31.25
4 0.1044 0.004 370.722 0.023 36 0.04 −178.4 0.40.83
5 0.1081 0.005 483.543 0.024 125.23 0.05 −35.630.09 −12.697 0.35 −09.425 0.40−11.69 0.05 −159.7 0.50.28
6 0.1141 0.006 627.520.025 127.42 0.06 −33.990.10 −12.497 0.40 −08.684 0.45−10.18 0.06 −142.0.6 −0.54
−
10 0.1733 0.010 2002.66 0.029 136.48 0.10 −28.010.14 −11.7240.60−06.1570.65−05.55 0.10 −87.9 0.99−134.8
120.94 0.03 −39.100.07 −13.103 0.25 −11.057 0.30−15.
123.07 0.04 −37.330.08 −12.899 0.30 −10.216 0.35−13.
1 5
7 0.1230 0.007 824.141 0.026 129.64 0.07 −32.410.11 −12.300 0.45 −07.989 0.50−08.82 0.07 −126.8 0.7−1.99
8 0.1351 0.008 1096.40 0.027 131.89 0.08 −30.890.12 −12.106 0.50 −07.337 0.55−07.60 0.08 −112.6 0.8−5.22
9 0.1515 0.009 1474.95 0.028 134.17 0.09 −29.420.13 −11.914 0.55 −06.727 0.60−06.52 0.09 −99.6 0.916.45

J. O. OKORO, C. I. NKEKI 481
Wdee efine the genral objective function
 




,t x

t,JtV,EuV

T X 

where

uV


t is the path of


Vt gih
strategy ne issi-
bp e
ven te portfolio

ortfolio
. Defi

V
gy that
to b
are
e the set of all adm
le stratV
F
- progressively me
u lv n
as-
rabe, and let

u


V t be a concave alue functio in


Vt such that





 


sup , ,
VJt
V


Then
 
UVtfies the HJB equation
sup ,
.
VEuVT Xtxt 




satis
UVt



sup,,0
VHtv 

t
U  (23)
subject to:

,,
v
UTv



 0,
where,












2
2
,,
1
2
1.
2
x
xx
Yx YY
H
tv
xt tU
xtU U
 
rx xtUU 







 
Finding the partial derivative of
 


,,Htv with re-
e optimal control spect to th


t and setting it to zero,
we obtain
 


1
*.
xYx
xx
UU
txU




 

 (24)
Substituting (24) into (23), we obtain the HJB equation
(25), we have


2
x
tx
MU
UrxU U


22
1
2
2
xx
Yx xYY x
xx xx
U
MU UU
UU
 


2
10.
2YY
U




 




 


where
Prop
(25)

1
M

 .
osition: Let
 

,,
vR t
Utv




  
Rt

v 

Rt
 
11
0;


1Rt 1M
2

1 
Y

R
trxv
M

vR  t




 
(26)






0,
be the solution to the HJB Equation (25), then,


*t
*Y
*
Xt * X. 1
MX  ttM
tt






Proof: We commence by obtaining the following par-
tial derivatives:
 
 (27)
 
1
t
UvRt Rt





1
x
UvRt

 

 
2
1
xx
UvRt





 
2
1
x
UvRt






1
UvRt

 

 
2
1UvRt




 
Substituting the partial derivatives abovto (25), we e in
obtain
 
 
1
11
1
21
0.
Y
M
Rt rxvRtRt
vRt MvRt


 








 
Again, substituting the partial derivatives into (24), we
obtain








*
Y
MXtttM 
*
**
.
1
tXt Xt





ortfolio value in the riskless asset is
obtain as

 

Therefore, the p
 






*
*
0**
1.
1
Y
M
Xt t
tM
tXt Xt







  (28)
The portfolio value (27) is made up of two parts. The
first part is the OVMP value and the second part is the
intertemporal hedging term that offset any shocks to the
stochastic salary of the PPM at time .
t
It is observe in
(28) that the flow of intertemporal term is a gradual
transfer fund from the risky assets to the riskless one
ov
the effective salary process of a PPM. It is also
a ratio of the PPM discounted value of expected future
contributions of a PPM to the optimal wealth process.
This strategy is strongly recommended for PPMs of
whom contributions are made compulsory. This will en-
su
ar
er time. The intertemporal hedging term, interestingly
is a function of financial market behaviour and volatility
vector of
re that the inflation risks in the portfolio of members
e hedged. We therefore say that (27) is a portfolio with
Open Access JMF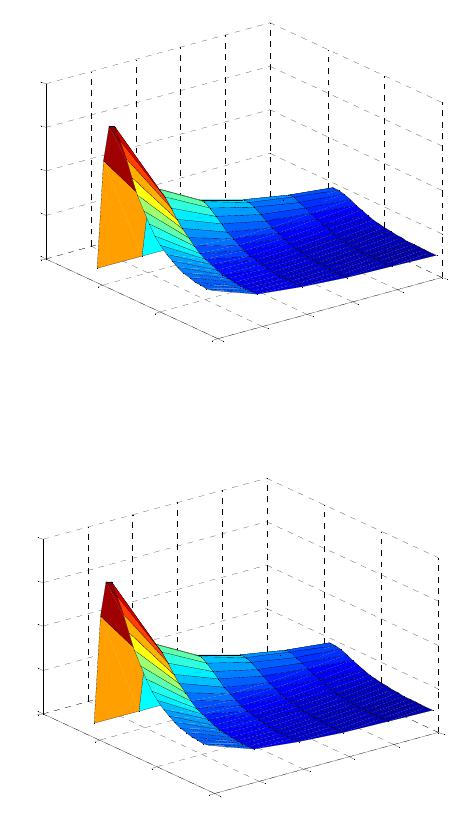

J. O. OKORO, C. I. NKEKI 482
inflation protection strategy. The solution to (26) can be
obtained numerically.
Numerical Example
Let 0.0292a, 0.04r, 10.18
Y

, 20.20
Y


,
0.09
z

, S0.30

, 0.40

, 0.09

, 0.01


,
0.80

,20T, 0.2
Q5


figures:
, 00.8y, 0.15c, we
Figures 1-3 are obtained for
have the following
0


ock that
ns for me
lio va
and for determi-
ni
in st inflation-linked
bond to ensure maximum returmbers at retire-
e portfolue in stock when
stic salary process. Figure 1 shows the portfolio value
of a PPM invested in inflation-linked bond for a period
of 20 years given that the wealth is between 1 to 6 mil-
lion. Similarly, Figure 2 shows the portfolio value of a
PPM invested in stock for the same period and the same
wealth. Figure 3 shows the portfolio value of a PPM in
cash account. It is observed that the portfolio values in
stock and inflation-linked bond are nonnegative, while in
cash account is negative over time. We therefore recom-
mend (based on these numerical examples) that the port-
folio value in cash account should be shorten by the
negative value to finance the risky assets (i.e., more
money should be borrowed from cash account to finance
the investment in stock and inflation-linked bond). It is
also observed that the wealth generated by stock is higher
than that of inflation-linked bond. This suggest that more
fund should be invested
ment. Figure 4 shows th
0


o
, and for thse salary stocFigure 5 shows
rtfolio val in Stock wh
e ca
the pue
hastic.
en 0


xe Fi
when
,
gure
for salar-
d lad.6 s the
portfolio value in cash account,
y sto
anrandomness is re showchastic
0

alary
stochastic. Figure 7 shows t
, and s
he lio value in cash
account, when 0
portfo

, salary stochastic and randomness
is relaxed. Figure 8 shows the portfolio value in infla-
tion-linked bond, when 0

, and salary is stochastic.
Figure 9 shows portfolio value in inflation-linked bond
for 0

, salary stochastic and randomness is relaxed.
Figures 4, 6, 8 are established for 0

 and for sto-
chastic salary process. These figures are made up of sev-
eral shocks and paths. These shock paths made it difficult
to make useful decisions, hence the need for us to relax
the randomness associated with the portfolios for ef-
fective decision making. We now have that the following
Figures 5, 7, 9 are special cases of Figures 4, 6, 8, re-
spectively. Similar behaviors exhibited by Figures 1-3
were also exhibited by Figures 5, 7, 9. The major differ-
ence is that the portfolio value under stochastic salary
yields higher returns that the deterministic salary. This
makes sense, since it is expected that, the higher the risk
taken, the higher the expected wealth. Interestingly, from
the numerical examples, the amount that was gradually
transferred from the risky assets to cash account seems to
een re-invested back to the risky assets overtime.
Figures 10-12 show the portfoliues for determi-
nistic salary and for 0
have b
o val

 in inflation-linked bond,
stock and cash account, respectively. bserved that
under this strategy, the entire fund should be invested in
stock for maximealth for the PPM at retirement.
Figures 13-15 show the portfolio values for stochastic
salary and 0
We o
um w

 in in-linked bond, stock and
cash account overtime. It should be noted that the shocks
associated with the portfolios arise from the salary risks
flation
of the PPM overtime.
5. Expected Wealth and Variance of the
Expected Wealth
In other to determine the expected wealth of the PPM at
time t, we find the mathematical expectation of (22) as
follows:
123456
0
10
20
30
0
10
20
30
40
Wealth
For Beta= 0 for Determ i n ist i c S alary
Time,t (in year)
Figure 1. The portfolio value in inflation-linked bond for
0
Portfolio Value


and salary deterministic.
123456
0
10
20
30
0
10
20
30
40
Fo r Be ta=0 for D eterm in i st ic S a lary
Wealth
Tim e,t (i n year)
Portfolio Va
Figure 2. The portfolio value of a PPM in stock for
lue
0


and salary deterministic.
Open Access JMF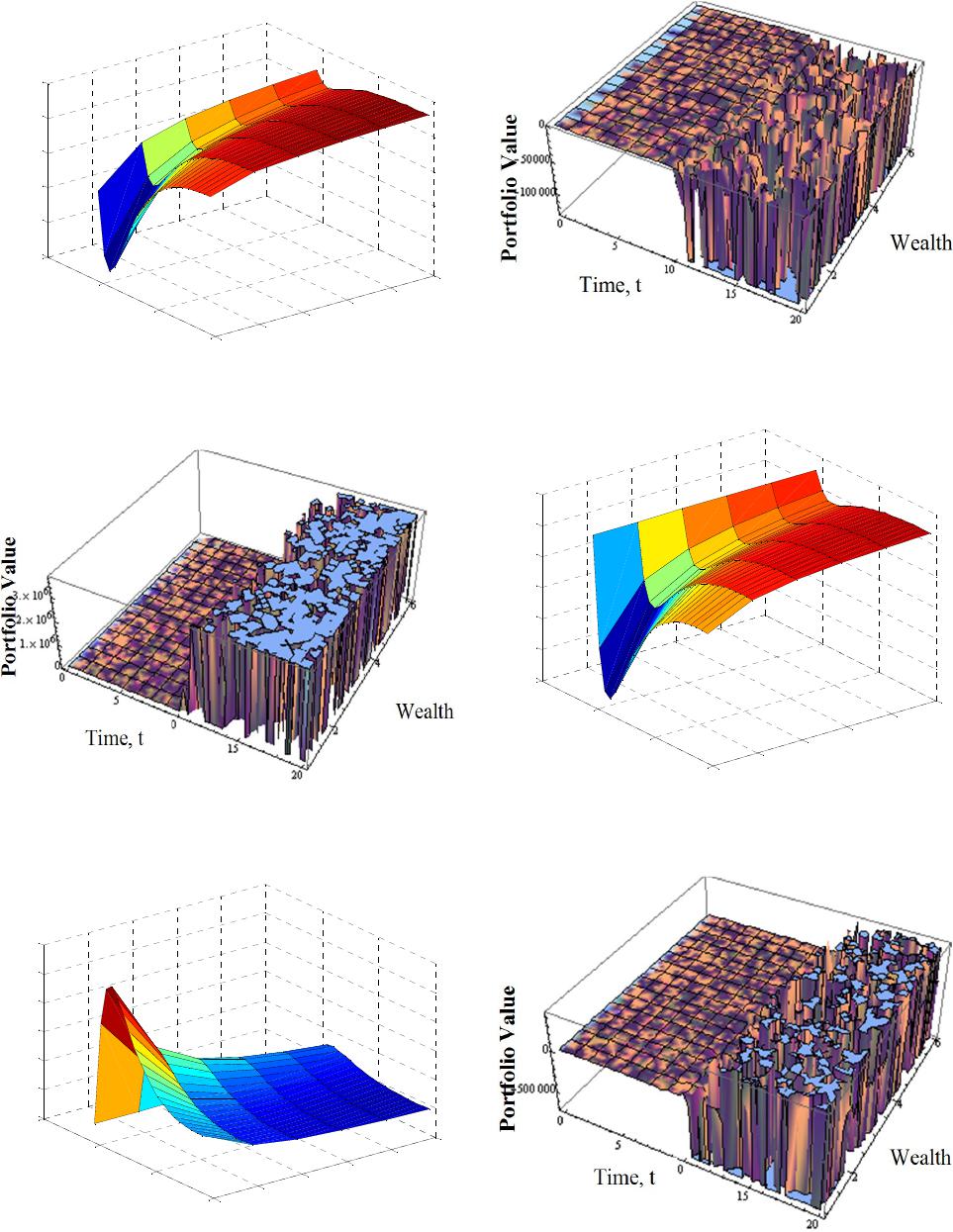

J. O. OKORO, C. I. NKEKI 483
123456
0
10
20
30
-50
-40
-30
-20
-10
0
Wealth
For Bet a=0 for Det ermi n i stic S alary
Time,t (in year)
Portfolio Value
Figure 3. The portfolio value of a PPM in cash account for
and salary deterministic. 0 
Figure 4. The portfolio value in stock. When 0

 , and
salary stochastic.
123456
0
10
20
30
0
5
10
15
20
25
30
Wealth
For Beta = 0 for S tochas tic Salary but normal i zed
Time,t (in year)
Portfolio Value
Figure 5. The portfolio value in stock. When 0


, and
Figure 6. The portfolio value in cash account. When 0

 ,
and salary stochastic.
123456
0
10
20
30
-30
-25
-20
-15
-10
-5
0
Wealth
For Beta=0 for Stochastic Salary but normalized
Time,t (in year)
Portfolio Value
Figure 7. The portfolio value in cash account. When 0

 ,
and salary stochastic randomness is relaxed.
Figure 8. The portfolio value in inflation-linked bond.
0 when

 , and salary stochastic.
salary stochastic and randomness is relaxe d.
Open Access JMF

J. O. OKORO, C. I. NKEKI 484
123456 0
10
20
30
0.05
0.06
0.07
0.08
0.09
Wealth
For Beta=0 for Stochastic Salary but normalized
Time,t (in year)
Portfolio Value
Figure 9. Portfolio value in inflation-linked bond. When
and salary stochastic and randomness is relaxed. 0  ,
Figure 10. The portfolio value in inflation-linked bond for
and deterministic salary. 0 
Figure 11. The portfolio value in stock for and de
terministic salary.
0  -
Figure 12. The portfolio value in cash account for 0

and deterministic salary.
Figure 13. The portfolio value in inflation-linked bond for
0

and for stochastic salary.
Figure 14. The portfolio value in stock for 0

and sa-
lary stochastic.
Open Access JMF

J. O. OKORO, C. I. NKEKI 485
Figure 15. The portfolio value in cash account for 0

and salary stochastic.


 





*
*
*
*
d
1
d
d.
1
Y
Vt
MV


t
rV t
rMttt
MVt
Wt

 













(29)
Taking the mathematical expectation (29), we have


 



 
*
*
d
1
d
Y
EV t
M
rEVt
rMtE tt












 

(30)
Solving (30), we have



 *ee
tts
t
EV tvf




 (31)

00ds s
where,
 







  


*2
*2 *
2
*2
,
1
d
22d
1
2d
1
Y
fsrMs Es
M
r
Vt
MM
VtftVt t
MVt
Wt









 

 






 


 





(32)
Taking the mathematical expectation of (32), we have




 

 

*2
dEV t
*2 *
2
22
d
1
MMEVtftEVtt 










 


(33)
Integrating (33), we have






 

*2 2
00
0
00
eee
eedd,
ts
tt
ts ts T
EVtvvfs
fsf s










ds
where,


2
2.
1
MM






 
Efficient Frontier
In this subsection, we presents the efficient frontier of the
three classes of assets.
At ,tT

we have








01
*2 2
02
e
e
T
T
T vT
EV TvT






*
EV
ss
dd
(34)
where



10ed
TTs
Tf




,




 

20
0
00
ee d
ee
Ts
T
Ts Ts T
Tv fss
f
sf s
 











Therefore, the variance of the portfolio is obtained as
(35)
(34) is the expected terminal wealth of the PPM and (35)
.
The efficient frontier of the three classes of assets is
obtain as





 



2
**2 *
2
2*
02
e.
T
Var VTE VTE VT
vTEVT



 
is variance of the expected terminal wealth of the PPM


 













2
*2*
02
2
1
*
2
02
2
1
*2
2
00
2
1
*2
2
02
2
1
*2
0
e
e
2e 2e
e2
e,
T
T
TT
TT
T
VarVTvTEVT
vEVTT
vEVT v
vEVT Tv
FTEVTv




0
e





 

 




 




 








Open Access JMF

J. O. OKORO, C. I. NKEKI
Open Access JMF
486
where,
 
2
02
2e
T
F
TvT

  .
Therefore, the efficient frontier (that is nonlinear and
of the portfolio process is have parabolic shape)




*
iVT
w,
1
*2
2
0
1
eT EV TvFT

  .
here
i1. If



*
20
VT FT
  ,
it implies that


1
*2
0eT
EV Tv

.
This shows that fund can be borrowed from the
optimal wealth at time for year.
6. Conclusion
In
portfolios with inflation protection strategy for a defined
contribution Pension scheme. The present values of PP
future contribution and sensitivity analysis of the presen
value of the contribution were established. The optimal
e, expected values of PPM’s terminal wealth
and variance as well as the efficient frontier were
tained.
REFERENCES
[1] L. Cao and Z. F. Guo, “Optimal Variance Swaps Invest-
ments,” IAENG International Journal of Applied Mathe-
matics, Vol. 41, No. 4, 2011, 5 Pages.
[2] L. Cao and Z. F. Guo, “Delta hedging through Deltas
from a Geometric Brownian Motion Process,” Proceed-
ings of International Conference on Applied Financial
Economics, London, 30 June-2 July 2011.
[3] P. E. Davis, “Portfolio Regulation of Life Insurance
Companies and Pension Funds,” Oxford University Press,
ford, 2000.
.org/dataoecd/30/39/2401884.pdf
[4] A. J. G. Cairns, D. Blake and K. Dow
ntrol, Vol. 30, No. 6, 2006, pp. 843-877.
http://dx.doi.org/10.1016/j.jedc.2005.03.009
namics & Co
[5] S. Brawne, A. M. Milevsky and T. S. Salisbury, “Asset
Allocation and the Liquidity Premium for Illiquid Annui-
975.t01-1-00062
ties,” The Journal of Risk and Insurance, Vol. 70, No. 3,
2003, pp. 509-526.
http://dx.doi.org/10.1111/1539-6
. Grasselli and P. Koehl, “Optimal design
ined Contribution Funds,” 2002.
[6] G. Deelstra, M
of the Guarantee for Def
http://www.amazon.com/Optimal-design-guarantee-defin
ed-contribution/dp/B000RQY19I
[7] G. Deelstra, M. Grasselli and P. Koehl, “Optimal Invest-
ment Strategies in the Presence of a Minimum Guaran-
tee,” Insurance: Mathematics and Economics, Vol. 33,
No. 1, 2003, pp. 189-207.
http://dx.doi.org/10.1016/S0167-6687(03)00153-7
[8] G. Deelstra, M. Grasselli and P. Koehl, “Optimal Design
of the Guarantee for Defined Contribution Funds,” Jour-
nal of Economics Dynamics and Control, Vol. 28, No. 11,
2004, pp. 2239-226.
http:/
0tT
/dx.doi.org/10.1016/j.jedc.2003.10.003
[9] C. R. Nwozo and C. I. Nkeki, “Optimal Investment Stra-
tegy for a Defon Plan in Nigeria
Using Dynamue,” Studies in Ma-
rantee and Infla-
Portfolio and
International Journal of Applied Mathe-
al Form of
236/jmf.2012.21015
this paper, we studied the optimal variational Merton ined Contributory Pensi
ic Optimization Techniq
M’s
t thematical Sciences, Vol. 2, No. 2, 2011, pp. 43-60.
[10] C. R. Nwozo and C. I. Nkeki, “Optimal Investment and
Portfolio Strategies with Minimum Gua
variational Merton portfolio processes with inter-tem-
poral hedging terms and inflation protection that offset
any shocks to the stochastic salary of a PPM are obtained.
Furthermor
tion Protection for a Defined Contribution Pension
Scheme,” Studies in Mathematical Sciences, Vol. 2, No. 2,
2011, pp. 78-89.
[11] C. R. Nwozo and C. I. Nkeki, “Optimal
ob- Strategic Consumption Planning in a Life-Cycle of a Pen-
sion Plan Member in A Defined Contributory Pension
Scheme,” IAENG
matics, Vol. 41, No. 4, 2011, p. 299.
[12] C. I. Nkeki, “On Optimal Portfolio Management of the
Accumulation Phase of a Defined Contributory Pension
Scheme,” Ph.D. Thesis, University of Ibadan, Ibadan,
2011.
[13] C. I. Nkeki and C. R. Nwozo, “Variation
Classical Portfolio Strategy and Expected Wealth for a
Defined Contributory Pension Scheme,” Journal of Mathe-
matical Finance, Vol. 2, No. 1, 2012, 132-139.
http://dx.doi.org/10.4
t under [14] C. I. Nkeki and C. R. Nwozo, “Optimal Investmen
Inflation Protection and Optimal Portfolios with Stocha-
stic Cash Flows Strategy,” To appear in IAENG Journal
of Applied Mathematics, Vol. 43, No. 2, 2013, p. 54.
Ox
http.//www.oecd
d, “Stochastic Life-
styling: Optimal Dynamic Asset Allocation for Defined
Contribution Pension Plans,” Journal of Economic Dy-