O. J. AKINRIBIDE ET AL.
332
consistency is accomplished by using standardized test-
ing techniques established and published by international
professional bodies. In several practical cases, the ulti-
mate ductile fracture strain determined with ten sile test is
accepted as a material plasticity measure [7]. In this case,
the plasticity has to be defined as an ability of a material
to accommodate high permanent strains until fracture
appears where this strain reaches certain value called
ultimate fracture strain. The strain value until fracture
depends not only on the material type, but also on other
several factors, as: strain speed, strain history, material
starting structure, temperature, specimen geometry, etc.
It is impossible to account for all factors in a single ma-
thematical description, due to a complexity of phenom-
ena and an insufficient state of the art, mainly for pheno-
mena present during a plastic strain. Several experiments
according to Bao and Wierzbicki [8], have demonstrated
that the material fracture process strongly depends on the
hydrostatic stress.
In Tensile Testing, the test specimen is deformed, usu-
ally until complete rupture or fracture occurs, with a
gradually applied increasing tensile load that is applied
uniaxially along the longitudinal axis of the specimen
(metals and non-metals) which could be circular, rectan-
gular with dimensions in accordance to internationally
acceptable standards (ASTM or BS). During testing, de-
formation is confined to the narrow center region which
has a uniform cross section along its length. The test spe-
cimen is clamped together in the machine with the aid of
upper and lower jaws that has grip ability designed to
firmly hold the test specimen. This work is focused at
design and producing alternative jaws grip that could
perform the same function meeting the required interna-
tional standard of material characterization by evaluating
the tensile properties of a material.
2. Materials and Method
2.1. Basic Development
The aim of this work is to design and develop jaw grips
for circular test piece which is an accessory commonly
used in commercially available universal mechanical
testing machine. The equipment accessory designed was
developed at minimum possible cost without compro-
mising the expected efficiency. The designed compo-
nents were modeled and analyzed using parametric 3-D
design software-Pro Engineer and machined using state-
of-the-art advanced manufacturing equipment which in-
clude, power Hacksaw, lathe, Computer Numerical Con-
trol (CNC) vertical Machining Center and surface grind-
ing machine.
Considering the expected uniform distribution in the
ap pli ed forces on the test specimen [8], a professional En-
gineering (Pro-E) software was used to design and model
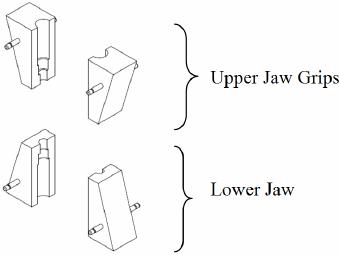
the jaws (upper and lower) as shown in Figure 1. Each
Figure 1. Model of the two pairs of the jaw grip required
for tensile test operation.
jaw is designed to have two stage stoppers on the speci-
men [9]; this is to avoid the likelihood of stress concentra-
tion at the end/edge of the gauge length of the specimen.
The maximum load of the machine used in this investi-
gation is 50 KN. To this effect, a suitable material (Aus-
tenitic Stainless Steel) that could withstand the load re-
quired-maximum of 30 KN to pull conventionally heat-
treated metallic materials to failure was selected, this is
as a result of its high strength, high resistance to oxida-
tion and its availability. The selected material was sub-
sequently cut with the aid of power Hacksaw to a spe-
cific configuration, drilled using drill bits and bored to
conform to the designed profile so as to ensure firm grip
on any specimen machined to its accepted configuration.
2.2. Results and Discussion
The model of the computer aided design of the jaw grips
are presented in the figures below:
Figure 2 shows the intricate parts of the designed jaw
grip. The jaw was designed and produced to have two
stage stopping points (first and second steps), the second
stopper is to further reduce or eliminate the possible
stress concentration at the end of the gauge length that
could have ensued if it is just one. Stress concentration at
a particular point of a material is a disadvantage that
leads to unexpected premature fracture or deformation in
the specimen. In the type of tensile testing machine tar-
geted for this design, the pins are required to hold the
grips at the designated position firmly thus enabling ri-
gidity during operation, for this reason, the pins were
incorporated in the design and developed as shown in
Figure 1 with their corresponding gro ove through which
they are being held firmly to the machine frame. As
shown in Figures 2 and 3(a), two pairs of grip are n eed-
ed to conduct any tensile test. Each of this pair consists
of two grips forming the upper and the lower jaw grips.
The newly produced jaws grips were subjected to test on
a Tensile Testing Machine [as shown in Figure 3(a)]
following the predetermined mounting setup shown in
Figure 3(b) to conduct several tensile tests on a circular
Open Access JMMCE