J. Serv. Sci. & Management. 2008, 1: 77-82
Published Online June 2008 in SciRes (www.SRPublishing.org/journal/jssm)
Empirical Research on Repo Rates Based on Exponen-
tial Smooth Transition Autoregressive Model
Qi-Zhi He
School of Statistics, Anhui University of Finance and Economics, Bengbu 233030, P.R.china
ABSTRACT
In the process of China's marketization of interest rates, researching the characteristics of interest rates has very im-
portant theoretical and practical significance. Based on Chinese interbank repo interest rates, the characteristics of
daily interest rates and monthly interest rates and their spreads have been researched, and unit root tests are paid to
the level, the first difference and the spread of daily interest rates and monthly interest rates based on the traditional
method and the exponential smooth transition autoregressive method (ESTAR) respectively. The results show: Firstly,
as for different term of repo interest rates, the characteristics are different. Secondly, both lists of daily rates and
monthly rates are integrated of order 1. Thirdly, the spread of daily interest rates and monthly interest rates is not sta-
tionary by use of ADF, but stationary by use of ESTAR. Finally, the long-run equilibrium relationship between daily
repo interest rates and monthly repo interest rates is stab le with nonlinear adjustment.
Keywords: Repo interest rates, Unit root, Nonlin ear, Augmented Dickey-Fuller (ADF), Exponential smooth tra nsition
autore gre ss i v e (ESTAR)
1. Introduction
Term structure of interest rates provides a characterization
of interest rates as a function of maturity. It is the bench-
mark of assets pricing, financial product design, risk
management and investment such as discussed in
[1,2,3].Because of its numerous uses, estimation of the
term structure has received considerable attention from
researchers and practitioners, such as Xie Chi and Wu
Xiong-wei (2002), Xie Chi (2004,2005,2006) [7], Zheng
Zhen-long and Lin Hai (2003,2004,2005,2006,2007),
ZHOU Rong-xie and QIU Wan-hua(2004), WANG
Xiao-Fang(2006), Fan Long-zhen(2006), He Qi-zhi
(2007)[4,5], etc..But most of the researches are only about
how to estimate the term structure of interest, and few
involved in the relationship between the different maturi-
ties of interest rates.
The expectation theory regarding the term structure of
interest rates is one of the bases of finance and mac-
roeconomy. According to the expectation theory, the yield
spread between different-term interest rates is stationary,
or different-term interest rates have the cointegration rela-
tionship with cointegrating vector (-1,1). Thus it is helpful
to judge the existence of the expectation theory by
checking the cointegration relationship between differ-
ent-term interest rates. Many documents have studied the
expectation theory by use of the traditional unit root tests
(DF and ADF)and cointegration tests (EG and AEG), such
as Campbell,J.Y. (1987, 1995) ,SHI Min,WANG
Shou-yang(2005)[6], and Wu Dan, Xie Chi(2005)[7],etc..
These traditional tests assume only linear adjustment.
There are, however, economic situations where a
non-linear adjustment process may exist [8]. For example,
policy intervention may take place only when the economy
deviates from equilibrium by a certain margin. The nature
of the policy action may also differ, depending on the di-
rection of that deviation. Another example is that arbitra-
geurs enter the market only if the price deviation of an
asset from its no-arbitrage equilibrium is sufficiently large
to compensate for transaction costs. As to the empirical
research of the expectation hypothesis of the term structure,
for the sake of simplicity, many researches have neglected
the inherent nonlinear adjustment of the term structure of
interest rate. In fact, sometimes only series of moderate
length are available and the number of observations is
small. The small number of observations and the market
friction including transaction costs in financial assets
markets is likely to lead to nonlinear speeds of conver-
gence to equilibrium of rates of return, and often lead to the
nonlinear adjustment of term structure of interest rates.
Recently, some authors have emphasized such nonlinear
features and adjustment of economic variables [9]. Typical
nonlinear time series models which appear useful in prac-
tice concern various forms of regime-switches. Since the
seminal articles of Ter asvirtaa && and Anderson (1992)[11]
and Ter asvirtaa && (1994) [11], smooth transition autore-
gressive (STAR) models have become one of most popular
classes of non-linear models in modern applied economics
[10]. The STAR models have been employed in modeling
the dynamics of various types of economic time series, for

78 Qi-Zhi He
example industrial production in Ter asvirtaa && and
Anderson(1992) [11],unemployment in Skalin and
Ter asvirtaa
&& (2002) [11], interest rates in van Dijk and
Franses (2000) [9], exchange rates in Taylor, Peel, and
Sarno (2001), real interest and exchange rates in George
Kapetanios, etc.(2003)[11], inter alia. Most recently, Maki,
Daiki (2005, 2006) [12, 13] investigated the term structure
of interest rates in Japan using the nonlinear unit root test:
ESTAR. His results provide strong evidence against the
unit root of the yield spread between long-term and
short-term interest rates, compared with standard unit root
tests assuming only linear adjustment.
The purpose of this paper is to investigate the term
structure of interest rates in china using the unit root test in
the exponential nonlinear smooth transition autoregressive
(ESTAR) framework, as proposed by Kapetanios (2003)
[11]. Their ESTAR approach tests for a unit root against a
nonlinear stationary process based on the STAR process.
In that paper they analyzed the implications of the exis-
tence of a particular kind of nonlinear dynamics for unit
root testing procedures, and provided an alternative
framework for a test of the null of a unit root process
against an alternative of a nonlinear exponential smooth
transition autoregressive (ESTAR) process.
The plan of the paper is as follows: section 2 addresses
the expectation theory and the traditional unit root test (DF,
and ADF). Section 3 introduces the nonlinear unit root test
proposed by Kapetanios (2003) [11] and applied by Maki,
Daiki (2005, 2006) [12] [13] in Japan. Section 4 presents
empirical applications in china. Section 5 provides a
summary of the paper, and contains some concluding re-
marks.
2. The Expectation Theory Regarding Term
Structure and the Unit Root Test
2.1. The expectation theory regarding term struc-
ture
The expectation hypothesis expressed by SHI Min,WANG
Shou-yang (2005) [6] is as follows:
1
()( )()
0
1k
nmn
tttim
i
rEr
k
θ
−
+
=
=+
∑ (1)
Where n and m represent respectively the long term and
short term, k equal to [n/m], ()n
t
r is the time t continu-
ously compounded yield to maturity of the n period, ()m
tim
r
+
is the time tim+ continuously compounded yield to
maturity of the m period, Et is the expectation operator
based on available information, and ()n
θ
denotes term
premium.
Both sides of equation (1) subtract()m
t
r:
1
(,)()( )( )( )
0
1
()( )()
01
1()
1
k
nmn mmm
ttt ttimt
i
ki
nmn
ttjm
ij
srr Err
k
Er
k
θθ
−
+
=
−
+
==
=− =−
+=Δ +
∑
∑∑
(2)
Known from equation (2), if ()n
t
r，()m
t
rhave a unit root,
()( )nm
tt
rr− will be a stationary process, or ()n
t
r and ()m
t
r
have the cointegration relationship with cointegrating
vector (-1, 1)’. Thus we can test for cointegration using
unit root tests including the traditional unit root tests (DF
and ADF).
2.2. The traditional unit root tests (DF and ADF)
From theoretical and applied point of view, the traditional
unit root tests (DF) can be represented as follows1:
1ttt
yyu
δ
−
Δ
=+ (3)
11ttt
yyu
β
δ
−
Δ
=+ + (4)
12 1ttt
ytyu
ββ
δ
−
Δ
=+ ++ (5)
Where
δ
, 12
,
β
β
is the parameter,
δ
represents the in-
tercept, {t
y} denote variable list, t denote time or trend
variable, t
u i.i.d. 2
(0, )
σ
.
A null hypothesis with a unit root implies that0
δ
=
.
The choice of formula (3), (4) or (5) is important since the
distribution of the test statistic under the null hypothesis
differs among these three cases.
When the errors in (3), (4) or (5) are serially correlated,
(3), (4) or (5) result in the following regression with
p-order augmentation (ADF):
1
1
m
ttitit
i
y
yyu δα
−−
=
Δ
=+Δ+
∑ (6)
11
1
m
ttitit
i
yy yu βδ α
−−
=
Δ
=++Δ +
∑ (7)
12 1
1
m
ttitit
i
y
ty yu ββ δα
−−
=
Δ
=+++Δ+
∑ (8)
3. The Nonlinear Unit Root Test (ESTAR) [11,
12, 13]
The traditional unit root tests only assume linear adjust-
ment, but the term structure of interest rates often has the
characteristics of inherent nonlinear adjustment because of
market frictions. Thus sometimes, wrong conclusions will
be drawn if using the traditional unit root tests for term
structure. In order to take into account such nonlinear ad-
justment, this paper employs the unit root test in the
1 To know whether the DF model should include the intercept, the
intercept and the time trend or neither in the test regression, see [14].

Empirical Research on Repo Rates Based on Exponential 79
Smooth Transition Autoregressive Model
nonlinear exponential STAR framework developed by
Kapetanios, G., Y. Shin, and A. Snell (2003) [11].
11
(;),1, ,
tt ttdt
y
yy ytT βγ θε
−− −
=+Θ +=L (9)
where t
ε
i.i.d.(0, 2
σ
), and
β
and
γ
are unknown pa-
rameters. The ESTAR model defines different regimes in
terms of small and large absolute deviations of the transi-
tion variable values from the threshold parameter value.
Hence, this model has a ‘sandwich’ structure with the outer
regime that is contrasted with the inner regime (Boriss
Siliverstovs, 2005) [10]. The transition function of the
exponential form is as follows:
2
( ;)1exp()
td
td
yy θθ
−
−
Θ=−− (10)
where it is assumed that0
θ
≥，and 1d≥ is the delay
parameter. The exponential transition function is bounded
between zero and 1;..ie Θ：R →[0, 1] has the properties:
(0)0; lim()1
xx →±∞
Θ= Θ=
and is symmetrically U-shaped around zero.
Substituting (6) into (5) Kapetanios, G., Y. Shin, and A.
Snell [11] obtain an exponential STAR (ESTAR) model,
2
11
[1 exp()]
tt ttdt
yy yy
βγ
θε
−− −
=+ −− + (11)
Both sides of equation (11) subtract1t
y
−:
2
11
[1 exp()]
tt ttdt
yy yy
φγ
θε
−− −
Δ=+− −+ (12)
where 1
φ
β =−.
The application that motivates the model is that of Sercu
et al. (1995) [17] and of Michaelet al. (1997) [1].These
authors analyse nonlinearities in the PPP relationship.
They adopt a null of a unit root for real exchange rates and
have an alternative hypothesis of stationarity, namely the
long run PPP. Their theory suggests that the larger the
deviation from PPP, the stronger the tendency to move
back to equilibrium. In the context of the model, this would
imply that while 0
ϕ
≥ is possible, we must have0
γ
<
and 0
ϕ
γ +<for the process to be globally stationary.
They claim that the ADF test may lack power against such
stationary alternatives and one of the contributions of this
paper is to provide an alternative test designed to have a
power against such an ESTAR processes.
More formally, geometric ergodicity and the associated
asymptotic stationarity can be established by the drift
condition of Tweedie (1975). A variant of the condition
states that an irreducible aperiodic Markov chain t
y
is
geometrically ergodic if there exists constants
1
δ
<,B,L <∞ and a small set C such that
1
[/],,
tt
EyyyyL y c δ
−=<+∀∉
1
[/], ,
tt
EyyyBy c
−
=
≤∀∈
The concept of the small set is the equivalent of a dis-
crete Markov chain state in a continuous context. For more
details see Tweedie (1975) [10], Balke and Fomby (1997)
[20] and Kapetanios (1999) [11].
Following the practice in the literature (e.g. Balke and
Fomby, (1997) [20], in the context of TAR models and
Michael et al., 1997 in the context of ESTAR models),
Kapetanios (2003) [11] and Daiki Maki (2005, 2006) [12]
[13] impose 0
ϕ
=
in [12], implying that t
y
follows a unit
root process in the middle regime. Kapetanios (2003) [11]
and Daiki Maki (2005,2006) [12] [13] consider a null
hypothesis that is a special case of a linear unit root which
in terms of the above model implies that 0
ϕ
=
and
0
θ
=
.Under the alternative hypothesis (0
ϕ
= but0
θ
>),
then t
yfollows a nonlinear but globally stationary process
provided that −2 <
γ
< 0, which we assume holds. In
practice, there is likely to be little theoretical or prior
guidance as to the value of the delay parameter d. We
would suggest that d be chosen to maximise goodness of
fit over d = {1, 2,max
,dL}.In what follows, to clarify ideas
and in keeping with empirical practice to date (as in for
example Michael et al.), Kapetanios (2003) [11] and Daiki
Maki (2005, 2006) [12] [13] set d = 1.
Imposing φ = 0 and d = 1 gives their specific ESTAR
model (12) as
2
11
[1 exp()],
ttt t
yyy u γθ
−−
Δ
=−−+ (13)
Hence we test
,0:
0
=
θ
H (14)
Against the alternative
0:
1>
θ
H. (15)
Obviously, testing the null hypothesis (14) directly is
not feasible, since γ is not identified under the null. If we
compute a first-order Talyor series approximation to the
ESTAR model under the null we get the auxiliary regres-
sion
1
3,
t
t
yyerror δ
−
Δ= + (16)
This suggests that we could obtain the t-statistic for δ =
0 against δ < 0 as
^^
/..(),
NL
tse
δ
δ = (17)
Where
^
δ
is the OLS estimate of
δ
and ^
..( )se
δ
is the
standard error of ^
δ
. Their test is motivated by the fact that
the auxiliary regression is testing the significance of the
score vector from the quasi-likelihood function of the
ESTAR model, evaluated at θ = 0. Unlike the case of

80 Qi-Zhi He
testing linearity against nonlinearity for the stationary
process, the NL t test does not have an asymptotic standard
normal distribution.
When the errors in (13) and (16) are serially correlated,
(13) and (16) result in the following regression with
p-order augmentation:
2
11
1
[1 exp()],
p
tjtjt tt
j
y
yy yu ργ θ
−− −
=
Δ=Δ +−−+
∑(18)
1
3
1
t
p
tjtj
j
y
yy error ρδ
−
−
=
Δ=Δ ++
∑ (19)
We can test the unit root via (18) instead of (13) and (19)
instead of (16).
4. Data and Empirical Results
In this paper, we employ the monthly interest rates of
treasury bonds repurchase trading of national interbank
market as long-term interest rates, expressed as R1M, daily
interest rates as short-term interest rates, expressed as R1.
It is because of the following reason to choose repurchase
interest rate data [15]. First, repurchase interest rate of in-
terbank market is the main variety of interest rate in
China’s money market. In regards to the trading structure
of money market, the amount of repurchase trade has a
larger proportion in total transaction amount than that of
trade in the Offered Market and Bond Market. Second,
repurchase interest rate of interbank market is not only the
tool of controlling and adjusting economics to every
country’s central bank, but also one of important standards
to decide the loan and deposit rate to commercial banks.
The daily data obtained from www.ChinaMoney.com.cn
consists of 572 periods between 2004:8-2006:1. Fig. 1
provides the change situations of R1, R1M and profit
spread (R1M-R1). According to Fig. 1 and footnote○
1, it
can be confirmed: Empirical tests to R1 and R1M should
include the intercept without the time trend, and empirical
test to profit spread=R1M-R1 should not include the con-
stant or the time trend. Tab.1 gives the simple statistics
characteristics of them.
4.1. Tests for nonlinear of interest rates
For simplicity, we estimate the nonlinear effect
θ
im-
posing 1
γ
=− on equation (12), similar to Kapet-
anios(2003) [11]、Daiki Maki (2005,2006) [12] [13]. From
Table 2, we can know that R1M does not have
θ
at a
significant level, and R1 and the yield spread has a sig-
nificant
θ
. This estimation shows that R1M do not have
nonlinear adjustment, but R1 and the yield spread have
nonlinear adjustment.
As for the criteria to determine the appropriate length of
the distributed lag, we use the Akaike info criterion (AIC),
Schwarz criterion (SC) and t-sig. As to the Akaike info
criterion (AIC) and Schwarz criterion (SC), we select the
model with the smallest information criterion. As to t-ing,
we set the maximum lag=12. t-ing selects the lag order k
via top-down testing. To begin with, we estimate the
equation with the maximum lag (here, the maximum lag
kmax=12). We use the lag order if the t-statistic of the pa-
rameter of the maximum lag is significant. If the t-statistic
is not significant, we estimate the equation with the
1
max
−
=
klag . That is, when the t-statistic of the pa-
rameter of the qklag
−
=
max is significant at a conven-
tional level, we employ the lag order [13].
4.2. Unit root tests
ADF and ESTAR denote the unit root tests by Dickey and
Fuller (1979) [17] and Kapetanios et al. (2003) [11], re-
spectively. As shown in Table 3, all of the tests do not re-
ject the unit root of interest rates at the level, but reject the
unit root of interest rates at first-order difference. There-
fore, the results show that interest rates is integrated of
order 1, namely I (1) process.
-0.01
0.00
0.01
0.02
0.03
0.04
R1 R1M SPREAD
2004-8-2 2005-6-7 2006-4-25 2006-1-12
Figure 1. Interest rates of repurchase trading
4.3. Cointegration tests
According to the expectation theory, if different term in-
terest rates are all integrated of order 1 :I(1),the yield
spread between different term interest rates are stationary,
or different term interest rates have the cointegration rela-
tionship with cointegrating vector (-1,1)’. Table 4 shows
the results of the unit root tests of the yield spread. The
results of ADF test fail to reject a unit root at a 1% sig-
nificance level according to either criterion, even at a 5%
according to AIC and t-ing criterions. In contrast, the test
by Kapetanios et al. (2003) [11] provides strong evidence
against the unit root of the yield spread at a 1% signifi-
cance level, even when different lag criterions are em-
ployed. This finding asserts that the long-run equilibrium
relationship between different term interest rates is stable
with nonlinear adjustment.
5. Conclusion
The paper has researched the characteristics of Chinese
interbank repo interest rates, and the relation between
Chinese interbank repo interest rates with different ma-
turities. The traditional unit root test ADF and the unit root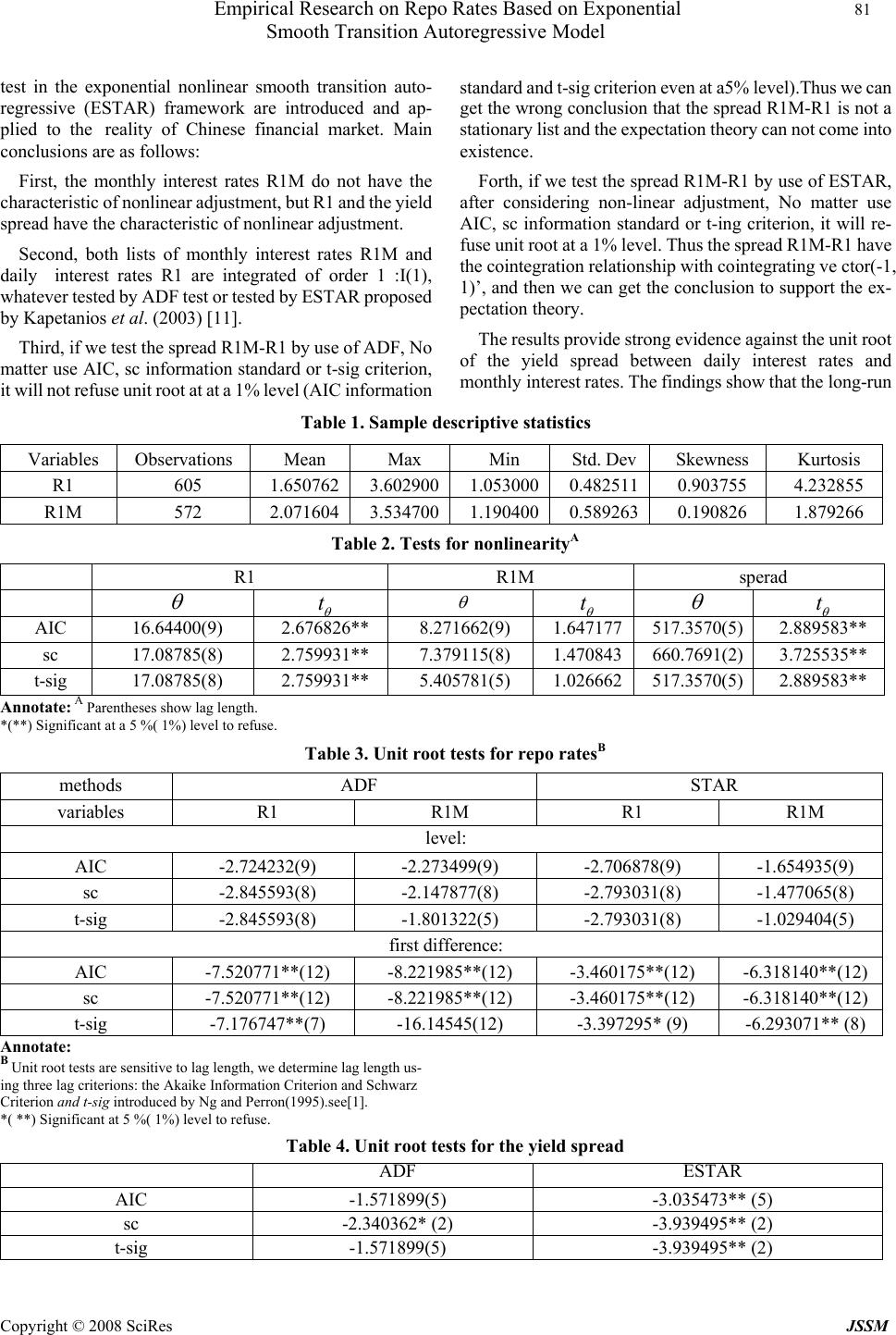

Empirical Research on Repo Rates Based on Exponential 81
Smooth Transition Autoregressive Model
test in the exponential nonlinear smooth transition auto-
regressive (ESTAR) framework are introduced and ap-
plied to the reality of Chinese financial market. Main
conclusions are as follows:
First, the monthly interest rates R1M do not have the
characteristic of nonlinear adjustment, but R1 and the yield
spread have the characteristic of nonlinear adjustment.
Second, both lists of monthly interest rates R1M and
daily interest rates R1 are integrated of order 1 :I(1),
whatever tested by ADF test or tested by ESTAR proposed
by Kapetanios et al. (2003) [11].
Third, if we test the spread R1M-R1 by use of ADF, No
matter use AIC, sc information standard or t-sig criterion,
it will not refuse unit root at at a 1% level (AIC information
standard and t-sig criterion even at a5% level).Thus we can
get the wrong conclusion that the spread R1M-R1 is not a
stationary list and the expectation theory can not come into
existence.
Forth, if we test the spread R1M-R1 by use of ESTAR,
after considering non-linear adjustment, No matter use
AIC, sc information standard or t-ing criterion, it will re-
fuse unit root at a 1% level. Thus the spread R1M-R1 have
the cointegration relationship with cointegrating ve ctor(-1,
1)’, and then we can get the conclusion to support the ex-
pectation theory.
The results provide strong evidence against the unit root
of the yield spread between daily interest rates and
monthly interest rates. The findings show that the long-run
Table 1. Sample descriptive statistics
Variables Observations Mean Max Min Std. DevSkewness Kurtosis
R1 605 1.650762 3.6029001.0530000.4825110.903755 4.232855
R1M 572 2.071604 3.5347001.1904000.5892630.190826 1.879266
Table 2. Tests for nonlinearityA
R1 R1M sperad
θ
t
θ
θ
t
θ
θ
t
θ
AIC 16.64400(9) 2.676826** 8.271662(9) 1.647177517.3570(5) 2.889583**
sc 17.08785(8) 2.759931** 7.379115(8) 1.470843660.7691(2) 3.725535**
t-sig 17.08785(8) 2.759931** 5.405781(5) 1.026662517.3570(5) 2.889583**
Annotate: A Parentheses show lag length.
*(**) Significant at a 5 %( 1%) level to refuse.
Table 3. Unit root tests for repo ratesB
methods ADF STAR
variables R1 R1M R1 R1M
level:
AIC -2.724232(9) -2.273499(9) -2.706878(9) -1.654935(9)
sc -2.845593(8) -2.147877(8) -2.793031(8) -1.477065(8)
t-sig -2.845593(8) -1.801322(5) -2.793031(8) -1.029404(5)
first difference:
AIC -7.520771**(12) -8.221985**(12) -3.460175**(12) -6.318140**(12)
sc -7.520771**(12) -8.221985**(12) -3.460175**(12) -6.318140**(12)
t-sig -7.176747**(7) -16.14545(12) -3.397295* (9) -6.293071** (8)
Annotate:
B Unit root tests are sensitive to lag length, we determine lag length us-
ing three lag criterions: the Akaike Information Criterion and Schwarz
Criterion and t-sig introduced by Ng and Perron(1995).see[1].
*( **) Significant at 5 %( 1%) level to refuse.
Table 4. Unit root tests for the yield spread
ADFESTA
R
AIC -1.571899(5) -3.035473** (5)
sc -2.340362* (2) -3.939495** (2)
t-sig -1.571899(5) -3.939495** (2)

82 Qi-Zhi He
Annotate :*(**) Significant at a 5 %( 1%) level to refuse.
equilibrium relationship between different term interest
rates is stable with nonlinear adjustment. Moreover, the
applied cointegration tests with non-linear adjustment
have multidimensional generalizations, and can be used
to many other variables. For example, the number of
observations of most macroeconomic variables, meas-
uring the business cycle, is small, because those vari-
ables are sampled only quarterly or annually. Thus,
there are also nonlinear properties in those macroeco-
nomic variables with a small number of observations.
We can also apply the ESTAR model to research the
relation between the variables.
6. Acknowledgements
The achievements of young fund project of humanities and
social science of education ministry（No. 07JC790028）;
The achievements of young fund project of Anhui Prov-
ince Office of Education(2007jql082); The achievements
of project of humanities and social science of Anhui
Province Office of Education(2007sk120).
REFERENCES
[1]. Martellini，L. and Priaulet，P.， Fixed-income
Securities， John Wiley& Sons,Ltd. ，Chichester，
2001.
[2]. ZHU Shi-wu, CHEN Jian-heng, “Empirical
Research of the Term Structure of Interest Rates of
Stock Exchange”, Journal of Financial Research,
2003, Vol.280(10), pp.63-73.
[3]. HE Qi-zhi, HE Jian-min, “Real Option Pricing
Method for R&D Investment under Changing
Risk-free Rate and Discount Rate”. Journal of
Southeast University, 2008, Vol,2.
[4]. HE Qi-zhi, “A New Method for Heteroscedasticity
of Term Structure Model Using Exponential
Splines”,IEEE. International Conference on
Communications, Services, Knowledge and
Engineering, Shanghai, 2007, pp.4068-4071.
[5]. He Qi-zhi, “Empirical Tests for Term Structure of
Interest Rates Based on Nonlinear Adjustment , ”
IEEE. International Conference on Wireless
Communications, Networking and Mobile
Computing, Shanghai, 2007, pp.4096-4099.
[6]. SHI Min, WANG Shou- yang,etc, “Empirical
analysis on term structure of China interbank offered
rates”, Journal Of Management Sciences in
China,2005,Vol. 5, pp.43-49.
[7]. Wu Dan, Xie Chi, “Test of the Expectations Theory
of the Term Structure of Treasury Market Among
China Banks”,Chinese Journal Of Management,
2005，Vol.9(5), pp.536-541.
[8]. Ying Liu, “Modeling Mortgage Rate Changes with a
Smooth Transition Error-Correction Model”.
Working paper, 2001.
[9]. Dick van Dijk, Philip Hans Frances, and Lucas，
“Testing for Smooth Transition Nonlinearity in the
Presence of Outliers”, working paper.
[10]. Siliverstovs, Boriss, “The Bi−parameter Smooth
Transition Autoregressive model”, Economics
Bulletin, 2005, Vol.3, No. 22, pp. 1−11
[11]. Kapetanios, G., Y. Shin, and A. Snell, “Testing for a
unit root in the nonlinear STAR framework”,
Journal of Econometrics, 2003,Vol. 112,
pp.359-379.
[12]. Daiki,Maki，“ Non-linear adjustment in the term
structure of interest rates: a cointegration analysis in
the non-linear STAR framework”, Applied Financial
Economics,2006, Vol.11, pp.1301-1307.
[13]. Daiki,Maki, “ The term structure of interest rates
with nonlinear adjustment: Evidence from a unit root
test in the nonlinear STAR framework”, Economics
bulletin,2005, Vol.5, pp.1-7.
[14]. ZOU Ping, Financial Econometrics, Shanghai
University of Finance & economics Press, Shaihai,
2005, 8.
[15]. Wen Bin, “An Empirical Study on the Choice of
Benchmark Interest Rate after Interest Rates
Liberalization in China”, Studies of International
Finance, 2004, Vol. 11, pp.54-60.
[16]. Duffee, G., “Term premia and interest rate forecasts
in affine models”, Journal of Finance , 2002 ,
Vol.57, pp.405-443.
[17]. Gerlach S,Smets F, “The term structure of Eurorates:
Some evidence in support of the expectations
hypothesis”,Journal of International Money and
Finance, 1997, Vol. 16(2), pp.305-321.
[18]. Hamilton J., Kim D. H, “A Reexamination of the
Predictability of Economic Activity Using the Yield
Spread”, Journal of Money, Credit, and
Banking,2002, Vol. 34(2), pp.340-344.
[19]. William Poole, “Understanding the Term Structure
of Interest Rates”, Federal reserve bank of st.louis
review, 2005, Vol. 9, pp.589-595.
[20]. Caner, M., Hansen, B.E., “Threshold autoregression
with a near unit root”. Econometrica, 2001, Vol, 69,
pp.1555-1596.
AUTHOR’S BIOGRAPHY
He Qi zhi (1974—), male, Lecturer, graduate. The paper is an extended version of the paper “Empirical Tests for Term
Structure of Interest Rates Based on Nonlinear Adjustment” accepted by Management Track within WiCOM: Engi-
neering, Services and Knowledge Management (EMS 2007). Email: