Technology and Investment
Vol.1 No.3(2010), Article ID:2493,10 pages DOI:10.4236/ti.2010.13022
Coordination of a Supply Chain with Advertising Investment and Allowing the Second Ordering
School of Management Science and Engineering, Nanjing University, Nanjing, China
E-mail: xiaotj@nju.edu.cn, yostyan@163.com
Received March 30, 2010; revised June 25, 2010; accepted June 27, 2010
Keywords: Advertising Investment, Supply Chain Management, Markdown Money-Cooperative Advertising Contract, Reorder, Game Theory
Abstract
This paper develops a game theoretic model of a one-manufacturer and one-retailer supply chain allowing the second ordering to investigate how to coordinate the order quantity and advertising investment via a markdown money-cooperative advertising contract. We focus on the effects of allowing the second ordering on equilibrium outcome and coordination mechanism. We find: the relationship between the unit wholesale prices and the chargeback rate depends on whether allowing the second ordering; the coordination mechanism is robust to demand uncertainty; the unit wholesale price in period 2 increases with the unit production cost in period 2, the unit delayed delivery cost and unit salvage value if and only if the chargeback rate is sufficiently small while that in period 1 is independent of them. In addition, we study the Pareto condition of coordination mechanism under which both manufacturer and retailer are better off using the coordination mechanism and find that the unit production costs in different periods may have contrary effects on the bounds of Pareto range.
1.Introduction
In business world, advertising is an important tool of sales promotion for retailer/seller, which raises the supply chain’s profitability. However, retailer only reaps a part of the benefit of advertising, which implies that the retailer may invest less in advertising than that of the centralized supply chain. For seasonal products, market demand is highly uncertain, which discourages the purchase behavior of the retailer. To stimulate the retailer’s order, the manufacturer may share the risk of demand uncertainty with the retailer, say, offering returns policy and markdown money policy. This paper focuses on how to coordinate the supply chain via a markdown moneycooperative advertising contract.
The members of supply chain usually cannot accurately make decisions under demand uncertainty, especially, order quantity and investment decisions. Hence, the retailer often orders a lower quantity to reduce operation risk. In order to satisfy the market demand, the manufacturer may allow the second ordering. Specifically, at the end of selling season, the retailer is allowed to make the second ordering for unsatisfied demand. They use this policy to reduce the loss incurred by demand uncertainty. The reorder policy becomes very important in business operation management. Lots of companies allow the retailers to reorder. For example, according to[1], Sport Obemeyer LTD is a company that sells fashion skiwear. If there were unsatisfied demand, Obemeyer would allow retailers to make the second ordering to replenish for popular items during the selling season. In fashion industry, the second ordering is often adopted, say Zara, Lilanz. This also happened in electronics industry, say, Irico group electronics company limited.
In this paper, we develop a game theoretic model of a supply chain consisting of one manufacturer and one retailer under demand uncertainty to investigate how to coordinate the order quantity and advertising investment decisions, and explore the effects of allowing the second ordering on the coordination mechanism. The manufacturer offers a markdown money-cooperative advertising contract to coordinate the supply chain. We assume that the manufacturer allows the retailer to make the second ordering at the end of selling season. The manufacturer uses a fast production mode to satisfy the second ordering, which incurs a higher unit production cost. We focus on the effect of some factors related to the second ordering on the coordination mechanism. We find that the relationship between the unit wholesale price and chargeback rate differs from that without the second ordering. In addition, we study Pareto condition of the coordination mechanism.
The remainder of this paper is organized as follows. Section 2 reviews related literature. Section 3 introduces the basic model. Section 4 investigates the coordination mechanism of the supply chain with general distribution function. Section 5 analyzes Pareto conditions of the coordination mechanism under uniform distribution. Finally, we summarize this paper and point out some directions for future research in Section 6.
2. Literature Review
This paper is closely related to cooperative advertising, coordination management and reorder policy.
It is well known that advertising can stimulate the market demand while also incurs an advertising cost. Thus, the seller must make a trade-off between the benefit and the cost when it determines advertising investment. Jørgensen et al. [2] pointed out that cooperative advertising is a popular incentive mechanism for advertising investment. Huang and Li [3] introduced a cooperative advertising model of a supply chain consisting of one manufacturer and one retailer, where the manufacturer invests in national advertising and pays the retailer a subsidy to stimulate the local advertising investment of the retailer. Nagler [4] offered an exploratory empirical investigation of the determinants of cooperative advertising participation rates and examined the relationship between participation rates and national advertising expenditures by brand. In this paper, we consider a cooperative advertising contract between one manufacturer and one retailer and investigate how to coordinate advertising investment.
About supply chain coordination contract, it has been widely studied in the literature, such as returns/buyback policy [5], markdown money [6,7], revenue-sharing contract [8], and option contract [9]. Donohue [10] investigated how to coordinate supply chain with forecast updating and two production modes. Zhang et al. [11] examined coordination of an assemble-to-order system involving a short-life-cycle product. Hsieh et al. [12] examined coordinated decisions in a decentralized supply chain faces random demand of a short-life-cycle product. Returns policy/buyback contract is a good coordination mechanism for the retailer to order more, where the retailer can return some or all unsold items at the end of selling season to the manufacturer and receives a full or partial refund. Kandel [13] investigated the allocation of responsibility for unsold items and concluded that monopolistic manufacturer prefers a buyback contract, while monopolistic retailer prefers a no-buyback policy. He et al. [14] developed a model to determine the optimal returns policy for single-period products in the presence of risk preferences and considered a markdown money contract stimulating order quantity. In a sense, markdown money contract is similar to buyback contract. Their difference lies in who disposes the leftovers to obtain the salvage value. Nair and Closs [15] evaluated the implications of coordinating price markdown policy with supply chain policies of inventory replenishment, and transportation expediting on retail performance of a short lifecycle product. Wang and Webster [7] pointed out that markdown money is frequently used between manufacturers and retailers selling perishable goods. In this paper, we combine markdown money contract with cooperative advertising contract to coordinate the supply chain.
There are many publications has discussed demand uncertainty [16-18]. Under demand uncertainty, there may be unsatisfied demand at the end of selling season. Some publications assumed that the unsatisfied demand is lost [18,19]. However, a few publications assumed that the seller reorders to satisfy the unsatisfied demand, say [20]. We consider the case where the retailer reorders to satisfy the unsatisfied demand at the end of selling season. Because of the delayed delivery, there is penalty cost for all unsatisfied demand. The reorder policy research mainly focused on two issues: reorder time and the second ordering. Most of the literature about reorder focused on reorder time. For example, Chen [21] compared the installation stock policy with the echelon stock policy to analyze the optimal reorder points. Seo et al. [22] defined the order risk policy to decide reorder time to develop the optimal reorder policy for a distribution system with one-warehouse and multiple retailers. Dogru et al. [23] used echelon stock newsvendor equations to optimize the reorder policy in an N-echelon stochastic serial inventory system with a given fixed batch size and linear penalty costs. Leng and Parlar [24] developed a simple profit-sharing contract to achieve supply chain coordination where the retailer manages the inventory system using reorder policy. A few publications only allowed the second ordering at the end of selling season and investigated the effect of allowing the second ordering. For example, Donohue [10] examined the problem of developing supply contracts and production decisions of high fashion, seasonal products operating in a two-mode production environment, and the second ordering was expensive but offered quick turnaround. Weng [20] developed a generalized newsvendor model to analyze the coordinated quantity decisions between the manufacturer and the buyer where allows the second ordering at the end of the period if the demand exceeds stock on hand. Seo [25] extended the order risk policy to general multi-echelon systems, and assumed that excessive customer demands at retailers are fully backordered and incur a linear penalty cost. We assume that the retailer makes the second ordering at the end of selling season and the second order quantity is equal to the quantity of unsatisfied demands, and focus on the effect of allowing the second ordering on the coordination mechanism. The unit production cost in the first setup often is lower than that in the second setup because the former has a longer delivery time. We incorporate this characteristic into model and investigate its effect on the coordination mechanism.
This paper is closely related to [26] that considered how to coordinate the order quantity and advertising investment decisions in a single period model with single production mode. However, we assume that the manufacturer has two production modes and explore how allowing the second ordering influences the equilibrium outcome and coordination mechanism. In addition, we consider how some factors influence the Pareto condition of coordination mechanism. We try to find the new results and managerial insights relative to [26]. In fact, we find some contrary results, for example, the relationship between the unit wholesale prices and chargeback rate depends on whether allowing the second ordering or not. We will point the main difference between them.
This paper complements the literature by investigating coordination of a two-stage supply chain allowing the second ordering to satisfy the unsatisfied demand at the end of selling season via a markdown money-cooperative advertising mechanism. Especially, we focus on the effects of allowing the second ordering on the coordination mechanism. In addition, we study Pareto condition of coordination mechanism when the random demand is uniformly distributed.
3. The Basic Model
We consider a supply chain consisting of one manufacturer and one retailer. The manufacturer produces a seasonal product and sells it through the retailer who carries out (local) advertising investment to stimulate market demand, where the second ordering is allowed. Owing to the market demand’s uncertainty, there may be some unsatisfied demands at the end of selling season. Thus, at the end of selling season, to set up a good reputation and obtain a higher profit, the retailer must reorder to satisfy all of unsatisfied demands, i.e., this paper allows backorder but shortage will incur a loss of goodwill. The unsatisfied customer demands incur a delayed delivery cost. We assume that the manufacturer has enough capacity to satisfy the retailer’s ordering within a given lead-time and only the second ordering is allowed at the end of selling season due to a long lead-time. The two players independently maximize their own expected profits.
Similar to [19], we assume that the retail price is exogenously given. Owing to the fact that there exists a long delivery lead-time and a short selling season, the manufacturer only allows the retailer to order two times, one occurring before the selling season, the other occurring at the end of selling season. In response to the retailer’s orders, the manufacturer should produce items over two periods. In the first period, the production mode is relatively cheap but needs a long lead-time. And in the second period, the manufacturer uses a faster but typically more expensive production mode. Similar to [10], we use two different production costs to express two different production modes.
The event sequence of this game is as follows:
1) the manufacturer determines the unit wholesale prices, cooperative advertising subsidy rate and chargeback rate;
2) the retailer decides the advertising investment level and the first order quantity;
3) if there are unsatisfied demands at the end of selling season, the retailer makes the second ordering to satisfy the market demand.
We have following notation:
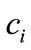 the unit production cost of the manufacturer in period
the unit production cost of the manufacturer in period 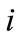 (
(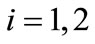 ),
),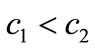 ;
;
 the unit wholesale price of the manufacturer in period
the unit wholesale price of the manufacturer in period 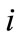 (
( ),
), ;
;
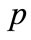 the unit retail price,
the unit retail price,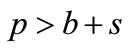 ;
;
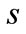 the salvage value per unit unsold item for the retailer,
the salvage value per unit unsold item for the retailer,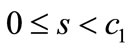 ;
;
 the first order quantity of the retailer;
the first order quantity of the retailer;
 the delayed delivery cost rate for per unit unsatisfied product,
the delayed delivery cost rate for per unit unsatisfied product, ;
;
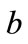 the chargeback rate per unit unsold product,
the chargeback rate per unit unsold product,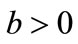 ;
;
 the advertising investment per unit expected demand for the retailer, referring to as advertising level,
the advertising investment per unit expected demand for the retailer, referring to as advertising level,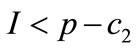 ;
;
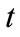 the fraction of advertising expenditure shared by the manufacturer,
the fraction of advertising expenditure shared by the manufacturer,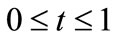 ;
;
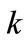 scaling constant for deterministic demand part,
scaling constant for deterministic demand part,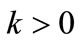 ;
;
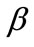 the advertising elasticity of the demand,
the advertising elasticity of the demand,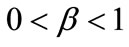 ;
;
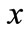 the stochastic demand for the retailer.
the stochastic demand for the retailer.
Similar to [26,27], we assume that the retailer faces a random demand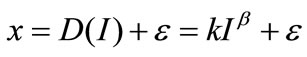 , where
, where  is distributed over
is distributed over  with a density function of
with a density function of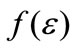 , a cumulative distribution function of
, a cumulative distribution function of 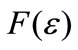 and a mean of
and a mean of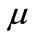 ,
, . Furthermore, the total advertising investment is
. Furthermore, the total advertising investment is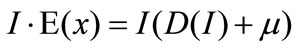 .
.
Since the market demand is uncertain, it is necessary to divide the profit function of the retailer into two cases, 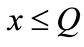 and
and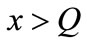 . At the end of selling season, if
. At the end of selling season, if , the unsold items are disposed in the secondary market by the retailer for a unit salvage value. Further, the retailer’s profit function is
, the unsold items are disposed in the secondary market by the retailer for a unit salvage value. Further, the retailer’s profit function is
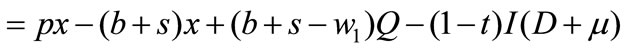
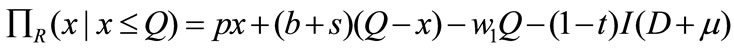
In the first line, the first term represents the selling revenue; the second term represents the total revenue of the leftovers from salvage value and chargeback money; the third term is the purchase cost; and the fourth term represents the advertising investment cost bear by the retailer.
If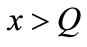 , the retailer makes the second ordering to satisfy all the unsatisfied demand. Similar to [22], unsatisfied demand incurs a shortage cost. In this paper, the retailer makes the second ordering to satisfy those unsatisfied demands. The customers at last receive those items a few days later, which incurs a unit delayed delivery cost
, the retailer makes the second ordering to satisfy all the unsatisfied demand. Similar to [22], unsatisfied demand incurs a shortage cost. In this paper, the retailer makes the second ordering to satisfy those unsatisfied demands. The customers at last receive those items a few days later, which incurs a unit delayed delivery cost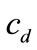 . And the retailer’s profit function is
. And the retailer’s profit function is
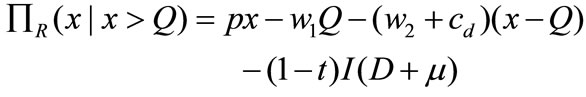
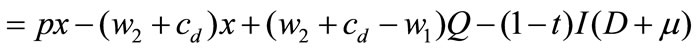
In the first line, the third term represents the sum of the reordering purchase cost and the delayed delivery cost.
Furthermore, the expected profit of the retailer is
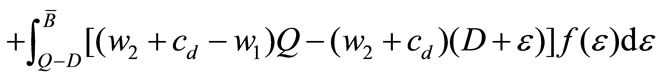


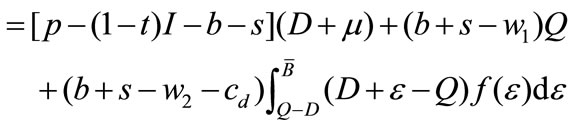 (1)
(1)
In (1), the term  represents the expected shortage quantity.
represents the expected shortage quantity.
If , the profit function of the manufacturer is
, the profit function of the manufacturer is
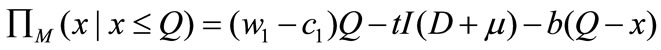
The first term represents the gross profit; the second term represents the advertising cost bear by the manufacturer; and the last term represents the chargeback cost for the leftovers. If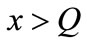 , the manufacturer setups the second production to satisfy the second ordering, and the manufacturer’s profit function is
, the manufacturer setups the second production to satisfy the second ordering, and the manufacturer’s profit function is
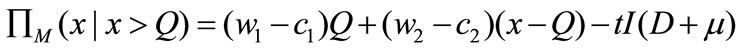 .
.
The second term represents the gross profit for the reorder quantity of the retailer. Furthermore, the expected profit of the manufacturer is

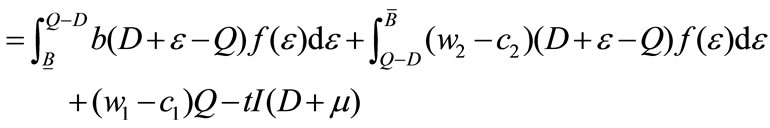
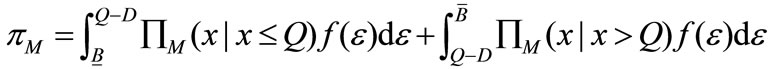 (2)
(2)
The total expected profit of supply chain is the sum of the expected profit functions of the retailer and the manufacturer. Thus, the total expected profit of supply chain is
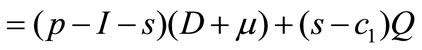
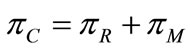
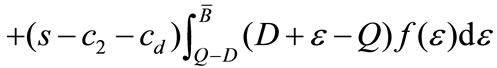 (3)
(3)
4. Coordination Mechanism
It is well known that the decentralized supply chain has a lower profitability than the centralized supply chain at the absence of supply chain competition. That is, coordinating the behavior of the member firms can improve the performance of supply chain. In order to coordinate the supply chain, the manufacturer offers a markdown money-cooperative advertising (MMCA) mechanism  to induce the retailer to replicate the optimal advertising level and order quantity of the centralized supply chain. When the supply chain is coordinated, the supply chain achieves the profit of the centralized system.
to induce the retailer to replicate the optimal advertising level and order quantity of the centralized supply chain. When the supply chain is coordinated, the supply chain achieves the profit of the centralized system.
4.1. Optimal Decisions in the Centralized Setting
To provide a benchmark, we first consider a centralized system where the central decision maker determines all decisions (advertising level and quantity) to maximize the channel profit .
.
From (3), we derive the following.
Proposition 1. In the centralized setting, the optimal solution of the channel profit satisfies the first-order conditions
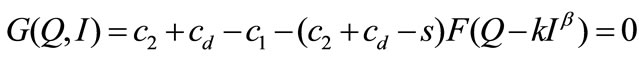 (for
(for )
)
 (for
(for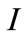 ).
).
Proposition 1 implies that the optimal advertising level is independent of the unit salvage value 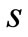 and the unit production cost
and the unit production cost 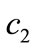 while the quantity depends on them. That is, when they change, the central decision-maker would like to adjust quantity to react to their effects. Let the optimal quantity and advertising level of the supply chain be
while the quantity depends on them. That is, when they change, the central decision-maker would like to adjust quantity to react to their effects. Let the optimal quantity and advertising level of the supply chain be 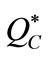 and
and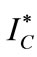 . The effects of
. The effects of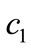 ,
, 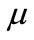 and
and 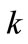 on
on 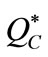 and
and 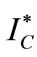 are similar to those in [26], omitting them. From Proposition 1, we find that
are similar to those in [26], omitting them. From Proposition 1, we find that 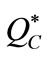 is an increasing function of
is an increasing function of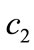 ,
, 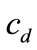 and
and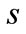 . Specifically, when the unit production cost
. Specifically, when the unit production cost  or the unit delayed delivery cost
or the unit delayed delivery cost  increases, the central decision maker should raise the production quantity in period 1 to reduce the cost for the shortage product. When the unit salvage value
increases, the central decision maker should raise the production quantity in period 1 to reduce the cost for the shortage product. When the unit salvage value 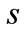 increases, the central decision maker raises the production quantity in period 1 due to a lower loss for the leftovers.
increases, the central decision maker raises the production quantity in period 1 due to a lower loss for the leftovers.
4.2. Coordination Mechanism
Now, we investigate how to coordinate the decentralized supply chain in which the manufacturer and the retailer maximize their own profits independently.
Similar to Proposition 1, we derive the following.
Proposition 2. The optimal decisions of the retailer satisfy the first-order conditions
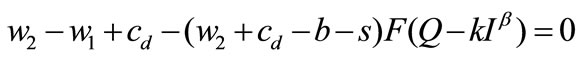 (for
(for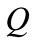 ) (4)
) (4)
 (for
(for ) (5)
) (5)
Proposition 2 implies that, a higher fraction (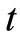 ) of advertising expenditure shared by the manufacturer induces a higher advertising level, which in turn induces a higher order quantity in period 1.
) of advertising expenditure shared by the manufacturer induces a higher advertising level, which in turn induces a higher order quantity in period 1.
When the supply chain is coordinated, the MMCA mechanism should induce the retailer to order quantity 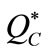 and invest
and invest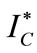 . Proposition 3 summarizes the MMCA mechanism.
. Proposition 3 summarizes the MMCA mechanism.
Proposition 3. The MMCA mechanism  with
with 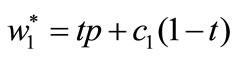 and
and

can coordinate the supply chain.
Proposition 3 implies that the MMCA coordination mechanism is robust to demand uncertainty, i.e., independent of the distribution of demand uncertainty, which differs from that in [26]. When the fraction 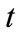 increases, the manufacturer will raise the unit wholesale prices in two periods to offset a part of the increased advertising cost. It is worthy to note that a higher chargeback rate is along with a lower unit wholesale price in period 2 and the unit wholesale price in period 1 is independent of the chargeback rate, which differs from that without the second ordering, see [19,26]. That is, if the manufacturer decreases the chargeback rate to reduce the excessive ordering, it should raise the unit wholesale price in period 2 to stimulate the order quantity in period 1. The unit wholesale price in period 1 is independent of the unit production cost
increases, the manufacturer will raise the unit wholesale prices in two periods to offset a part of the increased advertising cost. It is worthy to note that a higher chargeback rate is along with a lower unit wholesale price in period 2 and the unit wholesale price in period 1 is independent of the chargeback rate, which differs from that without the second ordering, see [19,26]. That is, if the manufacturer decreases the chargeback rate to reduce the excessive ordering, it should raise the unit wholesale price in period 2 to stimulate the order quantity in period 1. The unit wholesale price in period 1 is independent of the unit production cost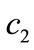 , the unit delayed delivery cost
, the unit delayed delivery cost 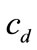 and the unit salvage value
and the unit salvage value 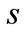 because they are not related to period 1. The unit wholesale price
because they are not related to period 1. The unit wholesale price 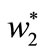 increases with the unit production cost
increases with the unit production cost 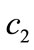 if and only if the chargeback rate is sufficiently low (
if and only if the chargeback rate is sufficiently low (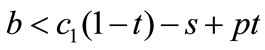 ); and increases with the unit delayed delivery cost
); and increases with the unit delayed delivery cost  and the unit salvage value
and the unit salvage value 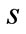 if and only if the chargeback rate is sufficiently low (
if and only if the chargeback rate is sufficiently low (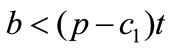 ). In addition, although a higher unit production cost in period 1 raises the unit wholesale price in period 1, it decreases the unit wholesale price in period 2 if the chargeback rate is sufficiently low (
). In addition, although a higher unit production cost in period 1 raises the unit wholesale price in period 1, it decreases the unit wholesale price in period 2 if the chargeback rate is sufficiently low (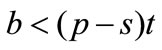 ), which results in a lower order quantity in period 1.
), which results in a lower order quantity in period 1.
5. Pareto Analysis of Coordination Mechanism under Uniform Distribution
In Section 4, we discuss the MMCA coordination mechanism without giving the optimal quantity and advertising level decisions in the setting with general distribution function. Now, we use a specific form of distribution function to obtain the optimal decisions and discuss the Pareto condition of the coordination mechanism. For analytical tractability, we use the uniform distribution function for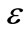 , defined over a finite range
, defined over a finite range ,
,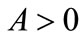 , which implies that the mean is
, which implies that the mean is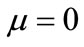 . Here, the density function is
. Here, the density function is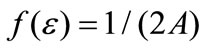 , the cumulative distribution function is
, the cumulative distribution function is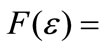
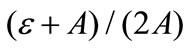 and
and 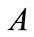 reflects the degree of demand uncertainty.
reflects the degree of demand uncertainty.
5.1. Equilibrium Outcome in the Centralized Setting
From Proposition 1, we derive the following.
Corollary 1. Under uniform distribution, the optimal decisions of the centralized system are
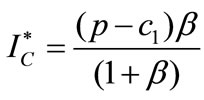 and
and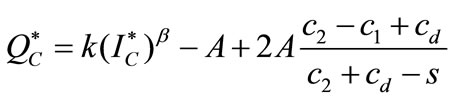 . The equilibrium channel profit is
. The equilibrium channel profit is

In the centralized setting, from Corollary 1 and [26], we know that the optimal advertising level is independent of whether allowing the second ordering while the optimal quantity depends on it. Corollary 1 implies that the channel profit is positive if and only if

That is, the channel can make a positive profit if and only if the demand uncertainty is not too large (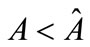 ). In the following, we assume that the condition
). In the following, we assume that the condition 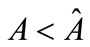 is satisfied. It follows from
is satisfied. It follows from 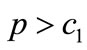 that both
that both 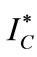 and
and 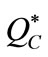 increase with
increase with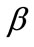 . It is surprising that the channel profit is decreasing with the advertising elasticity
. It is surprising that the channel profit is decreasing with the advertising elasticity 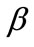 if
if . One expects that the advertising elasticity always have a positive effect on the channel profit because this raises the market demand. However, higher advertising elasticity also incurs a higher advertising cost (negative effect). As a consequence, if the unit net profit is sufficiently small (
. One expects that the advertising elasticity always have a positive effect on the channel profit because this raises the market demand. However, higher advertising elasticity also incurs a higher advertising cost (negative effect). As a consequence, if the unit net profit is sufficiently small (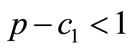 ) or the advertising elasticity
) or the advertising elasticity 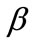 is sufficiently small, the channel profit decreases with the advertising elasticity because the negative effect is larger than the positive effect; otherwise, it increases. Corollary 1 implies that, when the retail price increases, the central decision maker increases the optimal advertising level to stimulate the market demand due to a higher unit profit.
is sufficiently small, the channel profit decreases with the advertising elasticity because the negative effect is larger than the positive effect; otherwise, it increases. Corollary 1 implies that, when the retail price increases, the central decision maker increases the optimal advertising level to stimulate the market demand due to a higher unit profit.
5.2. Equilibrium Outcome in the Decentralized Setting
Now, we discuss the decentralized system without coordination contract. Here, the manufacturer and the retailer maximize their profits independently. The manufacturer first jointly determines the unit wholesale price in two periods and then the retailer determines the order quantity and advertising level.
Similar to Section 3, when allowing the second ordering, we get the expected profit of the retailer is
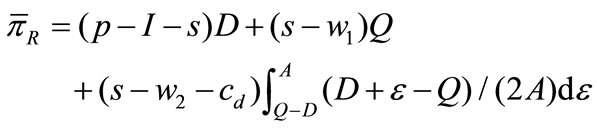
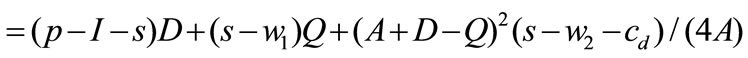 (6)
(6)
and the expected profit of the manufacturer is

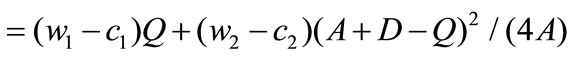 (7)
(7)
Similar to Corollary 1, from (6), it follows that, given the unit wholesale prices , the optimal reactions of the retailer are
, the optimal reactions of the retailer are  and
and

Inserting 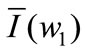 and
and 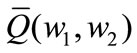 into (7), we can obtain the expected profit of the manufacturer
into (7), we can obtain the expected profit of the manufacturer . By search the maximum value of
. By search the maximum value of 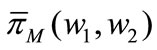 under the constraint
under the constraint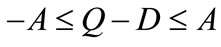 , we can obtain the optimal unit wholesale prices
, we can obtain the optimal unit wholesale prices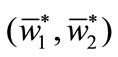 . Furthermore, we can obtain the equilibrium decisions of the retailer and the profits of the players. Let the optimal profit of the retailer be
. Furthermore, we can obtain the equilibrium decisions of the retailer and the profits of the players. Let the optimal profit of the retailer be 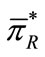 and that of the manufacturer
and that of the manufacturer 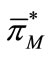 in the decentralized setting.
in the decentralized setting.
5.3. Pareto Analysis
When the supply chain is coordinated, the supply chain achieves the profit of the centralized system that is higher than that of the decentralized supply chain. However, the profit allocation of the coordinated supply chain depends on the specific MMCA contract. It is possible that a member of the coordinated supply chain gains a lower profit than that in the decentralized setting. Thus, it is necessary to study when both firms are better off using MMCA coordination mechanism, i.e., Pareto dominant.
Proposition 4 summarizes the Pareto condition of coordination mechanism.
Proposition 4. The MMCA mechanism is Pareto dominant over the decentralized setting if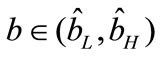 , where
, where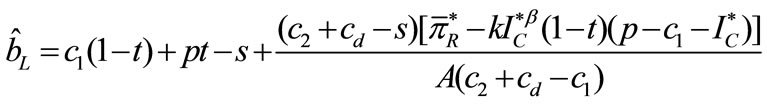 and
and 
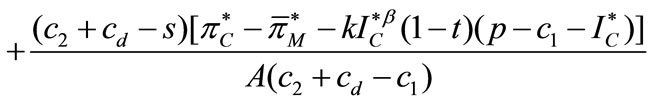 .
.
Proposition 4 implies that, the retailer is better off accepting the MMCA coordination mechanism only if the chargeback rate is not too low and the manufacturer is better off offering the MMCA mechanism only if the chargeback rate is not too high because a higher chargeback rate decreases the unit wholesale price in period 2 (see Proposition 3), which differs from that in [26]. That is, only when the chargeback rate is appropriate ( ), the two players are better off using the MMCA coordination mechanism.
), the two players are better off using the MMCA coordination mechanism.
Since it is difficult to find the analytic results on the bounds of chargeback rate, we investigate how some factors influence the results using a numerical example, where the default values of parameters are used as: ,
,  ,
,  ,
, 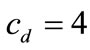 ,
, 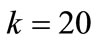 ,
,  ,
, 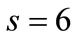 ,
, 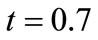 and
and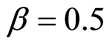 .
.
Figure 1 describes the effect of the chargeback rate on the profits of the players when the supply chain is coordinated. Figures 2-5 describe how the unit delayed cost, the unit production cost in period 2, the advertising elasticity and the fraction of advertising expenditure influences the bounds of chargeback rate. Since the effects of the unit production cost in period 1 and salvage value on the bounds are similar to those of the unit delayed delivery cost, we omit them. We also omit the effect of scaling constant because it is similar to that of advertising elasticity.
From Figure 1 and Proposition 3, we know that a higher chargeback rate is more beneficial to the retailer because the manufacturer charges the retailer a lower unit wholesale price in period 2 and the retailer obtains a higher chargeback for the unsold quantity in period 1, which is different from that in [26]. From Figure 2, we know that when the unit delayed delivery cost increases, the retailer has a higher incentive to use the MMCA mechanism while the manufacturer has a lower incentive to choose it because the manufacturer bears a part of the

Figure 1. Profits versus chargeback rate.
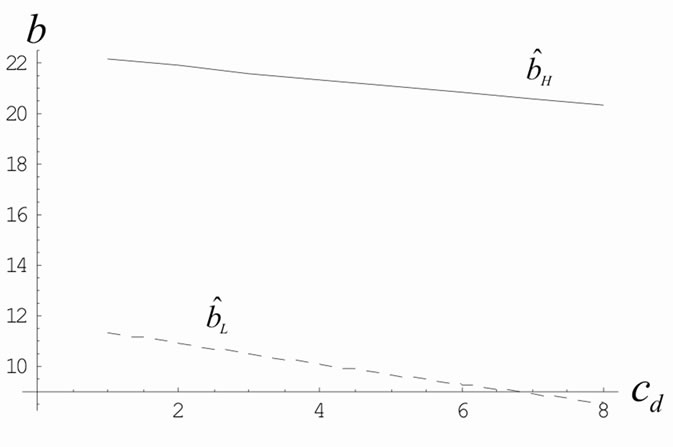
Figure 2. Bounds of chargeback rate versus delayed delivery cost.

Figure 3. Bounds of chargeback rate versus unit production cost.
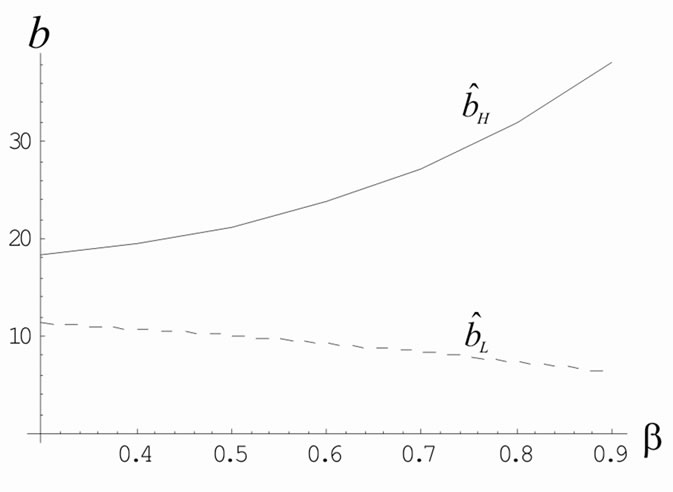
Figure 4. Bounds of chargeback rate versus advertising elasticity.

Figure 5. Bounds of chargeback rate versus the fraction.
delayed delivery cost in the coordinated setting. Figure 3 implies that, when the unit production cost in period 2 increases, the retailer has a lower incentive to use the coordination mechanism while the manufacturer has a higher incentive because the manufacturer can better transfer the production cost in period 2 to the retailer via the MMCA mechanism than the decentralized setting. Furthermore, the unit production cost difference between the two periods plays an important role in the motivation of the players to choose the MMCA mechanism. From Figure 4, we know that, when the advertising elasticity is not too small, higher advertising elasticity implies a larger range of chargeback rate in which both the manufacturer and the retailer are better off using coordination mechanism because the cooperative advertising can stimulate a higher advertising level and demand rate. From Figure 5, we know that, when the fraction  is sufficiently small, coordination is always beneficial to the retailer but harmful to the manufacturer. Thus, the manufacturer would like to offer a high fraction to stimulate the advertising investment. In fact, from Proposition 3, we know that the manufacturer offers a higher unit wholesale price to access a higher unit profit, which offsets a part cost of the advertising subsidy as the fraction increases. A higher fraction often is along with a higher chargeback rate because it needs a higher chargeback rate to induce the retailer to use coordination mechanism.
is sufficiently small, coordination is always beneficial to the retailer but harmful to the manufacturer. Thus, the manufacturer would like to offer a high fraction to stimulate the advertising investment. In fact, from Proposition 3, we know that the manufacturer offers a higher unit wholesale price to access a higher unit profit, which offsets a part cost of the advertising subsidy as the fraction increases. A higher fraction often is along with a higher chargeback rate because it needs a higher chargeback rate to induce the retailer to use coordination mechanism.
6. Conclusions
Seasonal products own high demand uncertainty such that there are often leftovers or shortage at the end of selling season. Local advertising plays an important role in promoting the marketing of seasonal products. This paper investigates how to coordinate the order quantity and advertising investment decisions via a MMCA mechanism when the second ordering is allowed.
We allow the retailer to make the second ordering to satisfy the market demand when there exists shortage at the end of selling season and focus on the effects of allowing the second ordering on equilibrium outcome and coordination mechanism. We find that whether allowing the second ordering influences the coordination mechanism to a large degree and even fully changes the results. For example, it inverts the relationship between the unit wholesale prices and chargeback rate and the motivation of the players to use the MMCA mechanism. In addition, we focus on the effects of the new factors related to allowing the second ordering (the unit production cost 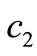 and the unit delayed delivery cost
and the unit delayed delivery cost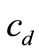 ) on the results and the characteristics of the unit wholesale price (
) on the results and the characteristics of the unit wholesale price (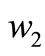 ) in period 2. We also illustrate the effects of the changing of economic environment on the Pareto range of coordination mechanism and find that the unit production cost difference between the two production modes remarkably influences the Pareto range, i.e., the unit production costs in different periods may have contrary effects on the bounds of Pareto range.
) in period 2. We also illustrate the effects of the changing of economic environment on the Pareto range of coordination mechanism and find that the unit production cost difference between the two production modes remarkably influences the Pareto range, i.e., the unit production costs in different periods may have contrary effects on the bounds of Pareto range.
This paper assumes that there is a monopoly retailer in the retail market. One may extend it to the case with multiple retailers to consider the effects of competition on equilibrium outcome and coordination mechanism. We assume that the manufacturer does not carry out (national) advertising investment. Incorporating the national advertising investment into our model may be interesting.
7. Acknowledgements
This research was supported in part by the National Natural Science Foundation of China under Grant 70971060, 70671055, 70971063 and 70731002.
8. References
[1] D. Simchi-Levi, P. Kaminsky and E. Simchi-Levi, “Designing & Managing Supply Chain: Concepts, Strategy & Case Studies,” McGraw-Hill, Irwin, 2003, pp. 76-90.
[2] S. Jørgensen, S. P. Sigué and G. Zaccour, “Dynamic Cooperative Advertising in a Channel,” Journal of Retailing, New York, Vol. 76, No. 1, 2000, pp. 71-92.
[3] Z. Huang and S. X. Li, “Co-op Advertising Models in Manufacturer-Retailer Supply Chains: A Game Theory Approach,” European Journal of Operational Research, Elsevier, Vol. 135, No. 3, December 2001, pp. 527-544.
[4] M. G. Nagler, “An Exploratory Analysis of the Determinants of Cooperative Advertising Participation Rates,” Marketing Letters, Springer Netherlands, Vol. 17, No. 2, April 2006, pp. 91-102.
[5] H. S. Lau and A. H. L. Lau, “Manufacturer’s Pricing Strategy and Return Policy for a Single-Period Commodity,” European Journal of Operation Research, Elsevier, Vol. 116, No. 2, July 1999, pp. 291-304.
[6] T. A. Taylor, “Supply Chain Coordination under Channel Rebates with Sales Effort Effects,” Management Science, INFORMS, Vol. 48, No. 8, August 2002, pp. 992-1007.
[7] C. X. Wang and S. Webster, “Markdown Money Contracts for Perishable Goods with Clearance Pricing,” European Journal of Operational Research, Elsevier, Vol. 196, No. 3, August 2009, pp. 1113-1122.
[8] Z. Yao, S. C. H. Leung and K. K. Lai, “Manufacturer’s Revenue-Sharing Contract and Retail Competition,” European Journal of Operational Research, Elsevier, Vol. 186, No. 2, April 2008, pp. 637-651.
[9] N. X. Xu and L. Nozick, “Modeling Supplier Selection and the Use of Option Contracts for Global Supply Chain Design,” Computers & Operations Research, Elsevier, Vol. 36, No. 10, October 2009, pp. 2786-2800.
[10] K. L. Donohue, “Efficient Supply Contracts for Fashion Goods with Forecast Updating and Two Production Modes,” Management Science, INFORMS, Vol. 46, No. 11, November 2000, pp. 1397-1411.
[11] X. H. Zhang, J. H. Ou and S. M. Gilbert, “Coordination of Stocking Decisions in an Assemble-to-Order Environment,” European Journal of Operational Research, Elsevier, Vol. 189, No. 2, September 2008, pp. 540-558.
[12] C. C. Hsieh, C. H. Wu and Y. J. Huang, “Ordering and Pricing Decisions in a Two-Echelon Supply Chain with Asymmetric Demand Information,” European Journal of Operational Research, Elsevier, Vol. 190, No. 2, October 2008, pp. 509-525.
[13] E. Kandel, “The Right to Return,” Journal of Law and Economics, University of Chicago, Vol. 39, April 1996, pp. 329-356.
[14] J. He, K. S. Chin, J. B. Yang and D. L. Zhu, “Return Policy Model of Supply Chain Management for SinglePeriod Products,” Journal of Optimization Theory and Applications, Springer Netherlands, Vol. 129, No. 2, May 2006, pp. 293-308.
[15] A. Nair and D. J. Closs, “An Examination of the Impact of Coordinating Supply Chain Policies and Price Markdowns on Short Lifecycle Product Retail Performance,” International Journal of Production Economics, Elsevier, Vol. 102, No. 2, August 2006, pp. 379-392.
[16] H. P. Marvel and H. Wang, “Inventories, Return Policy, and Equilibrium Price Dispersion under Demand Uncertainty,” China Center for Economic Research, Beijing University, Working Paper, 2002.
[17] K. Kogan and A. Herbon, “A Supply Chain under Limited-Time Promotion: The Effect of Customer Sensitivity,” European Journal of Operational Research, Elsevier, Vol. 188, No. 1, July 2008, pp. 273-292.
[18] Y. J. He and J. Zhang, “Random Yield Risk Sharing in a Two-Level Supply Chain,” International Journal of Production Economics, Elsevier, Vol. 112, No. 2, April 2008, pp. 769-781.
[19] C. H. Lee and B. D. Rhee, “Channel Coordination Using Product Returns for a Supply Chain with Stochastic Salvage Capacity,” European Journal of Operational Research, Elsevier, Vol. 177, No. 1, February 2007, pp. 214-238.
[20] Z. K. Weng, “Coordinating Order Quantities between the Manufacturer and the Buyer: A Generalized Newsvendor Model,” European Journal of Operational Research, Elsevier, Vol. 156, No. 1, July 2004, pp. 148-161.
[21] F. Chen, “Echelon Reorder Points, Installation Reorder Points, and the Value of Centralized Demand Information,” Management Science, INFORMS, Vol. 44, No. 12, December 1998, pp. S221-S234.
[22] Y. Seo, S. Jung and J. Hahm, “Optimal Reorder Decision Utilizing Centralized Stock Information in a Two-Echelon Distribution System,” Computers & Operations Research, Elsevier, Vol. 29, No. 2, February 2002, pp. 171-193.
[23] M. K. Dogru, G. J. Houtum and A. G. Kok, “Newsvendor Equations for Optimal Reorder Levels of Serial Inventory Systems with Fixed Batch Sizes,” Operations Research Letters, Elsevier, Vol. 36, No. 5, September 2008, pp. 551-556.
[24] M. Leng and M. Parlar, “Lead-Time Reduction in a Two-Level Supply Chain: Non-Cooperative Equilibria vs. Coordination with a Profit-sharing Contract,” International Journal of Production Economics, Elsevier, Vol. 118, No. 2, April 2009, pp. 521-544.
[25] Y. Seo, “Controlling General Multi-Echelon Distribution Supply Chain with Improved Reorder Decision Policy Utilizing Real-Time Shared Stock Information,” Computers & Industrial Engineering, Elsevier, Vol. 51, No. 2, October 2006, pp. 229-246.
[26] T. J. Xiao and X. X. Yan, “Coordinating a Two-Stage Supply Chain via a Markdown Money and Advertising Subsidy Contract,” International Journal of Information and Decision Sciences, Inderscience, 2010, in press.
[27] F. J. Arcelus, S. Kumar and G. Srinivasan, “Evaluating Manufacturer’s Buyback Policies in a Single-Period TwoEchelon Framework under Price-Dependent Stochastic Demand,” Omega, Elsevier, Vol. 36, No. 5, October 2008, pp. 808-824.
Appendix
Proof of Proposition 1. Differentiating  with respect to
with respect to , we can obtain the first-order condition
, we can obtain the first-order condition
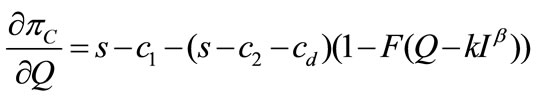
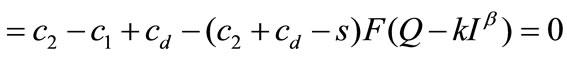 (A.1)
(A.1)
Note that  is a function of
is a function of . Differentiating
. Differentiating 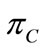 with respect to
with respect to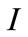 , we obtain the first-order condition
, we obtain the first-order condition
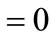

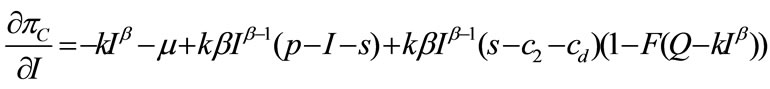 (A.2)
(A.2)
From (A.1), it follows that the first-order condition (A.2) is equivalent to
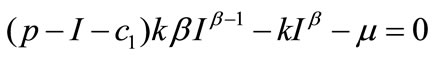 (A.3)
(A.3)
From (1), 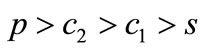 and
and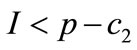 , it follows that, the second-order derivatives are
, it follows that, the second-order derivatives are
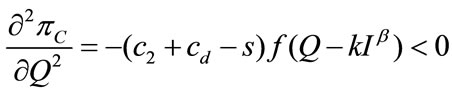
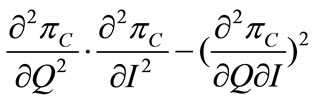
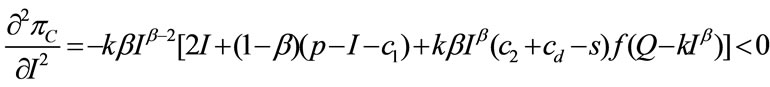
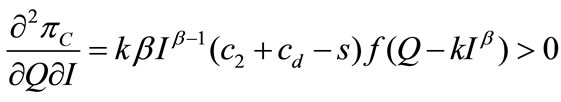
 .
.
Thus, 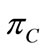 is a jointly concave function of
is a jointly concave function of , i.e., the second-order condition is satisfied. Thus, the solution of the first-order conditions is optimal.
, i.e., the second-order condition is satisfied. Thus, the solution of the first-order conditions is optimal.
Proof of Proposition 2. Given the MMCA mechanism of the manufacturer, the retailer determines  and
and 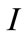 to maximize
to maximize 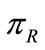 given by (1). Differentiating
given by (1). Differentiating  with respect to
with respect to  and
and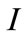 , we can obtain the first-order conditions
, we can obtain the first-order conditions

 (A.4)
(A.4)
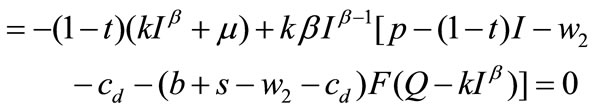
 (A.5)
(A.5)
From (A.4), it follows that the first-order condition (A.5) is equivalent to
 (A.6)
(A.6)
Similar to Proposition 1, we can show that  is a concave function of
is a concave function of , i.e., the second-order condition is satisfied.
, i.e., the second-order condition is satisfied.
Proof of Proposition 3. By comparing (A.1) with (A.4), we know that, if the manufacturer wants to induce the retailer to replicate the outcome of the centralized system, the optimal unit wholesale price for two periods should satisfy
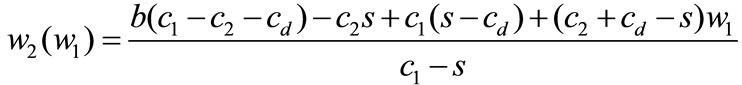
Rewriting (A.3) and (A.6), we have
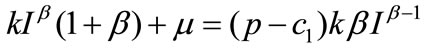 (A.7)
(A.7)
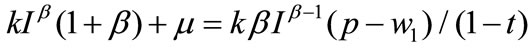 (A.8)
(A.8)
From (A.7) and (A.8), we know that
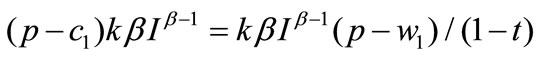 (A.9)
(A.9)
Solving (A.9) for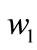 , we have
, we have

Proof of Corollary 1. From Proposition 1 and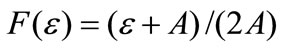 , it follows that the first-order conditions (A.1) and (A.3) are equivalent to
, it follows that the first-order conditions (A.1) and (A.3) are equivalent to
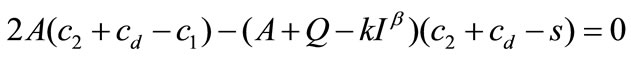 (A.10)
(A.10)
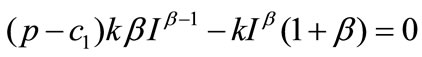 (A.11)
(A.11)
Solving (A.10) and (A.11) for 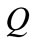 and
and , we obtain
, we obtain  and
and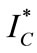 , given in Corollary 1.
, given in Corollary 1.
Proof of Proposition 4. Inserting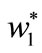 ,
, 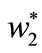 and
and 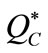 into (1), we have
into (1), we have
which is an increasing function of  following from
following from .
.
Solving 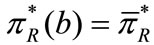 for
for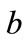 , we get
, we get
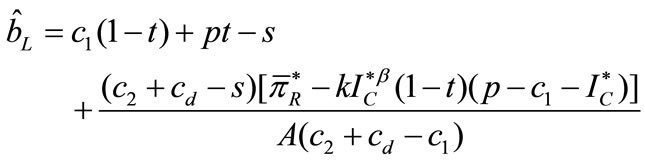
Thus, the retailer is better off using coordination mechanism if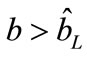 .
.
The equilibrium profit of the coordinated manufacturer is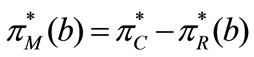 , which is a decreasing function of
, which is a decreasing function of . By solving
. By solving 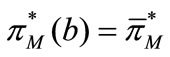 for
for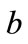 , we obtain
, we obtain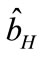 , given in Proposition 4. Furthermore, the manufacturer is better off using coordination mechanism if
, given in Proposition 4. Furthermore, the manufacturer is better off using coordination mechanism if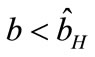 .
.

