Journal of Electromagnetic Analysis and Applications
 Vol.5 No.5(2013), Article ID:31435,8 pages DOI:10.4236/jemaa.2013.55033

Slice-Selective Transmit Array Pulses for Improvement in Excitation Uniformity and Reduction of SAR

BuSik Park1,2*, Kyunghyun Sung3, John McGarrity2, Suk-hoon Oh2,4, Zhipeng Cao1,2, Zhangwei Wang5, Christopher M. Collins1,2,4

1Department of Bioengineering, The Pennsylvania State University College of Medicine, Hershey, USA; 2Department of Radiology, The Pennsylvania State University College of Medicine, Hershey, USA; 3Department of Radiology, Stanford University, Stanford, USA; 4Department of Radiology, New York University, New York, USA; 5GE Healthcare, Aurora, USA.

Email: bu.park@fda.hhs.gov

Copyright © 2013 BuSik Park et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received March 15th, 2013; revised April 16th, 2013; accepted April 30th, 2013

Keywords: MRI; Composite Pulse; RF Shimming; SAR; MRI Simulator

ABSTRACT

To overcome challenges of inhomogeneous transmit B1 distribution and high specific energy absorption rate (SAR) in MRI, we compare slice-selective array-optimized composite pulse and RF shimming designed to both improve B1 uniformity and reduce SAR using an 8-channel transmit head array loaded with a head model at various RF pulse excitation times, and compare results with standard quadrature voltage distribution at 3T (128 MHz) and 7T (300 MHz). The excitation uniformity was estimated throughout the 3D brain region and SAR was calculated for the whole head. The optimized composite pulse could produce significantly better homogeneity and significantly better homogeneity when SAR was not constrained, and both significantly better homogeneity and lower SAR when the pulse duration was allowed to be twice that of the quadrature or RF shimmed pulse. When the total pulse durations were constrained to the same length, the relative advantages of the optimized composite pulse for producing better homogeneity and lower SAR simultaneously were diminished. Using the optimization results, the slice-selective composite pulse sequence was implemented on a 3D MRI simulator currently under development, and showed both effective slice selection and improvement in excitation uniformity compared to a conventional quadrature driving method.

1. Introduction

High field (3T and greater) magnetic resonance imaging (MRI) systems are used increasingly in clinical diagnosis and scientific research because of high Signal-to-Noise Ratio (SNR) and versatile soft tissue contrast. However, higher main magnetic field (B0) strengths require a higher frequency RF magnetic (B1) field resulting in more dramatic perturbations of the B1 field and more power absorbed by the human body or a sample for a given B1 field strength. Regarding the field perturbations, the wavelength inside the human body will be shorter at the higher field strengths, and much shorter in tissue than in free space. For example, in a 7T system (300 MHz), the wavelength inside the brain, having an average relative permittivity 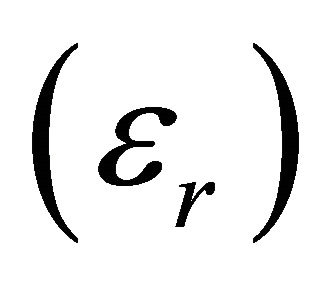of about 52 and conductivity (σ) of about 0.55 S/m, is approximately 13.9 cm, whereas in free space it is close to 100 cm. Because the human body has complex geometry consisting of highly inhomogeneous and lossy materials, strong electromagnetic interactions between the RF fields and the human body are expected. These interactions can lead to non-uniform, asymmetric, and complex current distributions on the RF coils as well as the inside of the human body. The distortions of the B1 field and increased absorbed power present significant challenges to the further advancement of MR.

A number of groups have introduced a variety of methods using arrays of coils or antennas in transmission, rather than the conventional single excitation coil, to simultaneously improve excitation homogeneity and reduce specific energy absorption rate (SAR) [1-11]. Some methods are limited to low flip angles and/or long pulse durations, some present challenges for slice-selective implementation, and some (those relying only on RF shimming) are limited by what can be accomplished within the bounds of the Maxwell equations for excitation uniformity. In this work, a slice-selective two-pulse array-optimized composite pulse [12] considering both B1 uniformity and SAR with a simple cost function, is designed and compared with RF shimming and the conventional quadrature driving method. The different excitation methods are compared in terms of both safety and excitation homogeneity with and without the constraint that the total duration of the RF pulses be equal. To implement our simulation results, MR images are acquired using a 3D MRI simulator (implementing the Bloch equations in 3D with no small-tip approximations) currently under development. Recent experimental comparison of the ability of composite pulses to achieve uniform excitation in comparison to RF shimming alone (without consideration of SAR) can be found elsewhere [13].

2. Method

The methods used here can be separated into three main portions: 1) finite difference time domain (FDTD) calculations using a transmit array and head model; 2) optimization of the transmit array pulsing method; and 3) implementation of the designed pulse sequences on an MRI system simulator. Each portion, especially the MR simulator, performs several calculations and therefore needs several subroutines and input files. Subsections devoted to each portion are given below. Briefly, the electromagnetic field distributions of each coil element (circularlypolarized magnetic field distributions, and, as well as electric field intensity, E), were calculated with the FDTD method. Using these calculated values, transmit array pulsing methods (RF shimming and optimized composite pulse) were developed using an optimization routine capable of considering the excitation uniformity and head average SAR simultaneously. The optimized current amplitude and phase of each channel were then used in the MR simulator with other input files (including sequence parameters and subject geometry) to calculate the k-space data using the Bloch equations. Finally, the k-space data from the MRI simulator was converted to image data using a fast Fourier transform (FFT) algorithm. Then the reconstructed image was evaluated with respect to excitation uniformity by comparing it to a simulated image acquired by the quadrature driving method.

2.1. FDTD Calculation Using Transmit Array and Head Model

An 8 channel transmit array (MR Instruments Inc, Minneapolis, Minnesota), having an inner diameter (ID) of 246 mm, a length (L) of 214 mm, and loaded with a human head was simulated at 128 MHz (3T) and 300 MHz (7T) (Figure 1). A conventional quadrature driving method using the same transmit array and head model was simulated for comparison. A human head model having 47 different tissue types with a 5 mm resolution was used for optimization to minimize calculation time (whereas a 2 mm resolution head model was used for the MR simulator). The original voxel-based model was acquired from the IT’IS foundation [14], and then transformed into a 3D grid of Yee cell cubes for use with the FDTD simulation method to calculate the B1 and electric field (E-field) produced by each element driven individually. Each element was excited with a voltage source having a magnitude of 1 V and with phase equal to the azimuthal position of the element in series with a 50 Ω resistor. All FDTD calculations were performed using commercially available software (xFDTD; Remcom, Inc.; State College, PA).

Before optimization, all electro-magnetic fields were normalized so that average 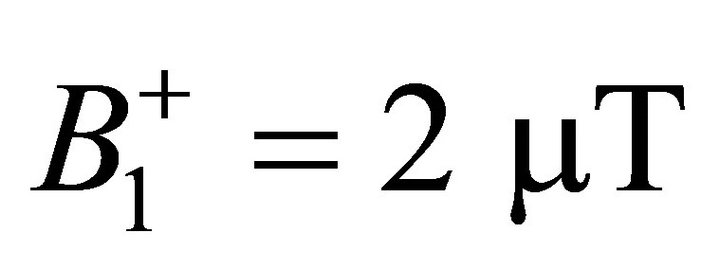within the brain volume (corresponding to a 3.0 ms 90o pulse) for quadrature driving, RF shimming, and optimized composite pulse having 3 ms duration of each component pulse [15], but with average for the optimized composite pulse having 1.5 ms duration for each component pulse.

2.2. Optimization of the Transmit Array Pulsing Method

For the optimized composite pulses, the magnitudes and phases of each element in both component pulses were optimized to produce the most homogeneous transverse magnetization 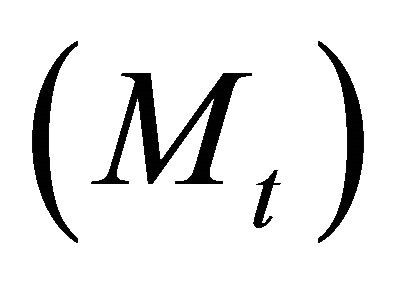at the end of the second component pulse and the lowest SAR throughout the pulse. During optimization, a simple cost function [8,9] was minimized,

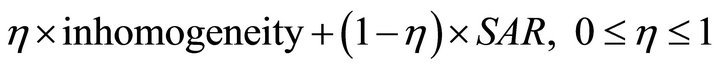(1)

The value for η was varied from 0 to 1 for evaluation of its effect on both excitation uniformity and head-average SAR. At this point the selection of η is empirically selected to give both good homogeneity and (in SARconstrained cases) significantly reduced SAR compared to when η is 1.

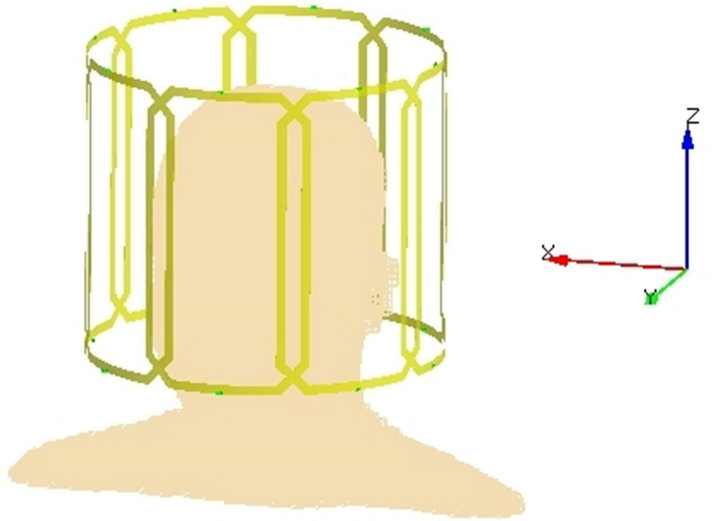
Figure 1. Geometry of 8 channel transmit array (MR Instruments Inc., MN, USA) and head model.

The transverse magnetization (Mxy) and degree of spin excitation, ignoring spin-lattice relaxation time (T1) and spin-spin relaxation time (T2) effects during the RF pulse, was calculated by the following portion of the Bloch equation [1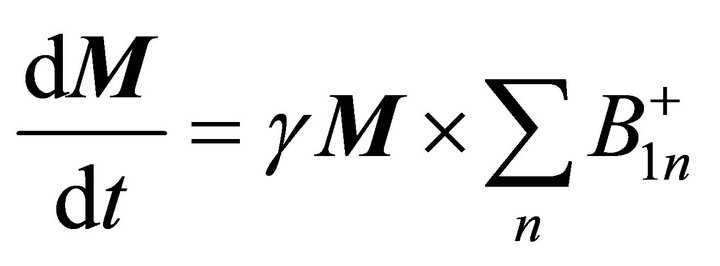2].

(2)

where represents the net spin magnetization vector, γ is the gyromagnetic ratio (42.58 MHz/T for the 1H), and 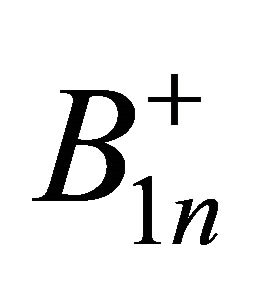is the complex circularly polarized component of the radiofrequency magnetic (B1) field rotating in the same directions of precession. For the purposes of the optimization process (not the MRI simulator), before the pulse was applied, 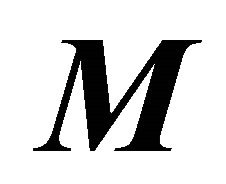was assigned an amplitude of 1 (arbitrary units, oriented in the z-direction) throughout the brain. Optimization for RF shimming followed a similar procedure, but with only one component pulse.

For all pulse types and drive configurations, excitation uniformity using the transverse magnetization (Mxy) was calculated as

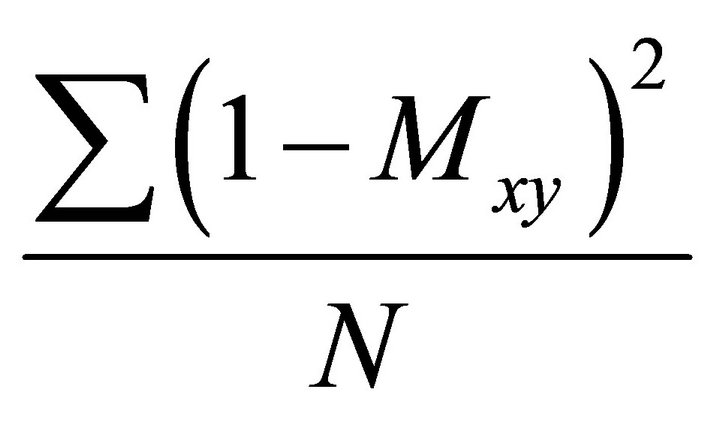(3)

where N is the total number of voxel in the region of interest.

The SAR was calculated as

(4)

where Ex, Ey, and Ez are amplitudes of orthogonal components of the electric field, 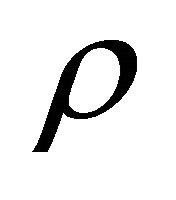is the mass density (kg/m3) and is the conductivity (S/m) of the local material.

For rectangular pulses, mean SAR for the RF shimming and quadrature driving considering the pulse excitation time is

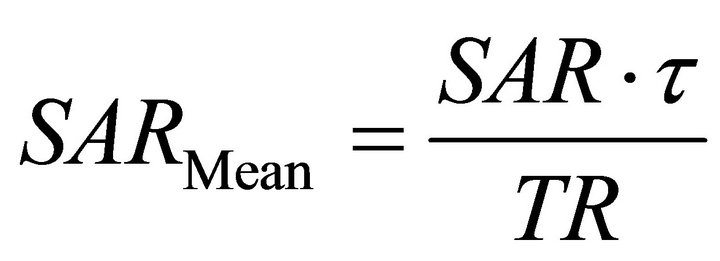(5)

where τ is the RF pulse excitation time, SAR is the average SAR within a head model at the certain time, and TR is the repetition time. Mean SAR for the composite pulse is

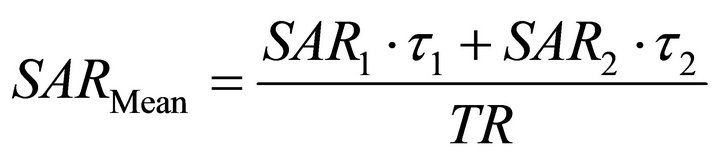(6)

where subscripts 1 and 2 indicate the first and second RF pulses. The Mt was calculated within a 3D brain region, whereas the whole head was used for the SAR calculations. Optimization was performed using home-built code in Matlab (The MathWorks, Inc., Natick, MA).

2.3. Calculation of the k-Space Data Using an MR Simulator

After optimization, amplitudes and phases of optimized currents for each channel were used to acquire MR images using a freely available Bloch-equation-based MR Simulator currently under development [16] with all pertinent information (e.g., T1, T2 and proton density of tissues, head geometry, B1 distribution of each coil element, and pulse sequences for all RF and gradients).

The transverse magnetization vector was tracked through time and space using the Bloch equation considering T1, T2, gradients and B0 inhomogeneity. The equation describing an interaction between tissue spin magnetization and applied fields during MRI scanning can be written as:

(7)

where 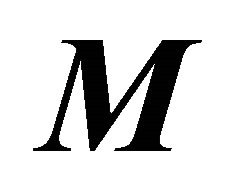is the spin magnetization vector (having components of Mx, My and Mz), t is time, are the relaxation constants, and M0 is the tissue spin magnetization at equilibrium without any applied fields except the main magnetic field (B0) determined by the proton density (ρ).

The local magnetic field, , can be written as [16]:

(8)

where B0 is the main magnetic field, 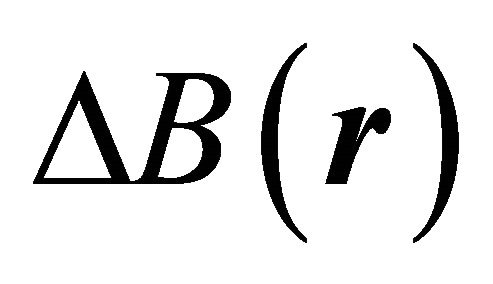is the local field variation caused by the tissue susceptibility and B0 inhomogeneity within the object, 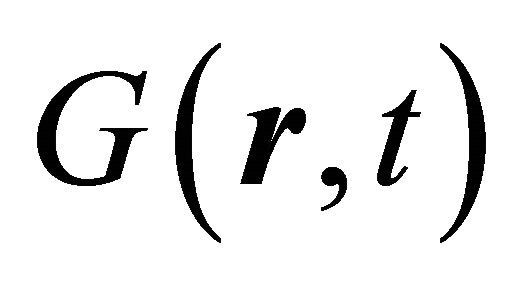is the applied gradient fields at a certain time, is the radio frequency (RF) magnetic field, and 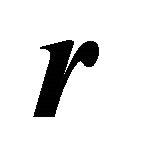is the spatial coordinate.

In a frame of reference rotating about the z axis at the Larmour frequency corresponding to B0, a discrete time solution of the Bloch equation can be expressed, as [17]:

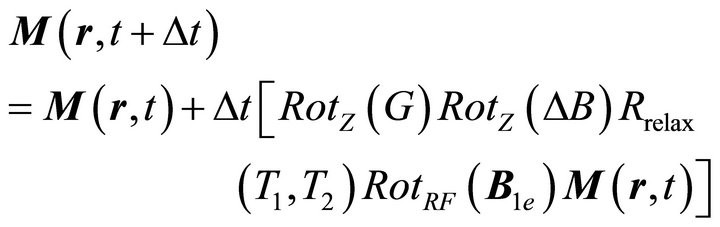(9)

where 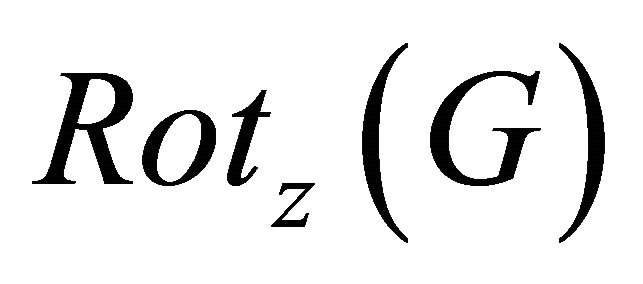is a rotation matrix about the z-axis associated to the applied gradient, 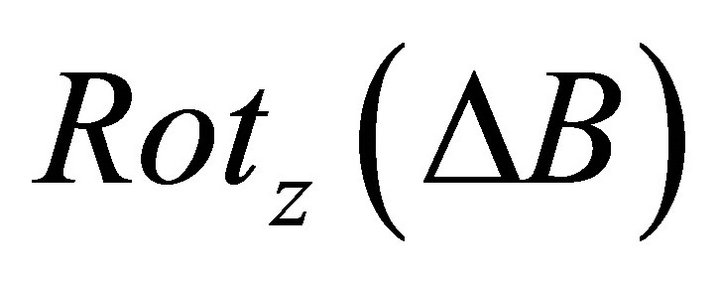is a rotation matrix about the z-axis associated with the difference between the applied main magnetic field (B0) and the actual local field strength caused by the susceptibility of the local tissue, 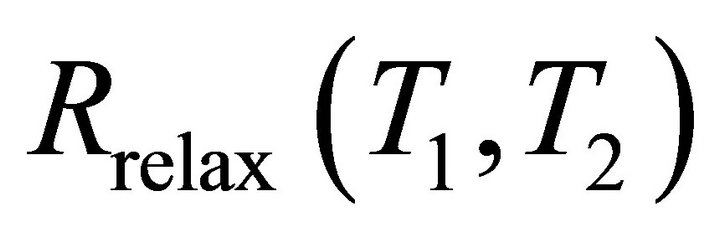describes the relaxation effect of T1 and T2, and represents the rotating effect of the applied effective B1 field.

The excitation uniformity was estimated using a proton density-weighted image (having parameters of TR = 2000 ms, TE = 20 ms) and a gradient echo sequence. T1- and T2-weighted images were acquired using the parameters of TR/TE = 100/10 ms and TR/TE = 2000/100 ms, respectively, where TR is repetition time and TE is the echo time.

3. Results

Figures 2 and 3 show at 128 MHz and 300 MHz, respectively, the distribution of SAR and Mt for the transmit array with quadrature drive (first column), RF shimming (second column) and optimized composite pulse (third column) throughout the region of interest (ROI), which is a 3D brain for Mt and the whole head for SAR.

The optimization without considering SAR (when η = 1) is presented in Figure 4 corresponding to 3T (128 MHz) and 7T (300 MHz).

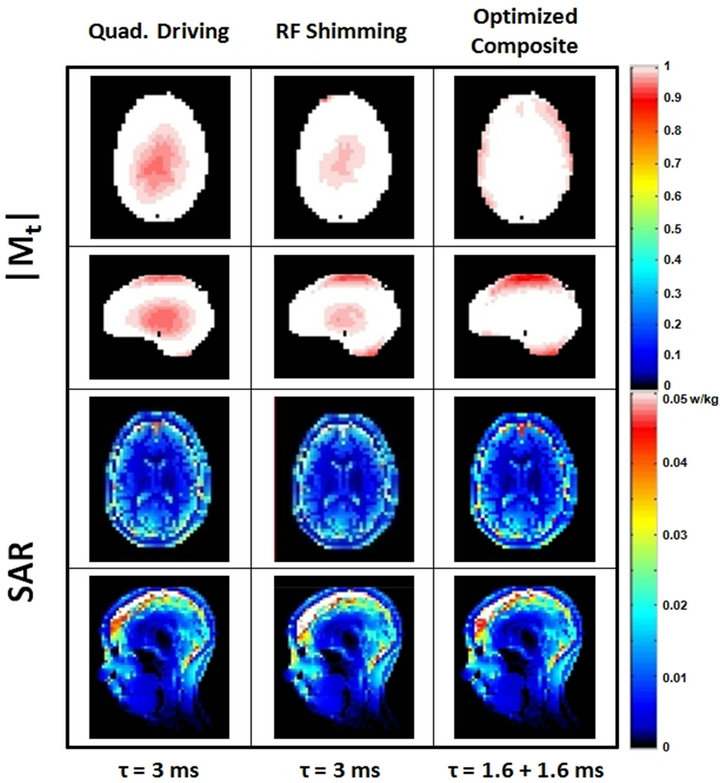
Figure 2. Distribution of SAR and Mt predicted during optimization throughout the selected slices of a head at 128 MHz (3T) for quadrature driving (first column), and transmit array with RF shimming having η of 0.75 (second column) and optimized composite having η of 0.2675 (third column). τ is the pulse excitation time.

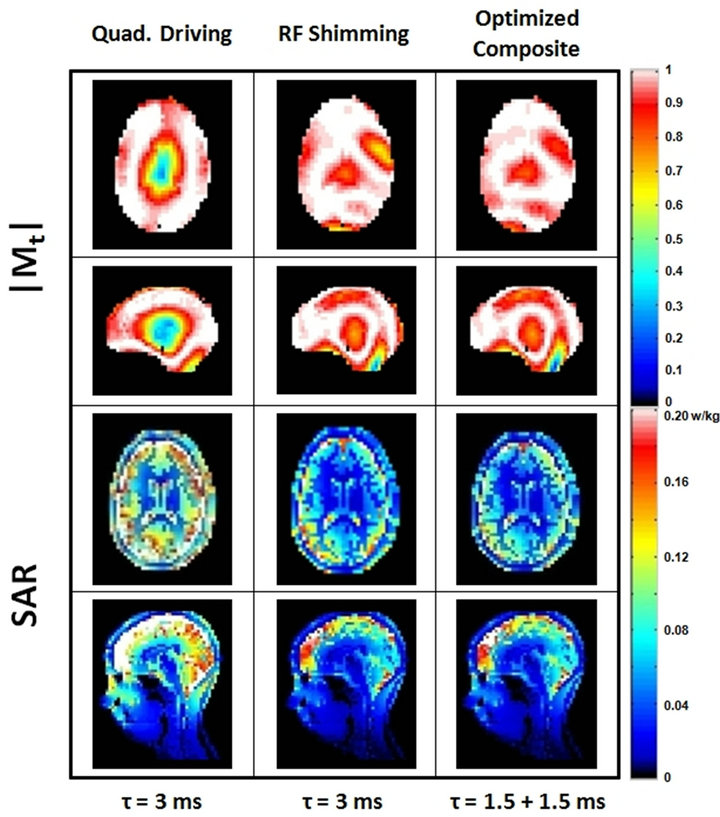
Figure 3. Numerical calculation results of SAR and Mt throughout the selected slices of a head with η of 0.51 (RF Shimming) and 0.5 (Optimized Composite) at 300 MHz (7T). Other parameters are the same as in Figure 2.

Figure 4. Distribution of transverse magnetization (Mt) throughout the selected slice of a head at 128 MHz (3T) and 300 MHz (7T) when η = 1 (considering only excitation uniformity).

The optimized composite pulse had better performance, both in excitation uniformity and SAR, compared to a quadrature drive. When η was increased from 0 to 1, the excitation uniformity calculated by Equation (2) was increased, whereas mean and maximum value of SAR calculated by Equation (5) was increased. A good compromise was seen when η was 0.2675 for 3T (Figure 2 and Table 1) and 0.5 for 7T (Figure 3 and Table 2) for the optimized composite.

When η was 1.0 for the optimized composite with τ of 1.5 ms, compared to the quadrature driving (Tables 1 and 2), the excitation uniformity was improved about 96% (3T) and 79% (7T) whereas the head average SAR was increased about 286% (3T) and 211% (7T).

To evaluate the excitation uniformity of the single slice image acquired by the optimized composite pulse and conventional quadrature drive, we acquired proton density images at 7T. The resulting signal intensity distributions on a 2D axial plane using this head model are shown in Figure 5. Results show that the array-optimized composite pulse has better excitation uniformity than the quadrature driving method. Figure 6 shows the designed pulse sequence for the optimized composite pulse and the acquired proton density weighted images without (top) and with the slice selection gradient of normal rectangular (middle) and triangular (bottom) using the variable-rate selective excitation (VERSE) method to minimize slew rate limitation and pulse duration.

4. Discussion and Conclusions

In this work we compare efficacy of a two-component array-optimized composite pulse for achieving homogeneous excitation balanced with constraints on head average SAR with comparison to efficacy of RF shimming alone for a variety of relative total pulse durations.

While other pulses have been shown to be able to consider both SAR and excitation homogeneity, they are typically not compared to competing pulses with critical consideration of relative pulse durations.

In this work we have chosen to perform evaluations with respect to whole-head SAR. The most recent IEC guidelines [18] clarify the distinction between suggested SAR limits for volume transmit coils and those for local transmit coils with no local (10 g) SAR limits given for volume transmit coils. These most recent guidelines also state that transmit arrays (or multi-channel transmit coils) can be treated as either volume transmit coils or local transmit coils depending on their use. In this case, where the transmit array surrounds the entire head volume and is used to excite the entire brain, it is clear that it is used as a volume transmit coil. For this reason we place first priority on head-average SAR.

It has previously been shown that a simple 2-pulse array-optimized composite pulse can provide homogeneous excitation over the entire brain at up to 600 MHz [11], and perform much better than RF shimming alone in im-

Table 1. Excitation uniformity (second column) and Mean SAR (third column) throughout the 3D slices of an entire head at 128 MHz (3T) for transmit array with quadrature driving (second row), RF shimming (third and fourth rows) and the composite pulse before (Quadrature Composite, fifth row) and after (from sixth to ninth row) optimization. τ is the RF pulse excitation time, Opt. is the abbreviation of optimization, and η is a variable for the cost function, η*inhomogeneity + (1 − η)*SAR.

Table 2. Excitation uniformity (second column) and mean SAR (third column) at 300 MHz (7T). Other parameters are the same as in Table 1.

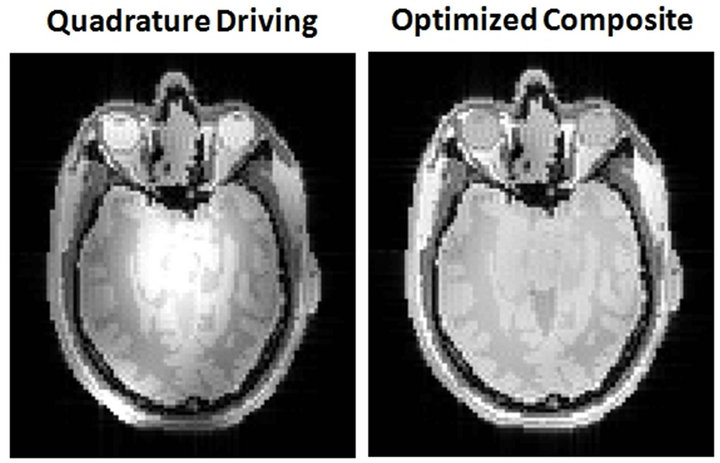
Figure 5. Acquired proton density images of quadrature driving (left) and optimized composite (right) in a 3D MRI simulator at 7T.

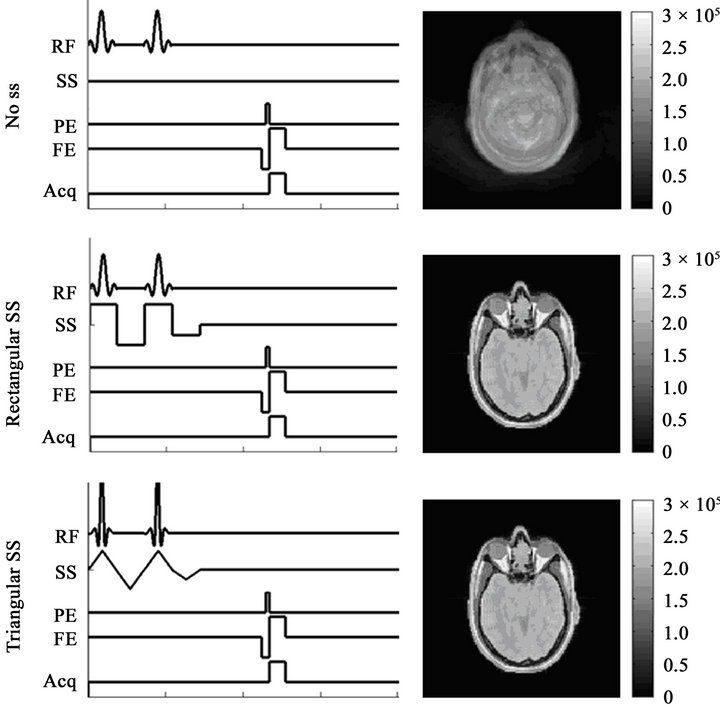
Figure 6. Acquired proton density images at 3T without slice selection (SS) gradient (top), with normal rectangular slice selection gradient (middle) and triangular slice selection gradient (bottom) using VERSE method.

proving homogeneity [11], or in simultaneously improving homogeneity and reducing SAR [12].

Based on the previous research, we showed RF pulse excitation time (τ) dependent optimization of both image homogeneity and SAR for RF shimming and composite pulses at 128 MHz (3T) and 300 MHz (7T) using an 8-channel transmit array and head model. In agreement with the previous results, when SAR is not a consideration, the optimized composite pulse can produce much better homogeneity than either the quadrature drive or RF shimming alone. If SAR is constrained during the optimization process but pulse duration of the optimized composite pulse is allowed to be longer than that of the other cases, the optimized composite pulse can again produce better homogeneity and lower SAR. If the total pulse duration of the optimized composite pulse is limited to that of the other pulse durations and SAR is a consideration, however, the advantages of the optimized composite pulse are more limited. In this case, it can still produce either better homogeneity or lower SAR than the RF shimmed case when SAR is not constrained, but it cannot necessarily produce both better homogeneity and lower SAR simultaneously. While other pulses that can achieve high homogeneity and slice selection have been published [2-4,9,10], they have not been compared to simple RF shimming or other competing pulses in terms of both homogeneity and SAR when all pulses are constrained to the same total duration. Spoke-type methods [9,10] were developed in parallel to array-optimized composite pulses [11,12] and share some similarities. Compared to current implementations of array-optimized composite pulses, spoke-type methods afford more degrees of freedom with use of transverse (in addition to slice-selection) gradients, but also rely on low-flip angle approximations. While there are methods to allow for fairly high flip angles with spoke-type methods, we believe that the current full-Bloch design for array-optimized composite pulses should afford some greater flexibility (especially if transverse gradients are also incorporated into array-optimized composite pulse design) though at a cost of greater computational requirements. 

Recent experiments show advantages of the array-optimized composite pulse compared to RF shimming alone for excitation homogeneity, but without constraints on SAR or pulse duration [13]. In order to illustrate the possibility of implementing the array-optimized composite pulse for very short pulse durations, here we demonstrated slice selection in the presence of B0 effects with an optimized composite pulse by implementing it on a 3D MRI simulator using the same coil geometries at both 3T and 7T using the VERSE technique [19]. While the simulator has no limitation in slew rate (so the slice-selective pulse with rectangular gradient waveforms could be as short as desired) in experimental implementation triangular gradient waveforms and the VERSE technique could be used to minimize pulse duration under the limitations of gradient slew rate (Figure 6) [19]. As shown here, the proton density image acquired using the optimized composite pulse has better excitation uniformity (Figure 5) than the quadrature driving. Thus, pulse duration can be very short, slice selection is possible, and both SAR and excitation uniformity can be improved with the array-optimized composite pulse in the head at 3T and 7T.

5. Acknowledgements

We thank Mark Watson, Scott Schillak and Labros Petropopolous for providing geometry of transmit array and helpful discussions. Funding provided in part by NIH through R01 EB000454, R01 EB006563, R01 EB000895, and the Pennsylvania Department of Health.

REFERENCES

  1. C. A. van den Berg, B. van den Bergen, H. Kroeze, L. W. Bartels and J. J. Lagendijk, “Simultaneous Homogenisation and SAR Hotspot Suppression by a Phased Array MR Transmit Coil,” Magnetic Resonance in Medicine, Vol. 57, No. 3, 2006, pp. 577-586.
  2. X. Wu, C. Akgun, J. T. Vaughan, K. Ugurbil and P.-F. Van de Moortele, “SAR Reduction in Transmit SENSE Using Adapted Excitation k-Space Trajectories,” Proceedings of the 15th Annual Meeting of ISMRM, Berlin, 19-25 May 2007, p. 673.
  3. X. Wu, C. Akgun, J. T. Vaughan, K. Ugurbil and P.-F. Van de Moortele, “SAR Analysis for Transmit SENSE at 7T with a Human Head Model,” Proceedings of the 15th Annual Meeting of ISMRM, Berlin, 19-25 May 2007, p. 3350.
  4. I. Graesslin, S. Biederer, F. Schweser, K.-H. Zimmermann, U. Katscher and P. Bornert, “SAR Reduction for Parallel Transmission Using VERSE and k-Space Filtering,” Proceedings of the 15th Annual Meeting of ISMRM, Berlin, 19-25 May 2007, p. 674.
  5. T. S. Ibrahim and L. Tang, “A Whole-Body 7 Tesla RF Excitation Scheme with Much Improved Field Homogeneity and Local/Global SARs over Quadrature Excitation,” Proceedings of the 15th Annual Meeting of ISMRM, Berlin, 19-25 May 2007, p. 1013.
  6. Z. Wang, J. C. Lin, W. Mao, W. Liu, M. B. Smith and C. M. Collins, “SAR and Temperature: Simulations and Comparison to Regulatory Limits for MRI,” Journal of Magnetic Resonance Imaging, Vol. 26, No. 2, 2007, pp. 437-441. doi:10.1002/jmri.20977
  7. Z. Wang, S.-H. Oh, M. B. Smith and C. M. Collins, “RF Shimming Considering both Excitation Homogeneity and SAR,” Proceedings of the 15th Annual Meeting of ISMRM, Berlin, 19-25 May 2007, p. 1022.
  8. G. McKinnon, “RF Shimming and SAR Considerations with an Eight-Element 3T Body Coil,” Proceedings of the 15th Annual Meeting of ISMRM, Berlin, 19-25 May 2007, p. 1085.
  9. A. C. Zelinski, K. Setsompop, V. Alagappan, B. A. Gagoski, L. M. Angelone, G. Bonmassar, U. Fontius, F. Schmitt, E. Adalsteinsson and L. L. Wald, “Pulse Design Methods for Reduction of Specific Absorption Rate in Parallel RF Excitation,” Proceedings of the 15th Annual Meeting of ISMRM, Berlin, 19-25 May 2007, p. 1698.
  10. A. C. Zelinski, V. K. Goyal, L. Angelone, G. Bonmassar, L. L. Wald and E. Adalsteinsson, “Designing RF Pulses with Optimal Specific Absorption Rate (SAR) Characteristics and Exploring Excitation Fidelity, SAR and Pulse Duration Tradeoffs,” Proceedings of the 15th Annual Meeting of ISMRM, Berlin, 19-25 May 2007, p. 1699.
  11. S.-H. Oh, G. Sylvie and C. M. Collins, “Array-Optimized Composite Excitation Pulse for Simultaneous Homogenous Excitation and Low SAR in a Human-Body Transmit-Array at 3.0T,” Proceedings of the 16th Annual Meeting of ISMRM, Toronto, 3-9 May 2008, p. 1309.
  12. C. M. Collins, Z. Wang, W. Mao, J. Fang, W. Liu and M. B. Smith, “Array-Optimized Composite Pulse for Excellent Whole-Brain Homogeneity in High-Field MRI,” Magnetic Resonance in Medicine, Vol. 57, No. 3, 2007, pp. 470-474. doi:10.1002/mrm.21172
  13. C. Sica, S. Oh and C. M. Collins, “pTX Array Optimized Composite Pulse for Inhomogeneity Compensation at 3T,” Proceedings of the ISMRM 21st Annual Meeting, Melbourne, 5-11 May 2012, p. 3481.
  14. A. Christ, et al., “Development of CAD Based Anatomical Human Body Models of Two Adults and Two Children,” EBEA 2007, abstr.S-4-2, 8th International Congress of the European Bioelectromagnetics Association (EBEA), Bordeaux, 10-13 April 2007.
  15. C. M. Collins and M. B. Smith, “Signal-to-Noise Ratio and Absorbed Power as Functions of Main Magnetic Field Strength, and Definition of ‘90˚’ RF Pulse for the Head in the Birdcage Coil,” Magnetic Resonance in Medicine, Vol. 45, No. 4, 2001, pp. 684-691. doi:10.1002/mrm.1091
  16. Z. Cao, C. T. Sica, S. Oh, J. McGarrity, T. Horan, B. S. Park and C. M. Collins, “An MRI Simulator for Effects of Realistic Field Distributions and Pulse Sequences, Including SAR and Noise Correlation for Array Coils,” Proceedings of ISMRM, Stockholm, 1-7 May 2010, p. 1456.
  17. H. Benoit-Cattin, G. Collewet, B. Belaroussi, H. SaintJalmes and C. Odet, “The SIMRI Project: A Versatile and Interactive MRI Simulator,” Journal of Magnetic Resonance, Vol. 173, No. 1, 2005, pp. 97-115. doi:10.1016/j.jmr.2004.09.027
  18. International Electrotechnical Commission, “International Standard, Medical Equipment—Part 2: Particular Requirements for the Safety of Magnetic Resonance Equipment for Medical Diagnosis,” 3rd Edition, International Electrotechnical Commission, Geneva, Vol. 601, 2010, pp. 2-33.
  19. K. Sung and K. S. Nayak, “Compensation in 3T Cardiac Imaging Using Short 2DRF Pulses,” Magnetic Resonance in Medicine, Vol. 59, No. 3, 2008, pp. 441- 446. doi:10.1002/mrm.21443

Journal Menu >>