Journal of Electromagnetic Analysis and Applications
Vol.5 No.6(2013), Article ID:32939,7 pages DOI:10.4236/jemaa.2013.56042
Chiral Maxwell’s Equations as Two Spinor System: Dirac and Majorana Neutrino
![]()
Escuela de Ingeniería Eléctrica Electrónica, Universidad de Tarapacá, Arica, Chile.
Email: htorres@uta.cl
Copyright © 2013 Héctor Torres-Silva. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 27th, 2013; revised March 28th, 2013; accepted April 5th, 2013
Keywords: Harmonic Current; Inversion; Torque Ripple; SPWM; Finite Element Method
ABSTRACT
This work clarifies the relation between Maxwell, Dirac and Majorana neutrino equations presenting an original way to derive the Dirac and neutrino equation from the chiral electrodynamics leading, perhaps, to novel conception in the mass generation by electromagnetic fields. In the present article, it is shown that Maxwell equations can be written in the same form as the two components Dirac and neutrino equations, that is the vector representation of electromagnetic theory can be factorized into a pair of two-component spinor field equations. We propose a simple approach with the electric field  parallel to the magnetic field
parallel to the magnetic field . Our analysis is based on the chiral or Weyl form of the Maxwell equations in a chiral vacuum. This theory is a new quantum mechanics (QM) interpretation for Dirac and neutrino equation. The below research proves that the QM of particles represents the electrodynamics of the curvilinear closed chiral waves. Electromagnetic properties of neutrinos are discussed.
. Our analysis is based on the chiral or Weyl form of the Maxwell equations in a chiral vacuum. This theory is a new quantum mechanics (QM) interpretation for Dirac and neutrino equation. The below research proves that the QM of particles represents the electrodynamics of the curvilinear closed chiral waves. Electromagnetic properties of neutrinos are discussed.
1. Introduction
Maxwell’s equations can be formulated in a number of diferent spinor representations: a) as a single four-component spinor equation whose transformation properties are almost identical with those of the Dirac equation; b) as a pair of uncoupled two‐component spinor equations, in two different representations. One of these is similar to the Weyl equation for the neutrino field and the other to the two‐component spinor form of the Dirac equation; c) as a single equation in which the field variables are 2 × 2 matrices. In terms of new field variables corresponding to chiral equations, we derived the Dirac equation and we reconsider the two-component Majorana equation. By making use of the chiral operator 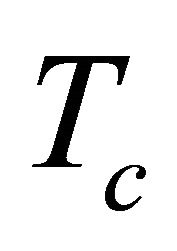 defined in Sections 2 and 3, we construct these equations with a mass term in a novel and manifestly covariant way, which reveal its intimate connection with the chiral electromagnetism.
defined in Sections 2 and 3, we construct these equations with a mass term in a novel and manifestly covariant way, which reveal its intimate connection with the chiral electromagnetism.
To do that, we must considerer the chiral vacuum. After the discovery of the weak interaction that violates parity (spatial reflection), we addressed the question on whether there may be any empirical evidence for the violation of parity in the electromagnetic interaction. If the chiral vacuum is take into account, then there is an implication in the experimental results that the electromagnetic and the nuclear forces also violate space-reflection symmetry, as well as time reversal symmetry.
The chiral vacuum is intended to explain the relation between electrodynamics in anisotropic material media and its analogous formulation in spacetime, with nonnull Riemann curvature tensor. The electromagnetism can be discussed via chiral differential forms, we point out the optical activity of a given material medium, closely related to topological spin, and the Faraday rotation, associated to topological torsion. Both quantities are defined in terms of the chiral magnetic and electric field.
In order to investigate the propagation of electromagnetic waves in material media, we think that it is analogous to consider the electromagnetic wave propagation in the vacuum, but in a curved spacetime, which is obtained by a deformation of the Lorenztian metric of Minkowski spacetime. Also, there exists a close relation between Maxwell equations in curved spacetime and in an anisotropic material medium, indicating that electromagnetism and spacetime properties are deeply related [1]. Besides, the geometrical aspects of wave propagation can be described by an effective geometry which represents a modification of the Lorentzian metric of Minkowski spacetime, i.e., a kind of spacetime deformation, that is a chiral vacuum. While the left circularly polarized (LCP) wave is transmitted straight through the chiral medium with no reflection and no refraction, the right circularly polarized (RCP) wave is scattered. The reverse can also occur. We call this effect as the chiral vacuum.
The chiral vacuum can be understood physically as follows. The polarization and magnetization of chiral medium is represented as a sum of electric and magnetic contributions, i.e.,  and
and . When the condition
. When the condition  is satisfied, the electric and magnetic contributions cancel each other out for one of the circular polarizations, and
is satisfied, the electric and magnetic contributions cancel each other out for one of the circular polarizations, and  is achieved. Thus the medium is equivalent to a vacuum only for one circular polarization [2-5].
is achieved. Thus the medium is equivalent to a vacuum only for one circular polarization [2-5].
A chiral medium can create an anisotropic electromagnetic environment, which leads to anisotropic quantum-vacuum fields (and observable quantum-vacuum effects) and the physical effects resulting from the quantum-vacuum fluctuation of leftand right-handed polarized modes will no longer be exactly canceled [6]. The aim of this work is to construct the Dirac equation and the neutrino equation in the Weyl representation through Maxwell’s equations in the chiral formulation. This possibility occurs only when the E field and H field are spatially parallel and the field distribution can generate mass. These fields are circulatory and stationary and under this condition we have no radiation and the vector Poynting  is zero. In Section 2, the Dirac equation in the Weyl representation is constructed through chiral Maxwell equations. In Section 3, we derive two spinor neutrino equations. The chiral electromagnetic neutrino is discussed in Section 4.
is zero. In Section 2, the Dirac equation in the Weyl representation is constructed through chiral Maxwell equations. In Section 3, we derive two spinor neutrino equations. The chiral electromagnetic neutrino is discussed in Section 4.
2. The Matrix Form of Chiral Maxwell Equation: Dirac Equation
The author of ref. [7] claims that no Maxwell-Dirac equivalence (MDE) may exist because F has six (real) degrees of freedom and ψ has eight (real) degrees of freedom. Here we show that it is possible to transform the Maxwell equation from six real components to four complex components and in this form to obtain two spinor equations in the Weyl representation. First, we will consider the Maxwell equations for a sourceless anisotropic chiral homogeneous medium following [8-13], but with the time variation as: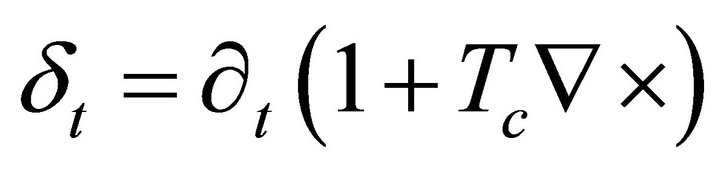 .
. 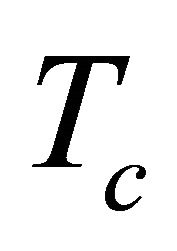 is a chiral parameter so the Maxwell’s equations without charges are expressed as [14-17]:
is a chiral parameter so the Maxwell’s equations without charges are expressed as [14-17]:
 (1)
(1)
 (2)
(2)
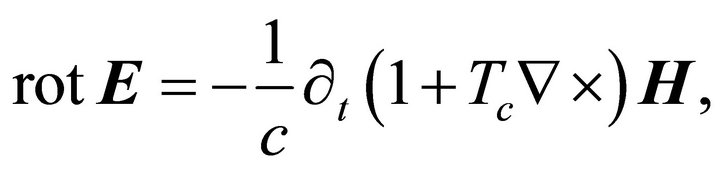 (3)
(3)
 (4)
(4)
If we multiply (4) and (1) by  and add them respectively to (2) and (3) we get
and add them respectively to (2) and (3) we get
 (5)
(5)
and
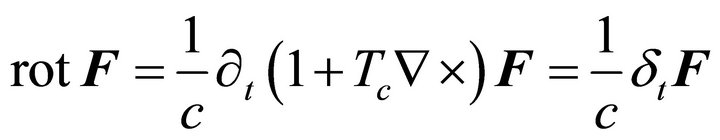 (6)
(6)
where
 (7)
(7)
Here,  ,
, 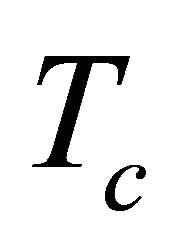 is the chiral scalar parameter,
is the chiral scalar parameter,  is the frequency and
is the frequency and  is the light velocity. Application of rot to (5) and (6) allows us to write the wave equation for
is the light velocity. Application of rot to (5) and (6) allows us to write the wave equation for .
.
 (8)
(8)
This chiral wave equation represents an equation of fourth order. For engineering of radiation and applications with artificial chiral metamaterials designed and fabricated at difference frequency ranges from microwaves to optical waves, the condition is 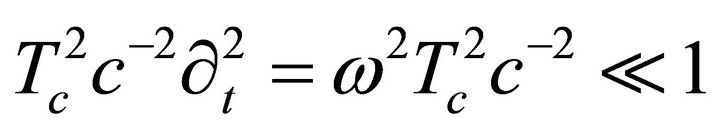 where we have the well known second order equation for chiral wave propagation [13]. Under this condition usually the E field and H field are not spatially parallel. Here we consider the new condition
where we have the well known second order equation for chiral wave propagation [13]. Under this condition usually the E field and H field are not spatially parallel. Here we consider the new condition
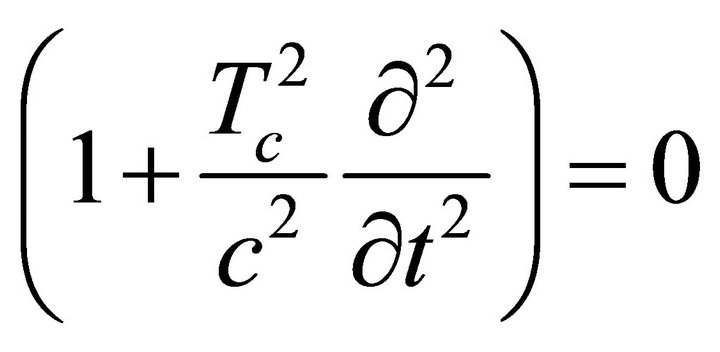 (9)
(9)
where Equation (8) is transformed from a fourth order equation to a first order one.
 (10)
(10)
and the electric field is parallel to the magnetic field . In terms of magnetic and electric polarization Equation (10) is equivalent to
. In terms of magnetic and electric polarization Equation (10) is equivalent to .,In this case we obtain the linear Beltrami Equation (10), which will be used to construct the Dirac equation in chiral or Weyl representation.
.,In this case we obtain the linear Beltrami Equation (10), which will be used to construct the Dirac equation in chiral or Weyl representation.
In [15], it was shown that the ordinary Dirac equation is equivalent to the chiral quaternionic equation  with
with 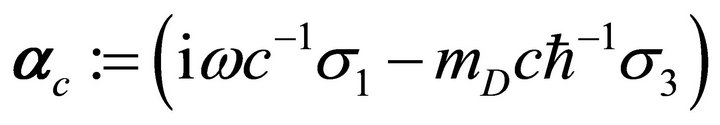 and the Maxwell Equations (5)-(8) are equivalent to the pair of chiral equations when the electric field
and the Maxwell Equations (5)-(8) are equivalent to the pair of chiral equations when the electric field  is parallel to the magnetic field
is parallel to the magnetic field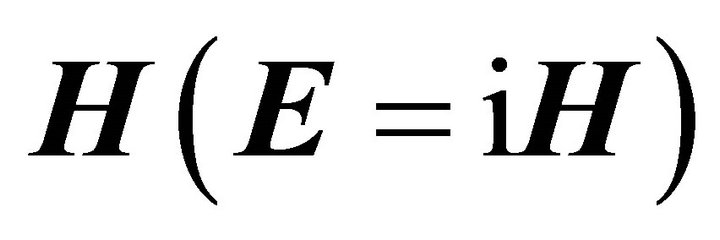 . Multiplying Equation (10) by
. Multiplying Equation (10) by  we have
we have
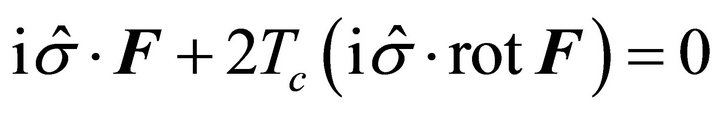 that is,
that is, 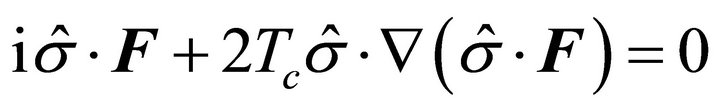
From this equation we can separate
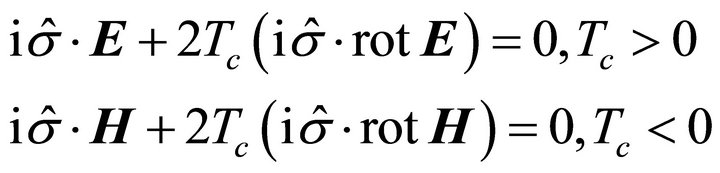
Defining  and making
and making  we obtain
we obtain
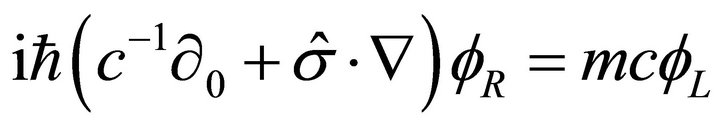 (11a)
(11a)
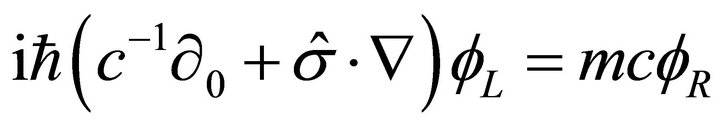 (11b)
(11b)
Equations (11) and (12) are equivalent to the quarternionic chiral Dirac equation obtained in reference [15], here  the Dirac mass. Solutions of (11) and (12) may be called the Beltrami fields (see, e.g., [13]). R and L, subscripts are associated with circularly polarized photons (right or left-handed spirals or chiral photons), that is photons that have closed trajectories to form standing waves that generate mass. If
the Dirac mass. Solutions of (11) and (12) may be called the Beltrami fields (see, e.g., [13]). R and L, subscripts are associated with circularly polarized photons (right or left-handed spirals or chiral photons), that is photons that have closed trajectories to form standing waves that generate mass. If , the Dirac equation in chiral or Weyl representation is
, the Dirac equation in chiral or Weyl representation is
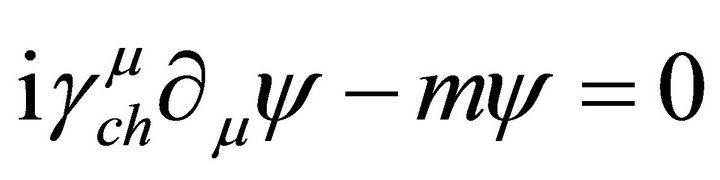 (12)
(12)
In the chiral Dirac field ,
,  and
and 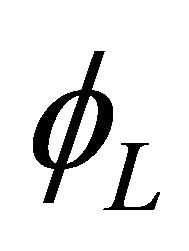 are two different types of 2-component spinor, they respectively correspond to the nonequivalent representations
are two different types of 2-component spinor, they respectively correspond to the nonequivalent representations  and
and 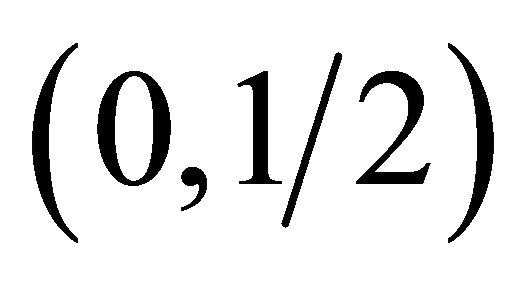 of the Lorentz group, and the chiral Dirac equation presents a relation between the two spinors. If we consider parity, then it is no longer sufficient to consider the 2-component spinors
of the Lorentz group, and the chiral Dirac equation presents a relation between the two spinors. If we consider parity, then it is no longer sufficient to consider the 2-component spinors  and
and 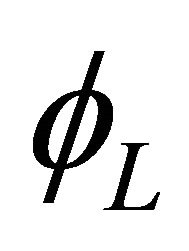 separately, but the 4-component spinor
separately, but the 4-component spinor .
.
This 4-component spinor is an irreducible representation of the Lorentz group extended by parity (i.e., the  representation).
representation).
Thus, relation between the Dirac operator and the Maxwell operators is valid if the condition (9) is fulfilled. This happen if  is parallel to
is parallel to , that is
, that is  and the vector Poynting is null.
and the vector Poynting is null.
3. Wave Equations in the New Representation: Neutrino Equations
If we write the Equations (5) and (6) explicitly in terms of the components 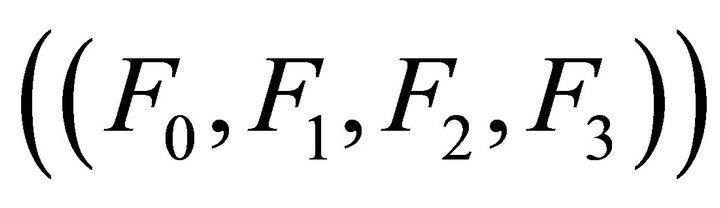 and following [11, 12] with
and following [11, 12] with 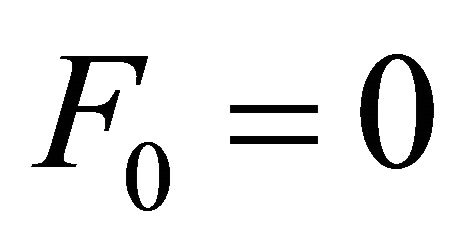 we have
we have

This expression becomes
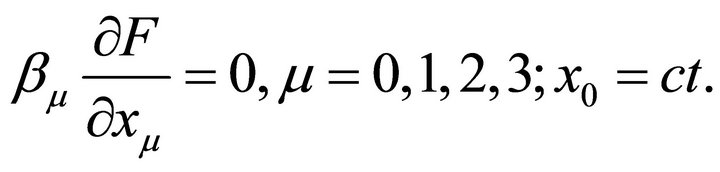 (13)
(13)
where
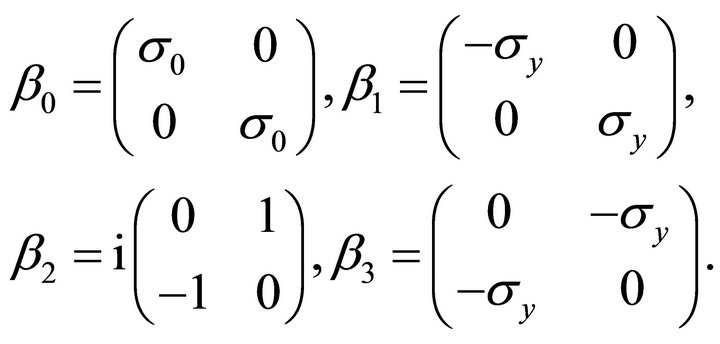
 are hermitians matrices
are hermitians matrices 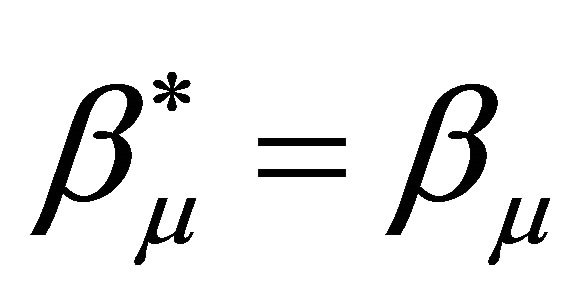 and obey the conmutation relations
and obey the conmutation relations 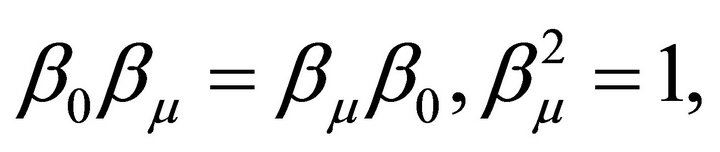 (no summation over
(no summation over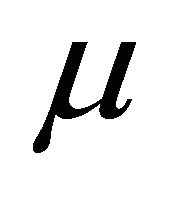 ),
), 
The description of electromagnetic phenomena in terms of a spinor language, leads to a generalization in the sense that the new formalism can make more predictions of physical observables than does the vector formalism. Some of these predictions are in one to one correspond-dence with all of the physical predictions of the vector representation of the theory. But the remaining predictions of the spinor theory have no counterpart in the vector theory [14-17], e.g., the condition of .
.
The factorization of Equation (8) is analogous to a consequence of Dirac’s factorization of the Klein Gordon equation, leading, for example to the energy coupling term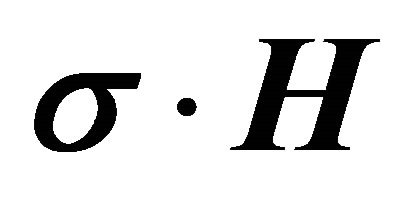 , which has no counterpart in the scalar formalism. The representation of the
, which has no counterpart in the scalar formalism. The representation of the  matrices of Equation (13) is inappropriate for the factorization of Equation (8) in two spinor equations. However Equation (13) can be reducible if we carry out the similarity transformation
matrices of Equation (13) is inappropriate for the factorization of Equation (8) in two spinor equations. However Equation (13) can be reducible if we carry out the similarity transformation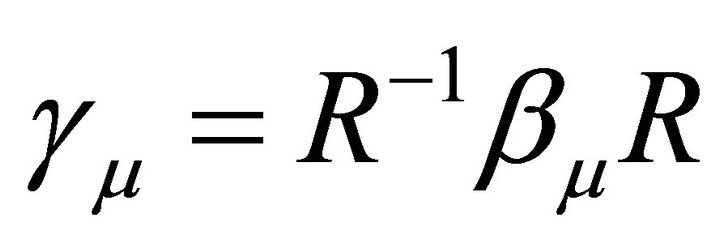 , then by means of the unitary matrix
, then by means of the unitary matrix
 (14)
(14)
Then we get the new representation
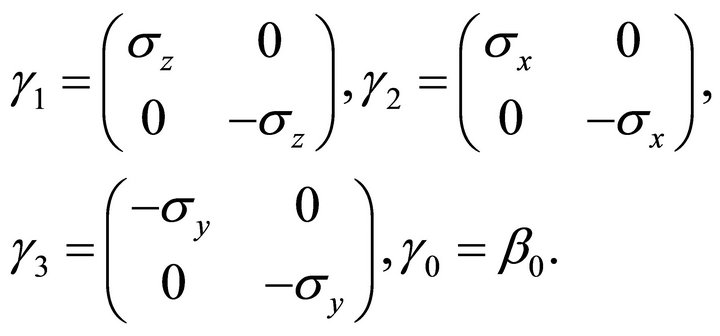
Also, we write

If we use a representation of the spin matrices  in which
in which 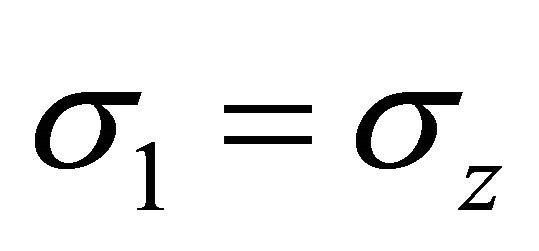 is diagonal so that
is diagonal so that
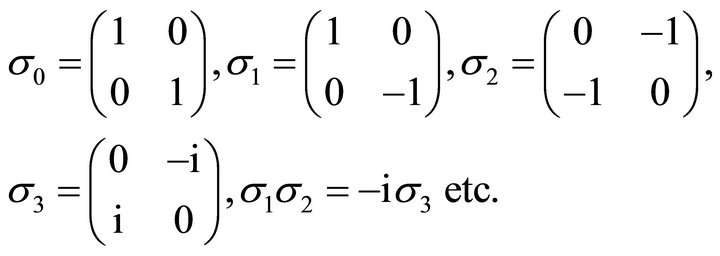 .
.
Here, we note that the well known Pauli matrices 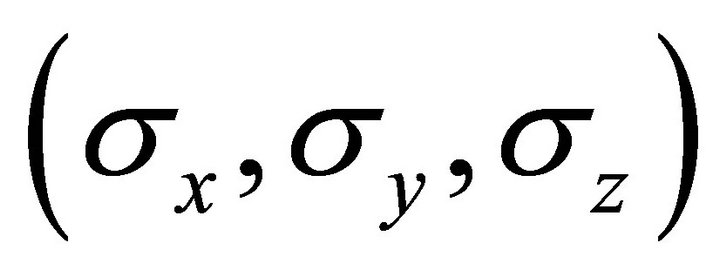 are
are  [11].
[11].
We can write

where * over  denotes the complex conjugate matrix, then Equation (13) in the new representation is
denotes the complex conjugate matrix, then Equation (13) in the new representation is
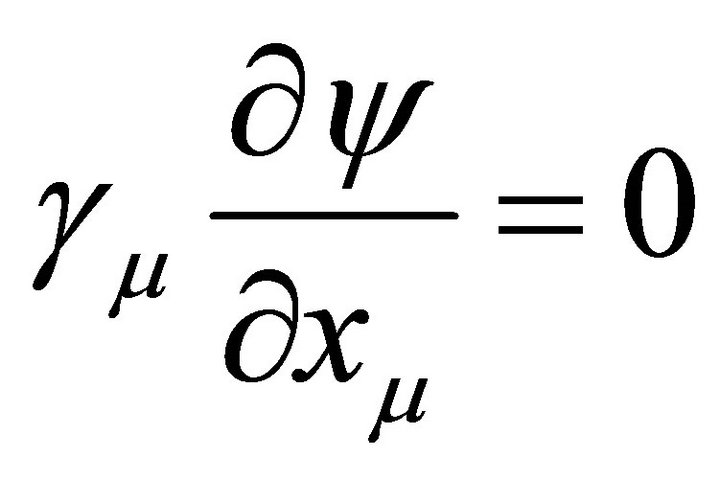 (15)
(15)
Here, we use the spinor expression

We can now write the wave Equation (15) in the new representation as a set of two equations
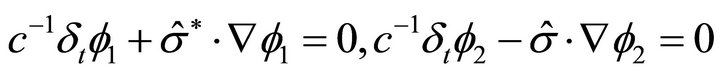 (15a, b)
(15a, b)
where 
If , these equations are formally the same as those proposed for the massless neutrino [16-18].
, these equations are formally the same as those proposed for the massless neutrino [16-18].
The difference is that in the present case the two equations are coupled through the chiral condition  when Equation (8) is factorized to Equation (10) and
when Equation (8) is factorized to Equation (10) and .
.
Now we are in conditions of generalize the concept of chirality. A chiral vacuum is defined as a vacuum for which the constitutive parameter  is a matrix. Such assumption would imply the chiral vacuum and therefore the universe itself may not have a center of symmetry.
is a matrix. Such assumption would imply the chiral vacuum and therefore the universe itself may not have a center of symmetry.
To see how the mass term appears, from Equation (10) and Equation (6) we write
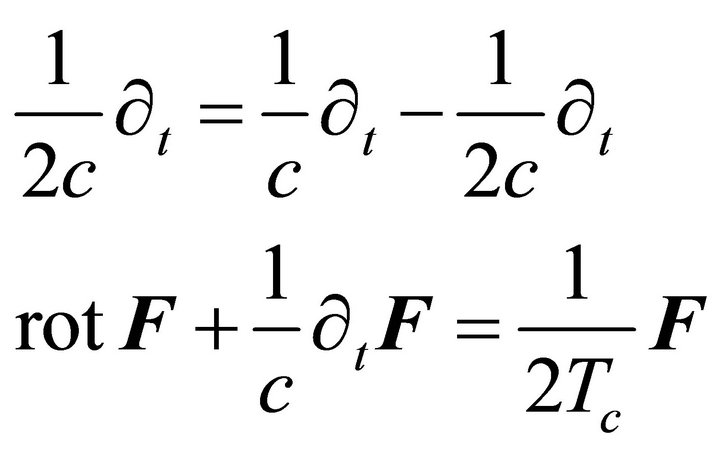
Equation (9) may be treated in scalar or matrix form. In scalar form we have 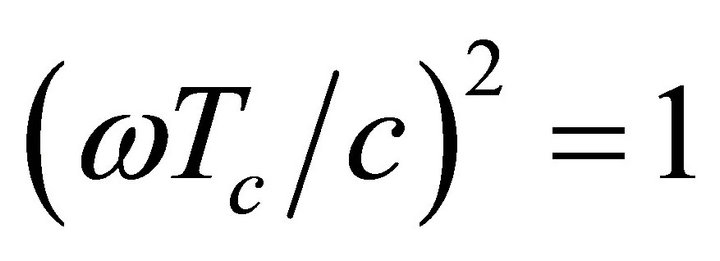 (see Section 2), but if we define the matrix
(see Section 2), but if we define the matrix  as
as , then the mass term can be associated to
, then the mass term can be associated to  the complex conjugate of
the complex conjugate of . Also,
. Also,  , and Equations (9) is transformed to matrix expression
, and Equations (9) is transformed to matrix expression
 (9’)
(9’)
Then, Equations (15a, b) are
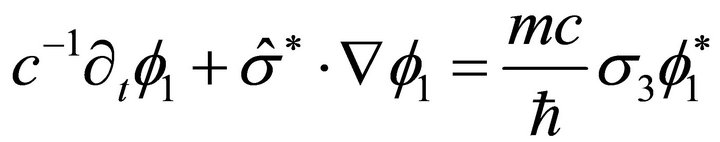 (16a)
(16a)
 (16b)
(16b)
Equations (16a) and (16b) are equivalents to the Maxwell system (5)-(10) with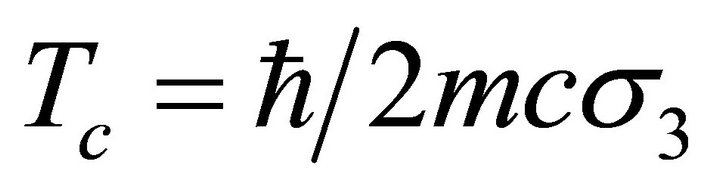 . Equations (16a) and (16b) was diagonalized following [8,10,11] and defining
. Equations (16a) and (16b) was diagonalized following [8,10,11] and defining
 (17)
(17)
where the unitary matrix  is given by (14).
is given by (14).
Thus, the two-component neutrino theory of Lee and Yang and of Landau can be obtained from (16a) or (16b). Also, it can be shown that for the free neutrino, their equations are equivalent to the Majorana equations, and thus are invariant under the full Lorentz group [18-20].
The electromagnetic interactions of neutrinos  can generate important effects, especially in astrophysical environments, where neutrinos propagate for long distances in magnetic fields both in vacuum and in matter. In the next section we discuss this problem
can generate important effects, especially in astrophysical environments, where neutrinos propagate for long distances in magnetic fields both in vacuum and in matter. In the next section we discuss this problem
4. Chiral Electromagnetic Neutrino
Dirac introduced the concept of antiparticles [21]. Now we know that for every particle there is an antiparticle.
However some particles could be self-conjugate, in the sense that particle and antiparticle could be the same. Of course such particles have to be electrically neutral.
The possibility of a self-conjugate fermion was first pointed out by Majorana [22], and hence they are called Majorana fermions while the other fermions (with distinct particles and antiparticles) are called Dirac fermions, Equations (11a) and (11b) [23]. Among the fermions of the Standard Model, only neutrinos are electrically neutral and hence qualify to be Majorana particles. But it is still an open question whether neutrinos are Majorana particles or Dirac particles. In our theory we can discriminate this situation if  with m =
with m =  or
or 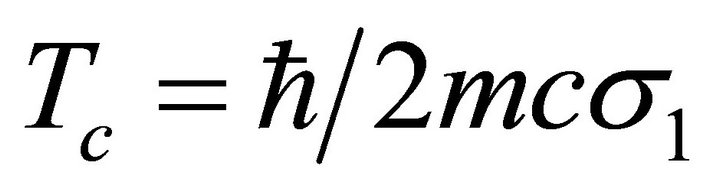 with
with  respectively (see Sections 2 and 3).
respectively (see Sections 2 and 3).
If neutrinos are Majorana particles, lepton number L is not conserved and this opens the door to generate an excess of leptons over antileptons in the early universe which can subsequently generate an excess of baryons over antibaryons, thus explaining how after annihilation of most of the particles with antiparticles, a finite but small residue of particles was left, to make up the present Universe.
To obtain the Majorana equation, the correct statement is an equation like Equation (16b)
 (18)
(18)
In the following, we will rename the field  by
by 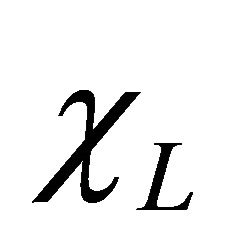 obeying Equation (18). A four-component spinor is
obeying Equation (18). A four-component spinor is
 (19)
(19)
Such that we can write Equation (18) in the chiral representation as follows 
 (20)
(20)
Or
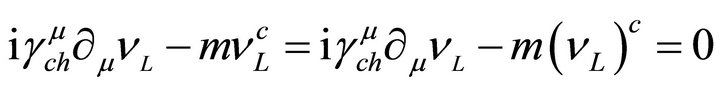 (21)
(21)
where the symbol c denotes charge conjugation as it is defined in the chiral representation. Now we can define a neutral four-component field
 (22)
(22)
Hence we have
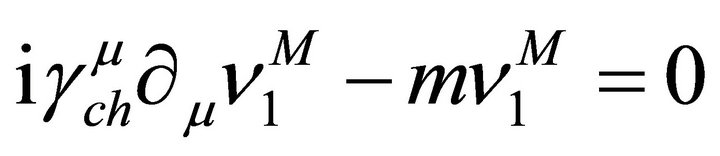 (23)
(23)
Equations (12) and (23) support the see-saw mechanism to explain why the neutrino masses, although not zero, are so tiny. With our theory, using Equations (12) and (23) it is possible to obtain a matrix mass
 (24)
(24)
The see-saw mechanism is a generic model used to understand the relative sizes of observed neutrino masses, of the order of eV. See‐saw mechanism may be the reason for the smallness of the neutrino mass . Here,
. Here,  is natural, since a
is natural, since a  mass term is forbidden by the SM symmetries,
mass term is forbidden by the SM symmetries, 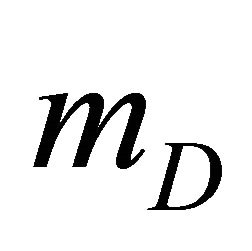 generated by the Higgs mechanism can be taken the order of the charged lepton masses and
generated by the Higgs mechanism can be taken the order of the charged lepton masses and  is not “protected” by the SM symmetries, and can be taken large.
is not “protected” by the SM symmetries, and can be taken large.
If 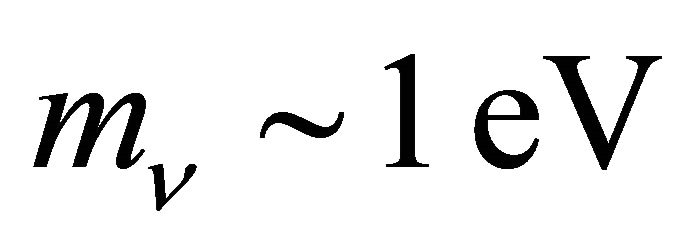 with
with 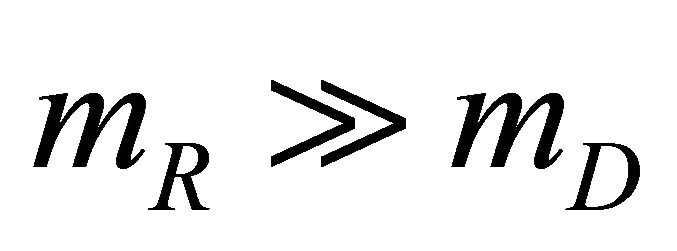 we obtain two Majorana particles, an electron neutrino light
we obtain two Majorana particles, an electron neutrino light  and a sterile heavy one
and a sterile heavy one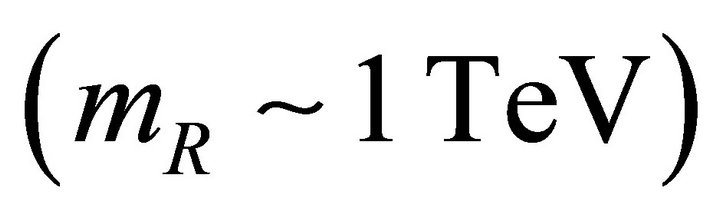 . In addition to the nonzero neutrino masses and mixing angles, the nonzero magnetic moment
. In addition to the nonzero neutrino masses and mixing angles, the nonzero magnetic moment 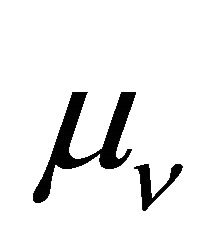 is another property of neutrinos beyond the standard model of particle physics. The importance of
is another property of neutrinos beyond the standard model of particle physics. The importance of  was first mentioned by Pauli [23]. Systematic theoretical studies of neutrino electromagnetic properties started after it was shown that in the extended Standard Model with right-handed neutrinos the magnetic moment of a massive neutrino is, in general, nonvanishing and that its value is determined by the neutrino mass [24,25].
was first mentioned by Pauli [23]. Systematic theoretical studies of neutrino electromagnetic properties started after it was shown that in the extended Standard Model with right-handed neutrinos the magnetic moment of a massive neutrino is, in general, nonvanishing and that its value is determined by the neutrino mass [24,25].
If neutrinos have a nonzero magnetic moment, it leads to precession between left and right-handed neutrinos in sufficiently strong magnetic fields [26]. In general, nondiagonal elements of the magnetic moment matrix are possible and neutrinos can be changed into different flavours and chiralities, see Equation (24). Furthermore, with the additional effect of coherent forward scattering by matter, neutrinos can be resonantly converted into those with different chiralities.
For a neutrino mass smaller than 1 eV, a Dirac neutrino has a non-zero magnetic moment proportional to the neutrino mass, that yields a very small value for the magnetic moment,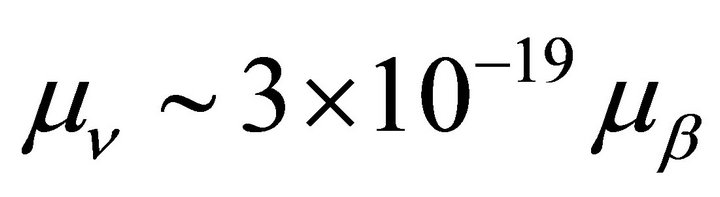 . As
. As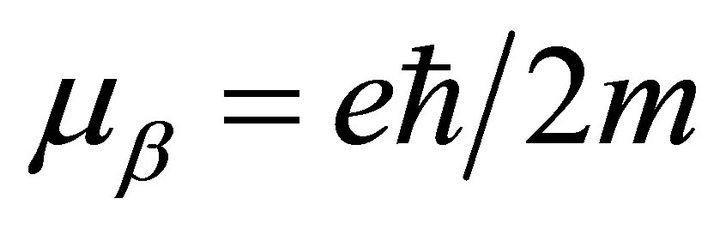 . From our theory, the Bohr magneton is proportional to
. From our theory, the Bohr magneton is proportional to  so in this case we have
so in this case we have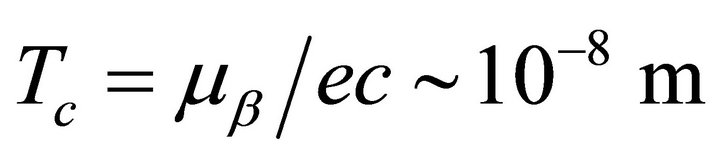 ). From data obtained of astrophysics (considering the cooling of red giant stars), we obtain
). From data obtained of astrophysics (considering the cooling of red giant stars), we obtain 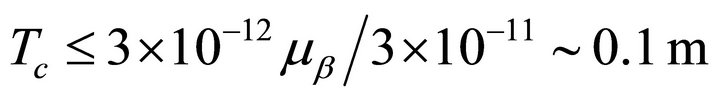 corresponding to neutrino
corresponding to neutrino . There is a gap of some orders of magnitude between the present experimental limits
. There is a gap of some orders of magnitude between the present experimental limits 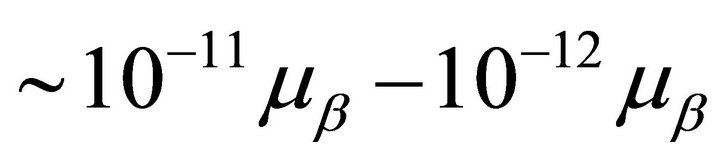 on neutrino magnetic moments and the predictions of different extensions of the Standard Model which hint at a range
on neutrino magnetic moments and the predictions of different extensions of the Standard Model which hint at a range  [24- 27]. The main problem in distinguishing Dirac from Majorana neutrino is the lack of neutrino with positive helicity. One way is to reverse the spin of the neutrino in an external magnetic field. The problem is that we need large neutrino magnetic moments and large magnetic field to obtain visible effects. However with our theory it is possible to reverse the spin using laser technology to have sufficient energy density to generate Dirac electron
[24- 27]. The main problem in distinguishing Dirac from Majorana neutrino is the lack of neutrino with positive helicity. One way is to reverse the spin of the neutrino in an external magnetic field. The problem is that we need large neutrino magnetic moments and large magnetic field to obtain visible effects. However with our theory it is possible to reverse the spin using laser technology to have sufficient energy density to generate Dirac electron
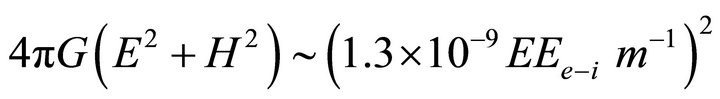 . Here
. Here 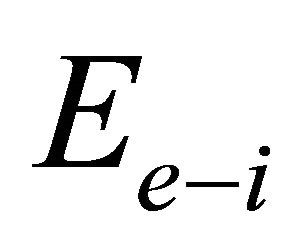 is the critical field for electron positron production
is the critical field for electron positron production  [27]. The terrestrial experimental constraints have been improved by only one order of magnitude during a period of about thirty years. Further improvements are very important, but unfortunately at the moment there is no new idea which could lead to fast improvements in the near future. However, we think that by measuring the chirality
[27]. The terrestrial experimental constraints have been improved by only one order of magnitude during a period of about thirty years. Further improvements are very important, but unfortunately at the moment there is no new idea which could lead to fast improvements in the near future. However, we think that by measuring the chirality  of the processes, we may have an improvement in the study of electromagnetic properties of neutrinos.
of the processes, we may have an improvement in the study of electromagnetic properties of neutrinos.
An example is the modeling of neutrinos propagation during core-collapse supernovae where very strong magnetic fields are believed to exist and in which the influence of neutrino electromagnetic properties has not yet been taken into account. Equation (20) is well suited to study the electromagnetic properties of neutrinos and Majorana particles [15,28,29] such as charge conjugation and time reversal, allowing for an experimental study of our Equations (16a) and (b).
5. Conclusions
In the present article we have shown that Maxwell equations can be written in the same form as the two component Dirac and neutrino equations, that is the vector representation of electromagnetic theory was factorized into a pair of two-component spinor field equations. We proposed a simple approach with the electric field  parallel to the magnetic field
parallel to the magnetic field . Our analysis is based on the chiral or Weyl form of the Maxwell equations in a chiral vacuum. This theory is a new quantum mechanics (QM) interpretation for Dirac and neutrino equation. Our research proves that the QM of particles represents the electrodynamics of the curvilinear closed chiral waves.
. Our analysis is based on the chiral or Weyl form of the Maxwell equations in a chiral vacuum. This theory is a new quantum mechanics (QM) interpretation for Dirac and neutrino equation. Our research proves that the QM of particles represents the electrodynamics of the curvilinear closed chiral waves.
The two-component Majorana equation, coming in two related forms (16a) and (16b) that are connected by a spin flip, represents the simplest possible covariant relativistic wave equation for a massive but uncharged fermion. The Dirac equation was directly derived by linearization of Equation (8), a procedure which leads to (11a, b) without explicit recourse to the Dirac theory. An important characteristic of neutrino electromagnetic properties is that they are different for Dirac and Majorana neutrinos. In particular, Majorana neutrinos cannot have diagonal magnetic or electric moments. Thus, studies of neutrino electromagnetic interactions from Equations (16a, b) can be used as a procedure to distinguish whether a neutrino is a Dirac or Majorana particle.
Moreover, CP invariance in the lepton sector puts additional constraints on the neutrino form factors and can be tested with experimental probes of neutrino electromagnetic interactions.
Also, our approach is related precisely to the polarization of photons so this theory may be important on study of uncertainly relations, specifically in the setting of quantum information and quantum cryptography, [30, 31], related with the polarization of a single photon. Our approach is related precisely linked to the polarization of photons, (See Equations (11a, 11b) and (21, 22)). Also, our theory lends itself to study mass generation in graphene devices.
5. Acknowledgements
This work has been supported by the Proyecto Mayor 8731-13, UTA-2013 of the Universidad de Tarapacá, Chile.
REFERENCES
- G. R. da Rocha, I. L. Freire R. da Rocha, et al., “Spacetime Deformations and Electromagnetism in Material Media,” Hadronic Journal, Vol. 30, No. 2, 2007, pp. 417- 446.
- Y. Tamayama, et al., “Observation of Brewster’s Effect for Transverse Electric Electromagnetic Waves in Metamaterials: Experiment and Theory,” Physical Review B, Vol. 73, No. 19, 2006, Article ID: 193104. doi:10.1103/PhysRevB.73.193104
- Y. Tamayama, et al., “An Invisible Medium for Circularly Polarized Electromagnetic Waves,” Optics Express, Vol. 16, No. 25, 2008, pp. 20869-20875. doi:10.1364/OE.16.020869
- Y. Tamayama, et al., “No-Reflection Phenomena for Chiral Media,” In: A. Petrin Ed., Wave Propagation, InTech, Rijeka, 2011, pp. 415-432. doi:10.5772/13828
- J. K. Gansel, et al., “Gold Helix Photonic Metamaterial as Broadband Circular Polarizer,”Science, Vol. 325, No. 6047, 2009, pp. 1513-1515. doi:10.1126/science.1177031
- M. Thiel, et al., “Three-Dimensional Chiral Photonic Superlattices,” Optics Letters, Vol. 35, No. 2, 2010, pp. 166-168. doi:10.1364/OL.35.000166
- A. Gsponer, “On the Equivalence of the Maxwell and Dirac Equations,” International Journal of Theoretical Physics, Vol. 41, No. 4, 2002, pp. 689-694. doi:10.1023/A:1015232427515
- W. I. Fushchyld, “On the Connection between Solutions of Dirac and Maxwell Equations,” In: W. I. Fushchyld, Ed., Scientific Works, Vol. 4, 2002, pp. 320-336.
- V. V. Dvoeglazov, “Generalized Maxwell and Weyl Equations for Massless Particles,” Revista Mexicana de Física, Vol. 49S1, 2003, pp. 99-103.
- R. H. Good, “Particle Aspect of the Electromagnetic Field Equations,” Physical Review, Vol. 105, No. 6, 1957, pp. 1914-1919. doi:10.1103/PhysRev.105.1914
- H. E. Moses, “Solution of Maxwell’s Equations in Spinor Notation,” Physical Review, Vol. 113, No. 6, 1959, pp 1670-1679. doi:10.1103/PhysRev.113.1670
- T. Vachaspati, “Maxwell Equations in the Form of Two Component Equations,” Proceedings of the Indian National Science India, Vol. 26 A, No. 4, 1959, pp. 359-363.
- A. Lakhtakia, “Beltrami Fields in Chiral Media,” World Scientific Series in Contemporary Chemical Physics, Vol. 2, No. 1, 1994, pp. 7-34.
- H. Torres-Silva and D. Torres, “Chiral Current in a Graphene Battery,” Journal of Electromagnetic Analysis and applications, Vol. 4, No. 10, 2012, pp. 426-431.
- H. Torres-Silva, “Chiral Dirac Equation Derived from Quaternionic Maxwell’s Systems,” Journal of Electromagnetic Analysis and applications, Vol. 5, No. 3, 2013. doi:10.4236/jemaa.2013.53017
- H. Torres-Silva, “Chiral Transverse Electromagnetic Standing Waves with E II H in the Dirac Equation and the Spectra of the Hydrogen Atom,” In: A. Akdagli, Ed., Behavior of Electromagnetic Waves in Different Media and Structures, Chapter 15, Book Intech, 2011, pp. 301-324.
- H. Torres-Silva and D. Torres Cabezas, “Chiral Seismic Attenuation with Acoustic Metamaterials,” Journal of Electromagnetics Analysis and Applications, Vol. 5, No. 1, 2013, pp. 10-15. doi:10.4236/jemaa.2013.51003
- L. Landau, “On the Conservation Laws for Weak Interaction,” Nuclear Physics, Vol. 3, No. 1, 1957, pp. 127-131. doi:10.1016/0029-5582(57)90061-5
- T. D. Lee and C. N. Yang, “Parity Non-Conservation and a Two-Component Theory of the Neutrino,” Physical Review, Vol. 105, No. 5, 1957, pp. 1671-1675. doi:10.1103/PhysRev.105.1671
- A. Salam, “on Parity Conservation and Neutrino Mass,” Nuovo Cimento, Vol. 5, No. 1, 1957, pp. 299-301. doi:10.1007/BF02812841
- P. M. A. Dirac, “The Quantum Theory of the Electron,” Proceedings of the Royal Society of London Series A, Containing Papers of a Mathematical and Physical Character, Vol. 117, No. 778, 1928, pp. 610-616. doi:10.1098/rspa.1928.0023
- E. Majorana, “Teoria Simmetrica Dell’ Elettrone E Del Positrone,” Il Nuovo Cimento (1924-1942), Vol. 14, No. 4, 1937, pp. 171-184. doi:10.1007/BF02961314
- W. Pauli, “Zur Quantenmechanik des Magnetischen Elektrons,” Zeitschrift für Physik A Hadrons and Nuclei, Vol. 43, No. 9-10, 1927, pp. 601-623. doi:10.1007/BF01397326
- C. Giunti and C. W. Kim, “Fundamentals of Neutrino Physics and Astrophysics,” Oxford University Press, Oxford.
- S. Bilenky, “Introduction to the Physics of Massive and Mixed Neutrinos,” Lecture Notes in Physics, Vol. 817, 2010. doi:10.1007/978-3-642-14043-3
- N. F. Bell, et al., “How Magnetic is the Dirac Neutrino?” Physical Review Letters, Vol. 95, 2005, Article ID: 151 802.
- H. Torres-Silva, “Physical Interpretation of the Dirac Equation with Electromagnetic Mass,” The Scitech, Journal of Science & Technology, 2012, pp. 127-133.
- A. Studenikin, “Neutrino Magnetic Moment,” Nuclear Physics B, Vol. 188, No. 1, 2009, pp. 220-222.
- J. Casanova, et al., “Quantum Simulation of the Majorana Equation and Unphysical Operations,” Physical Review X, Vol. 1, No. 2, 2011, Article ID: 021018. doi:10.1103/PhysRevX.1.021018
- L. Rozena, et al, “Violation of Heisenbergs’s Measurement-Disturbance Relationship by Weak Measurements,” Physical Review Letters, Vol. 109, 2012, Article ID: 100 404.
- J. Erhart, et al., “Experimental Demonstration of a Universally Valid Error-Disturbance Uncertainty Relation in Spin Measurements”, Nature Physics, Vol. 8, 2012, pp 185-189. doi:10.1038/nphys2194

