Journal of Electromagnetic Analysis and Applications
Vol.5 No.1(2013), Article ID:27313,7 pages DOI:10.4236/jemaa.2013.51004
Efficient MT-Based Compact FDTD Algorithm for Longitudinally-Magnetized Ferrite-Loaded Waveguides
![]()
Electronic Department, Faculty of Engineering Sciences, Mentouri University Constantine, Constantine, Algeria.
Email: abdelouahab.benouatas@gmail.com
Received November 9th, 2012; revised December 10th, 2012; accepted December 19th, 2012
Keywords: Compact 2D FDTD; Dispersion; Divergence Theorem; Mobius Transform; Longitudinally-Magnetized Ferrite
ABSTRACT
In this work, a compact finite-difference time-domain (FDTD) algorithm with a memory-reduced technique is proposed for the dispersion analysis of rectangular waveguides either fully or partially loaded with longitudinally-magnetized ferrite. In this algorithm, the divergence theorem is used to eliminate the longitudinal components of the electric and magnetic flux densities. The mobius transform (MT) technique is applied for the first time to obtain the equations relating the magnetic field to the magnetic flux density in a ferrite medium. Some examples are presented to validate the obtained algorithm with numerical results: good agreement is obtained with a significant reduction in the memory space requirement compared to the conventional algorithm.
1. Introduction
The compact 2D FDTD method was introduced for the aim of reducing the computational costs of the conventional 3D FDTD method. It appeared in two versions: complex [1,2] and real [3]. The later version was introduced to improve the efficiency of first; nevertheless, it was proved [4] that it does not apply to some cases of anisotropy.
The compact FDTD method has been applied to isotropic, dispersive [5-7] and leaky media [8-10]. Ferriteloaded waveguides have been analyzed by the complex version in [11]. In [12], it is shown that the real valued version applies also to ferrite materials. The method is based on the three fields D, B and H, i.e., nine field components are involved which requires large memory space for the storage of all field variables, especially in the case of a very large structure and a fine mesh.
On the other hand, a memory-efficient FDTD method was introduced in [13]. In this method, the divergence theorem is used to eliminate the longitudinal field components leading to a significant reduction in memory space requirements. This approach has been used to improve the efficiency of many other recent FDTD methods [14,15].
In this paper, the memory reduced technique described above is used in an attempt to improve the efficiency of the compact FDTD algorithm applied to rectangular waveguides loaded either fully or partially with longitudinally-magnetized ferrite. The linearity of the constitutive relation of these materials in the direction of propagation (which is also the direction of magnetization) allows the elimination of the longitudinal components of the electric and magnetic flux densities. The mobius transform technique is applied for the first time in this paper to obtain the equations relating the magnetic field to the magnetic flux in the longitudinally-magnetized ferrite medium using two different approaches. Some examples are given to validate the obtained algorithm with numerical results.
2. Derivation
From the curl Maxwell equations we obtain the following expressions for the transverse components of the electric and magnetic flux densities
 (1)
(1)
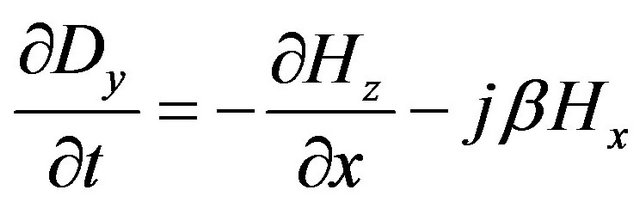 (2)
(2)
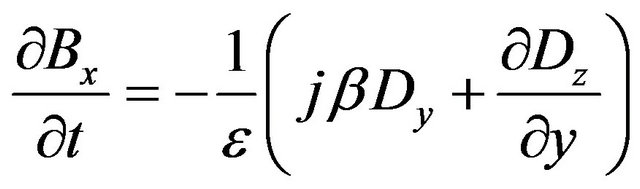 (3)
(3)
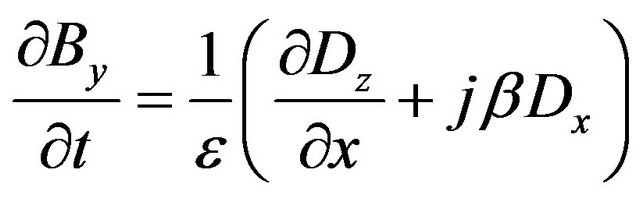 (4)
(4)
where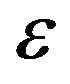 is the permittivity of the medium.
is the permittivity of the medium.
Two other expressions can be obtained for the longitudinal components from the divergence theorem of a charge free longitudinally-magnetized ferrite
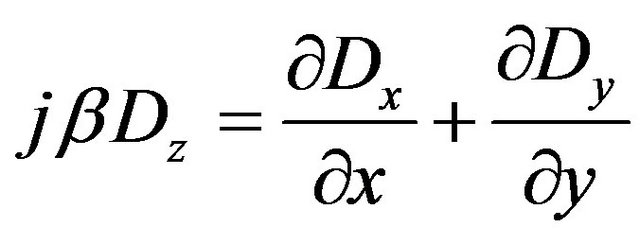 (5)
(5)
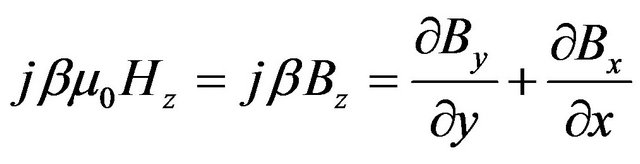 (6)
(6)
Eliminating 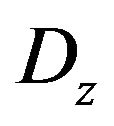 and
and  from (1)-(4) using (5) and (6), we obtain four complex valued equations for the transverse components
from (1)-(4) using (5) and (6), we obtain four complex valued equations for the transverse components
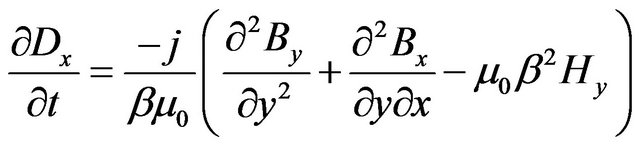 (7)
(7)
 (8)
(8)
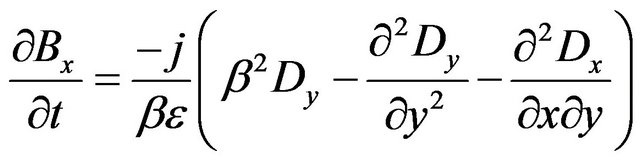 (9)
(9)
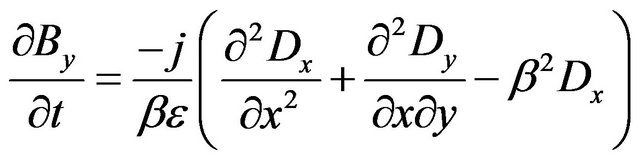 (10)
(10)
To transform them to real-valued equations, we introduce a phase shift between the group of TE mode components and the group of TM mode components as proposed in [3]; the following equations result
 (11)
(11)
 (12)
(12)
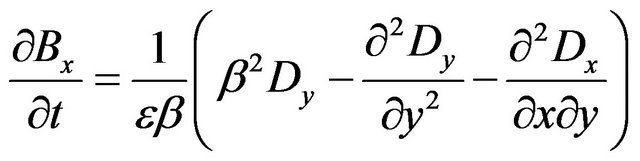 (13)
(13)
 (14)
(14)
The goal of the next section is to derive a suitable finite difference form for these equations. The equations relating the magnetic field to the magnetic flux density will be given later in Section 4.
3. Discretization and Boundary Treatment
Let’s take the Equation (13) for the 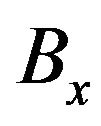 component as an example. To obtain the descretized form of (13) we start with the descretized form of (3), which is
component as an example. To obtain the descretized form of (13) we start with the descretized form of (3), which is
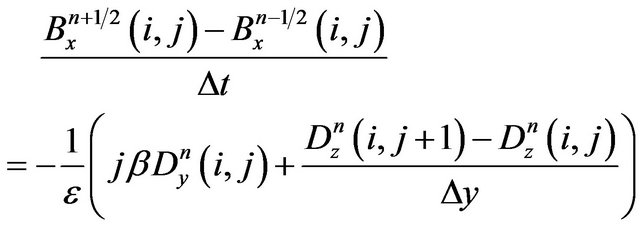 (15)
(15)
Here 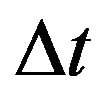 and
and 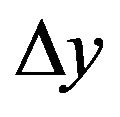 are the time and space increments respectively.
are the time and space increments respectively.
From the descretized form of (5) we obtain for 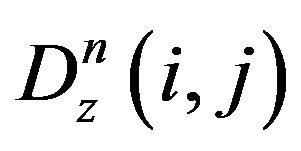 and
and 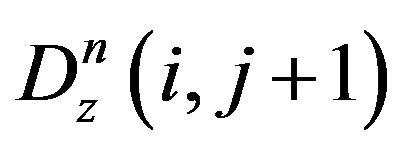 the expressions
the expressions
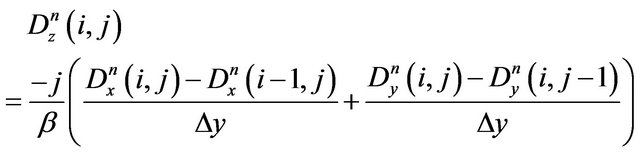 (16)
(16)
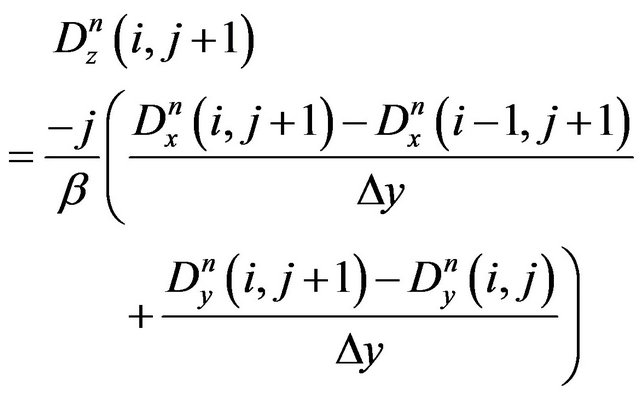 (17)
(17)
Substituting (16) and (17) into (15) to eliminate , applying the phase shift between the TE and TM mode components and after some arrangements we obtain
, applying the phase shift between the TE and TM mode components and after some arrangements we obtain
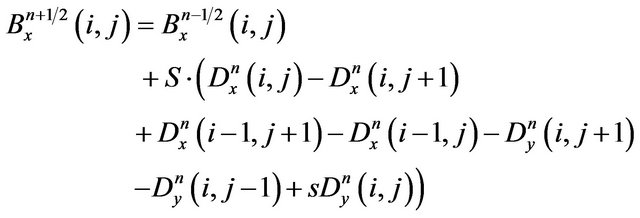 (18)
(18)
which is the discretized form of (13). Here we have: 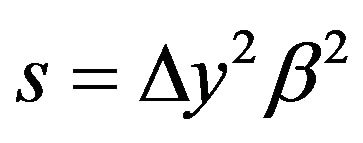 and
and .
.
For a guiding structure with perfectly conducting walls, the tangential electric and the normal magnetic flux densities are null at these walls. Suppose that the wall is located at the cell of index : since
: since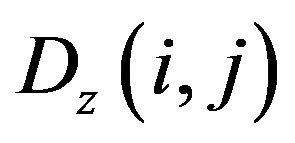 is null at this wall, the expression (15) reduces to
is null at this wall, the expression (15) reduces to
 (19)
(19)
Substituting (17) into (19) we obtain the following expression
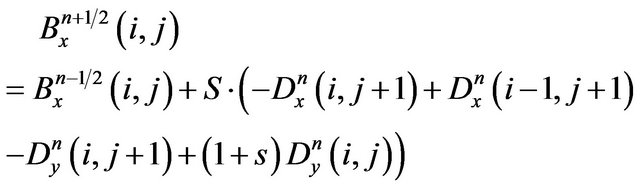 (20)
(20)
which is the modified form of (18) at the considered wall. Similarly we obtain the remaining expressions at the other walls of the guiding structure.
4. Mobius Transform Formulation
Dispersive media were studied in the 1990’s and many methods have been presented for the integration of their characteristics in the FDTD code. The most known among them are the recursive convolution (RC), the auxiliary differential equation (ADE) and the z transform (ZT).
A new technique was presented by Pereda and his co-workers in [16]. It consists in writing the frequencydependent constitutive relation of the dispersive media in the Laplace domain then maps it in the z domain using the mobius transform (MT). This technique was applied to chiral media in [17]; no application of this technique to ferrites is reported in literature so far.
In the following, the mobius transform technique is applied to obtain the equations relating the magnetic field to the magnetic induction in a ferrite medium following two different approaches. For the sake of clarity, the spatial indexes 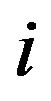 and
and  are omitted from the expressions of the fields.
are omitted from the expressions of the fields.
4.1. First Approach
Starting with constitutive relation of the longitudinallymagnetized ferrite in the frequency domain
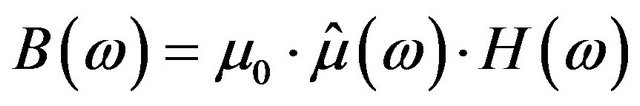 (21)
(21)
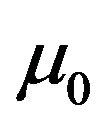 is the permeability of vacuum and
is the permeability of vacuum and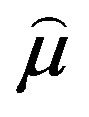 is the Polder tensor of the ferrite defined as:
is the Polder tensor of the ferrite defined as:
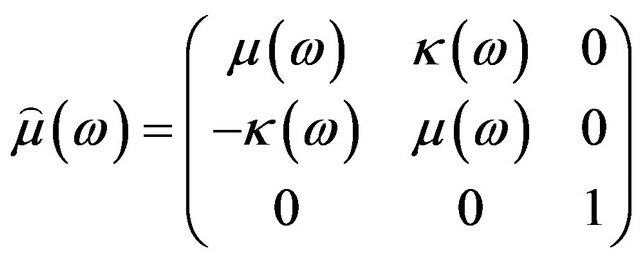 (22)
(22)
 (23)
(23)
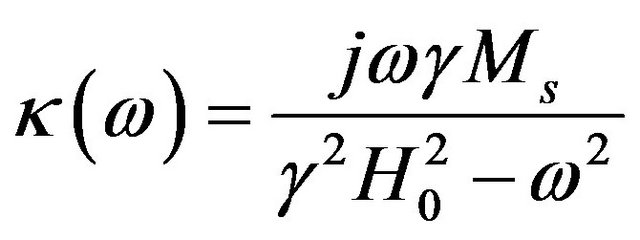 (24)
(24)
where  is the gyromagnetic ratio of the ferrite;
is the gyromagnetic ratio of the ferrite; 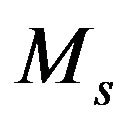 and
and  are magnetization to saturation and the static applied magnetic field respectively.
are magnetization to saturation and the static applied magnetic field respectively.
Writing the Polder tensor components in the La Place domain using: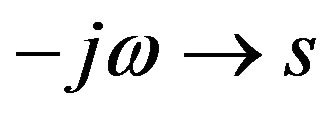 , we obtain
, we obtain
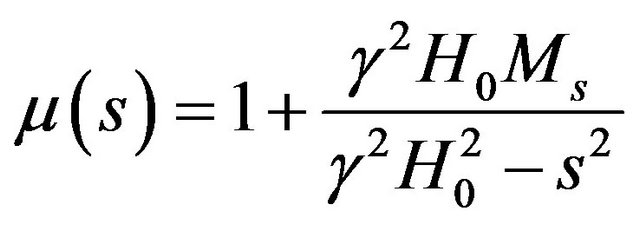 (25)
(25)
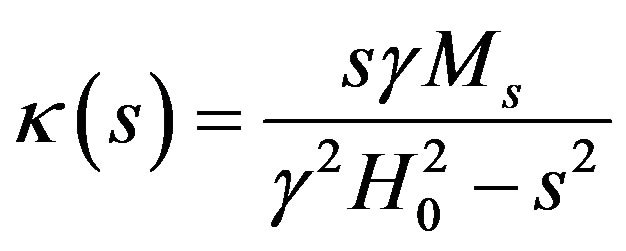 (26)
(26)
The constitutive relation in this case yields for the transverse components
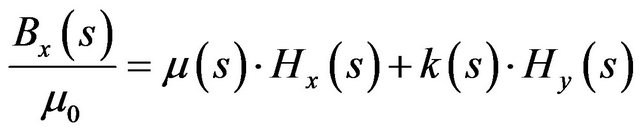 (27)
(27)
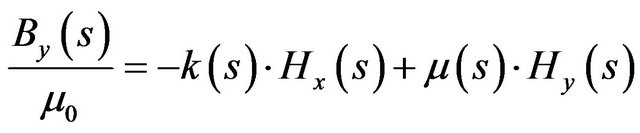 (28)
(28)
To map these equations in the z domain, we use the mobius transform
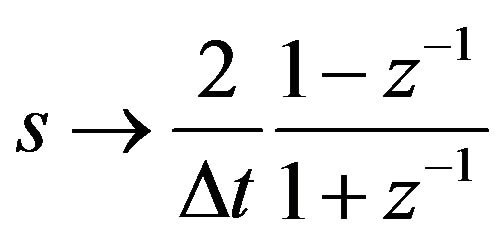 we obtain
we obtain
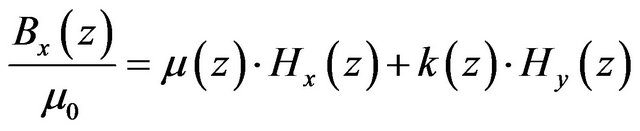 (29)
(29)
 (30)
(30)
where
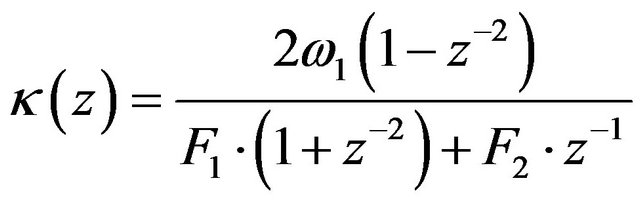 (31)
(31)
 (32)
(32)
and
 .
.
Apply to (29) and (30) the relation (
( denotes any field variable) to get to the sampled time domain and then separating the unknown entities (
denotes any field variable) to get to the sampled time domain and then separating the unknown entities ( and
and ) from the known ones
) from the known ones 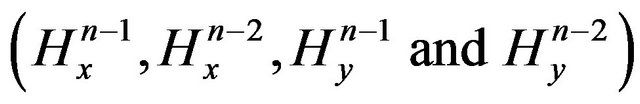 , we obtain
, we obtain
 (33)
(33)
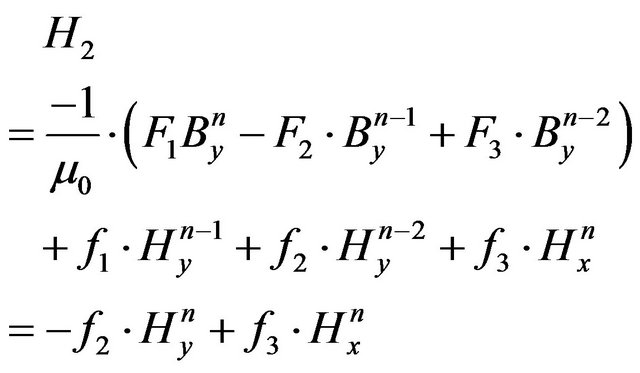 (34)
(34)
with: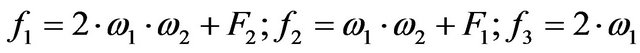 .
.
Finally, the magnetic field can be obtained by solving (33) and (34) for the unknowns and
and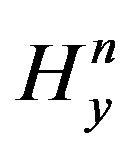
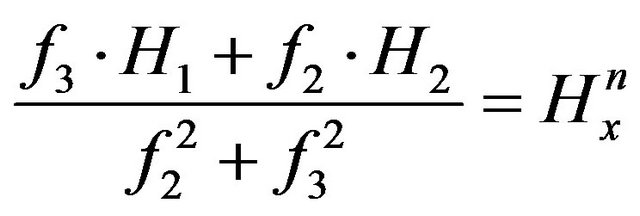 (35)
(35)
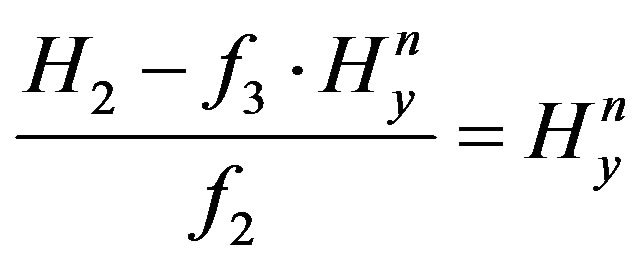 (36)
(36)
4.2. Second Approach
Starting with the frequency-dependent constitutive relations of ferrites
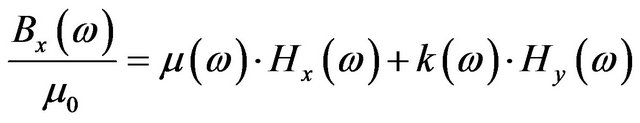 (37)
(37)
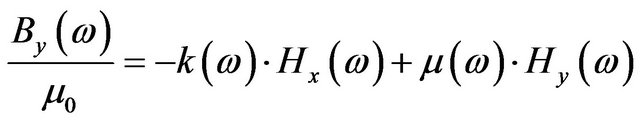 (38)
(38)
Developing the expression above then using the inverse Fourier transform  to get back to the time domain, we obtain
to get back to the time domain, we obtain
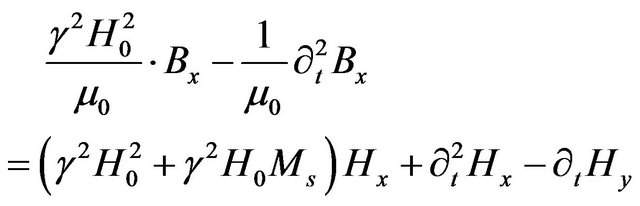 (39)
(39)
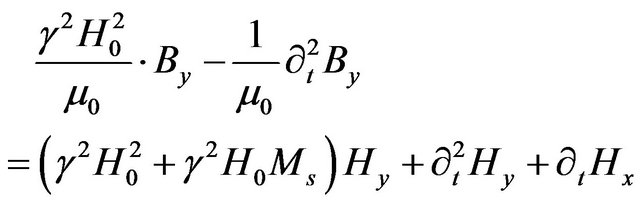 (40)
(40)
In [16], it is shown that the application of the mobius transform to the frequency-dependent relation of the medium is equivalent to the differentiation of this relation using the following approximating formulas [16]
 (41)
(41)
Here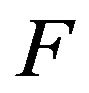 denotes any field component,
denotes any field component,  the order of the dispersive medium (equals 2 in our case) and
the order of the dispersive medium (equals 2 in our case) and 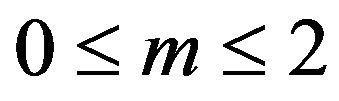 .
.
Using (41), we obtain the following approximating relations for the zero’th, the first and the second differentiation
 (42)
(42)
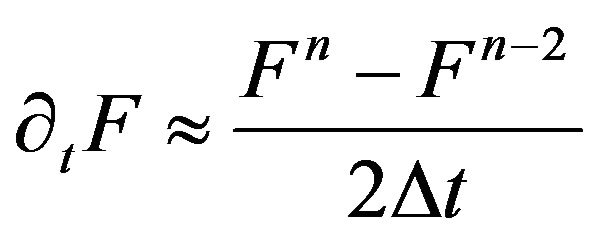 (43)
(43)
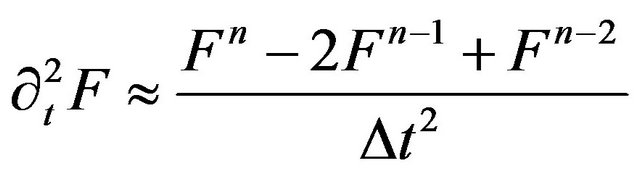 (44)
(44)
Using these formulas to approximate the time derivatives in (39) and (40) then solving these two equations for the two unknowns, we obtain the same algorithm obtained by the first approach.
5. Numerical Results
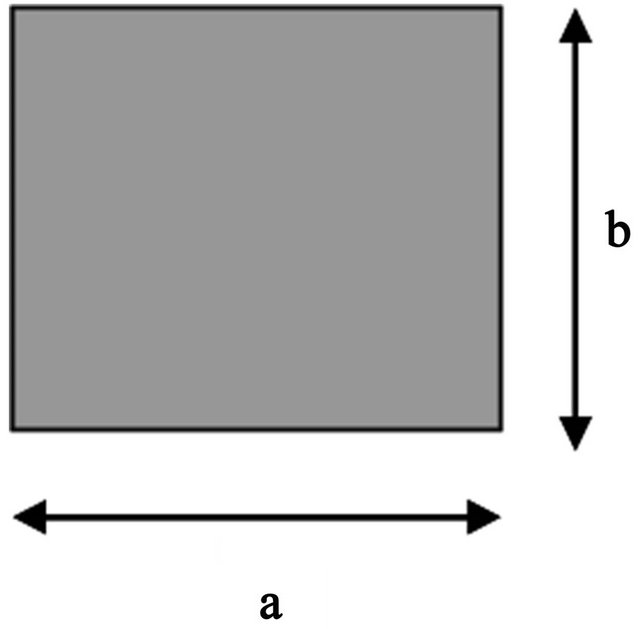
To show the validity of the algorithm above, we propose to calculate the dispersion characteristic of the dominant mode for the waveguides shown in Figure 1.
The first is a rectangular waveguide of height 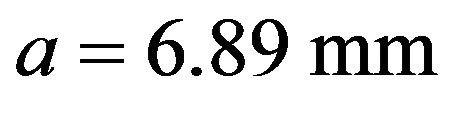 and width
and width , completely-filled with longitudinally-magnetized ferrite of relative permittivity
, completely-filled with longitudinally-magnetized ferrite of relative permittivity 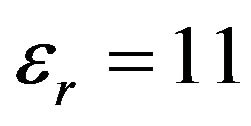 (Figure 1(a)). The static magnetization of the ferrites
(Figure 1(a)). The static magnetization of the ferrites 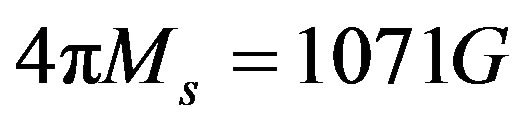 and the applied magnetic field is of strength
and the applied magnetic field is of strength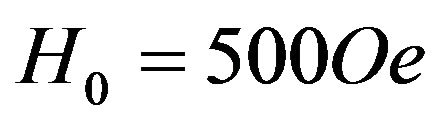 .
.
For the simulation of this waveguide, a rough mesh resolution 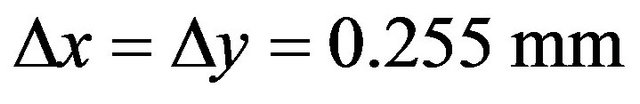 has been used, i.e.,
has been used, i.e.,  grid points in the
grid points in the 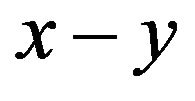 plane. A Gaussian pulse was chosen for the excitation. The value of the time step depends on the chosen value of the phase constant and the number of time iterations was set at 5000 for each simulation. The results obtained for the dominant mode of this waveguide are shown in Figure 2(a); good agreement with those found in literature [18].
plane. A Gaussian pulse was chosen for the excitation. The value of the time step depends on the chosen value of the phase constant and the number of time iterations was set at 5000 for each simulation. The results obtained for the dominant mode of this waveguide are shown in Figure 2(a); good agreement with those found in literature [18].
The second is a WR90 rectangular waveguide, partially filled with a symmetric ferrite slab 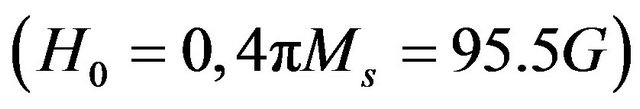 of relative permittivity
of relative permittivity  and of width
and of width  (Figure 1(b)).
(Figure 1(b)).
Similarly, a uniform grid with the dimensions  was used for the simulation of this waveguide which correspond to a grid size
was used for the simulation of this waveguide which correspond to a grid size . The source of excitation was a Gaussian pulse and the number of time iterations is 9000 for each simulation. The
. The source of excitation was a Gaussian pulse and the number of time iterations is 9000 for each simulation. The
 (a)
(a)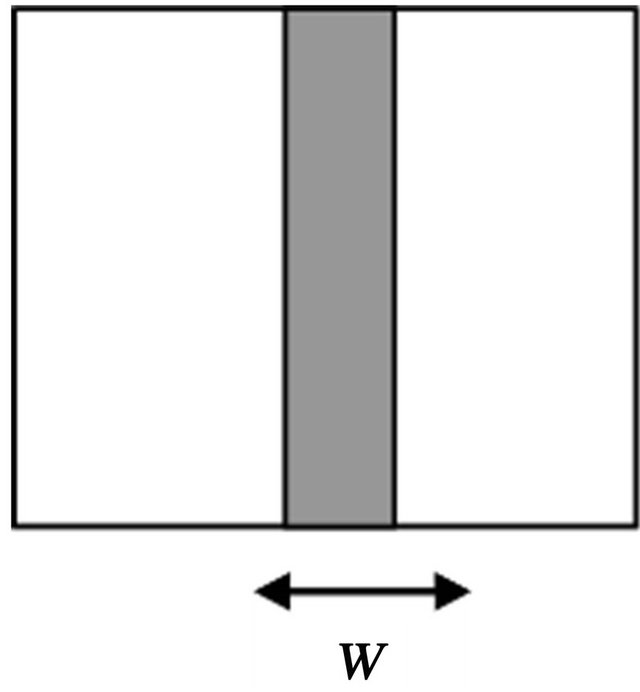 (b)
(b)
Figure 1. Different longitudinally-magnetized ferrite-loaded waveguides: (a) Completely-filled waveguide; (b) Partiallyfilled waveguide.
results obtained for the dispersion characteristic of the dominant mode for two values of the slab width are shown in Figure 2(b). Phase constant and frequency are normalized with respect to the vacuum wave number and the magnetization frequency respectively as described in [19] and the results obtained are in good agreement with those presented in the same reference.
A surface plot of the y-component of the electric field is shown in Figure 2(c). The field distribution of this field forms one lobe along the x-direction which correspond to the dominant TE10 mode.
The simulations were performed on Pentium III computer using Matlab 7.1.
A comparison of efficiency in calculating the dispersion curve of the dominant mode in the simple structure of Figure 1(a) between the present method and the ninecomponent is shown in Table 1.
As can be seen in the comparative table above, the time needed for the simulation is practically the same in the two methods, however, the memory space is reduced significantly (about 28.57%) in this method compared to the nine-component one.
In fact, much more efficient compact FDTD methods have been introduced recently, for instance: a compact FDTD method based on the alternating direction implicit (ADI) in which the time step is not limited by the CFL
 (a)
(a) (b)
(b)
Figure 2. Obtained results: (a) Phase constant versus frequency of the dominant mode of the completely-filled waveguide; (b) Normalized phase constant versus normalized frequency of the dominant mode of the waveguide of Figure 1(b) for two different values of the ferrite slab width; and (c) Surface plot of the Dy component of the dominant mode for the fully filled waveguide of Figure 1(a).
Table 1. Comparison of this method and the nine-component method.

criterion was presented in [20,21], a compact pseudo spectral time domain (PSTD) method in [22] and a compact FDTD method with weighted Laguerre polynomials in [23,24]. They have been applied to isotropic and anisotropic media; nevertheless, no application of these methods to anisotropic dispersive media characterized by a permittivity or permeability tensor with frequencydependent components (such as ferrites) has been reported, which make of this work the first to deal with this issue.
One of the limitations of the method presented here is that it does not apply to charged media and conductors because the divergence of the electric flux density is not null; nevertheless, an extension of this method to include these media is possible using the same approach presented in [13].
A null value for the phase constant can not be used also ( becomes singular); nevertheless, a sufficientlysmall value can be used instead. For the waveguide of Figure 1(a), we have taken
becomes singular); nevertheless, a sufficientlysmall value can be used instead. For the waveguide of Figure 1(a), we have taken 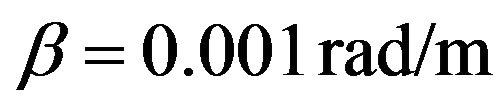 for the calculation of the cut-off frequency.
for the calculation of the cut-off frequency.
As can be seen in the comparative table above, the code complexity in this method is slightly increased compared to the conventional method. This is due to the boundary treatment of the fields. Consequently, a slight increase in the computational time results.
6. Conclusions
In this paper, an efficient compact FDTD algorithm was proposed for the dispersion analysis of waveguides loaded with longitudinally-magnetized ferrite. The divergence theorem is used to eliminate the longitudinal field components reducing hence the total number of field components. The obtained equations for the electric and magnetic flux densities are suitably descretized and a correction of the obtained equations at the perfectly conducting walls of the waveguide is given.
The mobius transform technique was applied for the first time in this paper to obtain the equations relating the magnetic field to the magnetic flux density following two different approaches. In the first, the constitutive relation written in the Laplace domain is mapped in the z domain using the mobius transform. The obtained equations are decoupled and the expressions for the transverse magnetic field components are obtained. In the second, the constitutive relation written in the frequency domain is transformed to differential equations in the time domain. The obtained differential equations are discretized using suitable approximating formulas. Both approaches lead to the same result.
The algorithm was applied for the calculation of dispersion of some rectangular waveguides partially or totally filled with longitudinally-magnetized ferrite. The obtained numerical results were in good agreement with those found in the literature and memory space requirements are reduced compared with those of the conventional compact FDTD algorithm.
REFERENCES
- S. Xiao, R. Vahldieck and H. Jin, “Full-Wave Analysis of Guided Wave Structures Using a Novel 2-D FDTD,” IEEE Microwave Guided Wave Letters, Vol. 2, No. 5, 1992, pp. 165-167. doi:10.1109/75.134342
- A. Asi and L. Shafai, “Dispersion Analysis of Anisotropic Inhomogeneous Waveguides Using Compact 2D-FDTD,” Electronic Letters, Vol. 28, No. 15, 1992, pp. 1451-1452. doi:10.1049/el:19920923
- S. Xiao and R. Vahldieck, “An Efficient 2-D FDTD Algorithm Using Real Variables,” IEEE Microwave Guided Wave Letters, Vol. 3, No. 5, 1993, pp. 127-129. doi:10.1109/75.217204
- A. P. Zhao, J. Juntunen and A. V. Raisanen, “Relationship between the Compact Complex and Real Variable 2- D FDTD Methods in Arbitrary Anisotropic Dielectric Waveguides,” IEEE MTT-S International Microwave Symposium, Denver, 8-13 June 1997, pp. 83-87.
- D. F. P. Pile, “Compact-2D FDTD for Waveguides Including Materials with Negative Dielectric Permittivity, Magnetic Permeability and Refractive Index,” Applied Physics B, Vol. 81, No. 5, 2005, pp. 607-613. doi:10.1007/s00340-005-1916-0
- J. J. Hu, G. Ren, X. Yu, G. Wang, P. P. Shum, C. Lu, K. T. V. Grattan and T. Sun, “A Generalized 2D FDTD Model for Photonic Crystal Fibers with Frequency Dependent Media,” Optical and Quantum Electronics, Vol. 39, No. 12-13, 2007, pp. 1133-1143.
- P. Dastmalchi, N. Granpayeh and M. R. Disfani, “ThreeDimensional Gap Plasmon Power Splitters Suitable for Photonic Integrated Circuits,” Optical and Quantum Electronics, Vol. 42, No. 4, 2010, pp. 231-239.
- M. Fujii and S. Kobayashi, “Accurate Analysis of Losses in Waveguide Structures by Compact Two-Dimensional FDTD Method Combined with Autoregressive Signal Analysis,” IEEE Transactions on Microwave Theory and Techniques, Vol. 44, No. 6, 1996, pp. 970-975.
- F. Xu and K. Wu, “A Compact 2-D Finite-Difference Time-Domain Method for General Lossy Guiding Structures,” IEEE Transactions on Antennas and Propagation, Vol. 56, No. 2, 2008, pp. 501-506.
- Q. Lu, W. Guo, D. C. Byrne and J. F. Donegan, “Compact 2-D FDTD Method Combined with Padé Approximation Transform for Leaky Mode Analysis,” Journal of Light Wave Technology, Vol. 28, No. 11, 2010, pp. 1638- 1645.
- N. Dib and L. Katehi, “Dispersion Analysis of Multilayer Planar Lines Containing Ferrite Regions Using an Extended 2D-FDTD Method,” IEEE Antennas and Propagation Society International Symposium Digest, Ann Arbor, 28 June-2 July 1993, pp. 842-845.
- Q. X. Chu, S. F. Zhang and B. Xiong, “A Compact 2-D FDTD Algorithm for the Analysis of Nonreciprocal Ferrite Phase Shifters,” Proceedings of the 3rd IEEE International Conference on Microwave and Millimeter Wave Technology, Beijing, 17-19 August 2002, pp. 1113-1116.
- G. D. Kondylis, F. De Flaviis, G. J. Pottie and T. Itoh, “A Memory-Efficient Formulation of the Finite-Difference Time-Domain Method for the Solution of Maxwell Equations,” IEEE Transactions on Microwave Theory and Techniques, Vol. 49, No. 7, 2001, pp. 1310-1320. doi:10.1109/22.932252
- G. W. Shao, S.-J. Lai and T. Z. Huang, “Compact 2D Full-Wave Order-Marching Time-Domain Method with a Memory Reduced Technique,” Progress in Electromagnetic Research Letters, Vol. 6, 2009, pp. 157-164. doi:10.2528/PIERL08111811
- Y. Yi, B. Chen, W.-X. Sheng and Y.-L. Pei, “A Memory-Efficient Formulation of the Unconditionally Stable FDTD Method for Solving Maxwell’s Equations,” IEEE Transactions on Antennas and Propagation, Vol. 55, No. 12, 2007, pp. 3729-3733. doi:10.1109/TAP.2007.910499
- J. A. Pereda, Á. Vegas and A. Prieto, “FDTD Modeling of Wave Propagation in Dispersive Media by Using the Mobius Transformation Technique,” IEEE Transactions on Microwave Theory and Techniques, Vol. 50, No. 7, 2002, pp. 1689-1695.
- J. A. Pereda, A. Grande, O. González and Á. Vegas, “FDTD Modeling of Chiral Media by Using the Mobius Transformation Technique,” IEEE Antennas and Wireless Propagation Letters, Vol. 5, No. 1, 2006, pp. 327-330. doi:10.1109/LAWP.2006.878902
- H. Sakli, H. Benzina, T. Aguili and J. W. Tao, “Propagation Constant of a Rectangular Waveguides Completely Full of Ferrite Magnetized Longitudinally,” Journal of Infrared, Millimeter, and Terahertz Waves, Vol. 30, No. 8, 2009, pp. 877-883.
- H. A. Elmikati, E. M. Eid, M. M. Abd-elrazzak and I. M. Eldiwani, “Analysis of Rectangular Waveguides Loaded with Longitudinally Magnetized Ferrite,” Proceedings of the 7th IEEE Mediterranean Electrotechnical Conference, Antalya, 12-14 April 1994, pp. 465-468.
- S. Ju and H. Kim, “Investigation of an Unconditionally Stable Compact 2D ADI-FDTD Algorithm: Formulations, Numerical Stability, and Numerical Dispersion,” IEEE of Antennas and Propagation Society International Symposium, 16-21 June 2002, San Antonio, pp. 639-642.
- P. Ding, G. Wang, H. Lin and B. Z. Wang, “A Compact Unconditionally Stable FDTD Method,” IEEE Antennas and Wireless Propagation Letters, Vol. 5, No. 1, 2006, pp. 520-524.
- G. Zhao and Q. H. Liu, “The 2.5-D Multidomain Pseudospectral Time-Domain Algorithm,” IEEE Transactions on Antennas and Propagation, Vol. 51, No. 3, 2003, pp. 619- 627.
- W. Shao, B. Wang, X. Wang and X. Liu, “Efficient Compact 2-D Time-Domain Method with Weighted Laguerre Polynomials,” IEEE Transactions on Electromagnetic Compatibility, Vol. 48, No. 3, 2006, pp. 442-448.
- X. Liu, B. Wang and W. Shao, “A Compact 2-D FullWave Algorithm Using Weighted Laguerre Polynomials for Exact Attenuation Constant Extraction of Lossy Transmission Lines,” IEEE of Antennas and Propagation Society International Symposium Albuquerque, 9-14 July 2006, pp. 1215-1218.

