Journal of Electromagnetic Analysis and Applications
Vol.4 No.11(2012), Article ID:24708,4 pages DOI:10.4236/jemaa.2012.411063
Computation of Optical Force on Nanoparticles Using Locally Non-Orthogonal Overlapping Yee FDTD Method
![]()
1Department of Mathematical Sciences, Delaware State University, Dover, USA; 2Arizona Center for Mathematical Sciences at Department of Mathematics, The University of Arizona, Tucson, USA.
Email: *jliu@desu.edu
Received August 30th, 2012; revised September 25th, 2012; accepted October 10th, 2012
Keywords: FDTD; Overlapping Yee; Optical Force; Nanoparticle
ABSTRACT
In this paper, a locally non-orthogonal overlapping Yee (OY) FDTD method is proposed in order to accurately calculates the optical force on dielectric and dispersive nanoparticles. It extends our previous work to geometries with sharp corners and dispersive materials. In addition to consistently achieving the smallest errors in comparison to the standard FDTD method, the OY approach is a stable non-orthogonal FDTD method that attains second-order convergence when sharp corners are present.
1. Introduction
Recent advances in optical trapping of nanoparticles, originated by Ashkin [1,2], have been successfully applied in both physics and biology [3]. Accurate and reliable algorithms for computation of the optical forces are critical in studying optical trapping [4]. It has been pointed out in [4] that the methods of using the Lorentz force [5] and the Maxwell stress tensor [6] are equivalent theoretically but accuracy of their numerical implementation may differ. Here we use the later approach. In the Maxwell stress tensor formulation, the total optical force acting on a particle due to a time-harmonic electromagnetic field is given by
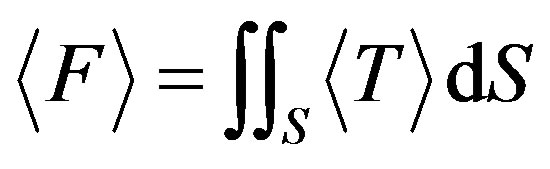 , (1)
, (1)
where T is the stress tensor
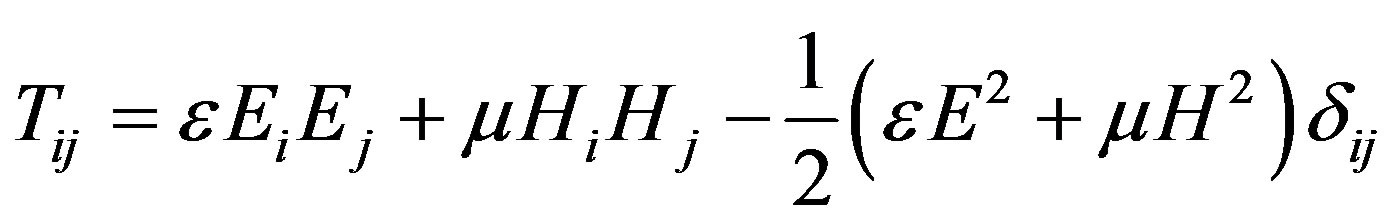 . (2)
. (2)
The ε and μ are the electric permittivity and magnetic permeability, respectively. S is a surface that encloses the object. The angle brackets indicate time-averaged values. A simple choice of the surface S is a cube surrounding the object.
Mie scattering theory gives accurate analytical solution of Maxwell’s equations but is limited to spherical objects. For arbitrary geometries, several methods have been used to compute optical forces, such as the coupled dipole method [7], the T-matrix method [8] and the finite-difference time-domain (FDTD) method [9].
The FDTD method (Yee’s scheme) [10,11] is a popular and very successful method for solving time-domain Maxwell’s equations. A major drawback of this method is the stair-casing approximation when modeling curved geometries that leads to large errors and reduced order of accuracy. Many methods have been proposed to eliminate the stair-casing error. The contour-path and locally conformal FDTD methods [12-14] deform the grid only locally to accommodate the curved surface. When dielectric material interfaces are present, the effective permittivity technique is applied [13-15], but the accuracy is reduced to first-order. The subpixel smoothing technique proposed in [16] achieves second-order accuracy by using an inverse dielectric tensor, and this method has been extended to anisotropic media [17], combined with a recently proposed stable FDTD scheme in anisotropic media [18]. However, as it has been pointed out in [16], a remaining challenge is to accurately handle objects with sharp corners, where the accuracy is still less than second-order.
In this paper, we show that the non-orthogonal Overlapping Yee (OY) method we developed in [19,20] can accurately model the optical force and achieve second order convergence. The OY method requires multiple Yee grids which lead to more memory and CPU costs. To improve the efficiency, we propose a locally non-orthogonal OY technique. In our new method, the computational cells are non-orthogonal and overlapped only in a small region near the curved geometry, and the rest of the computational domain is regular Yee grid. The interface between regular and overlapping cells is treated carefully to avoid instability. Numerical simulations on optical force computation confirm that in addition to consistently achieving the smallest errors in comparison to the standard FDTD method, the new approach is stable and attains second-order convergence when sharp corners are present.
2. The Locally Non-Orthogonal OY Algorithm
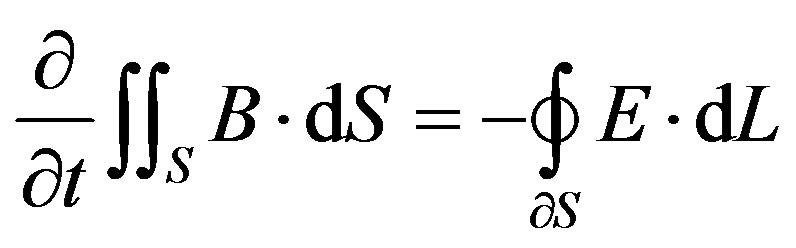 (3)
(3)
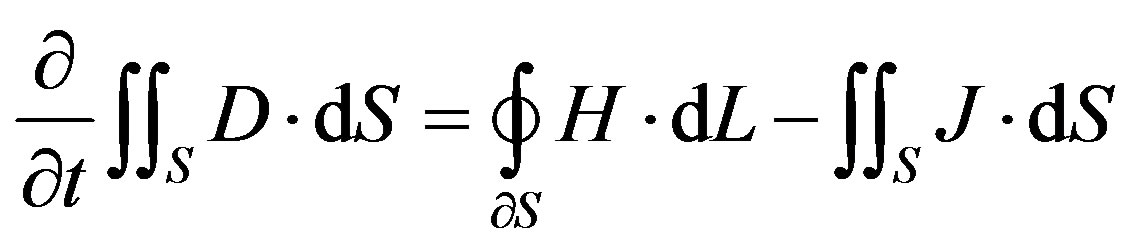 (4)
(4)
The OY FDTD method solves the integral form of the Maxwell’s Equations (3) and (4), for the magnetic and electric fluxes B and D over a non-orthogonal staggered grid with overlapping cells. J is the electric current density. The overlapping cells provide multiple pieces of information per computational cell. The components of the electric fluxes D are collocated and form a local basis that is used to determine the electric field E from the local constitutive relation D = ME, where the material matrix M is symmetric and positive definite. The same considerations hold for the magnetic field. The symmetry and positive definiteness of the material matrices guarantees that the CFL condition [11] is the only stability criterion for the OY method.
The diagonal split-cell model is an alternative way of constructing quadrilateral meshes for the OY method that avoids the permittivity averaging. The diagonal split-cell model has been discussed in Taflove’s book [11] for orthogonal Cartesian grid. We have extended this model to non-orthogonal grids. As shown in Figure 1, the quadrilateral mesh is constructed in such a way that the material interface does not go along cell edges but passes through the diagonal vertices of the cells using a smooth circle mapping method similar to the method proposed in [21]. Besides the simple test cases (e.g., cylinders and rectangles), our method can be applied to more complicated geometries, such as a triangular wedge as shown in Figure 2. By placing the magnetic fields at the cell centers and the electric fields along cell edges, this approach guarantees that no line integral of the electric field crosses the material interface so that the permittivity averaging is avoided. This approach is identified as the SplitCell Overlapping Yee (SC-OY) method. The split-cell mesh construction and some preliminary result of computing force on cylindrical particle were presented in [20].
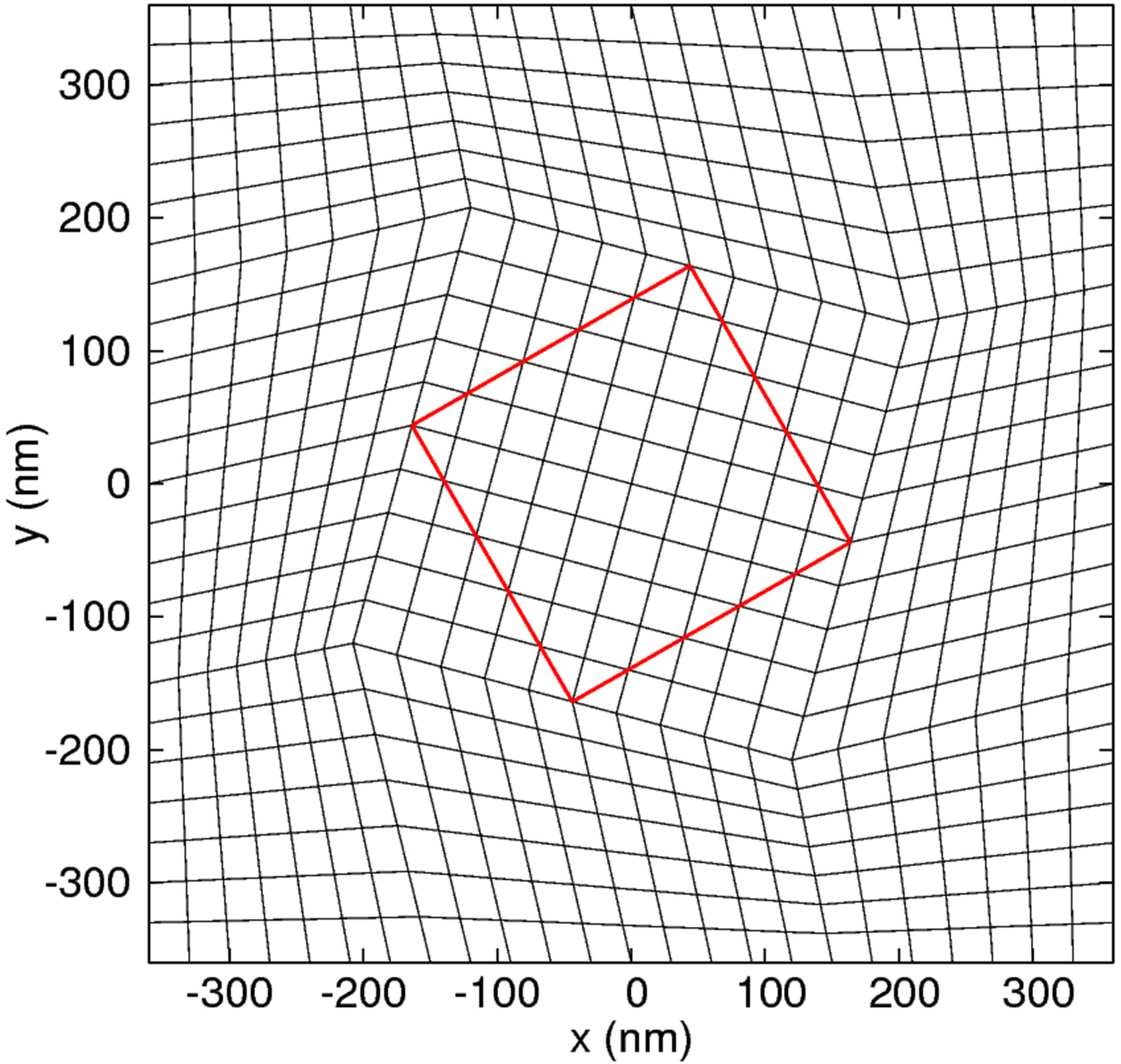
Figure 1. Non-orthogonal quadrilateral meshes near a tilted-square. The sides of the square (in red) go through the diagonal vertices of the grid cells.
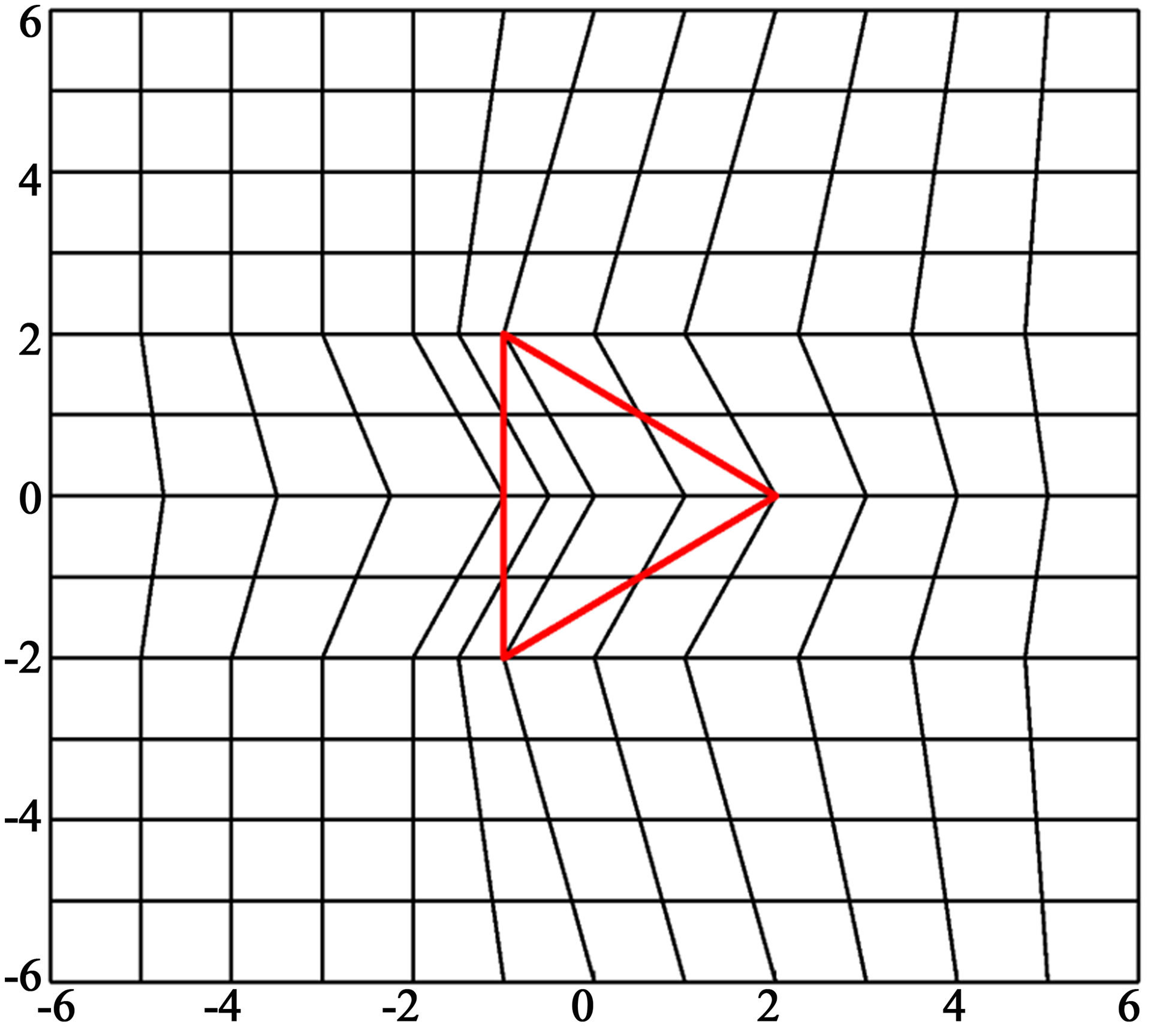
Figure 2. A sample non-orthogonal 8 by 8 quadrilateral mesh near a triangular wedge using diagonal split-cell model. The edges of the triangle (in red) go through the diagonal vertices of the grid cell.
In this paper, we focus on the extension of our previous work to geometries with sharp corners and dispersive materials. The non-orthogonal quadrilateral split-cell mesh for structures with sharp corners, such as a titled-square, is shown in Figure 1. The SC-OY method has at least two advantages: 1) it avoids permittivity averaging, so that the implementation is simplified; 2) it avoids tiny and near 180 degree angles for structures with large curvature so that the local error is smaller. A limitation of the split-cell approach is that it assumes nonmagnetic medium (μ is constant throughout the computational domain).
In general, the 2D OY technique requires two sets of Yee grids to be overlapped to each other, so it doubles the computational cost. In 3D, it quadruples the cost. To improve the efficiency of OY method, we have employed a locally non-orthogonal approach. That is, in our implementation, the computational cells are overlapped and non-orthogonal in a small region that near the nano-particle. The rest of the computational domain is rectangular. A sample mesh is shown in Figure 3. In the non-orthogonal region, the OY method is applied and the standard FDTD method is applied elsewhere. As shown in this figure, the non-orthogonal mesh is only about 10% of the whole computational domain, so that the overall computational cost decreases from 200% to 110%.
In 3D, this locally non-orthogonal technique will further improve the performance of numerical simulation.
An important step in designing the locally non-orthogonal OY algorithm is the treatment of the interface between regular rectangular cells and overlapping cells. As shown in Figure 4, for 2D TEz mode where only
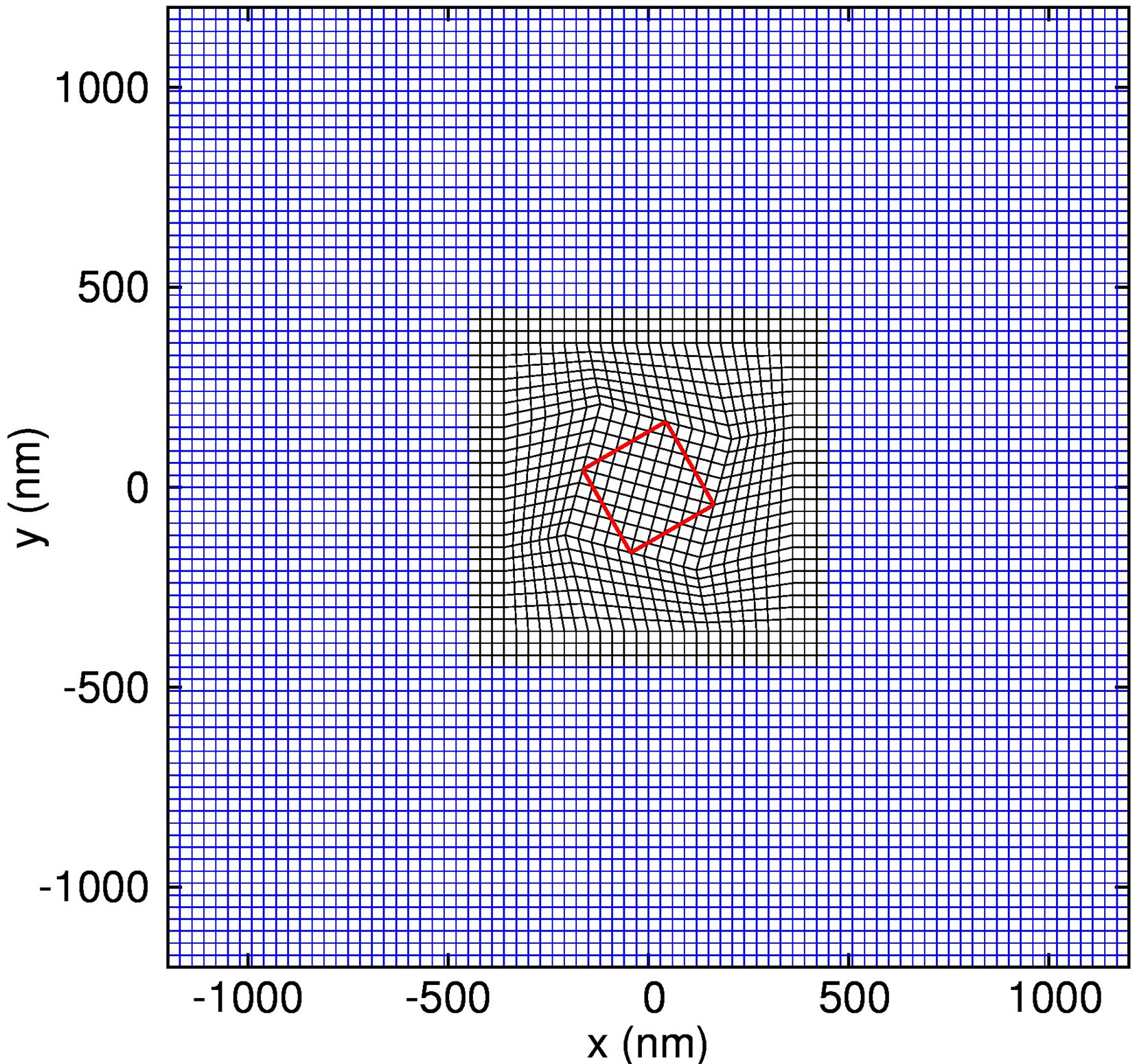
Figure 3. A locally non-orthogonal quadrilateral mesh near a tilted-square.
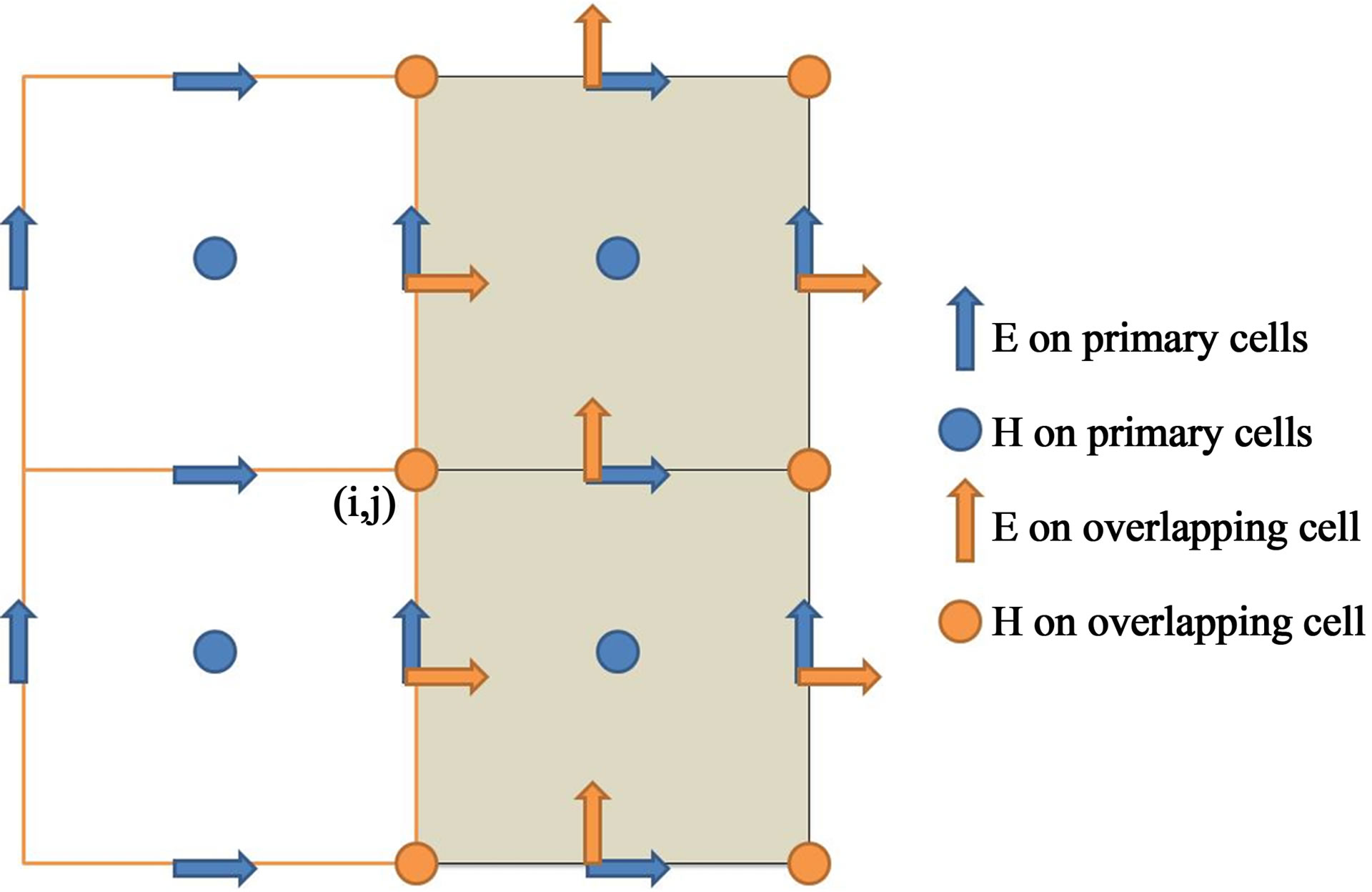
Figure 4. Computational cells near the interface of regular and overlapping cells.
 fields are involved, the magnetic field
fields are involved, the magnetic field 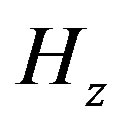 on primary grid is defined in the cell (at cell center) and the
on primary grid is defined in the cell (at cell center) and the 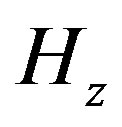 on the overlapping cell is defined at the corner of the cell. Our algorithm follows the following three steps:
on the overlapping cell is defined at the corner of the cell. Our algorithm follows the following three steps:
1) Update the solution inside the regular grid (Yee mesh) by using the standard FDTD method;
2) Update the solution inside the OY region using the OY FDTD algorithm;
3) Calculate the magnetic field 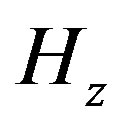 on the interface by averaging the neighbor values on the primary grid. The formula is given as
on the interface by averaging the neighbor values on the primary grid. The formula is given as
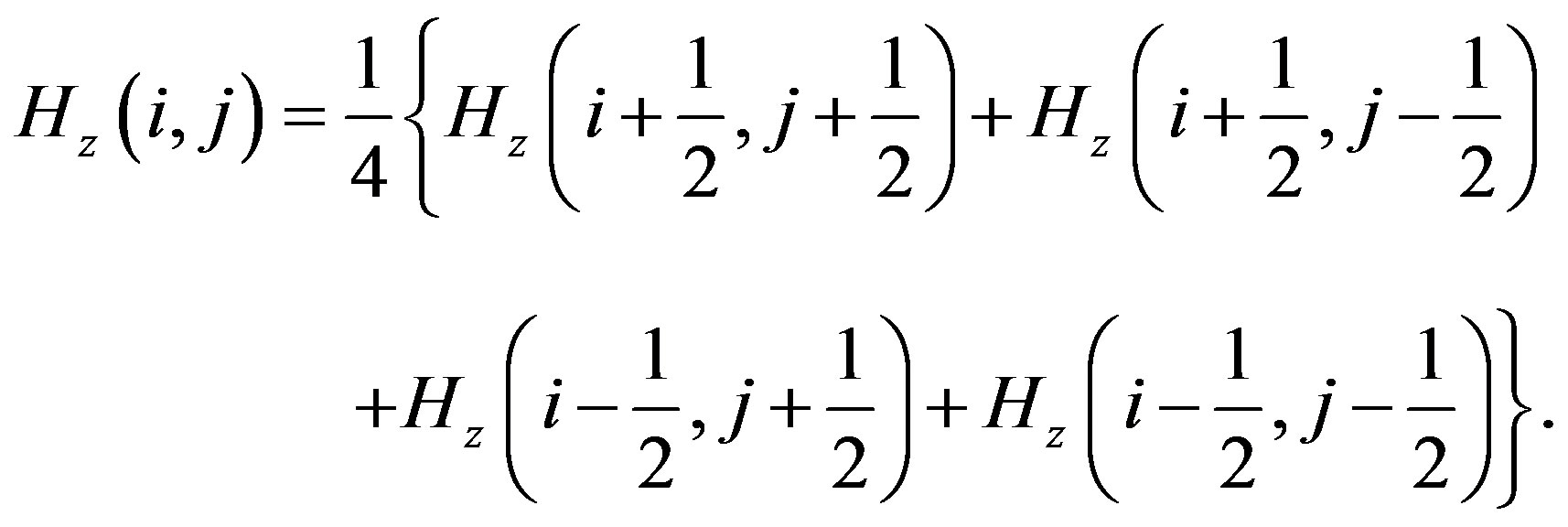
Similarly, for TMz mode, in step 3 the magnetic field 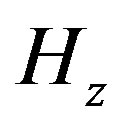 is replaced by the electric field
is replaced by the electric field  in our algorithm.
in our algorithm.
3. Numerical Simulations
In our numerical examples, we apply the technique we proposed to compute the optical force on a tilted-square. The side length of the square is 240 nm and it is titled for 30 degrees. The wavelength of the incident plane wave propagating in the x-direction is  The computational domain is surrounded by the uniaxial perfectly matched layer (UPML) boundaries in all directions. A sample computational mesh is shown in Figure 3.
The computational domain is surrounded by the uniaxial perfectly matched layer (UPML) boundaries in all directions. A sample computational mesh is shown in Figure 3.
Figure 5 shows the relative errors of the computed optical forces on dielectric and metallic particles. The relative permittivity inside the dielectric particle is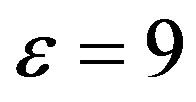 . The metallic (gold) particle is simulated using the linear Drude dispersive model with frequency dependent permittivity:
. The metallic (gold) particle is simulated using the linear Drude dispersive model with frequency dependent permittivity:
 where
where 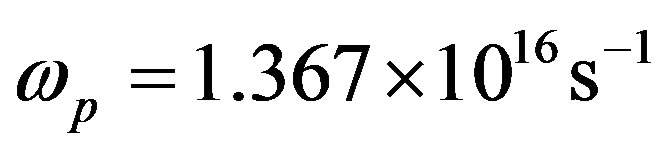 and
and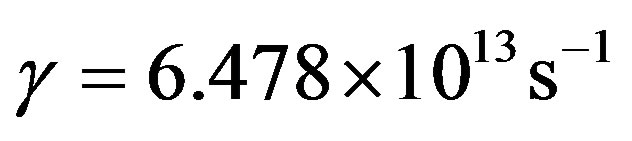 . The numerical result at very fine mesh
. The numerical result at very fine mesh 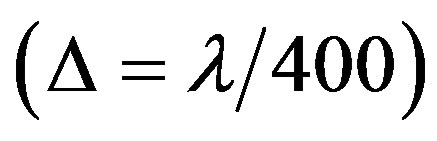 is used as the exact solution. As shown in Figure 5, for both dielectric and metallic particles, the FDTD method converges linearly, while the OY method is second-order accuracy. For grid size
is used as the exact solution. As shown in Figure 5, for both dielectric and metallic particles, the FDTD method converges linearly, while the OY method is second-order accuracy. For grid size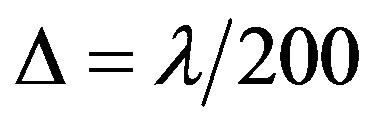 , the relative error of the OY result is about one order of magnitude smaller than the FDTD result. Our numerical results also show that the OY solution with
, the relative error of the OY result is about one order of magnitude smaller than the FDTD result. Our numerical results also show that the OY solution with 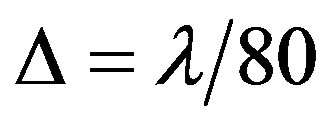 and the FDTD solution with
and the FDTD solution with 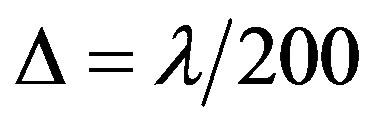 have comparable errors (about 0.5%), but the OY method requires only half in memory usage and less than 25% in CPU usage.
have comparable errors (about 0.5%), but the OY method requires only half in memory usage and less than 25% in CPU usage.
 (a)
(a)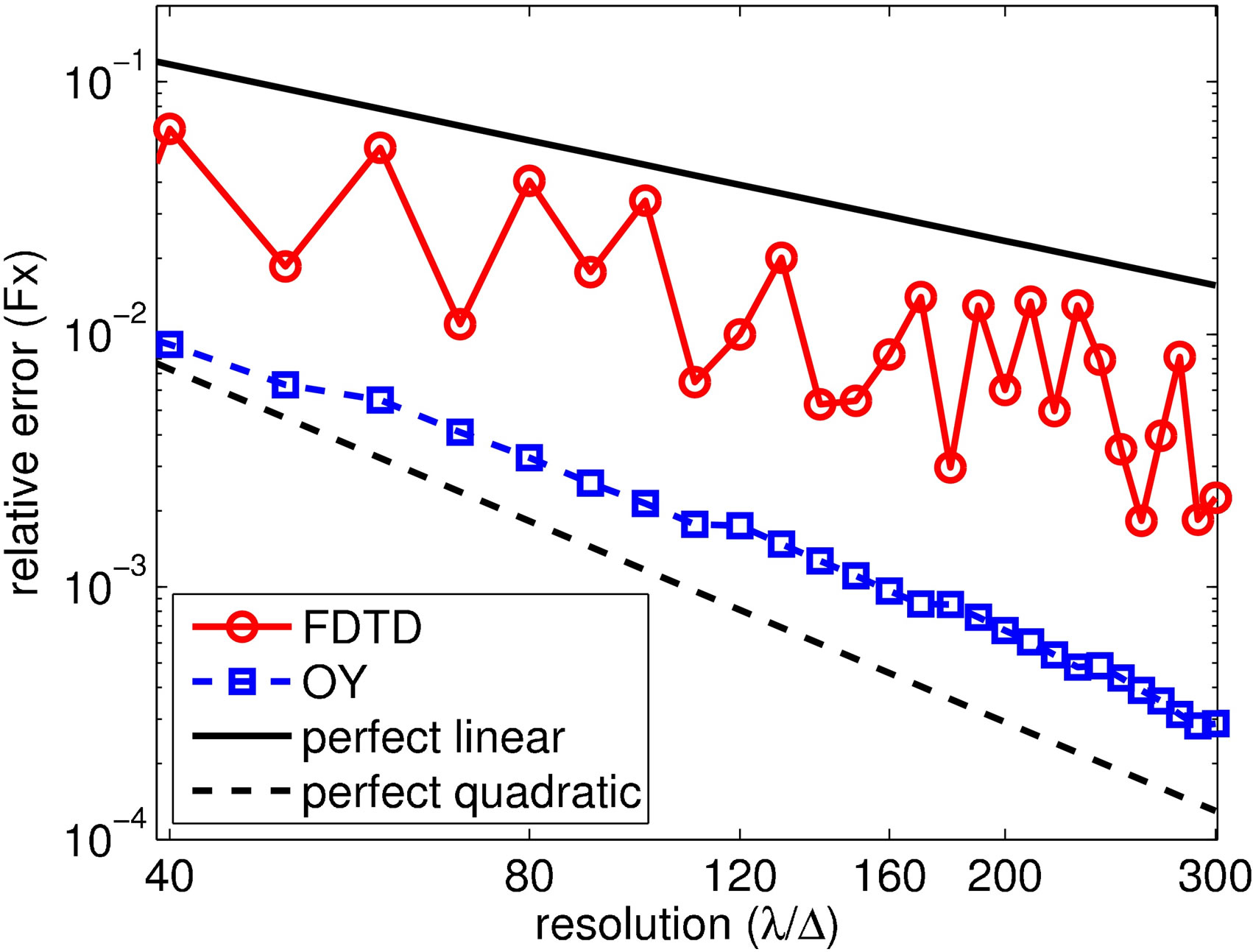 (b)
(b)
Figure 5. Relative errors of force versus resolution for tilted-square illuminated by TEz plane wave for (a) Dielectric medium (ε = 9); (b) Dispersive medium.
4. Conclusion
We have implemented local non-orthogonal OY FDTD method that was applied to the optical force computation. Our numerical simulations showed that in addition to consistently achieving the smallest errors in comparison to the standard FDTD method, the OY approach is a stable non-orthogonal FDTD method that attains better efficiency and second-order convergence even when sharp corners are present.
5. Acknowledgements
The authors would like to thank Dr. Colm Dineen and Dr. Yong Zeng for their invaluable discussions. This work is supported by the Air Force Office of Scientific Research (AFOSR) under Grant numbers FA9550-10-1-0127 and FA9550-10-1-0064.
REFERENCES
- A. Ashkin, “Acceleration and Trapping of Particles by Radiation Pressure,” Physical Review Letters, Vol. 24, No. 4, 1970, pp. 156-159. doi:10.1103/PhysRevLett.24.156
- A. Ashkin and J. M. Dziedzic, “Optical Levitation by Radiation Pressure,” Applied Physics Letters, Vol. 19, No. 8, 1971, pp. 283-285. doi:10.1063/1.1653919
- K. C. Neuman and S. M. Block, “Optical Trapping,” Review of Scientific Instruments, Vol. 75, No. 9, 2004, pp. 2787-2809. doi:10.1063/1.1785844
- M. Dienerowitz, M. Mazilu and K. Dholakia, “Optical Manipulation of Nanoparticles: A Review,” Journal of Nanophotonics, Vol. 2, No. 1, 2008, Article ID: 021875. doi:10.1117/1.2992045
- A. R. Zakharian, M. Mansuripur and J. V. Moloney, “Radiation Pressure and the Distribution of Electromagnetic Force in Dielectric Media,” Optics Express, Vol. 13, No. 7, 2005, pp. 2321-2336. doi:10.1364/OPEX.13.002321
- J. D. Jackson, “Classical Electrodynamics,” 2nd Edition, Wiley, New York, 1975. doi:10.1103/PhysRevB.61.14119
- P. C. Chaumet and M. Nieto-Vesperinas, “Coupled Dipole Method Determination of the Electromagnetic Force on a Particle over a Flat Dielectric Substrate,” Physical Review B, Vol. 61, No. 20, 2000, pp. 14119-14127.
- M. I. Mishchenko, L. D. Travis and D. W. Mackowski, “T-Matrix Computations of Light Scattering by Nonspherical Particles: A Review,” Journal of Quantitative Spectroscopy & Radiative Transfer, Vol. 55, No. 5, 1996, pp. 535-575. doi:10.1016/0022-4073(96)00002-7
- K. Okamoto and S. Kawata, “Radiation Force Exerted on Subwavelength Particles near a Nanoaperture,” Physical Review Letters, Vol. 83, No. 22, 1999, pp. 4534-4537. doi:10.1103/PhysRevLett.83.4534
- K. S. Yee, “Numerical Solution of Initial Boundary Value Problems Involving Maxwell’s Equations in Isotropic Media,” IEEE Transactions on Antennas and Propagation, Vol. 14, No. 3, 1966, pp. 302-307. doi:10.1109/TAP.1966.1138693
- A. Taflove and S. Hagness, “Computational Electrodynamics: The Finite-Difference Time-Domain Method,” 3rd Edition, Artech House, Norwood, 2005.
- T. G. Jurgens, A. Taflove, K. R. Umashankar and T. G. Moore, “Finite-Difference Time-Domain Modeling of Curved Surfaces,” IEEE Transactions on Antennas and Propagation, Vol. 40, No. 4, 1992, pp. 357-366. doi:10.1109/8.138836
- S. Dey and R. Mittra, “A Conformal Finite-Difference Time-Domain Technique for Modeling Cylindrical Dielectric Resonators,” IEEE Transactions on Microwave Theory and Techniques, Vol. 47, No. 9, 1999, pp. 1737- 1739. doi:10.1109/22.788616
- A. Mohammadi, H. Nadgaran and M. Agio, “Contour path Effective Permittivities for the Two-Dimensional Finite-Difference Time-Domain Method,” Optics Express, Vol. 13, No. 25, 2005, pp. 10367-10381. doi:10.1364/OPEX.13.010367
- N. Kaneda, B. Houshmand and T. Itoh, “FDTD Analysis of Dielectric Resonators with Curved Surfaces,” IEEE Transactions on Microwave Theory and Techniques, Vol. 45, No. 9, 1997, 1645-1649. doi:10.1109/22.622937
- A. Farjadpour, D. Roundy, A. Rodriguez, M. Ibanescu, P. Bermel, J. D. Joannopoulos, S. G. Johnson and G. W. Burr, “Improving Accuracy by Subpixel Smoothing in the Finite-Difference Time Domain,” Optics Letters, Vol. 31, No. 20, 2006, pp. 2972-2974. doi:10.1364/OL.31.002972
- A. F. Oskooi, C. Kottke and S. G. Johnson, “Accurate Finite-Difference Time-Domain Simulation of Anisotropic Media by Subpixel Smoothing,” Optics Letters, Vol. 34, No. 18, 2009, pp. 2778-2780. doi:10.1364/OL.34.002778
- G. R. Werner and J. R. Cary, “A Stable FDTD Algorithm for Non-Diagonal, Anisotropic Dielectrics,” Journal of Computational Physics, Vol. 226, No. 1, 2007, pp. 1085- 1101. doi:10.1016/j.jcp.2007.05.008
- J. Liu, M. Brio and J. V. Moloney, “Overlapping Yee FDTD Method on Nonorthogonal Grids,” Journal of Scientific Computing, Vol. 39, No. 1, 2009, pp. 129-143. doi:10.1007/s10915-008-9253-1
- J. Liu, M. Brio and J. V. Moloney, “A Diagonal Split Cell Model for the Overlapping Yee FDTD Method,” Acta Mathematica Scientia, Vol. 29, No. 6, 2009, pp. 1670- 1676. doi:10.1016/S0252-9602(10)60009-4
- D. A. Calhoun, C. Helzel and R. J. LeVeque, “Logically Rectangular Grids and Finite Volume Methods for PDEs in Circular and Spherical Domains,” SIAM Review, Vol. 50, No. 4, 2008, pp. 723-752. doi:10.1137/060664094
NOTES
*Corresponding author.

