Journal of Electromagnetic Analysis and Applications
Vol.4 No.6(2012), Article ID:20334,18 pages DOI:10.4236/jemaa.2012.46034
Statistical Characteristics of Scattered Radiation in Medium with Spatial-Temporal Fluctuations of Electron Density and External Magnetic Field
1Department of Physics, Georgian Technical University, Tbilisi, Georgia; 2Dynamics of Geophysical fields and Computing Geophysics, TSU M. Nodia Institute of Geophysics, Tbilisi, Georgia.
Email: *jandieri@access.sanet.ge
Received April 13th, 2012; revised May 15th, 2012; accepted May 25th, 2012
Keywords: Fluctuations; Correlation function; Scattering; Magnetized Plasma; Phase portrait; Extraordinary Wave
ABSTRACT
Influence of temporal fluctuations of both electron density and external magnetic field fluctuations on scattered ordinary and extraordinary waves in magnetized plasma is investigated using the ray-(optics) method. Transport equation for frequency fluctuations of scattered radiation has been derived. Broadening of the spatial power spectrum and amplification of the intensity of frequency fluctuation taking into account geometry of the task and the features of turbulent magnetized plasma is analyzed for the anisotropic Gaussian correlation function using the remote sensing data. It is shown that spatial-temporal fluctuations of electron density and external magnetic field, anisotropy and angle of inclination of prolate irregularities relative to the external magnetic field may lead to the exponential amplification of the intensity of frequency fluctuations of scattered electromagnetic waves in the collisional magnetized plasma.
1. Introduction
Many papers are devoted to the theoretical investigation and observations of statistical characteristics of scattered radiation in the ionosphere [1,2]. The geomagnetic field plays a key role in the dynamics of plasma in the ionosphere and irregularities have different spatial scales usually elongating in the direction of an external magnetic field. Investigation of statistical moments in randomly inhomogeneous magnetized plasma is of a great practical importance. Scintillation effects and the angleof-arrival of scattered electromagnetic waves by anisotropic collision magnetized ionospheric plasma slab for both power-law and anisotropic Gaussian correlation functions of electron density fluctuations were investigated analytically [3] in the complex geometrical optics approximation on the basis of stochastic eikonal equation and numerically [4] by statistical simulation using the Monte Carlo method. Second order statistical moments of scattered electromagnetic waves in the ionospheric plasma at random variations of geomagnetic field magnitude in the ray-(optics) approximation were considered in [5] and the influence of directional fluctuations of an external magnetic field by the perturbation method in [6]. The Stokes parameters and the Faraday angle of scattered ordinary and extraordinary waves by magnetized plasma slab were calculated in [7]. In these papers fluctuating plasma parameters were random functions only of spatial coordinates. The influence of temporal fluctuations of both electron density and external magnetic field on scattered ordinary and extraordinary waves in turbulent collisional magnetized plasma has not been considered till now. These fluctuations in absorptive medium can lead to the amplification of frequency of scattered radiation. Conditions of the exponential amplification caused due to electron density and external magnetic field fluctuations are obtained in geometrical optics approximation.
Geometrical optics approximation imposes well-known restrictions on the distance traveled by the wave in inhomogeneous medium. Build-up effect of fluctuations of wave parameters is revealed most vividly at great distances from a source. Regular absorption in a nonstationary medium leads to the fluctuations growing with distance from the power law to the exponential one [8]. Therefore investigation of waves having different nature propagating in a smoothly inhomogeneous nonstationary medium is of interest. In Section 2 the dispersion equation of the complex phase and stochastic differential equation for phase fluctuations are derived at spatialtemporal fluctuations of electron density and external magnetic field fluctuations in collisionless magnetized plasma. The solution satisfies the boundary condition. Second order statistical moment-broadening of the spatial (angular) power spectrum (SPS) of scattered electromagnetic waves by turbulent magnetized plasma slab is obtained for arbitrary correlation functions of randomly varying plasma parameters. In section 3 transfer equation for the frequency fluctuations in collisional magnetized plasma is derived taking into account temporal fluctuations of both turbulent magnetized plasma parameters and external magnetic field, and anisotropy factors of ionospheric irregularities. Second order statistical moment of the frequency fluctuations has been calculated. The influence of weak absorption on the growing of the variance of frequency fluctuations characterizing broadening of the spectrum of scattered radiation is analyzed. Numerical calculations are carried out in Section 4 for anisotropic Gaussian correlation function including anisotropy factor of electron density inhomogeneities and the angle of inclination of prolate irregularities with respect to the geomagnetic field using experimental data. Conclusion is given in section 5.
2. Formulation of the Problem
Electric field E satisfies nonstationary wave equation:
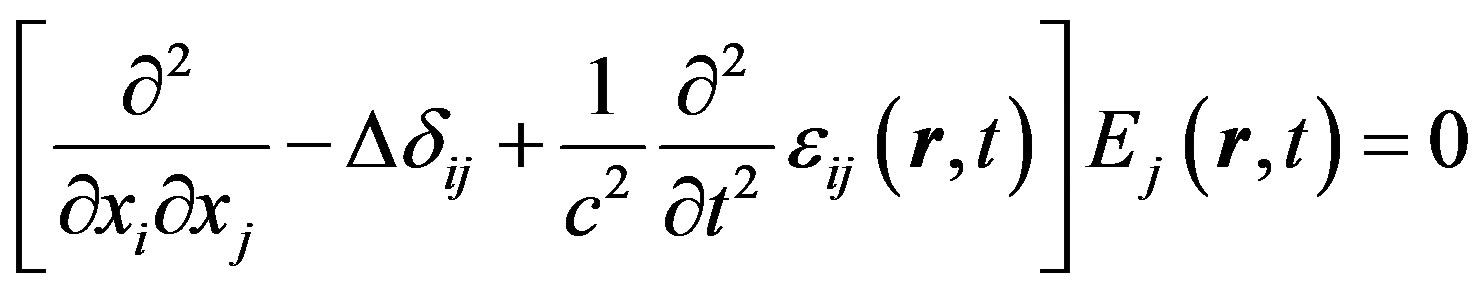. (1)
where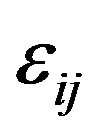 
is the second rank tensor [9]:
,
, 
,
;
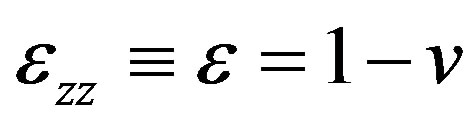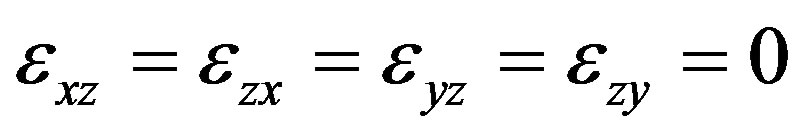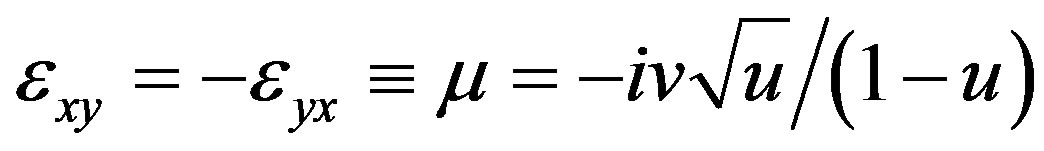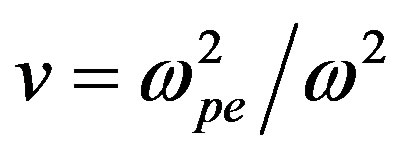and 
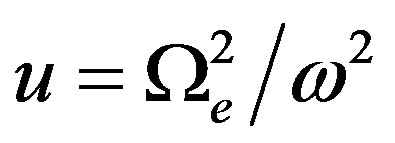non-dimensional plasma parameters, 
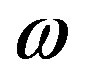is the angular frequency of an incident wave, 
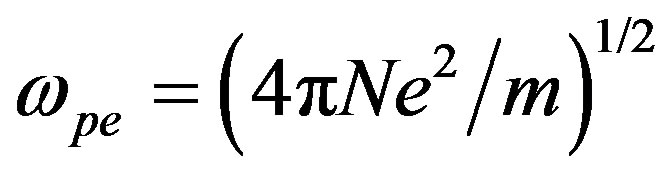is the angular plasma frequency, N is electron density, e and m are the charge and the mass of an electron, 
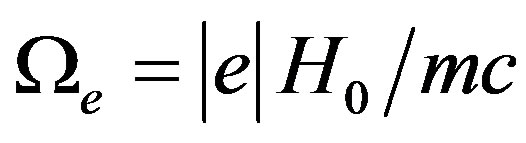is the angular gyrofrequency for the magnetic field, 
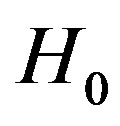is the strength of an external magnetic field directing along the z axis, c is the speed of light in the vacuum.
In ray-(optics) approximation [10] substituting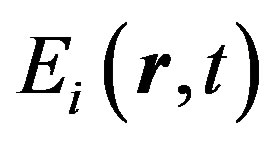 
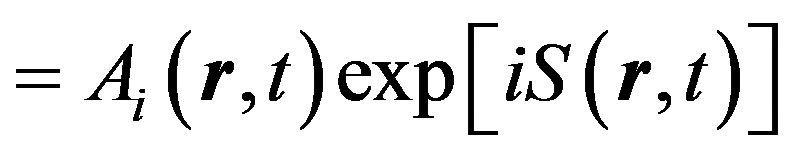in the Equation (1) and taking into account that phase fluctuations substantially exceed amplitude fluctuations, we obtain the dispersion equation for the complex phase:
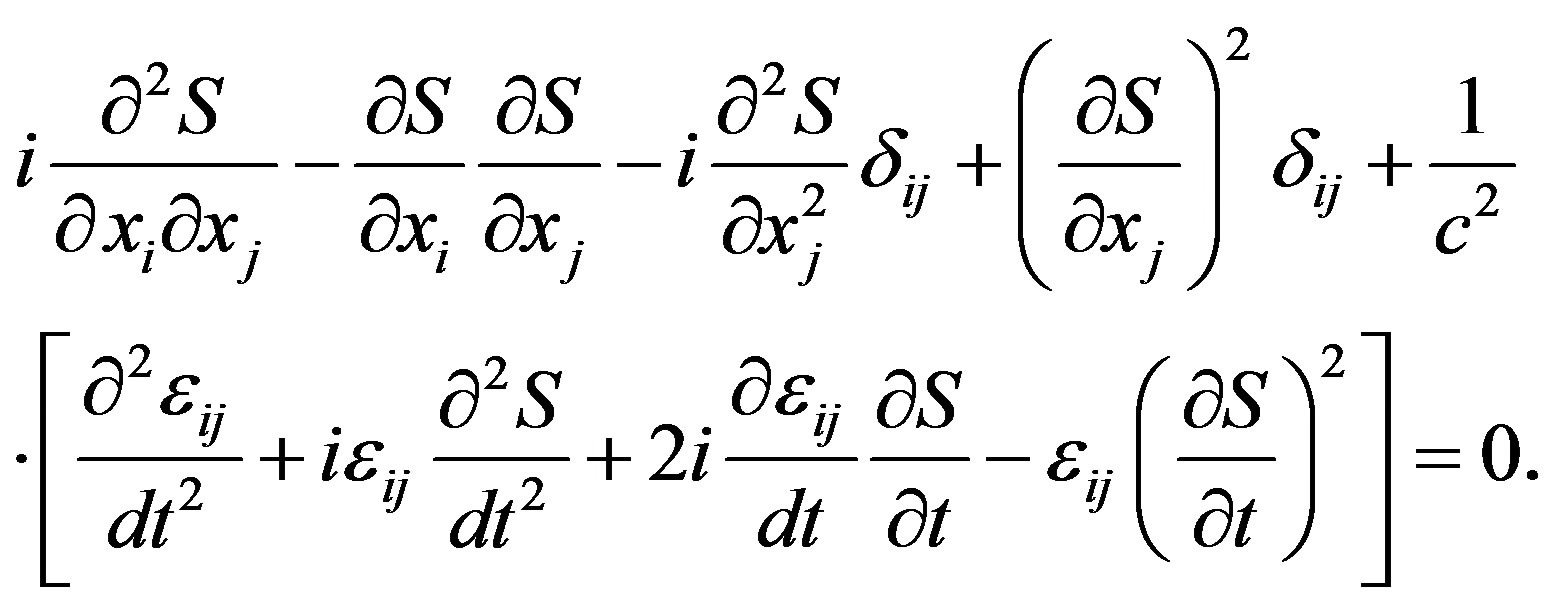(2)
Using the perturbation method electron density and external magnetic field we present as the sum of constant mean and small fluctuating terms, which are random functions of the spatial coordinates and time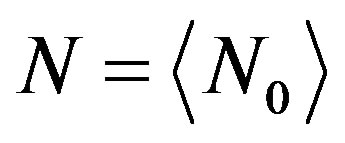 
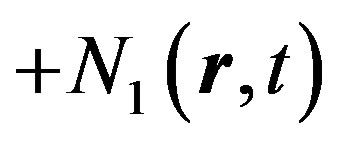and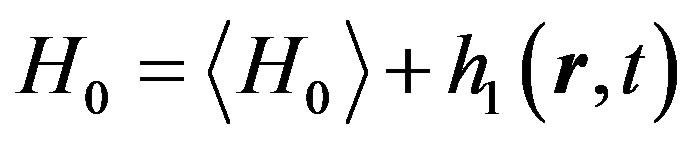 
(angular brackets denote statistical average);
, 
,
:
,
, 
,
,
;
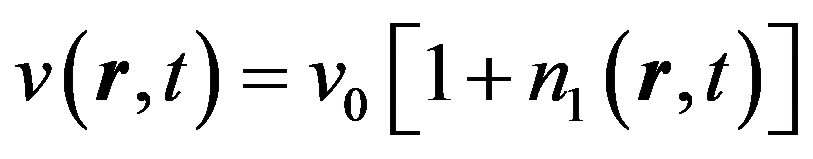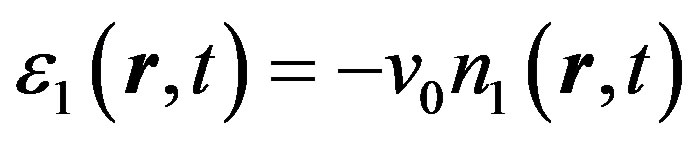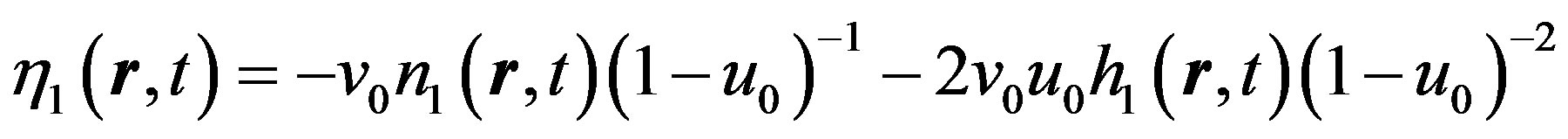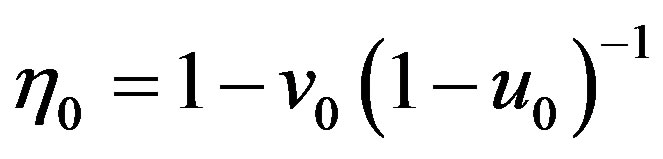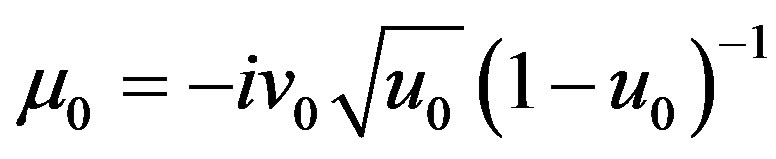
or permittivity tensor is the sum of 
and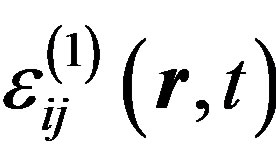
. Hence, the phase has the regular
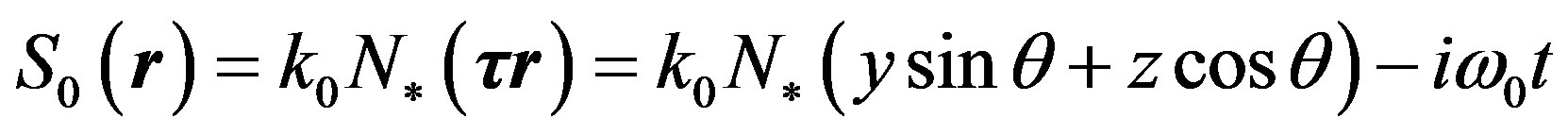
and fluctuating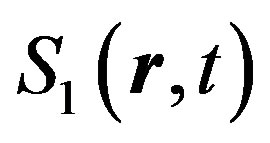 
components. Vector 
of an incident wave lies in the 
plane (principle plane),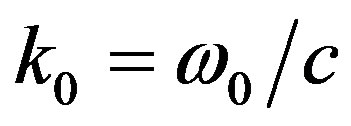 
, 
is the angle between the imposed magnetic field and the direction of a wave vector of the incident wave. For collisionless magnetized plasma the refractive index is given [9] as:
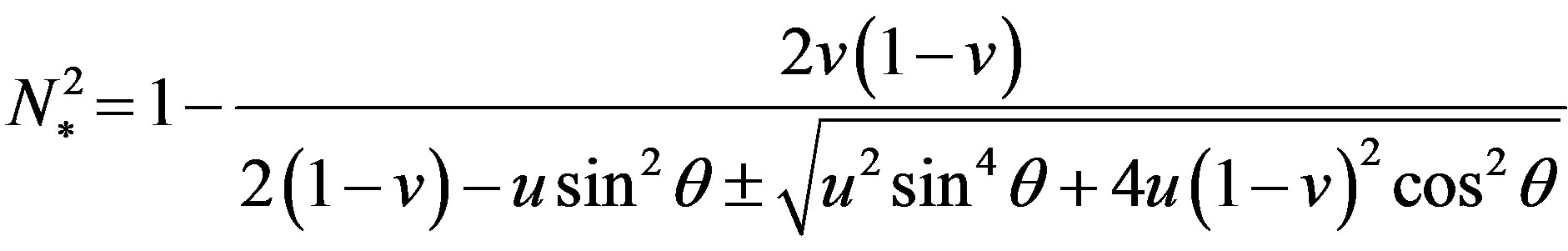,(3)
sign “+” corresponds to the ordinary wave, sign “–” devoted to the extraordinary wave. After linearization of Equation (2) the real part of regular phase coincides with the expression obtaining in [5] for collisionless magnetized plasma and the solution of the task reduces to the calculation of the determinant:
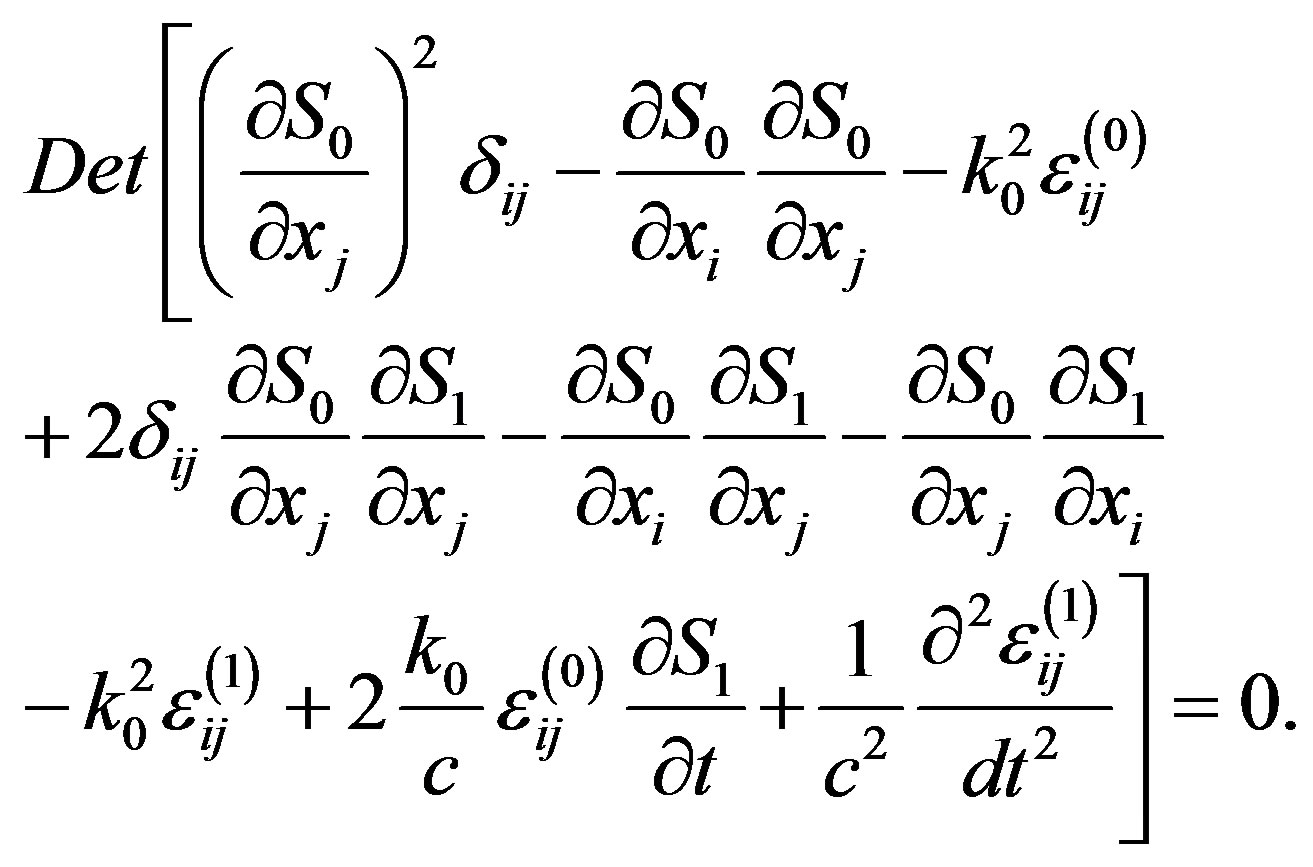(4)
In a zeroth approximation at θ = 0˚ for the refractive index of the collisionless magnetized plasma we obtain the well-known expression [9]
.
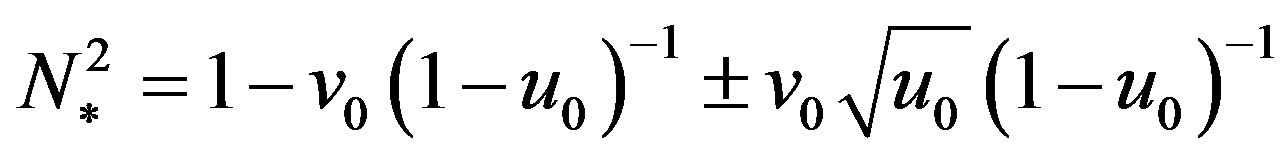The fluctuating term of the complex phase satisfies the stochastic differential equation:
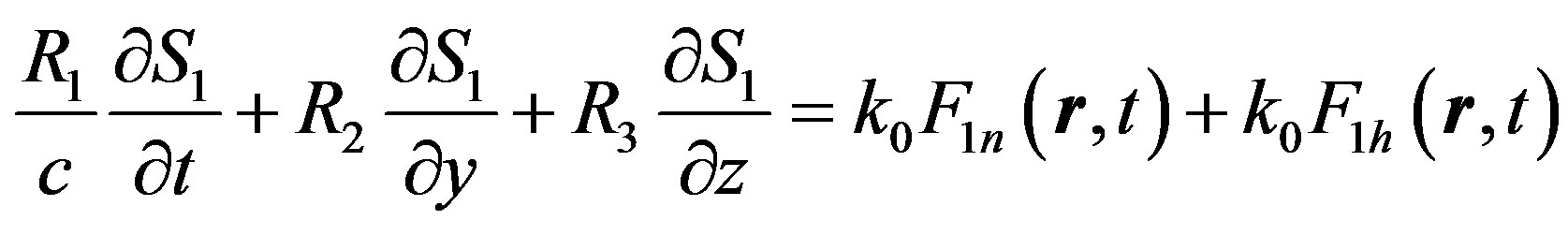, (5)
where
,
,
,
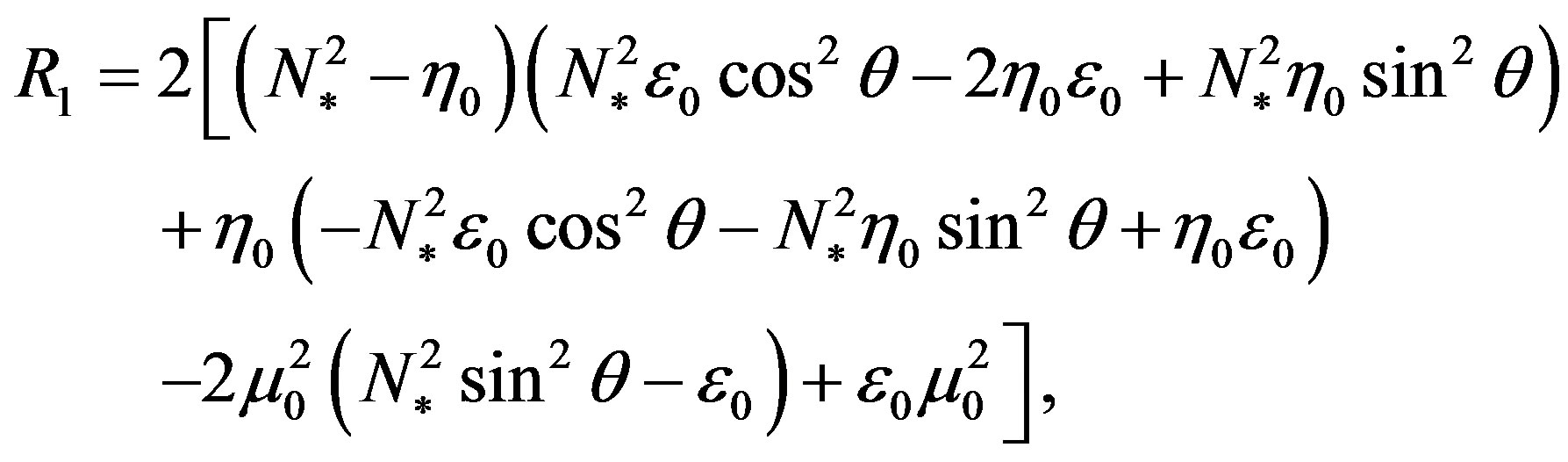
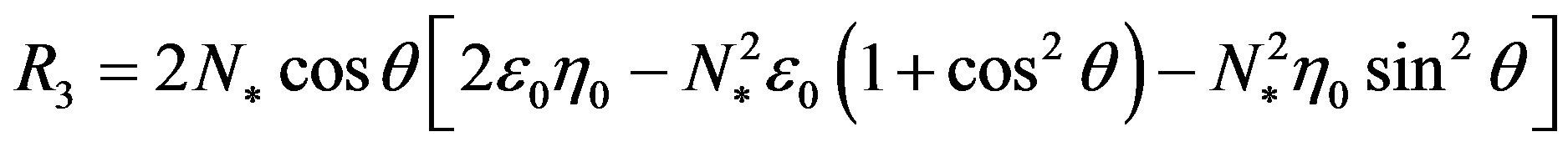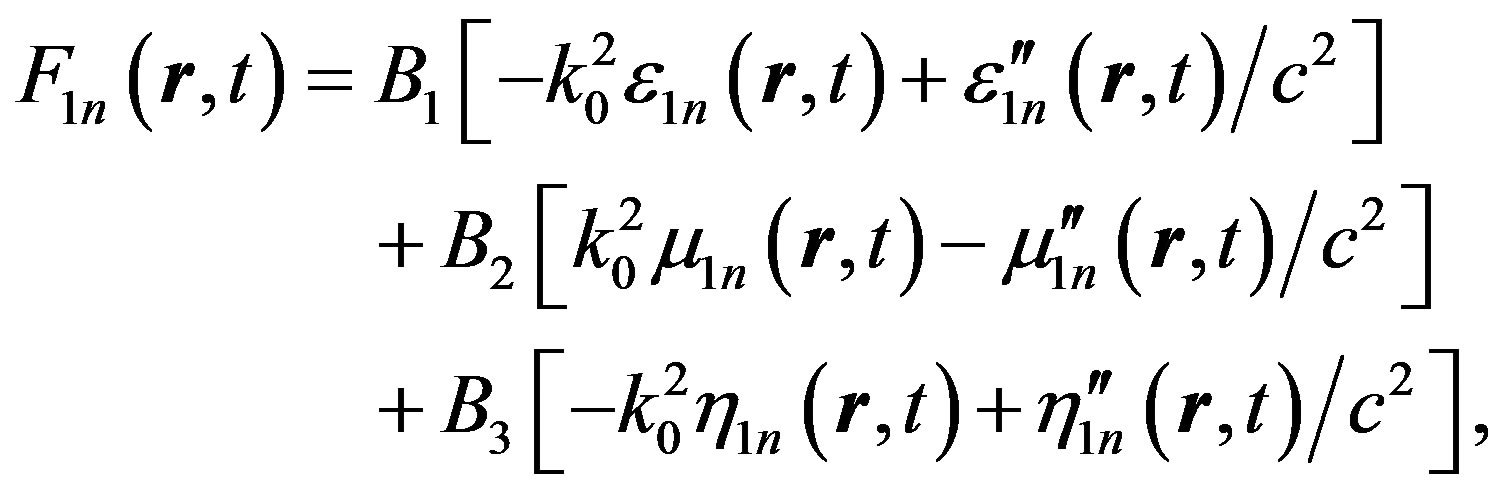
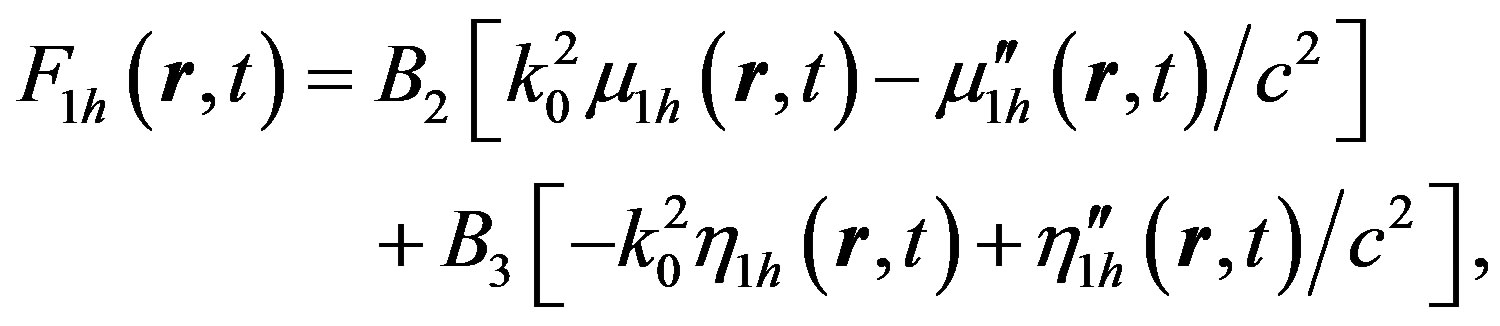
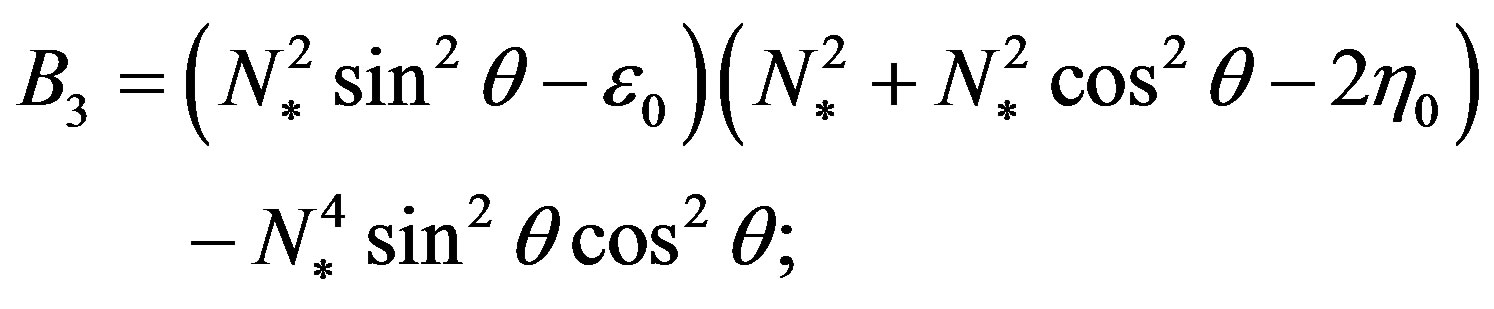
indices n and h determine electron density and magnetic field fluctuations, respectively; index “0” indicate regular components of the tensor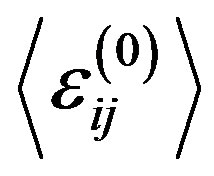
; functions 
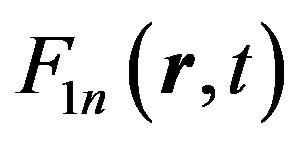and 
contain temporal derivatives of fluctuating terms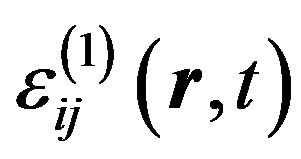
. Solving Equation (5) and applying the Fourier transformation:
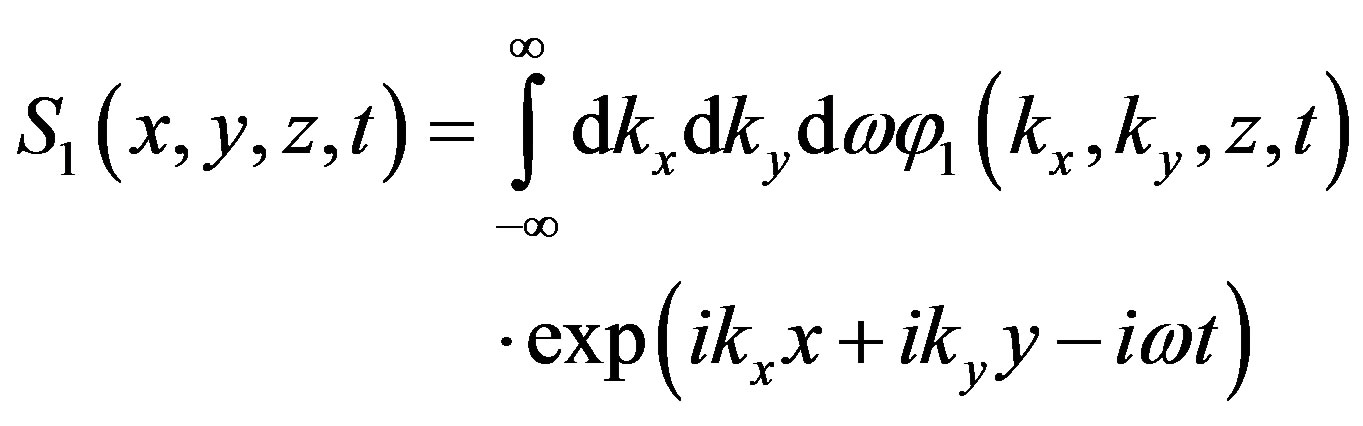
for two-dimensional spectral density of the phase fluctuations we obtain:
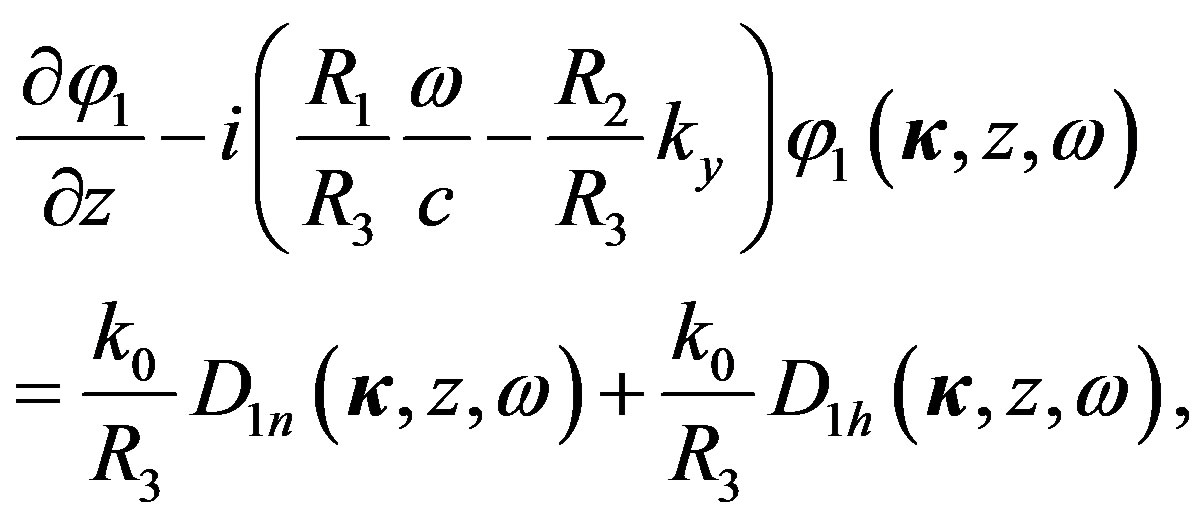(6)
. Solving this equation and taking into account the boundary condition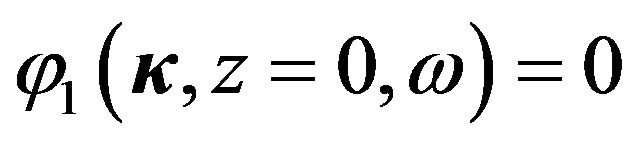
, for the phase fluctuation we have:
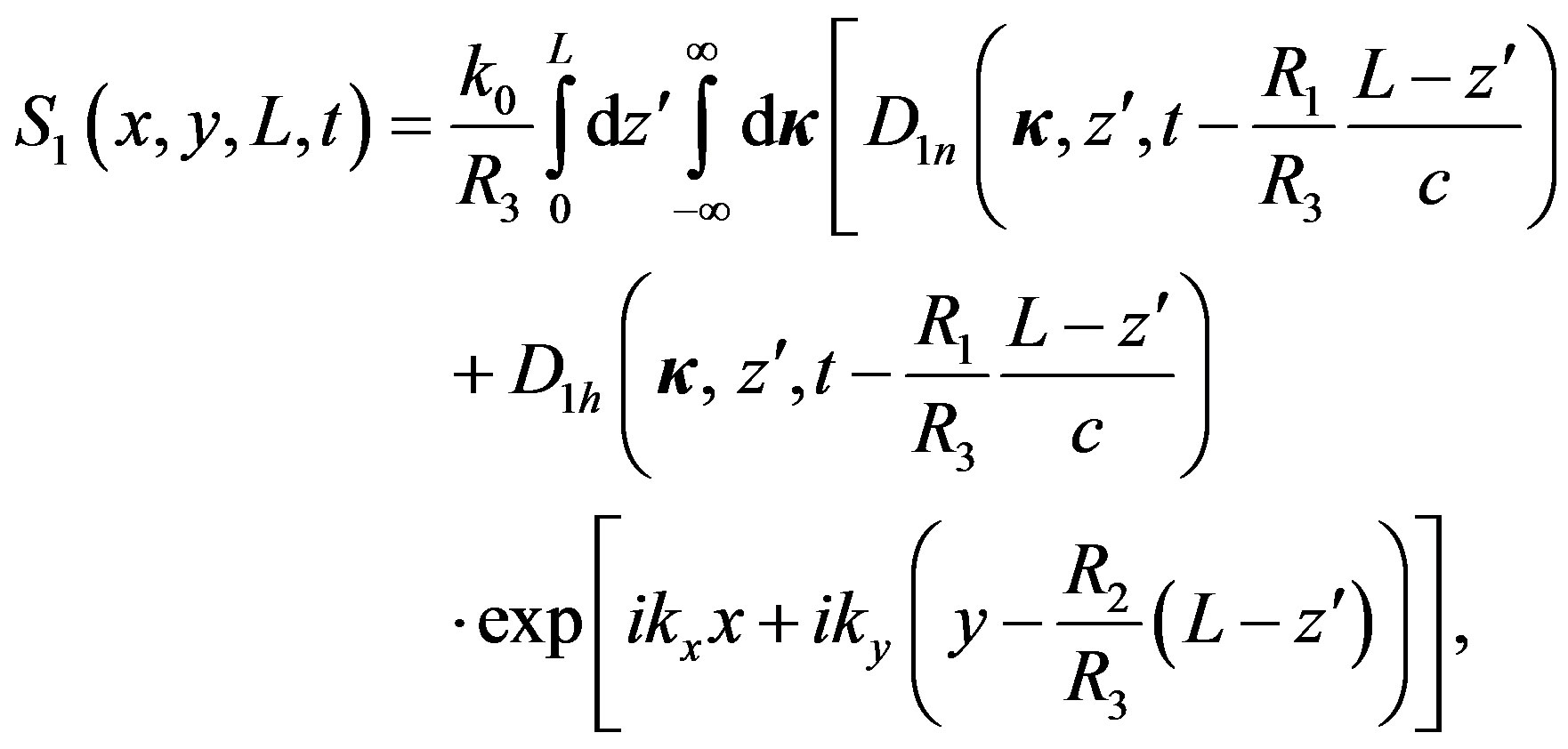(7)
where 
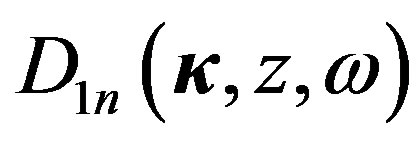and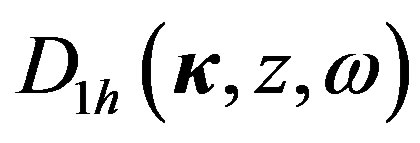 
are easily determined:
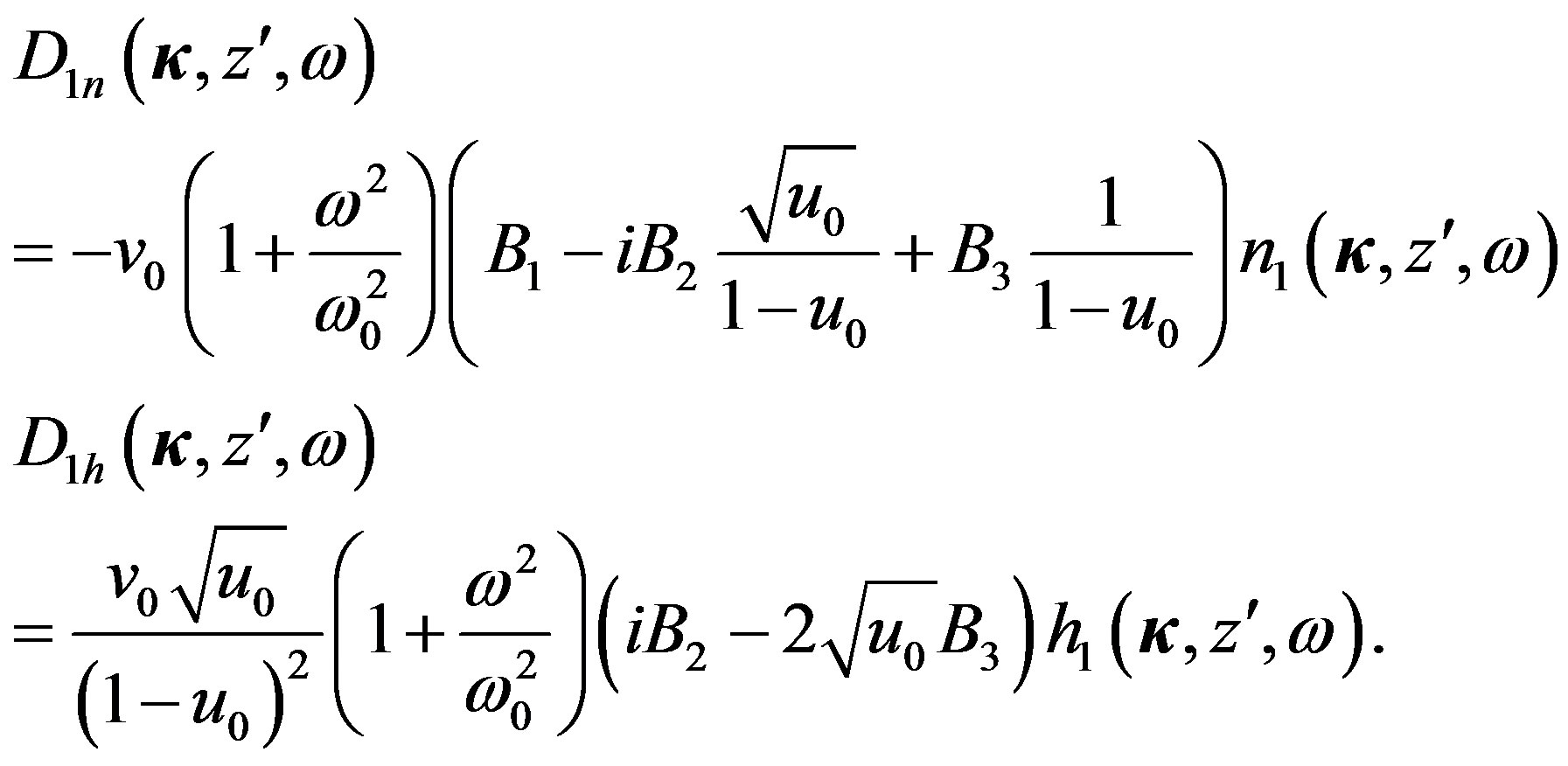(8)
Application of the geometrical optics method impose the well-known restriction on the path length traveling by the wave in random medium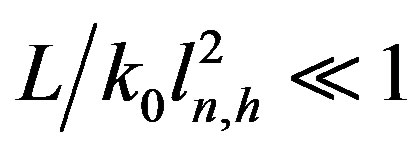 
(
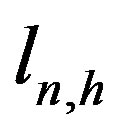are characteristic spatial scales of electron density and magnetic field fluctuations, respectively, L-distance traveling by the wave in turbulent magnetized plasma) [10-12].
Correlation function of the phase fluctuation of scattered radiation at fixed moment t for two receiving antennas spaced apart at small distances 
and 
has the following form:
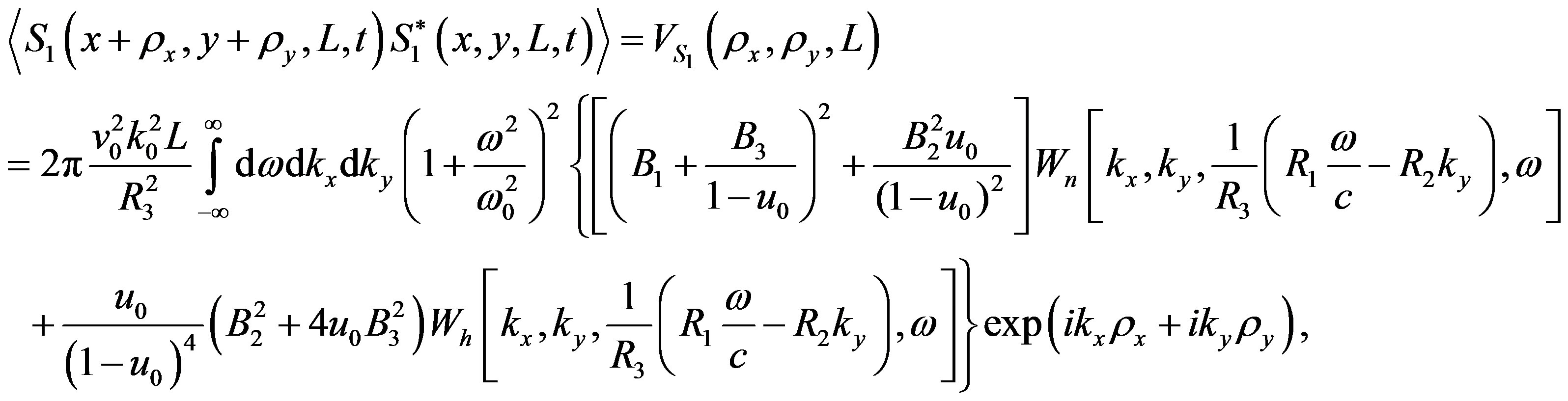(9)
where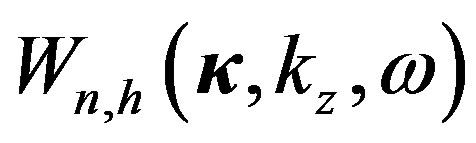 
are the arbitrary correlation functions of electron density and external magnetic field fluctuations. Particularly, in the absence of an external magnetic field, at θ = 0˚ (quasi-longitudinal propagation of waves), 
(one receiving antenna), for the isotropic Gaussian correlation function of electron density fluctuations (not taking into account temporal pulsations of plasma parameters), we obtain the well-known expression for the variance of the phase fluctuations 
[13],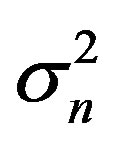 
is the variance of electron density fluctuations.
Knowledge of the phase correlation function allows us to calculate other statistical characteristics of scattered electromagnetic waves, particularly SPS which is equivalent to the ray intensity (brightness) in radiation transfer equation [10,11]. It can be obtained by Fourier transformation from the correlation function of scattered field and has a Gaussian form for strong fluctuations of the phase [14]:
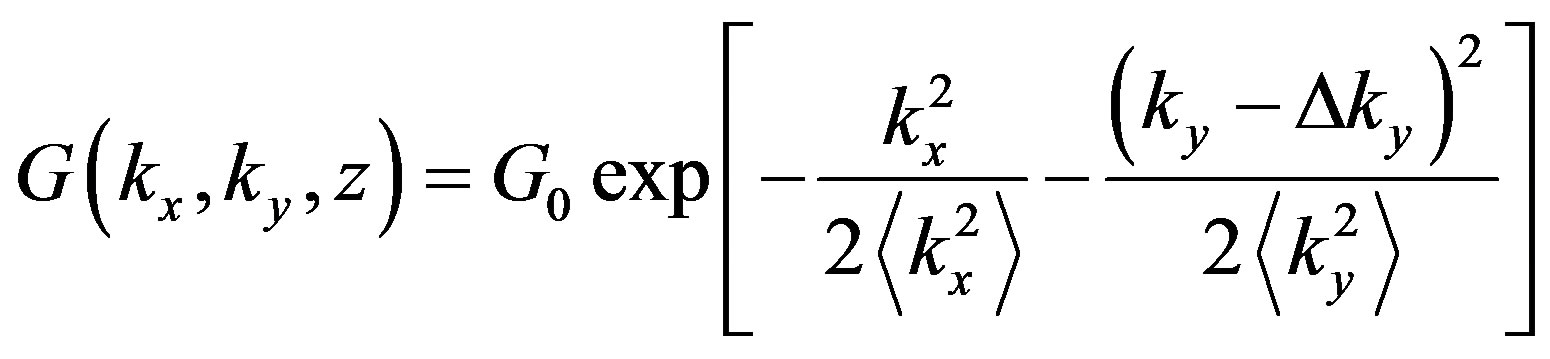, (10)
where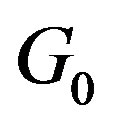 
is the amplitude of spectral curve, 
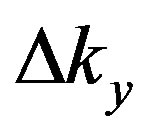determines the displacement of spectral maximum, 
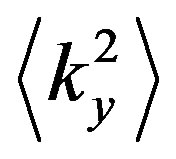and 
are the broadening of the SPS in the principle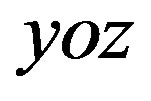 
and perpendicular 
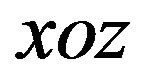planes, respectively:
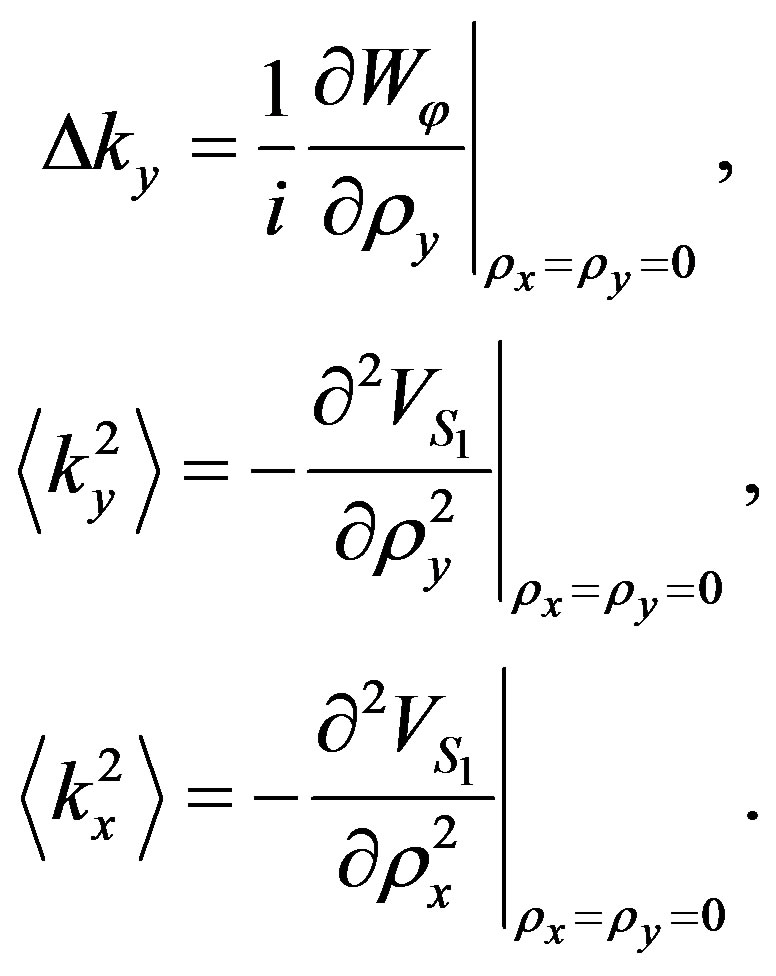(11)
The derivatives of the phase correlation function are taken at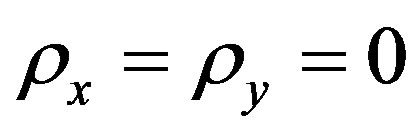
.
3. Transfer Equation for Frequency Fluctuations in Weakly Absorptive Turbulent Magnetized Plasma
At waves propagation in the atmosphere besides the amplitude and phase fluctuations we are also interested in the frequency fluctuations as far as they impose definite restrictions on the measurements accuracies. In contactless diagnostics of nonstationary plasma the most important is the temporal spectrum of a scattered wave. Therefore, we analyze the expression of fluctuating part of an instantaneous complex frequency of the wave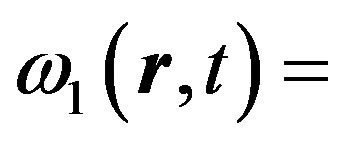 
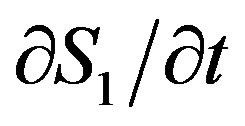. Differentiating (5) with respect to time, after Fourier transformation:
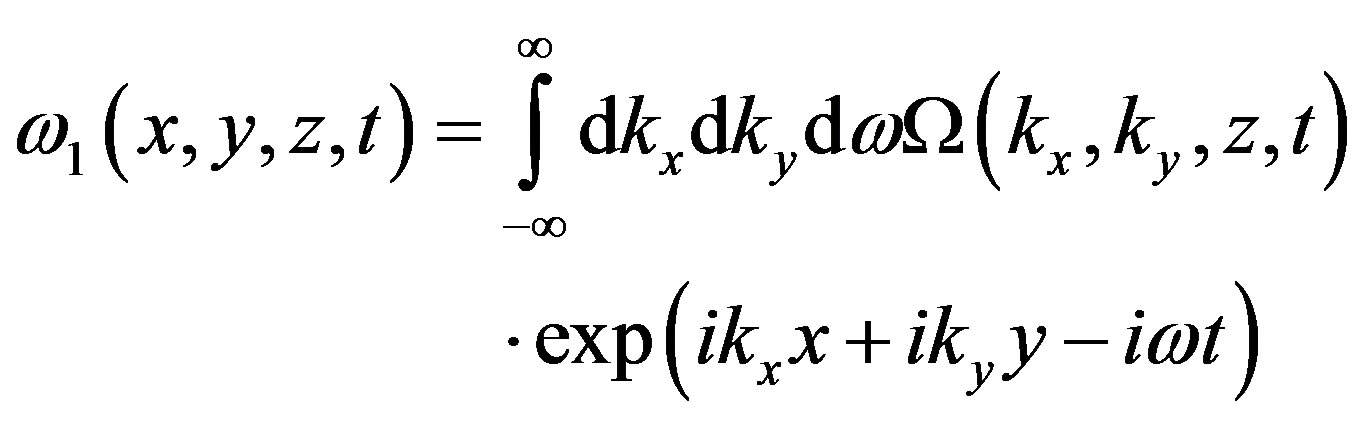
we obtain transfer equation for two-dimensional spectral density of the frequency fluctuations of scattered electromagnetic field caused due to spatial-temporal pulsations of both electron density and the external magnetic field fluctuations having different characteristic spatialtemporal scales:
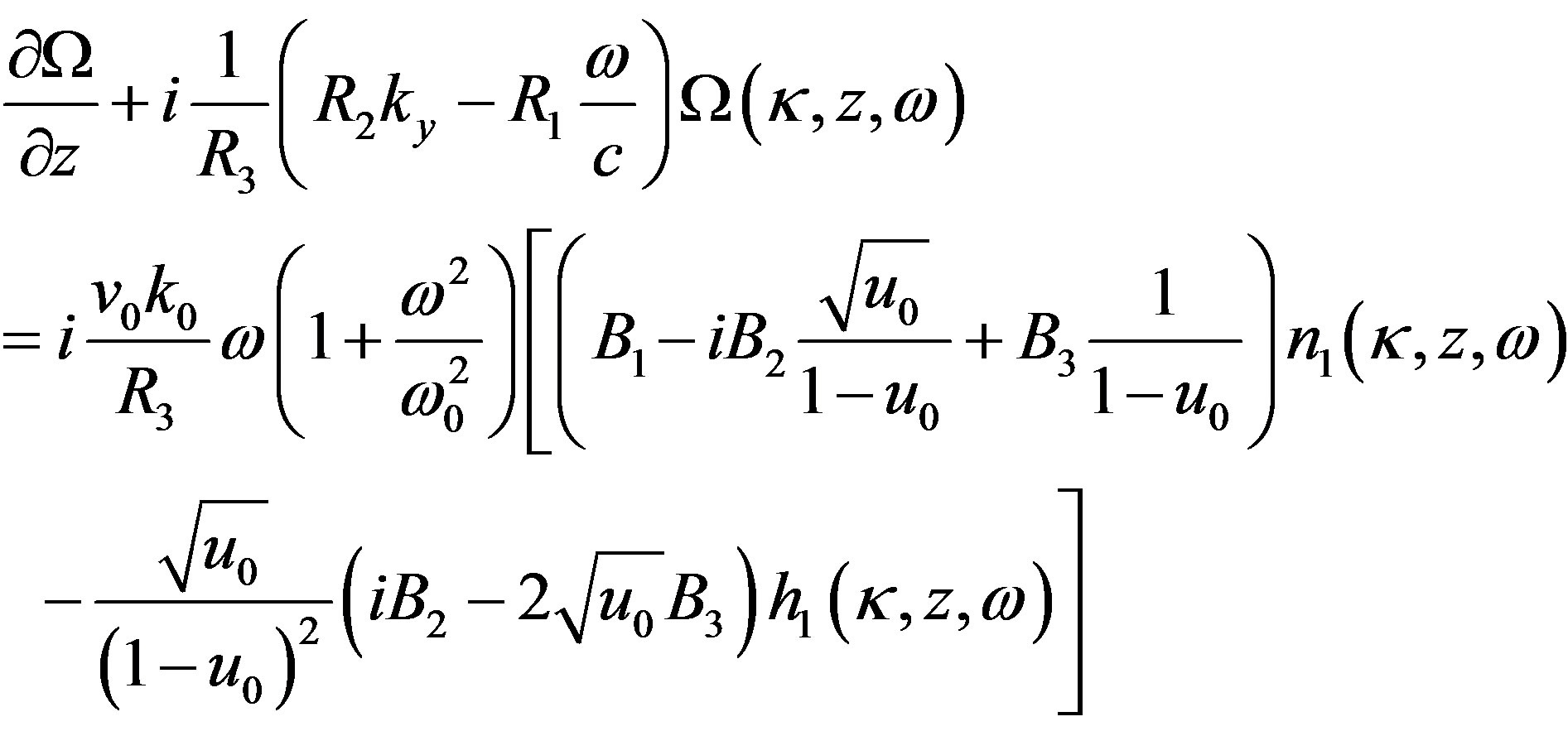, (12)
Consider the simplest case of quasi-longitudinal propagation of waves (θ = 0˚) in collisional magnetized plasma with
,
,
, 
, 
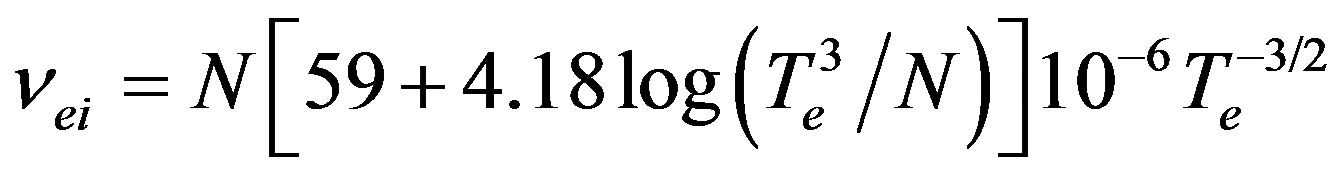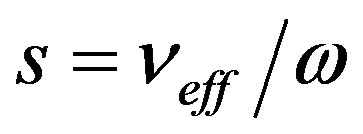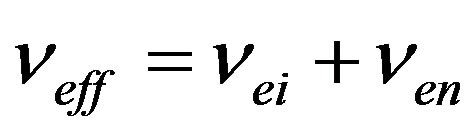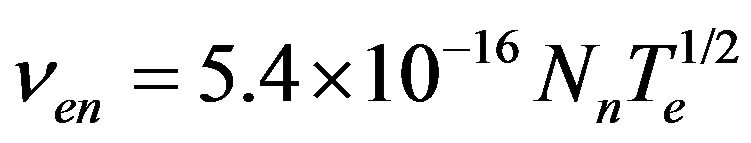are the electron-ion and electron-neutral collision frequencies, respectively [15]. Complex refractive index 
takes into account absorption caused due to collision of electrons with the neutral and other plasma particles:
,
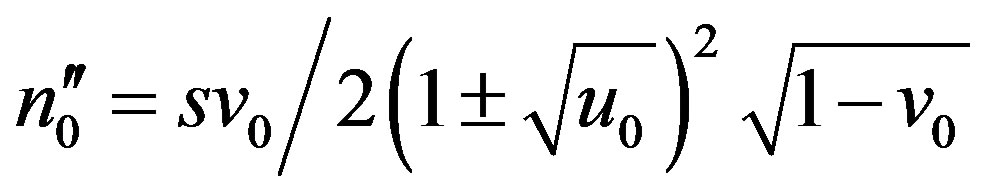; hence components of the second rank tensor (2) at θ = 0˚ and 
can be written as [5]:
, 
,
;
, 
, 
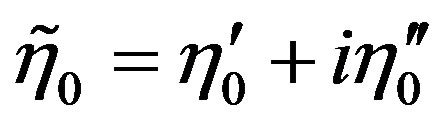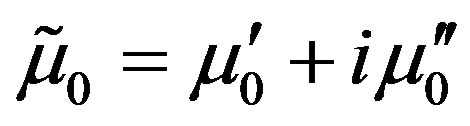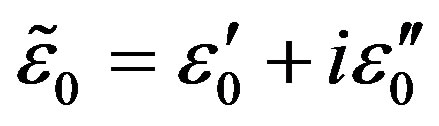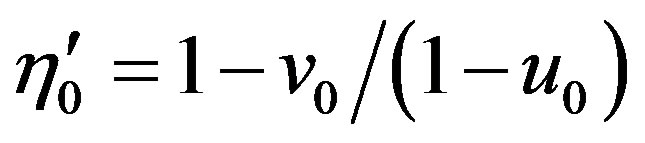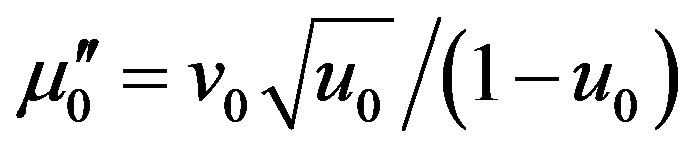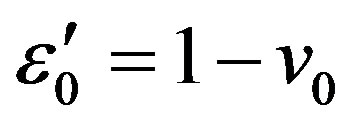
imaginary parts of these components are connected with the absorption:
,
,
.
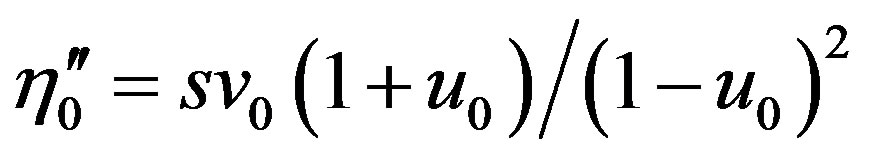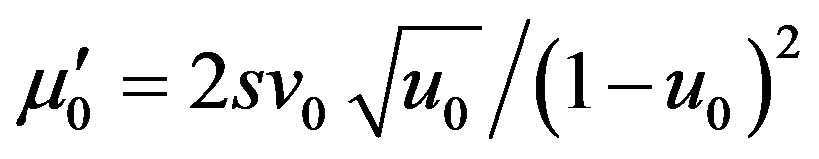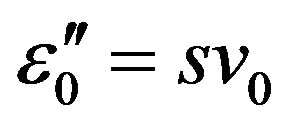Solving Equation (12) taking into account the boundary condition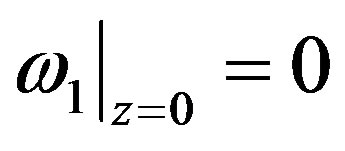
, correlation function of the frequency fluctuations for arbitrary spatial-temporal spectra of correlation functions of the electron density 
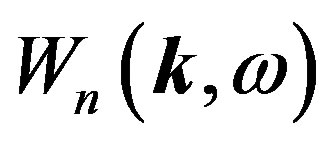and magnetic field fluctuations 
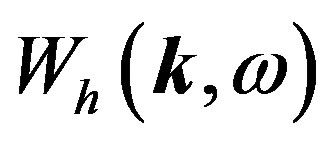can be written as:
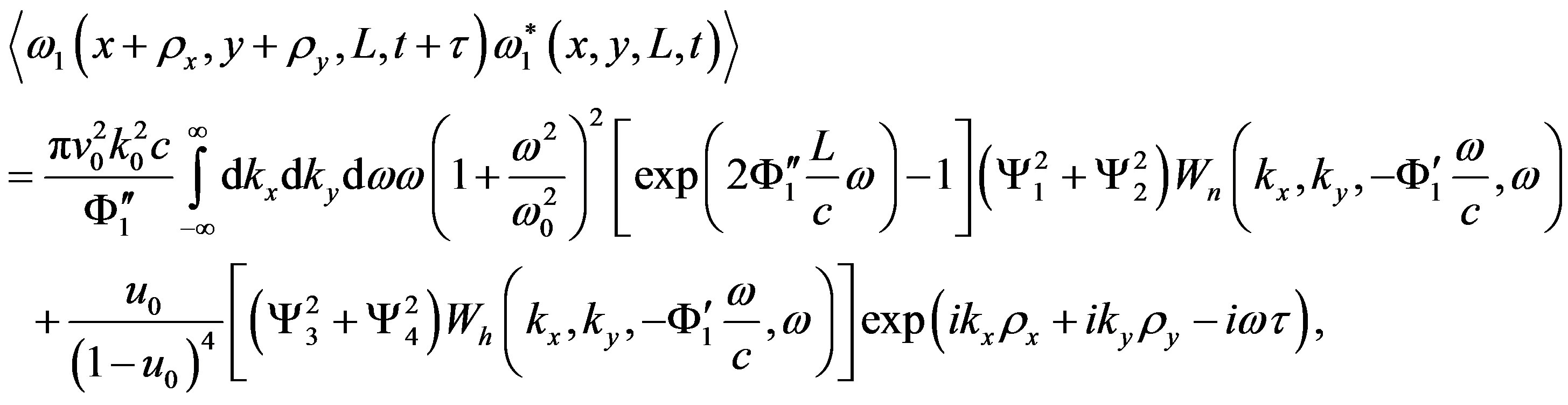(13)
where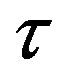 
is the observation time,
,
, 
, 
,
,
,
,
, 
,
,
,
,
,
, 
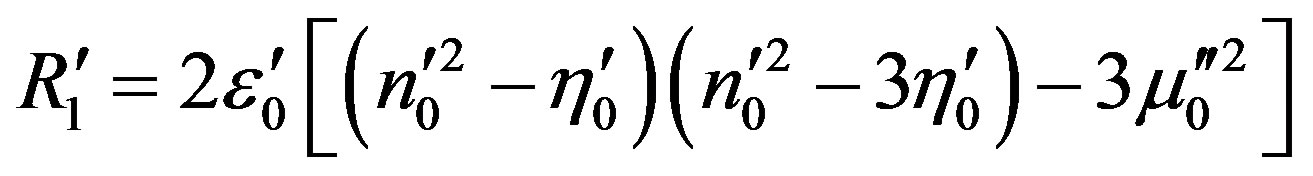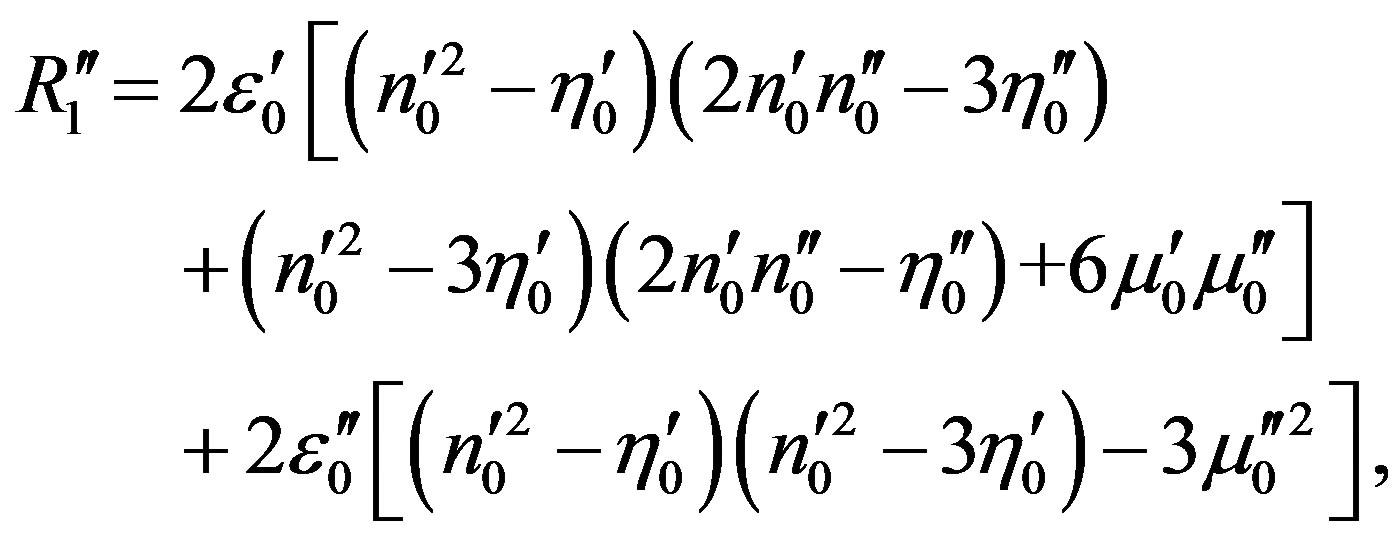
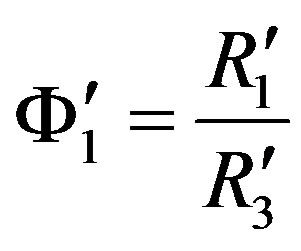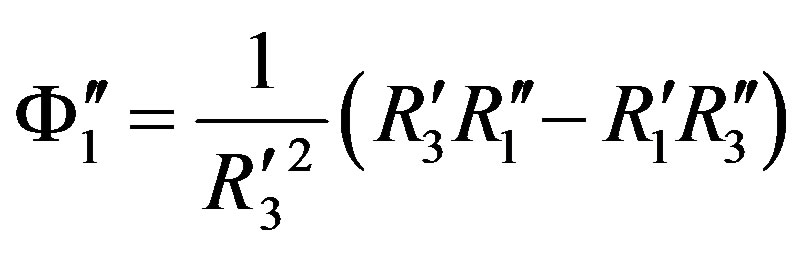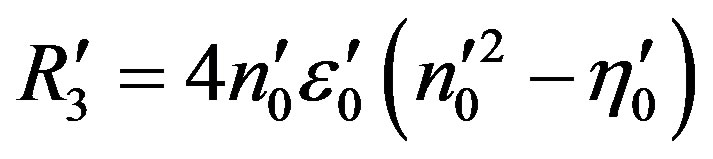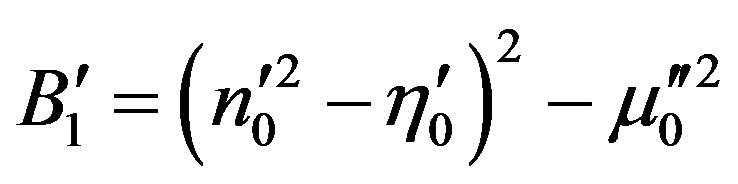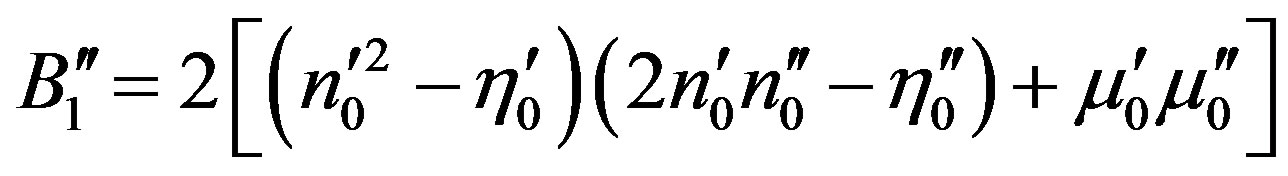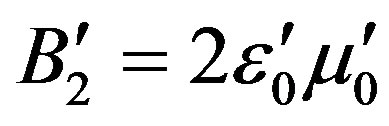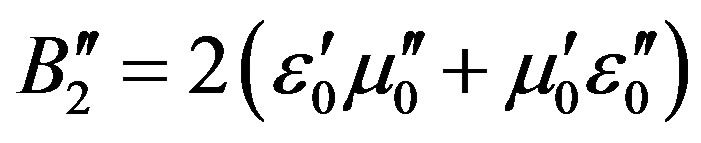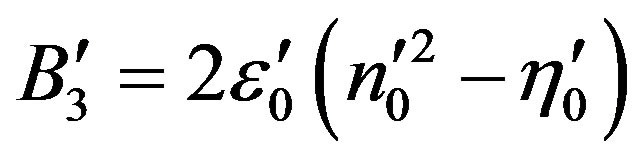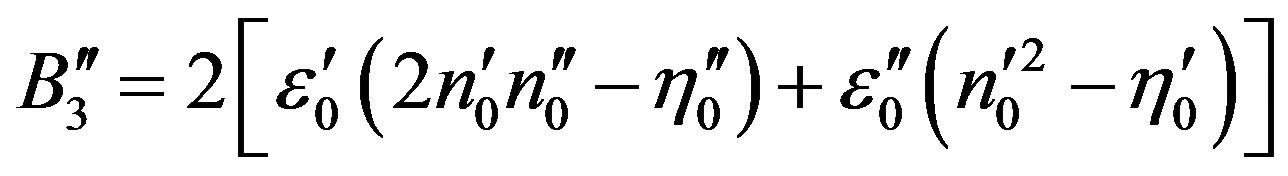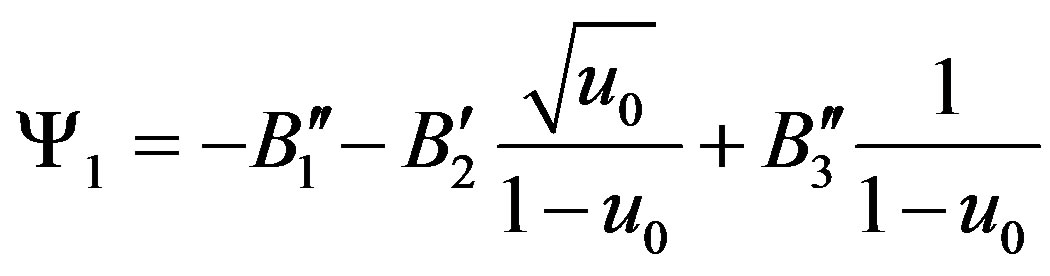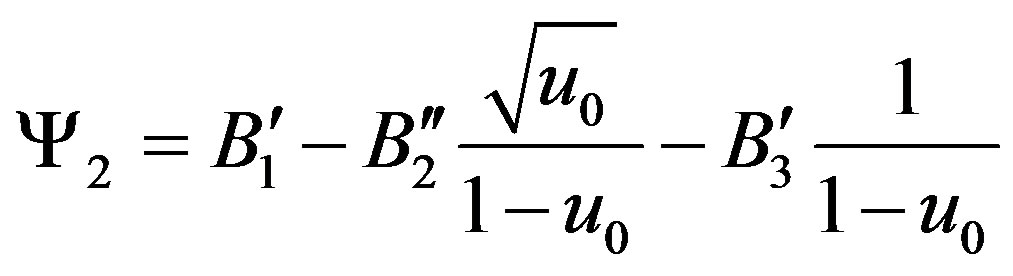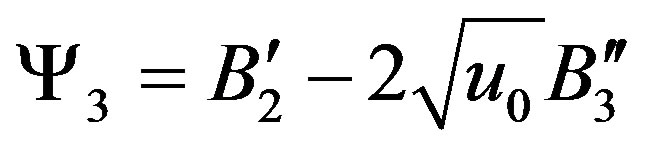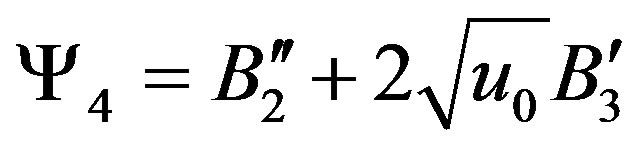
The variance of the frequency fluctuations of scattered electromagnetic waves
determines the width of the temporal power spectrum measured by experiments. First term for arbitrary correlation function of electron density fluctuations has the following form:
(14)
where
,
.
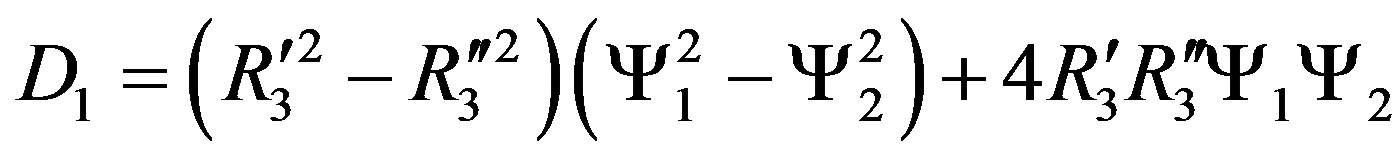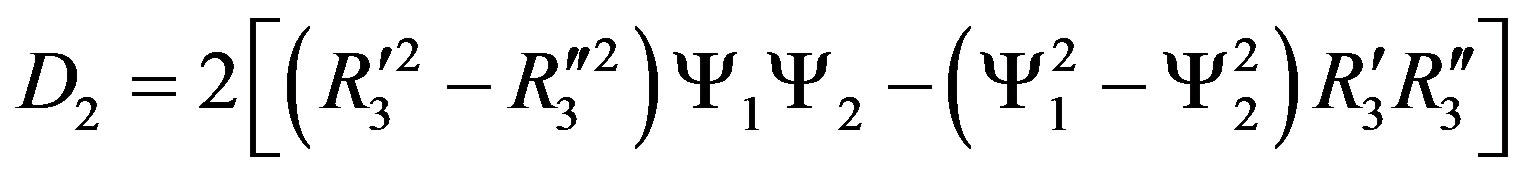Estimations show that at big distances L the expression
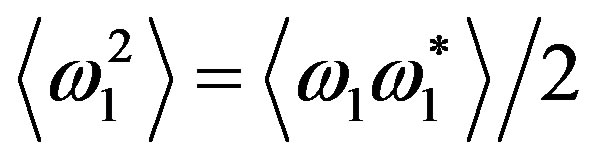is valid. Therefore, it is not necessary to calculate the combination
.
Hence, in general, intensity of the frequency fluctuations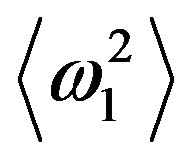 
of scattered ordinary and extraordinary waves depends on: 1) the geometry of the task (thickness of a turbulent collisional magnetized plasma slab, angle of an incident wave on the slab boundary, angle between the wave vectors of an incident wave and external magnetic field); 2) characteristic spatial-temporal scales of both electron density (taking into account anisotropy factor and the angle of inclination of prolate irregularities with respect to the external magnetic field) and external magnetic field fluctuations; 3) absorption caused by collision of electrons with other plasma particles. On the other hand, correlation function of frequency fluctuations is calculated as:
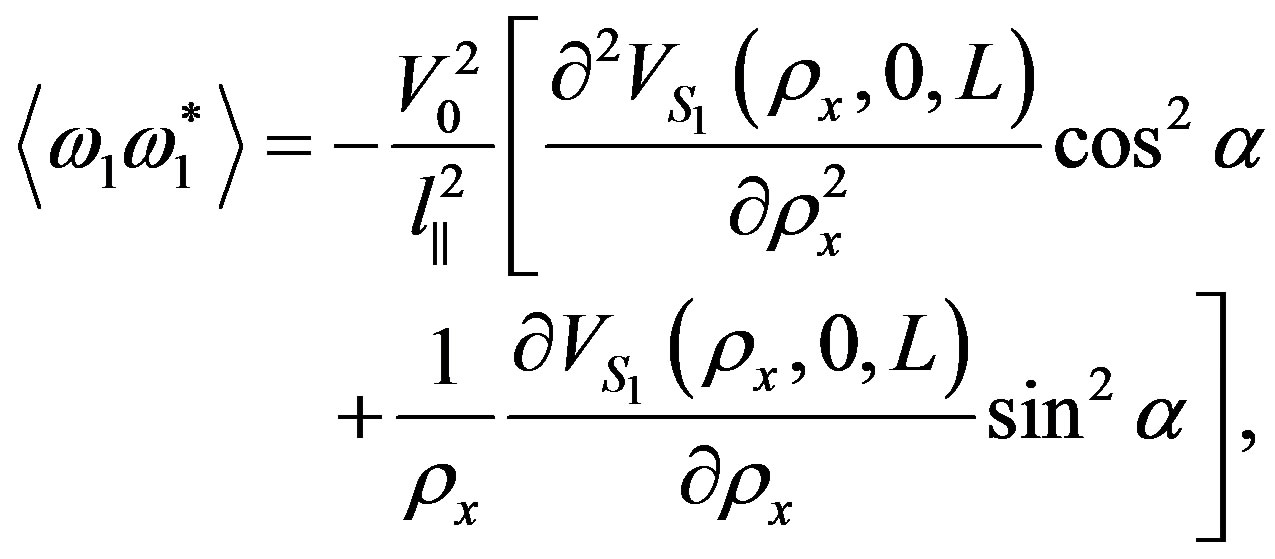(15)
where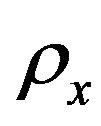 
is the distance between observation points in the plane perpendicular to the direction of wave propagation, 
is the angle between the direction of drift velocity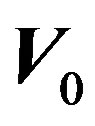 
of frozen irregularities and vector
. In this case, correlation function of frequency fluctuations is anisotropic due to the presence of the wind direction even at isotropic correlation function of phase fluctuations. From (13) and (15) it is possible to calculate and measure the horizontal drift velocity of plasma motion if other parameters are known or vice-versa.
4. Numerical Results and Discussions
The most widely used spectral density function is the Gaussian, which has certain mathematical advantages. In the theoretical study forward scattering assumption is valid when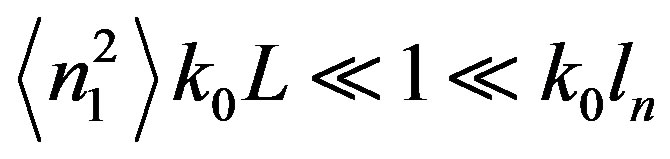
, where 
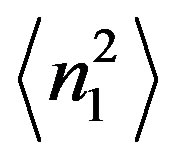is the variance of the medium fluctuations. If the single scattering condition is also fulfilled 
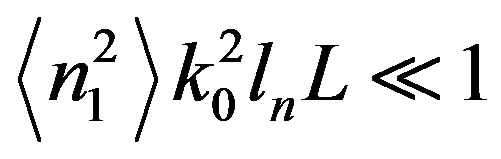a medium is characterized by the Gaussian irregularity spectrum [16]. Anisotropic Gaussian correlation function of electron density fluctuation in the principle 
plane has the following form [17]
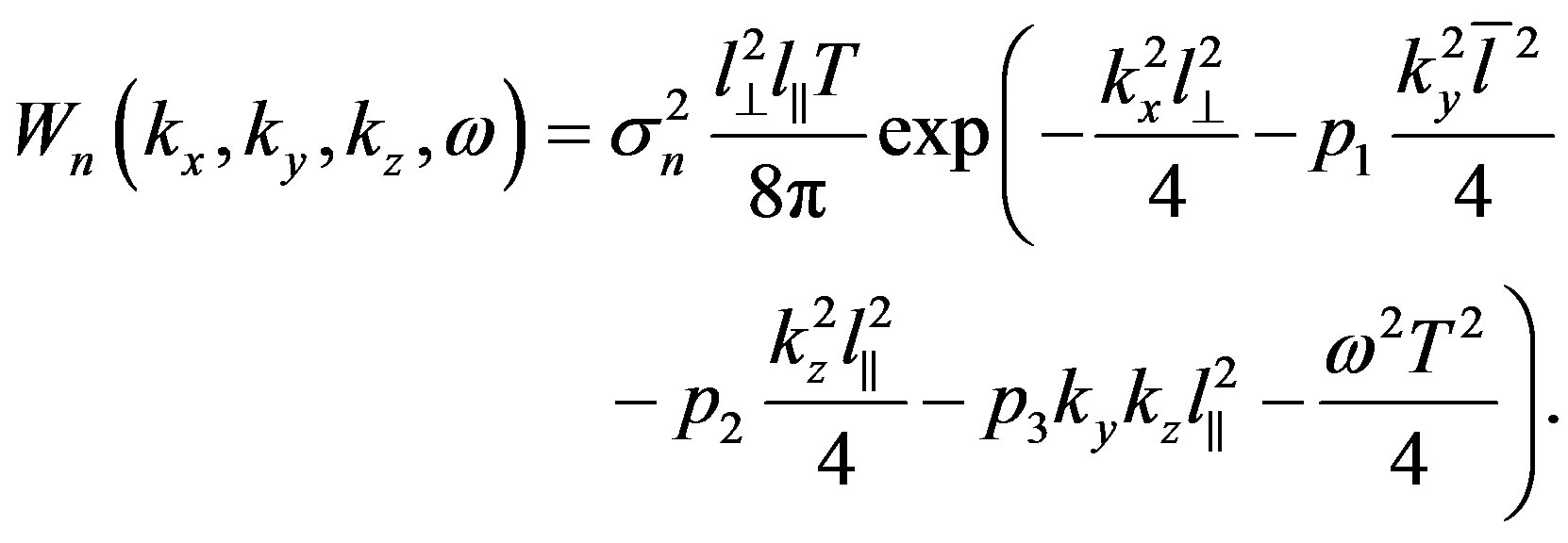(16)
This function is characterized by anisotropy factor of irregularities 
(ratio of longitudinal and transverse linear scales of plasma irregularities with respect to the external magnetic field) and the inclination angle of prolate irregularities with respect to the external magnetic field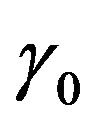
, 
is the relative fluctuations of the plasma density,
,
,
,
.
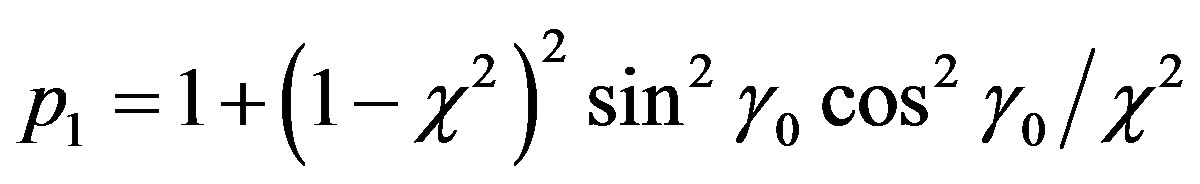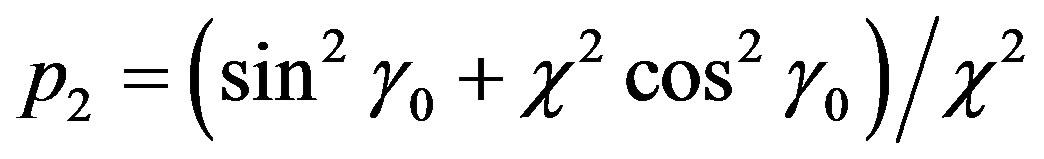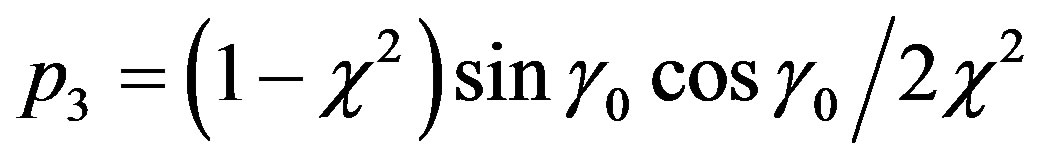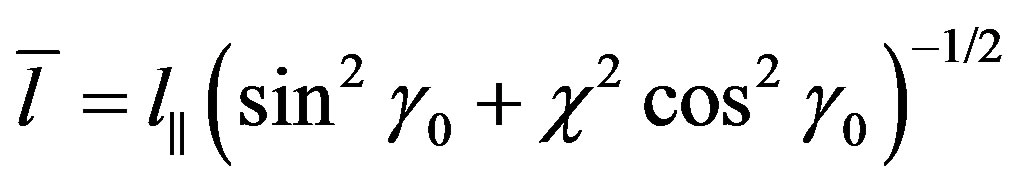For correlation function of magnetic field fluctuations we use the anisotropic Gaussian model:
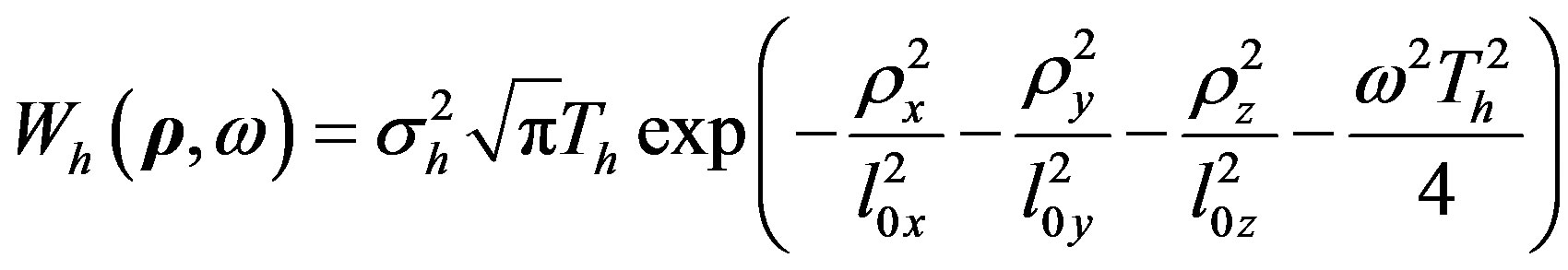(17)
where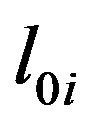 
and 
are characteristic spatial and temporal scales of an external magnetic field fluctuations. As far as scalar and solenoid vector fields are statistically independent [12], investigation of statistical characteristics of scattered electromagnetic waves would be carried out independently from electron density pulsations and external magnetic field fluctuations.
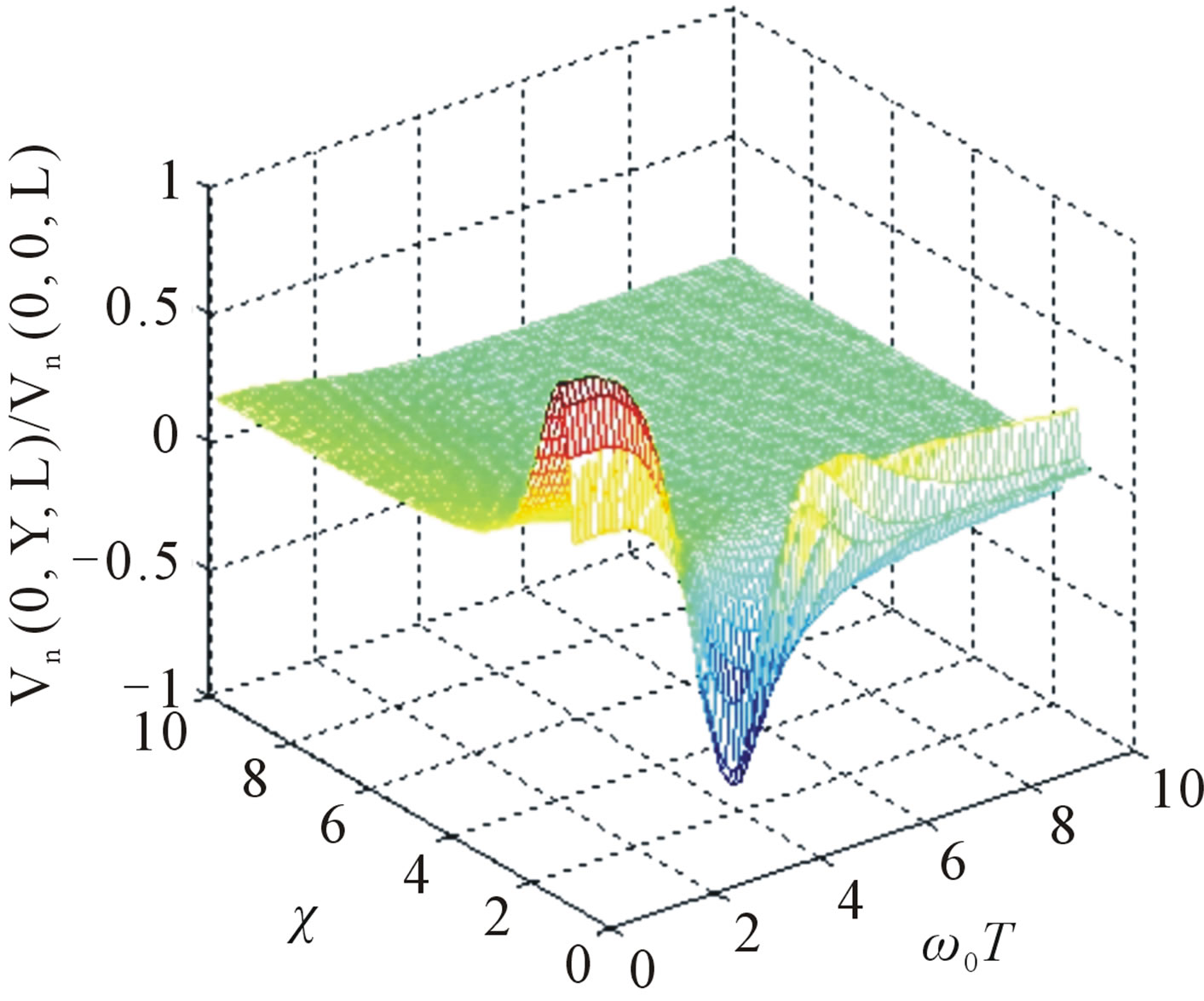
Numerical calculations are carried out for ionospheric F layer. Frequencies of an incident electromagnetic waves are equal 0.1 MHz (k0 = 0.28 × 10−2 m−1, plasma parameters: v0 = 0.28, u0 = 0.22) and 40 MHz (k0 = 0.84 m−1, plasma parameters: v0 = 0.0133, u0 = 0.0012). Figure 1 shows dependences of three-dimensional surfaces of normalized correlation functions of phase fluctuations for ordinary and extraordinary waves versus anisotropy factor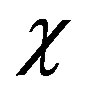 
and non-dimensional frequency parameter characterizing temporal pulsations of turbulent medium 
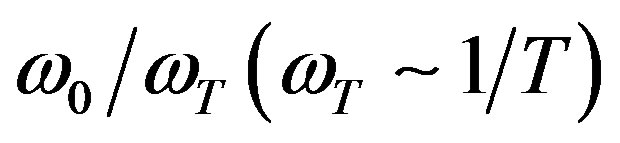using anisotropic Gaussian correlation function of electron density fluctuations (16). At γ0 = 0˚ (inhomogeneities are stretched along external magnetic field), increasing anisotropy parameter
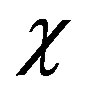, phase fluctuations connecting with scattering of the ordinary wave on electron density fluctuations of magnetized plasma substantially depend on the degree of elongation of inhomogeneities. In Figure 1 at 
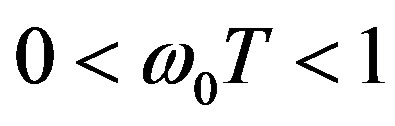temporal pulsations of plasma electrons density have more substantial effect on the ordinary wave than that on the extraordinary one. The curves corresponding to the extraordinary wave become smoother with increasing
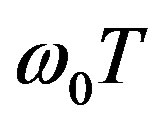. Maximums of upper and middle curves correspond to the
(a)
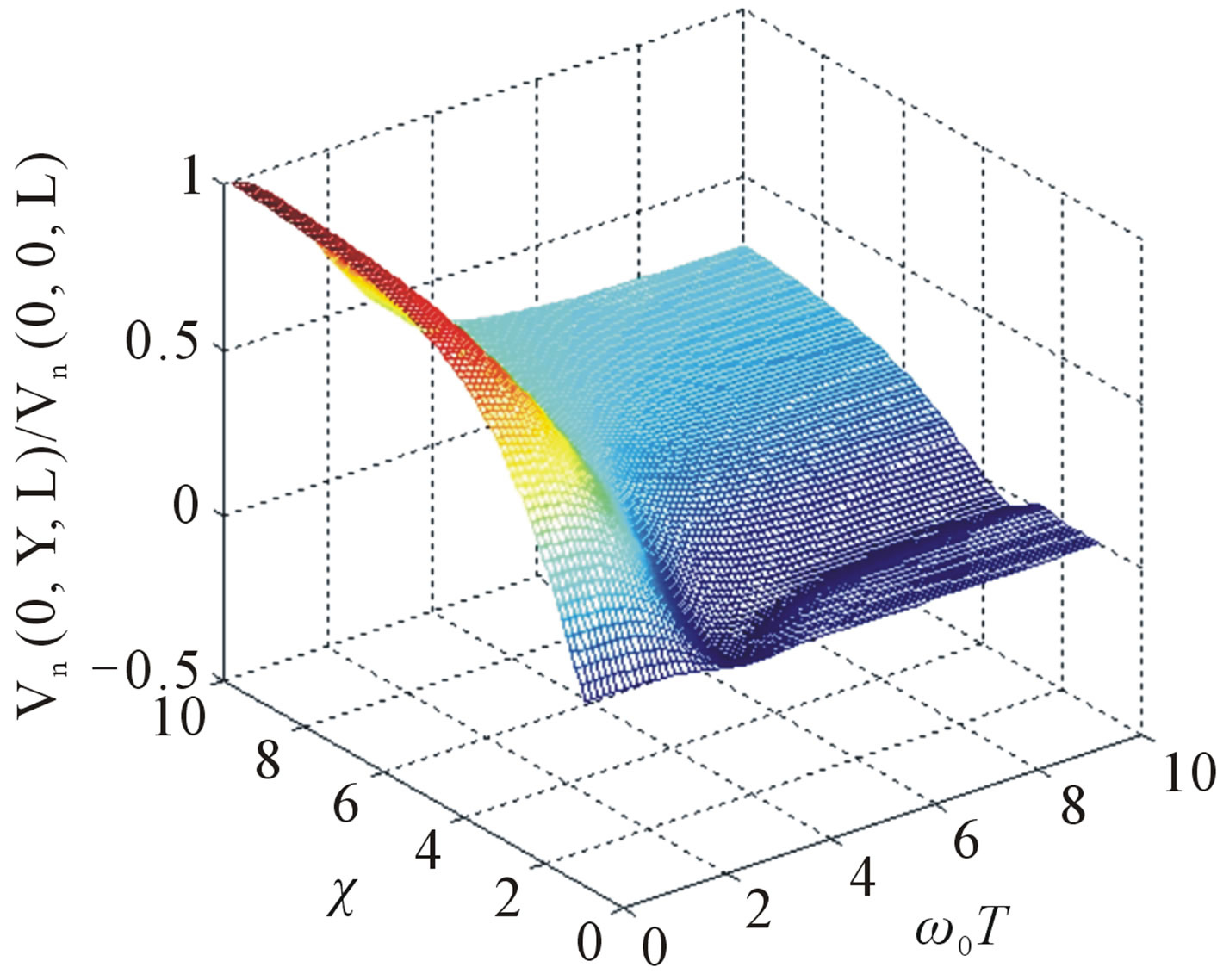(b)
Figure 1. Three-dimensional picture of the normalized correlation function of the phase fluctuation versus anisotropy coefficient of prolate irregularities χ and characteristic nondimensional temporal scale of electron density pulsations (ω0T) in turbulent magnetized plasma slab for the ordinary (a) and extraordinary (b) waves at Y = 0.1, γ0 = 0˚, θ = 5˚, l|| = 10 km.
case when the frequency of pulsation of electrons density twice exceeds the frequency of an incident wave; maximum of the lower curve arises at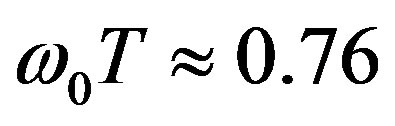
. The saturation for the ordinary waves begins at 
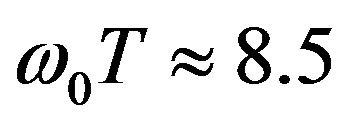and for extraordinary waves at
.
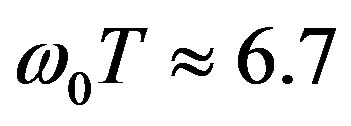Figure 2(b) presents the curves of the dependence of broadening of the SPS in principal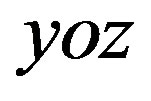 
plane versus parameter of anisotropy of electrons density at different values of an inclination angle of prolate irregularities with respect to the external magnetic field. Broadening of the spectrum is caused by both anisotropy and spatialtemporal fluctuations of electron density. Broadening of the spectrum is maximum for the ordinary wave at 
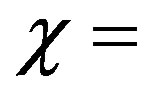5,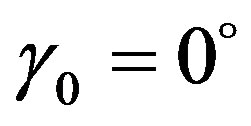 
(upper curve) and at
, 
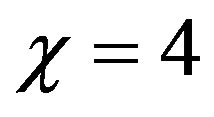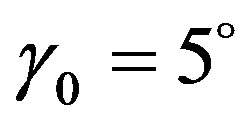(lower curve), and for the extraordinary wave at
, 
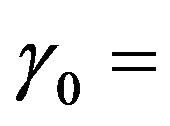0˚ (upper curve) and at
, 
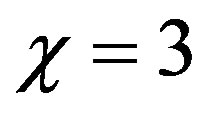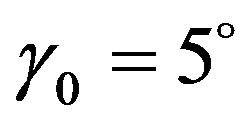(lower curve). Broadening of the spatial spectrum is the same for both waves beginning from
.
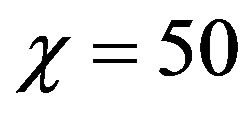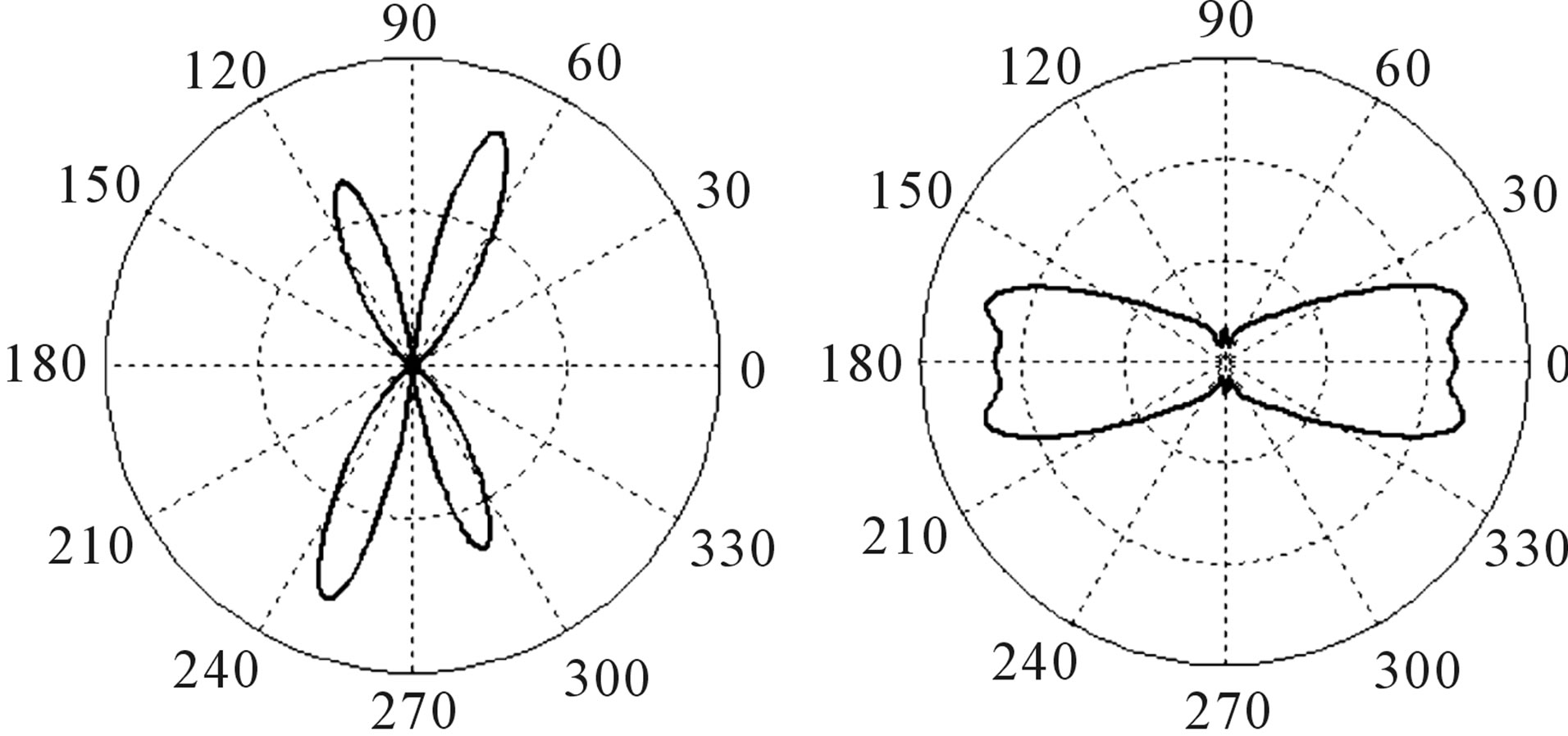
Phase portraits of the normalized correlation function of scattered radiation, caused by temporal pulsations of an external magnetic field in the polar coordinate system are given in Figures 3 and 4 for the ordinary wave at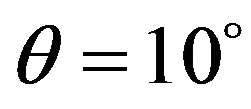
. In Figure 3 the curves are constructed at fixed distances between the receiving antennas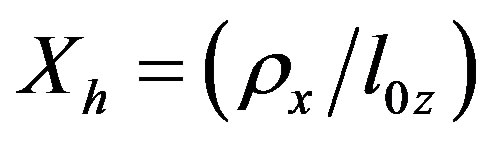 
,
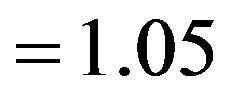. When the frequency of temporal pulsations of turbulent plasma increases and exceeds the frequency of an incident wave (
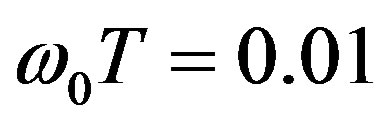and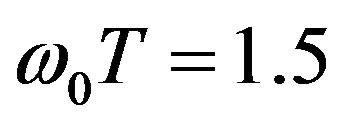
), phase portraits are substantially deformed. Figure 4 shows the evolution of phase portrait when distance between observation points decreases at fixed value
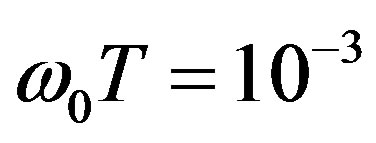. Numerical calculations show that deformation of phase portrait of the phase correlation function caused by electrons density fluctuations substantially depends on: the collision frequency of electrons with other plasma particles, characteristic linear scales of an external magnetic field fluctuations, distance between receiving antennas, incident angle of electromagnetic wave on a boundary of magnetized plasma and frequency of temporal pulsations of electrons density.
Phase portraits of the normalized correlation function of scattered radiation, caused by temporal pulsations of an external magnetic field in the polar coordinate system are given in Figures 3 and 4 for the ordinary wave at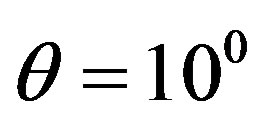
. In Figure 3 the curves are constructed at fixed distances between the receiving antennas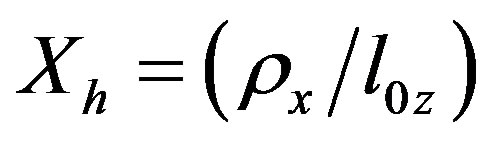 
,
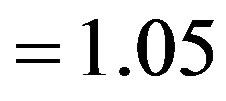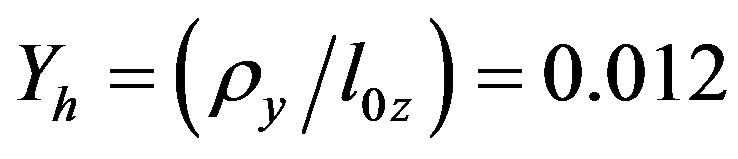. When the frequency of temporal pulsations of turbulent plasma increases and exceeds the frequency of an incident wave (
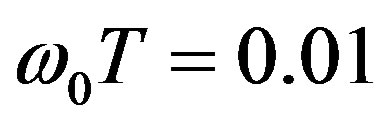and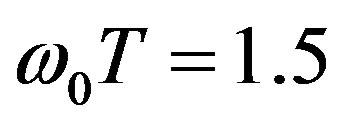
), phase portraits are substantially deformed. Figure 4 shows the evolution of phase portrait when distance between observation points decreases at fixed value
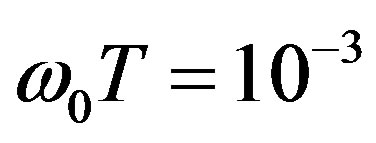. Numerical calculations show that deformation of phase portrait of the phase correlation function caused by electrons density fluctuations substantially depends on: the collision frequency of electrons with other plasma particles, characteristic linear scales of an external magnetic field fluctuations, distance between receiving antennas, incident angle of electromagnetic wave on a boundary of magnetized plasma and frequency of temporal pulsations of electrons density.
Substituting (16) into (13), assuming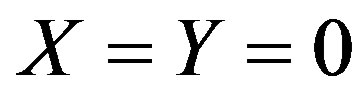
, amplification condition of the intensity of frequency fluctuations of scattered ordinary and extraordinary waves caused by spatial-temporal pulsations of electron density
(a) (b)
Figure 2. Dependence of the normalized correlation function of the phase fluctuations versus characteristic temporal scale of electron density pulsations (ω0T) for the ordinary and extraordinary waves at different χ and γ0 (a). Dependence of the broadening of the angular power spectrum in the principle plane (at θ = 10˚, ω0T = 50) versus anisotropy parameter χ (solid line-γ0 = 0˚, dashed line-γ0 = 5˚).
(a) (b)
Figure 3. Phase portraits of the normalized phase correlation function of scattered ordinary electromagnetic waves caused due to temporal pulsations of an external magnetic field at (l0x/l0z) = 0.07, (l0y/l0z) = 0.03, Xh = 1.05, Yh = 0.012, loz = 50 km; ω0T = 0.01 (a), ω0T = 1.5 (b).
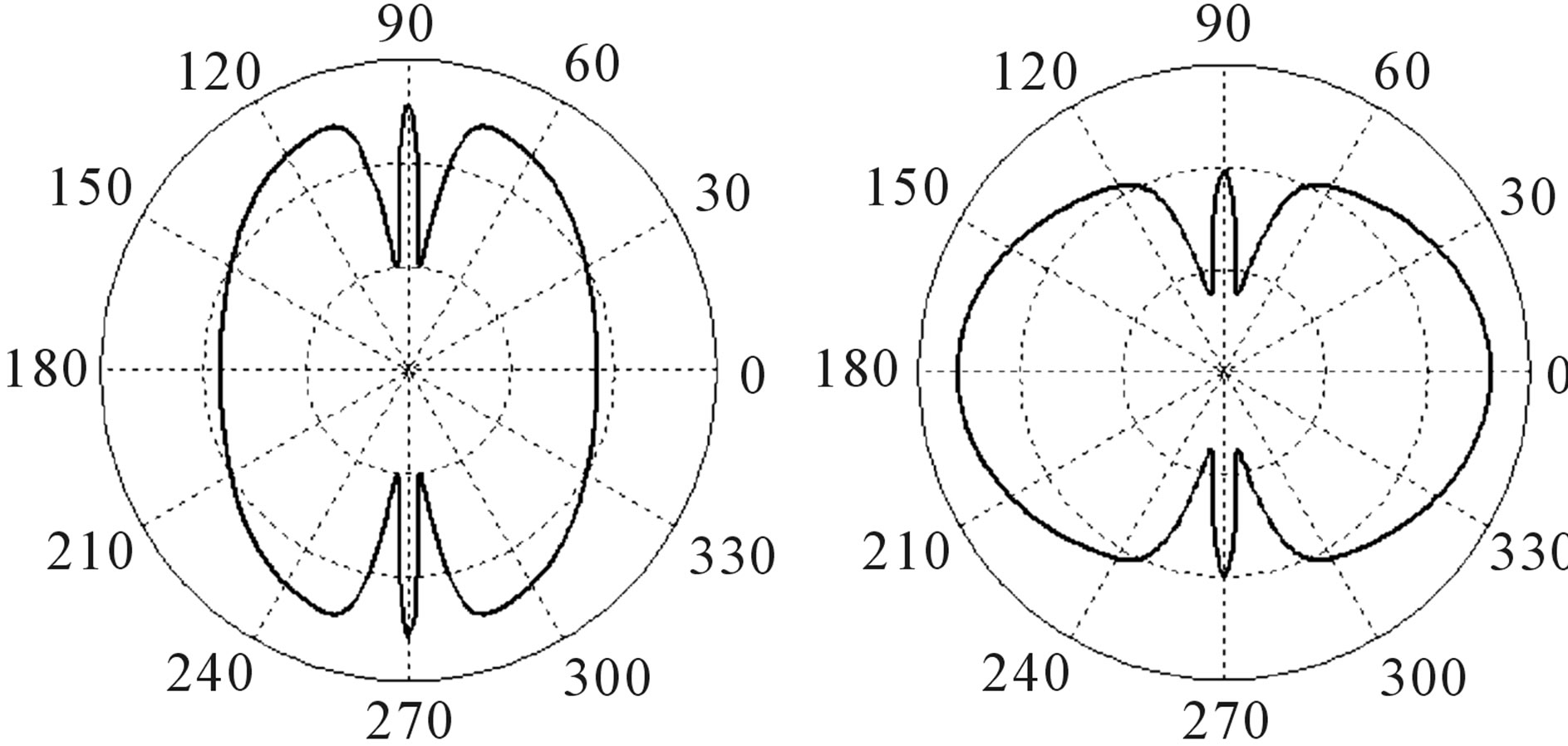(a) (b)
Figure 4. Phase portraits of the normalized phase correlation function of scattered ordinary electromagnetic waves caused due to temporal pulsations of an external magnetic field at ω0T = 0.001, (lox/loz) = 3.2, (loy/loz) = 3.7, Yh = 0.009, loz = 100 km; Xh = 30 (a), Xh = 15 (b).
at normal incidence of wave (θ = 0˚) at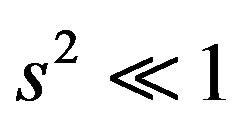 
can be written as:
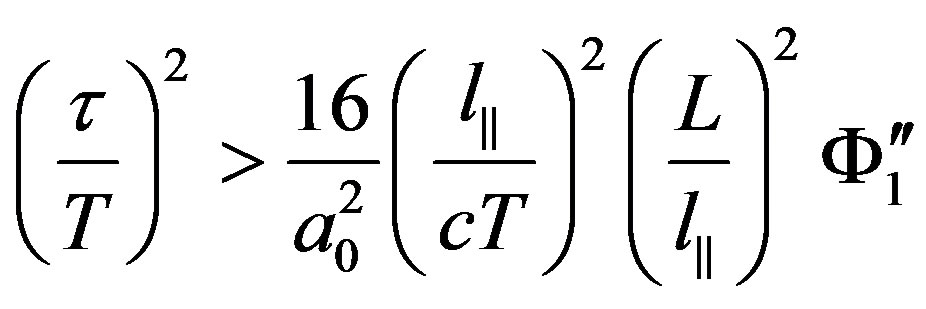, (18)
where:
,
.
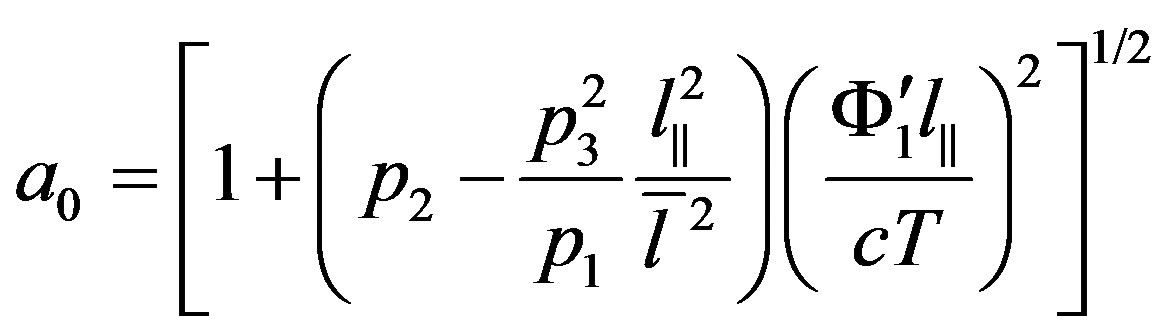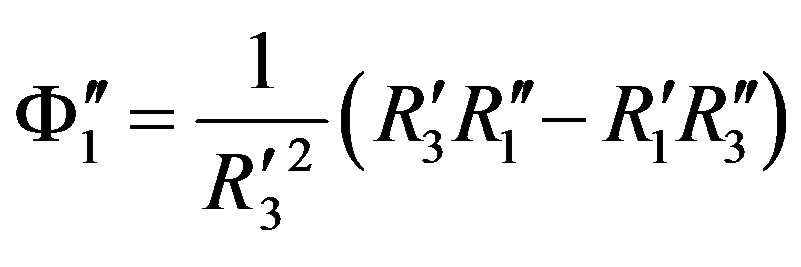It also considers anisotropic properties of prolate irregularities relative external magnetic field. If the condition (18) is not fulfilled waves fast attenuate. Numerical calculations show that the condition (18) is fulfilled for frequencies 0.1 MHz and 40 MHz when distance traveling by the wave in turbulent plasma is L = 100 - 200 km and characteristic linear scale of electrons density fluctuation of is equal to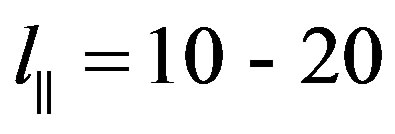
.
5. Conclusions
In the complex geometrical optics approximation on the basis of stochastic tensor wave equation the peculiarities of the influence spatial-temporal fluctuations of both electron density and external magnetic field on statistical characteristics of the ordinary and extraordinary waves scattered in the turbulent magnetized plasma are studied. Linearized stochastic differential equation is obtained for phase fluctuation and second order statistical moments of phase fluctuation are calculated for arbitrary correlation functions of electron density and external magnetic field fluctuations. Numerical calculations are carried out for anisotropic Gaussian correlation functions of fluctuating plasma parameters using experimental data. The amplification conditions of the intensity of frequency fluctuation are obtained taking into account geometry of the task and the features of turbulent magnetized plasma. It is shown that weak absorptive nonstationary plasma, anisotropy and angle of inclination of prolate irregularities relative to the external magnetic field may lead to the exponential amplification of the intensity of frequency fluctuations of scattered electromagnetic waves. Simultaneous presence of both nonstationary and absorption lead to fast broadening of the spectrum of scattered radiation.
Statistical characteristics of scattered waves depend on correlation properties of temporal parameters of a chaotically inhomogeneous medium, dispersion law and waves type. It should be noted that the obtained results are valid on the distances from the source where amplitude fluctuations of the wave are small. However, in many cases phase characteristics of scattered electromagnetic waves calculated by the smooth perturbation method are correct in the region of strong fluctuations as well, and therefore there are the reasons to hope that these formulas will have wide application in the ionospheric plasma, in nonstationary media with different dispersion law, particularly in semiconductor plasma and ferrites. A new “compensation effect” connected with the oblique incidence of wave on a magnetized plasma slab and the influence of spatial-temporal fluctuations of both electron density (power-law model of the correlation function) and external magnetic field on the transfer equation of frequency fluctuation of the ordinary and extraordinary waves in collisional magnetized plasma will be considered in a separate paper.
REFERENCES
- V. L. Frolov, N. V. Bakhmet’eva, V. V. Belikovich, G. G. Vetrogradov, V. G. Vatrogradov, G. P. Komrakov, D. S. Kotik, N. A. Mityakov, S. V. Polyakov, V. O. Rapoport, E. N. Sergeev, E. D. Tereshchenko, A. V. Tolmacheva, V. P. Uryadov and B. Z. Khudukon, “Modification of the earth’s ionosphere by High-Power High-Frequency Radio Waves,” Physics-Uspekhi, Vol. 50, No. 3, 2007, pp. 315-324. doi:10.1070/PU2007v050n03ABEH006282
- Z.-S. Wu, H.-Y. Wei, R.-K. Yang and L.-X. Guo, “Study of Scintillation Considering Inner and Outer-Scales for Laser Beam Propagation on the Slant Path through the Atmospheric Turbulence,” Progress in Electromagnetics Research, PIER, Vol. 80, 2008, pp. 277-293. doi:10.2528/PIER07112505
- V. G. Gavrilenko, A. V. Sarokin, G. V. Jandieri and V. G. Jandieri, “Some properties of the Angular Power Distribution of Electromagnetic Waves Multiply Scattered in a Collisional Magnetized Turbulent Plasma,” Plasma Physics Report, Vol. 31, No. 7, 2005, pp. 604-615. doi:10.1134/1.1992588
- G. V. Jandieri, A. Ishimaru, K. Yasumoto, A. G. Khantadze and V. G. Jandieri, “Angle-of-arrival of Radio Waves Scattered by Turbulent Collisional Magnetized Plasma Layer,” International Journal of Microwave and Optical Technology, Vol. 4, No. 3, 2009, pp. 160-169.
- G. V. Jandieri, A. Ishimaru, V. G. Jandieri, A. G. Khantadze and Z. M. Diasamidze, “Model computations of Angular Power Spectra for Anisotropic Absorptive Turbulent Magnetized Plasma,” Progress in Electromagnetics Research, PIER, Vol. 70, 2007, pp. 307-328. doi:10.2528/PIER07013103
- G. V. Jandieri, A. Ishimaru, N. N. Zhukova, T. N. Bzhalava and M. R. Diasamidze, “On the influence of fluctuations of the direction of an External Magnetic Field an phase and Amplitude Correlation Functions of scattered Radiation by Magnetized Plasma Slab,” Progress in Electromagnetics Research B, PIER B, Vol. 22, 2010, pp. 121- 143. doi:10.2528/PIERB10051402
- G. V. Jandieri, A. Ishimaru and V. G. Jandieri, “Depolarization effects of Incoherently Scattered Electromagnetic Waves by Inhomogeneous Magnetized Plasma Slab,” Journal of Electromagnetic Analysis and Applications, Vol. 3, No. 11, 2011, pp. 471-478.
- V. G. Gavrilenko, V. N. Konkov and N. A. Churilina, “On the influence of absorption on the Statistical Characteristics of wave in medium with Smooth Spatial-Temporal Fluctuations,” in Russian, Izv. Vuzov, Radiophysics, vol. 21, No. 10, 1978, pp. 1537-1540.
- V. L. Ginzburg, “Propagation of Electromagnetic Waves in Plasma,” Gordon and Beach, New York, 1961.
- A. Ishimaru, “Wave Propagation and Scattering in Random Media, Vol. 2, Multiple Scattering, Turbulence,” Rough Surfaces and Remote Sensing, IEEE Press, Piscataway, 1997.
- S. M. Rytov, Y. A. Kravtsov and V. I. Tatarskii, “Principles of Statistical Radiophysics. vol. 4. Waves Propagation Through Random Media,” Springer, Berlin, 1989.
- V. I. Tatarskii, “Wave Propagation in a Turbulent Medium,” McGraw-Hill, New York, 1961.
- B. N. Gershman, L. M. Erukhimov and Y. Y. Yashin, “Wave phenomena in the Ionosphere and Space Plasma,” in Russian, Nauka, Moscow, 1984.
- V. G. Gavrilenko, A. A. Semerikov and G. V. Jandieri, “On the effect of absorption on Multiple Wave Scattering in a Magnetized Turbulent Plasma,” Wave Random Media, Vol. 9, No. 3, 1999, pp. 427-440. doi:10.1088/0959-7174/9/3/310
- H. Rishbeth and O. K. Garriott, “Introduction to Ionospheric Physics,” Academic Press, New York, 1969.
- A. W. Wernik and C. H. Liu, “Ionospheric Irregularities Causing Scintillation of GHz Frequency Radio Signals,” Journal of Atmospheric and Terrestrial Physics, Vol. 36, No. 5, 1974, pp. 871-879. doi:10.1016/0021-9169(74)90032-4
- G. V. Jandieri, A. Ishimaru and V. G. Jandieri, “A Radio Scintillation in the Turbulent Collision Magnetized Plasma,” Proceeding of the 2007 World Congress in Computer Science, Computer Engineering and Applied Computing, Las Vegas, 25-28 June 2007, pp. 189-195.
NOTES
*Corresponding author.