Journal of Electromagnetic Analysis and Applications
Vol. 3 No. 10 (2011) , Article ID: 8144 , 4 pages DOI:10.4236/jemaa.2011.310065
Fault Tolerant Neuro-Robust Position Control of DC Motors
![]()
North Carolina A & T State University, Greensboro, USA.
Email: rzhang@ncat.edu
Received July 2nd, 2011; revised August10th, 2011; accepted August 23rd, 2011.
Keywords: Fault-Tolerant, Neuro-Robust, Position Control, DC Motors
ABSTRACT
DC motors are widely used in industry such as mechanics, robotics, and aerospace engineering. In this paper, we present a high performance control method for position control of DC motors. Fault-tolerant control model are also addressed to combine with neuro-robust control approach. It is shown that with the proposed control algorithms, external disturbances and coupled dynamics inherent in the system are effectively compensated using neural network unit in which no analytical estimation on the upper bound of the reconstruction error and uncertainties is needed. Simulations results of the position control also confirm the effectiveness of the proposed methods.
1. Introduction
In this paper, we proposed a neuro-robust position control of DC motors incorporating a fault-tolerant control model with the condition of parameter uncertainty and unknown load torque. DC motors are widely used in industry such as mechanics, robotics, and aerospace engineering. In recent years, some methods are applied for the position control of DC motors. For example, an adaptive PID control tuning was proposed to cope with the control problem for a class of uncertain chaotic systems with external disturbance [1]. Sliding mode control (SMC) is one of the popular strategies to deal with uncertain control systems [2-4]. Based on certain assumptions, various control approaches, such as model-based control, nonlinear inverse control, and neural network based control (and others) have been proposed [5-6].
This work is concerned with position control of DC motors by neuro-robust control. A nonlinear model is considered incorporate with fault-tolerant model in which modelling uncertainties and nonlinearities are explicitly addressed. The NN unit is designed to cope with the disturbances and coupled dynamics. Unlike traditional NN based method, there is no need to analytically estimate the upper bound of the reconstruction error and uncertainties in the proposed approach. Both theoretical analysis and simulation studies verify the effectiveness of the control algorithms.
2. Problem Formulation
2.1. Modeling of DC Motors
The DC motors dynamics is given by
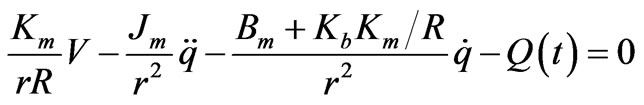 (1)
(1)
where 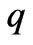 is the position of link,
is the position of link, 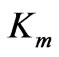 is the torque constant,
is the torque constant, 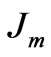 is the motor inertia,
is the motor inertia, 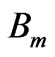 is the damping coefficient,
is the damping coefficient, 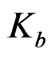 is the back emf constant, R is the armature resistance, r is the gear ratio, Q(t) is the load torque, and V is the control input in voltage [7].
is the back emf constant, R is the armature resistance, r is the gear ratio, Q(t) is the load torque, and V is the control input in voltage [7].
Our control objective is to make the position q tracking to the desired position qd. From (1), we have
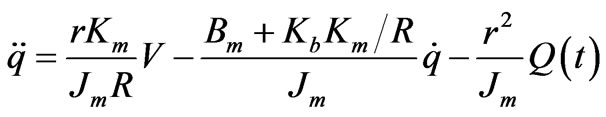 (2)
(2)
For later development, we can express (2) in the following compact form with 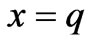 as
as
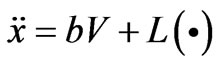 (3)
(3)
where
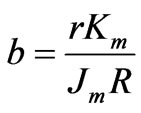 (4)
(4)
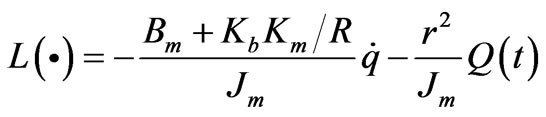 (5)
(5)
A direct measurement of the load torque is difficult because high cost equipment is required. Thus, the load torque Q(t) is usually considered to be unknown. The control objective is to design V so that the actual position trajectory q tracks the desired qd asymptotically.
2.2. Fault Tolerant Control Model
As actuator failures represent the most typical and devastate faults, we should explicitly address such faults in control design. The preceding control failures can be modeled for each control by the following model
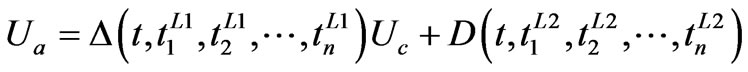 (6)
(6)
with
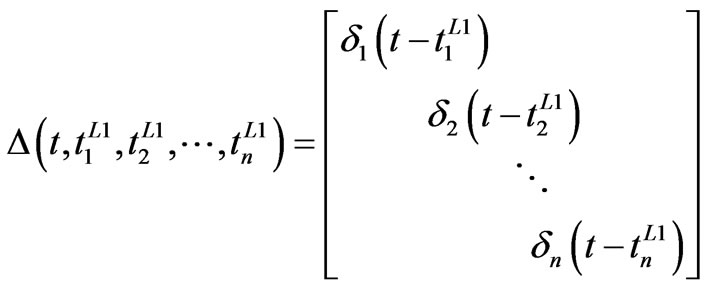 (7)
(7)
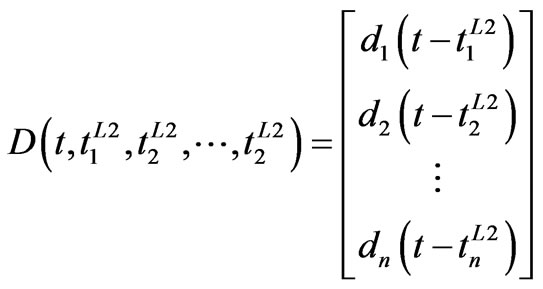 (8)
(8)
where 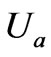 is the applied controller,
is the applied controller, 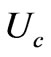 is the demanded control to be designed,
is the demanded control to be designed, 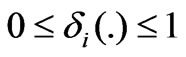 and
and 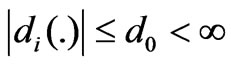 are the actuation health indicator and un-adjustable portion of the actuator. In general,
are the actuation health indicator and un-adjustable portion of the actuator. In general, 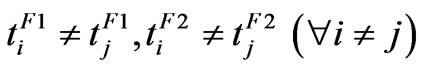 and
and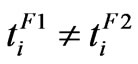 . It should be mentioned that the proposed fault model includes the commonly used fault model as a special case [8,9]. With the proposed actuator fault model (6), we can model all the possible actuation faults as mentioned earlier with
. It should be mentioned that the proposed fault model includes the commonly used fault model as a special case [8,9]. With the proposed actuator fault model (6), we can model all the possible actuation faults as mentioned earlier with 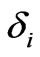 and
and  defined properly, as follows:
defined properly, as follows:
Fault Case 1)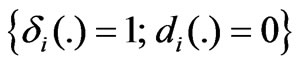 : healthy Fault Case 2)
: healthy Fault Case 2) : fading power but partially controllable Fault Case 3)
: fading power but partially controllable Fault Case 3)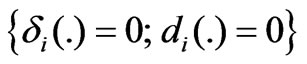 : completely shut down Fault Case 4)
: completely shut down Fault Case 4)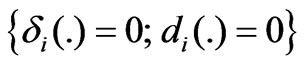 : completely uncontrollable Fault Case 5)
: completely uncontrollable Fault Case 5)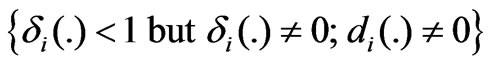 : fading power but partially controllable with uncontrollable portion.
: fading power but partially controllable with uncontrollable portion.
Most existing fault-tolerant control methods such as [8,9] are based on constant  and D(.) which is practically restrictive. In our design, we treat both
and D(.) which is practically restrictive. In our design, we treat both 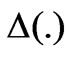 and D(.) as completely unknown time-varying. Presently, there is no technique available to anticipate/predict such faults precisely. We design a control scheme that does not explicitly use any information about
and D(.) as completely unknown time-varying. Presently, there is no technique available to anticipate/predict such faults precisely. We design a control scheme that does not explicitly use any information about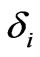 ,
, 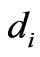 ,
, 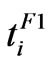 ,
,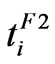 . Namely, we assume that not only the type and the magnitude of the faults are unknown, the time profile of fault occurrence are also unpredictable.
. Namely, we assume that not only the type and the magnitude of the faults are unknown, the time profile of fault occurrence are also unpredictable.
Let us define ua = V, and substitute for ua from (6), we get
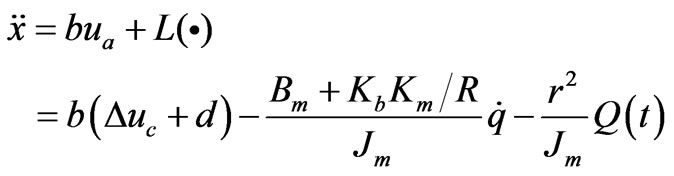 (9)
(9)
which can be expressed as
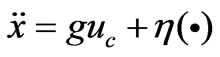 (10)
(10)
where
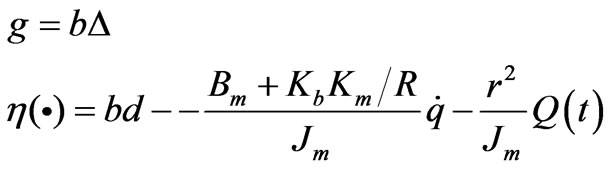 (11)
(11)
Thus, the model of DC motor has been constructed, and the uc is the control input. We will consider the case that all the actuator partially loses its effectiveness in that 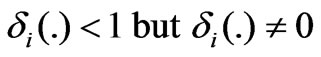 in the following control design.
in the following control design.
3. Control Design
As the first step, we define the position acking error
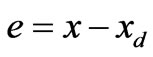 (12)
(12)
where xd is the desired position, and the filtered error variable
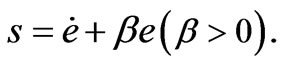 (13)
(13)
Because of (7), it is seen that the control objective is realized as long as s is driven to zero as time goes by. Therefore, we focus on designing u to stabilize s. From (3) and (5) we have
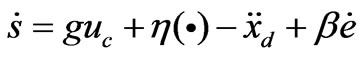 (14)
(14)
Due to the existence of the uncertainties, as lumped by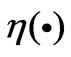 , traditional model-based control is not applicable. In this work, we design the neuro-robust control scheme based on the unavailable part
, traditional model-based control is not applicable. In this work, we design the neuro-robust control scheme based on the unavailable part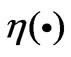 , which is to compensated by the following neural network unit,
, which is to compensated by the following neural network unit,
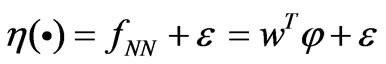 (15)
(15)
where 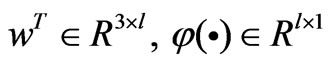 are the optimal weight matrix and basic function vector of the neural network, respectively, and
are the optimal weight matrix and basic function vector of the neural network, respectively, and 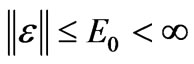 is the reconstruction error with unknown upper bound. For this case, we construct the following controller
is the reconstruction error with unknown upper bound. For this case, we construct the following controller
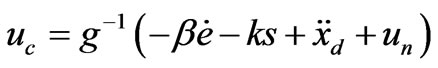 (16)
(16)
where 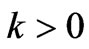 is control parameter chosen by designer. With the control scheme (16), it is seen that the closedloop dynamics become
is control parameter chosen by designer. With the control scheme (16), it is seen that the closedloop dynamics become
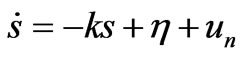 (17)
(17)
the NN based compensation is given as follows,
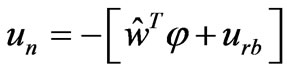 (18)
(18)
with
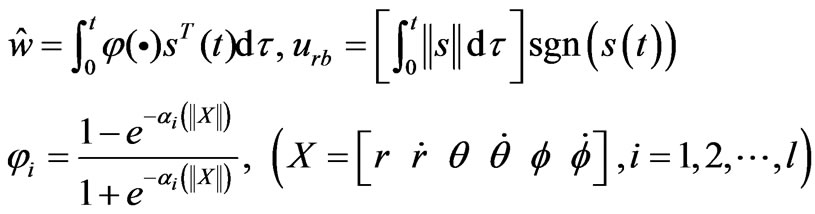
The overall control block diagram is shown in Figure 1. To address the stability, we consider the following Lyapunov function candidate,
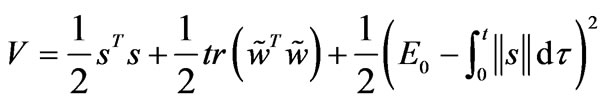 (19)
(19)
where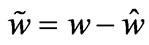 , it can be shown that
, it can be shown that
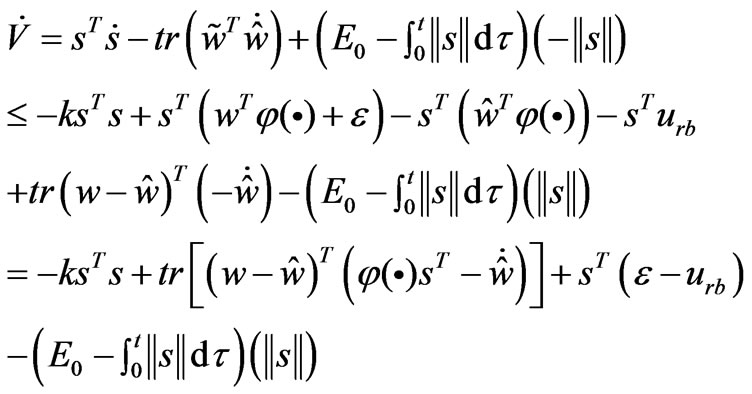 (20)
(20)
Note that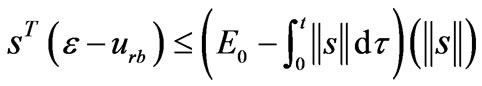 , it follows that
, it follows that
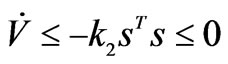
Thus
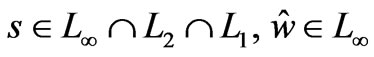
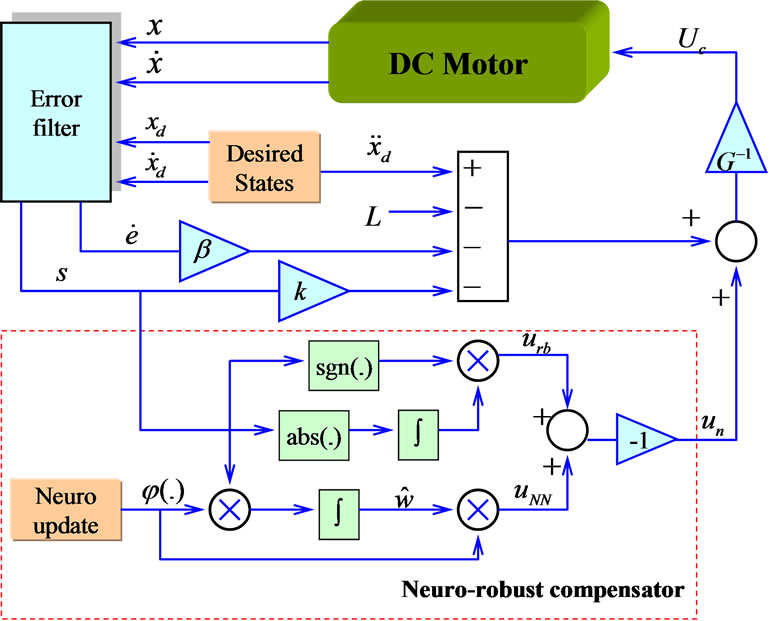
Figure 1. Block diagram of the proposed neuro-robust controller.
We can also show that s is uniformly continuous because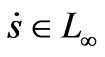 . By Babalart lemma, we conclude that
. By Babalart lemma, we conclude that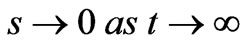 , then
, then 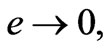 and
and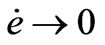 , as
, as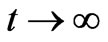 , i.e:
, i.e: 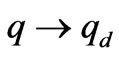 and
and 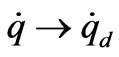 as
as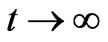 .
.
Remark 1. The control scheme, consisting of (16) and (18), has simple structure, and does not involve analytical estimation of the upper bound on the reconstruction error, making the design process simple and easy for implementation easy.
4. Simulation Results
To verify the effectiveness of the controller, a numerical simulation study was conducted. The following functions were used in the simulation,
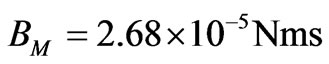 ;
;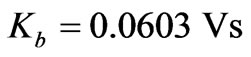 ;
;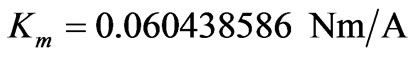 ;
;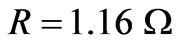 ;
;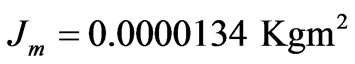 ;
; 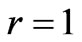
Simulation results are given in Figures 2 and 3, where Figure 2 is a plot of the position tracking. The initial values are all set 0 at the very beginning for the two figures. The actual position is tracking to the desired position very quick and smooth in both cases. In first case, a one time position tracking is set, and in the second case, there is one more desired position set after the 4th second. Figure 3 is the tracking error for both position tracking. Note that although precise descriptions of system dy-
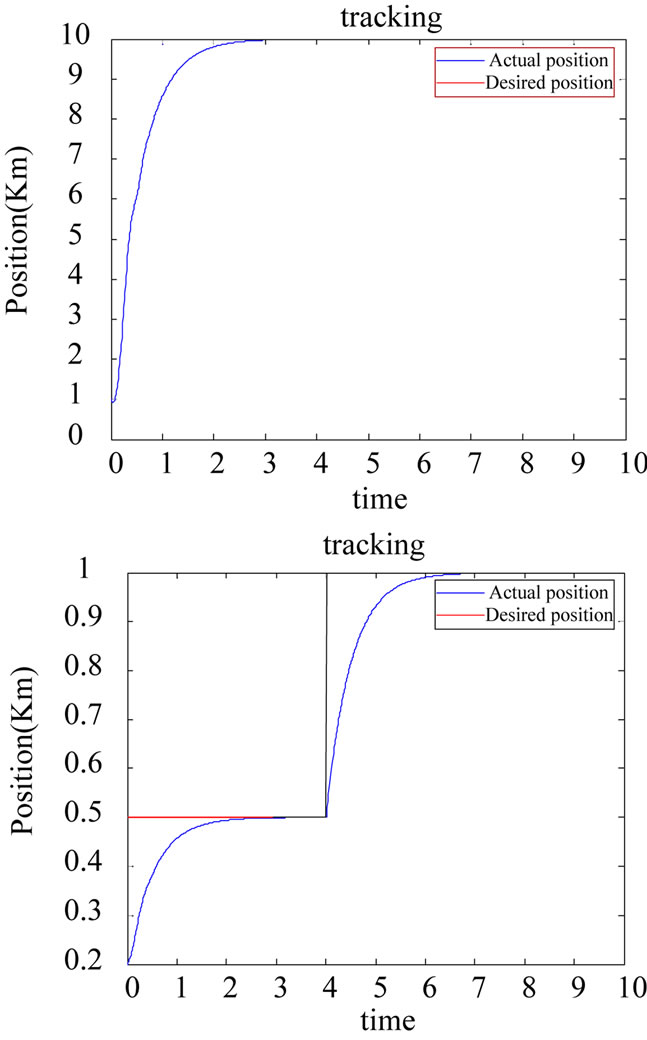
Figure 2. Tracking process.

Figure 3. Tracking error.
namics and external disturbances are unavailable, good tracking precision via the proposed neurorobust adaptive control still maintains with smooth control action and satisfactory position tracking
5. Conclusions
The paper explored the fault-tolerant control problem of DC motors. Using neuro-robust approach, control algorithms achieve high precision position tracking of DC motors under uncertainties and disturbances. The salient feature of the proposed method lies in its flexibility and simplicity in design and implementation. There is no need to redesign or reprogram the control scheme for the different conditions, and no need of analytical estimation on the upper bound of the reconstruction error and uncertainties. A numerical example was simulated as a verification of the effectiveness of the proposed control algorithms.
REFERENCES
- W. D. Chang and J. J. Yan, “Adaptive Robust PID Controller Design Based on a Sliding Mode for Uncertain Chaotic Systems,” Chaos Solitions & Fractals, Vol. 26, No. 1, 2005, pp. 167-175. doi:10.1016/j.chaos.2004.12.013
- J. Y. Hung, W. Gao and J. C. Hung, “Variable Structure Control: A Survey,” IEEE Transactions on Industrial Electronics, Vol. 40, No. 1, 1993, pp. 2-22. doi:10.1109/41.184817
- K. D. Young, V. I. Utkin and Ü. Özgüner, “A control Engineer’S Guide to Sliding Mode Control,” IEEE Transactions on Control Systems Technology, Vol. 7, No. 3, 1999, pp. 328-342. doi:10.1109/87.761053
- A. S. I. Zinober, “Variable Structure and Lyapnuov Control,” Springer-Verlag, Berlin, 1994. doi:10.1007/BFb0033675
- A. Calise and R. Rysdyk, “Nonlinear Adaptive Flight Control Using Neural Networks,” Control Systems Magazine, Vol. 18, No. 6, 1998, pp. 14-25. doi:10.1109/37.736008
- F. Lewis, “Nonlinear Network Structures for Feedback Control,” Asian Journal of Control, Vol. 1, No. 4, 1999, pp. 205-228. doi:10.1111/j.1934-6093.1999.tb00021.x
- H.-L. Choi, Y.-H. Chang, Y. Oh and J.-T. Lim, “On Robust Position Control DC Motor by PID Controller and Its Application to Humanoid Robot Arms,” Proceedings of the 17th IFAC World Congress, Seoul, 6-11 July 2008.
- J. D. Boskovic, R. K. Prasanth and R. K. Mehra, “Reconfigurable Fault-tolerant Flight Control: Algorithms, Implementation and Metrics,” AIAA Guidance, Navigation and Control Conference and Exhibit, Keystone, 21-24 August 2006.
- M. Bodson and J. Groszkiewicz, “Multivariable Adaptive Algorithms for Reconfigurable Flight Control,” IEEE Transactions on Control Systems and Technology, Vol. 5, No. 2, 1997, pp. 217-229. doi:10.1109/87.556026

