Journal of Electromagnetic Analysis and Applications
Vol. 2 No. 5 (2010) , Article ID: 1917 , 10 pages DOI:10.4236/jemaa.2010.25039
Economic Design of Three-Phase Induction Motor by Particle Swarm Optimization
![]()
1Department of Electrical Engineering, Faculty of Engineering and Technology, Annamalai University, Tamil Nadu, India; 2Institute for Energy Systems, Economics and Sustainability, Tallahassee, USA; 3Department of Electrical Engineering, Faculty of Engineering and Technology, Annamalai University, Tamil Nadu, India.
Email: vp.sakthivel@yahoo.com, boonisridhar@rediffmail.com, profdrmani@gmail.com
Received January 27th, 2010; revised March 22nd, 2010; accepted March 25th, 2010.
Keywords: Design Optimization, Induction Motor, Particle Swarm Optimization
ABSTRACT
A Particle Swarm Optimization (PSO) based design of three-phase induction motors are proposed. The induction motor design is treated as a non-linear and multivariable constrained optimization problem. The annual material cost and the total annual cost of the motor are chosen as two different objective functions. The PSO is used to find a set of optimal design variables of the motor which are then used to predict performance indices and the objective functions. The proposed method is demonstrated for two sample motors, and it is compared with the genetic algorithm (GA) and the conventional design methods. The results show that the PSO-based method effectively solved the induction motor design problems and outperforms the other methods in both the solution quality and computation efficiency.
1. Introduction
The ever increasing imbalance between the demand and supply of energy has focused our attention towards energy conservation. Numerous attempts have been made to achieve this either by harnessing energy from renewable sources or by improving the operating efficiency of devices used in generation, transmission and utilization of electrical energy. Induction motors are used in large number in a variety of applications. Any significant improvement in the operating efficiency of induction motor will, therefore, help our effort at energy conservation. This can be achieved by taking recourse to design optimization techniques.
Induction motors are the main energy consuming devices in industries contributing to more than 80% of electromechanical energy conservation. However, their operating efficiency is often far from satisfactory. The design optimization of energy efficient induction motor is therefore the need of the day. In the past, the design of induction motor has been attempted for achieving better performance characteristics and/or reducing the cost. These were trial and error based which were solely attributed by professional experience. Digital computer has made it possible to use well known optimization techniques in the design of electrical machines.
For the design optimization of induction motors, the most frequently used objective functions are material cost and the operating cost of the motor. If the objective function represents the manufacturer’s viewpoint, then it is equal to the material cost [1-5]. The objective function, in the form of a weighted sum of the material and operating costs, represents the consumer’s viewpoint [4-6].
Several techniques such as GA [7], evolutionary algorithm [8], neural networks [9] and fuzzy logic [10] are used to solve the induction motor design problems. However, these techniques do not always guarantee the globally optimal solution, they will provide suboptimal solution.
The PSO [11-15] algorithm is one of the modern evolutionary algorithms. This algorithm was first proposed by Kennedy and Eberhart. PSO is a population-based search algorithm characterized as conceptually simple, easy to implement and computationally efficient. As it is reported in [13], this optimization technique can be used to solve many problems as GA and does not suffer from some of GA’s difficulties. PSO has also been found to be robust in solving problems featuring non-linearity, non-differentiability and high dimensionality.
In this paper, a PSO based approach to the induction motor design problem is proposed. The method is applied on two sample motors and the results are compared with the GA and the conventional design method [16,17].
2. Optimization Problem
The design optimization of induction motor can be expressed mathematically as follows:
Find X (x1, x2, …….., xn) such that F(X) is a minimum (1)
Subject to:
gj (X) ≥ 0 j = 1, 2, ………m
and
xLi ≤ xi ≤ xUi i = 1, 2, ………n
where X (x1, x2, …….., xn) is the set of independent design variables with their lower and upper limits as xLi and xUi, for all ‘n’ variables. F (X) is the objective function to be optimized and gj (X) are the constraints imposed on the design.
2.1 Design Variables
The following quantities are chosen as the principle design variables for the optimization (X):
1) Stator bore diameter (x1);
2) Average air gap flux density (x2);
3) Stator current density (x3);
4) Air gap length (x4);
5) Stator slot depth (x5);
6) Stator slot width (x6);
7) Stator core depth (x7);
8) Rotor slot depth (x8);
9) Rotor slot width (x9).
The remaining parameters can be expressed in terms of these variables or may be treated as fixed for a particular design.
2.2 Objective Functions
The objective function to be minimized is F(X). This may be based on the performance indices, weight, or some form of cost of the motor. In the present work, the following two objective functions have been considered:
1) Annual active material cost;
2) Total annual cost of the motor (Annual material cost, annual power loss cost and annual energy loss cost).
The expression of the objective function, in terms of the motor design variables are as follows:
2.2.1 Annual Active Material Cost
Annual iron material cost,
 (2)
(2)
where,
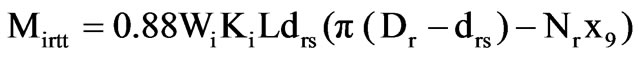
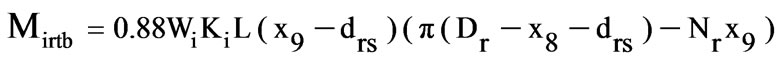
Annual copper material cost,
 (3)
(3)
where,
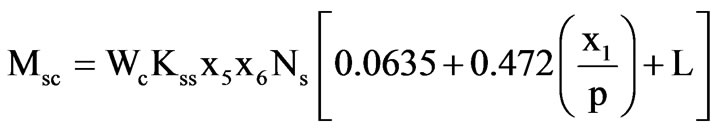
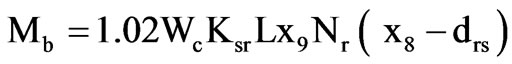
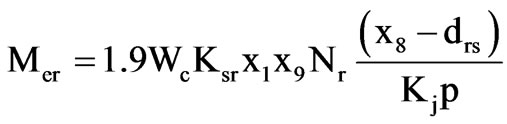
Annual active material cost is given by
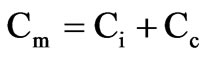 (4)
(4)
2.2.2 Annual Active Power Loss Cost
Annual iron loss cost,
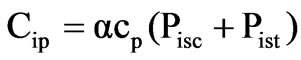 (5)
(5)
where,
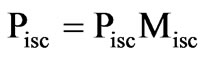

where, pisc and pist are the specific iron loss corresponding to Bsc and Bst respectively. Bsc and Bst are given as follows
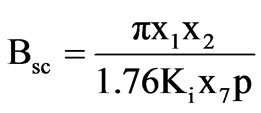
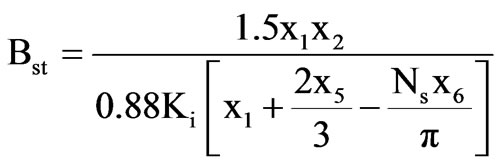
Annual copper loss cost,
 (6)
(6)
where,
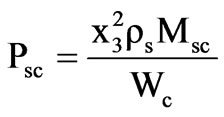
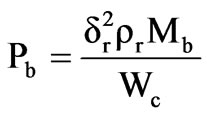
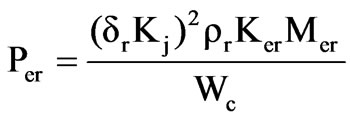
Annual friction and windage loss cost,
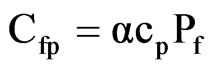 (7)
(7)
where,
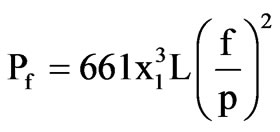
The stray loss is assumed to reduce the efficiency by 0.5%, so that:
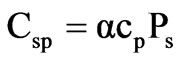 (8)
(8)
where,
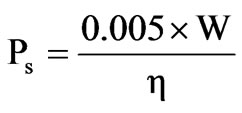
The total annual active power loss cost is thus:
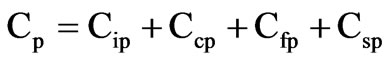 (9)
(9)
2.2.3 Annual Energy Loss Cost
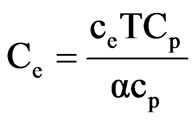 (10)
(10)
The first objective function is given by:
 (11)
(11)
The second objective function is given by:
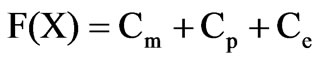 (12)
(12)
2.3 Constraints
The following constraints (g1, ….. g6) are imposed on the design optimization problem:
1) Maximum to full-load torque ratio (g1);
2) Starting to full-load torque ratio (g2);
3) Starting to full-load current ratio (g3);
4) Full-load efficiency (g4);
5) Full-load power factor (g5);
6) Maximum temperature rise (g6);
The expression of the constraint functions is as follows:
2.3.1 Maximum to Full-Load Torque Ratio
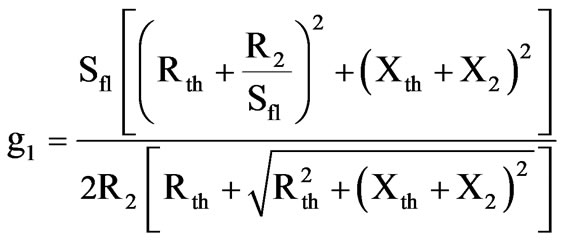 (13)
(13)
2.3.2 Starting to Full-Load Torque Ratio
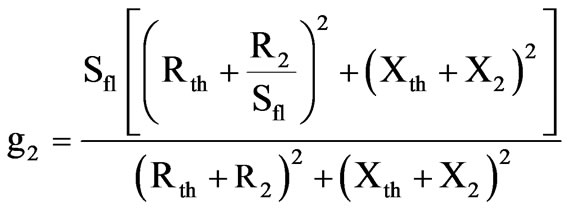 (14)
(14)
2.3.3 Starting to Full-Load Current Ratio
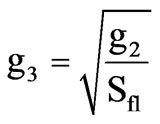 (15)
(15)
2.3.4 Full Load Power Factor
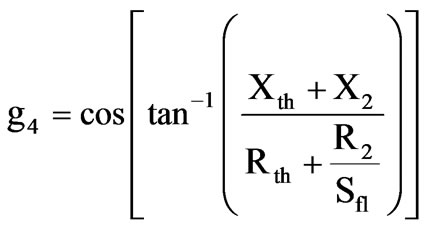 (16)
(16)
2.3.5 Full Load Efficiency
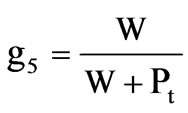 (17)
(17)
where, 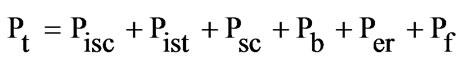
2.3.6 Maximum Temperature Rise
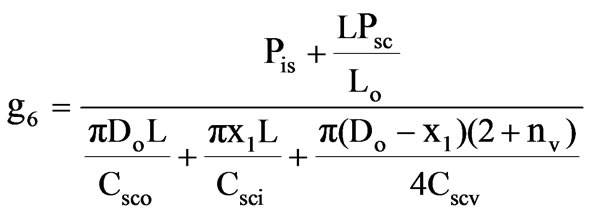 (18)
(18)
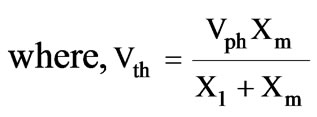 ,
,  ,
, 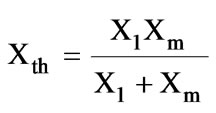
The equivalent circuit parameters R1, R2, X1, X2 and Xm can be found in terms of the design variables [16,17].
3. Overview of PSO
PSO is one of the modern heuristic algorithms developed by Kennedy and Eberhart. It is a multi-agent search technique that traces its evolution to the emergent motion of a flock of birds searching for food. It uses a number of particles that constitute a swarm. Each particle traverses the search space looking for the global minimum (or maximum). In a PSO system, particles fly around in a multidimensional search space. During flight, each particle adjusts its position according to its own experience, and the experience of neighboring particles, making use of the best position encountered by itself and its neighbors. The swarm direction of a particle is defined by the set of particles neighboring the particle and its history experience. Compared to other evolutionary techniques, the advantages of PSO are as follows:
1) PSO is easy to implement, and only few parameters have to be adjusted;
2) Unlike the GA, PSO has no evolution operators such as crossover and mutation;
3) In GAs, chromosomes share information so that the whole population moves like one group, but in PSO, only global best particle (gbest) gives out information to the others. It is more robust than GAs;
4) PSO can be more efficient than GAs; that is, PSO often finds the solution with fewer objective function evaluations than that required by GAs;
5) Unlike GAs and other heuristic algorithms, PSO has the flexibility to control the balance between global and local exploration of the search space.
Let X and V denote the particle’s position and its corresponding velocity in search space respectively. At iteration K, each particle i has its position defined by 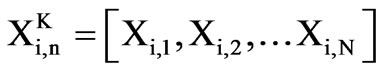 and a velocity is defined as
and a velocity is defined as 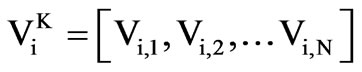 in search space N. Velocity and position of each particle in the next iteration can be calculated as:
in search space N. Velocity and position of each particle in the next iteration can be calculated as:
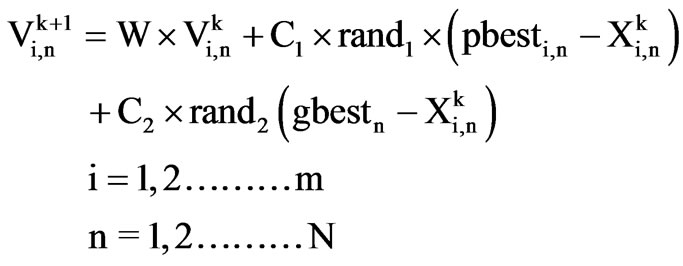 (19)
(19)
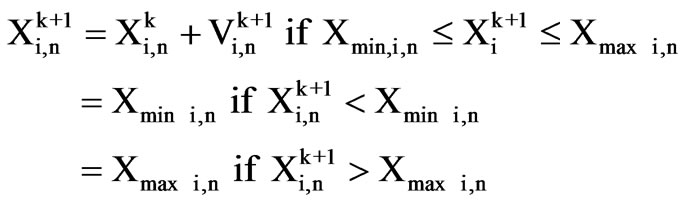 (20)
(20)
where, m number of particles in the swarm;
N number of dimensions in a particle;
K pointer of iterations (generations);
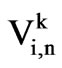 velocity of particle i at iteration k;
velocity of particle i at iteration k;
W weighting factor;
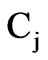 acceleration factor;
acceleration factor;
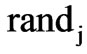 random number between 0 and 1;
random number between 0 and 1;
 current position of particle i at iteration k;
current position of particle i at iteration k;
 personal best of particle I;
personal best of particle I;
gbest global best of the group.
In the above procedures, the convergence speed of each particle could be influenced by the parameters of acceleration factors C1 and C2. The optimization process will modify the position slowly, if the value of  is chosen to be very low. On the other hand, the optimization process can become unstable, if the value of
is chosen to be very low. On the other hand, the optimization process can become unstable, if the value of 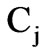 is chosen to be very high. The first term of Formula (2) the initial velocity of particle which reflects the memory behavior of particle; the second term “cognition part” which represents the private thinking of the particle itself; the third part is the “social” part which shows the particles behavior stem from the experience of other particles in the population.
is chosen to be very high. The first term of Formula (2) the initial velocity of particle which reflects the memory behavior of particle; the second term “cognition part” which represents the private thinking of the particle itself; the third part is the “social” part which shows the particles behavior stem from the experience of other particles in the population.
Suitable selection of weighting factor W provides a balance between global and the local explorations. In general, the weignting function is set to the following equation:
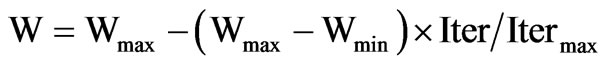 (21)
(21)
where Wmax and Wmin are initial and final weight respectively. Itermax is maximum number of generations and Iter is current number of generations.
4. Constraints Handling Strategy
Induction motor design problem is associated with inequality constraints. In this paper, a penalty-parameter-less penalty approach is used for constraints handling. The fitness function is given by:
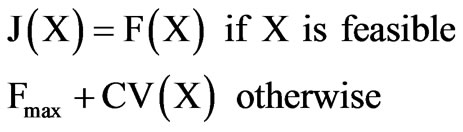 (22)
(22)
where, Fmax is the objective function of the worst feasible solution in the population. CV(X) is the overall constraint violation of solution X. It is calculated as follows:
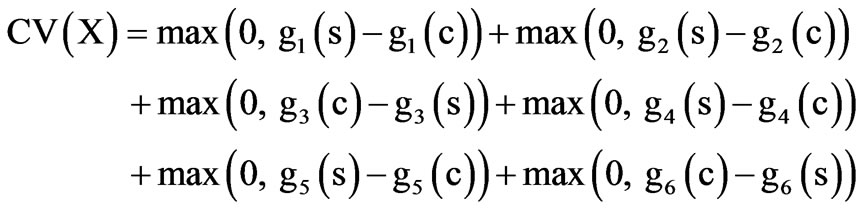 (23)
(23)
where c and s denote the computed and specified constraint values respectively.
In this method, the objective function value is not computed for any infeasible solution. Since all feasible solution has zero constraint violation and all infeasible solutions are evaluated according to their constraint violation only, both objective function and constraint violation are not combined in any solution in the population. Thus, there is need to have any penalty parameters for this approach.
5. Design Procedure of Induction Motor Using PSO
In this design, the PSO is used to find a set of design variables which ensure that the function F(X) has a minimum value and all the constraints are satisfied. The penalty-parameter-less approach is used to optimize the design. Hence the optimal design problem reduces to obtaining the design variables which correspond to the minimum value of an unconstrained function J(X).
The procedure for optimal design of induction motor is as follows:
1) Read specifications and performance indices of the motor;
2) Initialize PSO parameters such as Wmax, Wmin, C1, C2 and Itermax;
3) Generate initial population of N particles (design variables) with random positions and velocities;
4) Compute objective value and performance indices of the motor;
5) Calculate fitness: Evaluate the fitness value of current particle using Equation (22);
6) Update personal best: Compare the fitness value of each particle with its pbests. If the current value is better than pbest, then set pbest value to the current value;
7) Update global best: Compare the fitness value of each particle with gbest. If the current value is better than gbest, set gbest to the current particle’s value;
8) Update velocities: Calculate velocities Vk+1 using Equation (19);
9) Update positions: Calculate positions Xk+1 using Equation (20);
10) Return to step (4) until the current iteration reaches the maximum iteration number;
11) Output the optimal design variables and their corresponding annual costs of the motor in the last iteration.
6. Results and Discussions
To illustrate the performance of the proposed method, two sample motors (5 HP and 10 HP motors) are tested. The specifications of the sample motors are given in Appendix B. The results of the proposed method are also compared with the GA and the conventional design methods. The value of design constants is given in Appendix C. The parameters of PSO used were the following: Population size = 20; initial inertia weight wmax = 0.9; final inertia weight wmin =0.1; acceleration factor C1 = C2 = 1.5 and maximum iteration Itermax = 50.
Two different designs (objectives) are considered as follows:
Design 1: The annual material cost is used as objective.
Design 2: the total annual cost of the motor is used as objective.
The results obtained from PSO, GA and conventional based design methods are given in Tables 1 and 3 respectively for motors 1 and 2. From these results, the following important points can be noted.
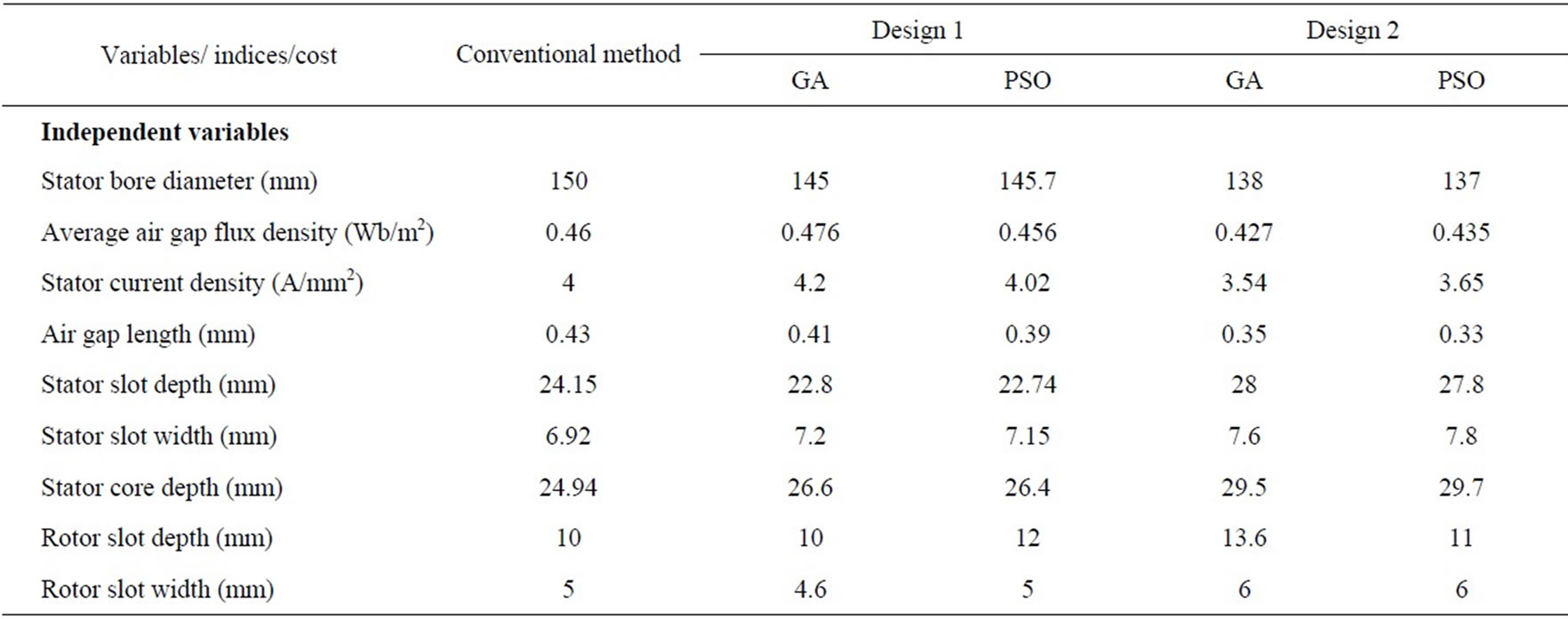
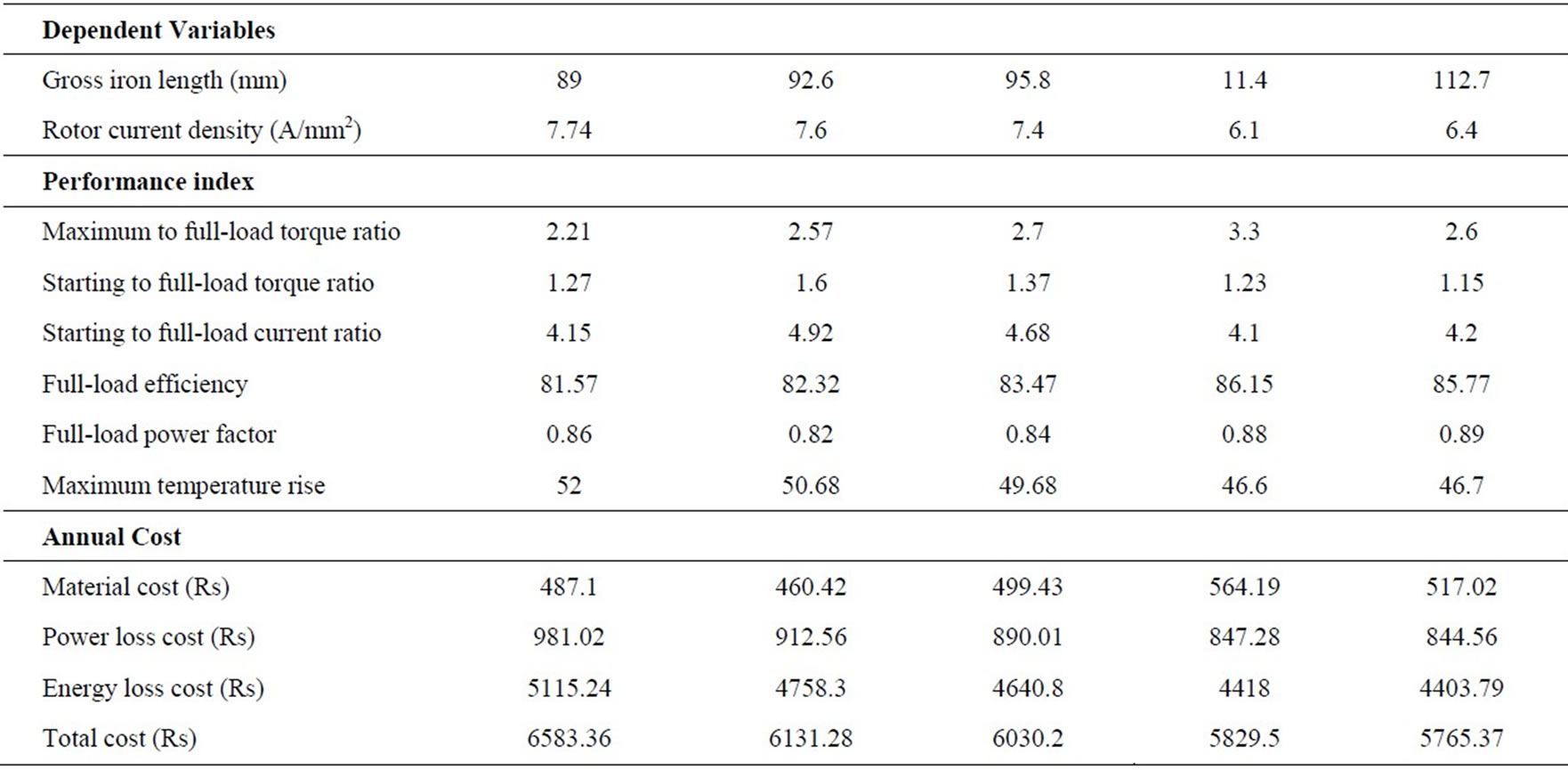
Table 1. Optimum design results of motor 1 for different methods
The optimum value of the annual material cost is observed to be higher one for the Design 2 as compared to the Design 1. The total annual cost is found to decrease marginally in Design 2. The air gap density and stator current density values are decreased in Design 2. These design variables are inversely proportional to the efficiency of motor. Thus the efficiency of the Design 2 is improved. But the maximum torque and the starting torque are affected. However, their values remain within the limits.
The convergence characteristics of GA and PSO methods for the sample motors are shown in Figures 1 and 2. From Figures, it is seen that the PSO converges quickly and explore higher quality solution than the GA.
To test the robustness of GA and PSO, 20 independent trials are carried out. The obtained results by each method are given in Tables 2 and 4. From tables, it is clear that the minimum, average and standard deviations of costs obtained by PSO are better than GA.

Table 2. Comparison of different methods for motor 1 (20-trials)
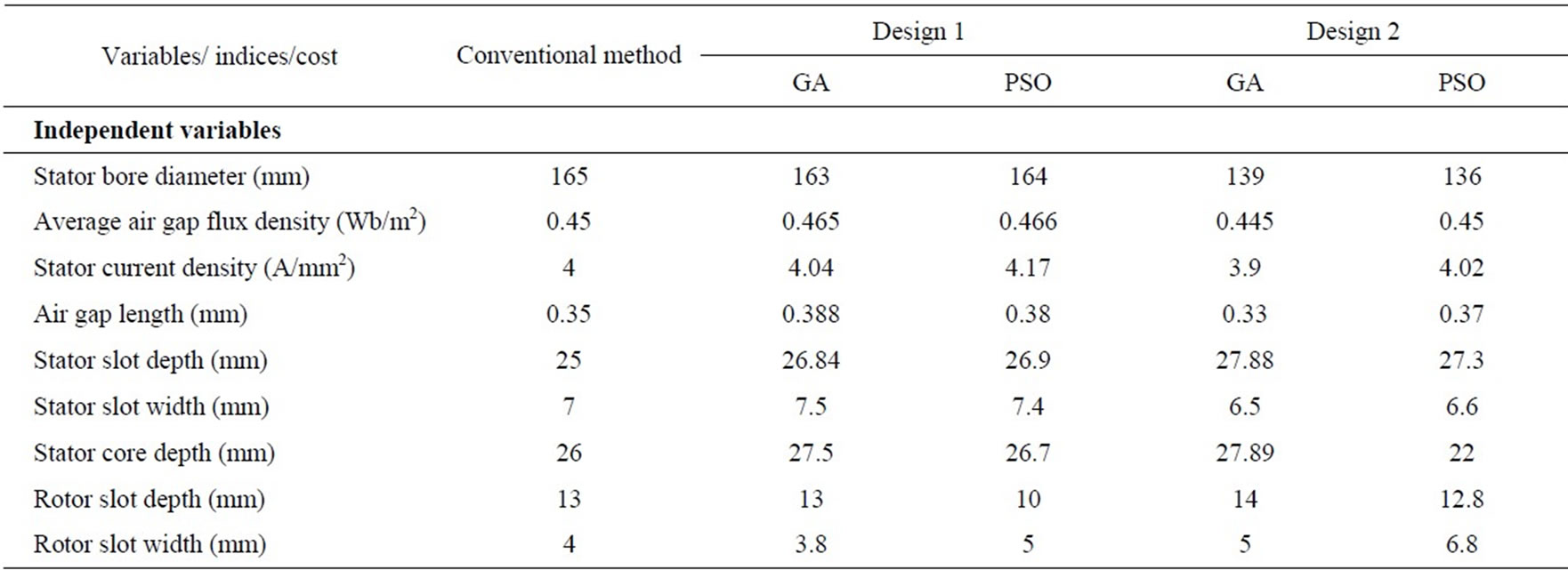

Table 3. Optimum design results of motor 2 for different methods

Table 4. Comparison of different methods for motor 2 (20-Trials)
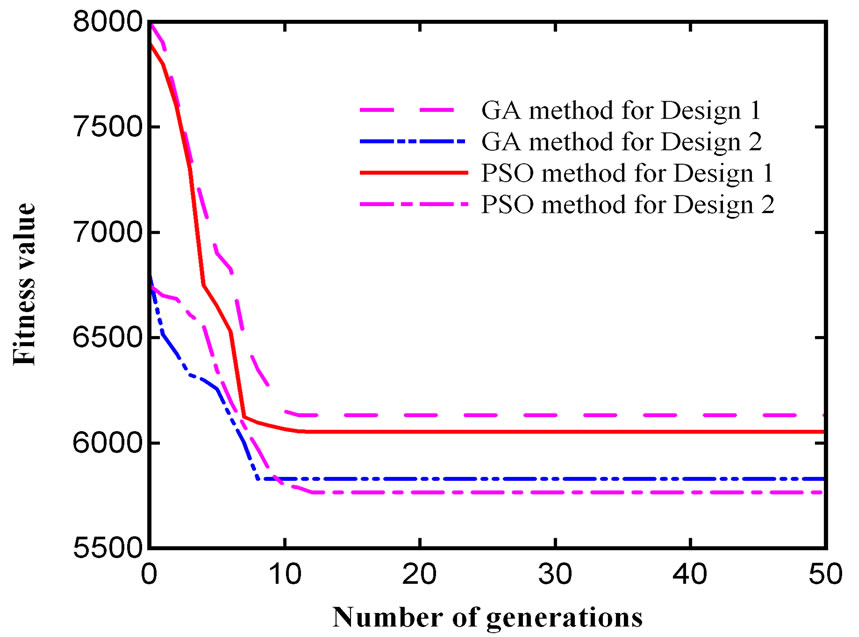
Figure 1. Convergence characteristic of GA and PSO methods for motor 1
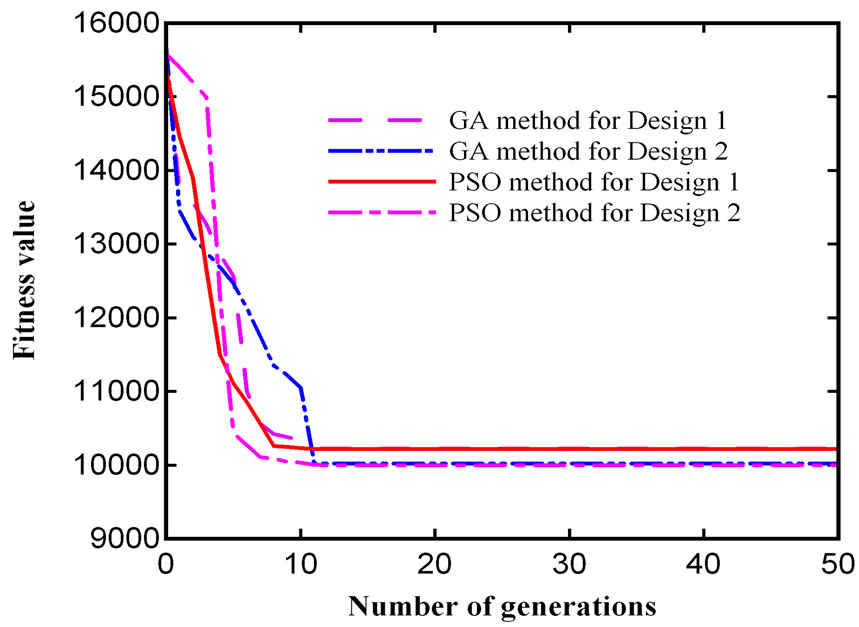
Figure 2. Convergence characteristic of GA and PSO methods for motor 2
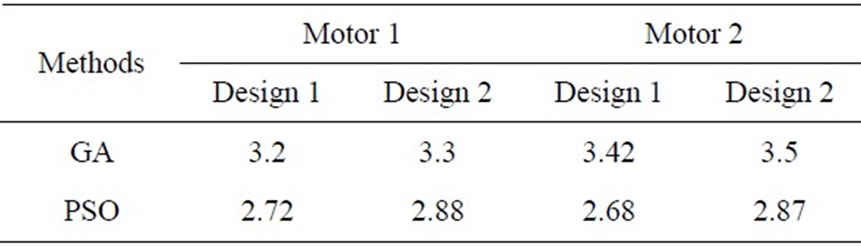
Table 5. Comparison of average computation time (in seconds) of PSO and GA methods (20-Trials)
Computational efficiencies of GA and PSO methods are compared based on the average CPU times taken by each algorithm are given in Table 5. From table, it is evident that the average convergence time for PSO is minimum.
7. Conclusions
The PSO based design optimization of induction motors is presented in this paper. Two different objective functions such as annual material cost and total annual cost of the motor are considered. The method has been applied in two sample motors and the results are compared with the GA and the conventional design methods. The results show that the PSO method is simple, robust and reliable for the design optimization of induction motors.
REFERENCES
- R. Ramarathnam and B. G. Desai, “Optimization of PolyPhase Induction Motor Design-A Nonlinear Programming Approach,” IEEE Transactions Power Apparatus and Systems, Vol. 90, No. 2, 1971, pp. 570-578.
- B. G. Bharadwal, K. Venkatesen and R. B. Saxena, “Experience with Direct and Indirect Search Methods Applied to Cage Induction Motor Design Optimization,” Electric Machines and Electromechanics, Vol. 4, No. 1, 1979, pp. 85-93.
- C. Li and A. Rahman, “Three-Phase Induction Motor Design Optimization Using the Modified Hooke-Jeeves Method,” Electrical Machines and Power Systems, Vol. 18, No. 1, 1990, pp. 1-12.
- J. Appelbaum, E. F. Fuchs and J. C. White, “Optimization of Three-Phase Induction Motor, Part I: Formation of the Optimization Technique,” IEEE Transactions on Energy Conversion, Vol. 2, No. 3, 1987, pp. 407-415.
- J. Appelbaum, I. A. Khan, E. F. Fuchs and J. C. White, “Optimization of Three-Phase Induction Motor, Part II: The Efficiency and Cost of an Optimum Design,” IEEE Transactions on Energy Conversion, Vol. 2, No. 3, 1987, pp. 415-422.
- N. H. Feith and H. M. EI-Shewy, “Induction Motor Optimum Design Including Active Power Loss Effect,” IEEE Transactions on Energy Conversion, Vol. 1, No. 3, 1986, pp. 155-160.
- G. F. Uler, O. A. Mohammed and C.-S. Koh, “Design Optimization of Electrical Machines Using Genetic Algorithms,” IEEE Transactions on Magnetics, Vol. 31, No. 3, 1995, pp. 2008-2011.
- J. P. Wieczorek, O. Gol and Z. Michalewiez, “An Evolutionary Algorithm for the Optimal Design of Induction Motors,” IEEE Transactions on Magnetics, Vol. 34, No. 6, 1998, pp. 3882-3887.
- G. T. Bellarmine, R. Bhuvaneswari and S. Subramanian, “Radial Basis Function Network Based Design Optimization of Induction Motor,” Proceedings of IEEE SOUTHEASTCON 2006, Memphis, Tennessee, 2006, pp. 75-80.
- R. Bhuvaneswari and S. Subramanian, “Fuzzy Logic Approach to Three-Phase Induction Motor Design,” Proceedings of the International Conference on Computer Applications in Electrical Engineering Recent Advances - CERA-05, IIT Roorkee, 28 September-1 October 2005, pp. 505-509.
- J. Kennedy and R. Eberhart, “Particle Swarm Optimization,” Proceedings of the IEEE Conference on Neural Networks-ICNN’95, Perth, Vol. 4, 1995, pp. 1942-1948.
- Y. Shi and R. C. Eberhart, “Empirical Study of Particle Swarm Optimization,” Proceedings of the IEEE International Congress Evolutionary Computation, Anchorage, Vol. 3, 1999, pp. 101-106.
- R. Eberhart and J. Kennedy, “A New Optimizer Using Particle Swarm Optimization,” Proceedings of the 1995 Sixth International Symposium on Micro Machine and Human Science, Nagoya, pp. 39-43.
- R. C. Eberhart and Y. Shi, “Comparing Inertia Weights and Constriction Factors in Particle Swarm Optimization,” Proceedings of the IEEE International Congress Evolutionary Computation, San Diego, Vol. 1, 2000, pp. 84-88.
- K. T. Chaturvedi, M. Pandit and L. Srivastava, “Particle Swarm Optimization with Time Varying Acceleration Coefficients for Non-Convex Economic Power Dispatch,” Electrical Power and Energy Systems, Vol. 31, No. 6, 2009, pp. 249-257.
- M. G. Say, “Alternating Current Machines,” Pitman, London, 1983.
- R. K. Agarwal, “Electrical Machine Design,” 3rd Edition, S. K. Katarai and Sons, Delhi, 1997.




