Int'l J. of Communications, Network and System Sciences
Vol.7 No.6(2014), Article
ID:47135,7
pages
DOI:10.4236/ijcns.2014.76021
Analysis of Rate One Quasi-Orthogonal Space-Time Block Coding over Rayleigh Fading Channel
Md. Abdullah Al Amin Ranju, Ragib Shakil Rafi
Electronics & Communication Engineering, Khulna University, Khulna, Bangladesh
Email: ranju.ece@gmail.com, ku.08rafi@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 April 2014; revised 26 May 2014; accepted 10 June 2014
ABSTRACT
Full-rate is very important in any data transmission coding. For transmitting data at low bit rate than full-rate code, higher modulation scheme is required. But it is impossible to design full rate orthogonal designs with complex constellation for more than two transmit antennas. Only Alamouti code provides full-rate for two transmit antennas. In this paper, Bit Error Rate (BER) is calculated for Quasi-Orthogonal Space-time Block Coding (QOSTBC). Here we work with Rayleigh fading channel. We consider the codes which decodes pairs of symbols instead of simple separate decoding like Orthogonal Space-Time Block Coding. In Quasi-Orthogonal Space-time Block Code full-rate is achieved but full-diversity is sacrificed. Diversity is the most important techniques for providing reliable communication over fading channels. One of the diversity techniques that uses multiple transmit and/or receive antennas is space diversity. Multiple antenna technique provides a space diversity to struggle with the fading without necessarily sacrificing bandwidth resources, so the excellent solutions of removing the fading of the channel for broadband wireless communications is using space diversity. Then, with the constellation rotation of the symbol, rotated version of Quasi-Orthogonal Space-Time Block Code is generated. It provides full diversity. We simulate BER for QOSTBC, rotated QOSTBC, orthogonal STBC and for uncoded system. The simulation result shows that QOSTBC and rotated QOSTBC perform better than other systems. It shows that QOSTBC provides a full transmission rate but that rotated QOSTBC provides the full rate with the full diversity.
Keywords:Orthogonal Space-Time Block Coding, Quasi-Orthogonal Space-Time Block Coding, Rayleigh Fading, Rotated Quasi-Orthogonal Space-Time Block Coding

1. Introduction
The transmission path in the wireless communication is air or free space for transmitting the electromagnetic signal to the destination. The transmitted signal may reach the receiver directly (Line-of-Sight) or through multiple reflections on local objects. When waves coming from these different paths are interacting with one another and for this received signal’s amplitude and power fluctuates with time and if this fluctuation is rapid over a short period of time, then it is known as small-scale fading. The Rayleigh distribution [1] is commonly used to describe the statistical time varying nature of the received fading signal. The fading can be removed by using diversity and space diversity [2] is one of the diversity techniques that use multiple transmit and/or receive antennas. The possibility of deep fading over all paths’ signals is greatly reduced by space diversity creating many independent propagation paths from transmitter to receiver. Information data are transmitted in a block-by-block fashion. Data transmission in an ST system is carried out in two dimensions, the space dimension and the time dimension, as the acronym ST suggests. The space dimension is spanned by multiple transmit-antennas while the time dimension is spanned by multiple time intervals over which multiple blocks are transmitted. By using STBC, QOSTBC [3] decreases the fading problem and provides partial diversity. But rotated QOSTBC [3] offers full-diversity. We simulate the BER and make a comparison for QOSTBC and rotated QOSTBC with OSTBC.
2. Space-Time Block Codes
We review the space-time block codes which provide maximum possible diversity for multiple transmit antennas in wireless communications. One example of space time block code is Alamouti code [3] . The generator matrix of this code to emphasize the indeterminate variables x1 and x2 in the design:
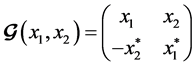 (1)
(1)
The Alamouti code is the only example of a full-rate full-diversity complex space-time block code using orthogonal design.
In general, a complex orthogonal space-time code is given by ![]() generator matrix
generator matrix . Here T and N represents the number of time slots for transmitting one block of symbols and the number of transmit antennas respectively. The generator matrix
. Here T and N represents the number of time slots for transmitting one block of symbols and the number of transmit antennas respectively. The generator matrix 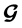 is chosen so that the rows and columns of each matrix are orthogonal to each other (i.e. the dot product of each row with another row is zero) and Orthogonal Design Theory provides this. Orthogonal Design Theory is two types, one for real numbers and other for complex numbers. Radon and Hurwitz [4] [5] provided the Real Orthogonal Designs and Complex Orthogonal Design is created from Real Orthogonal Design. The elements of the matrix are linear combinations of determinates
is chosen so that the rows and columns of each matrix are orthogonal to each other (i.e. the dot product of each row with another row is zero) and Orthogonal Design Theory provides this. Orthogonal Design Theory is two types, one for real numbers and other for complex numbers. Radon and Hurwitz [4] [5] provided the Real Orthogonal Designs and Complex Orthogonal Design is created from Real Orthogonal Design. The elements of the matrix are linear combinations of determinates  and their conjugates.
and their conjugates.
It is required that
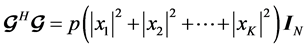 (2)
(2)
where, 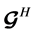 is the Hermitian of
is the Hermitian of ,
,  is the
is the ![]() identity matrix and p is a constant.The code rate of
identity matrix and p is a constant.The code rate of 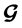 is defined to be
is defined to be . This is due to the fact that the code transmits
. This is due to the fact that the code transmits ![]() constellation symbols in
constellation symbols in 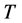 time slots. The rate is defined as the transmission rate relative to the maximum possible rate of a full-diversity code. It has been shown in [3] that the rate of a full-diversity code is less than or equal to one
time slots. The rate is defined as the transmission rate relative to the maximum possible rate of a full-diversity code. It has been shown in [3] that the rate of a full-diversity code is less than or equal to one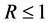 .
.
3. Quasi-Orthogonal Space-Time Block Code
3.1. Encoding
The encoding of QOSTBCs is very similar to the encoding of orthogonal STBCs. To transmit 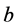 bits per time slot, we use constellations containing 2b points. Using 4b bits, constellation symbols
bits per time slot, we use constellations containing 2b points. Using 4b bits, constellation symbols  are selected. Setting
are selected. Setting 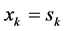 for
for  in generator matrix
in generator matrix , we arrive at a codeword matrix
, we arrive at a codeword matrix 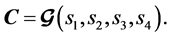 Then, at time t, the four elements in the tth row of
Then, at time t, the four elements in the tth row of ![]() are transmitted from the four transmit antennas. Since four symbols
are transmitted from the four transmit antennas. Since four symbols 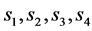 are transmitted in four time slots presents a rate one code.
are transmitted in four time slots presents a rate one code.
3.2. Transmission Model
A wireless communication system is considered with N transmit antennas and M receive antennas [3] . The channel is assumed to be quasi-static slow flat fading and the path gain from transmit antenna n to receive antenna m is denoted by . The path gains are modeled as samples of independent complex Gaussian random variables. The variance is 0.5 for both imaginary part and real part of path gain. The channel is quasi-static so that the path gains are constant over a time frame of length T and vary independently from one frame to another. Channel estimation is done with training/pilot sequences in regular intervals during the transmission. The received signal
. The path gains are modeled as samples of independent complex Gaussian random variables. The variance is 0.5 for both imaginary part and real part of path gain. The channel is quasi-static so that the path gains are constant over a time frame of length T and vary independently from one frame to another. Channel estimation is done with training/pilot sequences in regular intervals during the transmission. The received signal 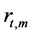 at time t and antenna m is given by,
at time t and antenna m is given by,
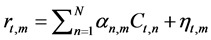 (3)
(3)
where, the noise samples 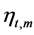 are independent samples of a zero-mean complex Gaussian random variable and the code symbol
are independent samples of a zero-mean complex Gaussian random variable and the code symbol 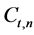 is transmitted from n transmit antenna at time t. The real part and imaginary part of noise symbols have equal variance N/(2SNR). The average energy of the transmitted symbols from each antenna is normalized to be 1, so that the average power of the received signal at each receive antenna is N and the signal-to-noise ratio is SNR.
is transmitted from n transmit antenna at time t. The real part and imaginary part of noise symbols have equal variance N/(2SNR). The average energy of the transmitted symbols from each antenna is normalized to be 1, so that the average power of the received signal at each receive antenna is N and the signal-to-noise ratio is SNR.
3.3. Decoding Algorithm
Assuming perfect channel state information is available. So the receiver computes the decision metric [6] ,
 (4)
(4)
Overall possible 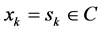 and decides in favor of the constellation symbols
and decides in favor of the constellation symbols  that minimized the sum. We get from Alamouti code [3] ,
that minimized the sum. We get from Alamouti code [3] ,
 (5)
(5)
Now let us consider N = T = K = 4. So the generator matrix,
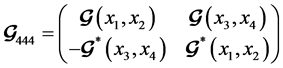 (6)
(6)
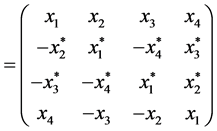 (7)
(7)
It is easy to see that the minimum rank of matrix 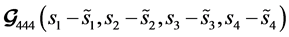 is two [2] . The matrix constructed from
is two [2] . The matrix constructed from 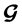 by replacing xi with
by replacing xi with  is 2. Therefore diversity of 2M is achieved and code rate = 1. Now, if we define
is 2. Therefore diversity of 2M is achieved and code rate = 1. Now, if we define , i =1, 2, 3, 4 as the ith column of
, i =1, 2, 3, 4 as the ith column of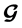 , it is easy to see that,
, it is easy to see that,

where, 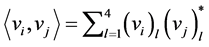 is the inner product of vector
is the inner product of vector 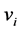 and
and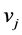 . The subspace created by
. The subspace created by 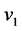 and
and
 is orthogonal to the subspace created by
is orthogonal to the subspace created by  and
and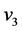 . Using this orthogonality, the maximum-likelihood decision metric (4) is equivalent to minimizing these two terms independently. The ML decision metric can be calculated as the sum of two terms
. Using this orthogonality, the maximum-likelihood decision metric (4) is equivalent to minimizing these two terms independently. The ML decision metric can be calculated as the sum of two terms 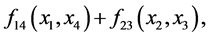 where,
where, 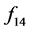 is independent of
is independent of ![]() and
and 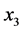 and
and 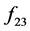 is independent of
is independent of 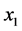 and
and![]() . Thus the minimization of these two terms independently. Other words, first the decoder finds the pair
. Thus the minimization of these two terms independently. Other words, first the decoder finds the pair 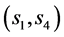 that minimizes
that minimizes  among all possible values of
among all possible values of 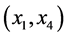 pair. Then, or in parallel, the decoder selects pair
pair. Then, or in parallel, the decoder selects pair 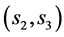 similarly. Simple manipulation of Equation (4) becomes,
similarly. Simple manipulation of Equation (4) becomes,
 (8)
(8)
 (9)
(9)
where, the real part of a is denoted by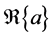 . It is clear that decoding pairs of symbols for the QOSTBCs is more complex than decoding single symbols for the space time block codes.
. It is clear that decoding pairs of symbols for the QOSTBCs is more complex than decoding single symbols for the space time block codes.
4. Rotated Quasi-Orthogonal Space-Time Block Code
The minimum rank of the difference matrix  is two for QOSTBCs in (7) for regular symmetric constellations same as PSK and QAM. For M receive antennas, a diversity of 2M is achieved while the code rate is one. The minimum diversity of 4M for a rate one complex orthogonal code is impossible in this case if all symbols are chosen from the same constellation [3] . For different transmitted symbols if we use different constellations we get full diversity. This means that we may rotate half of the symbols before transmission. This is called Rotated Quasi-Orthogonal Space Time Block Codes (Rotated QOSTBCs). This code is very powerful because it provides the full diversity, rate one, and simple pair wise decoding with satisfactory performance. The encoding algorithm and the transmission model are same as the QOSTBCs.
is two for QOSTBCs in (7) for regular symmetric constellations same as PSK and QAM. For M receive antennas, a diversity of 2M is achieved while the code rate is one. The minimum diversity of 4M for a rate one complex orthogonal code is impossible in this case if all symbols are chosen from the same constellation [3] . For different transmitted symbols if we use different constellations we get full diversity. This means that we may rotate half of the symbols before transmission. This is called Rotated Quasi-Orthogonal Space Time Block Codes (Rotated QOSTBCs). This code is very powerful because it provides the full diversity, rate one, and simple pair wise decoding with satisfactory performance. The encoding algorithm and the transmission model are same as the QOSTBCs.
Decoding
The generator matrix of QOSTBC from (7) is recall here,
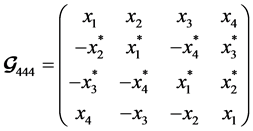 (10)
(10)
For rotated QOSTBC 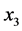 and
and ![]() are get from the rotated version of
are get from the rotated version of 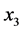 and
and![]() . They are rotated before transmission and is denoted by
. They are rotated before transmission and is denoted by 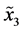 and
and![]() . Here,
. Here, 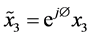 and
and  and
and ![]() is the constellation rotation angle.
is the constellation rotation angle.
Now for rotated QOSTBC the generator matrix (10) becomes:
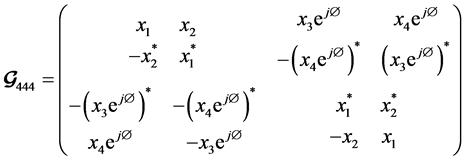 (11)
(11)
We can see that the decoding decision for symbols 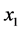 and
and ![]() are obtained by minimizing the metric
are obtained by minimizing the metric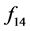 , similarly the decoding decision for symbol
, similarly the decoding decision for symbol ![]() and
and 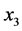 are obtained by minimizing the metric
are obtained by minimizing the metric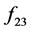 . Clearly decoding of
. Clearly decoding of 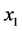 and
and ![]() can be performed separately from the decoding of
can be performed separately from the decoding of ![]() and
and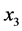 . Since
. Since 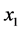 and
and ![]() (
(![]() and
and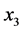 ) are each a complex symbol their decoding requires the joint detection of two complex symbols (i.e. four real symbols) in total.
) are each a complex symbol their decoding requires the joint detection of two complex symbols (i.e. four real symbols) in total.
So, the simple manipulation of decision metric becomes:
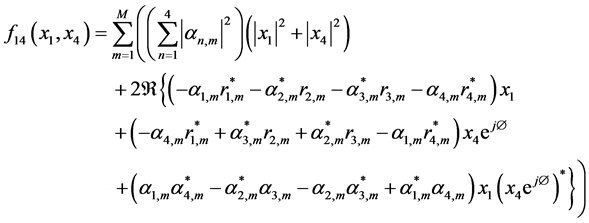 (12)
(12)
 (13)
(13)
The decoding algorithm in (12) and (13) are more complex than the QOSTBC in (8) and (9). Where in (12) and (13) 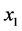 and
and ![]() are non-rotated complex constellation symbols. The rotated QOSTBC decoding algorithm in (13) and (13) can be decoded with joint detection of only two real symbols, while still achieving full transmit diversity and full code rate.
are non-rotated complex constellation symbols. The rotated QOSTBC decoding algorithm in (13) and (13) can be decoded with joint detection of only two real symbols, while still achieving full transmit diversity and full code rate.
5. Simulation Results
In this section, we provide simulation results for the QOSTBC in (7) and the Rotated QOSTBC in (11) and compare it with the other codes. These codes have a definite code rate and use different modulation scheme depends on the transmission bit rate. So, we have used the suitable modulation scheme due to the transmission bit rate for different STBCs. In all simulation result we consider different types of transmit antenna and one receive antenna and a given transmission bit rate on the Rayleigh fading channel. Then using this result the performance of each QOSTBC is provided. For, a fair comparison the modulation type and code size are varied with a view to maintaining a constant bit rate. As a result proper combination of QOSTBC and constellations are very essential. There is a constellation diagram which contains ![]() point for uncoded system with one transmission antenna or a full-rate OSTBCs transmission bit rate is b bits/(sHz). For a QOSTBCs with rate R, the transmission bit rate is Rb bits/(sHz). Since only for real signal constellation a full-rate full-diversity code exists. For complex signal constellations full-rate OSTBCs exist only for two transmit antenna and this code is provided by Alamouti. This code has a great advantage that, one can transmit the desire transmission bit rate while only depends on the modulation techniques. If one wants to be transmit 1 bits/(sHz) he may use BPSK, for 2 bits/(s Hz) use QPSK and continues for higher modulation technique. But code rate less than one need higher modulation technique for same transmission bit rate that obtained by Alamouti code. For half rate code needs QPSK where Alamouti codes need BPSK.
point for uncoded system with one transmission antenna or a full-rate OSTBCs transmission bit rate is b bits/(sHz). For a QOSTBCs with rate R, the transmission bit rate is Rb bits/(sHz). Since only for real signal constellation a full-rate full-diversity code exists. For complex signal constellations full-rate OSTBCs exist only for two transmit antenna and this code is provided by Alamouti. This code has a great advantage that, one can transmit the desire transmission bit rate while only depends on the modulation techniques. If one wants to be transmit 1 bits/(sHz) he may use BPSK, for 2 bits/(s Hz) use QPSK and continues for higher modulation technique. But code rate less than one need higher modulation technique for same transmission bit rate that obtained by Alamouti code. For half rate code needs QPSK where Alamouti codes need BPSK.
In case of full-rate code one can transmit more bits than lower code rate by using same modulation scheme. This is why full-rate code is more efficient code than lower rate code. For complex constellation and more than two transmit antennas full-rate is possible only by QOSTBC. So it is clear that it is more efficient than regular OSTBC. But there is no advantage in using QOSTBC of (7) and BPSK that results in the transmission bit rate of 1 bits/(sHz) because a full-rate full-diversity code exist for real signal constellation. So, here we consider the simulation result of transmission bit rate of 2 bit/(sHz). Figure 1 shows the comparison among QOSTBC, rotated QOSTBC and OSTBC. Figure 2 shows the simulation results of varying transmit antennas using QOSTBCs.
Figure 1 shows the simulation result for OSTBC, QOSTBC and rotated QOSTBC of the transmission bit rate of 2 bit/(sHz). These graphs are plotted against Bit Error Probability versus Signal-to-Noise Ratio (SNR) in dB.
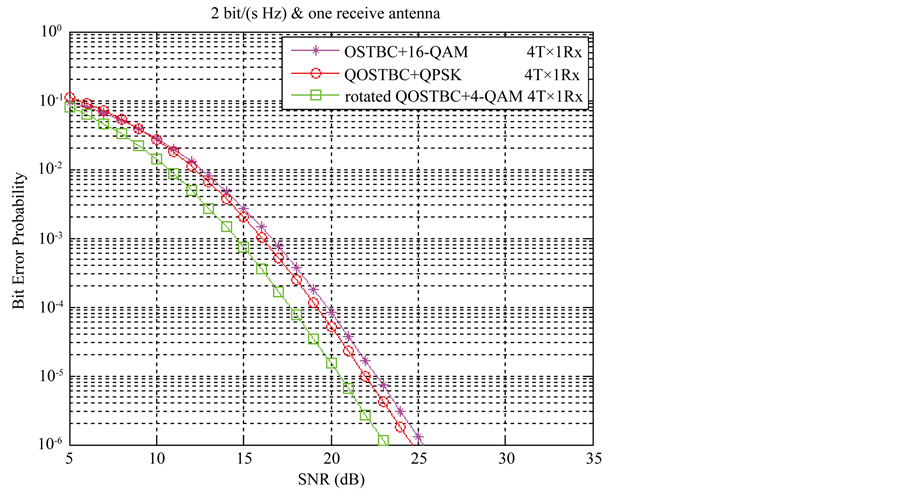
Figure 1. Bit error probability versus signal-to-noise ratio at 2 bits/(sHz).
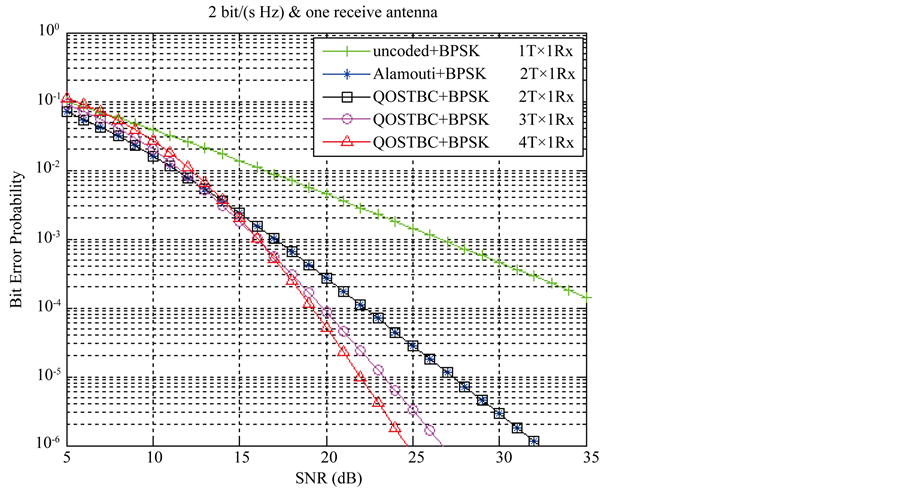
Figure 2. Bit error probability versus signal-to-noise ratio at 2 bits/(sHz) with varying transmit antennas.
For transmission of the QOSTBC in (7) use QPSK modulation scheme, contains four message points. For OSTBC, it uses 16-QAM modulation scheme, contains sixteen message points and transmission bit rate is 2 bits/(sHz). Rotated QOSTBC uses 4-QAM modulation scheme, contains four message points.
At the reference point 10−4 QOSTBC provides about 0.7 dB less SNR than OSTBC. Rotated QOSTBC is about 1.4 dB less SNR than QOSTBC.
Therefore, full-rate QOSTBCs SNR is lower and rotated QOSTBCs SNR is the lowest. So, QOSTBC performs better than OSTBC and rotated QOSTBC performs best from OSTBC and QOSTBC for 2 bits/(sHz).
Figure 2 shows the comparison among the different number of transmit antennas for rate one code, any number of antennas it uses QPSK modulation scheme for transmission bit rate 2 bit/(sHz) and four message points.
For two transmit antenna, QOSTBC 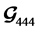 code in (7) becomes
code in (7) becomes 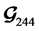 by removing of two columns.
by removing of two columns.
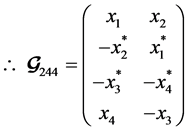 (14)
(14)
The Alamouti code in (5) and the QOSTBC 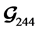 code in (14) provide same curve in the graph so the performance of both codes are same for two transmit antennas.
code in (14) provide same curve in the graph so the performance of both codes are same for two transmit antennas.
The 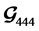 code in (7) becomes a three transmit antenna QOSTBC
code in (7) becomes a three transmit antenna QOSTBC 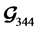 code by removing one column.
code by removing one column.
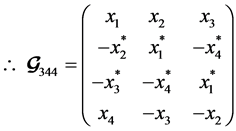 (15)
(15)
The SNR of the four transmit antenna 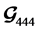 code in (7) is about 0.7 dB less than
code in (7) is about 0.7 dB less than 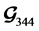 code in (15) and
code in (15) and 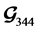 code is about 2.25 dB less than the
code is about 2.25 dB less than the 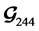 code in (14). The uncoded curve is shown in the graph only for a fair comparison.
code in (14). The uncoded curve is shown in the graph only for a fair comparison.
Therefore, if the number of transmit antenna increases, the SNR decreases. So, it performs better with increasing the number of transmit antenna.
6. Conclusions
Simulation results show that the QOSTBC performs better than OSTBC and rotated QOSTBC performs better than the QOSTBC. If the number of transmit antenna increases rate one code performs better. In fact, since the slope of the BER-SNR curve depends on the diversity, the QOSTBC curve also starts from a better point in the BER-SNR curve. It decodes the pair of symbol so decoding complexity is higher than the OSTBC but both codes have very low decoding complexity. The encoding complexity is very small and same. For two transmit antenna Alamouti scheme and QOSTBC provide same SNR and same BER.
So, the performance of QOSTBC and rotated QOSTBC is better than OSTBC. We work only with Rayleigh flat fading channel. So, there may also few options to works with fast or, slow fading channel or another fading channel like Rician or, Nakagami fading channel. Yet everybody works with four transmit antenna for QOSTBC. One can study for the maximum possible rate for a given number of transmit antenna that will provide full-rate and full-diversity.
References
- Simon, M.K. and Alouni, M.-S. (2000) Digital Communications over Fading Channels: A Unified Approach to Performance Analysis. John Wiley & Sons, Ltd., Hoboken, 4-20, 70-265.
- Xiong, F.Q. (2000) Digital Modulation Techniques. Artech House, Inc., Boston.
- Jafarkhani, H. (2005) Space-Time Codes: Theory and Practice. Cambridge University Press, Cambridge, 1-125. http://dx.doi.org/10.1017/CBO9780511536779.004
- Proakis, J.G. (2001) Digital Communications. 4th Edition, McGraw-Hill, New York.
- Jafarkhani, H. (2001) A Quasi-Orthogonal Space-Time Block Code. IEEE Transactions on Communications, 49, 1-4. http://dx.doi.org/10.1109/26.898239
- Jankirman, M. (2004) Space-Time Codes and MIMO Systems. Artech House, Boston, London, 15-22, 47-50, 75-105.

