Int'l J. of Communications, Network and System Sciences
Vol. 6 No. 5 (2013) , Article ID: 31333 , 8 pages DOI:10.4236/ijcns.2013.65026
Utility-Based Node Cooperation Mechanism in Wireless Sensor Networks
Shenzhen Key Lab of Advanced Communications and Information Processing, Faculty of Information Engineering, Shenzhen University, Shenzhen, China
Email: *xhlin@szu.edu.cn
Copyright © 2013 Xiaohui Lin et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 14, 2013; revised April 12, 2013; accepted May 6, 2013
Keywords: Wireless Sensor Networks; Selfish Node; Game Theory; Reputation; Energy
ABSTRACT
In wireless sensor networks, due to the energy and resource constraints, nodes may be unwilling to forward packets for their neighbors. This can render severe deteriorations in the network performance and malfunctions of the system. To tackle such selfish behaviors and enhance the cooperation among sensors, based on reputation and energy consumption of each node, we present a utility function to punish the malicious nodes and encourage cooperation among nodes. Specifically, we firstly give a mixed strategy Nash equilibrium solution for the two nodes. Then we extend the model to multi-nodes scenario. With the unity function, each sensor’s reputation is evaluated according to its degree of cooperation. The extensive simulation results have shown the effectiveness of the mechanism, in that the cooperative behaviors are encouraged, which can ensure the normal functioning of the network system.
1. Introduction
Wireless sensor networks (WSNs) have recently penetrated deeply into our society and drawn considerable attentions from the academia and industry. WSNs are composed of a large number of cheap and tiny senor nodes deployed in monitored areas. Compared with traditional networks, wireless sensor networks have dynamic topology and are characterized by their non-centralized structure, self-organized and multi-hop features. As a novel technology in acquiring and processing information, WSN has been widely applied in many fields, such as military affairs, industry, agriculture, health care, and environmental monitoring, etc. [1].
However, in the deployment of WSN, one of the key concerns is the limited energy constraint, which has restricted the capabilities of sensor nodes in data communication, computing, and information processing.
Specifically, to conserve limited energy, some selfish nodes may be unwilling to forward data for their neighboring nodes, which can cause the decrease in network throughput and the severe deterioration in system performance. Therefore, to guarantee network performance, cooperation among sensors should be definitely encouraged, and reasonable incentive mechanisms [2-4] should also be designed to fulfill this target.
2. Related Work
Thus far, many different methods have been proposed to tackle the selfish issues of nodes. Generally, they can be classified into three categories.
2.1. Reputation Based Mechanism
In this mechanism [5,6], if a node successfully forwards data packets for its neighbors, the reputation of this node will be increased; otherwise if it drops packets, the reputation will be decreased. When the reputation value drops below a threshold, the node is either punished or isolated. In [7], Marti uses a watchdog algorithm to identify misbehaving nodes. In addition, they also design a path rater to enhance the routing quality by deleting these selfish nodes from the path. Similarly, by using the idea of Watchdog, authors in [8] propose CONFIDANT (Cooperation of Nodes Fairness in Dynamic Ad-hoc Networks) protocol, which aims at detecting and isolating misbehaving nodes.
2.2. Credit-Payment Mechanism
This mechanism is similar to reputation-based one. The difference is that the mechanism introduces a concept of virtual currency or credits as payment to a cooperating neighbor from which a node has received service. A sending node will pay its neighbor who has successfully forwarded packets for it. On the other hand, if a noncooperative neighbor refuses to provide service, it will forfeit its virtual currency or credits as a punishment. If the virtual currency is used up, it cannot send its own packets anymore [9].
In [10], Buttyaan et al. propose Packet Purse Model (PPM), in which, a type of virtual currency called “nuglets” is used. In PPM, each packet is loaded with nuglets by the source. Each forwarding node can take some amount of nuglets as reward for the forwarding services, thus stimulating the cooperative behaviors of the neighbors.
2.3. Game Theory Mechanism
Game theory provides analytical tools to predict the outcome of complex interactions among rational entities. A game consists of a set of players, a set of strategies available to players, and a specification of payoffs for each combination of strategy [11,12]. The cooperation among sensors can also be model as a game. By properly designing the utility function in the game, the high throughput can be guaranteed and energy consumption can also be balanced [13,14]. In [15], a repeated game model for WSN is proposed, and punishment mechanism is also employed to encourage the cooperation of sensor nodes.
3. Model and Assumptions
In this paper, we will design a utility function based on reputation and energy consumption of nodes to encourage cooperation among nodes. We will also propose a mechanism to monitor the malicious nodes and selfish nodes. Firstly, we give the system model and basic concepts and assumptions.
3.1. Node Entity
A node has the following attributes:
1)1) ID-Every node has its unique ID.
2)2) Type. The nodes are categorized into three types— normal nodes, malicious nodes and selfish nodes. Normal nodes always cooperate. Malicious nodes always drop packets from neighbors. Selfish nodes occasionally participate in forwarding packets (with some probability). We assume that, at the beginning, selfish nodes drop packets more often. When their reputation values fall below a certain threshold, they begin to behave like normal nodes and forward more packets for others.
Transmission Range. Nodes can only communicate with their neighbors which are within their transmission range. The distance between two nodes can be written as
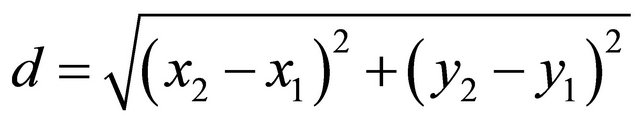
where,  are coordinates of two nodes. If the value of
are coordinates of two nodes. If the value of ![]() is less than or equal to the transmission range (in this paper, we set
is less than or equal to the transmission range (in this paper, we set ![]() to 10), the two nodes can be considered as neighbors.
to 10), the two nodes can be considered as neighbors.
4)1) Reputation. We assume the initial reputation of every node is . Nodes participating in packets forwarding can gain some reputation as a reward (this increment of reputation is defined as
. Nodes participating in packets forwarding can gain some reputation as a reward (this increment of reputation is defined as ), while those who act selfishly will lose some reputation as a punishment (this decrement of reputation is defined as
), while those who act selfishly will lose some reputation as a punishment (this decrement of reputation is defined as ).
).
2) Energy. The initial energy level of all nodes at the beginning in the network is . When sending/forwarding and receiving packets, node will consume some amount of energy. A node will die when its energy is depleted.
. When sending/forwarding and receiving packets, node will consume some amount of energy. A node will die when its energy is depleted.
3.2. Network Setup
In this paper, the simulated network is demonstrated in Figure 1. The area is  with 10 nodes, which are numbered from 0 to 9. Neighbors are connected by straight line. One malicious node (node 6) and two selfish nodes (node 0 and 4) are included into the network.
with 10 nodes, which are numbered from 0 to 9. Neighbors are connected by straight line. One malicious node (node 6) and two selfish nodes (node 0 and 4) are included into the network.
3.3. Cooperation Modeling
We assume each node will send packets to each other in the network. Each packet is included the following information-sequence number, source node, and destination node.
We design a utility function, which takes node reputation and energy consumption into consideration. The utility function can be expressed as
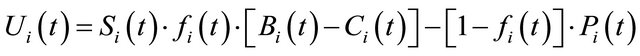 (1)
(1)
where 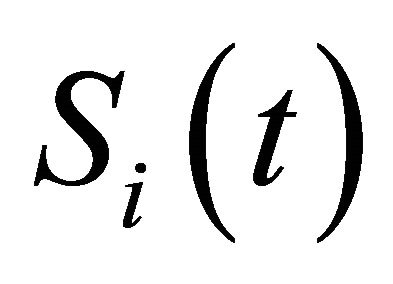 is a Boolean variable, which indicates whether node
is a Boolean variable, which indicates whether node  can participate in packet forwarding based on its residual energy
can participate in packet forwarding based on its residual energy .
.
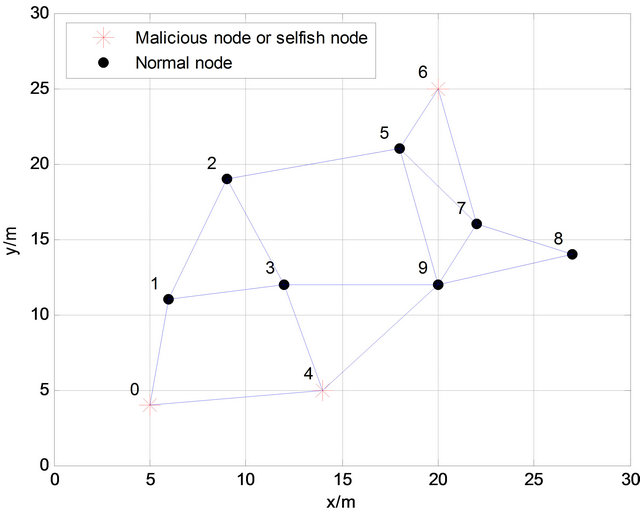
Figure 1. Node topology (30 × 30 m).

Only when the residual energy level of node  is higher than the minimum energy threshold
is higher than the minimum energy threshold , can it participate in the packet forwarding. Otherwise, it will be excluded from the network if its energy falls below the threshold level.
, can it participate in the packet forwarding. Otherwise, it will be excluded from the network if its energy falls below the threshold level.  is the forward probability, which has to be decided by the game strategy. We set the average value of total utility
is the forward probability, which has to be decided by the game strategy. We set the average value of total utility 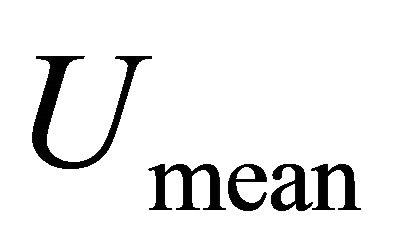 as the threshold (will be illustrated later, see Equation (7)), and when the utility of a neighboring node is less than this threshold, node
as the threshold (will be illustrated later, see Equation (7)), and when the utility of a neighboring node is less than this threshold, node  will drop packets from this neighbor.
will drop packets from this neighbor.  and
and  denote the benefit, cost and punishment in a node’s packet forwarding respectively. Specifically, benefit and punishment refer to the increment and decrement of reputation, respectively, while cost refers to the energy consumed by node in packet forwarding.
denote the benefit, cost and punishment in a node’s packet forwarding respectively. Specifically, benefit and punishment refer to the increment and decrement of reputation, respectively, while cost refers to the energy consumed by node in packet forwarding.
We average the reputation values that all neighbors assign to a node at the end of each round and get reputation of that node. In Table 1 we list the definitions of the parameters to be used in the paper. According to the above definitions, we have:

Table 1. Parameters and descriptions.

In the paper, we only consider alive nodes, thus we let . Therefore, Equation (1) can be written as
. Therefore, Equation (1) can be written as
 (2)
(2)
We consider the packet forwarding at the relay nodes. The packet forwarding decision making at a node is illustrated in Figure 2. In the proposed utility function, if a node is always forwarding packets for its neighbors, then we have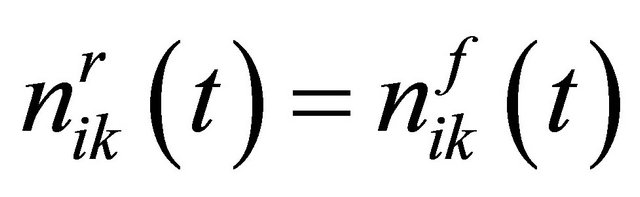 . Therefore, the above equation can be rewritten as
. Therefore, the above equation can be rewritten as
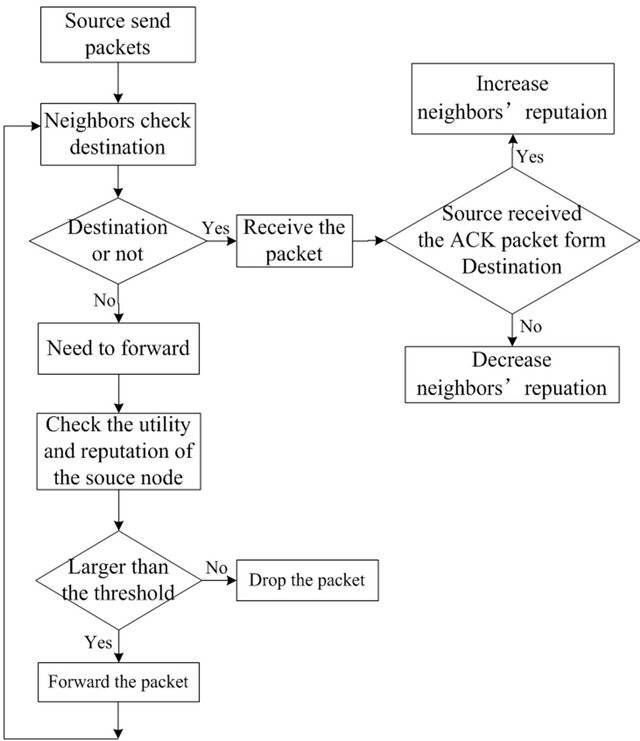
Figure 2. Packet delivery at sensor node.
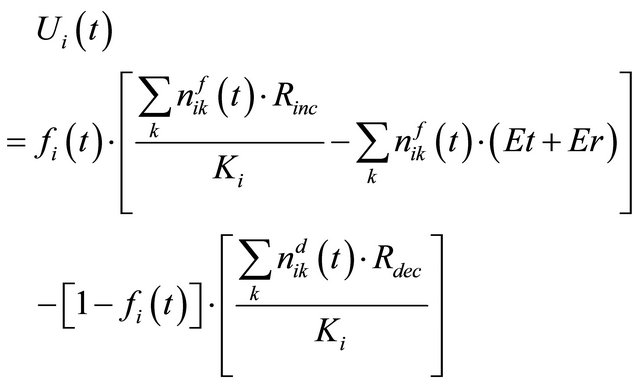
where ,
,
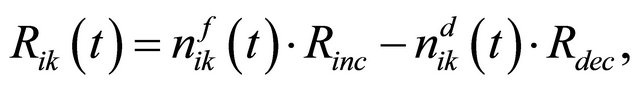
Let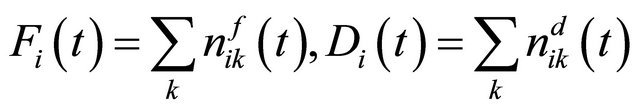 and
and  can be further simplified as
can be further simplified as
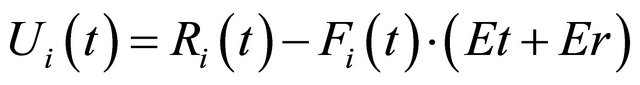 (3)
(3)
After normalization, 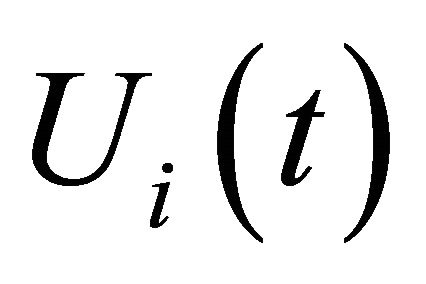 can be expressed as:
can be expressed as:
 (4)
(4)
Note that, the above utility function consists of two parts. The first part is the ratio of the current global reputation value of the node to the initial reputation value, and the second part is the ratio of the forwarding energy consumption of the node to the total energy consumption.
To reflect the effects of reputation and energy on the utility, we add two adjustable weight factors—α and β, and have the newly defined utility function given by:
 (5)
(5)
The total utility of the n nodes in the network is given by
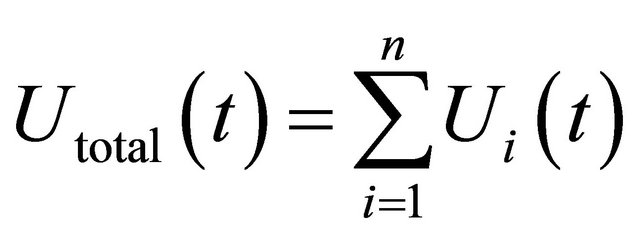 . (6)
. (6)
The average utility of total utility is
 . (7)
. (7)
4. Game Model
4.1. Two Nodes Game Model
In this model, we let nodes i and j be two forwarding nodes. According to above analysis, the behaviors of two nodes can be described as the classic “prisoner dilemma problem”. The payoff matrix of nodes i and j can be expressed as listed in Table 2 [12].
We consider packets forwarding between the two neighboring nodes, and let . So the energy consumption can be written as
. So the energy consumption can be written as

Table 2. Payoff matrix of two nodes.
 . Let
. Let , now we need to find the proper
, now we need to find the proper .
.
The behaviors of different nodes can be complicatednormal nodes always cooperate, and malicious nodes never cooperate, and selfish nodes only participate in packet forwarding with a certain probability. Let the forwarding probability of node and
and  be
be  and
and 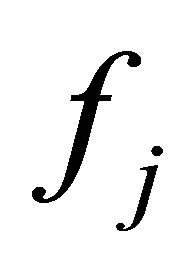 respectively, then the mixed strategies for the two nodes are
respectively, then the mixed strategies for the two nodes are 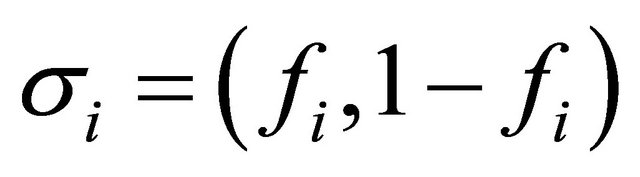 and
and 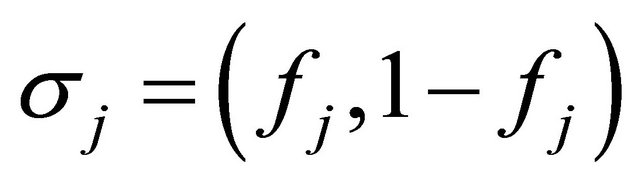 respectively. Thus the expected payoff of node
respectively. Thus the expected payoff of node  is given by:
is given by:
 (8)
(8)
We differentiate this payoff with respect to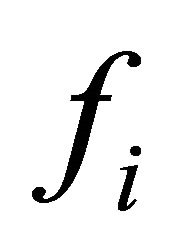 , and let the differentiation value equal to zero:
, and let the differentiation value equal to zero:
 (9)
(9)
Then we have:
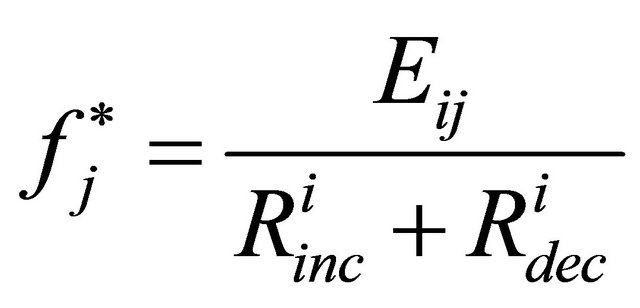 (10)
(10)
Similarly, for the other node, we have:
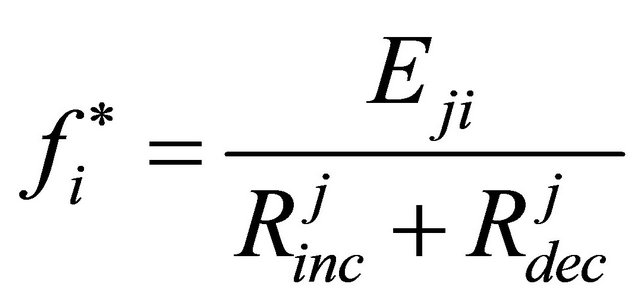 (11)
(11)
With Equations (10) and (11), the best-responses of the two nodes are shown in Figure 3. We get three Nash Equilibrium points-mixed strategy NE (Nash equilibrium), and two pure strategies NE (both nodes cooperate, and neither nodes cooperates). From the results, we can see that the strategy-(cooperate, cooperate) has the highest payoff for the two nodes, with which we can achieve Pareto Optimality [16]. Therefore, cooperation is the best strategy for a node.
4.2. Multi-Node Game
Then we extend the two-node game to multi-node sce-

Figure 3. The best responses of two neighbor nodes.
nario. Without loss of generality, we consider the utility of node . To encourage cooperation among nodes, the utility of cooperation should be larger than that of noncooperation, i.e.,
. To encourage cooperation among nodes, the utility of cooperation should be larger than that of noncooperation, i.e.,
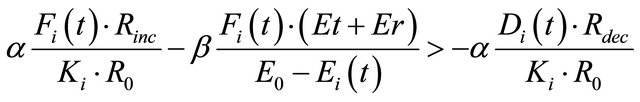
which can be further simplified as:
 (12)
(12)
5. Performance Analysis and Simulation Results
We calculate the NE of the proposed game model with C++ and MATLAB, and set the node’s strategy according to these NEs. We use DSDV as the routing protocol. Table 3 shows the parameter setting.
We firstly compare the proposed mechanism with the scenario that without incentive. The simulated results are shown in Figure 4. We can observe that, if there is no incentive, nodes will be unwilling to forward packets, which will lead to high drop packet rate. While the selfish behavior of nodes is effectively restricted by the proposed mechanism, which can remarkably lower the packet loss rate as shown in the figure.
It is observed that the proposed mechanism can restrict the behaviors of selfish nodes. Specifically, a selfish node should avoid being isolated by increasing the forwarding probability (with more cooperation behaviors). Note that a malicious node never cooperates. We set a utility threshold 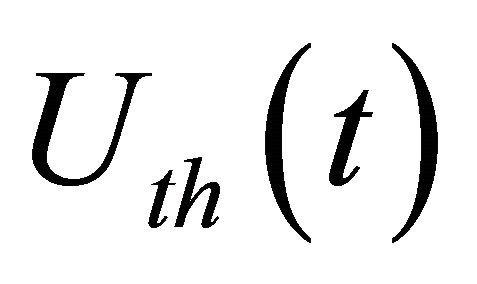 to differentiate the selfish nodes from malicious nodes (if the utility is lower than the threshold, the node will be treated as malicious node and excluded from the network). Hence the selfish nodes can increase the forwarding probability when its utility is
to differentiate the selfish nodes from malicious nodes (if the utility is lower than the threshold, the node will be treated as malicious node and excluded from the network). Hence the selfish nodes can increase the forwarding probability when its utility is

Table 3. Parameters setting in the experiment.
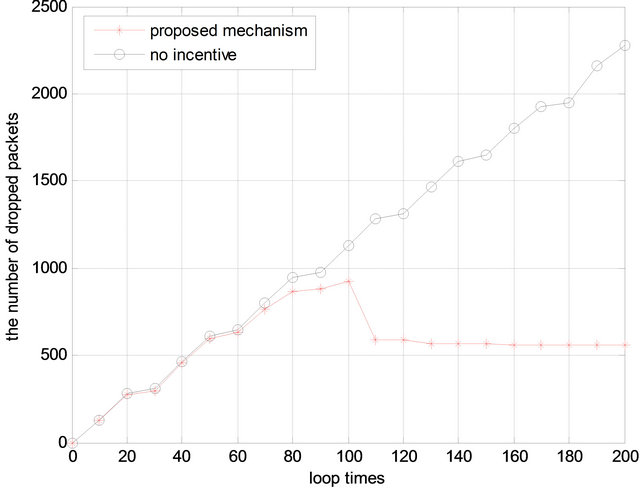
Figure 4. Number of packets dropped with time.
lower than the threshold (we set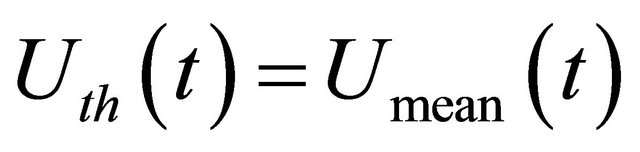 ). In some papers [e.g. 4,5], the utility function is simply based on reputation, and selfish nodes will be excluded from the network once identified. The isolation of these malicious nodes can lead to the decrease in the number of packet drop as shown in Figure 5.
). In some papers [e.g. 4,5], the utility function is simply based on reputation, and selfish nodes will be excluded from the network once identified. The isolation of these malicious nodes can lead to the decrease in the number of packet drop as shown in Figure 5.
In Figure 5, compared with the proposed mechanism, the reputation-based mechanism can reduce the packet loss rate to zero when the malicious nodes are identified and isolated (after round time 100). This, however, can lead to unbalance in energy consumption among nodes, which can further incur early energy depletion for the nodes in the reputation-based mechanism as illustrated in Figure 6. Instead, in the proposed game approach, as the selfish nodes are rational, each node adaptively adjusts its forwarding probability to maximize its own utility and avoid being isolated, thus more nodes will survive and packet relay is more evenly distributed among the network. This can definitely extend the network lifetime.
Another problem need to solve is setting of 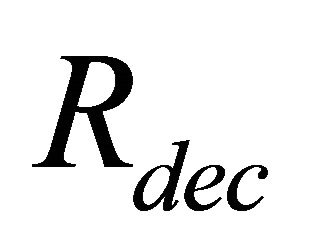 and
and . We let
. We let , and substitute these values into Equation (12), then we have
, and substitute these values into Equation (12), then we have

which can be further Simplified as:
 (13)
(13)
We determine the range of 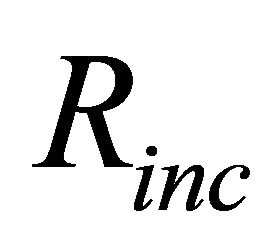 through extensive experiments and find that
through extensive experiments and find that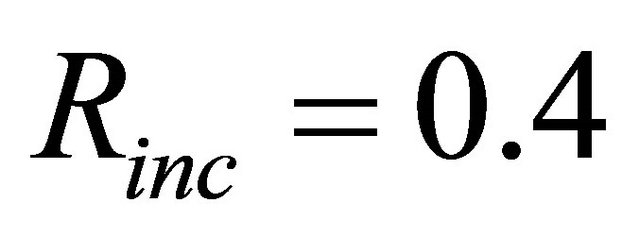 ,
, 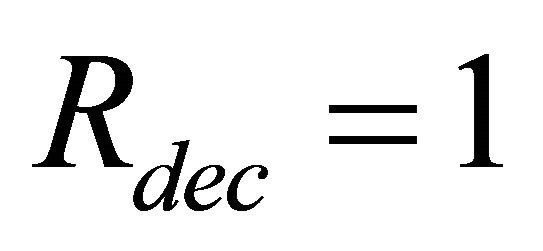 is the proper parameter set that can ensure the cooperation of nodes.
is the proper parameter set that can ensure the cooperation of nodes.
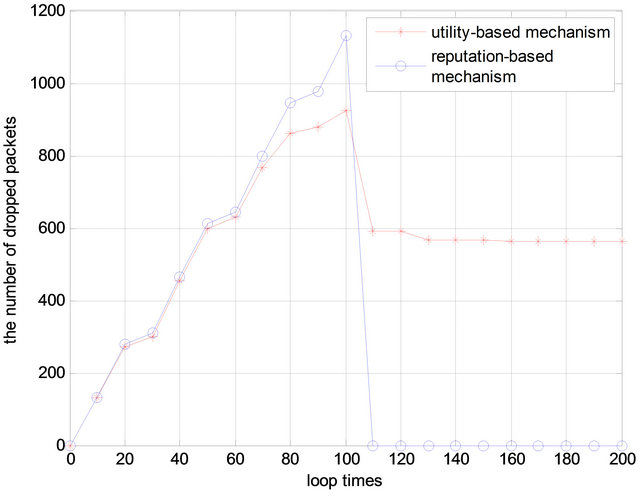
Figure 5. Number of packets dropped.
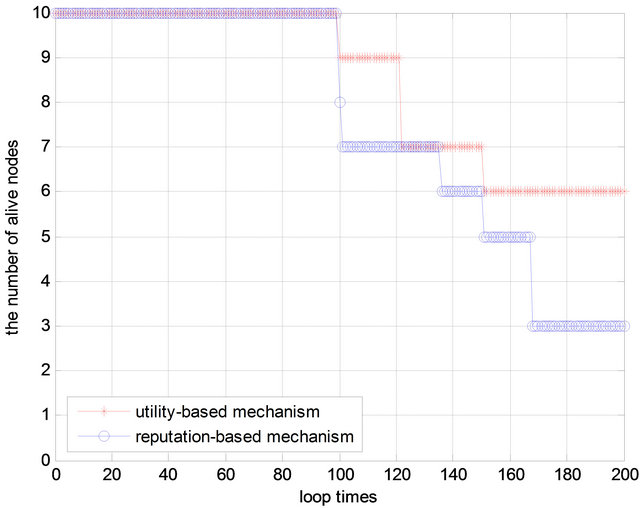
Figure 6. Number of nodes alive versus time.
5.1. The Effect of Reward and Punishment
We let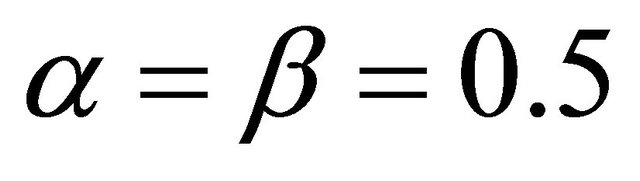 , and simulate four scenarios using different values of Reward and Punishment. Obviously, the smaller the
, and simulate four scenarios using different values of Reward and Punishment. Obviously, the smaller the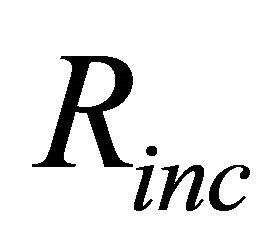 , the smaller the reward achieved, and relatively the harsher the punishment. The reward and punishment parameters are set as the follows:
, the smaller the reward achieved, and relatively the harsher the punishment. The reward and punishment parameters are set as the follows:
1) Scenario 1: 
2) Scenario 2: 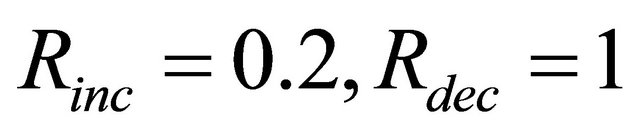
3) Scenario 3: 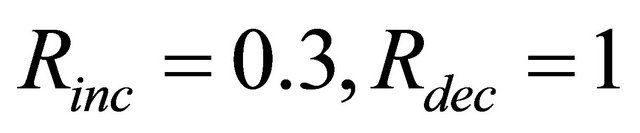
4) Scenario 4: 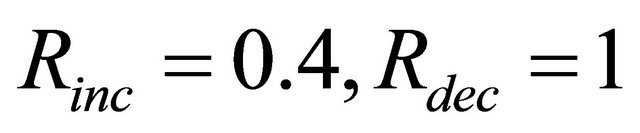
5) Scenario 5: 
It can be seen from Figure 7, the packet loss rate is high in either scenario 1 (small reward value) or scenario 5 (large reward value). This phenomenon is reasonable since when the reward for packet forwarding is small, selfish nodes can only get low incentive in packet forwarding (utility is low), thus its strategy is to decrease the forwarding probability and save energy. On the other hand, a large reward value can lead to longer time in identifying the selfish nodes, which can lead to more packet drop by the selfish nodes. Scenario 4 shows the best performance. In the 100th round, the packet loss rate dropped rapidly because the malicious node is identified and excluded from the network. Also, with the incentive mechanism, the selfish nodes can gradually adjust its probability and cooperate more in packet forwarding.
Figure 8 is the number of nodes alive with time. In the 100th round, the malicious node is identified and excluded from the network. Nodes in scenario 1 have the longest lifetime, and hence, with regard to lifetime, parameter setting in scenario 1 is optimal. However, it also shows bad performance in packet loss rate. Thus, depending on different criteria and preference, the parameter setting should be flexible and adjustable.
5.2. Eight Effects
We set 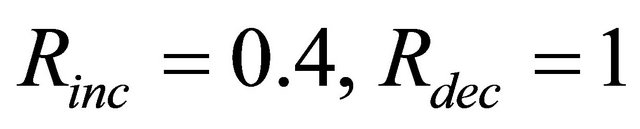 and simulate three scenarios with different values of α and β.
and simulate three scenarios with different values of α and β.
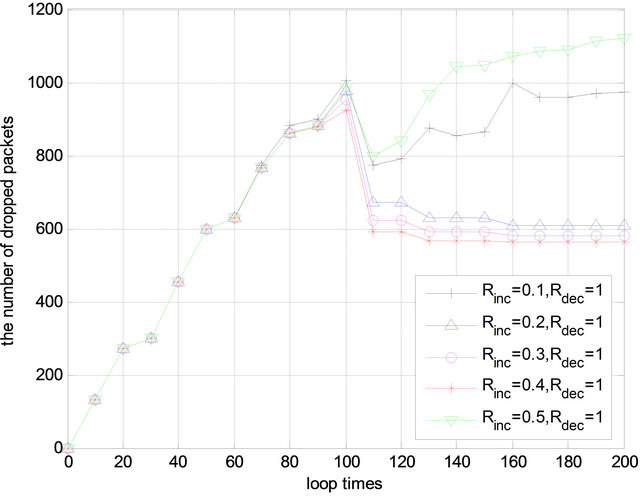
Figure 7. Number of packets dropped.

Figure 8. Number of nodes alive versus time.
1) Scenario 1: 
2) Scenario 2: 
3) Scenario 3: 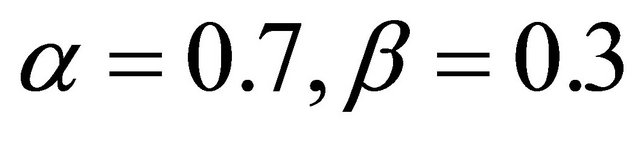
Figure 9 is the number of packets dropped with time. It is observed that parameters in scenario 1 show the best performance. The packet loss rate in scenario 2 is much higher than the other two. That’s because the utility function assigns large weight to the energy part while small weight to reputation part, which causes selfish nodes to care more about energy saving instead of the reputation, leading to a high packet loss rate. By assigning equal weights to both parts, scenario 1 can strike a balance in between. We can also observe that, before the first 100 rounds, the packet loss rate increased steadily because the malicious node has not been identified. Afterwards malicious node is identified and isolated, and also due to the effect of incentive mechanism, the network performance can be maintained at a steady level.
Figure 10 is the number of node alive with time. It is shown that scenario 2 has the best performance. As ana-
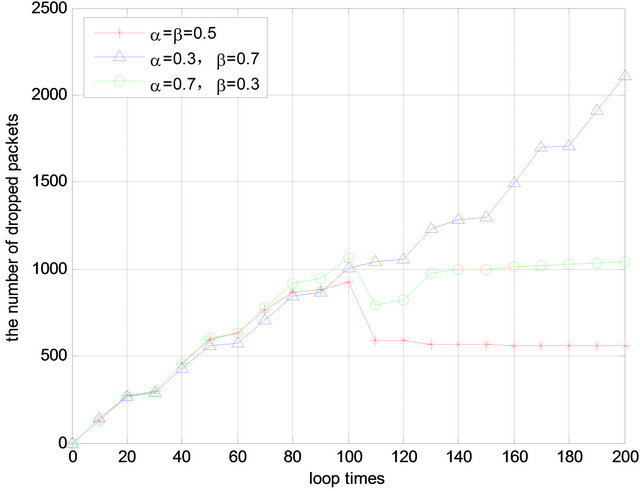
Figure 9. Number of packets dropped.

Figure 10. Number of nodes alive versus time.
lyzed above, in scenario 2, nodes care more about energy saving. Therefore, there is a tradeoff between energy consumption and performance, and we should find a balance point in between (e.g. ).
).
6. Conclusion
In this paper, we propose a utility-based game mechanism to enhance the cooperation among sensor nodes. In the mechanism, reputation and energy of the nodes are taken into consideration. We have also derived the Nash equilibrium solution to the game and extended it to a multiple-node scenario. With the mechanism, by properly tuning the related parameters, malicious node can be identified and isolated, and at the same time, selfish behaviors can also be restricted. Additionally, simulation results show that the network performance of our mechanism is better than that of conventional punishment mechanism, in which selfish nodes will be directly removed from the network once identified. Instead, in the proposed method, selfish node is not excluded, and with the incentive mechanism, the selfish node can adjust its behavior, thus balancing the energy consumption and enhance the network lifetime. Finally, we have also illustrated the effects of different parameters on the network, which can provide a guideline for the optimization of the mechanism.
7. Acknowledgements
The research was jointly supported by research grant from Natural Science Foundation of China under project numbers NSFC60602066, NSFC60773203, NSFC60902 016, NSFC61001182 and NSFC61171071, 973 Program under the project number 2013CB336700, and grants from Foundation of Shenzhen City under project numbers JC201005250035A, JC201005250047A, JC201005 280404A JC201005280556A, JCYJ20120613115037732, and ZDSY20120612094614154.
REFERENCES
- I. F. Akyildiz, S. Weilian, Y. Sankarasubramaniam, et al., “A Survey on Sensor Networks,” IEEE Communications Magazine, Vol. 40, No. 8, 2002, pp. 102-114. doi:10.1109/MCOM.2002.1024422
- S. Vikram, N. Pavan, C. F. Chiasserini, et al., “Cooperation in Wireless Ad Hoc Networks,” Proceedings of the INFOCOM 2003 Twenty-Second Annual Joint Conference of the IEEE Computer and Communications, San Franciso, 30 March-3 April 2003.
- E. Altman, A. A. Kherani, P. Michiardi and R. Molva. “Non-Cooperative Forwarding in Ad-hoc Networks,” Technical Report INRIA Report No. RR-5116, 2004..
- P. Marbach and Q. Ying, “Cooperation in Wireless Ad Hoc Networks: A Market-Based Approach,” IEEE/ACM Transactions on Networking, Vol. 13, No. 6, 2005, pp. 1325-1338. doi:10.1109/TNET.2005.860109
- P. Michiardi and R. Molva, “Core: A Collaborative Reputation Mechanism to Enforce Node Cooperation in Mobile Ad Hoc Networks,” Proceedings of the IFIP TC6/ TC11 6th Joint Working Conference on Communications and Multimedia Security, Deventer, 3-5 September 2002, pp. 107-121.
- S. Bansal and M. Baker, “Observation-Based Cooperation Enforcement in Ad Hoc Networks,” Technical Paper, 2003.
- S. G. Marti, T. J. Giuli and K. Lai, “Mitigating Routing Misbehavior in Mobile Ad Hoc Networks,” MOBICOM, Boston, 2000, pp. 255-265.
- S. Buchegger and J. L. Boudec, “Performance Analysis of the CONFIDANT Protocol Cooperation of Nodes-Fairness in Dynamic Ad-Hoc Networks,” ACM International Symposium on Mobile Ad Hoc Networking and Computing, Lausanne, 9-11 June 2002, pp. 226-236. doi:10.1145/513800.513828
- S. Zhong, J. Chen and Y. R. Yang, “Sprite: A Simple, Cheat-Proof, Credit-Based System for Mobile Ad-Hoc Networks,” Proceedings of the INFOCOM 2003 TwentySecond Annual Joint Conference of the IEEE Computer and Communications, San Franciso, 30 March-3 April 2003.
- L. Buttyaan and J. P. Hubaux, “Nuglets: A Virtual Currency to Stimulate Cooperation in Self-Organized Mobile Ad Hoc Networks,” Technical Report No. DSC/2001/001, Swiss Federal Institute of Technology (EPFL), Lausanne, 2001.
- R. Gibbons, “Game Theory for Applied Economists,” Pricenton University Press, Princeton, 1992.
- M. J. Osborne and A. Rubinste, “A Course in Game Theory,” The MIT Press, Cambridge, 1994.
- D. Levin, “Punishment in Selfish Wireless Networks: A Game Theoretic Analysis,” Proceedings of the ACM Workshop on the Economics of Networked Systems (NetEcon 2006), Ann Arbor, 11 June 2006.
- H. Zhu, J. Zhu and K. J. R. Liu, “A Cartel Maintenance Framework to Enforce Cooperation in Wireless Networks with Selfish Users,” IEEE Transactions on Wireless Communications, Vol. 7, No. 5, 2008, pp. 1889-1899. doi:10.1109/TWC.2008.061014
- Y. Lu, J. Shi and L. Xie, “Repeated-Game Modeling of Cooperation Enforcement in Wireless Ad Hoc Network,” Journal of Software, Vol. 19, 2008, pp. 755-756. doi:10.3724/SP.J.1001.2008.00755
- J. Harsanyi and R. Selten, “A General Theory of Equilibrium Selection in Games,” Cambridge University Press, Cambridge, 1988.
NOTES
*Corresponding author.

