Int'l J. of Communications, Network and System Sciences
Vol. 6 No. 2 (2013) , Article ID: 28163 , 9 pages DOI:10.4236/ijcns.2013.62012
An Efficient Priority Based Routing Technique That Maximizes the Lifetime and Coverage of Wireless Sensor Networks
1Department of Computer Science, The University of Jordan, Amman, Jordan
2Department of Computer Science, Fahd Bin Sultan University, Tabuk, KSA
Email: i.salah@ju.edu.jo, mshrideh@ju.edu.jo, salsharaeh@yahoo.com
Received November 26, 2012; revised December 15, 2012; accepted January 4, 2013
Keywords: Wireless Sensor Networks; Energy-Aware Routing; Sensors Deployment; Priority Based Technique
ABSTRACT
Recent development in sensor technologies makes wireless sensor networks (WSN) very popular in the last few years. A limitation of most popular sensors is that sensor nodes have a limited battery capacity that leads to lower the lifetime of WSN. For that, it raises the need to develop energy efficient solutions to keep WSN functioning for the longest period of time. Due to the fact that most of the nodes energy is spent on data transmission, many routing techniques in the literature have been proposed to expand the network lifetime such as the Online Maximum Lifetime heuristics (OML) and capacity maximization (CMAX). In this paper, we introduce an efficient priority based routing power management heuristic in order to increase both coverage and extend lifetime by managing the power at the sensor level. We accomplished that by setting priority metric in addition to dividing the node energy into two ratios; one for the sensor node originated data and the other part is for data relays from other sensors. This heuristic, which is called pERPMT (priority Efficient Routing Power Management Technique), has been applied to two well know routing techniques. Results from running extensive simulation runs revealed the superiority of the new methodology pERPMT over existing heuristics. The pEPRMT increases the lifetime up to 77% and 54% when compared to OML and CMAX respectively.
1. Introduction
Recent advances in Nano-electromechanical systems (NEMS) paved the way to new applications for Wireless sensor networks [1-3]. Sensor networks comprise a large number of small-size nodes with sensing, computation, and wireless communication capabilities. These nodes collaborate together by performing desired measurements, process measured data, and transmitting it to some special nodes, commonly referred to as sink node [2]. One limitation to sensor nodes is the limited battery capacity [2,3]. Usually, the sensor nodes are deployed in a hard to reach areas. For that, it has a limited lifetime. Many researches in the literature have the objective to maximize the lifetime of sensor nodes by developing new routing techniques [4]. Hence, it is vital to develop solutions that are energy efficient and maximizing the network lifetime [1,4].
Energy depletion is mainly due to data reception and transmission, where the later is large when compared to data reception [2]. There are many ways for data to be received (collected) or propagate to end (sink node) node. Either by, single-hop transmission [5,6], multi-hop transmission, or cluster-based transmission [1]. Single-hop transmission is the simplest transmission method which tries to communicate directly with the sink node, but this consumes higher power rates. Multi-hop transmission delivers data by forwarding it to one of its adjacent nodes, which are closer to the sink node; the data propagate from the source node to the sink from one node to another until it reaches the sink node. A drawback of this methodology, nodes closer to the sink must forward data received from other nodes as well as transmitting their own data to the sink base station. For that, their batteries drain quickly more than others, and as results produce blind areas and cause network partitions. In cluster based transmission [5,6], nodes are grouped into clusters and one node which is the cluster head is responsible of sending other nodes data to the sink.
In our work, we are concerned with the first two methods and we try to balance between them when necessary to gain higher lifetimes and coverage as we will see later in the discussion. We accomplished this by developing energy-aware routing heuristics (pERPMT) that tries to optimize network lifetime by managing routes in a way that will save power as much as possible so that the lifetime of the network is maximized.
Prolonging the lifetime is the same as increasing the coverage of WSN. By prolonging the lifetime of sensor node, the vicinity of sensor node area is kept covered [2,3]. One of our purposes was to keep all or most of the network nodes active (alive) most of the network lifetime.
The reminder of the paper is organized as follows: Section 2 introduces the wireless sensor networks mathematical model. In Section 3, we provide simulation and modeling of pERPMT. Simulation data and discussion of pERPMT is introduced in Section 4. Section 5 is concluding the paper.
2. Literature Review
The main problem in most of energy-aware routing heuristics is that they find the lowest energy route and use it for every communication [2,7,8]. Using low energy path more frequently will leads to energy depletion of the nodes along that path especially the nodes closer to the sink. Once the sensor node dies it leads to network partition that cause blind areas (areas that can not be sensed by any node). Some heuristics have been proposed to solve this problem by taking into account the residual energy at nodes and delay the depletion of nodes that are already low in energy [9,10]. In [11], the researchers proposed the MRPC (Maximum Residual Packet Capacity) lifetime-maximization, which depends not only on the residual battery energy on a node, but also on the expected energy spent in forwarding a packet over a specific link. MRPC selects the path that has the largest packet capacity at the node which has the smallest residual packet transmission capacity. They also present CMRPC, a conditional variant of MRPC that switches from MRPC only when the packet forwarding capacity of nodes falls below a predetermined threshold. In [12], they proposed the CMAX (Capacity Maximization). The capacity is the number of messages routed over some time period, heuristic which provides a single path for each message (no multiple paths) chosen with respect to the link weights. The heuristic makes admission control. That is, it rejects some routes that are possible in order to increase lifetime. In [13,14], the authors introduced localized heuristics to maximize lifetime in which they define a new power cost metric based on both nodes life time and distance-based power metrics. They also show that the required transmission power can be reduced if additional nodes placed at desired locations between two nodes at distance D. Park and Sahni [15] proposed the OML (Online Maximum Lifetime) heuristic where two shortest path computations are done to route each message. In order to maximize lifetime, we need to delay as much as possible the depletion of a sensor’s energy to a level below that needed to transmit to its closest neighbor. Al-Sharaeh, et al. [16], introduced a Multi-Dimensional Poisson Distribution Heuristic to better evaluate the routing heuristics; by taking into account earth’s terrain and the multi-dimensional concept and this is done by the method of placement of sensors and the probability of the connections between sensors nodes. The positions of the sensors (x and y-coordinates) are chosen either from a Uniform or Poisson distributions. A major effect on the performance of different routing heuristics was gained. In [17], they introduced a study of the deployment strategy effect on maximizing the lifetime of the wireless sensor networks; it shows that changing the statistical techniques of distribution—such as Poisson Distribution— that meet real environment requirements affect the performance of maximizing lifetime routing heuristics in many aspects, such as average lifetime and network capacity. In [9] the authors prolonged the life time by proposing new heuristic based-on dividing the energy of nodes into two parts. The heuristic named an Efficient Routing Protocol Management Technique (ERPMT). The Alpha part reserved to own data transmission, while the Beta part for other nodes data (i.e. to relay other nodes data). One draw back of their work is that, the nodes close to the sink nodes, say, one hop, deplete their energy very fast as compared to two hops.
In this work, we proposed a heuristic that delays the depletion of one-hop nodes by adding a priority metric. The priority number that we have is based on two factors. One is the number of hopes and the second is based on the energy level of the node. In order to have fair comparison, we perform a battery power management at the node level with and without priority based scheme, such that the total power of the sensor battery is divided into two parts; the first is dedicated for sending data generated by the sensor itself, while the other is for data relays from other sensors [9,10]. Our approach can be used along with any existing routing heuristics. For that, we compared pERPMT against two well known routing heuristics: OML, CMAX, and ERPMT.
3. WSN Mathematical Model
A wireless sensor network is represented by a directed graph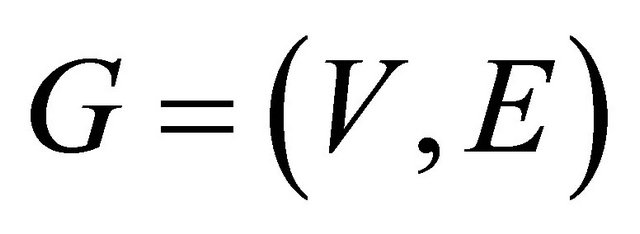 , where V is the set of nodes, and E is the set of edges between these nodes, there will be a directed edge from node v to node u (i.e.
, where V is the set of nodes, and E is the set of edges between these nodes, there will be a directed edge from node v to node u (i.e.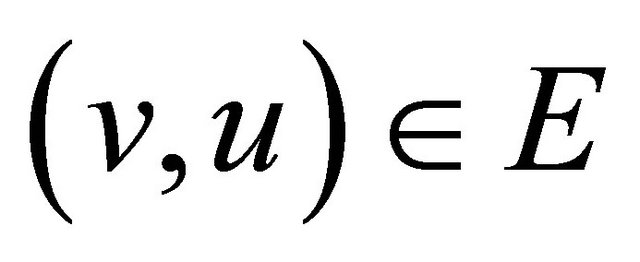 ) if u and v in the range of each others. Such modeling can be used to represent Wireless Sensor Networks (WSN). for each
) if u and v in the range of each others. Such modeling can be used to represent Wireless Sensor Networks (WSN). for each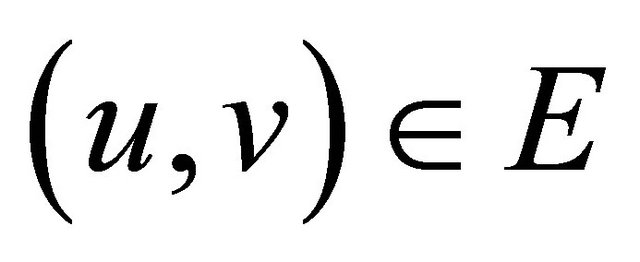 , in case of single hop transmission from sensor u to sensor v, the current energy in sensor u, ce(u) is represented by Equation (1) [12]
, in case of single hop transmission from sensor u to sensor v, the current energy in sensor u, ce(u) is represented by Equation (1) [12]
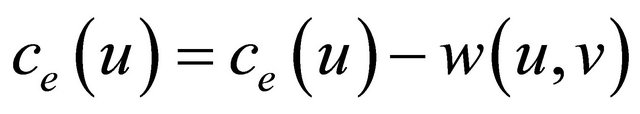 (1)
(1)
where ce(u) is the current energy in sensor u, such as 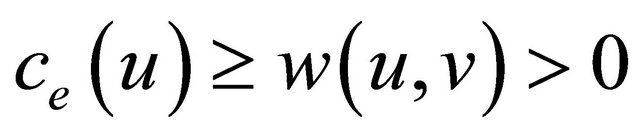 and
and 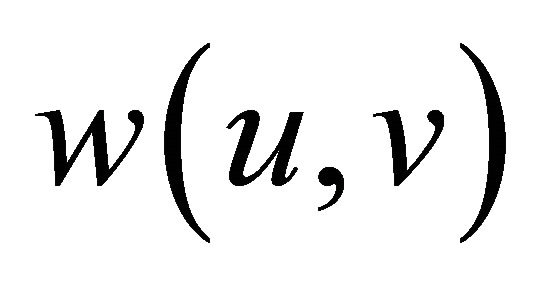 is the energy required to make a single hop transmission from sensor u to sensor v, such that
is the energy required to make a single hop transmission from sensor u to sensor v, such that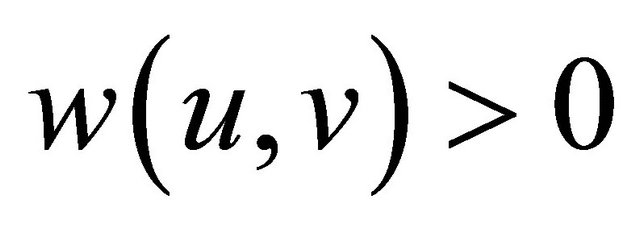 . We also assume that the receiver of a message consumes no energy during message reception. Thus, the current energy in sensor (v) is not affected by the transmission from u to v. In our work the energy is divided into two ratios, one for data originated from the node (α), the other is for relays from other sensors (β); if the data is originated from the node itself, it will use the energy from the first ratio otherwise it will use energy from the other ratio.
. We also assume that the receiver of a message consumes no energy during message reception. Thus, the current energy in sensor (v) is not affected by the transmission from u to v. In our work the energy is divided into two ratios, one for data originated from the node (α), the other is for relays from other sensors (β); if the data is originated from the node itself, it will use the energy from the first ratio otherwise it will use energy from the other ratio.
An adjacency matrix can be used to represent directed graphs of WSN [12-16]. The adjacency matrix of a finite directed graph G on n vertices (where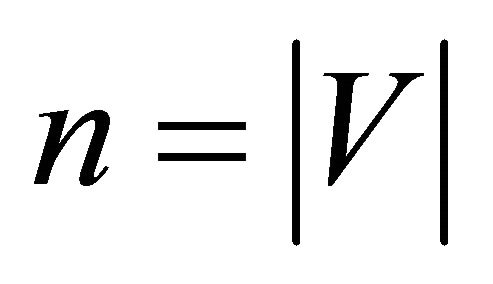 ), is the n × n matrix such that, the non-diagonal entry
), is the n × n matrix such that, the non-diagonal entry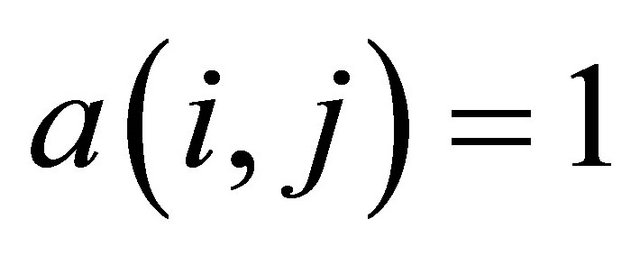 , represents the existence of an edge from sensor i to sensor j. While the diagonal entry
, represents the existence of an edge from sensor i to sensor j. While the diagonal entry 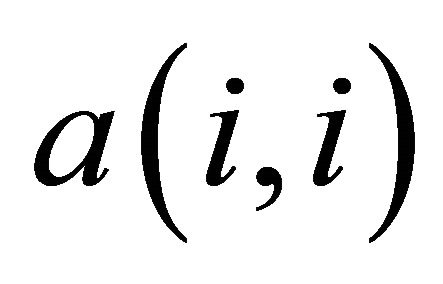 is assigned by zeros here because we assume that there is no internal loops in the WSN.
is assigned by zeros here because we assume that there is no internal loops in the WSN.
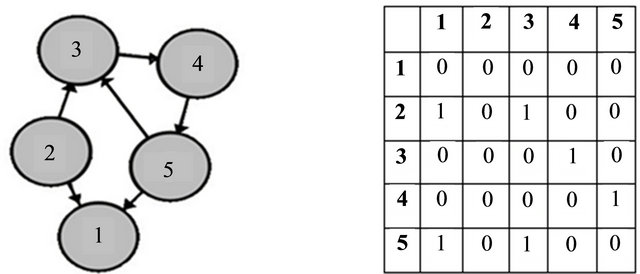
There exists a unique adjacency matrix for each graph. For example, Figure 1(a) shows a simple representation for sensor network S. A directed graph is used, where the represented nodes are sensors, and the edges represent the existence of edges between the sensor nodes. Figure 1(b) shows the adjacency matrix of the sensor network S modeled in Figure 1(a). It is obvious that Figure 1(b) depicts a network that has been implemented using one dimension to represent sensors. Such representation for sensors has been used by Al-Sharaeh, et al. [16].
In most of the studies to represent a sensor location as well as connectivity a random number from Uniform distribution was used [12]. It is better to use the Uniform distribution for flat terrain environment, because the sensors can be distributed evenly as shown in Figure 2, but the real environment usually characterized by terrains, such as in case of sensors deployed in high mountains or deep oceans. In this case, the Uniform distribution does not give a good realistic that match the terrain changes. For that, it is better to use Poisson distribution as it is best fits the asymmetric environment [16,17]. Figure 3
 (a) (b)
(a) (b)
Figure 1. Representation of wireless sensor network, (a) Simple graph network representation; (b) Corresponding adjacency matrix representation.
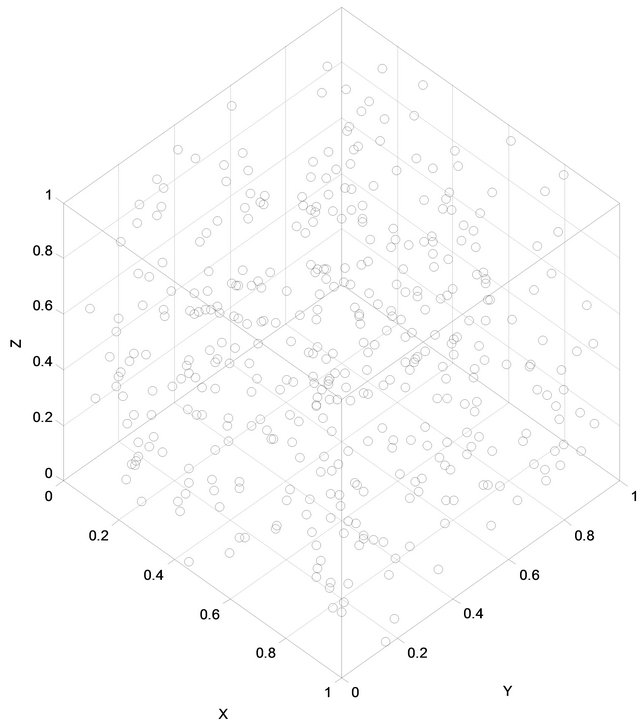
Figure 2. 3D Sensor nodes distribution based on Uniform distribution.
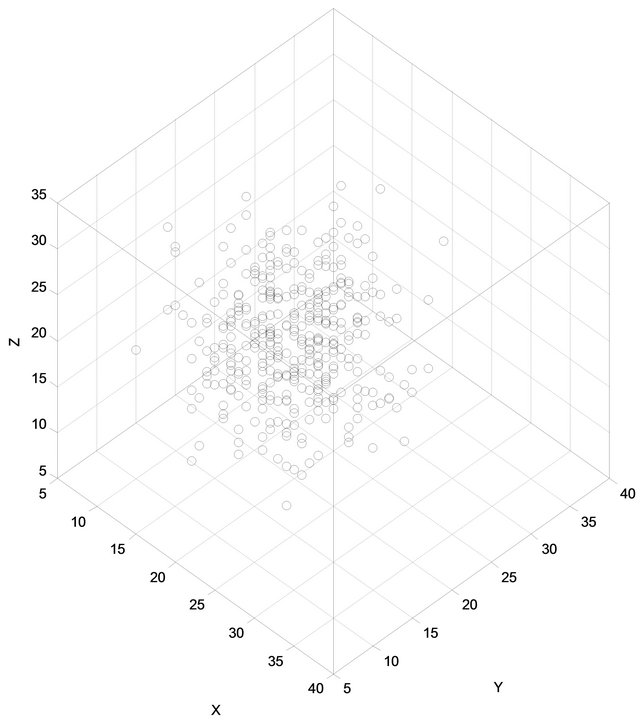
Figure 3. 3D Sensor nodes distribution based-on Poisson distribution.
shows sensor nodes distribution based on Poisson distribution, it is clear that the sensors location concentrated around the mean. This kind of deployment imitates a deployment of sensors via airplane in a terrain that is close to valleys. For fair comparisons with the heuristics in the literature we used Uniform distribution.
An example of sensor deployment application is avalanching predictions, mountainous terrains portrait all the challenges that may face sensor deployment in order to make full coverage. For that, deployment strategy has a major effect on evaluating a routing heuristic. This is due to the fact of terrain changes of real life environment. Figure 4 depicts the landscape of typical environment that ranges from flat land, hilltop, cliffs, valleys, to mountains top. In order to make fair comparison between different routing protocols, a major attention should be paid to the deployment strategy. This factor can be taken into consideration by the way we generate the random graph that both simulate the position as well as the connectivity that at the end will simulate the way the sensors are connected.
To determine connectivity between the nodes, we used a threshold which was equal to the mean of the dimensions of network nodes. All nodes were recursively checked by comparing their X-, Yand Z-dimension in case of 3D deployment with the mean of the Euclidian dimensions for these 3 dimensions (X, Y, and Z) for all network nodes. For the case of 1D, we only work with just the X dimension. Each node with a dimension value greater than or equal to the mean of the same dimension will be considered connected, otherwise it will be disconnected [16].
4. pERPMT Heuristic
We have used two well known heuristics to apply pERPMT on, these two different heuristics were proposed to extend the lifetime of the network and they obtained the best lifetime in the literature, CMAX and OML.
Figure 5 shows the details of our proposed heuristic, which is pERPMT_C and it is an enhancement over the CMAX, where we assume that the current energy in each sensor is divided in two ratios, the first is for the sensor originated data (α), the other is for relays from other sensors (β). For each routing step there are three steps. In

Figure 4. Mountains terrains for avalanche detection WSN application.

Figure 5. pERPMT based on CMAX heuristic.
step one; every edge with a sensor that has not adequate energy to make a single hop transmission is eliminated from the graph. Then each remaining link is assigned a weight using Equation (2):
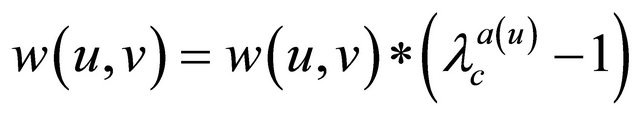 (2)
(2)
where 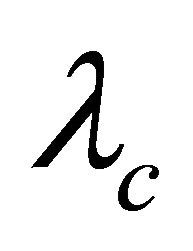 is a heuristic parameter,
is a heuristic parameter, 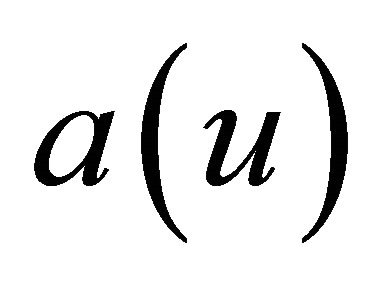 is the percentage of the initial energy that has already been spent at the sensor node and calculated as in Equation (3):
is the percentage of the initial energy that has already been spent at the sensor node and calculated as in Equation (3):
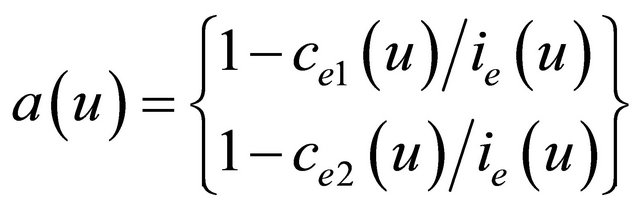 (3)
(3)
In the second step, the source-to-destination path in the modified Graph is computed. If a path is not found, then the request failed. Otherwise it is used unless it is larger than a specified threshold σ. In the third step, we assign a priority number; it is range depends on the number of paths. The set value for the priority number depends on the average power of the path. Furthermore, since through extensive simulation runs we concluded that those nodes close to the sink depleted fast, for that we excluded those nodes from our computations. Since we excluded the nodes that are one hop far from the sink, only that path that has at least one node in the range of sink is selected. For the case if there is no node in the range of the sink, we include the one hope node in the calculated paths.
Assumption: Divide the current energy of each sensor into 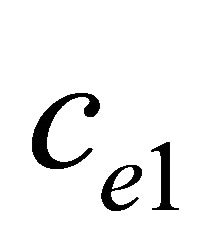 and
and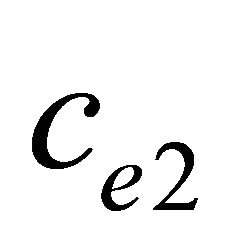 :
:
 and
and 
For each routing request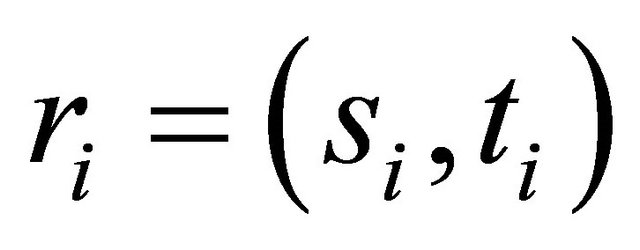 :
:
Step 1: [Initialize]
Eliminate from G every edge 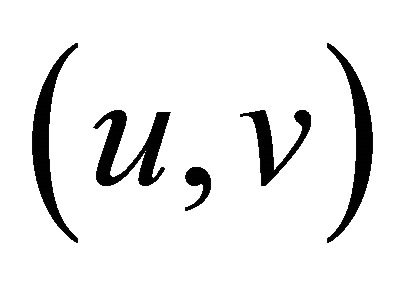 for which:
for which:
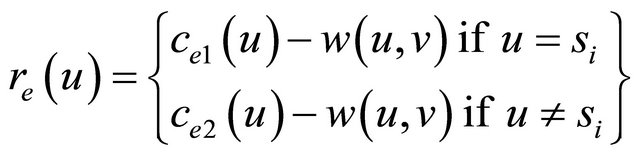
Change the weight of every remaining edge 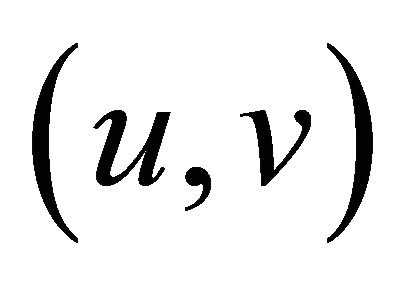 to:
to:
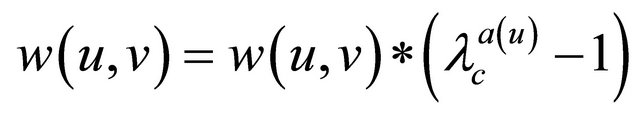
where 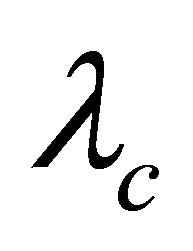 is a heuristic parameter, a(u) is the percentage of the initial energy that has already been spent at the sensor node and it is calculated as:
is a heuristic parameter, a(u) is the percentage of the initial energy that has already been spent at the sensor node and it is calculated as:
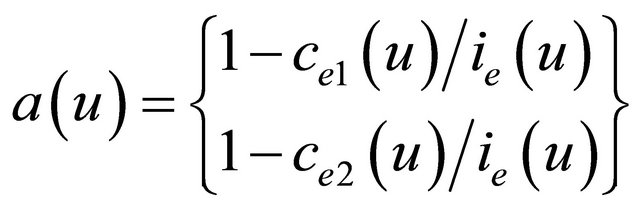
Step 2: [Shortest Paths]
Let 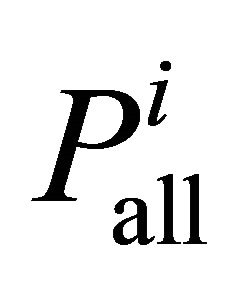 be all shortest source-to-destination path in the modified Graph, and let
be all shortest source-to-destination path in the modified Graph, and let 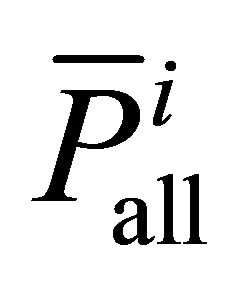 be the average path power.
be the average path power.
Step 3: [Path Selection that has highest priority]
Figure 6 details of the second heuristic (ERPMT based on OML) are shown. As in ERPMT based on CMAX, we assume that the energy in each sensor is divided into two ratios α and β. Then for each routing request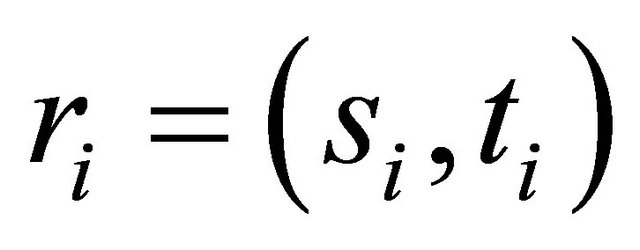 ,two steps are done:
,two steps are done:
Step 1: [Compute G′′] :
All edges are removed from G such that 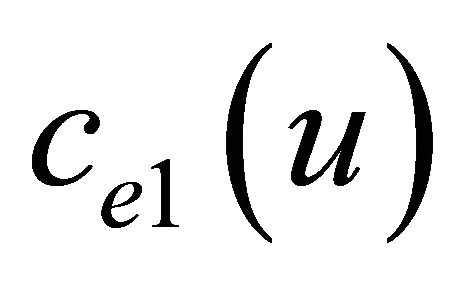 or
or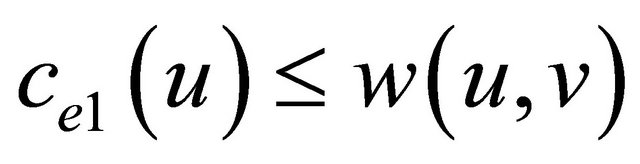 ; as these edges have less power than required for a single transmission. The resulting graph is
; as these edges have less power than required for a single transmission. The resulting graph is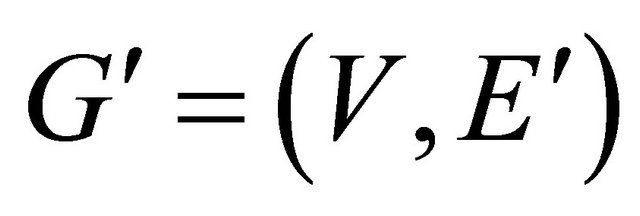 . Determine the minimum energy path
. Determine the minimum energy path 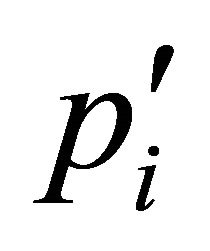 from
from ![]() to
to 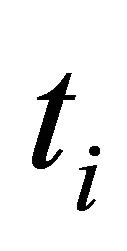 in
in . This is done using a shortest path algorithm based on Dijikstra’s Algorithm. If there is no path from the source s to destination t, then the routing request fails, but if routing request exists, then
. This is done using a shortest path algorithm based on Dijikstra’s Algorithm. If there is no path from the source s to destination t, then the routing request fails, but if routing request exists, then 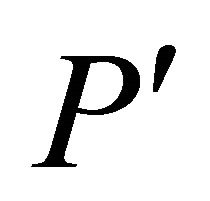 is used to compute the residual energy using Equation (4):
is used to compute the residual energy using Equation (4):
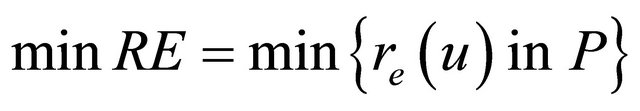 (4)
(4)
Then the graph 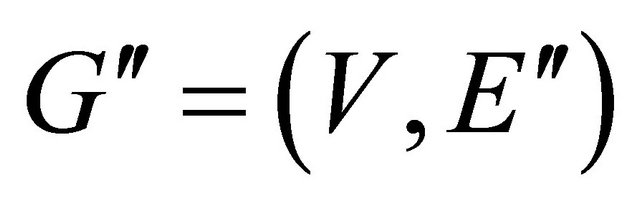 can be obtained by removing all edges
can be obtained by removing all edges 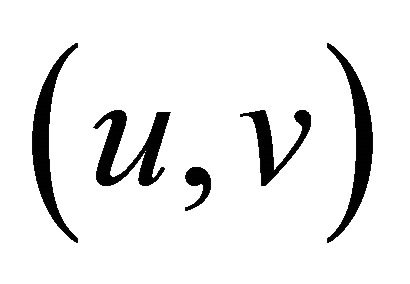 in
in  with
with 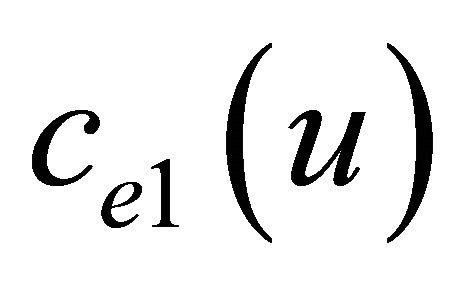 or
or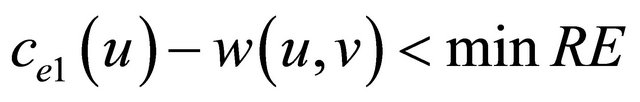 . As a result, all the edges with residual energy below (minRE) will be pruned from the graph and the reduction of energy from sensors that are low on energy could be prevented.
. As a result, all the edges with residual energy below (minRE) will be pruned from the graph and the reduction of energy from sensors that are low on energy could be prevented.
The second step in the procedure is to find the path to be used to route the request r, we begin with 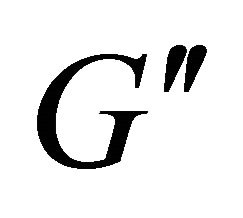 and assign weights to each
and assign weights to each 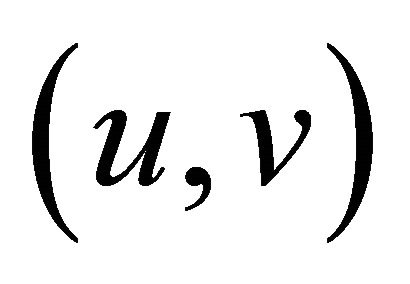 in
in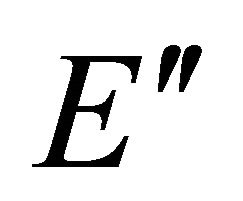 ; this is done to balance the desire to minimize total energy consumption as well as the desire to prevent the depletion of a sensor’s energy.
; this is done to balance the desire to minimize total energy consumption as well as the desire to prevent the depletion of a sensor’s energy.
Let eMin (the energy needed by sensor u to transmit a message to its nearest neighbor in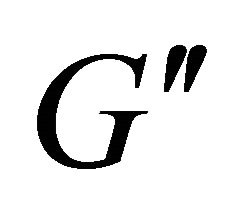 ) as expressed in Equation 5:
) as expressed in Equation 5:
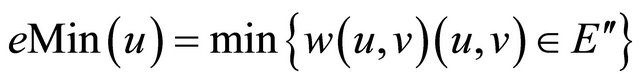 (5)
(5)
Now, let be defined as in the following equation:
be defined as in the following equation:
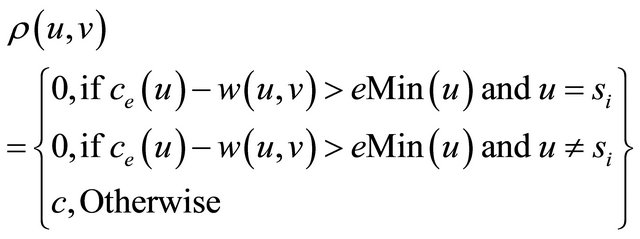 (6)
(6)
where the c symbol is a non-negative constant and it is an

Figure 6. pERPMT based on OML heuristic.
algorithm parameter. Then a (u) is defined for each u in V as a 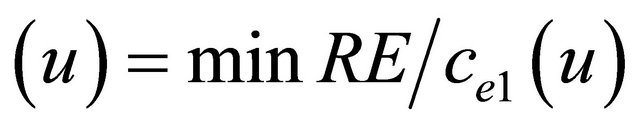 or
or 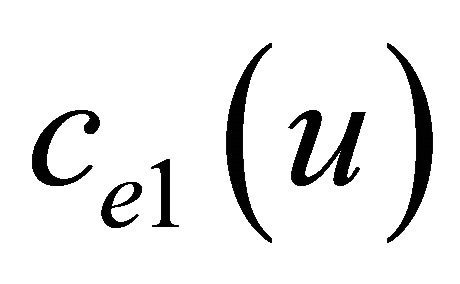 and the weight
and the weight 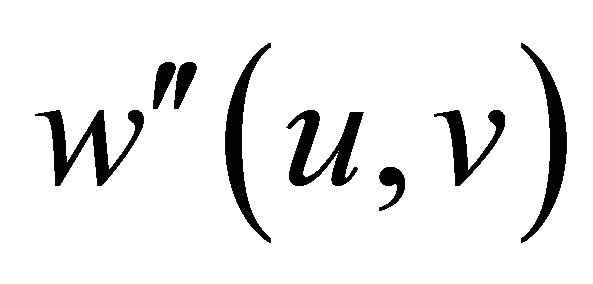 assigned to edge
assigned to edge 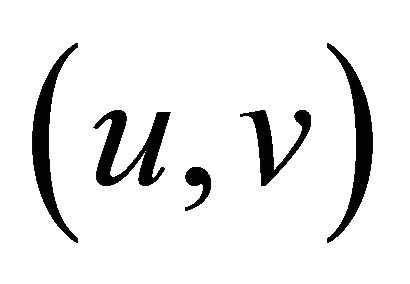 in
in 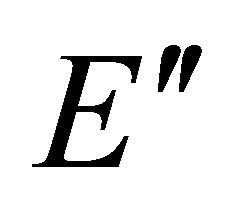 is computed using Equation (7):
is computed using Equation (7):
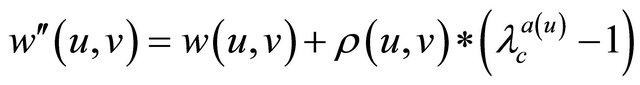 (7)
(7)
where 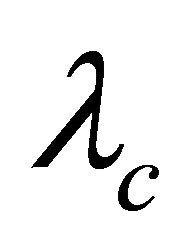 is another non-negative constant an algorithm parameter.
is another non-negative constant an algorithm parameter.
As can be seen, the weighting function, through 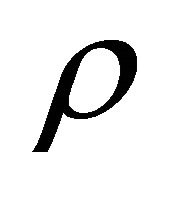 , assigns a high weight to edges whose use on a routing path causes a sensor’s residual energy to become low.
, assigns a high weight to edges whose use on a routing path causes a sensor’s residual energy to become low.
Also, all edges emanating from a sensor whose current energy is small relative to minRE are assigned a high weight because of the term. Thus the weighting function discourages the use of edges whose use on a routing path is likely to result in the failure of a future route. Finally, we Find the shortest path 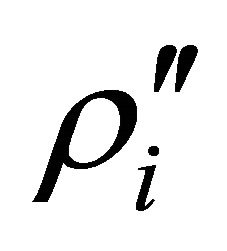 in
in 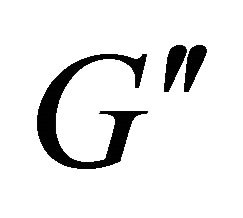 and use it to route from s to t.
and use it to route from s to t.
5. Expremintals Results
The pERPMT is implemented using  software running on a Operating System of Windows XP SP3 installed on a PC with 3.20 GHz processor and 2 GB of RAM. The OML and the CMAX were implemented using the new power management technique (pERPMT) based on Uniform. In each of 10 networks 20 sensors were randomly populated based on Uniform distribution. The energy required by a single-hop transmission between two sensors was assumed to be
software running on a Operating System of Windows XP SP3 installed on a PC with 3.20 GHz processor and 2 GB of RAM. The OML and the CMAX were implemented using the new power management technique (pERPMT) based on Uniform. In each of 10 networks 20 sensors were randomly populated based on Uniform distribution. The energy required by a single-hop transmission between two sensors was assumed to be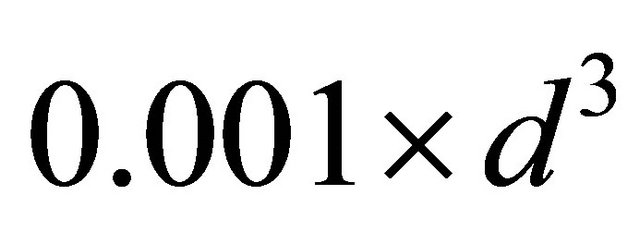 , and the Euclidean distance between two sensors is
, and the Euclidean distance between two sensors is![]() . And the transmission radius and initial energy for each sensor were set to 5100 respectively. Finally, the c was set to
. And the transmission radius and initial energy for each sensor were set to 5100 respectively. Finally, the c was set to 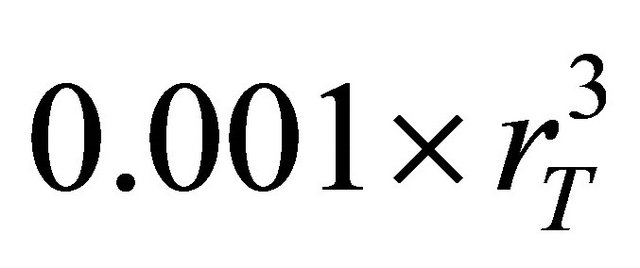 , where
, where 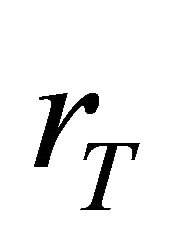 is the transmission radius [12]. The simulation results show the effects of applying the power management technique in different distribution types on the network lifetime.
is the transmission radius [12]. The simulation results show the effects of applying the power management technique in different distribution types on the network lifetime.
A. Dedicating power less than or equal to β for α
Here α was 50%, 40%, 30%, 20%, and 10% of total node energy.
1) Average lifetime for 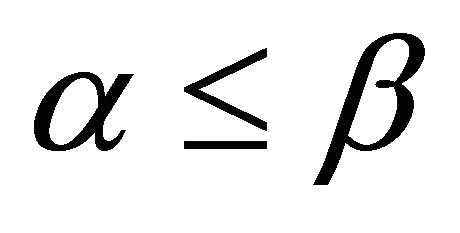
A twenty sensor networks were deployed to be randomly distributed. Figure 7 depicts the average lifetime for 10 networks with 20 sensors in each network for the OML and pERPMT_O (pERPMT based on OML) heuristic. It is obvious that when applying our pERPMT technique the lifetime has increased in all cases.
The same observation is found when as we use CMAX, depicted in Figure 8. As previous researches in [16,17], we conclude that the CMAX has less lifetimes than OML.
B. Dedicating more power for α than β
In these experiments α was larger than β, α was set to 60%, 70%, 80%, 90%, 100%.
1) Average lifetime for α > β
Figure 9 shows the results of applying the pERPMT on the OML (pEPRMT_O). It is clear that as the power dedicated for the sensor own generated data increases, the lifetime decreases. This decrease in lifetime is a result of increasing the value of α more than 50% of total power. That is, the probability for a node to find a path to route through, get decreases, and as a result the lifetime of network decreases.
Figure 10 shows results of the same experiments, but we used ERPMT based on CMAX (pERPMT_C). The same conclusions apply, but as we discussed before that CMAX is less affected to changes of the values of α, and that is because the stability of the CMAX heuristic.
Table 1 depicts the percentage difference in lifetime between OML, ERPMT_O, and pERPMT_O in different cases, by using Equation (8). Note that, if the result is negative then there is a reduction in lifetime, otherwise, it is an improvement. The enhancement of lifetime for the pERPMT_O is better than OML by 79% and 67% for ERPMT_O for cases when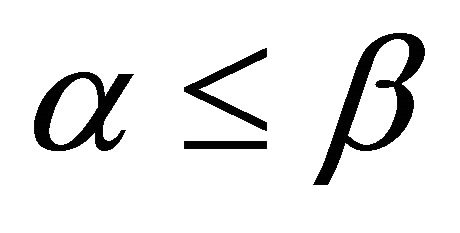 .
.
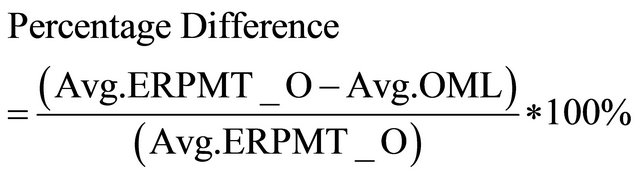 (8)
(8)
For Table 2, it depicts the percentage difference in lifetime between CMAX, ERPMT_C, and pERPMT_C. The enhancement of lifetime for the pERPMT_C is
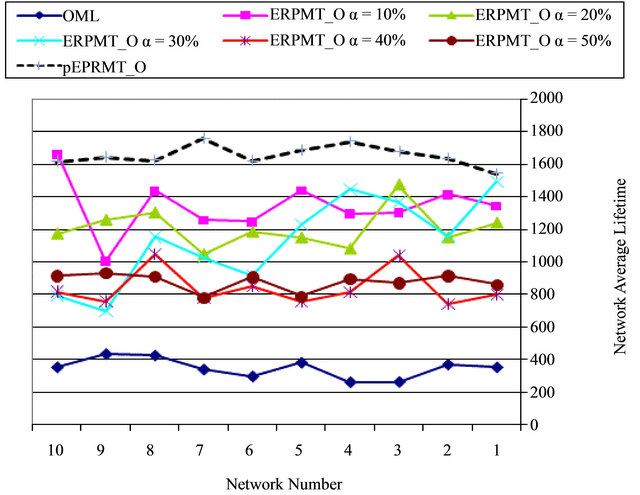
Figure 7. Average lifetime routing for OML and ERPMT_O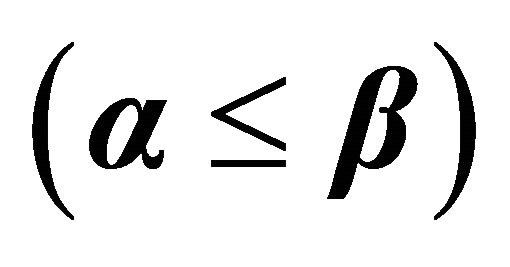 .
.
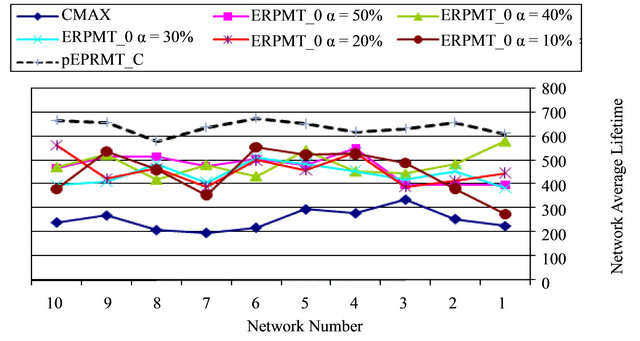
Figure 8. Average lifetime routing for CMAX and ERPMT_C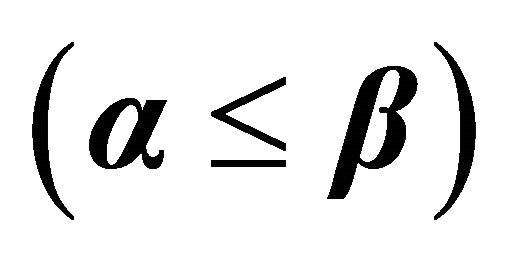 .
.
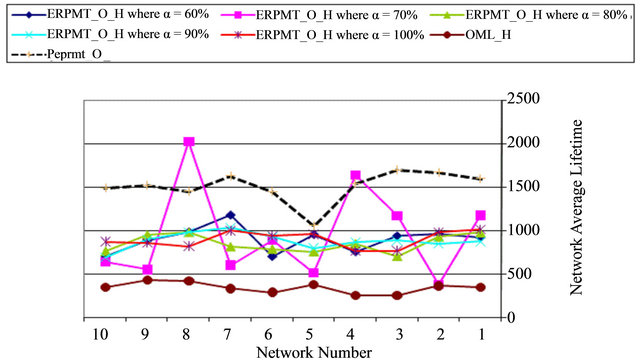
Figure 9. Average lifetime routing for OML and ERPMT_O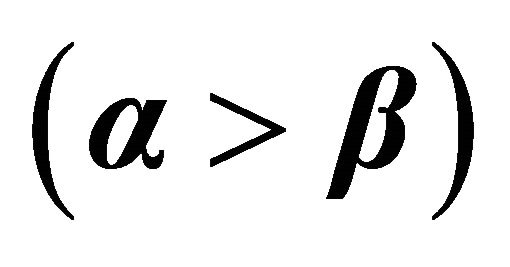 .
.
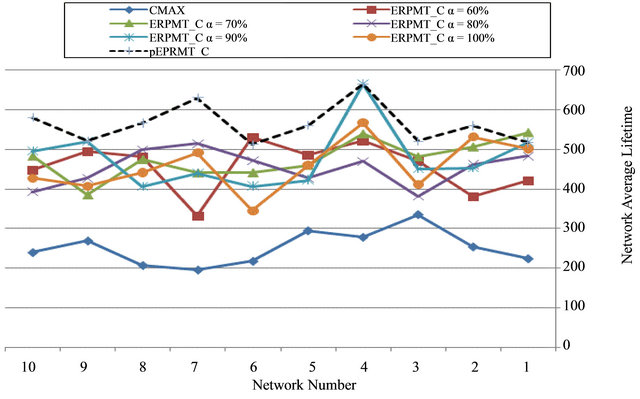
Figure 10. Average lifetime routing for CMAX and ERPMT_C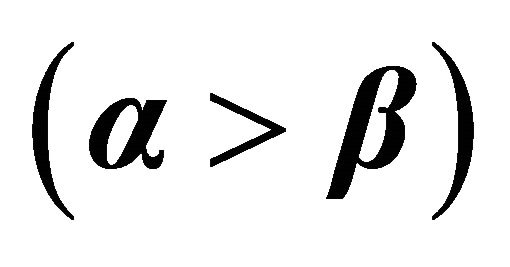 .
.
better than CMAX by 61% and 45% for ERPMT_O for cases when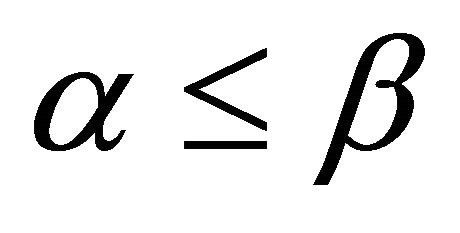 .
.
The percentage differences in lifetime between OML, ERPMT_O, and pERPMT_O show an enhancement of lifetime for the pERPMT_O over OML by 76% and 61% for ERPMT_O for case when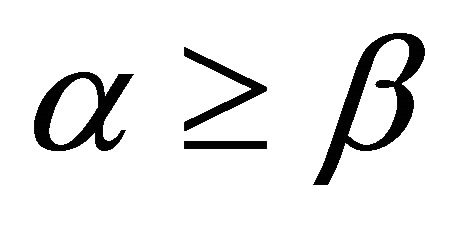 as depicted in Table 3.
as depicted in Table 3.
Table 4 depicts the percentage difference in lifetime between CMAX, ERPMT_C, and pERPMT_C. The enhancement of lifetime for the pERPMT_C is better than CMAX by 47% and for ERPMT_C is 46% when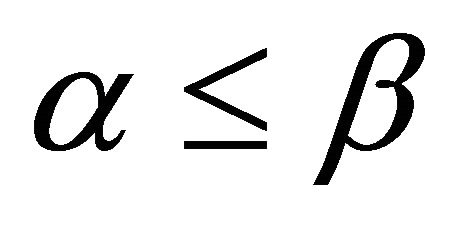 .
.
Based on the previous results, Table 5 shows the enhancement of the proposed heuristics pERPMT for the cases of 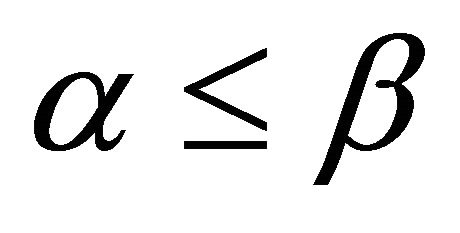 and
and 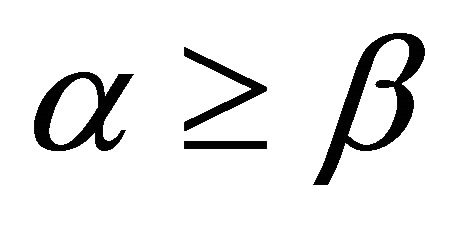 for the two well known heuristics, OML and CMAX. It is evident that when
for the two well known heuristics, OML and CMAX. It is evident that when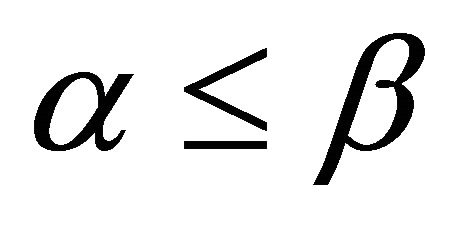 , pERPMT significantly outperform OML and CMAX by 61% and 79% respectively. For
, pERPMT significantly outperform OML and CMAX by 61% and 79% respectively. For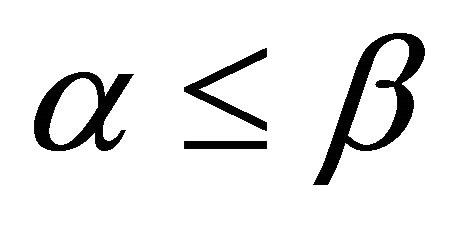 , it means more power dedicated for other nodes data transmission than it is own data. Through an exhaustive simulation runs using OML and CMAX individually where we read the energy values on
, it means more power dedicated for other nodes data transmission than it is own data. Through an exhaustive simulation runs using OML and CMAX individually where we read the energy values on  hop nodes throughout the lifetime of WSN, where
hop nodes throughout the lifetime of WSN, where  is a sensor node with an
is a sensor node with an  hope away from the sensor and
hope away from the sensor and ![]() is the total number of nodes. We conclude that the life of WSN ends because of the depletion of the nodes that are one hop away from the sink. And when we used the pERPMT we shifted the burden of forwarding the aggregated data, to the nodes in the middle (i.e.
is the total number of nodes. We conclude that the life of WSN ends because of the depletion of the nodes that are one hop away from the sink. And when we used the pERPMT we shifted the burden of forwarding the aggregated data, to the nodes in the middle (i.e. , where
, where  is the hop count from the sink), as well as using
is the hop count from the sink), as well as using 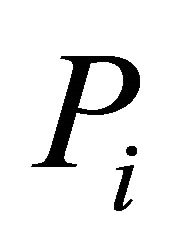 that has high priority.
that has high priority.
Table 1. The percentage difference between OML and proposed heuristics for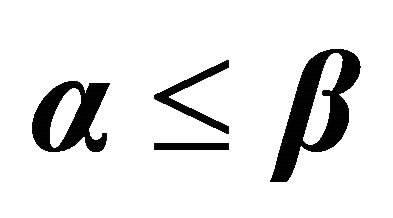 .
.

Table 2. The percentage difference between CMAX and proposed heuristics for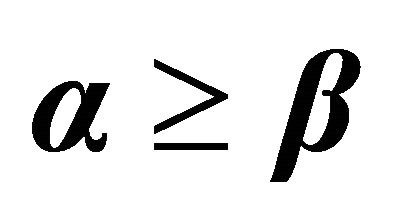 .
.

Table 3. The percentage difference between OML and proposed heuristics for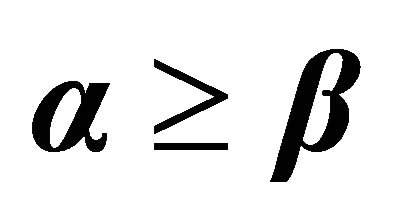 .
.

Table 4. The percentage difference between CMAX and proposed heuristics for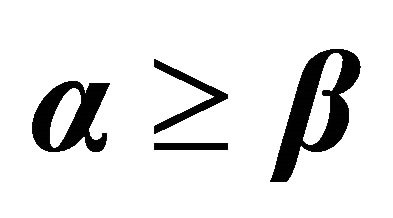 .
.

Table 5. Performance of pERPMT vs. CMAX and OML.

Table 2 shows the percentage difference for ERPMT with α > β. ERPMT is 18.3% better than OML for case of α = 60%. As α increase, we notice a decrease in the lifetime. OML is 17.9 better than ERPMT with α = 70%. As α increase more decrease in the network lifetime.
6. Conclusions and Future Work
WSN play an important role for various applications such as but not limited to volcano eruption mentoring, border control, and nondestructive testing. Since WSN is usually deployed randomly and in a hard to reach areas, limited battery capacity raises researcher concerns on the network lifetime. Many researchers proposed routing techniques to prolong the WSN lifetime. In this paper, an efficient priority routing power management heuristics have bas been proposed and analyzed (pERPMT). Various performing metric parameters have been evaluated. It is observed that the pEPRMT outperformed existing routing heuristics in the literature such as OML and CMAX by 77% and 54% on average, respectively. This is especially true when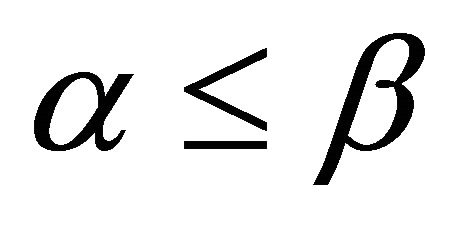 . It is evident that WSN lifetime can be prolonged if we shift data aggregation re-transmission to the sink node to one of the intermediate nodes, given that at least you can find one node in the transmission range of the sink. Otherwise, one of the nodes that are one hope away from the sink is used.
. It is evident that WSN lifetime can be prolonged if we shift data aggregation re-transmission to the sink node to one of the intermediate nodes, given that at least you can find one node in the transmission range of the sink. Otherwise, one of the nodes that are one hope away from the sink is used.
We believe that additional investigation is needed to consider the locality of sensor nodes that depends on the deployment process. Furthermore, the dimension of deployment should be taken into account. We plan to look at different distributions of sensor nodes as well as movable sink node.
REFERENCES
- W. Wilson and G. Atkinson, “Wireless Sensors for Space Applications,” Sensors & Tranducers Journal, Vol. 13, Special Issue, 2011, pp. 1-9.
- I. F. Akyildiz, W. Su, Y. Sankarasubramaniam and F. Cayirci, “Wireless Sensor Networks: A Survey, Computer Networks,” Computer Networks, Vol. 38, No. 4, 2002, pp. 393-422. doi:10.1016/S1389-1286(01)00302-4
- J. N. AL-Karaki and A. E. Kamal, “Routing Techniques in Wireless Sensor Networks: A Survey,” IEEE Wireless Communications, Vol. 11, No. 6, 2004, pp. 6-28.
- F. L. Lewis, “Wireless Sensor Networks, Smart Environments: Technology, Protocols, and Applications,” In: D. J. Cook and S. K. Das, Eds., Smart Environments: Technologies, Protocols, and Applications, John Wiley, New York, 2004. doi:10.1002/047168659X
- J. Lei, R. Yates and L. Greenstein, “A Generic Model for Optimizing Single-Hop Transmission Policy of Replenishable Sensor,” IEEE Transactions on Wireless Communications, Vol. 8, No. 2, 2009, p. 54.
- J. Wang, Y. Niu, J. Cho and S. Lee, “Analysis of Energy Consumption in Direct Transmission and Multi-Hop Transmission for Wireless Sensor Networks,” 3rd International IEEE Conference on Signal-Image Technologies and Internet-Based System, Shanghai, 16-18 December 2007, pp. 275-280.
- K. Akkaya and M. Younis, “A Survey on Routing Protocols for Wireless Sensor Networks,” Elsevier Computer Networks Journal, Vol. 38, No. 4, 2003, pp. 393-422.
- D. Chen and P. K. Varshney, “QoS Support in Wireless Sensor Networks: A Survey,” Proceedings of 2004 International Conference on Wireless Networks (ICWN 2004), Las Vegas, 21-24 June 2004, pp. 227-233.
- S. Al-Sharaeh, R. Hasan and I. Salah, “An Efficient Routing Technique That Maximizes the Lifetime and Coverage of Wireless Sensor Networks,” 2nd International Conference on Digital Information and Communication Technology and It’s Applications (DICTAP), Bangkok, 16-18 May 2012, pp. 13-18.
- M. Alqbilat, “An Efficient Power Management Heuristic That Minimizes The Power Consumption of Wireless Sensor Networks,” Master Thesis, The University of Jordan Library, Amman, 2010.
- O. Ozdemir, R. Niu, P. K. Varshney, A. L. Drozd and R. Loe, “Feature Aided Probabilistic Data Association Filter for Ballistic Missile Tracking,” Proceedings of the SPIE, Orlando, Vol. 8064, 2011, pp. 806406-806406-11.
- A. Misra and S. Banerjee, “MRPC: Maximizing Network Lifetime for Reliable Routing in Wireless Environments,” Proceedings of the IEEE Wireless Communications and Networking Conference, Orlando, March 2002, pp. 800- 806.
- K. Kar, M. Kodialam, T. V. Lakshma and L. Tassiulas, “Routing for Network Capacity Maximization in EnergyConstrained Ad-Hoc Networks,” IEEE Societies of the 22nd Annual Joint Conference of the IEEE Computer and Communications, San Franciso, 30 March-3 April 2003, pp. 673-681.
- I. Stojmenovic and X. Lin, “Power-Aware Localized Routing in Wireless Networks,” IEEE Transactions on Parallel and Distributed Systems, Vol. 12, No. 11, 2001, pp. 1122- 1133. doi:10.1109/71.969123
- J. Park and S. Sahni, “An Online Heuristic For Maximum Lifetime Routing in Wireless Sensor Networks,” IEEE Transactions on Computer Journal, Vol. 55, No. 8, 2006, pp. 1048-1056. doi:10.1109/TC.2006.116
- S. H. Al-Sharaeh, A. Sharieh, A. Abu Dalhoum, R. Hosny and F. Mohammed, “Multi-Dimensional Poisson Distribution Heuristic for Maximum Lifetime Routing in Wireless Sensor Network,” World Applied Sciences Journal, Vol. 5, No. 2, 2008, pp. 119-131.
- S. H. Al-Sharaeh, A. Sharieh and R. AbuElayyan, “Deployment Strategy Effect on Maximizing the Lifetime of Wireless Sensor Networks,” 24th International Conference on Computers and Their Applications, New Orleans, 8-10 April 2009, pp. 122-129.

