Int'l J. of Communications, Network and System Sciences
Vol. 5 No. 6 (2012) , Article ID: 19656 , 5 pages DOI:10.4236/ijcns.2012.56043
TUP: A New eCK-Secure AKE Protocol under the CDH Assumption
School of Information and Engineering, Zhengzhou University, Zhengzhou, China
Email: ieqlzhou@zzu.edu.cn, hp4880@163.com
Received March 4, 2012; revised April 20, 2012; accepted May 14, 2012
Keywords: Authenticated Key Exchange; Provable Security; eCK Model; Computational Diffie-Hellman Assumption; Trapdoor Test
ABSTRACT
The design and analysis of authenticated key exchange protocol is an important problem in information security area. At present, extended Canetti-Krawczyk (eCK) model provides the strongest definition of security for two party key agreement protocol, however most of the current secure protocols can not be prove to secure without Gap assumption. To avoid this phenomenon, by using twinning key technology we propose a new two party key agreement protocol TUP which is obtained by modifying the UP protocol, then in conjunction with the trapdoor test, we prove strictly that the new protocol is secure in eCK model. Compared with previous protocols, the security assumption of new proposal is more standard and weaker, and it also solves an open problem in ProvSec’09.
1. Introduction
Authenticated key Exchange (AKE) protocol allows two parties to negotiate a session key through the exchange of some information in order to ensure the security of communications. Unlike key distribution protocol, the communicating parties do not need to have a pre-shared secret information and do not require a trusted third-party participation. In addition, the two sides can have the same contribution to generation of new session key. Therefore, the analysis and design of the AKE protocol become one of the important topics in the field of information security.
For the formal analysis of the AKE protocol, Canetti and Krawzcyk proposed a well-known security model denoted by CK model [1] in 2001. Recently, LaMacchia, Lauter and Mityagin Extend the former CK model (eCK [2]) that captures almost all the security properties. As it can reduce the dependence of the certificate authority (CA), relax the assumption on the ability of the attacker, maximize the information the protocol leak, the eCK model provides the strongest definition for two parties key agreement protocol and been widely recognized.
At present most of the key agreement protocols are based on the Diffie-Hellmn protocol which is more efficient and simpler than protocols that are based on digital signature or public key encryption to achieve authentication, such as MQV [3], HMQV [4] and so on. But these protocols are insecure in eCK model. In 2007, with a new ephemeral public key derivation (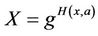 ), LaMacchia, Lauter and Mityagin proposed a new protocol (NAXOS [2]) which is secure in the eCK model under the GDH assumption [5]. In 2008, According to slightly modify the NAXOS+ protocol, Lee and Park proposed NAXOS+ protocol [6] which is secure under the CDH assumption. Besides, in 2009, Ustaoglu proposed CMQV protocol [7] which is obtained from (H) MQV and NAXOS, and proof its eCK security. Then, in 2010, Lijiang Zhang modified the CMQV protocol and introduced CMQV+ [8] which has a tight security reduction.
), LaMacchia, Lauter and Mityagin proposed a new protocol (NAXOS [2]) which is secure in the eCK model under the GDH assumption [5]. In 2008, According to slightly modify the NAXOS+ protocol, Lee and Park proposed NAXOS+ protocol [6] which is secure under the CDH assumption. Besides, in 2009, Ustaoglu proposed CMQV protocol [7] which is obtained from (H) MQV and NAXOS, and proof its eCK security. Then, in 2010, Lijiang Zhang modified the CMQV protocol and introduced CMQV+ [8] which has a tight security reduction.
However, according to recent studies, the NAXOS technique is vulnerable to side channel attacks and disclosure the discrete logarithm of ephemeral public keys. To avoid this attack, Ustaoglu proposed UP protocol [9] with postponed ephemeral key derivation, in which  is seen as ephemeral public key,
is seen as ephemeral public key,  is seen as pseudo static key. At present, almost all the protocol use these two technologies to achieve eCK security. Like (H,C)MQV protocol which used the forking technology [10] to construct its security, In 2011, Jiaxin P and Libin W< proposed TMQV [11] protocol which is secure under the CDH assumption, they also propose UP+ protocol [12] which admits higher security level with the same efficiency.
is seen as pseudo static key. At present, almost all the protocol use these two technologies to achieve eCK security. Like (H,C)MQV protocol which used the forking technology [10] to construct its security, In 2011, Jiaxin P and Libin W< proposed TMQV [11] protocol which is secure under the CDH assumption, they also propose UP+ protocol [12] which admits higher security level with the same efficiency.
In order to remove the GDH assumption with the help of trapdoor test and postponed ephemeral key derivation (this is also an open problem proposed by Ustaoglu in ProvSec’09), we use the twin key technology [13] to extend the UP protocol and to propose TUP protocol. The new proposed protocol also has a tight security reduction. Here we denote long-term private key as , regard
, regard 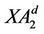 as postponed ephemeral key and
as postponed ephemeral key and  as pseudo static key. Unlike the TMQV protocol, the forking leama is not necessary for the security argument.
as pseudo static key. Unlike the TMQV protocol, the forking leama is not necessary for the security argument.
2. Preliminaries
2.1. Assumption
Let G denote a multiplicative cyclic group of prime order q, generated by . The discrete logarithm function DLOG (U) takes as input an element
. The discrete logarithm function DLOG (U) takes as input an element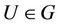 , and returns u such that
, and returns u such that . The computational Diffie-Hellman function CDH (
. The computational Diffie-Hellman function CDH ( ) takes as input a pair or elements
) takes as input a pair or elements , and returns
, and returns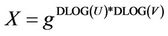 . The CDH problem is defined as follows: Given
. The CDH problem is defined as follows: Given 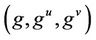 with uniformly random choices of
with uniformly random choices of , and compute CDH
, and compute CDH . We say that G satisfies the CDH assumption if no feasible adversary can solve the CDH problem with non-negligilbe probability.
. We say that G satisfies the CDH assumption if no feasible adversary can solve the CDH problem with non-negligilbe probability.
2.2. Trapdoor Test
Since we need to use trapdoor test [9] to analysis the new protocol TUP, we state it briefly without proof.
Trapdoor test: Let G be a cyclic group or prime order q, generated by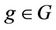 , suppose U1, r, s, Y, Z1, Z2 are independent random variables, where U1, Y, Z1, Z2 takes values in G, and r, s, are uniformly distributed over Zq, compute
, suppose U1, r, s, Y, Z1, Z2 are independent random variables, where U1, Y, Z1, Z2 takes values in G, and r, s, are uniformly distributed over Zq, compute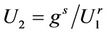 , then we have 1) U2 is uniformly distributed over G2) U1 and U2 are independent3) The probability that the truth value of
, then we have 1) U2 is uniformly distributed over G2) U1 and U2 are independent3) The probability that the truth value of  does not agree with the truth value of
does not agree with the truth value of 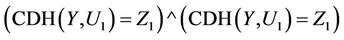 is at most
is at most .
.
2.3. eCK Model
In this section,we recall the eCK model [2] which will be used to analysis the new proposed protocol TUP. In this article, we use 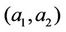
 denote the long term public and private keys, X, x denote ephmeral public and private keys for some party A.
denote the long term public and private keys, X, x denote ephmeral public and private keys for some party A.
Parties. Each participant (denoted as A, B), which is modeled as probabilistic polynomial time (PPT) Turing Maching, can simultaneously execute multiple sessions, the session identifier (sid) involved in the identity of both sides and the information they exchanged. Every honest party has a secure channel to connect with certificate authority (CA) to register their public keys without any checks such as proof of possess corresponding private keys.
Adversary. An adversary M, which is also modeled as PPT turning maching, has full control over communication network between honest parties. In eCK model, we allow M to execute the following oracle queries disorderly and adaptive
1) Send (A, B, comm): Get a response from A on behalf of B, when comm is null, M can active A to execute a session with B.
2) StaticTermKeyReveal (A): Reveal the long_term key of A.
3) EphemeralKeyReveal (sid): Reveal the ephemeral key of session sid.
4) SessionKeyReveal (sid): Reveal the session key of sid which is completed.
5) EstablishParty (A): Register to CA with the public key of honest party A.
6) Test (sid): Pick 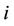 from {0, 1} randomly, if i = 0, set
from {0, 1} randomly, if i = 0, set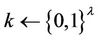 , otherwise set
, otherwise set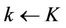 , then return k.
, then return k.
Freshness. The key of session sid can be seen as determined by the set , as long as
, as long as 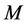 dose not execute the above query to get
dose not execute the above query to get 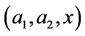 or
or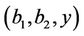 , and M does not execute SessionKeyReveal query on behalf of sid or its matching session
, and M does not execute SessionKeyReveal query on behalf of sid or its matching session , then we said sid is fresh.
, then we said sid is fresh.
eCK security. After execute a test query to a fresh session, M guess a number j, we say an AKE protocol is secure if the value of the following formula is negligible.

3. Proposed AKE Protocol: TUP
In this section, According to modify the UP protocol with twin key technology, we propose a new protocol TUP, and it is secure under the CDH assumption which is more stander than the GDH assumption. Figure 1 depicts the new protocol.
System initialization: Let  be the security parameter and G be a cyclic group of prime order q, H1, H2 are hash functions modeled as random oracles where
be the security parameter and G be a cyclic group of prime order q, H1, H2 are hash functions modeled as random oracles where 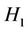 outputs integers that are half the bit-size of q. For each part A, we pick
outputs integers that are half the bit-size of q. For each part A, we pick 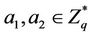 randomly as its long term private key, compute its public key
randomly as its long term private key, compute its public key 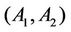 and then register to CA, the party B is simulated in the same way.
and then register to CA, the party B is simulated in the same way.
Running steps: As to avoid the attack of NAXOS protocol, In the information transfer phase, when A receives the activation message, he pick  randomly, compute its ephemeral public key
randomly, compute its ephemeral public key  and then send it to B. After receive the message from A, B do it in the same way.
and then send it to B. After receive the message from A, B do it in the same way.
Session key derivation: to avoid the Cremers attack, we bind session key with the session state. At the end of session, both A and B can compute d, e, σ1, σ2, σ3 and than the session key as described in Figure 1.
Brief analysis: As we can see from the derivation, compare to the UP protocol, the TUP protocol is of the same structure execept extening long-term private key to double the privious bit-size, even ignoring the σ3, it achieves stronger security under the same environment.
In the following section, we will give its strick proof in the eCK model under the CDH assumption. Restricted by space, we simplify some parts which are same as UP protocol.
4. Security Analysis
Theorem 1. If H1 and H2 is modeled as random oracle, and G is a group where the CDP assumption holds, then the TUP is eCK secure AKE protocol.
Actually, let λ denote the denote the security parameter, M be a polynomially bound adversary, if M could attack TUP protocol in time at most t, involves at most n honest parties and activates at most k sessions, then we can construct a solver S which can solve the GDH problem with non-negligible probability. More precisely

Proof: Since the session key of the test session is computed as K = H (σ) = H (σ1, σ2, σ3, A, B, X, Y) for some 7-tuple σ, the adversary M has only two ways to distinct K from random value.
1) Forging attack. At some point M queries random oracle on the same 7-tuple σ.
2) Key-replication attack. M succeeds in forcing the establishment of another session that has the same session key as the test session.
As the ephemeral public key is randomly generated, idel hash function H2 produce no collisions (collisions happen with probability ), M must perform a forging attack to win the test game. Next we show if M can mount a successful forging attack, then we can construct a CDH solver S which uses M as a subroutine through providing M a indistinguishable simulation en-
), M must perform a forging attack to win the test game. Next we show if M can mount a successful forging attack, then we can construct a CDH solver S which uses M as a subroutine through providing M a indistinguishable simulation en-
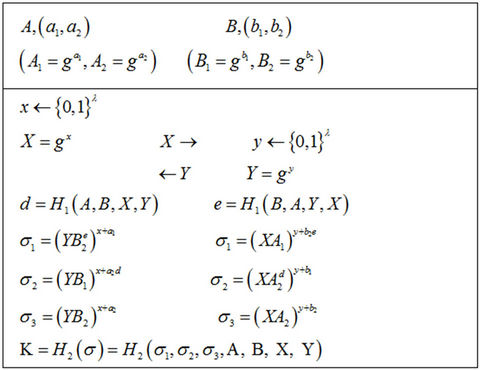
Figure 1. The TUP protocol.
vironment and then solve the CDH problem with nonnegligible probability.
Given a CDH challenge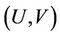 , S randomly picked long-term and ephemeral private key from
, S randomly picked long-term and ephemeral private key from 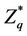 for the n paries which was involved by M and then compute the corresponding public key. Now S can answer all kinds of oracle query from M because he knows all the secret information. Then S randomly select two honest parties A, B and randomly select two sessions (denote as
for the n paries which was involved by M and then compute the corresponding public key. Now S can answer all kinds of oracle query from M because he knows all the secret information. Then S randomly select two honest parties A, B and randomly select two sessions (denote as  and
and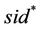 ) executed by them from all the k sessions, S will guess them with probability at least
) executed by them from all the k sessions, S will guess them with probability at least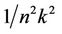 .
.
In the following step, according to the freshness principle, we will consider the following complementary events:
1) There exists session 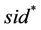 matching to the test session sid and M does not issues EphemeralKeyReveal (
matching to the test session sid and M does not issues EphemeralKeyReveal (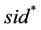 ); and either of the following:
); and either of the following:
a) M does not issues StaticTermKeyReveal (A)—E1a.
b) M does not issues EphemeralKeyReveal (sid)—E1b.
2) M does not issues StaticTermKeyReveal (B), but may issues EphemeralKeyReveal ( ) if
) if  exists; and either of the following:
exists; and either of the following:
a) M does not issues StaticTermKeyReveal (A)—E2a.
b) M does not issues EphemeralKeyReveal (sid)—E2b.
Actually, event E1a consider the case when M does not obtain (a1, a2, y), E1b consider the case when M does not obtain (x, y), E2a consider the case when M does not obtain (a1, a2, b1, b2), E2b consider the case when M does not obtain (x, b1, b2). In any other scenario M will break freshness of the test session. For each of the complementary cases, S randomly chooses  and modifies environment as follows:
and modifies environment as follows:
Event. E1a: S resets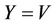

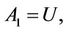 , according to the definition of E1a, M can not distinguish with non-negligilbe probability. For each 7-tuple (σ1, σ2, σ3, A, B, X, Y), M queries to H2, S computes
, according to the definition of E1a, M can not distinguish with non-negligilbe probability. For each 7-tuple (σ1, σ2, σ3, A, B, X, Y), M queries to H2, S computes
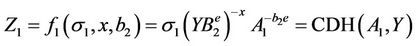

If  then S can answers
then S can answers  According to the trapdoor test, the probability S will fail is
According to the trapdoor test, the probability S will fail is 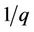 which is negligible.
which is negligible.
Event. E1b: S resets ,
, . For each 7-tuple (σ1, σ2, σ3, A, B, X, Y), M queries to H2, S computes
. For each 7-tuple (σ1, σ2, σ3, A, B, X, Y), M queries to H2, S computes
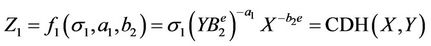

If 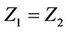 then
then 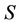 can answers
can answers 
Event. E2a: S resets ,
,  ,
, 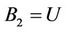 ,
,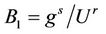 . In the case that the maching session may not exists, as M has the ability to alter or insert messages between honest parties, S may not known DLOG (
. In the case that the maching session may not exists, as M has the ability to alter or insert messages between honest parties, S may not known DLOG ( ). This is the reason that TUP need one more exponentiation (σ3) than UP in the computation of shared secrets. For each 7-tuple σ, M queries to H2, S computes
). This is the reason that TUP need one more exponentiation (σ3) than UP in the computation of shared secrets. For each 7-tuple σ, M queries to H2, S computes
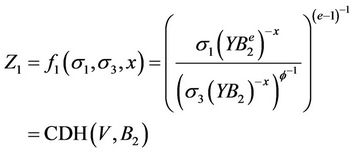
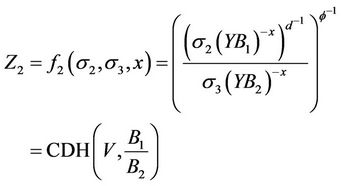
If 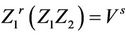 then S can answers
then S can answers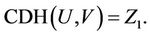
Event. E2b: 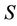 resets
resets ,
,  ,
,  , For each 7-tuple σ, M queries to H2, S computes
, For each 7-tuple σ, M queries to H2, S computes
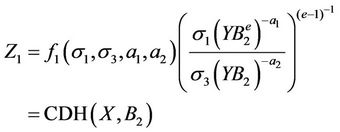
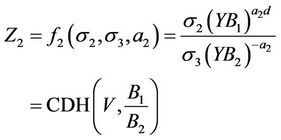
Similarly, If 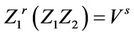 then S can answers
then S can answers 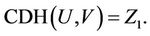
5. Protocols Comparison
In Table 1, we compare the new proposed protocol TUP with other previous typical protocols in some aspects. The comparison mainly focuses on the numbers of exponentiations, security assumption, tightness of security reduction and so on. For every protocol the adversary can obtain either  as in NAXOS or
as in NAXOS or 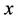 as in HMQV.
as in HMQV.
By contrast, we can see the TUP protocol has the following advantages:
1) In message exchange satage, TUP derives ephemeral key x as in MQV, so it can avoids the side channel attacks.
2) With the use of twin key technology, It can achieves security under the CDH assumption which is more stander and weaker than GDH assumption.
3) Unlike (H,C,T)MQV protocol, we did not use forking technology in security analysis, so the security reduction is more tight.
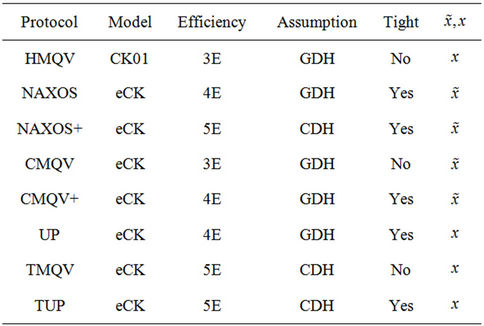
Table 1. Protocols comparison.
Unfortunately, compared with previous protocol, the new proposed protocol has no advantages in efficiency.
6. Conclusion
In this paper, we proposed a new authenticated key exchange protocol TUP which is obtained by using twin key technology in UP protocol and added one more exponentiation in shared secrets computation. The proposed protocol also can solve an open problem in ProvSec’09. However, there is no obvious advantage regarding efficiency. So in improving the security level, to make the AKE protocol more efficient is an important goal for future work.
REFERENCES
- R. Canetti and H. Krawczyk, “Analysis of Key-Exchange Protocols and Their Use for Building Secure Channels,” Lecture Notes in Computer Science, Vol. 2045, 2001, pp. 453-474. doi:10.1007/3-540-44987-6_28
- B. LaMacchia, K. Lauter and A. Mityagin, “Stronger Security of Authenticated Key Exchange,” Lecture Notes in Computer Science, Vol. 4784, 2007, pp. 1-16. doi:10.1007/978-3-540-75670-5_1
- L. Law, A. Menezes, M. Qu, J. Solinas and S. Vanstone, “An Efficient Protocol for Authenticated Key Agreement,” Designs, Codes and Cryptography, Vol. 28, No. 2, 2003, pp. 119-134. doi:10.1023/A:1022595222606
- H. Krawczyk, “HMQV: A High-Performance Secure Diffie-Hellman Protocol,” Lecture Notes in Computer Science, Vol. 3621, 2005, pp. 546-566. doi:10.1007/11535218_33
- T. Okamoto and D. Poincheval, “The Gap-Problems: A New Class of Problems for the Security of Cryptogrphic Schemes,” Lecture Notes in Computer Science, Vol. 1992, 2001, pp. 104-118. doi:10.1007/3-540-44586-2_8
- J. Lee and J. H. Park, “Authenticated Key Exchange Secure under the Computational Diffe-Hellman Assumption,” Cryptology ePrint Archive, Report 2008/344, 2008.
- B. Ustaoglu, “Obtaining a Secure and Efficent Key Agreement Protocol from (H) MQV and NAXOS,” Designs, Codes and Crytography, Vol. 46, No. 3, 2008, pp. 329- 342. doi:10.1007/s10623-007-9159-1
- L. J. Zhang, “A Provably Secure Authenticated Key Exchange Protocol,” IEEE International Conference on Wireless Communications, Networking and Information Security, Beijing, 25-27 June 2010, pp. 292-297.
- B. Ustaoglu, “Comparing SessionStateReveal and EphemeralKeyReveal for Diffe-Hellman Protocol,” Lecture Notes in Computer Science, Vol. 5848, 2009, pp. 183-197. doi:10.1007/978-3-642-04642-1_16
- D. Pointcheval and J. Stern, “Security Arguments for Digital Signatures and Blind Signatures,” Journal of Cryptology, Vol. 13, No. 3, 2000, pp. 361-396. doi:10.1007/s001450010003
- J. X. Pan and L. B. Wang, “TMQV: A Strongly eCKSecure Diffie-Hellman Protocol without Gap Assumption,” Lecture Notes in Computer Science, Vol. 6890, 2011, pp. 380-388. doi:10.1007/978-3-642-24316-5_27
- J. X. Pan, L. B. Wang and C. S. Ma, “Analysis and Improvement of an Authenticated Key Exchange Protocol,” Lecture Notes in Computer Science, Vol. 6672, 2011, pp. 417-431. doi:10.1007/978-3-642-21031-0_31
- D. Cash, E. Kiltz and V. Shoup, “The Twin Diffe-Hellman Problem and Applications,” ” Lecture Notes in Computer Science, Vol. 4965, 2008, pp. 127-145. doi:10.1007/978-3-540-78967-3_8

