Int'l J. of Communications, Network and System Sciences
Vol.3 No.2(2010), Article ID:1266,7 pages DOI:10.4236/ijcns.2010.32019
Selection of Design Parameters for Generalized Sphere Decoding Algorithms
Department of ECE, McGill University, 3480 University, Montréal, Canada
Email: pingwang.mcgill@gmail.com, tho.le-ngoc@mcgill.ca
Received November 11, 2009; revised December 15, 2009; accepted January 7, 2010
Keywords: Sphere Decoding (SD), Generalized Sphere Decoding (GSD), Maximum-likelihood (ML), Integer Least-Square (ILS), MIMO, λ-GSD, Multi-User Detection (MUD), CDMA, MC-CDMA
Abstract
Various efficient generalized sphere decoding (GSD) algorithms have been proposed to approach optimal ML performance for underdetermined linear systems, by transforming the original problem into the full-column-rank one so that standard SD can be fully applied. However, their design parameters are heuristically set based on observation or the possibility of an ill-conditioned transformed matrix can affect their searching efficiency. This paper presents a better transformation to alleviate the ill-conditioned structure and provides a systematic approach to select design parameters for various GSD algorithms in order to high efficiency. Simulation results on the searching performance confirm that the proposed techniques can provide significant improvement.
1. Introduction
Sphere decoding (SD) is an efficient searching method to obtain maximum-likelihood (ML) solution for NP-hard integer least-square (ILS) problems. SD can have polynomial time average complexity for many practical communication problems [1]. It offers large complexity reduction over the exhaustive search method in numerous applications, e.g., lattice decoding [2], multi-input, multi-output (MIMO) detection [3] and multi-user detection (MUD) [4]. However, when the problem is underdetermined, zero elements appear in the diagonal terms of the upper-triangular matrix generated by QR or Cholesky decomposition before searching, and the standard SD searching cannot apply. Such underdetermined ILS problems arise in many areas, e.g., MIMO detection with the number of transmit antennas larger than that of receiver antennas; MIMO detection with strongly correlated channel gains [5] or MUD for overloaded CDMArelated systems [8]. To solve such problems efficiently, generalized SD (GSD) algorithms, fully or partly based on SD, have been developed [6–12] for underdetermined or rank-deficient MIMO systems.
The GSD algorithms in [6,7] modify the underdetermined problem for constant-modulus constellation (e.g., QPSK) into a full-column-rank one by introducing a design parameter purely based on observations and then uses SD on the modified problem. For non-constantmodulus ones, e.g., 16/64QAM, they have to be transformed into multiple QPSKs, leading to larger dimension and hence increased complexity. To avoid this problem and obtain better efficiency, the λ-GSD algorithm proposed in [8], performs transformation without expanding the size of M-ary QAMs. Unlike the GSD algorithms in [6,7], the design parameter can be is upper-bounded [8,13] to guarantee near-ML performance for high QAMs and has little effect on the efficiency of λ-GSD [14].
In this paper, we first present an improved version of the λ-GSD algorithm to alleviate the ill-conditioned problem in the transformed matrix of [8]. Then we study the setting of the design parameter for the improved version of λ-GSD, as well as GSD in [6,7]. A more systematic approach is proposed to select design parameters for the above GSD algorithms to achieve high efficiency.
The remainder of the paper is as follows. Section 2 summarizes transformations employed in several popular GSD algorithms. Section 3 presents the improved version of λ-GSD over [8] and briefly discusses its performance characteristics; then we proceed to propose a systematic approach to choose the design parameter for it and also for that of [6,7] in Section 4. Section 5 provides illustrative results under flat-fading underdetermined MIMO scenarios. Section 6 concludes the paper.
2. Transformations by G SD Algorithms
The objective of ILS problem is to find the least-square (LS) solution for a linear system with integer unknowns. When the transmitted vectors (the unknowns) are from a finite set A in communications, i.e.,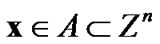 , where
, where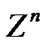 denotes the n-dim vector space with integer entries, the objective function is
denotes the n-dim vector space with integer entries, the objective function is

 , for
, for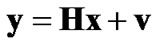 , (1)
, (1)
where 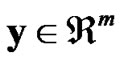 is a
is a 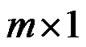 vector for a real-valued system1,
vector for a real-valued system1, 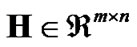 the system matrix typically with full column rank (i.e., rank(
the system matrix typically with full column rank (i.e., rank( )=n) and
)=n) and  a
a  zero-mean Gaussian noise vector,
zero-mean Gaussian noise vector,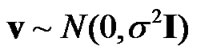 . It’s well known that SD algorithm and its variants are efficient approaches to solve such problems: it reduces the complexity of exhaustive-search greatly by conducting search within a hyper-sphere but still guarantees the ML optimality. One advantage of SD algorithms is that the search can be divided into layered enumeration of integer values in one-dimensional interval, so that it can efficiently decide which points are inside the hyper-sphere. However, SD algorithm was originally designed for full-column-rank system only. For underdetermined ILS problem when
. It’s well known that SD algorithm and its variants are efficient approaches to solve such problems: it reduces the complexity of exhaustive-search greatly by conducting search within a hyper-sphere but still guarantees the ML optimality. One advantage of SD algorithms is that the search can be divided into layered enumeration of integer values in one-dimensional interval, so that it can efficiently decide which points are inside the hyper-sphere. However, SD algorithm was originally designed for full-column-rank system only. For underdetermined ILS problem when  has rank (
has rank ( ) =m,
) =m,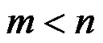 in (1), the original SD algorithms can not proceed efficiently, as on certain searching layers, the candidate point set is no longer in a 1D-interval. [6–8] introduce transformations for underdetermined problem so that SD can be utilized on the transformed full-column-rank system. The transformations used are as follows.
in (1), the original SD algorithms can not proceed efficiently, as on certain searching layers, the candidate point set is no longer in a 1D-interval. [6–8] introduce transformations for underdetermined problem so that SD can be utilized on the transformed full-column-rank system. The transformations used are as follows.
The original underdetermined problem for constantmodulus constellation (e.g., QPSK) was modified into a full-column-rank system [6] and the equivalent new objective function is
 , (2)
, (2)
where  is a design parameter. (2) is equivalent to
is a design parameter. (2) is equivalent to
 , (3)
, (3)
where 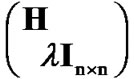 in (3) is full-column-ranked with
in (3) is full-column-ranked with . If
. If  is from constant-modulus constellations,
is from constant-modulus constellations,  is constant and (3) is the same as(1); and when applying SD on the new problem (3), ML performance can still be achieved. For high QAMs, in order to guarantee ML performance, high QAMs are transformed into multiple QPSKs in [6] before using the above transformation, e.g., 16QAM vector
is constant and (3) is the same as(1); and when applying SD on the new problem (3), ML performance can still be achieved. For high QAMs, in order to guarantee ML performance, high QAMs are transformed into multiple QPSKs in [6] before using the above transformation, e.g., 16QAM vector  can be represented as
can be represented as  where
where 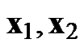 are from QPSK. The 16QAM system is transformed into a QPSK one with
are from QPSK. The 16QAM system is transformed into a QPSK one with
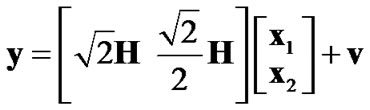 . (4)
. (4)
Hence the transformation in (3) can be used on (4) and SD can then be applied efficiently. Despite the fact that the complexity of the GSD algorithm in [6] depends on λ, the parameter is set arbitrarily in [6].
The transformation of high QAMs into multiple QPSK ones in [6] unavoidably lead to larger problem size for the ILS problem and increased search complexity. To avoid this problem, another transformation is utilized in [8] for both the constant-modulus and non-constant modulus constellations, i.e.,
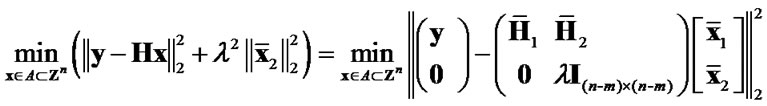 (5)
(5)
where  is subset of
is subset of 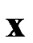 =[
=[ ] with length (n-m). SD searching is applied on (5) directly for both QPSK and high QAMs. Consequently, exact ML performance can be achieved for QPSK constellation with arbitrary value of λ whist close-to-ML performance can be achieved with sufficient small λ [8]. Moreover, an upper bound is provided in [8] for λ in high QAMs to approach ML performance with negligible loss and it’s also shown that the efficiency is quite insensitive to λ [14] for λ-GSD, unlike GSD in [6]. Therefore, the choice of λ can be randomly set for QPSK and judiciously set to be within the upper bound for high QAMs.
] with length (n-m). SD searching is applied on (5) directly for both QPSK and high QAMs. Consequently, exact ML performance can be achieved for QPSK constellation with arbitrary value of λ whist close-to-ML performance can be achieved with sufficient small λ [8]. Moreover, an upper bound is provided in [8] for λ in high QAMs to approach ML performance with negligible loss and it’s also shown that the efficiency is quite insensitive to λ [14] for λ-GSD, unlike GSD in [6]. Therefore, the choice of λ can be randomly set for QPSK and judiciously set to be within the upper bound for high QAMs.
Later in [7], by noticing the structure of the transformation in (5) is less efficient2 and also targeting to alleviate the size expansion problem in [6,7] considers to utilize a transformation of adding the  part of
part of 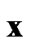 =[
=[ ] with length (n-m+1) instead of (n-m), and then apply SD to achieve ML performance for constant-modulus constellations. The resulted new ILS problem is
] with length (n-m+1) instead of (n-m), and then apply SD to achieve ML performance for constant-modulus constellations. The resulted new ILS problem is

 (6)
(6)
For non-constant-modulus constellations, [7] adopts the same strategy as [6], i.e., to transform high QAMs into multiple QPSKs in order to achieve exact-ML performance in a similar way as [6,7] also suggests a value

Figure 1. Histogram of condition number distribution of MIMO system matrices over 104 runs @12dB, QPSK. (a) 12x12 real matrices of regular i.i.d. 6x6 complex-valued matrices; (b) transformed 12x12 real matrices of λ-GSD at λ=10-3; (c)transformed 14x12 real matrices of improved λ-GSD at λ=10-3.
of λ purely based on experimental observations though apparently the efficiency depends on λ.
3. Improved Transformation Structure to Speed up λ-GSD Algorithm
For a negligible performance loss, λ-GSD keeps the problem size intact for high QAMs as mentioned, and hence it is more efficient than [6,7] for high QAMs. However, despite of the high efficiency of λ-GSD compared to its counterparts, the efficiency of λ-GSD is still significantly higher than SD on regular full-column-rank system. Ill-conditioned structure of the transformed matrix of λ-GSD partly accounts for the inefficiency. It is known that well-conditioned matrix generally leads to more efficient searching than ill-conditioned ones [16]. Figure 1 illustrates histograms for the occurrence of the condition number of the three categories of matrices over 104 runs for a QPSK MIMO system at 12dB, where (a) is for the 12x12 real-valued matrices of the i.i.d. regular 6x6 complex-valued system with full-column-rank; (b) is for the transformed 12x12 real matrices of λ-GSD in a 4x6 complex-valued system. (c) is for an improved version of λ-GSD to be proposed in this section. Comparing Figure 1(a) and (b), we can see that over 104 runs, the condition number of transformed matrices of λ-GSD is centered at around 8x103 whilst that of the regular full-column-rank ones is only centered at around 10. Next we will propose an improved version of λ-GSD, which combines the transformation in [7] and the idea of keeping problem size intact of λ-GSD. The modified version of λ-GSD to alleviate the ill-conditioned problem can be presented as follows.
Consider a real-valued underdetermined system 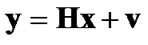 in (1) where 2< rank(
in (1) where 2< rank( )=m< n. Partition
)=m< n. Partition  where
where 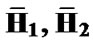 are
are  and
and  matrices respectively, instead of
matrices respectively, instead of 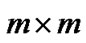 and
and 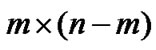 in the original λ-GSD (5). Then partition
in the original λ-GSD (5). Then partition  so that
so that 

 . Adding an equation
. Adding an equation 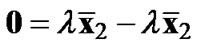 where 0 is a zero-vector with length (n-m+2) and
where 0 is a zero-vector with length (n-m+2) and >0 is a weighting factor, the transformed new ILS problem becomes,
>0 is a weighting factor, the transformed new ILS problem becomes,
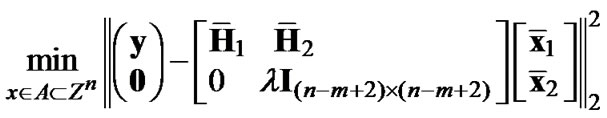

(7)
Again, SD algorithms then can be used on (7) to solve the transformed full-column-rank ILS problem. Note that the transformation in (7) appears very analogous3 to that used in [2], i.e., (6), yet they are distinct for the case of high QAMs: the improved version of λ-GSD keeps the problem size intact for high QAMs and hence SD algorithm is directly applied on (7) without further transformation. Performance of the modified approach can be analyzed following the analysis for λ-GSD in [13], and the conclusions are similar. Specifically, for constant-modulus modulations, the modified GSD can achieve exact ML performance and for high QAMs, the choice of λ has to be sufficiently small to keep the performance close to optimal. Here we omit the detailed upper bound analysis for simplicity and only provide the conclusions for a 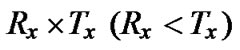 complex linear system using uncoded square M-QAM with average symbol energy Es: Approximately, assuming ε denotes the difference in the upper bound error probability between λ-GSD and ML performance, the upper bound for λ is
complex linear system using uncoded square M-QAM with average symbol energy Es: Approximately, assuming ε denotes the difference in the upper bound error probability between λ-GSD and ML performance, the upper bound for λ is .
.
Compared to original λ-GSD, we expect the improved version is more efficient as it has better transformed matrix structure, which can be seen from the illustrative histogram of condition number in Figure 1(c) for the transformed 14x12 real-valued matrices in the improved version of λ-GSD over 104 runs for a QPSK MIMO system. We can see that the condition number in this example is centered at around 6x103. Compared to 8x103 in Figure 1(b), the ill-conditioned situation gets alleviated. The complexity efficiency of the improved version of λ-GSD will be illustrated in Section 5 via simulations.
4. Selection of Design Parameters for the GSD Algorithms
It was mentioned in [6,7] that there may exist an optimal value for the design parameter in their GSD algorithms. It is very hard, if not impossible, to derive a closed-form expression for the optimal value in a strict sense. In this section, alternatively, we propose one criterion to choose design parameters for these GSD algorithms, which enables the underlying algorithms with high efficiency. The proposed criterion also works for the improved version of λ-GSD algorithm in QPSK systems, since the underlying transformation shares similarity with that for GSD in [7]. Therefore, we mainly derive the design parameter for the improved version of λ-GSD in QPSK systems for simplicity, which can be applied to GSD in [7] as well. Note that for high QAMs, the selection of the design parameter for the improved version of λ-GSD is limited by the upper bound as mentioned in previous session.
For SD searching, if the first point found is closer to ML point, the search tends to be faster [15]. For the improved version of λ-GSD and GSD in [6,7], the first point obtained in search is different for various values of λ. Let us consider the transformation (5) of GSD [6] first. Since the first point using Shnorr-Euchner enumeration4 is the midpoint, hence, the elements of the first point can be written as [15]
 (8)
(8)
where 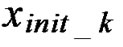 is the ZF-DFE point [15] for the transformed ILS problem;
is the ZF-DFE point [15] for the transformed ILS problem;  where(
where(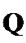 ,
,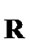 ) are the resulted matrices after QR decomposition of the transformed matrix;
) are the resulted matrices after QR decomposition of the transformed matrix; 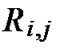 is the (i,j)-th element of
is the (i,j)-th element of  and
and 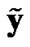 is the equivalent received vector for the transformed ILS problem. Then at k=n, based on (5), we have
is the equivalent received vector for the transformed ILS problem. Then at k=n, based on (5), we have


(9)
Clearly,  depends on λ. From (8) and (9), we
depends on λ. From (8) and (9), we

Figure 2. Avg. searching FLOPS vs. λ @ 2x4 MIMO, 16QAM, 28dB, 104 runs.
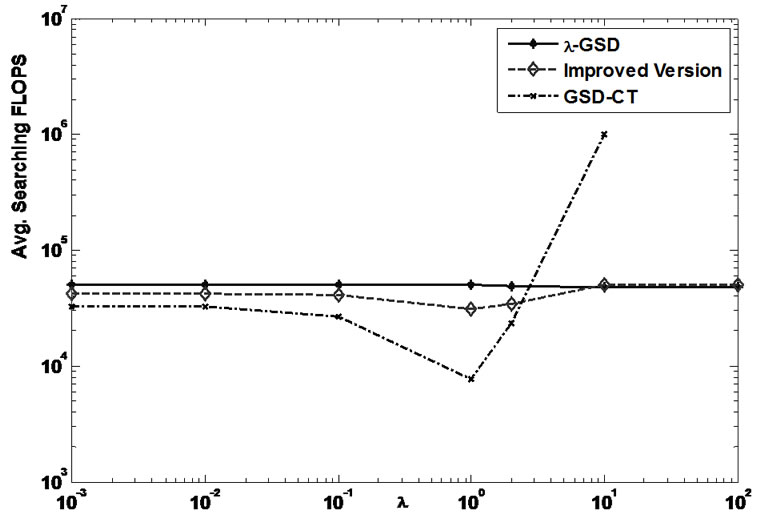
Figure 3. Avg. searching FLOPS vs. λ @ 4x8 MIMO, QPSK, 12dB, 104 runs.
know that when λ is 0, the first element of (9),  , is the first element of ZF-DFE point of the original ILS, i.e,
, is the first element of ZF-DFE point of the original ILS, i.e, ; Thus, the first point,
; Thus, the first point,  , is its ZF-DFE point. On the other hand, when λ is equal to
, is its ZF-DFE point. On the other hand, when λ is equal to , where
, where  represents the SNR ratio, (9) becomes
represents the SNR ratio, (9) becomes 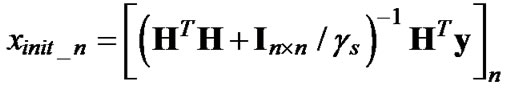 which is the first element of MMSE-DFE point for the original ILS, i.e,
which is the first element of MMSE-DFE point for the original ILS, i.e,  and
and 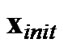 is the MMSEDFE point. It’s known that MMSE detector is the best linear estimator to the ILS problem based on meansquare error criterion and MMSE-DFE is generally closer to the optimal ML point than ZF-DFE; Using MMSE-DFE point as the first point in the searching procedure could lead to a fast convergence [15]. Therefore, to achieve high efficiency, we suggest using
is the MMSEDFE point. It’s known that MMSE detector is the best linear estimator to the ILS problem based on meansquare error criterion and MMSE-DFE is generally closer to the optimal ML point than ZF-DFE; Using MMSE-DFE point as the first point in the searching procedure could lead to a fast convergence [15]. Therefore, to achieve high efficiency, we suggest using  in GSD [6], so that the first valid point is the MMSEDFE point of the original ILS.
in GSD [6], so that the first valid point is the MMSEDFE point of the original ILS.
Next, we continue to derive the suggested value of λ for the improved version of λ-GSD for QPSK system as follows. From (8), we obtain  in the improved version of λ-GSD:
in the improved version of λ-GSD:

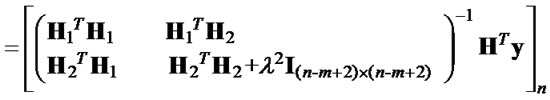
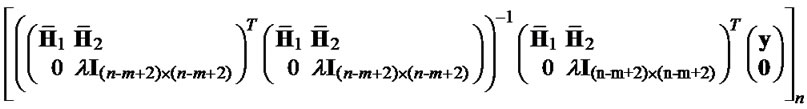
(10)
Comparing with the first element of MMSE-DFE point,


(11)
We would like to choose λ such that (10) and (11)are as similar as possible. Thus, we propose to choose λ such that the two following matrices,  in (10) and
in (10) and  in(11) are as similar as possible. One way to measure the similarity between the two matrices is the norm of the difference. Here we use Frobenius norm to measure the difference and choose λ to minimize
in(11) are as similar as possible. One way to measure the similarity between the two matrices is the norm of the difference. Here we use Frobenius norm to measure the difference and choose λ to minimize , i.e.,
, i.e.,

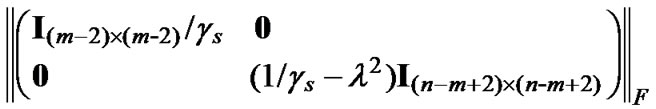

(12)
Clearly, when ,
,  achieves the minimum, zero.
achieves the minimum, zero.
5. Illustrative Results
This section illustrates the merits of the improved ver-

Figure 4. Avg. searching FLOPS vs. λ @ 4x8 MIMO, QPSK, 12dB, 104 runs.

Figure 5. Avg. searching FLOPS vs. λ @ 4x8 MIMO, QPSK, 12dB, 104 runs.
sion of λ-GSD and verify the efficiency of the selection of design parameter for the improved version of λ-GSD and GSD [6] via simulation in a flat fading underdetermined MIMO channel with n transmit and m receive antennas (m< n ). In simulations, we use the “accelerated” standard SD algorithm in [17] as the sub-algorithm for GSDs. The received signal can be represented as , where
, where  is the transmitted vector from M-QAM and
is the transmitted vector from M-QAM and  is an
is an  AWGN noise vector with variance
AWGN noise vector with variance .
.  is an underdetermined
is an underdetermined  matrix where
matrix where  follows Rayleigh fading model
follows Rayleigh fading model . We define
. We define 
 , where Es is the average M-ary QAM symbol energy. Note that the complex model would be transformed into an equivalent real model with 2n unknowns (from
, where Es is the average M-ary QAM symbol energy. Note that the complex model would be transformed into an equivalent real model with 2n unknowns (from  -PAM equivalently) before using
-PAM equivalently) before using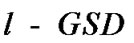 . The average searching FLOPS are counted as complexity measurement for simulation comparison for the GSDs.
. The average searching FLOPS are counted as complexity measurement for simulation comparison for the GSDs.
Figure 2 provides the average searching FLOPS comparison between the original λ-GSD and the improved version for various λ values under a 2x4 16QAM flat-fading MIMO scenario at 28dB. Note that the upper bound for λ in these two GSD algorithms with ε=1% is 0.0167 and 0.0149 respectively. We can see that the complexity is reduced by about 5% with the better structure. Besides, Figure 2 indicates that in the improved version of λ-GSD for 16QAM, the complexity is quite insensitive to the choice of the design parameter λ as long as the value of λ is within the upper bound, similar to the case of the original λ-GSD.
Figure 3 plots the complexity comparison of three GSD algorithms for 4x8 QPSK flat-fading MIMO scenarios at SNR=12dB, including the original λ-GSD, the improved version and GSD in [6] (i.e., GSD-CT). Figure 3 shows the average searching FLOPS w.r.t. various values for the design parameter in all the three GSD algorithms for QPSK system. We can see that the complexity of the original λ-GSD is insensitive to the choice of the design parameter; yet the other two GSD algorithms are more sensitive to the design parameter and apparently there is an optimal value for the lowest complexity as expected.
Thus, we calculate the λ =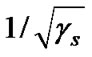 value for a 4x8 MIMO QPSK system at 12dB and the resulted value for λ is λ0=0.710468. Then we simulate the complexity for different λ values in the range (0.1, 2) in Figure 4, which indicates that the lowest complexity is achieved approximately at λ0=0.710468, i.e., choosing λ equal to λ0 can lead to very good efficiency. Correspondingly, we calculate the
value for a 4x8 MIMO QPSK system at 12dB and the resulted value for λ is λ0=0.710468. Then we simulate the complexity for different λ values in the range (0.1, 2) in Figure 4, which indicates that the lowest complexity is achieved approximately at λ0=0.710468, i.e., choosing λ equal to λ0 can lead to very good efficiency. Correspondingly, we calculate the 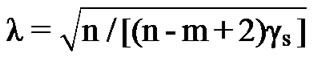 value of the improved version of λ-GSD for the same 4x8 MIMO QPSK system at 12dB and the resulted value for λ is λ0= 0.8987. Then we simulate its corresponding complexity for different λ value in the range of (0.1, 2). Figure 5 indicates that the lowest complexity is achieved for λ around λ0, i.e., choosing λ equal to the suggested value of λ0= 0.8987 also can lead to very good efficiency for the improved version of λ-GSD.
value of the improved version of λ-GSD for the same 4x8 MIMO QPSK system at 12dB and the resulted value for λ is λ0= 0.8987. Then we simulate its corresponding complexity for different λ value in the range of (0.1, 2). Figure 5 indicates that the lowest complexity is achieved for λ around λ0, i.e., choosing λ equal to the suggested value of λ0= 0.8987 also can lead to very good efficiency for the improved version of λ-GSD.
6. Conclusions
An improved version of λ-GSD algorithm was first proposed for underdetermined linear systems by transforming the original problem into a full-column-rank one with better structure, so that standard SD can be efficiently applied. As the introduced transformation maintains the original problem dimension and has better system structure than the original one, lower complexity can be obtained compared to its counterparts, especially for high QAMs. Selection of design parameter  was then studied for the improved version of λ-GSD. The resulted systematic approach to select the design parameter can also be used for GSD in [6], [7] in which the design parameters were only selected randomly or based on observations. Simulation results confirmed the high efficiency achieved by such choices of design parameters for these GSDs.
was then studied for the improved version of λ-GSD. The resulted systematic approach to select the design parameter can also be used for GSD in [6], [7] in which the design parameters were only selected randomly or based on observations. Simulation results confirmed the high efficiency achieved by such choices of design parameters for these GSDs.
7. References
[1] E. Agrell, T. Eriksson, A. Vardy, and K.Zeger, “Closest point search in lattices,” IEEE Transactions Information Theory, pp. 2201–2214, August 2002.
[2] O. Damen, A. Chkeif. and J. C. Belfiore, “Lattice code decoder for space-time codes,” IEEE Communication Letters, pp. 161–163, May 2000.
[3] H. Vikalo, B. Hassibi, and T. Kailath, “Iterative decoding for MIMO channels via modified sphere decoding,” IEEE Transactions on Wireless Communication, Vol. 3, No. 6, pp. 2299–2311, November 2004.
[4] L. Brunel, “Multiuser detection techniques using maximum likelihood sphere decoding in multicarrier CDMA systems,” IEEE Tranactions on Wireless Communication, Vol. 3, No. 3, pp. 949–957, May 2004.
[5] T. Cui and C. Tellambura, “An efficient generalized sphere decoder for rank-deficient MIMO systems,” IEEE VTC. Fall, 2004.
[6] T. Cui and C. Tellambura, “An efficient generalized sphere decoder for rank-deficient MIMO systems,” IEEE Communication Letters, Vol. 9, No. 5, pp. 423–425, May 2005.
[7] X. Chang and X. Yang, “An efficient regularization approach for underdetermined MIMO system decoding”, IWCMC, Hawaii, USA, August, 2007.
[8] P. Wang and T. Le-Ngoc, “An efficient multi-user detection scheme for overloaded group-orthogonal MCCDMA systems,” IET Communications, Vol. 2, No. 2, pp.346–352, February 2008.
[9] M. Damen, K. A. Meraim, and J. C. Belfiore, “Generalised sphere decoder for asymmetrical space-time communication architecture,” Electronics Letters, Vol. 36, No. 2, pp. 166–167, January 2000.
[10] P. Dayal and M. K. Varanasi, “A fast generalized sphere decoder for optimum decoding of under-determined MIMO systems,” 41st Annual Allerton Conference on Communication Control and Computer, October 2003.
[11] Z. Yang, C. Liu, and J. He, “A new approach for fast generalized sphere decoding in MIMO systems,” IEEE Signal Processing Letters, Vol. 12, No. 1, pp. 41–44, January 2005.
[12] X. W. Chang and X. H. Yang, “A new fast generalized sphere decoding algorithm for underdetermined sphere decoding algorithm for underdetermined MIMO systems,” 23rd Biennial symposium on Communications, Kingston, ON, Canada, pp. 18–21, June 2006.
[13] P. Wang and T. Le-Ngoc, “A low complexity generalized sphere decoding approach for underdetermined linear communication systems: performance and complexity evaluation,” IEEE Transactions on Communications, Vol. 57, No. 11, pp. 3376–3388, November 2009.
[14] P. Wang and T. Le-Ngoc, “On the expected complexity analysis of a generalized sphere decoding algorithm for underdetermined linear communication systems,” IEEE International Conference Communication (ICC), Glasgow, June 2007.
[15] M. O. Damen, H. E. Gamal, and G. Caire, “On maximum-likelihood detection and the search for the closest lattice point,” IEEE Transactions on Information Theory, Vol. 49, No. 10, pp. 2389–2402, October 2003.
[16] H. Artes, D. Seethaler, and F. Hlawatsch, “Efficient detection algorithms for MIMO channels: a geometrical approach to approximate ML detection,” IEEE Transactions on Signal Processing. Vol. 51, No. 11, pp. 2808–2820, November 2003.
[17] J. Boutros, N. Gresset, L. Brunel, and M. Fossorier, “Soft-input soft-output lattice sphere decoder for linear channels,” IEEE Globecom 2003, pp. 1583–1587, 2003.
NOTES
1For complex-valued communication systems, linear transformations are generally used to obtain real-valued ones and apply SD.
2to be discussed in Section 3.
3The only difference in transformation is the length of (n-m+2) in 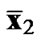 is used in improved version of λ-GSD, instead of (n-m+1) in [7]. Using (n-m+2) in real-valued ILS problem is actually equivalent to using ((n-m)/2+1) in corresponding complex-valued problem; i.e,, “+1” is assumed to operate in complex-valued domain, whilst [7] applies “+1” directly on real-valued domain.
is used in improved version of λ-GSD, instead of (n-m+1) in [7]. Using (n-m+2) in real-valued ILS problem is actually equivalent to using ((n-m)/2+1) in corresponding complex-valued problem; i.e,, “+1” is assumed to operate in complex-valued domain, whilst [7] applies “+1” directly on real-valued domain.
4Shnorr-Euchner enumeration refers to the ordering of the integer points in each layer in a zig-zag manner, which is more efficient than natural ordering and recommended to be used for SD searching recently.

