Int'l J. of Communications, Network and System Sciences
Vol.3 No.1(2010), Article ID:1171,5 pages DOI:10.4236/ijcns.2010.31004
A Maximum Likelihood TOA Based Estimator for Localization in Heterogeneous Networks
University of Rennes 1, IETR Labs, Rennes, France
E-mail: Mohamed.laaraiedh@univ-rennes1.fr
Received October 10, 2009; revised November 14, 2009; accepted December 23, 2009
Keywords: Localization, TOA, Ranging, Weighted least square, Maximum Likelihood, Hybrid Data Fusion, UWB, WLAN, Cramer Rao Lower Bound
Abstract
In this paper, we exploit the concept of data fusion in hybrid localization systems by combining different TOA (Time of Arrival) observables coming from different RATs (Radio Access Technology) and characterized by different precisions in order to enhance the positioning accuracy. A new Maximum Likelihood estimator is developed to fuse different measured ranges with different variances. In order to evaluate this estimator, Monte Carlo simulations are carried out in a generic environment and Cramer Rao Lower Bounds (CRLB) are investigated. This algorithm shows enhanced positioning accuracy at reasonable noise levels comparing to the typical Weighted Least Square estimator. The CRLB reveals that the choice of the number, and the configuration of Anchor nodes, and the type of RAT may enhance positioning accuracy.
1. Introduction
The integration of heterogeneous technologies (2G, 3G, WLAN, UWB, etc.) is the key idea that springs from the B3G vision. Next generations of telecommunication networks will give the mobile user the capability to be connected to the network every time and everywhere. This objective supposes that the mobile station (MS) should be able to support different kinds of Radio Access Technologies (RAT). In this heterogeneous web of networks, the location information may be of interest to enhance the performances of the network and to give new valuable services to the user.
In such heterogeneous networks, the problem of the lack of necessary data for positioning is reduced. In fact, in 2D scenarios, at least 3 observables are necessary to get position using Least Square approximation [1]. These observables can be Time of Arrival (ToA), Time Difference of Arrival (TDOA), or Received Signal Strength (RSS). In a single RAT based network, this amount of observables may not be available in all cases. Thus, the use of heterogeneous observables coming from different RATs is a good alternative to estimate position. Nevertheless, the fusion of these heterogeneous observables (called Hybrid Data Fusion) should be done smartly since the nature and the precision of these observables are quite different.
As the Ultra Wide Band (UWB) technology is more and more used nowadays and the Wireless LAN (WLAN) networks are implemented world wide, TOA observables can be easily obtained via ranging techniques. Proposed ranging techniques are able to achieve good precision on TOA estimation especially in Impulse Radio UWB technology (IR-UWB) [2–5]. Thus, in this paper a new Maximum Likelihood (ML) estimator is developed in order to estimate the position using hybrid TOAs with different precisions. This proposed estimator shows better performances than typical Weighted Least Square (WLS) estimator usually used in previous works [1]. Moreover, based on the mathematical formulation of this estimator, the Cramer Rao Lower Bound (CRLB) of TOA-based estimation of position is reviewed and new formulation is given and investigated.
The rest of the paper is organized as follow. A short review about TOA ranging techniques is presented in Section 2. The new proposed TOA based estimator of position is developed in Section 3. The formulation of the Cramer Rao Lower Bound is investigated in Section 4. The performances of the proposed estimator are shown in Section 5. Finally, our concluding remarks are given in Section 6.
2. TOA Based Ranging Techniques
ToA-based ranging techniques are usually based on the estimate of the distance between transmitter and receiver from the TOA under the radio Line of Sight (LOS) assumption. To obtain this distance, several techniques are proposed such as One Way Ranging (OWR) and Two Way Ranging (TWR). In [6], Power Delay Profile (PDF) is also used in order to estimate TOA in Line of Sight (LoS) conditions. Nevertheless, TOA ranging is affected by relative clock drift between link sides, clock accuracy, the path loss, and radio propagation phenomena such as shadowing, multipath and Non LoS propagation conditions [3].
In WLAN networks, many previous works define TOA based ranging techniques. In [4] and [7], authors define and implement a TOA-based ranging technique over IEEE 802.11 networks. This approach is based on Round Trip Time (RTT) measurements using standard IEEE 802.11 link layer frames and a statistical post-processing to mitigate the noise of the measurements. In [5], another method, also based on RTT, estimates TOA between WLAN nodes without using extra hardware.
3. The Proposed New TOA Based Location Estimator
The proposed localization scenario is defined by a set of wireless nodes and one targeted MS to be positioned. The K wireless nodes (ANk)k=1..K are assumed to be either indoor access points (AP) or cellular Base Stations (BS) with known positions. The targeted MS for which the position estimation will be performed is assumed to be connected to all K nodes. We consider the problem of estimating the unknown position x of the MS, exploiting the ranges obtained through TOA-based ranging techniques thanks to a set of K anchor nodes xk. The output of ranging procedures is a set of ranges with their associated variances. We distinguish the following notations:
• true distance: dk = |x - xk|
• Gaussian distributed estimated range centered on dk: rk ~ N (dk,σrk2)
• variance of estimated range: σrk2
The ranges rk are supposed to be independent. If the true positions (x1,…,xK) of anchor nodes are perfectly known, we have the classical result that ML estimator is equivalent to the following minimization problem:
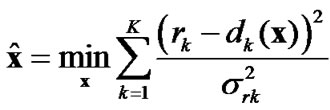 (1)
(1)
Let F be:
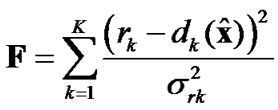 (2)
(2)
It can be readily shown that the ML estimator follows then the following implicit relation:
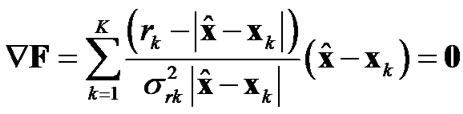 (3)
(3)
where is the gradient of F.
is the gradient of F.
In [8], the author presents a semi-definite programming approach to resolve this minimization problem. In this paper, an iterative approach based on the downhill simplex algorithm is used. The ML estimate is then obtained via this classical iterative optimization algorithm giving an initial guess which can be taken randomly or equal to the WLS solution.
is then obtained via this classical iterative optimization algorithm giving an initial guess which can be taken randomly or equal to the WLS solution.
4. Cramer Rao Bound of the Proposed Estimator
In this section, the mathematical formulation of the Cramer Rao Bound is presented. To proceed, let J(x) defines the Fisher Information Matrix (FIM) for x. J(x) is defined by:
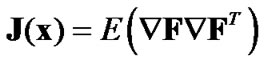 (4)
(4)
where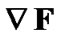 is given by the Equation (3).
is given by the Equation (3).
Thus, assuming independence between the estimated ranges, J(x) becomes:
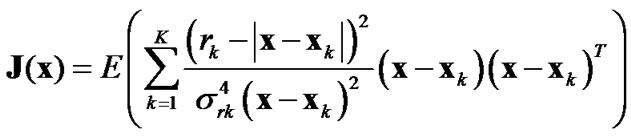 (5)
(5)
 (6)
(6)
The CRLB of x is defined by cov(x) ≥ J(x)-1. Hence, the CRLB on the variance of the TOA based location estimation is:
 (7)
(7)
Developing (7) leads to this expression of the CRLB:
 (8)
(8)
This expression reveals that the CRLB depends on at least three factors:
• The number (K) of measured TOA observables.
• The precision of these ranges given by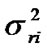 .
.
• The configuration of the anchor nodes involved in the localization process.
5. Simulation Results and Discussions
In this section, we evaluate the performances of the proposed TOA based estimator described in Section 3 through Monte Carlo simulations. Two criteria are chosen to perform the evaluation: Positioning error and CRLB.
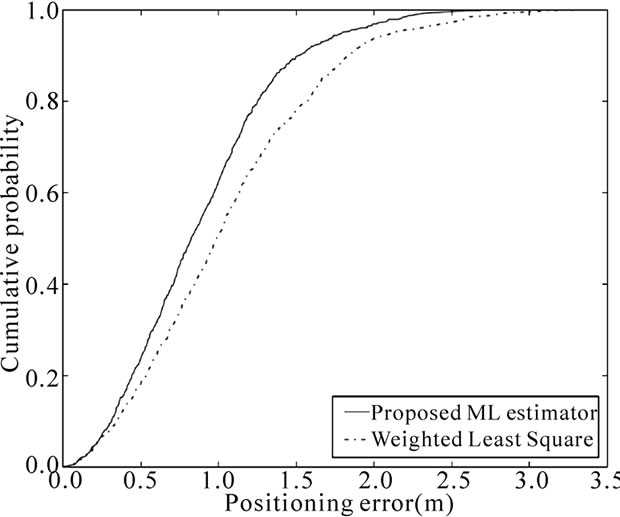
Figure 1. Compared cumulative density function of proposed estimator and WLS estimator for L = 15 meters and K=4.
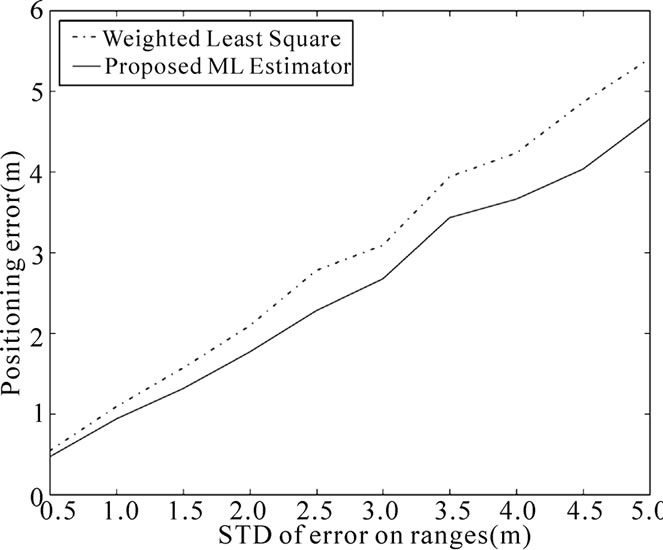
Figure 2. Evolution of positioning error with respect to the standard deviation of introduced error on ranges for L = 15 meters and K=4.
5.1. Positioning Error
The different steps of the simulation are the following:
• K random ANs and one targeted MS are uniformly drawn in an area of L by L m2.
• A Gaussian random range is drawn centered on the true distance between the MS and each AN. the used standard deviation of ranging σr is token equal to 1 meter.
• All simulations have been done with a number of trials NTrial equal to 1000.
In Figure 1, the cumulative density function (CDF) of the proposed estimator is plotted and compared to the CDF of the WLS estimator. In this figure, we assume that only K TOA observables are available. Ranges are then obtained by multiplying the TOA by the speed of light c. The proposed estimator (3) is then applied on these ranges in order to estimate position. In Figure 2, we plot the evolution of the positioning error with respect to the standard deviation σr of the introduced ranging error for a fixed length of area L chosen equal to 15 meters. The positioning error at each value of σr is calculated as the average of errors given after NTrial=1000 random iterations of the targeted MS.
These two figures show that the new proposed estimator outperforms than the typical WLS estimator based on trilateration and the linearization of at least three circle equations in 2D space [9]. Compared to the typical WLS position estimator, the proposed new estimator merges smartly the different observables with different associated variances, and overcomes positioning error caused by the stage of linearization [10]. Furthermore, Figure 2 reveals that the proposed estimator is more robust to ranging error. Indeed, the gap between average errors for WLS and ML estimators respectively is as greater as σr is higher. We believe that it is more interesting, in situations where the information is poor, to use this kind of iterative scheme instead of using more straightforward and cheaper linear implementation of the estimator.

Figure 3. Cramer Rao Lower Bound for 4 TOAs for L = 15 meters and K=4.
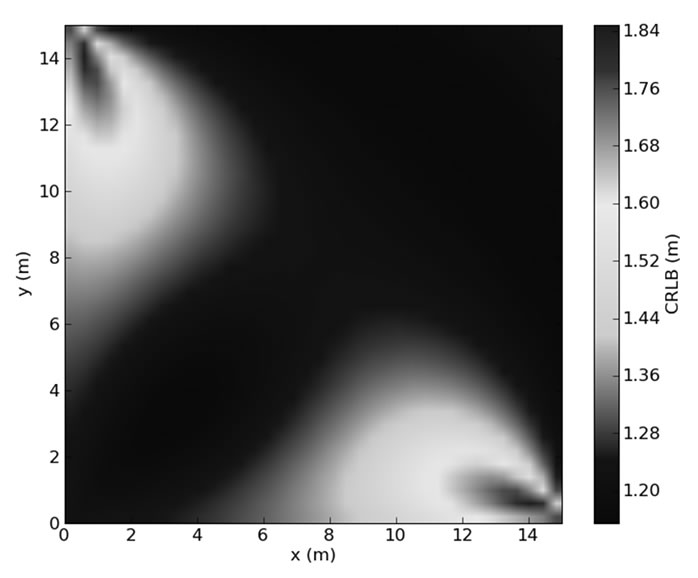
Figure 4. Cramer Rao Lower Bound for 3 TOAs in (0.0,0.0), (0.0,15.0) and (15.0,0.0).
5.2. Cramer Rao Lower Bound
Simulations are done assuming these rules:
• Four anchor nodes are first placed in the four corners of an L by L area.
• For each point in the L by L area, we compute the CRLB for 4 TOAs.
• The standard deviation of ranging σr is token equal to 1 meter.
Giving these assumptions, Figure 3 plots the CRLB over the L by L area. This figure shows the values of calculated CRLB in each point of the area. As expected, the figure is symmetric since the reference ANs are put on the four corners. The figure reveals that the positioning is as accurate as the MS is equidistant from the reference anchor nodes. The positioning becomes more difficult when the MS approaches an anchor node. This difficulty of positioning may be overcome by hybrid data fusion techniques of TOA and RSS observables [11].
In Figure 4, we supposed that the MS has no range estimate from the AN placed on the corner (15.0,15.0). Comparison between this figure and Figure 3 shows that performances are as better as the number of TOAs increases. Moreover, these figures reveal that the configuration of anchor nodes affects the performances of positioning algorithm and may enhance or deteriorate the positioning accuracy. Thus, the choice of the best and the sufficient anchor nodes is a decisive factor to enhance positioning accuracy especially when we aim to perform the positioning service without causing too much overhead on the network.
Figure 5 shows the average CRLB for 4 TOAs placed in the four corners over the entire area for varying sizes of the area and for different values of σr. This figure reveals that the average CRLB does not depend on the size of area and that the accuracy of TOA based ranging affects the accuracy of positioning. This second remark is confirmed by Figure 6 where the average CRLB is plotted with respect to the precision of TOA ranges. This precision may depends on the used technique of ranging, the Radio Access Technology RAT (UWB, WLAN,...), and others factors as the clock offset and the multipath. Nevertheless, the proposed estimator is still able to perform localization even with different RATs. We believe that the proposed estimator defines a good tool to merge different ranges from different RATs.
In conclusion, the Cramer Rao Lower Bound presents a good criterion to choose the best number, type, and associated positions of observables in order to perform a service with the required accuracy. We suggest that this criterion should be involved in tracking system giving, hence, the capability of choosing the best configurations of anchor nodes and observables. Thus, the system may enhance the performed services, reduce the cost of implementation, and preserve the resources.
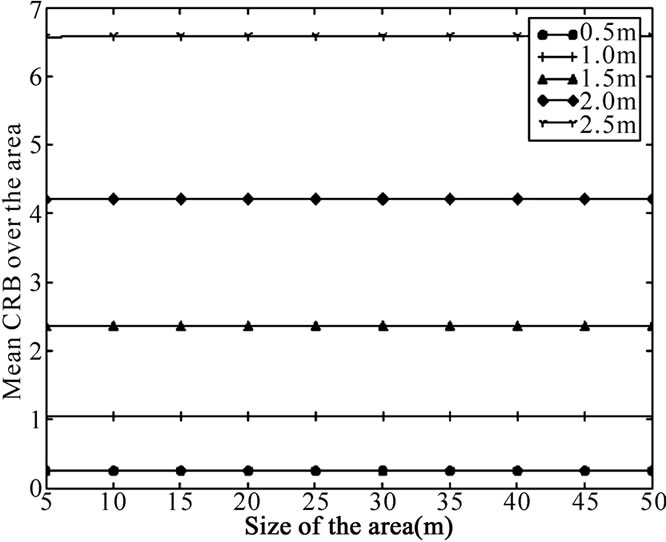
Figure 5. Mean Cramer Rao Lower Bound with respect to the size of area for different values of ranging error variances for K=4.
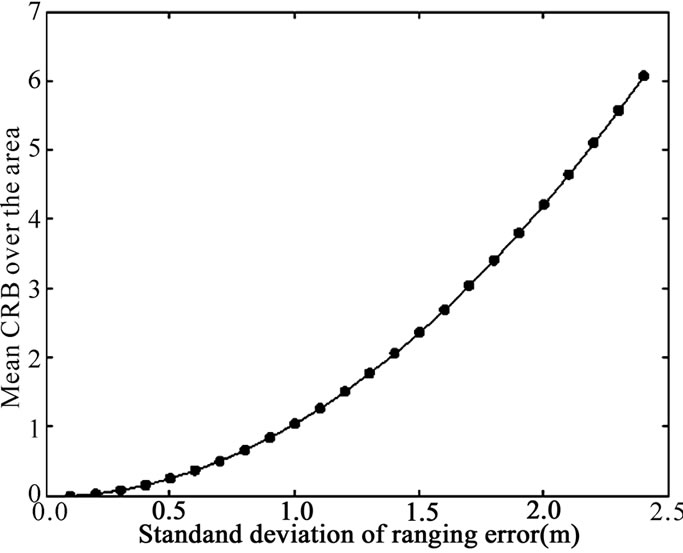
Figure 6. Mean Cramer Rao Lower Bound with respect to the ranging error for L = 15 meters and K=4.
6. Conclusions
In this paper, we proposed an hybrid TOA localization scheme based on a new Maximum Likelihood estimator. We believe that this proposed ML estimator is able to merge smartly different TOA observables while considering associated variances. This estimator performs better than typical weighted least square estimator. The effect of additional TOAs on the performances is studied using positioning error and Cramer Rao Lower Bound. We believe that the number and the position of anchor nodes implied in TOA-based ranges and their associated precisions should be smartly chosen in order to perform the requested positioning accuracy. We suggest that the CRLB may be a good criterion to choose the best configuration and number of anchor nodes implied on the positioning scheme. Next step will be to evaluate performance in more realistic scenarios and to combine TOA observables with other observables such as TDOA and RSS.
7. Acknowledgment
The work presented in this paper has been performed in the framework of the ICT-217033 WHERE project funded by the European Union.
8. References
[1] G. Shen, R. Zetik, and R. Thoma, “Performance comparison of TOA and TDOA based location estimation algorithms in los environment,” WPNC’08, 2008.
[2] Z. Sahinoglu, S. Gezici, and I. Guvenc, “Ultra-wideband positioning systems : Theoretical limits, ranging algorithms, and protocols,” Cambridge University Press, New York, 2008.
[3] B. Denis, J. Keignart, and N. Daniele, “Impact of nlos propagation upon ranging precision in UWB systems,” IEEE Conference on Ultra Wide Band and Systems and Technologies, 2003.
[4] M. Ciurana, F. Barcelo-Arroyo, and F. Izquierdo, “A ranging method with IEEE 802.11 data frames for indoor localization,” WCNC’07, 2007.
[5] A. Gunther and C. Hoene, “Measuring round trip times to determine the distance between WLAN nodes,” Networking, 2005.
[6] C. Mazzucco, U. Spagnolini, and G. Mulas, “A ranging technique for UWB indoor channel based on power delay profile analysis,” IEEE VTC Spring, 2004.
[7] M. Ciurana, F. Barcelo-Arroyo, and F. Izquierdo, “A ranging system with IEEE 802.11 data frames,” IEEE Radio and Wireless Symposium, January 2007.
[8] K. Cheung, W. K. Ma, and H. So, “Accurate approximation algorithm for TOA-based maximum likelihood mobile location using semidefinite programming,” IEEE International Conference on Coustics, Speech, and Signal Processing, 2004.
[9] M. Laaraiedh, S. Avrillon, and B. Uguen, “Enhancing positioning accuracy through direct position estimators based on hybrid RSS data fusion,” IEEE VTC Spring, 2009.
[10] W. Kim, J. Lee, and G. Jee, “The interior-point method for an optimal treatment of bias in trilateration location,” IEEE Transactions on Vehicular Technology, Vol. 55, July 2006.
[11] M. Laaraiedh, S. Avrillon, and B. Uguen, “Hybrid data fusion techniques for localization in UWB networks,” WPNC’09, March 2009.

