Journal of Intelligent Learning Systems and Applications
Vol.5 No.2(2013), Article ID:31486,9 pages DOI:10.4236/jilsa.2013.52011
Randomized Algorithm for Determining Stabilizing Parameter Regions for General Delay Control Systems*
![]()
Department of Electrical and Computer Engineering, National University of Singapore, Singapore City, Singapore.
Email: yuchao@nus.edu.sg, binhnguyen.le@nus.edu.sg, lixian@nus.edu.sg, elewqg@nus.edu.sg
Copyright © 2013 Chao Yu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 29th, 2013; revised March 25th, 2013; accepted April 2nd, 2013
Keywords: Stabilizing Parameter Regions; Delay Control Systems; Randomized Sampling; LMI Stability Criterion; Support Vector Machines
ABSTRACT
This paper proposes a method for determining the stabilizing parameter regions for general delay control systems based on randomized sampling. A delay control system is converted into a unified state-space form. The numerical stability condition is developed and checked for sample points in the parameter space. These points are separated into stable and unstable regions by the decision function obtained from some learning method. The proposed method is very general and applied to a much wider range of systems than the existing methods in the literature. The proposed method is illustrated with examples.
1. Introduction
Finding stabilizing regions for control systems in parameter space becomes important in recent years. Stabilizing parameter regions will be instructive for controller tuning with greatest robustness or controller optimization with regard to other specific indexes. Most papers in the literature discuss about the stabilizing parameter regions for proportional-integral-derivative (PID) controllers. Wang et al. [1] designed a quasi-Linear Matrix Inequality method to compute the stabilizing parameter regions of multi-loop PID controllers, but it only dealt with systems with no time delays. Lee et al. [2-4] established some stability conditions by simple P or PI controllers for a class of unstable processes with time delays, but the application of their methods is confined to single-input single-output (SISO) systems whose transfer functions only have one zero. Nie et al. [5] gave a frequency method to calculate the loop gain margins of multivariable feedback system. Liu et al. [6] introduced a fast calculation approach for PI controller stable region based on D-partition method. Wang et al. [7] presented an effective graphical method to obtain exact P controller gain ranges for two input two output (TITO) systems with input time delay. However, this approach could not handle systems with state-delays. Some other methods can be found in [8-13]. All the methods seek the solutions for the stabilizing parameter regions for limited classes of plants or controllers.
In this paper, we design a general algorithm for determining stabilizing parameter regions for delay control systems based on randomized sampling. Each unknown parameter is assumed to follow the uniform distribution in a given range and a certain number of independent and identically distributed (i.i.d.) random sample points are generated in the parameter space based on the randomized algorithms [14]. Next, given a delay control system, we convert it into a unified state-space form. Efficient LMI stability criterion is developed for a control system with multiple delays in both input and state. Then each point in the parameter space is checked by the developed stability criterion. After that, these points are separated into stable and unstable regions by the decision function obtained from some learning method. The effectiveness of the proposed method is illustrated by simulation examples.
The rest of this paper is organized as follows. Section 2 presents the idea of proposed method. Section 3 develops the stability criterion. Determining stabilizing parameter regions is discussed in Section 4. Section 5 gives simulation examples and Section 6 concludes the paper.
2. The Proposed Method
We consider a unity feedback control system as shown in Figure 1. The plant may have some unknown parameters that may affect the system stability and the parameters of the controller are also needed to be designed. Hence, knowing stabilizing parameter regions is instructive for robustness analysis and design. Some methods [2-4] can give analytical solutions for stabilizing parameter regions, but these methods usually have many constraints and could only be applied to limited plants or controllers. Some numerical methods [11,12] also have some restrictions on system structures and their algorithms might be difficult to be implemented. The objective of this paper is to provide stabilizing parameter regions with a new approach which is totally different from the existing methods in this specific area. We illustrate the idea of our method with a simple example.
We consider the model in [10] as follows,
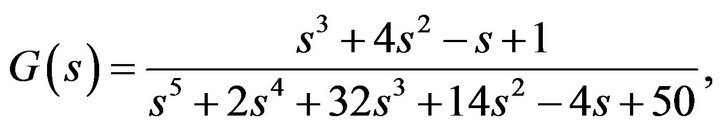
with a PI controller
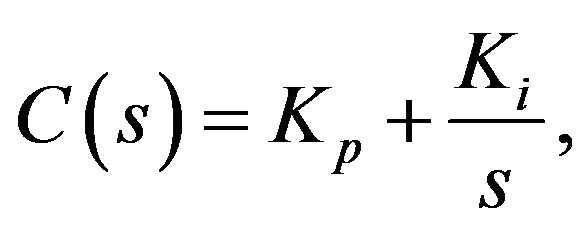
where 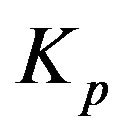 and
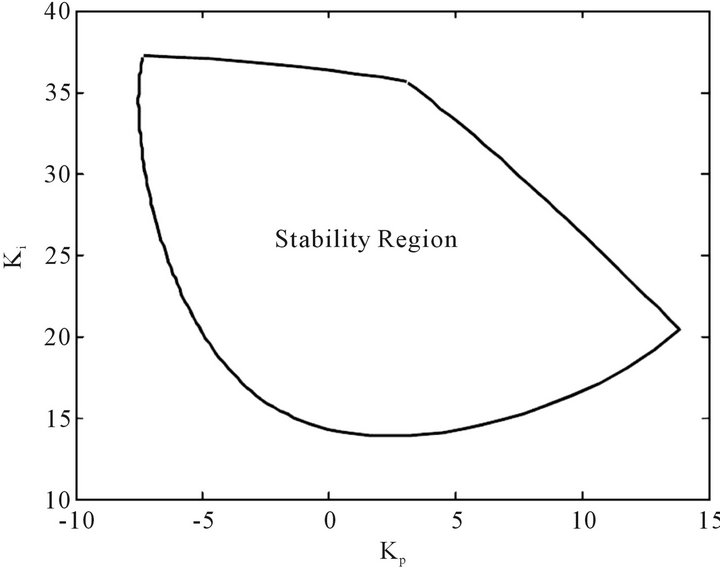
and 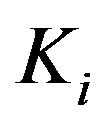 are unknown parameters. With the method in [10], the stabilizing parameter region is shown in Figure 2(a).
are unknown parameters. With the method in [10], the stabilizing parameter region is shown in Figure 2(a).
The randomized algorithms have been applied to design robust controllers [14]. In their context, a fixed single controller is obtained for an uncertain plant. The uncertainty lies in some plant parameters. These parameters are sampled randomly to get a set of plants which represent and replace the original uncertain plant. One single controller (fixed controller parameters) is found to meet a performance measure such as 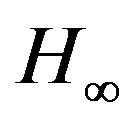 for these sampled points. In our context, we want to find the entire regions of controller parameters which stabilize a plant. Furthermore, the plant may also have some uncertain parameters such as delay. In the later case, we want to find the regions of combined parameter vector p from the controller and the plant which stabilize the control system. We employ the idea of randomized sampling. Suppose that each unknown parameter follows the uniform distribution in a given range, that is
for these sampled points. In our context, we want to find the entire regions of controller parameters which stabilize a plant. Furthermore, the plant may also have some uncertain parameters such as delay. In the later case, we want to find the regions of combined parameter vector p from the controller and the plant which stabilize the control system. We employ the idea of randomized sampling. Suppose that each unknown parameter follows the uniform distribution in a given range, that is ,
,  and they distribute uniformly in their re
and they distribute uniformly in their re
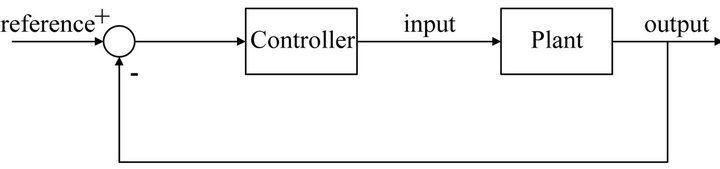
Figure 1. Unity feedback control system.
 (a)
(a)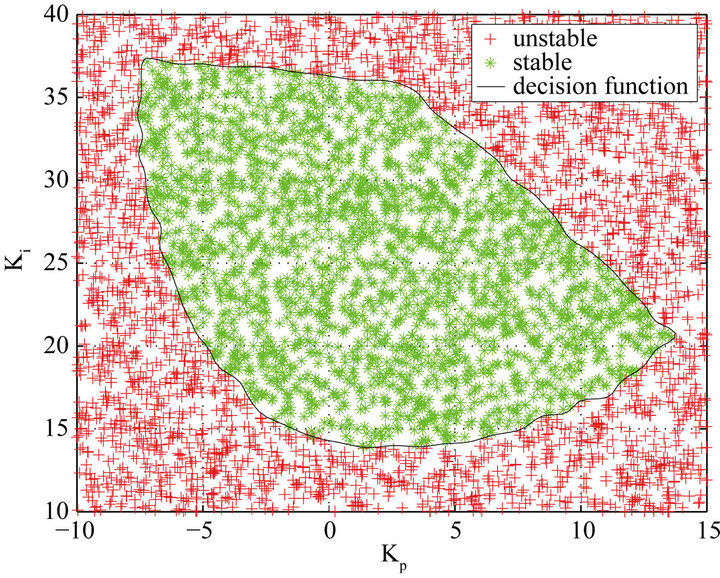 (b)
(b)
Figure 2. Stabilizing parameter region for the example in [10]. (a) Result in [10]; (b) Result with the proposed method.
spective range. Then a certain number of i.i.d. random points are sampled in the parameter space. Repeated samples are omitted. According to the randomized algorithms [14], the number of points, N, should satisfy
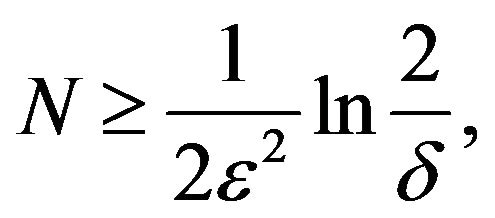 (1)
(1)
where we set a priori 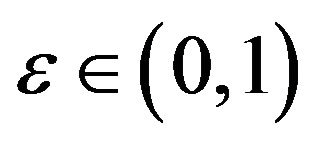 as the accuracy parameter and
as the accuracy parameter and 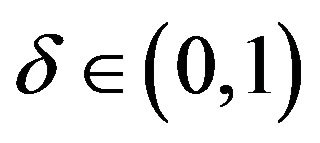 as the confidence level. Both
as the confidence level. Both 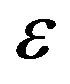 and
and  are usually taken small values, say less than 0.1. We choose
are usually taken small values, say less than 0.1. We choose 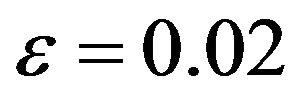 and
and 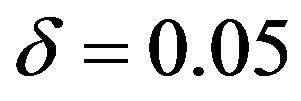 for our example. It could be calculated from (1) that
for our example. It could be calculated from (1) that 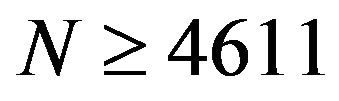 and then we choose
and then we choose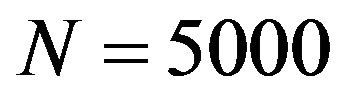 . Throughout this paper,
. Throughout this paper, 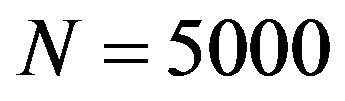 is used for all simulation cases.
is used for all simulation cases.
Next, we check whether each of these points could stabilize the system by some stability criterion. The characteristic equation of the closed-loop system is
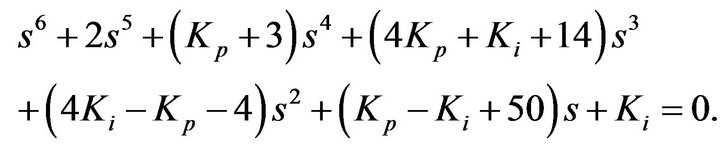
We can simply calculate the closed-loop poles for stability testing. If a point of 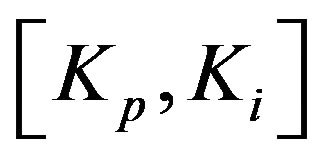 could stabilize the system, it is labeled as “stable”. Otherwise, if a point could not stabilize the system, it is labeled as “unstable”. However, calculating the closed-loop poles is not possible for systems with time delays. In this case, we present a Linear Matrix Inequality (LMI) stability criterion which will be discussed in next section.
could stabilize the system, it is labeled as “stable”. Otherwise, if a point could not stabilize the system, it is labeled as “unstable”. However, calculating the closed-loop poles is not possible for systems with time delays. In this case, we present a Linear Matrix Inequality (LMI) stability criterion which will be discussed in next section.
Lastly, the points in the parameter space are divided into stable and unstable regions by the decision function obtained from some learning method, such as the Neural Networks and the Support Vector Machines (SVM) [15]. We choose SVM as the classification tool and employ the LibSVM [16] kit with its arguments “-t” = 2 (Radial Basis Function (RBF) as kernel) and “-c” = 1,000,000 (penalty parameter) to solve the problem. The resulting stabilizing parameter region is shown in Figure 2(b). It is seen from Figures 2(a) and (b) that the stable region from the proposed method is almost same as that in [10]. Hence, our method is effective and straightforward.
3. Stability Criterion
As stated in previous section, it is impossible to calculate the closed-loop poles for systems with time delays. Therefore, in this section, we present an effective algorithm for stability testing which can be applied to a much wider range of systems. Given a delay system with PI or PID controller, we first convert it into a unified statespace form, which is a generalization of the method in [17] where a delay-free system is considered. Next, we present a conversion of delay systems with general dynamic controllers. Lastly, we present an LMI stability criterion for the unified state-space form.
3.1. PI Control for Input-Delay Plant
Consider a plant:
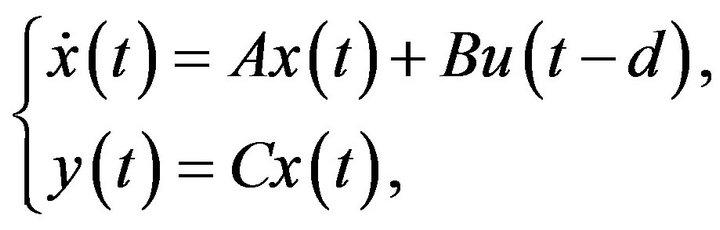 (2)
(2)
with a PI controller:
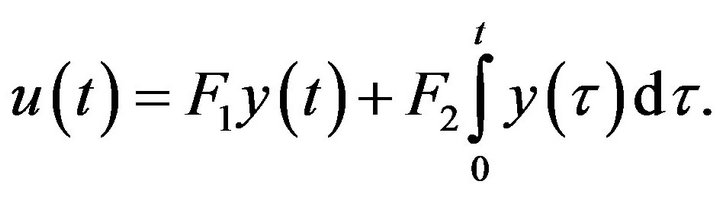
Let
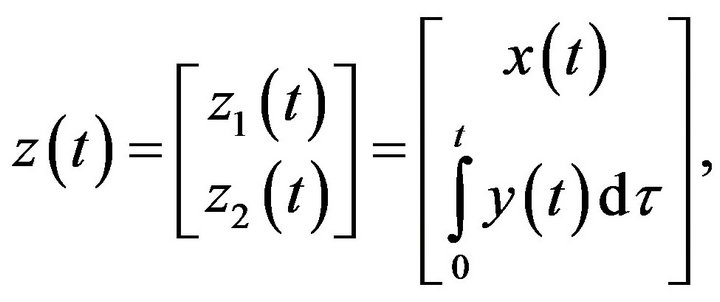
so that
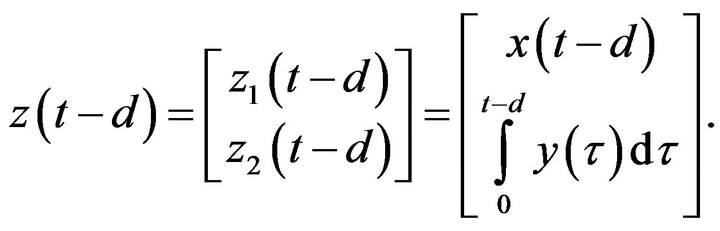
The vector 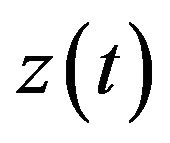 can be viewed as a new state variable of the system, whose dynamics is governed by
can be viewed as a new state variable of the system, whose dynamics is governed by
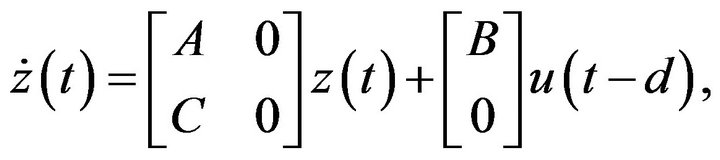 (3)
(3)
where
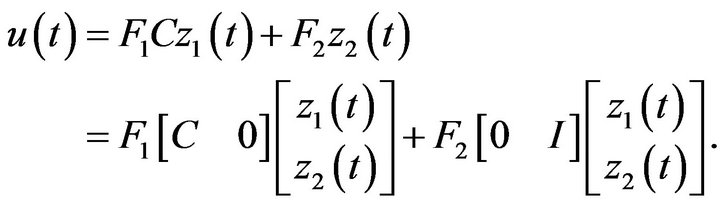 (4)
(4)
Let 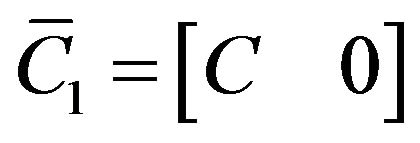 and
and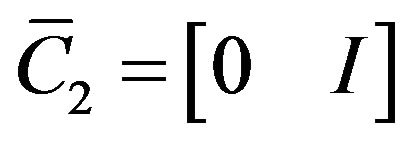 . Equation (4) can be rewritten as
. Equation (4) can be rewritten as
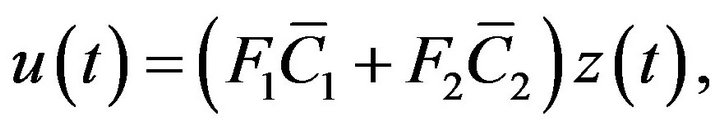
or
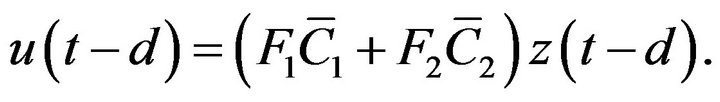 (5)
(5)
Substituting (5) into (3) yields
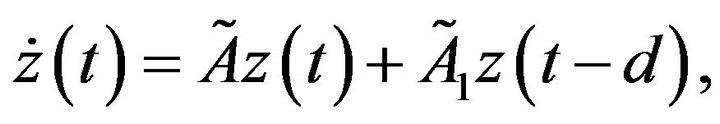 (6)
(6)
where
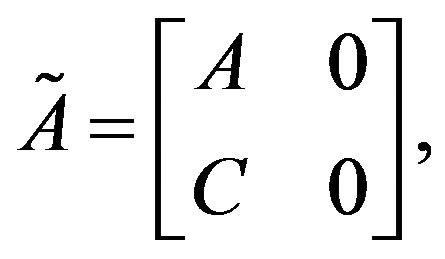
and
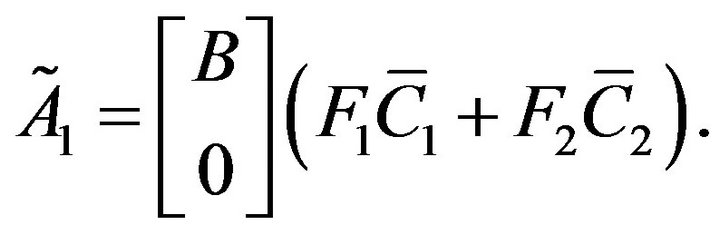
When (2) is with a PID controller
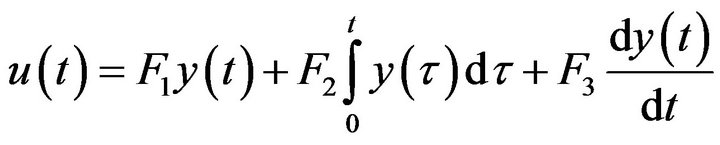 the conversion could not be proceeded. This is because
the conversion could not be proceeded. This is because 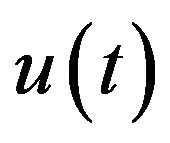 depends on
depends on 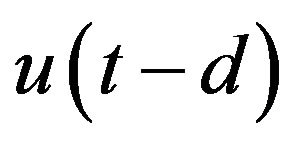 since
since
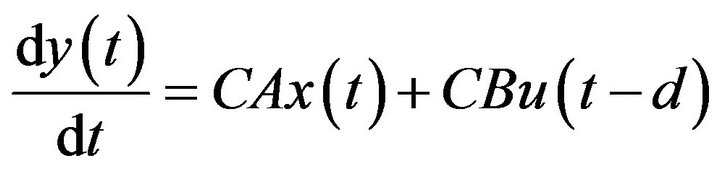 . Then the control signal cannot be expressed only by state vectors as (4) or (5). In such a case, we could use a practical D controller:
. Then the control signal cannot be expressed only by state vectors as (4) or (5). In such a case, we could use a practical D controller:
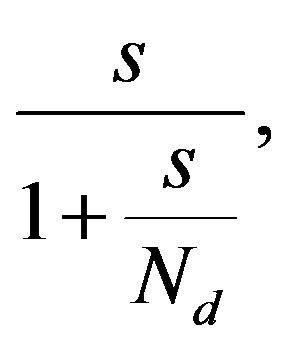
where 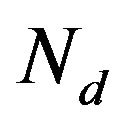 is chosen by users to limit derivative gain on higher frequencies. Then, the practical PID controller falls in a format of general dynamic controller, which is handled in Section 3.3 below.
is chosen by users to limit derivative gain on higher frequencies. Then, the practical PID controller falls in a format of general dynamic controller, which is handled in Section 3.3 below.
3.2. PID Control for State-Delay Plant
Consider a plant:
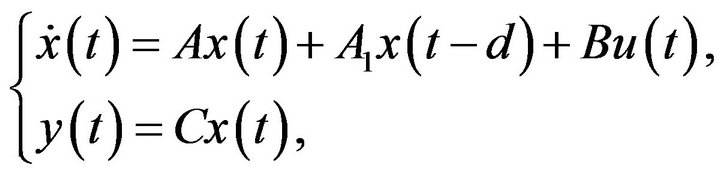 (7)
(7)
with a PID controller:
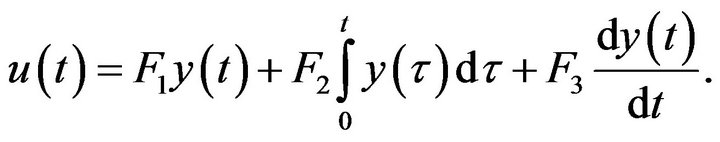
Let 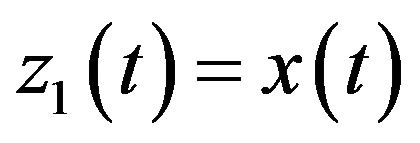 and
and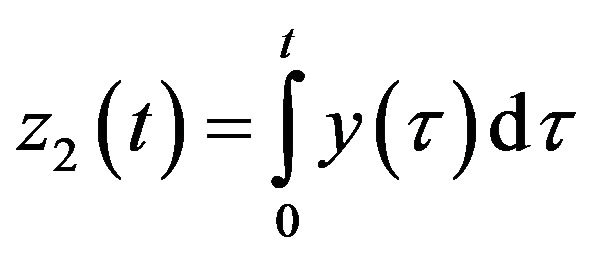 . We have
. We have
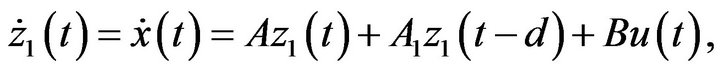
and
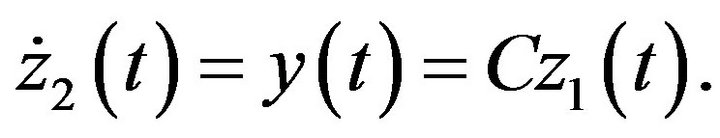
Denoting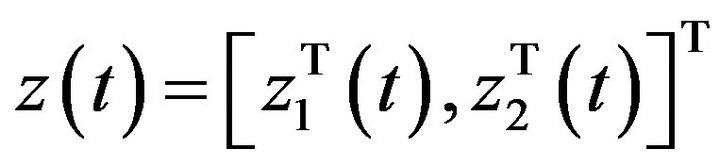 , we have
, we have
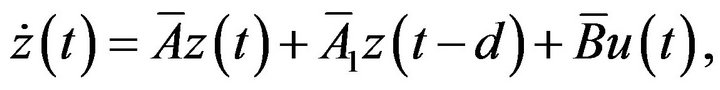
where
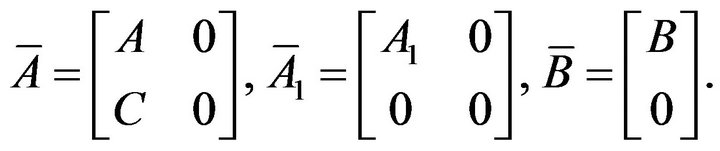
Combining (7) and the definition of  yields
yields
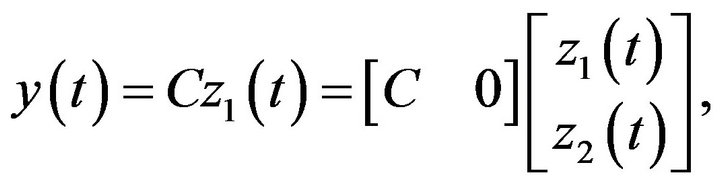
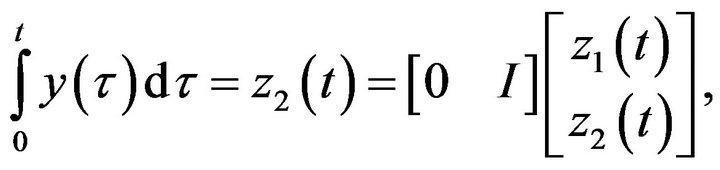
and
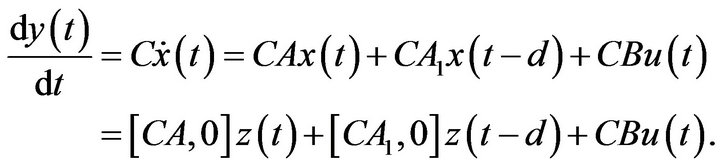
Denoting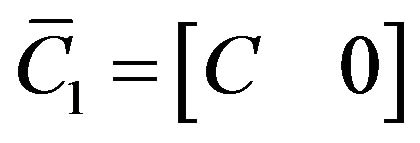 ,
, 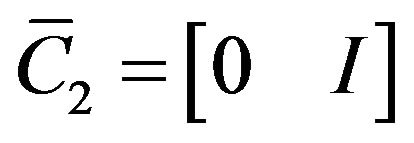 ,
, 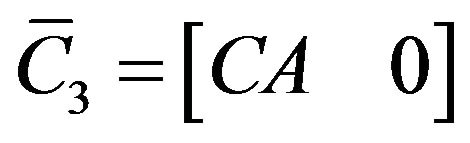 ,
,
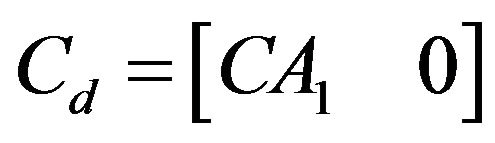 ,
, 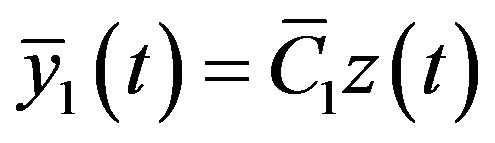 ,
, 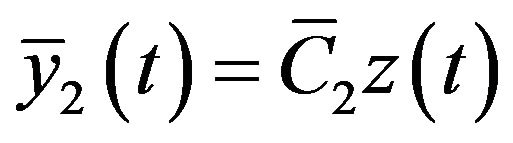 and
and
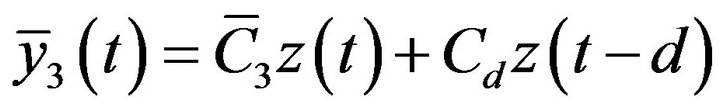 , we have
, we have
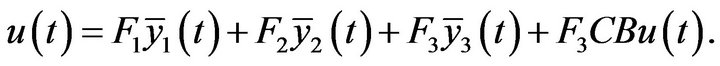
Suppose that 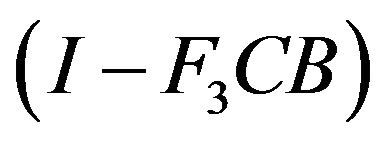 is invertible. Let
is invertible. Let
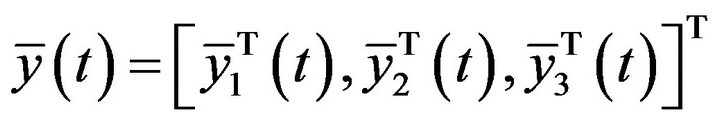 ,
, 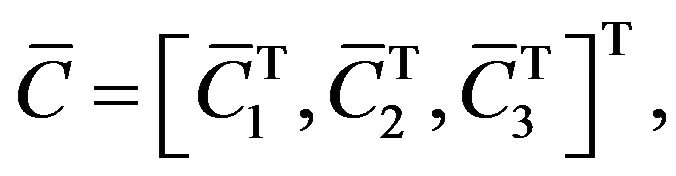
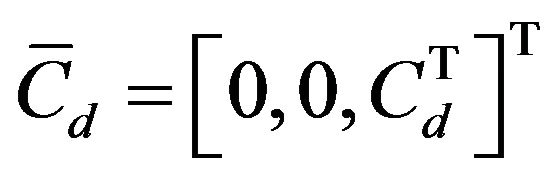 , and
, and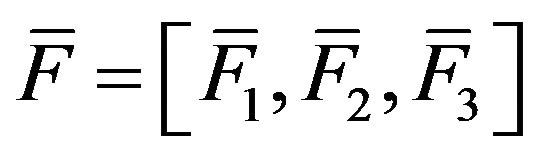 , where
, where
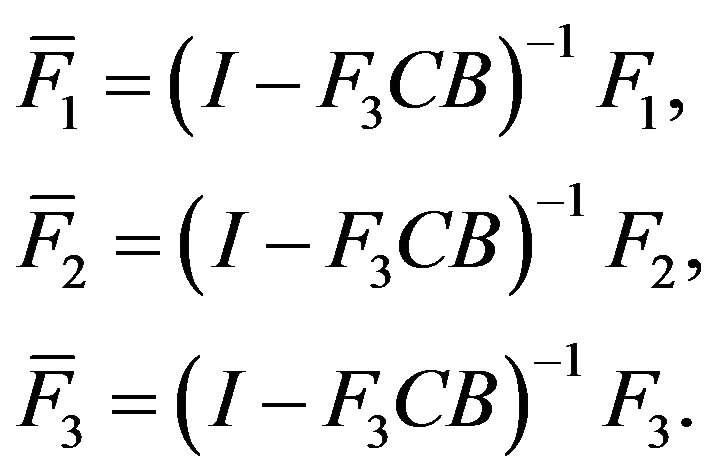
Then (7) is equivalent to
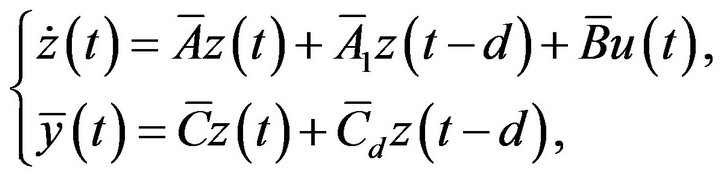
with
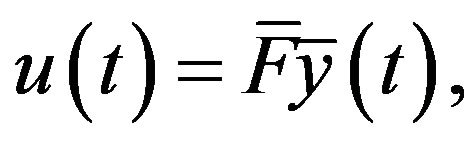
i.e.,
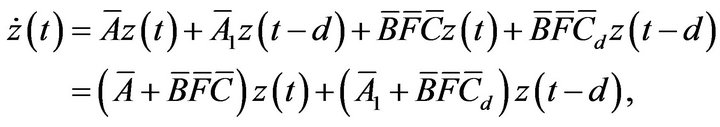 (8)
(8)
which is also in the form of (6) with 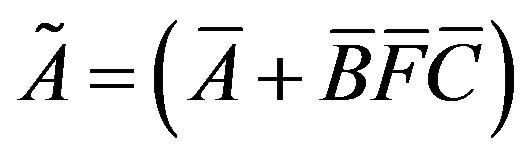 and
and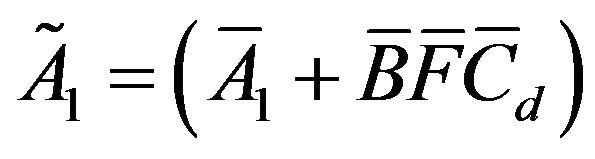 .
.
Remark 1. The systems (2) and (7) only contain one time delay. However, it would not be difficult to make conversion for systems with multiple time delays, which is omitted here for brevity.
The previous two cases only tackle delay systems with PI or PID controller whose parameters appear in a linear form. In practical control systems, the controllers may be of higher orders and the parameters of controllers may also appear in a nonlinear form, such as the lead-lag compensators [18]. Thus, we consider the conversion for delay systems with general dynamic controller as follows.
3.3. General Dynamic Controller for a Plant with Multiple Delays in Input and State
Consider a plant (9)
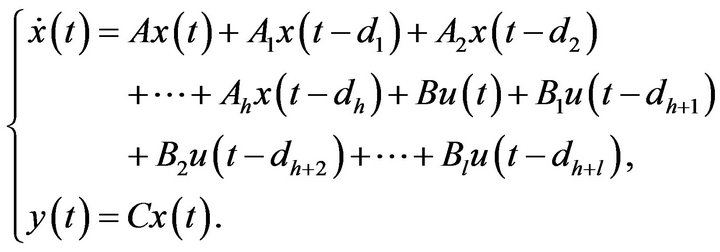 (9)
(9)
under the following dynamic controller:
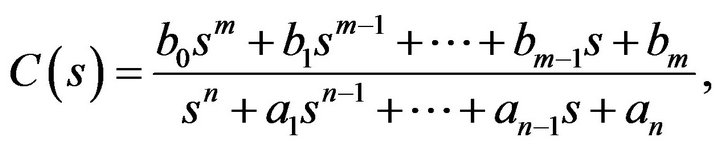
whose minimal state-space realization can be expressed by
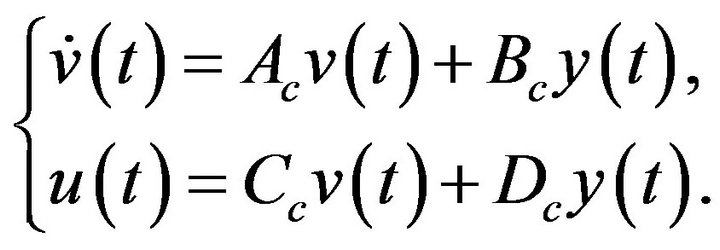
Let 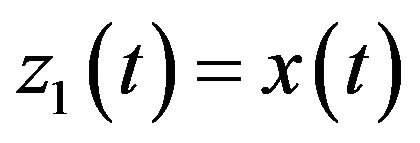 and
and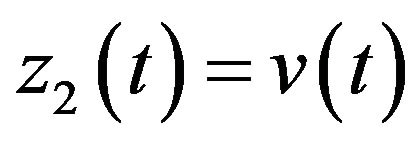 . Denoting
. Denoting
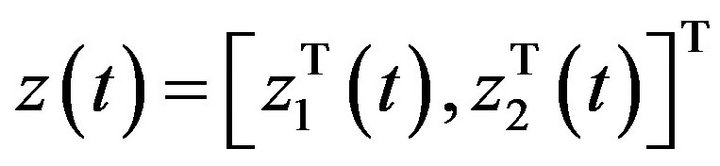 , we have
, we have
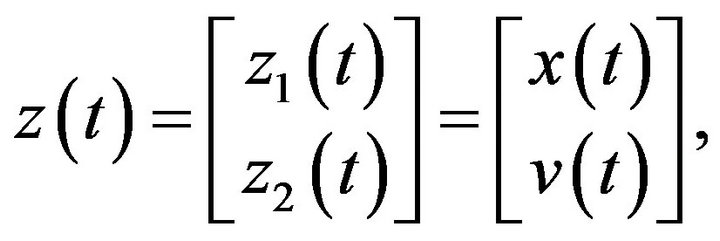
and
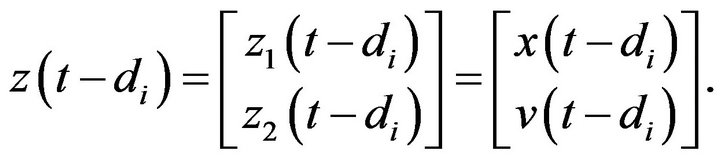
Combining the above expressions gives (10)
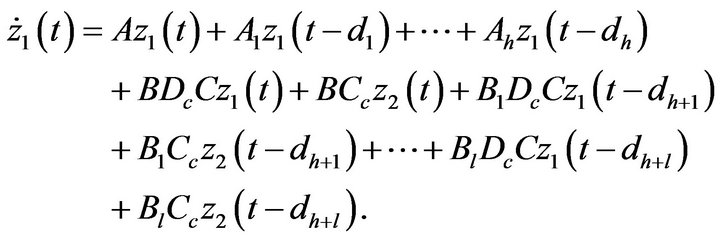 (10)
(10)
and
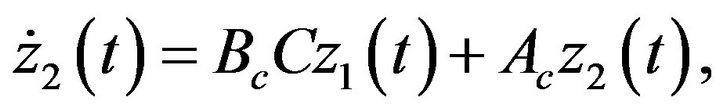
i.e.,
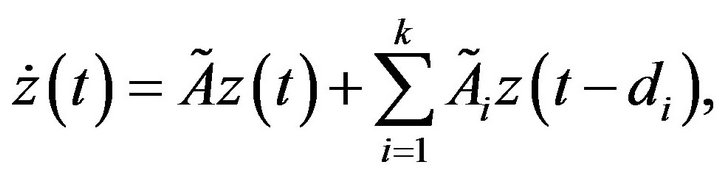 (11)
(11)
where
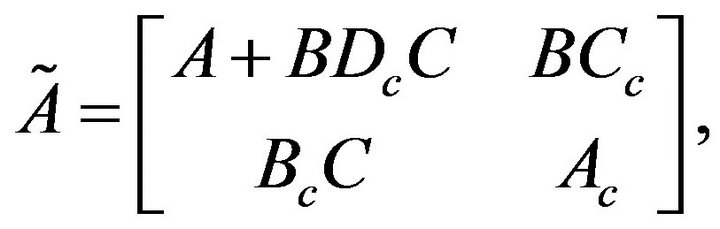
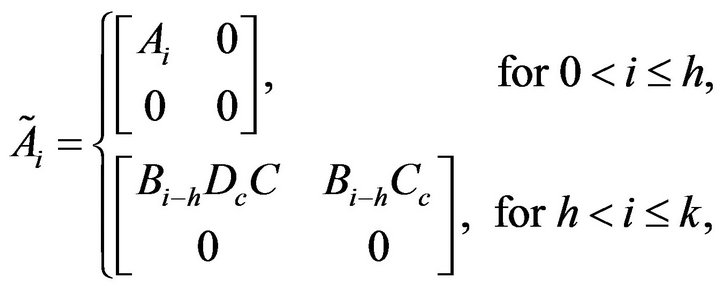
and 
Remark 2. The system (6) is a special case of (11).
3.4. The LMI Stability Criterion for a System with Multiple Delays in Input and State
Theorem 1. The system (11) is asymptotically stable if there exist symmetric positive definite matrices 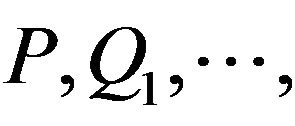
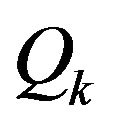 , and
, and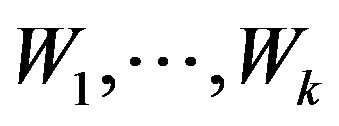 , such that
, such that
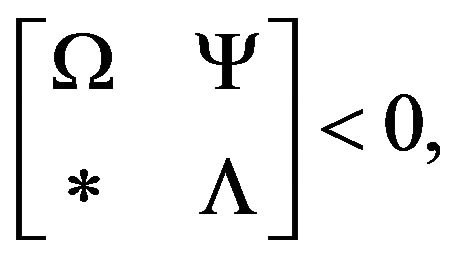 (12)
(12)
where (13) holds,
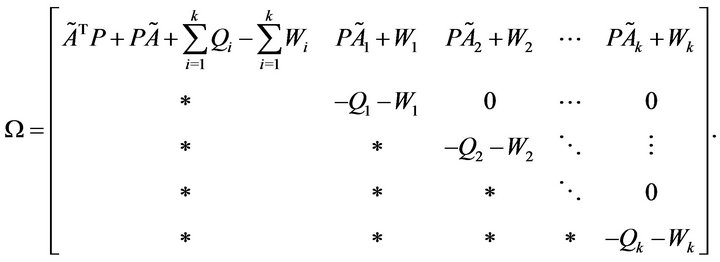 (13)
(13)
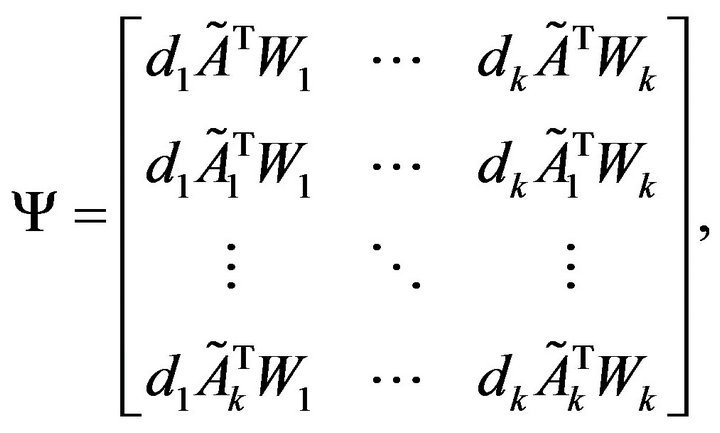 and
and 
Here and in the sequel, a block induced by symmetry is denoted by an ellipsis *.
Proof. Define the Lyapunov functional as
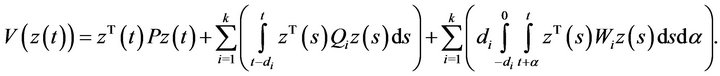
The derivative of  is
is

It follows from Jensen’s inequality [19] that
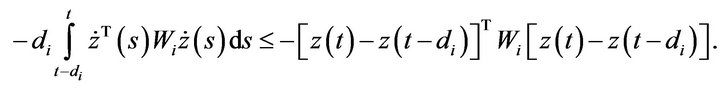
Then we have (14).
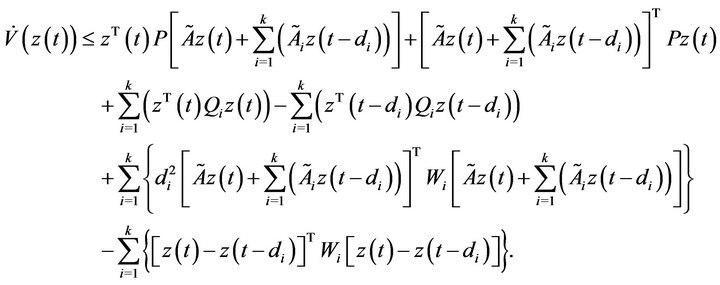 (14)
(14)
Let
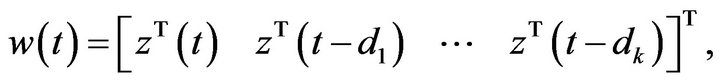
and
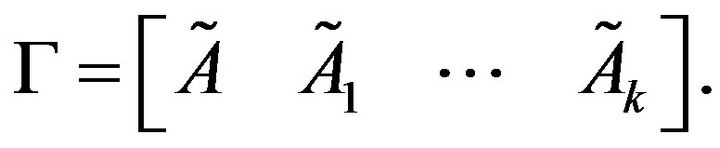
One sees
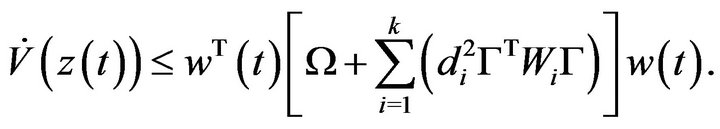
By Schur complement, (12) guarantees
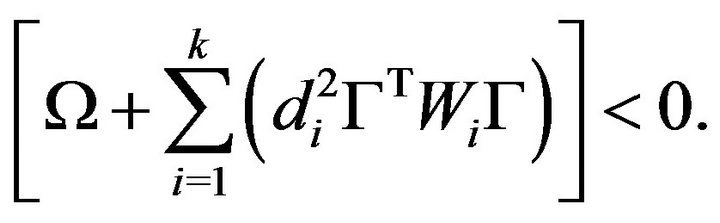
Therefore, the system (11) is asymptotically stable.
4. Stabilizing Parameter Regions
Each point in the parameter space corresponds to a sample of the parameter vector p, which is denoted by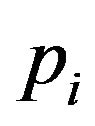 ,
,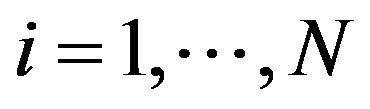 . We check whether each of these points could stabilize the system by the developed LMI stability criterion. If a point
. We check whether each of these points could stabilize the system by the developed LMI stability criterion. If a point 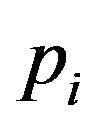 could stabilize the system, it is labeled as “stable”. Otherwise, if
could stabilize the system, it is labeled as “stable”. Otherwise, if 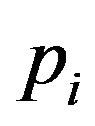 could not stabilize the system, it is labeled as “unstable”.
could not stabilize the system, it is labeled as “unstable”.
The points in the parameter space can be separated into stable and unstable regions by the decision function obtained from some learning method. In this paper, we choose SVM as the learning method due to its superior performance in a wide range of applications. Support Vector Machines (SVM), which was first introduced by Vapnik [20], has shown many attractive features in the fields of small sample, non-linear and high dimensional pattern recognition [21]. It can be promoted to classification and regression problems. It employs the Structural Risk Minimization principle [21]. The goal of SVM is to find a decision function that minimizes the structural risk, which could be converted into a quadratic programming problem. In addition, the solution of an SVM problem is a globally optimal solution [22].
In this paper, SVM is employed to solve a binary classification problem. Given the data set 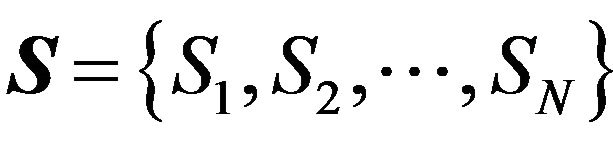 with
with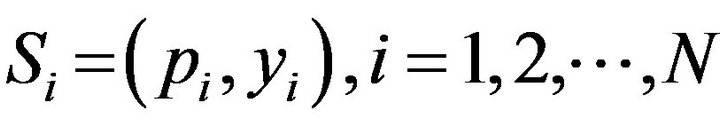 , where
, where 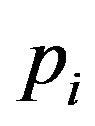 is a point in the parameter space and
is a point in the parameter space and 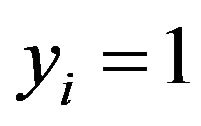 (stable) or −1 (unstable) is the label of the point, SVM is to solve the following problem:
(stable) or −1 (unstable) is the label of the point, SVM is to solve the following problem:
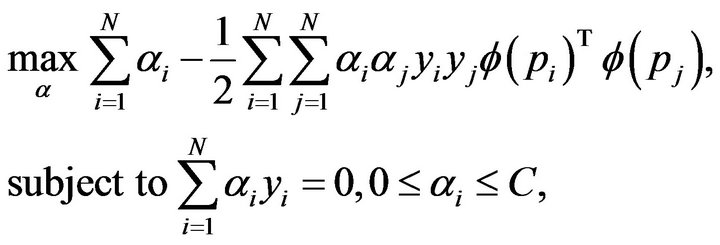
where 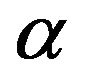 is the Lagrange multiplier,
is the Lagrange multiplier, 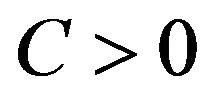 is the penalty parameter which can be set by users and
is the penalty parameter which can be set by users and 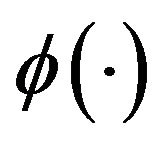 is a mapping from
is a mapping from 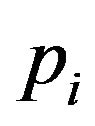 to a higher dimensional space.
to a higher dimensional space.
There have already been many SVM tool kits that can be used to solve the classification problems. LIBSVM [16] is a simple and effective one developed by Chih-Jen Lin’s research group. Throughout this paper, the LibSVM kit is employed to do simulation with proper arguments.
5. Simulation Examples
In this section, four examples are presented to illustrate the effectiveness of the proposed method.
Example 1. The analytical method in [2] cannot deal with a process containing multiple zeros, while our method does not have this constraint. Consider the plant:

with a P controller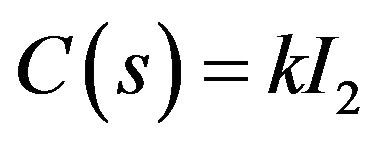 . This control system is converted to the form in (11) with
. This control system is converted to the form in (11) with
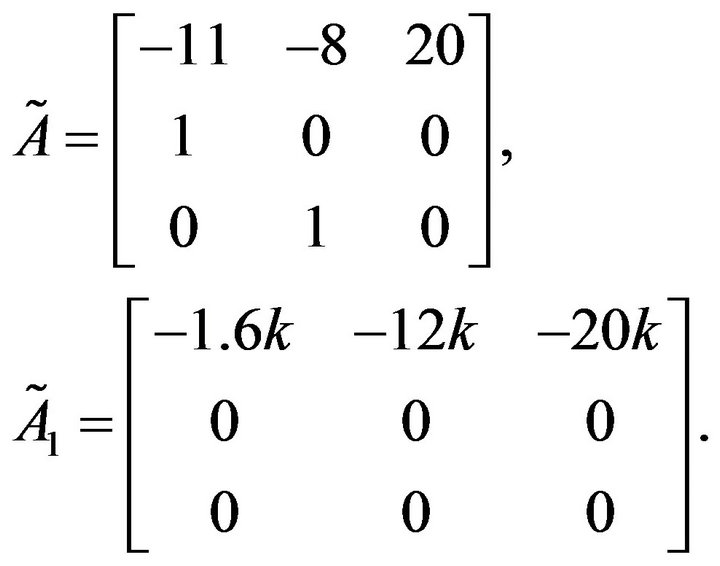
Let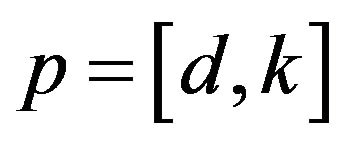 . Performing our method with the LibSVM arguments “-t” = 2 and “-c” = 100, the stabilizing parameter region is obtained and shown in Figure 3.
. Performing our method with the LibSVM arguments “-t” = 2 and “-c” = 100, the stabilizing parameter region is obtained and shown in Figure 3.
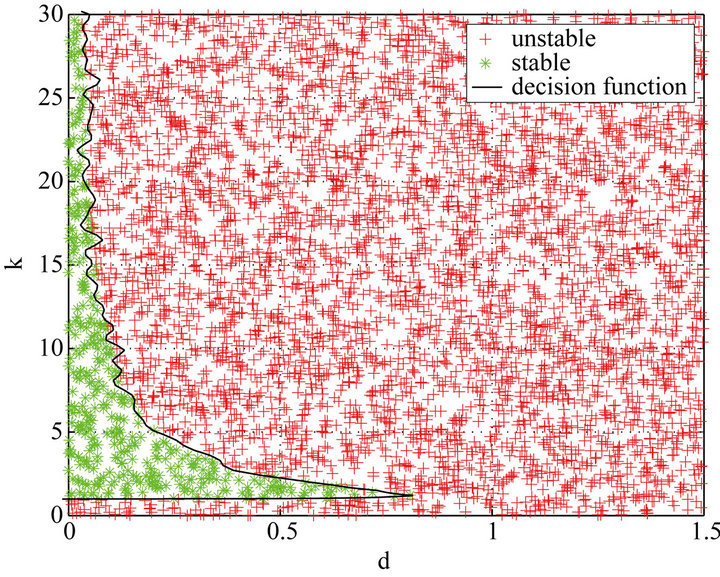
Figure 3. Stabilizing parameter region for Example 1.
Example 2. The graphical method in [7] cannot deal with a process containing state-delays. However, our method does not have this restriction. Consider the plant:
 (15)
(15)
with a P controller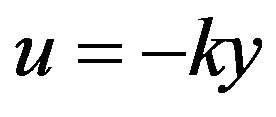 . This control system is converted to the form in (11) with
. This control system is converted to the form in (11) with
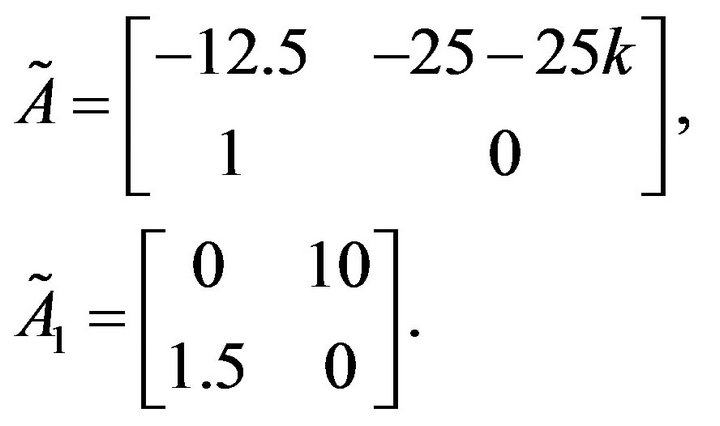
Let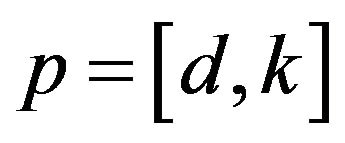 . Performing our method with “-t” = 2 and “-c” = 1000, the stabilizing parameter region is obtained and shown in Figure 4.
. Performing our method with “-t” = 2 and “-c” = 1000, the stabilizing parameter region is obtained and shown in Figure 4.
Example 3. Consider the plant (15) with 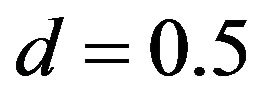 under the controller
under the controller
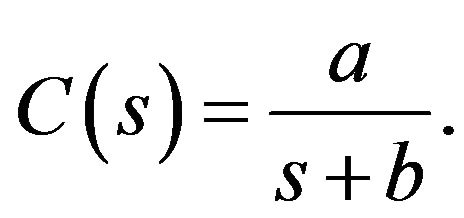 (16)
(16)
Note that b appears in a nonlinear fashion, which is different from parameters of PID controllers. We can rewrite (16) as
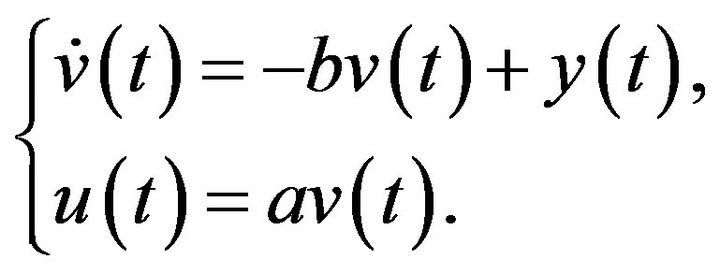
This control system is converted to the form in (11) with
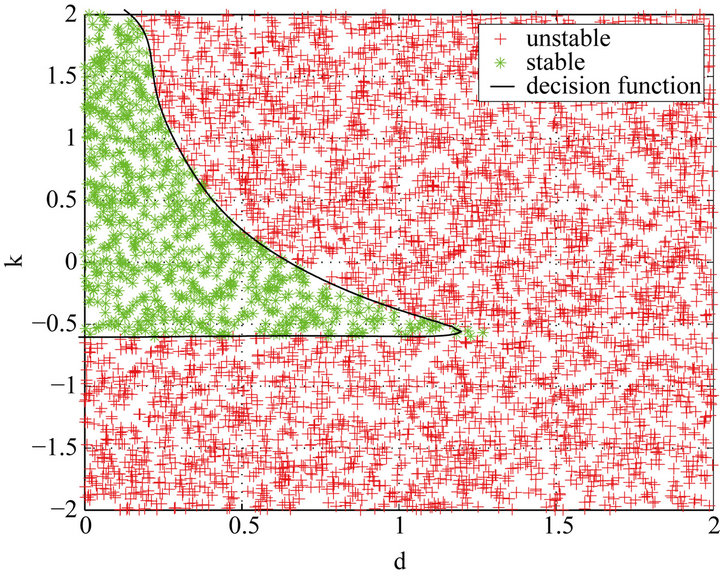
Figure 4. Stabilizing parameter region for Example 2.
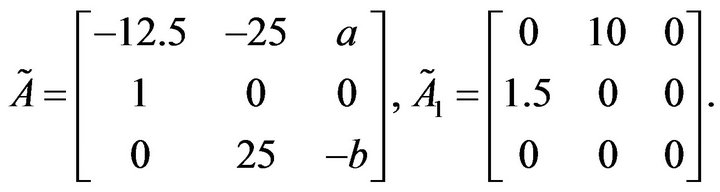
Let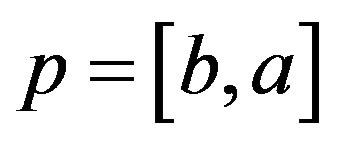 . Performing our method with “-t” = 2 and “-c” = 1000, the stabilizing parameter region is obtained and shown in Figure 5.
. Performing our method with “-t” = 2 and “-c” = 1000, the stabilizing parameter region is obtained and shown in Figure 5.
Example 4. The proposed method also works well with a high-dimensional parameter space. Consider the plant:
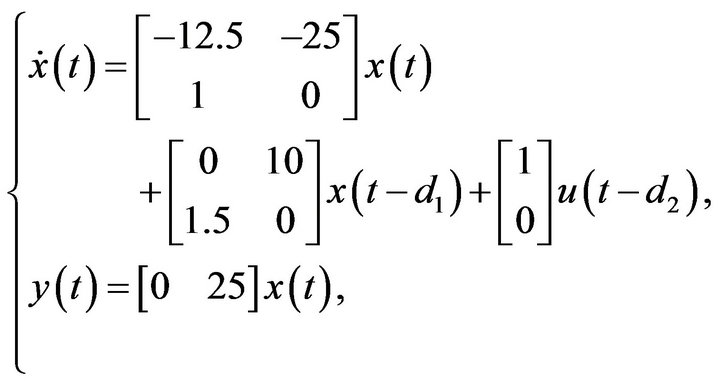
with a controller:
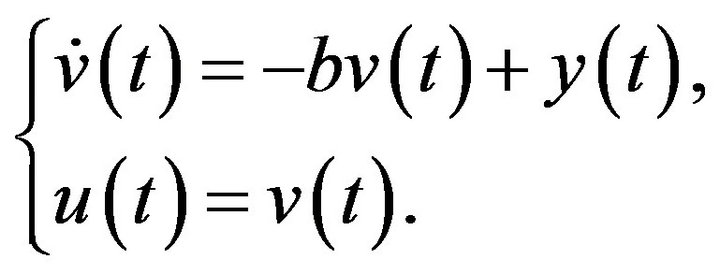
This control system is converted to the form in (11) with
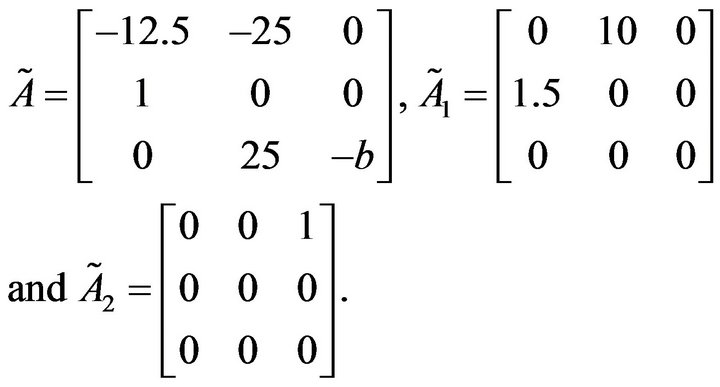
Let . Performing our method with “-t” = 2 and “-c” = 1000, the stabilizing parameter region is obtained and shown in Figure 6.
. Performing our method with “-t” = 2 and “-c” = 1000, the stabilizing parameter region is obtained and shown in Figure 6.
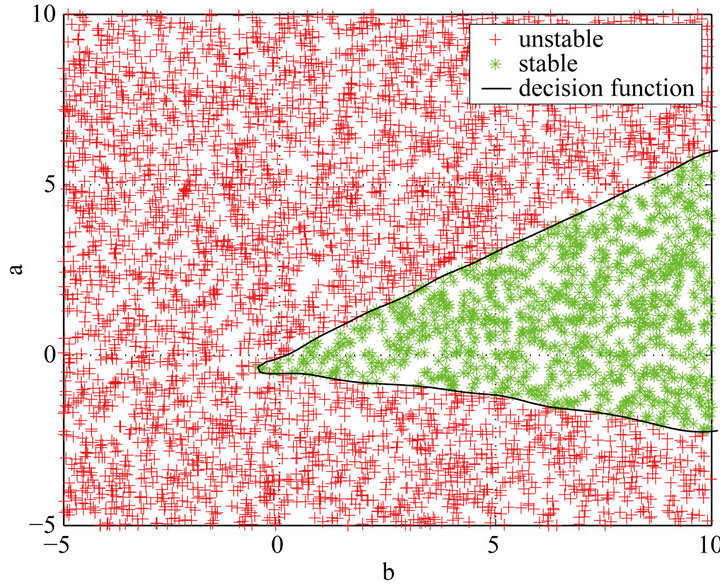
Figure 5. Stabilizing parameter region for Example 3.
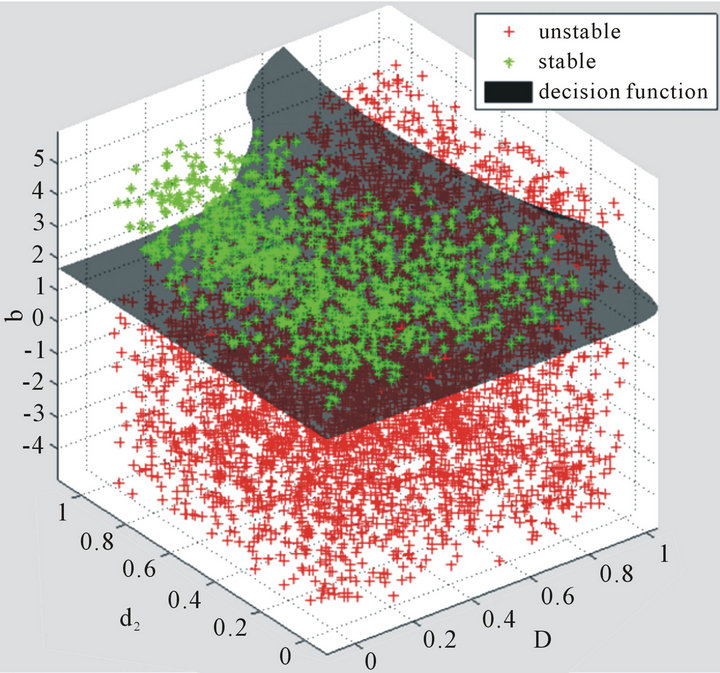
Figure 6. Stabilizing parameter region for Example 4.
The above examples have well illustrated the effectiveness of the proposed method which can be applied to a much wider range of systems than the existing methods in the literature.
6. Conclusions
This paper proposes a new and general method for determining the stabilizing parameter regions for delay control systems. We first take a certain number of random sample points in the parameter space. Next, we represent a delay control system in a unified state-space form. Then the numerical stability condition is developed and checked for sample points in the parameter space. These points are divided into two classes according to whether they can stabilize the system. The stabilizing parameter regions could be well defined by the decision function obtained from some learning method. The effectiveness of the proposed method is well illustrated with examples. The proposed method does not have essential constraints and has a wide range of applications. Note that our method could be applied to a higher-dimensional parameter space, though the stabilizing parameter regions are difficult to be shown by graphics.
It should be pointed out that the presented LMI stability criterion is only sufficient since it is based on Lyapunov theory. A sufficient and necessary stability criterion and the additional potential values of the proposed method are to be investigated in future works.
REFERENCES
- Q. Wang, C. Lin, Z. Ye, G. Wen, Y. He and C. Hang, “A Quasilmi Approach to Computing Stabilizing Parameter Ranges of Multi-Loop Pid Controllers,” Journal of Process Control, Vol. 17, No. 1, 2007, pp. 59-72. doi:10.1016/j.jprocont.2006.08.006
- S. Lee and Q. Wang, “Stabilization Conditions for a Class of Unstable Delay Processes of Higher Order,” Journal of the Taiwan Institute of Chemical Engineers, Vol. 41, No. 4, 2010, pp. 440-445. doi:10.1016/j.jtice.2010.03.001
- S. Lee, Q. Wang and C. Xiang, “Stabilization of All-Pole Unstable Delay Processes by Simple Controllers,” Journal of Process Control, Vol. 20, No. 2, 2010, pp. 235-239. doi:10.1016/j.jprocont.2009.05.005
- S. Lee, Q. Wang and L. Nguyen, “Stabilizing Control for a Class of Delay Unstable Processes,” ISA transactions, Vol. 49, No. 3, 2010, pp. 318-325. doi:10.1016/j.isatra.2010.03.006
- Z. Nie, Q. Wang, M. Wu and Y. He, “Exact Computation of Loop Gain Margins of Multivariable Feedback Systems,” Journal of Process Control, Vol. 20, No. 6, 2010, pp. 762-768. doi:10.1016/j.jprocont.2010.04.006
- L. Jinggong, X. Yali and L. Donghai, “Calculation of Pi Controller Stable Region Based on d-Partition Method,” 2010 International Conference on Control Automation and Systems (ICCAS), Gyeonggi-do, 27-30 October 2010, pp. 2185-2189.
- Q. Wang, B. Le and T. Lee, “Graphical Methods for Computation of Stabilizing Gain Ranges for Tito Systems,” 2011 9th IEEE International Conference on Control and Automation (ICCA), Santiago, 19-21 December 2011, pp. 82-87.
- Q. Wang, Y. He, Z. Ye, C. Lin and C. Hang, “On Loop Phase Margins of Multivariable Control Systems,” Journal of Process Control, Vol. 18, No. 2, 2008, pp. 202-211. doi:10.1016/j.jprocont.2007.06.004
- M. S¨oylemez, N. Munro and H. Baki, “Fast Calculation of Stabilizing Pid Controllers,” Automatica, Vol. 39, No. 1, 2003, pp. 121-126. doi:10.1016/S0005-1098(02)00180-2
- N. Tan, I. Kaya, C. Yeroglu and D. Atherton, “Computation of Stabilizing Pi and Pid Controllers Using the Stability Boundary Locus,” Energy Conversion and Management, Vol. 47, No. 18, 2006, pp. 3045-3058. doi:10.1016/j.enconman.2006.03.022
- B. Fang, “Computation of Stabilizing Pid Gain Regions Based on the Inverse Nyquist Plot,” Journal of Process Control, Vol. 20, No. 10, 2010, pp. 1183-1187. doi:10.1016/j.jprocont.2010.07.004
- E. Gryazina and B. Polyak, “Stability Regions in the Parameter Space: D-Decomposition Revisited,” Automatica, Vol. 42, No. 1, 2006, pp. 13-26. doi:10.1016/j.automatica.2005.08.010
- K. Saadaoui, S. Testouri and M. Benrejeb, “Robust Stabilizing First-Order Controllers for a Class of Time Delay Systems,” ISA transactions, Vol. 49, No. 3, 2010, pp. 277- 282. doi:10.1016/j.isatra.2010.02.001
- G. Calafiore, F. Dabbene and R. Tempo, “Research on Probabilistic Methods for Control System Design,” Automatica, Vol. 47, No. 7, 2011, pp. 1279-1293. doi:10.1016/j.automatica.2011.02.029
- T. Hastie, R. Tibshirani and J. H. Friedman, “The Elements of Statistical Learning: Data Mining, Inference, and Prediction,” Springer, New York, 2009. doi:10.1007/978-0-387-84858-7
- C. C. Chang and C. J. Lin, “LIBSVM: A Library for Support Vector Machines,” ACM Transactions on Intelligent Systems and Technology (TIST), Vol. 2, No. 3, 2011, p. 27. doi:10.1145/1961189.1961199
- F. Zheng, Q. Wang and T. Lee, “On the Design of Multivariable PID Controllers via LMI Approach,” Automatica, Vol. 38, No. 3, 2002, pp. 517-526. doi:10.1016/S0005-1098(01)00237-0
- G. Franklin, J. Powell, A. Emami-Naeini and J. Powell, “Feedback Control of Dynamic Systems,” , Vol. 3, Addison-Wesley, Reading, 1994.
- K. Gu, V. Kharitonov and J. Chen, “Stability of TimeDelay Systems,” Birkhauser, Boston, 2003. doi:10.1007/978-1-4612-0039-0
- V. Vapnik, “The Nature of Statistical Learning Theory,” 1995.
- S. R. Gunn, “Support Vector Machines for Classification and Regression,” ISIS Technical Report, Vol. 14, 1998.
- P. H. Chen, C. J. Lin and B. Schölkopf, “A Tutorial on ν- Support Vector Machines,” Applied Stochastic Models in Business and Industry, Vol. 21, No. 2, 2005, pp. 111- 136.
NOTES
*This research is funded by the Republic of Singapore’s National Research Foundation through a grant to the Berkeley Education Alliance for Research in Singapore (BEARS) for the Singapore-Berkeley Building Efficiency and Sustainability in the Tropics (SinBerBEST) Program. BEARS has been established by the University of California, Berkeley as a center for intellectual excellence in research and education in Singapore.

