Journal of Intelligent Learning Systems and Applications
Vol.4 No.2(2012), Article ID:19257,7 pages DOI:10.4236/jilsa.2012.42011
Clustering Analysis of Stocks of CSI 300 Index Based on Manifold Learning
![]()
1International School of Software, Wuhan University, Wuhan, China; 2Institute of High Energy Physics, Chinese Academy of Sciences, Beijing, China.
Email: *hjcai@whu.edu.cn
Received November 5th, 2011; revised March 2nd, 2012; accepted March 10th, 2012
Keywords: Manifold Learning; Isomap; Nonlinear Dimensionality Reduction; Stock Clustering
ABSTRACT
As an effective way in finding the underlying parameters of a high-dimension space, manifold learning is popular in nonlinear dimensionality reduction which makes high-dimensional data easily to be observed and analyzed. In this paper, Isomap, one of the most famous manifold learning algorithms, is applied to process closing prices of stocks of CSI 300 index from September 2009 to October 2011. Results indicate that Isomap algorithm not only reduces dimensionality of stock data successfully, but also classifies most stocks according to their trends efficiently.
1. Introduction
Clustering analysis of stocks is necessary when investigating in stocks, Yu and Wang [1] proposed an approach in which kernel principal component analysis is used to reduce the dimensionality of data and k-means clustering method is used to cluster the reduced data so that stocks can be divided into different categories in terms of their financial information. Xu et al. [2] apply unsupervised self-organizing map network, also called SOM, to analyze and cluster stocks. Zhou et al. [3] apply clustering analysis in stock investment. By a synthetic evaluation index system to measure the similarity of stocks, investors can use the evaluation deciding scope and supposing possible variation of stock price. All above studies used financial indicators of the companies, like asset ratio, current ratio, EPS (Earning per share), ROE (Return on Equity), as foundation of estimation dividing stocks into Blue-chip stocks and junk stocks. The results provided us with a good basis of assessing merits of stocks. Assaleh et al. [4] predict stock price in the Dubai Financial Market from historical price data using the Polynomial Classifiers (PC) and Artificial Neural Networks (ANN). Qin Qin et al. [5] use two different types of prediction models and multiple technical indicators to predict the Shanghai Composite Index returns and price volatility. These methods are proved to be effective by experiments.
In this paper, we will use closing price of stocks and cluster these stocks according to their trends. Stock movement is volatile and uncertain. But from stock charts, difference of trends between different stocks reflects on their price, whether they are rising or dropping and the degree of their movements. That is to say, though stock data is high-dimensional and nonlinear, there are only three underlying parameters. As for how to find these underlying parameters, manifold learning provides a good solution.
Manifold learning is an important field of machine learning which acquires very good achievements in exploring inner law of nonlinear data. It assumes data is even sampled from a low dimensional manifold embedded in a high dimensional Euclidean space. The purpose of manifold learning is to learn this low dimensional manifold from high dimensional data, to get the relevant embedded mapping and finally to reduce the dimension of the data and realize visualization.
Isomap (Isometric Feature Mapping) and LLE (Locally Linear Embedding) are two very famous nonlinear dimensionality reduction algorithm. Isomap which is proposed by Tenenbaum [6] and his workmates get approximate geodesic distance from shortest path of nearest neighbor graph firstly to instead Euclidean distance which cannot represent the inner manifold structure. And then input geodesic distances into MDS to find the low dimensional coordinate embedded in high dimensional space. LLE which is proposed by Roweis and Saul [7] can map high dimensional input data to a global low dimensional coordinate, and maintain relation of neighbors, thus keep original topology structure for data after dimensionality reduction.
Some scholars use these data dimensionality reduction methods into other fields and get many interesting results. Reference [8] use shapes of mouth as input of LLE and get a low dimensional manifold. Then finding curves of each word formed on manifold, by analyzing these curves we can read the lip language. Reference [9] improve the conventional Isomap algorithm by utilizing class membership for measuring distance of data pair so as to find a low-dimensional manifold preserving the distance between classes as well as the distance between data points. Through computational experiments on artificial data sets and real facial data sets, they confirm that the proposed method gives better performance than the conventional Isomap. Reference [10] does the emulation experiment of EEG (electroencephalogram) generation source by combining Isomap and SVM (Support Vector Machine). Combining with Rényi entropy, manifold learning is used on face recognition in Reference [11].
The present paper is organized as follows. In section 2, the source of experiment data and their pre-processing is introduced. In section 3, Isomap is applied to stocks’ clustering. In section 4, we compare the results of stocks’ clustering using LLE with using Isomap. And section 5 concludes the whole paper.
2. Data Selection and Pre-Processing
CSI (China Securities Index) 300 Index reflects overall trends of A-share market and review of changes of stocks prices of Chinese stock market whose samples cover 60% of capitalization of Shanghai and Shenzhen market. It has a good representation of market. So we choose stocks of CSI 300 Index as our experimental subjects.
We take closing price of these 300 stocks for 500 days from September 22nd, 2009 to October 18th, 2011. When the stock stopped quotation on the exchange, we use the closing price of the day before to fill the gap. If the listing of a stock was after September 22nd, 2009, we use closing price of its first day of listing to fill the data of early days.
So we can get 300 data points, the dimensionality of each data point is 500. Since we don’t care about the exact price of each stock, but their trends compared to others. To eliminate the influence of absolute price, we normalize them to z-score on the basis of a local mean and standard deviation. The standardized data are consistent with normal distribution, that is to say, their means equal zero and standard deviations equal one. The formulas are as follows:
 (1)
(1)
 , (2)
, (2)
 (3)
(3)
 represents original data of row i column j,
represents original data of row i column j,  represents standardized data of row i column j,
represents standardized data of row i column j,  represents mean of original data of column j,
represents mean of original data of column j,  represents standard deviation of original data of column j. In this experiment, i is from 1 to 500, j is from 1 to 300. With so many data points to observe, we number them from 1 to 300 and divide them into 5 groups, each group corresponds to one color on the distribution graph, and data points of same color are not necessarily in a same classification.
represents standard deviation of original data of column j. In this experiment, i is from 1 to 500, j is from 1 to 300. With so many data points to observe, we number them from 1 to 300 and divide them into 5 groups, each group corresponds to one color on the distribution graph, and data points of same color are not necessarily in a same classification.
3. Clustering Analysis of CSI 300 Stocks Using Isomap
3.1. Dimensionality Reduction of the Stocks
We run Isomap codes1 on MATLAB 7.6 (R2008a). By changing the value of parameter k, we get a series of residual variance graphs and data distribution graphs which are low dimensional embedding recovered by Isomap. Residual variance graph (Figure 1) can help to test the effectiveness of dimensionality reduction and decide the low dimension in which data embedded. Data distribution graph (Figure 2) can help to observe results of stock clustering directly.
Figure 1 shows the residual variance graph when k = 7. When changing the value of k, we get nearly same results, so we use k = 7 as an example to analyze the results. X-Label represents dimensionality; Y-Label represents residual variance. Residual variance decreases as the dimensionality is increased [10]. With increasing of dimensionality, it is getting close to true dimension, error between current and true dimension is reducing, so value of residual variance is decreasing. Curves in Figure 1 reduced as dimensionality increased, so dimensionality reduction of stock data by Isomap is successful.
The “intrinsic” dimensionality of the data can be estimated by looking for the “elbow” at which this curve ceases to decrease significantly with added dimensions [6]. Before the “elbow point”, error between current and true dimensionality is huge. After the “elbow point”, errors of these dimensionalities between true dimensionality are nearly the same. Since we need to observe how data points distribute after dimensionality reduction directly, we need to choose a low dimension while keep the error as small as possible. So “elbow point” is the best choice. In Figure 1, arrow marks the true or approximate dimensionality which is two, so the data points distribute on a two-dimensional rectangular plane coordinate system.

Figure 1. Residual variance graph when k = 7.

Figure 2. Data point distribution graph of stocks of CSI 300 Index when k = 7 (because of so much points, we use different colors to distinguish them). Trend curves of 8 groups (A1-A8) of stocks circled in this figure will be compared in Figure 3, each number in this graph represents a stock listed in Table 1.
3.2. Clustering Analysis of the Stocks
During the process of dimensionality reduction, Isomap produces data point distribution graph in which data points distribute on a two-dimensional rectangular plane coordinate system (Figure 2). As we can see, except a pile of points at left bottom,most points on the map distribute evenly. We choose 8 groups of them to compare their trends curves. Information of these stocks is in Table 1. Points of each group are close to each other in Figure 2, if Isomap can cluster stocks according to their trends, stocks in same group should have similar trend.
From comparisons of these stock trends in Figure 3, we can see stocks of same group from A1 to A6 are similar both in overall trends and the ups and downs at the same time. While stocks trend curves of same group in A7 and A8 are different from each other. In Figure 2, group A1 and A6 are far apart whose trends are different from each other (Figure 3). So points with different trend do not distribute together.
4. Comparison of LLE and Isomap
We also use LLE2, another manifold learning algorithm to processing and clustering the same stocks. In this experiment, we reduce the dimensionality of stock data to 2, and map these data to a two-dimensional rectangular plane coordinate system (Figure 4). We also choose 8 groups of points to compare their trend curves. The results are in Figure 5.
From the comparison in Figure 5, we can see that LLE can clustering the stocks that have similar trend curves, but the similarity is not as high as Isomap.
We also conduct following experiments: 1) the chosen stocks distribute together after being processed using Isomap, and are apart from each other after being processed using LLE. The trends of these stocks are highly similar; 2) the chosen stocks distribute together after being processed using LLE, and are apart from each other after being processed using Isomap. The trends of these stocks are not so similar with each other. We conclude that Isomap is more effective in clustering stocks.
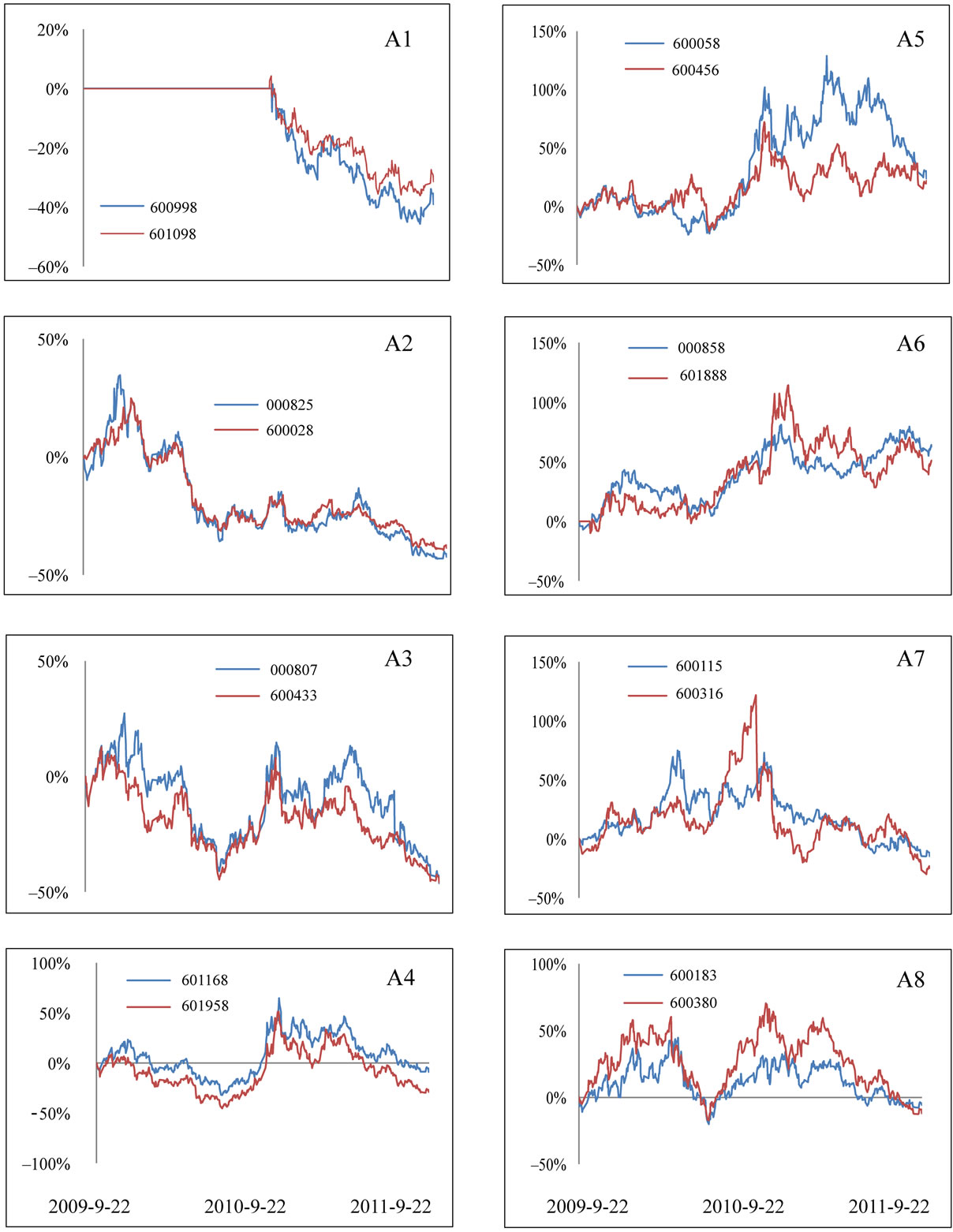
Figure 3. Comparison of trend curves of sample stocks chosen in Figure 2, horizontal axis represents time; vertical axis represents relative variation of stock price.

Figure 4. Data point distribution graph of stocks of CSI 300 Index after being processed using LLE. Trend curves of 8 groups (B1-B8) of stocks circled in this figure will be compared in Figure 5, each number in this graph represents a stock listed in Table 2" target="_self"> Table 2.

Figure 5. Comparison of trend curves of sample stocks chosen in Figure 4, horizontal axis represents time, vertical axis represents relative variation of stock price.
5. Conclusions
In this paper, we use Isomap processing closing price of stocks of CSI 300 Index. Results show that Isomap algorithm can reduce dimensionality of these high dimensional data. Reduced data points distribute in a two-dimensional coordinate system. By choosing and observing sample points, we find that for most points which distribute together have similar trend, for which distribute away from each other have different trend. There are also points with different trends distributing together. Since most stocks clustering are successful, we think Isomap can cluster stocks according to their trend.
By comparing the effects of clustering by Isomap and by LLE, we consider Isomap as a more effective method. Isomap is a global geometric manifold learning algorithm which is based on MDS (Mutidimensional Scaling). It makes every effort to keep the intrinsic geometry of data points, which is to preserve the geodesic distances between two points. For neighboring points, input-space distance provides a good approximation to geodesic distance. For faraway points, geodesic distance can be approximated by adding up a sequence of “short hops” between neighboring points [6]. While LLE recovers global nonlinear structure from locally linear fits [7]. Isomap plays a better role.
6. Acknowledgements
This study is partly supported by the Basic Research Program of China/973 Project, Basic Research on Data Storage System Theory and Technology for Complex Application Environment, 2011CB302306. The authors would like to thank reviewers for their helpful comments.
REFERENCES
- L.-A. Yu and S.-Y. Wang, “Kernel Principal Component Clustering Methodology for Stock Categorization,” System Engineering—Theory & Practice, Vol. 29, No. 12, 2009, pp. 1-8.
- Z.-C. Xu, Y.-C. Liang and X.-H. Shi, “Analysis Method of SOM-Based of Stock Clustering,” Computer Engineering and Design, Vol. 29, No. 9, 2008, pp. 2426-2428.
- Z.-H. Zhou, W.-N. Chen and Z.-Y. Zhang, “Application of Cluster Analysis in Stock Investment,” Journal of Chongqing University, Vol. 25, No. 7, 2002, pp. 122-126.
- K. Assaleh, H. El-Baz and S. Al-Salkhadi, “Predicting Stock Prices Using Polynomial Classifiers: The Case of Dubai Financial Market,” Journal of Intelligent Learning Systems and Applications, Vol. 3, No. 2, 2011, pp. 82-89.
- Q. Qin, Q.-G. Wang, S.-Z. S. Ge and G. Ramakrishnan, “Chinese Stock Price and Volatility Predictions with Multiple Technical Indicators,” Journal of Intelligent Learning Systems and Applications, Vol. 3 No. 4, 2011, pp. 209-219.
- J. B. Tenenbaum, V. de Silva and J. C. Langford, “A Global Geometric Framework for Nonlinear Dimensionality Reduction,” Science, Vol. 290, No. 5500, 2000, pp. 2319-2323. doi:10.1126/science.290.5500.2319
- S. T. Roweis and L. K. Saul, “Nonlinear Dimensionality Analysis by Locally Linear Embedding,” Science, Vol. 290, No. 5500, 2000, pp. 2323-2326. doi:10.1126/science.290.5500.2323
- M. Aharon and R. Kimmel “Representation Analysis and Synthesis of Lip Images Using Dimensionality Reduction,” International Journal of Computer Vision, Vol. 67, No. 3, 2006 , pp. 297-312, doi:10.1007/s11263-006-5166-3
- M. Cho and H. Park “Nonlinear Dimension Reduction Using ISOMap Based on Class Information,” Proceeding of International Joint Conference on Neural Networks, Atlanta, June 14-19, 2009, pp. 2830-2834.
- J. Liu, “Isomap Algorithm and Its Application to the Classification of EGG Generation Source,” Hebei University of Technology, Tianjin, 2006.
- W.-M. Cao and N. Li, “Face Recognition Based on Manifold Learning and Rényi Entropy,” Journal of Intelligent Learning Systems and Applications, Vol. 2 No. 1, 2010, pp. 49-53.



