Journal of Water Resource and Protection
Vol.08 No.07(2016), Article ID:67491,19 pages
10.4236/jwarp.2016.87059
Reciprocal Analysis of Sensible and Latent Heat Fluxes in a Forest Region Using Single Height Temperature and Humidity Based on the Bowen Ratio Concept
Toshisuke Maruyama*, Manabu Segawa
Faculity of Environmental Science, Ishikawa Prefectural University, Ishikawa, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 April 2016; accepted 17 June 2016; published 20 June 2016
ABSTRACT
Evapotranspiration in forests has been researched for a long time because it serves an important role in water resource issues and biomass production. By applying the reciprocal analysis based on the Bowen ratio concept to the canopy surface, the sum result of sensible and latent heat fluxes, i.e., actual evapotranspiration (ET), is estimated from engineering aspect using the net radiation (Rn) and heat flux into the ground (G). The new method uses air temperature and humidity at a single height by determining the relative humidity (rehs) using the canopy temperature (Ts). The validity of the method is confirmed by the latent heat flux (lE) and sensible heat flux (H) observed by mean of eddy covariance method. The heat imbalance is corrected by multiple regression analysis. The temporal change of lE and H at the canopy surface is clarified using hourly and yearly data. Furthermore, the observed and estimated monthly evapotranspiration of the sites are compared. The research is conducted using hourly data and the validation of the method is conducted using observed covariance at five sites in the world using FLUXNET.
Keywords:
Bowen Ratio, Eddy Covariance, Reciprocal Determination, Estimation of Evapotranspiration, Canopy Surface Temperature and Humidity

1. Introduction
Reasonable water resource planning requires estimation of actual evapotranspiration. Many relevant research projects have provided useful results; however, the research is still incomplete. Existing research uses theoretical, observational (eddy covariance and Bowen ratio methods), and experimental approaches (the complementary relationship method). All of the above approaches are based on aerodynamic theory, including the heat balance approach, but excluding the complementary relationship.
The eddy covariance method [1] is very useful for estimating evapotranspiration. Latent heat flux (lE) has been observed directly by the eddy covariance method, but the heat balance relationship sometimes is not guaranteed [2] . On the other hand, the value of eddy covariance represents only the sensible heat flux (H); therefore, the latent heat flux (lE) must be estimated to determine by the heat imbalance. Unfortunately, the observation sites of eddy covariance are rarely included in common climate observations although evapotranspiration remarkably affected by regional ecosystem and local climate elements.
In contrast, the Bowen ratio method [3] is commonly used, but its evaluation requires the air temperature and humidity at least two heights. Unfortunately, two heights are rarely included in common climate observations despite their usefulness.
The complementary relationship method is based on the hypothesis that the actual plus potential evapotranspiration is twice the equilibrium evaporation [4] - [6] . However, the method has a limited ability to evaluate the equilibrium evaporation state. The method sometimes uses an empirical coefficient [7] , but this constant is still unclear because it varies by location.
In the natural world, the air temperature and humidity is determined by H and lE from the net radiation (Rn) and heat flux into the ground (G). Thus, our research attempts the reciprocal estimation of H and lE from the not observed humidity (rehs) while satisfying the heat balance relationship using the canopy surface temperature (Ts). The concept is different from that of the other relevant methods, and it only requires Rn, G and common climate measurements, including the air temperature and humidity at a single height.
In the proposed method, the unknown variables, relative humidity at the canopy surface (rehs) were determined reciprocally with keeping heat balance relationship by the non-linear optimization technique known as the general reduced gradient (GRG) attached in the Excel Solver (Appendix 1).
2. Methods
2.1. Theoretical Background
2.1.1. Fundamental Concept of the Model
The proposed model considers the above of near-canopy as shown in Figure 1. Net radiation moves from the air to the canopy and soil surface, and it is portioned into sensible, latent and underground fluxes. Ts is the canopy surface temperature including plant zone, Tz is the air temperature above the canopy at height z, q (Tz) is the specific moisture at height z, rehz is the relative humidity in air at height z, q (Ts) is the unsaturated specific moisture on the canopy surface including plant zone, and qsat (Ts) is the saturated specific moisture at the same height of q (Ts). In addition, the meaning of observed Tz and rehz in the method describe in discussion section.
The fundamental formulae of the model satisfy the following well known heat balance relationship [3] . The relationship, i.e., energy conservation theorem, is a fundamental concept in the natural world that must be guaranteed at anywhere and anytime.
Heat balance relationship:
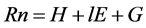 (1)
(1)
Here, Rn is the net radiation flux (W∙m−2), G is the heat flux into the canopy and ground (W∙m−2), H is the sensible heat flux (W∙m−2), and lE is the latent heat flux (W∙m−2). In addition, although there is heat flux stored in the canopy and plant zone, the effect of stored heat flux appeared on G, Ts and rehs.
On the other hand, the Bowen ratio (H∙lE−1) is defined as follows with assuming continuity relationship of the H and lE between two heights [3] :
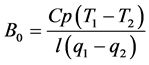 (2)
(2)
We apply the relationship on the canopy zone (including plant zone) as in Figure 1, i.e., the Bowen ratio con- cept is applied to the layer between the canopy zone and the observation height of the air temperature and humidity by assuming Ts and q (Ts). The reason is as follows: The Ts and q (Ts) in the canopy zone are usually
Figure 1. Component of the model and the relevant symbols.
unknown and difficult to observe. If we try to observe, the observation position usually can’t be specify. This application results in the following:
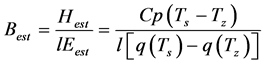 (3)
(3)
The specific moisture on the canopy zone is expressed as follows as a function of Ts:
 (4)
(4)
Here, l is the latent heat flux of evaporation (kJ∙kg−1), Cp is the specific heat of the air at a constant pressure (1.004 kJ∙kg−1∙K−1).
According to the above definition of Ts and rehs, the two items are somewhat symbolic and comprehensive concept that did not specify the position. The other variables in Equation (3) and Equation (4) can be expressed by the following well-known equations:
Saturated specific moisture:
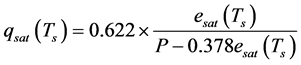 (5)
(5)
Saturated vapor pressure:
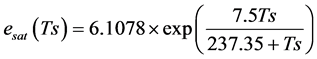 (6)
(6)
Latent heat flux of evaporation
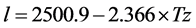 (7)
(7)
where P is the atmospheric pressure (hPa).
2.1.2. Governing Equation for Determining the Unknown Variables by the Proposed Method
The purpose of the optimization is to determine the unknown variables Ts and q (Ts) in Equation (3) without measurements, but with Ts sometimes observed. The governing equation to be solved is obtained by inserting Equation (3) into Equation (1). Initially, if Ts was observed, rehs is only assumed because
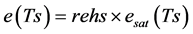 . Equation (1) is not as closed as Equation (8) because of the assumptions for rehs. The equation is expressed as follows:
. Equation (1) is not as closed as Equation (8) because of the assumptions for rehs. The equation is expressed as follows:
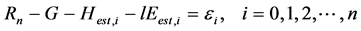 (8)
(8)
The objective function is εi that goes to a minimum by repeating calculation using Equation (8) and Equation (3) in the optimization process.
The rehs can be unified mathematically because a governing Equation (8) determined a variable rehs.
After optimization completed, i.e., Best in Equation (3) goes to B0, lE and H can be obtained as follows.
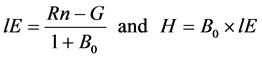 (9)
(9)
The equation is nonlinear for Ts and q (Ts). Thus, an analytical solution is not available. Therefore, a numerical method was applied. Note that the other factors were obtained from observations or calculated independently using the aforementioned relationships. In addition, the analysis was conducted essentially using hourly data and summarized daily because the climate element change remarkably throughout a day.
The rehs in Equation (4) for estimating q (Ts) was assumed initially to be rehz because the humidity on the canopy has not remarkably different. The rehs was automatically modified.
The calculation follows a non-linear optimization procedure that employs a General reduced Gradient (GRG) algorithm, which can be applied with the Excel Solver on a personal computer (Appendix 1 and Appendix 2).
2.2. Investigation Site and Equipment
To examine the validity of proposed method, five sites were chosen throughout the world as identified in Table 1: one site in Japan, China and Europe and two sites in the USA. The data of all sites were prepared by FLUXNET [8] - [12] . Table 1 shows the name of the sites, country, state/province, location, elevation, vegetation, tower height, canopy height and year of data examination. The examined year was chosen to minimize the data gaps.
Table 2 describes the type of applied instruments with the variables of the heat balance components, unit and description of those measurements, including soil temperature (To) measurement depth Tx. The temperature Ts is obtained by calculation from observed RglOut by radiometer that is setting at higher position than the canopy height. Therefore, the Ts represent the temperature not only canopy surface but also inside of canopy including ground surface.
2.3. Heat Balance Relationship at the Observed Sites
To investigate the accuracy of observed data, Table 3 describes the heat balance relationship of observations at the tested sites expressed in heat flux. The imbalance was estimated by 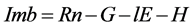 using yearly data and an imbalance ratio defined as
using yearly data and an imbalance ratio defined as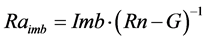 . The Raimb ranged from −0.05 (US-Slt) to 0.37 (CN-Cha) with an average of 0.16 (the upper low of Table 3 in each of the sites). Especially, although the coefficient for H at CN-Cha show remarkably different of the other sites. The results are almost the same as those of Wilson’s [13] . The annual precipitation of the examined year is also shown in Table 3.
. The Raimb ranged from −0.05 (US-Slt) to 0.37 (CN-Cha) with an average of 0.16 (the upper low of Table 3 in each of the sites). Especially, although the coefficient for H at CN-Cha show remarkably different of the other sites. The results are almost the same as those of Wilson’s [13] . The annual precipitation of the examined year is also shown in Table 3.
Table 1. Features of the tested sites.
Table 2.Measurement instruments of the tested sites including Tx.
Table 3. Heat balance relationship of the tested sites (unit: heat flux).
Observed: Observed by eddy covariance method. Corrected: Corrected by multiple regression analysis. Raimb =: Imb∙(Rn + G) −1. *Annual average precipitation.
2.4. Correction of the Heat Imbalance by Multiple Regression Analysis
The heat imbalance mentioned above is well known as a “closure issue”. Twine et al. [14] indicate approximately under 10% - 30% variation in H and lE. Wilson et al. [13] also indicate approximately under 20% of the imbalance. Allen [2] suggests that the under-measurement of lE is approximately 40%. Table 1 describes the imbalance in the heat energy. Therefore, the data should be correct. According to Allen’s procedure, we corrected the data by multiple regression analysis using the observed data as follows.

Here: Rn is the net radiation, G is the heat flux into the ground, lE is the latent heat flux, H is the sensible heat flux. A is the regression coefficient for lE, B is the regression coefficient for H.
In Equation (10), Rn and G is fixed due to observed error will be small than lE and H [2] .
Table 3 also describes the corrected data that are applied in the regression analysis. To guarantee the heat balance relationship, all of the sites primarily used the corrected data. In addition, the correction is conducted using the daily data.
2.5. Initial Values for Ts and rehs and the Constraints for Estimation
The initial values of Ts and rehs are key factors for obtaining a reliable result. The value of Ts is chosen from observed values collected by the radiometer on the canopy surface, the initial value of rehs is set to be the same as the rehz. The reason describe in discussion section.
The ε values have very small values on the order of 10−15 W∙m−2 initially (before optimization) because Best, by the assumptions of Ts and rehs, nearly satisfies the heat balance relationship. Therefore, the objective function is multiplied by 1015. The small value has not influenced the accuracy of analysis because the Best is a ratio of Hest and lEest, even if a slight residual can be expected in the objective function (ԑ). To avoid abnormal fluctuations of H and lE, constraints on those variables are set at less than (Rn − G). Also, the constraints for Best are set at −100 < B0 < 100 by referring to the actual data, even though there are some exceptions. The reason for these exceptions is described in the discussion section. In addition, Equation (8) applied for the data of each unit time.
3. Results
3.1. Conversion of Observed Data (Hobs and lEobs) into Corrected Data (Hcor and lEcor, or Himb and lEimb)
Observed data does not achieve the heat balance relationship, as shown in Table 3. To maintain the heat balance relationship, multiple regression analysis is applied using Equation (10). Figure 2 describes the relationship (Rn − G) versus (H + lE) of the original and corrected data in which the observed data are shown in the red circle while the corrected data are shown in the blue circle. The slope of the five tested sites increased and approached to 1.0. The regression coefficients described in Table 4 are A for H and B for lE. The coefficients differ site by site, having no comprehensive tendency. The correction coefficients ranged from 0.966 to 1.570 for H with an average of 1.169 and ranged from 0.755 to 1.534 for lE with an average of 1.178. The observed data are corrected using these coefficients for all of the tested sites. The corrected data of H and lE also describes in Table 3 as “corrected”. In addition, the imbalance is corrected in another way: 

The corrected result describe in the corrected column (lower low) in Table 3 that resulted in −0.05 ~ 0.05 of the Raimb resulting in remarkably improved the heat balance relationship.
Figure 2. Correction of observed data by multiple regression analysis P value of any cases were less than 0.05.
Table 4. Regression coefficients for H and lE.
3.2. Comparison of the Hourly Change of lE and H
To confirm the validity of the method, Figure 3 compares the hourly change in the corrected latent and sensible heat flux, lEcor and Hcor with estimated lEest and Hest at five sites in summer. The lEest agreed well with lEcor and the Hest agreed with Hcor but there were small differences. The small differences in lEest were reflected in Hest.
On the other hand, the fluctuation may occur due to the unstable B0 estimated. However, the heat balance is not achieved instantaneously because of heat storage; it requires a few hours [3] . Thus, the figure adjusts to a five-hour moving average. The pattern of the lE and H changes was quite similar for all of the sites of for both the observed and estimated. This fact describes the reasonability of our method.
3.3. Comparison of the Observed versus Estimated lE and H
To confirm the validity of the method, Figure 4 compared, the observed versus estimated data of lE and H by the proposed method using the observed Ts by long wave radiation (radiometer) at five sites. All sites of estimated values almost consistent with observed because the gradient (slope of the straight line) of the observed
Figure 3. Hourly change of the observed and estimated lE and H (W∙m−2).
Figure 4. Comparison of observed and estimated lE and H (W∙m−2). P value of any cases were less than 0.05.
versus estimated relationship is very near 1.0; In detail, For lEcor, FR-Pue, JP-Tom, CN-Cha and US-Slt almost coincide (<±15%), but a little smaller at US-WCr (>±15%). For Hcor CN-Cha and US-Slt are a little smaller than 1.0 (<±15%) while the other sites are more smaller. The R2 determination coefficient for the five cases in the lE shows good coincidence (>±60%) except JP-Tom while not so good for H except CN-Cha and US-Slt. From the above facts, the estimated lE and H coincided well with the observed data.
3.4. Temporal Change of the Estimated and Observed lE, H, rehs and B0
To investigate the temporal change in the estimated and observed lE and H, Figure 5 describes the changes of those variables throughout the year for the five sites.
The estimated lE and H were almost all reproduced well by the observed throughout the year. However, the late summer in FR-Pue, spring in JP-Tom and spring and autumn in US-WCr have a small difference in lE. H is
Figure 5. Temporal change of observed and estimated lE and H (W∙m−2).
almost all well reproduced but summer in US-WCr has a small difference. The B0 changes remarkably in winter while is relatively stable in other seasons (B0 are not shown). If the constraints (−100 < B0 < 100) cannot be applied, the abnormal changes of B0 occurred not only winter but also in another season.
The pattern of the temporal change of lE, H and B0 was quite similar for all sites. From the above results, the proposed method was satisfactory in describing the aspects of temporal change of the data.
3.5. Hourly Change of Humidity and Temperature
To investigate more detail the humidity and temperature. Figure 6 describes those changes. Left side of Figure 6 shows the relationship between rehz and rehs. The estimated rehs approaches track rehz in all times. Right
Figure 6. Hourly change of humidity and temperature.
side of Figure 6 describes the relationship of observed temperatures. The blue line indicate the difference Ts and Tz. The red line indicate the difference of To and Tz, To is temperature near the soil surface, The both line changes to opposite side periodically with site specific features. The difference of the blue line (Ts-Tz) and red line (Ts-To) is storage effect of the heat flux. The lag time of the peaks between (Ts-Tz) and (Ts-To) is required several hours, i.e., the time between red line to blue line peak. That justifies the five hour moving average of calculated data aforementioned.
3.6. Temporal Change of Humidity and Temperature
To investigate the temporal change in the estimated and observed relative humidity, left side of Figure 7 describes the changes of rehz and rehs throughout the year for the five sites. The estimated rehs track rehz in all seasons. The right side of Figure 7 describes the relationship of observed temperatures. The blue line indicates the difference Ts and Tz. The line moves around zero, but a little lower at FR-Pue, JP-Tom and US-Slt whereas a little higher at CN-Cha and US-WCr at early Spring.
Figure 7. Temporal change of humidity and temperature.
3.7. Monthly Change in Evapotranspiration (ET)
The monthly change of the ETcor and ETest is described in Figure 8 at the five sites. The ET is estimated at 100 W∙m−2 equivalent for 3.53 mm/day [15] , which assumes the latent heat is constant. The ET per month is an estimated monthly average except for the abnormal data. The figure shows that the observed values of ETcor were mostly reproduced by the estimates of ETest at the five sites. However, the feature is site specific. The ETcor well consistent at FR-Pue, CN-Cha and US-Slt while the other sites indicate slight difference. The observed values were not consistent at FR-Pue, JP-Tom, CN-Cha while relatively consistent at US-Slt (not shown). This fact indicates that the proposed method functioned reasonably well as an estimation of ET.
Total amount of evapotranspiration ETest, ETcor, ETobs and ETimb described in Table 5. The total amount of ETest in year well reproduced ETcor. This fact describes the reasonability of the proposed method in aspect of total ET in a year which utilize for water resources planning.
Figure 8. Monthly change of evapotranspiration (ET) (mm∙month−1).
Table 5. Yearly evapotranspiration of various methods for the tested sites (mm∙year−1).
Note: ETest: Estimation by proposed method. ETcor: Corrected by multiple regression analysis. ETimb: Imbalnce by eddy correlation. ETobs: Observed by eddy correlation. Latent heat flux 100 w/m2 equivalent for 3.53 mm∙day−1 of evaporation (Kondo 2015).
4. Considerations
4.1. Effect on Initial Values of rehs on lE and H at JP-Tom and CN-Cha
The selection of the initial value of rehs is a very important issue because of the sensitivity of rehs on the convergence of Equation (8) is not so remarkable. Table 6 describes the effect of the initial values on the estimated and observed lE and H by various rehs, as an example, in case of the initial values changes 0.90, 0.95, 1.00, 1.05
Table 6. Slope of estimated versus observed lE and H with initial values of rehs∙rehz−1 (daily).
and 1.10 times of the rehz, respectively. The slope shows a slight difference in the converged values, the case of rehs = 1.0 is mostly reasonable because the slopes of the observed and estimated lE and H approach to balanced. Therefore, the initial value of rehs is set at 1.0 in the research. The rehs on the canopy will be nearly equals as the rehz observed.
4.2. Effect on Observed Data Correction (JP-Tom)
The observed data are corrected in three ways: using multiple regression analysis, imbalance and the observation itself because the observed data do not guarantee the heat balance relationship. To investigate the effect of the correction on lE and H, Figure 9 describes the relationship among three methods at the JP-Tom site, as an example. The corrected data describes relatively reasonable in lEest but not so reasonable in Hest, whereas lEobs and Hobs indicate the opposite tendency of the correction. The slope of lEimb and Himb describes an underestimation. The lEobs versus lEest describes the lowest in lE while the highest in H. The data corrected by regression analysis were not always guaranteed reasonability, therefore, the other method should be referred. In other word, the specification of better method among correction, observed and imbalance is difficult at present.
4.3. Comparison of Another Method of Correction of H and lE
To compare another method of correction of lE and H for all sites investigated, Table 7 describes the slope of the various methods versus that estimated by our method.
Case 1 (first column) of Table 7 describes the results of the analysis of the revised data using the multiple regression. Case 2 (second column) describes the results of the analysis of the original (observed) data itself, and Case 3 (third column) describes the results of the analysis using the imbalance data (lEimb = Rn − G − H). Case 2 and Case 3 are references of Case 1. If the slope is greater than 1.0, i.e., overestimate, while a slope less than 1.0 is an underestimate, as mentioned previously. The data describes relatively site specific.
For Case 1, the underestimation (>15%) of lE occurs for US-WCr, while the underestimation not occurs. The underestimation of H occurs for FR-Pue, JP-Tom and US-WCr, while the overestimation not occurs. For Case 2, the overestimation (>1.15) of lE occurs for FR-Pue and CN-Cai while underestimation occurs for JP-Tom and US-Slt. Overestimation of Hobs occurs at CN-Cha while underestimation occurs at FR-Pue, while underestimation occurs at FR-Pue. For Case 3, the underestimation of lE occurs at JP-Tom, CN-Cha and US-WCr, while for H it occurs for all sites. The overestimation of lEimb and Himb not occurs.
4.4. Exceptions of the Abnormal Estimated and Observed Data
The observed data contain some abnormal data that may reflect the observational quality. Abnormal data, defined as (Rn − G) > (lE or H), sometimes appear at or near 0˚C in the winter and in the early morning in other seasons. This criteria needs in convergence process rather than actual phenomena to prevent the abnormal fluctuation i.e., overestimation of H reflect to underestimation of lE and vice versa. The analyses were conducted without the abnormal data.
5. Discussion
5.1. Abnormal Fluctuation of Best
In the convergence process, if Ts approaches zero apparently, when the difference of Ts and Tz is constant at
Figure 9. Comparison of lE versus H by corrected, observed and imbalance at JP-Tom (W∙m−2). P value of any cases were less than 0.05.
Table 7. Slope between estimated and observed lE and H (daily).
1.0˚C for example, the Best is remarkably increased around zero from the opposite side, both positive and negative, as shown in Figure 10. This tendency (singularity) is almost independent of (Ts-Tz) even though there are small differences. Actually, when rehs approaches to rehz∙[qsat (Tz)∙qsat (Ts)−1], the abnormal Best appeared. The phenomenon occurs sometimes in the winter season because Ts approaches zero ˚C and occurs sometimes in the
Figure 10. Relationship between B0 and temperature Ts when Ts-Tz = 1.0˚C.
early morning or night. To avoid this conflict, Best is limited to (−100 < B0 < 100) as aforementioned, referring to the observed data approximately.
5.2. Relationship of the Penman and the Penman-Monteith Method with Proposed Method
The Penman method uses to evaluate the evaporation from the saturated soil surface that corresponds to our method as rehs equals to 100%. In detail, the former uses the slope of temperature and vapor pressure at Tz whereas the latter uses the slope between Ts and Tz In this view point, our proposed method a little reasonable because of utilize the Ts rather than Tz only. In the Bulk Transfer method, if the sensible transfer coefficient CH sets as equals to latent heat transfer coefficient CE, result of the penman method can be reproduced.
The Penman-Monteith method has shortfalls how to determine the stomata resistivity. The resistivity may be determined using actual evapotranspiration [16] . Our method considered mainly the upper space of the plant canopy and plant layer itself, thus, the estimated evaporation or evapotranspiration already include the resistivity of the plant. Therefore, the hourly change of lEest in our method can be utilized for the evaluation of stomata resistivity in the Penman-Monteith Method.
5.3. Advantage of the Tz and rehz as Variables for Partitioning H and lE
The H and lE i.e., evaporation or evapotranspiration affected by various items such as climate elements (wind speed, soil moisture, local boundary layer size and effect of regional advection) and ecosystem structure (canopy height and leaf area density profile, stomata conductance), etc. The observed Tz, Ts and rehz will be determined by the effect of above various climate elements and regional ecosystem structure, therefore, the determined lE and H are already include the above very complicated elements comprehensively.
5.4. Quality of Observed lE and H
The quality of the observed lE and H is one of the most important issues. The observed lE and H have a considerable gap in the heat balance relationship, as shown in Table 3, which is well known as the “closer issue” [13] . Therefore, the observed lE and H are corrected by multiple regression analysis as lEcor and Hcor. However, the correction is not a sufficient but only conventional. Recently Frank et al., [17] researched the accuracy of sonic anemometer and structural need for shadowing correction for H, the knowledge will be consider in future.
For data correction, Allen [2] assumed the observation error for G, but we did not assumed error because the effect of G will be small by cyclic change in a day. And also heat flux storage under the canopy zone already taking into consider blindly in Tz and rehz Therefore, the partitioning H and lE, using Tz and rehz may be reasonable.
5.5. Issues to Be Solved in the Future
The data for the heat balance components in Table 3 show some imbalance. The reason for this phenomenon is not clear. The imbalance problem remains to be solved in the future. In addition, the results of the optimization show some differences in the initial values of rehs; therefore, the selection of the initial value of rehs in the optimization process is also an important issue to be solved in the future.
6. Conclusions
In the natural world, the air temperature and humidity reflect the partitioning of sensible and latent heat flux from Rn and G. Based on this concept, we attempt to reciprocally estimate the H and lE, i.e., the actual evapotranspiration ET, from Rn and G. By applying the Bowen ratio concept on the canopy and inside of plant layer using radiometer temperature Ts, the unknown variables q (Ts), i.e., rehs, are estimated by an optimization procedure from engineering aspect as satisfying the heat balance relationship. The validation of the method was conducted using five forest sites in the world where observations of lE and H by the eddy covariance method were collected by help of FLUXNET. The analysis conducted on an hourly basis and was summarized daily. The main results are as follow:
1) The observed data were corrected by regression analysis because it does not guarantee the heat balance relationship.
2) The hourly change in the estimated lE and H coincided well with that observed at all the sites.
3) The estimated lE coincides satisfactorily with that observed. The estimated H also consistent with observed at two site, but the other site are underestimated.
4) The temporal change in year for the estimated H and lE was clarified. The estimates of those items were well reflected in the observed data.
5) The estimated monthly evapotranspiration ETest satisfactorily coincides with ETcor, not only distribution but also total amount of yearly.
6) Through the above analysis, the interrelationship among heat balance components was clarified.
The estimated results have not completely reproduced the observed data, but the results are almost satisfactory for estimation of lE and H. This fact shows that the method is useful for estimation of lE. The remarkable feature of this method is that it is applicable for the data of single height temperature and humidity with Rn and G.
We conclude that ET is controlled by energy conservation in nature. Realistically, the observed temperature and humidity are strongly affected by the partitioning of H and lE and vice versa. Therefore, using the observed temperature, humidity and common climate elements, lE and H values can be reciprocally approximated by the optimized techniques.
Acknowledgements
We express sincere thanks to the Ameri Flux, Euro Flux and Asia Flux principal investigation for data accessed July 5, 2015. We thank Dr. Fujihara Yooich and Dr. Takimoto Hiroshi for providing valuable comments for the optimization procedure. We also thank the staff at the Ishikawa Forest Experiment Station.
We acknowledge the following Ameri Flux sites for their data records: site IDs. In addition, funding for Ameri Flux data resources was provided by the US Department of Energy’s Office of Science.
Cite this paper
Toshisuke Maruyama,Manabu Segawa, (2016) Reciprocal Analysis of Sensible and Latent Heat Fluxes in a Forest Region Using Single Height Temperature and Humidity Based on the Bowen Ratio Concept. Journal of Water Resource and Protection,08,724-742. doi: 10.4236/jwarp.2016.87059
References
- 1. Kondo, J. (1996) Meteorology on Water Environment, 5. Wind and Its Turbulence near Soil Surface. Asakura Publishing Ltd., Tokyo, 99-127.
- 2. Allen, R. (2008) Quality Assessment of Weather Data and Micrometeorological Flux Impact on Evapotranspiration Calculation. Journal of Agricultural Meteorology, 64, 191-204.
http://dx.doi.org/10.2480/agrmet.64.4.5 - 3. Kondo, J. (1996) Meteorology on Water Environment, 6. Water and Heat Balance on Soil Surface. Asakura Publishing Ltd., Tokyo, 128-159.
- 4. Morton, F.I. (1978) Estimating Evapotranspiration from Potential Evaporation. Journal of Hydrology, 38, 1-32.
- 5. Brutsaert, W. and Striker, H. (1979) An Advection Aridity Approach to Estimate Actual Regional Evapotranspiration, Water Resources Reseach, 15, 443-450.
- 6. Otsuki, K., Mitsuno, T. and Maruyama, T. (1984) Comparison between Water Budget and Complementary Relationship Estimates of Catchment Evapotranspiration Studies on the Estimation of actual Evapotranspiration (II). Transactions of The Japanese Society of Irrigation, Drainage and Reclamation Engineering, 112, 17-23.
- 7. Preistley, C.H.B. and Taylor, R.J. (1972) On the Assessment oh Surface Heat Flux and Evaporation Using Large-Scale Parameters. Monthly Weather Review, 100, 81-92.
http://dx.doi.org/10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2 - 8. Rambal, S. and Ourcival, J.-M. (2008) Puechabon (FR-Pue) European Fluxes Database Cluster L2 Data.
http://gaia.agraria.unitus.it/home/data/request-data - 9. Saigusa, N., Hirata, R. and Hirano, T. (2002) Tomakomai Flux Research Site (TMK), AsiaFlux Data.
https://db.cger.nies.go.jp/asiafluxdb/ - 10. Guan, D.X., Zhang, J.H. and Wu, J.B. (2005) Changbaishan Site (CBS) AsiaFlux Data.
https://db.cger.nies.go.jp/asiafluxdb/ - 11. Clark, K.L. (2012) Silas Little Experimental Forest (US-Slt) AmeriFlux L2 Data.
http://cdiac.esd.ornl.gov/programs/ameriflux/data_system/aaSilas_Little_Experimental_Forest_pf.html - 12. Bolstad, Paul, Desai, Ankur (2005) Willow Creek (US-WCr) AmeriFlux L2 Data.
http://cdiac.esd.ornl.gov/programs/ameriflux/data_system/aaWillow_Creek_pf.html - 13. Wilson, K., Goldstein, A., Falge, E., Abbinet, M., Baldocchi, D., Berbingier, C., Ceulemans, R., Dolman, H., Field, C., Grelle, A., Ibrom, A., Law, B., Kowalski, A., Meyers, T., Moncrieff, J., Monson, R., Oechel, W., Tenhunen, J., Valentini, R. and Verma, S. (2002) Energy Balance Closure at FLUXNET Sites. Agricultural and Forest Meteorology, 113, 223-243.
http://dx.doi.org/10.1016/S0168-1923(02)00109-0 - 14. Twine, T.E., Kustas, W.P., Norman, J.M., Cook, D.R., Houser, P.R., Meyers, T.P., Prueger, J.H., Staks, P.J. and Wesely, M.L. (2000) Correcting Eddy-Covariance Flux under Estimates over a Grassland. Agricultural and Forest Meteorology, 103, 279-300.
http://dx.doi.org/10.1016/S0168-1923(00)00123-4 - 15. Kondo, J. (2015) Heat Balance and Climate on Soil Surface.
http://www.asahi-net.or.jp/~rk7j-kndu/kenkyu/ke03.htm - 16. Urano S.-I. (2012) Study on Bowen Ratios in the Penman and Priestly·Taylor Equations. Geophysical Bulletin of Hokkaido University, Sapporo, 15, 91-107.
- 17. Frank, J.M., William, J.M, Edoward, S., Herb, A.Z. and Brent, E.E. (2016) All Sonic Anemometers Need to Correct for Transducer and Structural Shadowing in Their Velocity Measurement. Journal of Atmospheric and Oceanic Technology, 33, 149-167.
http://dx.doi.org/10.1175/JTECH-D-15-0171.1
Appendix 1
The GRG Nonlinear Solving Method for nonlinear optimization: developed by Leon Lasdon, University of Texas at Austin, and Alan Waren, Cleveland State University, and enhanced by Front line System, Inc.
For more information about the other solution algorithms or advice on building effective Solver models and solving larger scale problems, contact: Frontline System. Inc.
Website: http://www.solver.com, E-mail: info@solver.com.
Appendix 2
Using modules of Visual Basic for Applications(VBA) in the manuscript
Sub Macro “ Number1( )
' Macro ”Number 1”:GRG method
Dim r As Long
Dim lastRow As Long
lastRow = Range(“〈Column Alphabet〉” & Rows Count).End(xlUp).Row
SolverReset
For r = 〈Start row number〉 To 〈End row number〉
SolverReset
SolverOptionsPrecision :=0.000001, Convergence:=0.0001, StepThru:=False, Scaling:=False _
, AssumeNonNeg:=False, Derivatives:=2
SolverOkSetCell:="Row" & r, MaxMinVal:=2, ValueOf:=0_
,ByChange:=Range(Cells(r, 〈First column number〉), Cells(r, 〈Last column number〉))
SolverAddCellRef:="$ 〈rehs’s Column Alphabet〉" &r, Relation:=1, FormulaText:=0.9999
SolverAddCellRef:="$ 〈rehs’s Column Alphabet〉" &r, Relation:=3, FormulaText:=0.0001 SolverAddCellRef:="$ 〈RTs’s Column Alphabet〉" &r, Relation:=1, FormulaText:=5
SolverAddCellRef:="$ 〈RTs’s Column Alphabet〉" &r, Relation:=3, FormulaText:=-5
SolverAddCellRef:="$ 〈Hestimated’s Column Alphabet〉" &r, Relation:=1, FormulaText:= "$ 〈Rn-G observed’ s Column Alphabet〉$ &r
SolverAddCellRef:="$ 〈LEestimated’s Column Alphabet〉" &r, Relation:=1, FormulaText:= "$ 〈Rn-Gobserved’s Column Alphabet〉$ &r
SolverAddCellRef:="$ 〈Boestimated’s Column Alphabet〉" &r, Relation:=3, FormulaText:=-100
SolverAddCellRef:="$ 〈Boestimated’s Column Alphabet〉" &r, Relation:=1, FormulaText:=100
SolverSolveUserFinish :=True, ShowRef:="DummyMacro"
Next
End Sub
Submit your manuscript at: http://papersubmission.scirp.org/
NOTES
*Corresponding author.















