Journal of Water Resource and Protection
Vol.06 No.18(2014), Article ID:52469,15 pages
10.4236/jwarp.2014.618150
Influence of Vertical Motion on Initiation of Sediment Movement
Ishraq Alfadhli*, Shu-Qing Yang, Muttucumaru Sivakumar
School of Civil, Mining and Environmental Engineering, University of Wollongong, Wollongong, Australia
Email: *ia179@uowmail.edu.au
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 September 2014; revised 3 October 2014; accepted 25 October 2014
ABSTRACT
This paper makes an attempt to answer why the observed critical Shields stress for incipient sediment motion deviates from the Shields curve. The measured dataset collected from literature show that the critical Shields stress widely deviates from the Shields diagram’s prediction. This paper has re-examined the possible mechanisms responsible for the validity of Shields’ diagram and found that, among many factors, the vertical velocity in the sediment layer plays a leading role for the invalidity of Shield’s prediction. A closer look of the positive/negative deviation reveals that they correspond to the up/downward vertical velocity, and the Shields diagram is valid only when flow is uniform. Therefore, this diagram needs to be modified to account for hydraulic environments when near bed vertical velocities are significant. A new theory for critical shear stress has been developed and a unified critical Shields stress for sediment transport has been established, which is valid to predict the critical shear stress of sediment in both uniform and nonuniform flows.
Keywords:
Critical Shear Stress, Nonuniform Flows, Shields Diagram, Vertical Velocity, Decelerating/Accelerating Flows

1. Introduction
The initiation of sediment motion is one of the most important topics in sedimentology and geomorphology as well as hydraulic/hydrological engineering. Generally, there are two methods available in the literature to express the incipient motion that is the shear stress approach and velocity approach [1] . The first researcher who used the shear stress approach is probably [2] who used dimensional analysis to determine the dimensionless parameters and the well-known Shields diagram was developed using the Shields number (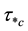 ) as:
) as:
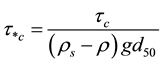 (1)
(1)
where 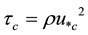 is the critical shear stress for the median grain size,
is the critical shear stress for the median grain size, 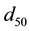 ,
, 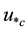 is critical shear velocity, g is the gravitational acceleration,
is critical shear velocity, g is the gravitational acceleration, 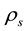 and
and  are the sediment and fluid densities, respectively. The shear stress exerted by the fluid must exceed the critical shear stress
are the sediment and fluid densities, respectively. The shear stress exerted by the fluid must exceed the critical shear stress 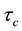 for the initiation motion of grains at the bed. Based on his experimental data, Shields found that
for the initiation motion of grains at the bed. Based on his experimental data, Shields found that 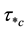 depends only on the particle Reynolds number (
depends only on the particle Reynolds number (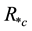 ) that is:
) that is:
 (2)
(2)
where ν is the kinematic viscosity of the fluid.
The original Shields diagram has been reproduced and modified by many researchers. A comprehensive review has been done by [3] , [4] and others, in which some significant deviations of the observed critical shear stress from the standard Shields curve were observed. This has attracted extensive research by notable investigators for example [3] , [5] -[7] , and some factors leading to the data scatter have been identified and discussed.
Some of them believe that the definition of the incipient motion may cause the invalidity of Shields diagram as the experimenter is very difficult to define precisely the status of sediment particles. Consequently, the incipient motion depends more or less on the experimental observers’ subjective judgment. To address this, criteria like “individual initial motion”, “several grains moving” and “weak movement” have been introduced to express the incipient motion [1] .
Other researchers attribute the large discrepancy to the stochastic nature of turbulence and sediment itself, in which grain shape, orientation, exposure, protrusion, etc. can affect the critical Shields stress for example [8] - [11] . It is understandable that when the material is nonuniform, it is very difficult to determine the condition of incipient motion. For example the coarse particles could move relatively easily than the smaller ones because they are sheltered [5] . In reality, in order to simplify the experimental works and also the calculation of Shields stress, the median grain size (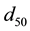 ) is generally used to represent the grain size in a mixture for critical condition.
) is generally used to represent the grain size in a mixture for critical condition.
Over eight decades, the incipient motion of sediment transport has been extensively investigated again and again [3] , and it is certain that the Shields diagram cannot exactly predict the threshold of sediment transport in some circumstances. As mentioned, the reason of invalidity is not fully understood, some investigators ascribe the large scatters to sediment’s characteristics, and some believe these deviations are caused by the flow condition that is nonuniformity [12] .
Probably, [13] was the first one who linked the wide scatter in Shields diagram with flow’s nonuniformity, as he observed that when the same sediment was applied, the observed critical shear stress in non-uniform flows is highly different from that in uniform flows even when the same “subjective judgment criteria” was applied. [14] also observed very large critical shear stress deviation compared to Shields diagram and these large values can be due to some non-uniformity in sediments. While in decelerating nonuniform flow, [12] confirmed experimentally the critical shear stress is considerably below the Shields’ prediction, and their experimental data are in complete disagreement with the Shields diagram. Similar results are obtained by [15] , [16] , etc. It was concluded that “…there is no universal value for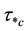 ” [12] , [3] also suggested “less emphasis should be given on choosing a universal
” [12] , [3] also suggested “less emphasis should be given on choosing a universal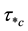 ”.
”.
A group of researchers make some attempts to explain the large discrepancy between predicted and measured critical shear stress using channel’s characteristics, such as the channel shape and bed slope [16] -[22] . For example, [23] found that “the well-known Shields criterion is insufficient for large slope”. On the other hand, this contradicts with people’s intuition which the steep slope would reduce sediment stability as the slope increases as a result of the influence of the downstream gravitational force [24] . [24] re-visited and examined almost all published datasets, and found that the critical Shields stress for incipient motion of sediment in open-channel flow increases with channel slope, this is contrary to people’s intuition that predicts increased mobility with increasing channel slope due to the added gravitational force in the downstream direction. They studied the cause of this discrepancy by using a simple force-balance model as well as “increased drag from channel walls and bed morphology, variable friction angles, grain emergence, flow aeration, and changes to the local flow velocity and turbulent fluctuations”. Their analysis implies that incipient motion is affected by turbulent fluctuations in a significant manner basically because fluctuations increase the drag and lift forces that are exerted on the particle thereby increasing the mobility for all channel slopes. Although they used different forces which have the influence on sediment particles, the vertical velocity generated from flow velocity or the forces generated from ground water was not taken into account. However, [18] experiments in very steep channels show that the critical shear stress is decreased, contrary to the conclusion of [24] .
Therefore, the brief literature review shows that more research is needed to clarify why the critical shear stress for sediment motion depends on channel-bed slope and nonuniformity, and why Shields diagram cannot predict the critical shear stress well. The primary objectives of the present study are to 1) investigate why sometimes the Shields curve cannot express the incipient motion of sediment transport; 2) explain the dependence of Shields number on the variation of water depth along the open channel flow or channel slope; 3) establish a universal relationship between τ* and the particle Reynolds number; and 4) verify the newly established equations using data from the literature.
2. Theoretical Consideration of Influence of Vertical Velocity on the Critical Shear Stress
In this study, we hypothesized that the upward/downward velocity in sediment layer caused by nonuniformity or seepage plays an important role for the invalidity of Shields’ diagram. It is ubiquitous as shown in Figure 1 that a river flow always interchanges with groundwater and the vertical velocity exists in the porous sediment layer, the suctions and injections caused by groundwater happen in flood/dry seasons alternatively. It is reasonable to infer that the upward flow increases the sediment particles’ mobility, or the threshold shear stress required is reduced due to the upward motion. This can be seen from its effective settling velocity when its ambient water has an upward velocity that is:
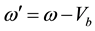 (3)
(3)
where ω = particle’s settling velocity in still water and ω' = the net falling velocity subject to the vertical velocity, Vb in the sediment layer. A spherical particle’s falling velocity ω in still water (Vb = 0) can be expressed as:
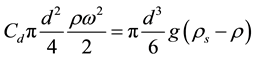 (4)
(4)
where d is the particle diameter, Cd is the drag coefficient which is dependent on the Reynolds number that is
The above simple discussion clearly shows that the presence of vertical velocity Vb in a sediment layer could

Figure 1. The upward and downward vertical velocity generating from seepage face (a) injection seepage (b) suction seepage.
lead to the invalidity of Shields diagram. This inference has been confirmed experimentally by many researchers like [25] and others who observed the critical shear stress subject to injection and suction flows, and a comprehensive literature review can be found from [26] . The influence of seepage on the critical shear stress has been discussed by many researchers. The parameters used to express the seepage include 1) the hydraulic gradient for example [27] ; 2) the pressure variation for example [28] ; or 3) the apparent water density. But, there is no research available to investigate the role of time-averaged vertical velocity on the incipient motion of sediment transport.
In this study, the reduction of settling velocity as shown in Equation (3) can be achieved by introducing “apparent sediment density”. As the presence of vertical velocity can alter the net settling velocity, the upward velocity promote sediment’s mobility, thus the critical shear stress is reduced with seepage similar to the critical shear stress of lightweight material without seepage, even other parameters like particle sizes are identical. Similarly, the downward velocity increases the net sediment falling velocity or its effect can be alternatively expressed by increasing the apparent density, subsequently its stability.
The introduction of apparent sediment density is similar to the treatment of [28] . Instead of modifying the sediment density, they modified the water’s density to eliminate the effect of pressure variation on sediment’s critical shear stress. Their results show that higher pressure yields higher “apparent water density”, and lower pressure corresponds to lower “apparent water density”. In this study, the concept of apparent sediment density is introduced and the parameter of settling velocity is modified by the presence of vertical velocity in the sediment layer. Therefore, it is necessary to establish a relationship between the apparent sediment density and the settling velocity. In other words, after the introduction of apparent density, the effect of pressure variation or seepage on sediment transport is eliminated, a “lightweight particle” with settling velocity ω' should have same effect on its mobility as a real sediment particle whose settling velocity is ω' in the environment without seepage/pressure variation, and vice versa. Hence, the introduction of apparent density can simplify this mathematical treatment for the complex interaction between horizontal and vertical motions in open channel flows. In the environment with ambient velocity, the relationship between the modified settling velocity and the apparent density can be expressed by:

where 

Equation (6) shows that if Vb is equal to zero, then 



As the vertical velocity Vb in Figure 1 has the similar effect for the particles’ stability as the buoyancy effect that is the submerged weight of the particles is no longer


Substituting Equation (6) into Equation (7), one obtains:

or

where
Equation (8) or Equation (9) generally expresses the influence of vertical velocity Vb on the critical shear stress, and it is useful to show why the vertical velocity, V is ubiquitous in open channel flows and how the vertical velocity can be induced by nonuniform flows.
3. Influence of Nonuniform Flow on the Critical Shields Stress
In natural streams and laboratory flumes, the uniform flow is very rare, most of them are nonuniform. As shown in Figure 2, even the flow rate is constant; the flow could still be either accelerating or decelerating dependent of its water depth variation that is dh/dx (≠ 0). The 2-D continuity equation for incompressible flows can be written as follows:

where 


Equation (11) shows that accelerating flows that is 


where Q = discharge; U is the depth-averaged streamwise velocity, h is the water depth and b is the channel width. In Equation (12), Q/b could be constant if both Q and b remains unchanged in x direction, thus one has:

The vertical velocity 

where 
Figure 2. Non-uniform flows in open channel and the variation of water depth, in which u and v are mean velocities in x and y direction, respectively.

Equation (15) shows that the decelerating flow generates 



[4] replaced the Reynolds number in Shields’ diagram by dimensionless particle diameter:

Similarly, d* needs modification by introducing the apparent density with the following form:

Inserting Equation (6) into Equation (17), one has

or

Therefore, the empirical equation of Shields curve by [29] can be modified with the following form:

For the fall velocity, many empirical equations are available in the literature. [4] related cd in Equation (4) with the particle diameter d* and obtained the following explicit form:

It should be clarified that in Equation (3), only the real settling velocity is needed, so the d* in Equation (21) should not be replaced by
Although the incipient motion driven by a uniform flow has been extensively investigated, to the authors’ knowledge no one investigates the influence of vertical velocity on incipient motion of sediment particles, this vertical flow may not be measurable or large enough to induce discernible seepage, thus it is useful to estimate the vertical velocity using some measured parameters. The average vertical velocity can be written in a similar way as shown in Equation (15) that is:

where U, the depth-average streamwise velocity, is a measurable parameter, rather than
The near bed vertical velocity that influences sediment incipient motion can be induced by either the groundwater or the surface variation as shown in Equation (22), the joint effect can be obtained by assuming it is proportional to V and the nominal seepage velocity Vs that is

where λ and λs are the coefficients, Vs = nominal seepage velocity defined by Darcy (Vs = ki, k = hydraulic conductivity, i = hydraulic gradient), ε0 = porosity of granular materials. All parameters in Equation (23) are measurable.
Generally in laboratory flumes the second term of Equation (23) is negligible that is Vs = 0, but in natural streams both the river flow and underground water flow can generate the velocity at the river bed, thus two terms co-exist in Equation (23).
4. Re-Analyse the Data on the Original Shields Diagram
To verify whether Equation (20) is applicable to nonuniform flows, we have comprehensively compiled 329 datasets from [12] [14] [23] [27] [30] -[38] . The hydraulic conditions of these experimental data sets are summarized in Table 1, and the experimental conditions are briefly outlined as follows:
The experiments by [14] were conducted in a flume 0.9 (m) wide and 5 (m) long with different particle sizes and densities. Among the data obtained, 11 data points are obviously above the Shields curve. The data obtained by [30] were collected from a recirculating flume 6 (m) long and 0.3 (m) wide, uniform sediment with diameter between (0.016 - 2.2) (mm) was used. The experimental datasets by [31] include 35 runs with d50 from 0.127 to 1.79 (mm) and specific gravity of 2.65, and 11 runs with d50 from 0.09 to 0.18 (mm) and specific gravity of 4.7. Figure 3 shows that almost all his data points are located below the Shields’ prediction. The data from [32] was collected from a narrow natural stream and in a broad stream. [23] measured the critical shear stress in a flume 16.8 (m) long, 0.6 (m) wide and 0.8 (m) high, gravel sediment with uniform size was used. [33] used a flume to study the effect of relative depth on the incipient motion of coarse uniform sediments. The experimental data from [37] was conducted in a horizontal, rectangular glass walled flume with dimensions of 6 (m) long, 0.5 (m) wide and 0.7 (m) deep, different types of noncohesive materials were used ranged from d50 = 0.91 to 4.36 (mm).
[27] conducted their experiments to investigate the influence of upward seepage on the critical conditions of incipient motion, the experiments were conducted in a horizontal flume 7.6 (m) long, 0.21 (m) wide and 0.4 (m) deep, and uniform particle sizes with d50 = 0.63, 1.02 and 1.95 (mm) were used, and the seepage velocity (injection) was measured with a range between (0 - 0.0138) (m/s). They found that the upward seepage reduces significantly the critical shear stress required by Shields curve. [35] conducted experiments in a 7.5 (m) long, 0.6 (m) wide flume with both injection and suction seepage using sediment particle of d50 = 0.16, 0.5 and 1.2 (mm)
Table 1. Summary of experimental conditions by previous researchers.
Figure 3. Measured critical shear stress versus d* and its comparison with Shields curve or Equation (20) at Y = 0.
and the observed value of seepage velocity that is Vs is range between (−0.0026 - 0.00223) (m/s). [38] observed the critical shear stress for sediment with a median diameter of 0.9 (mm) in the presence of downward seepage with the range of downward seepage velocity between (−0.00314 - 0) (m/s). Their experiment was conducted in a glass-sided flume that was 30 (m) long, 0.7 (m) wide and 0.6 (m) deep, they found that the upward seepage (injection) decreases the critical shear velocity while the downward seepage (suction) increases it.
Nineteen flume experiments from [34] are also included in Figure 3; they investigated the initiation of sediment motion under nonuniform sediment mixtures. [12] conducted experiments to investigate the effect of nonuniformity on the critical shear stress in a channel 14 (m) long, 0.6 (m) width and 0.5 (m) depth; the sediment size of d50 = 8 (mm) was used for their observation. Different from the prediction of [24] , their experimental data reveal that the value of critical shear stress is smaller than Shields’ prediction by at least 50%. Similarly, the experiments by [36] were also conducted in accelerating and decelerating flow conditions, in a rectangular flume of 14 (m) long, 0.6 (m) wide and 0.6 (m) deep. The sediment size d50 = 0.8 and 1.3, 1.8 (mm) was used for a total 72 data sets, in order to achieve nonuniform flow conditions, negative and positive bed slope (±0.7%, ±0.9%, ±1.25% and ±1.5%) were used. They found that the critical shear stress and Shields parameter for incipient motion in accelerating flow are higher than those predicted by Shields in uniform flow while their values in decelerating flow are considerably lower than that in accelerating flow.
These data are plotted in the form of the Shields diagram based on their original definitions as shown in Figure 3. It can be seen that the observed critical shear stress highly deviates from the standard Shields curve, this has been noticed and reported by many researchers for example [3] , [24] , etc., and this discrepancy cannot be simply attributed to measurement errors. In Figure 3, the three lines represent the Equation (20) (Y = 0) ±100% error band.
5. Dependence of Critical Shields Stress on Channel Slope
In the literature, many researchers attribute the deviations from the Shields curve to channel’s slope. For example [18] proposed that

where ϕ = angle of stream wise bed slope, θ = angle of repose. Equation (24) shows that the Shields number decreases with the increase of channel slope.
However, the formula given by [24] shows that the steep channel has a higher Shields number with the following form:

where X = 0.407ln(142S), and the slope S is in the regime 10−4 < S < 0.5.
Figure 4 shows the comparison of the measured data from Table 1 and Equations (24) and (25), it can be seen that these equations cannot express the data points well as the measured τ* could be largely different even the sediment and channel slope are set to constant. Hence, one can conclude that the invalidity of Shields prediction cannot be simply explained by the dependence of channel slope, and more research works need to be carried out for the discrepancy.
6. Effect of Seepage on Critical Shields Stress
Figure 4 shows that particles of the same particle size and same channel slope behave largely different, and none of the existing theory can effectively explain the invalidity of Shields curve. Equation (23) states that the scatter could be caused by either groundwater or the main flow, or both of them. To simplify the discussion, the effect of seepage on the critical shear stress is discussed first. The experimental data by [27] [35] and [38] are presented in Figure 5.
The modified Shields number in Equation (7) should remain unchanged if the apparent sediment density is introduced that is:

Using Equation (6), one obtained the critical shear stress in the following form:

Figure 5 also includes the critical shear stress predicted by Equation (27) and the empirical factor λs is found to be 8.5. The good agreement between the measured and predicted critical shear stress indicates that the introduction of apparent sediment density is acceptable.
Figure 4. Dependence of critical shear stress on the channel slope.
Figure 5. Comparison of measured and predicted critical shear stress subject to seepage.
Different from Equation (27), [27] expressed their data using the following empirical way:

where Vsc is the critical seepage velocity in a quick state and m = 1 ~ 2 and depends on the characteristics of sediments, they proposed the following equation to express Vsc:

It is clearly seen that Equations (27) and (28) are functionally similar to each other, and both Equations (27) and (28) give 
[28] also developed an empirical equation to express the critical shear stress under the influence of seepage, it has the following form:

Comparing Equations (27), (28) and (30), one can find that the conditions for 

It is interesting to compare these three pre-requites for 



7. Effect of Nonuniformity on the Critical Shear Stress
Figure 3 shows that the Shields’ curve could be totally invalid sometimes, these noticeable deviations imply that the nonuniformity could affect the predictability of Shields curve, for example, the data point of [12] locate below the curve when the flow was decelerating, while [36] measured critical shear stress was far higher than the Shields’ prediction, and his data points were collected from accelerating flows. Therefore the large deviation from Shields curve shown in Figure 3 may be mainly caused by the vertical velocity as predicted by Equation (23), and the V could be induced by flow’s nonuniformity.
To ascertain whether the deviations from Shields curve are caused by the nonuniformity, the data without seepage in Table 1 are used to determine the water depth variation 

where 

The energy slope Sf in Equation (32) can be determined from the Manning equation using the hydraulic radius R that is:

For all data without seepage listed in Table 1, the calculated 


Figure 6. The variation of water depth dh/dx has different values based on the influence of vertical velocity on the initial motion, where (−0.024 < dh/dx < 0.0526) for all data sets from Figure 3.
the accelerating flow increases particles’ stability, and decelerating flow increases sediment’s mobility. In Figure 6, the calculated positive 

8. The Modification of Shields Diagram
To investigate whether all data points shown in Figure 3 can be expressed by Equation (20), we analyzed the datasets without artificial seepage or with negligible groundwater effects, only those data are analyzed in which Vb is caused by the nonuniformity in the main flow. Therefore, Equations (22) and (23) can be simplified as follows:

Experiments by [12] , [31] , [36] and [37] are analyzed first. They reported that their measured critical shear stress is lower than Shields’ prediction. Besides, the datasets by [14] and [36] are examined; they claimed that higher values of critical shear stress were observed.
In these studies, flow discharge Q or mean flow velocity U; flow depth h or hydraulic radius R; median sediment size d50; bed slope S0 were comprehensively measured. The experimental data sets from the collected data related to the nonuniform flow are plotted in Figure 7 in which the empirical factor l is found to be 8.5 for both accelerating and decelerating flow. The comparison of the measured and predicted critical shear stress presented in Figure 7 shows that the agreement is reasonably good, and it could be better if different l is used in the fitting as l could be a function of sediment gradation and shapes, turbulence, etc. In this research we only assume that sediment particle size is uniform and can be represented by d50.
Figure 8 shows the comparison of predicted and the measured critical shear stress, the datasets include [23] , [30] , [32] -[34] . It can be seen that even the observed critical shear stress largely deviates from Shields diagram represented by the solid line (Y = Vs/ω = 0), all data points can be covered by Equation (8) or Equation (9) when the parameter Y is introduced.
Figure 7. Comparison of experimental results on threshold condition without seepage with Equation (27) where Y = Vb/ω.
Figure 8. Influence of vertical velocity on critical shear stress, the solid line is the original curve (or Y = 0) and other lines are calculated from Equation (20) with different Y.
9. Discussions
As mentioned, some researchers found the dependence of the critical shear stress on the channel slope [24] , but it is still an open question why the observed Shields number changes when the bed slope is large, thus it is worthwhile to explore the reasons for this dependence.
This study re-examined the data available in the literature and found that the deviation from the shields curve could be caused by the vertical velocity, the Shields curve is valid only when the flow is uniform, which implies that the vertical velocity is zero. As the true uniform is very rare in laboratory or nature, thus it is understandable why Shields curve is invalid to express most of observed critical shear stress. Hence, a natural question to ask is whether the dependence of τ* on the channel slope is also caused by the vertical flow or flow’s nonuniformity.
Equations (22) and (23) indicate that in almost all cases, there always exists the vertical velocity caused by either the exchange of groundwater and river water or the flow’s nonuniformity. Therefore, the widely observed dependence like those reported by [24] is possibly caused by the parameter Y (≠0). To ascertain the statement, we only need to check whether the data used by [24] are obtained from uniform flows. All data used by Lamb et al. to support their claim are listed in Table 2, in which only the laboratory data are included as his field data were certainly collected from nonuniform conditions. The last column of Table 2 shows the length of flumes, and from it one can see that almost half of the flumes were less than 10 (m). [39] measured the developing zone of a flume and found that to achieve the uniform flows a channel should be longer than 10 (m) as there is a developing zone from the flume’s entrance and its tailgate. Even for those data from flumes longer than 10 (m), the flow still could be nonuniform also when the parameter 
We took [18] as an example, their observation is opposite to the prediction of [24] , but they also claimed the dependence of critical shear stress on the channel slope based on their experimental data. In their experiments, the channel slope was specially designed to vary within a range of −10˚ to 31˚, but their channel lengths were 4 (m) and 2 (m) only. Obviously, their experiments were conducted in the nonuniform flow conditions as the 2 - 3 (m) length is too short to form a uniform flow. In other words, both conclusions drawn by [24] and [18] are not very convincing as they did not check the parameter of
10. Conclusions
This paper investigates why the observed critical shear stress widely deviates from the Shields curve. Its validity
Table 2. Previously reported data selected from [24] .
or discrepancy could be caused by many factors like sediment gradation, shapes, channel-bed slopes, measurement errors, turbulence, etc. However, this study found that the vertical motion plays an important role to initiate sediment motion or bed load transport; the vertical velocity could be induced by seepage, nonuniformity and turbulence alike. By re-examining 329 datasets available in the literature, we can draw the following conclusions:
1) The upward velocity promotes sediment mobility and downward velocity promotes sediment stability. The sediment’s mobility or stability can be equivalently expressed by its apparent sediment density which is able to eliminate the effect of vertical velocity as shown in Equation (6). This provides a useful tool to simplify the influence of nonuniformity on the incipient motion of sediment.
2) There exists vertical velocity on the channel bed and this vertical velocity could be induced by seepage or nonuniformity, the amount of the vertical velocity may be very small, but its influence to sediment incipient should not be underestimated. The joint effect can be expressed by Equation (23). For nonuniform flow, Equation (6) indicates that the sediment tends to move in decelerating flows, but it becomes more difficult to move in accelerating flows.
3) The Shields diagram is valid only when the flow is uniform, but after the introduction of apparent sediment density, the Shields diagram could be extended to express complex flows. An improved critical Shields stress for sediment transport has been established, that can predict the critical shear stress in both uniform and nonuniform flows well.
4) A new parameter Y has been proposed to express the influence of nonuniformity or seepage, this parameter should be included in the models of sediment transport. According to available experimental data in the incipient motion in nonuniform flows or in the seepage cases, good agreements between the measured and predicted values can be achieved if Y is included in the existing model, but more research is needed to determine the coefficients λs and λ in Equation (23), they could be a function of sediment gradation and shapes, turbulence, etc.
References
- Yang, C.T. (1996) Sediment Transport: Theory and Practice. Krieger Pub, Malabar.
- Shields, A. (1936) Application of Similarity Principles and Turbulence Research to Bed-Load Movement. California Institute of Technology, Pasadena (Translate from German).
- Buffington, J.M. and Montgomery, D.R. (1997) A Systematic Analysis of Eight Decades of Incipient Motion Studies, with Special Reference to Gravel-Bedded Rivers. Water Resources Research, 33, 1993-2029. http://dx.doi.org/10.1029/96WR03190
- Julien, P.Y. (1995) Erosion and Sedimentation. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139174107
- Garde, R.J. and Ranga Raju, K.G. (1985) Mechanics of Sediment Transportation and Alluvial Stream Problems. Wiley Eastern, New Delhi.
- Lavelle, J. and Mofjeld, H. (1987) Do Critical Stresses for Incipient Motion and Erosion Really Exist? Journal of Hydraulic Engineering, 113, 370-385. http://dx.doi.org/10.1061/(ASCE)0733-9429(1987)113:3(370)
- Wilcock, P.R. (1992) Flow Competence: A Criticism of a Classic Concept. Earth Surface Processes and Landforms, 17, 289-298. http://dx.doi.org/10.1002/esp.3290170307
- Wiberg, P.L. and Smith, J.D. (1987) Calculations of the Critical Shear Stress for Motion of Uniform and Heterogeneous Sediments. Water Resources Research, 23, 1471-1480. http://dx.doi.org/10.1029/WR023i008p01471
- Wilcock, P.R. (1988) Methods for Estimating the Critical Shear Stress of Individual Fractions in Mixed-Size Sediment. Water Resources Research, 24, 1127-1135. http://dx.doi.org/10.1029/WR024i007p01127
- Kirchner, J.W., Dietrich, W.E., Iseya, F. and Ikeda, H. (1990) The Variability of Critical Shear Stress, Friction Angle, and Grain Protrusion in Water-Worked Sediments. Sedimentology, 37, 647-672. http://dx.doi.org/10.1111/j.1365-3091.1990.tb00627.x
- Johnston, C.E., Andrews, E.D. and Pitlick, J. (1998) In Situ Determination of Particle Friction Angles of Fluvial Gravels. Water Resources Research, 34, 2017-2030. http://dx.doi.org/10.1029/98WR00312
- Afzalimhr, H., Dey, S. and Rasoulianfar, P. (2007) Influence of Decelerating Flow on Incipient Motion of a Gravel- Bed Stream. Sadhana, 32, 545-559. http://dx.doi.org/10.1007/s12046-007-0041-7
- Iwagaki, Y. (1956) Fundamental Study on Critical Tractive Force. Transactions of the Japan Society of Civil Engineer, 41, 1-21. http://dx.doi.org/10.2208/jscej1949.1956.41_1
- Neill, C.R. (1967) Mean Velocity Criterion for Scour of Coarse Uniform Bed Material. Proceeding of the 12th Congress of the International Association of Hydraulics Research, 3, 46-54.
- Kuhnle, R. (1993) Incipient Motion of Sand-Gravel Sediment Mixtures. Journal of Hydraulic Engineering, 119, 1400- 1415. http://dx.doi.org/10.1061/(ASCE)0733-9429(1993)119:12(1400)
- Dey, S. and Raju, U. (2002) Incipient Motion of Gravel and Coal Beds. Sadhana, 27, 559-568. http://dx.doi.org/10.1007/BF02703294
- Andrews, E.D. (1994) Marginal Bed Load Transport in a Gravel Bed Stream, Sagehen Creek, California. Water Resources Research, 30, 2241-2250. http://dx.doi.org/10.1029/94WR00553
- Chiew, Y.M. and Parker, G. (1994) Incipient Sediment Motion on Non-Horizontal Slopes. Journal of Hydraulic Research, 32, 649-660. http://dx.doi.org/10.1080/00221689409498706
- Church, M., Hassan, M.A. and Wolcott, J.F. (1998) Stabilizing Self-Organized Structures in Gravel-Bed Stream Channels: Field and Experimental Observations. Water Resources Research, 34, 3169-3179. http://dx.doi.org/10.1029/98WR00484
- Patel, P.L. and Ranga Raju, K.G. (1999) Critical Tractive Stress of Nonuniform Sediments. Journal of Hydraulic Research, 37, 39-58. http://dx.doi.org/10.1080/00221689909498531
- Dey, S. and Debnath, K. (2000) Influence of Streamwise Bed Slope on Sediment Threshold under Stream Flow. Journal of Irrigation and Drainage Engineering, 126, 255-263. http://dx.doi.org/10.1061/(ASCE)0733-9437(2000)126:4(255)
- Erich, R.M., Pitlick, J. and Nelson, J.M. (2005) Variation in the Reference Shields Stress for Bed Load Transport in Gravel-Bed Streams and Rivers. Water Resources Research, 41, Article ID: W04006-10.
- Graf, W.H. and Suszka, L. (1987) Sediment Transport in Steep Channels. Journal of Hydroscience and Hydraulic Engineering, 5, 11-26.
- Lamb, M.P., Dietrich, W.E. and Venditti, J.G. (2008) Is the Critical Shields Stress for Incipient Sediment Motion Dependent on Channel-Bed Slope? Journal of Geophysical Research: Earth Surface, 113, Article ID: F02008.
- Rao, A. and Sitaram, N. (1999) Stability and Mobility of Sand-Bed Channels Affected by Seepage. Journal of Irrigation and Drainage Engineering, 125, 370-379. http://dx.doi.org/10.1061/(ASCE)0733-9437(1999)125:6(370)
- Lu, Y., Chiew, Y.M. and Cheng, N.S. (2008) Review of Seepage Effects on Turbulent Open-Channel Flow and Sediment Entrainment. Journal of Hydraulic Research, 46, 476-488. http://dx.doi.org/10.3826/jhr.2008.2942
- Cheng, N.S. and Chiew, Y.M. (1999) Incipient Sediment Motion with Upward Seepage. Journal of Hydraulic Research, 37, 665-681. http://dx.doi.org/10.1080/00221689909498522
- Francalanci, S., Parker, G. and Solari, L. (2008) Effect of Seepage-Induced Nonhydrostatic Pressure Distribution on Bed-Load Transport and Bed Morphodynamics. Journal of Hydraulic Engineering, 134, 378-389. http://dx.doi.org/10.1061/(ASCE)0733-9429(2008)134:4(378)
- Yalin, M.S. and Da Silva, A.F. (2001) Fluvial Processes. IAHR Monograph, IAHR, Delft, 197 p.
- White, S.J. (1997) Plane Bed Thresholds of Fine Grained Sediments. Nature, 228, 152-153. http://dx.doi.org/10.1038/228152a0
- Everts, C.H. (1973) Particle Overpassing on Flat Granular Boundaries. ASCE Journal of Waterways Harbors Coastal Engineering Division, 99, 425-438.
- Carling, P.A. (1983) Threshold of Coarse Sediment Transport in Broad and Narrow Natural Streams. Earth Surface Processes and Landforms, 8, 1-18. http://dx.doi.org/10.1002/esp.3290080102
- Shvidchenko, A.B. and Pender, G. (2000) Flume Study of the Effect of Relative Depth on the Incipient Motion of Coarse Uniform Sediments. Water Resources Research, 36, 619-628. http://dx.doi.org/10.1029/1999WR900312
- Sarker, L.K. and Hossain, M.M. (2006) Shear Stress for Initiation of Motion of Median Sized Sediment of No Uniform Sediment Mixtures. Journal of Civil Engineering, 34, 103-114.
- Kavcar, P.C. and Wright, S.J. (2009) Experimental Results on the Stability of Non-Cohesive Sediment Beds Subject to Vertical Pore Water Flux. American Society of Civil Engineers, 342, 3562-3571.
- Emadzadeh, A., Chiew, Y.M. and Afzalimehr, H. (2010) Effect of Accelerating and Decelerating Flows on Incipient Motion in Sand Bed Streams. Advances in Water Resources, 33, 1094-1104. http://dx.doi.org/10.1016/j.advwatres.2010.06.014
- Gaucher, J., Marche, C. and Mhdi, T.F. (2010) Experimental Investigation of the Hydraulic Erosion of Noncohesive Compacted Soils. Journal of Hydraulic Engineering, 136, 901-913. http://dx.doi.org/10.1061/(ASCE)HY.1943-7900.0000274
- Liu, X. and Chiew, Y.M. (2012) Effect of Seepage on Initiation of Cohesionless Sediment Transport. Acta Geophysica, 60, 1778-1796. http://dx.doi.org/10.2478/s11600-012-0043-7
- Kirkgöz, M. and Ardiçlioğlu, M. (1997) Velocity Profiles of Developing and Developed Open Channel Flow. Journal of Hydraulic Engineering, 123, 1099-1105. http://dx.doi.org/10.1061/(ASCE)0733-9429(1997)123:12(1099)
- Paintal, A.S. (1971) Concept of Critical Shear Stress in Loose Boundary Open Channels. Journal of Hydraulic Research, 9, 91-113. http://dx.doi.org/10.1080/00221687109500339
- Ashida, K. and Bayazit, M. (1973) Initiation of Motion and Roughness of Flows in Steep Channels. Proceedings of the 15th Congress of the International Association for Hydraulic Research, 1, 475-484.
- Fernandez Luque, R. and Van Beek, R. (1976) Erosion and Transport of Bed-Load Sediment. Journal of Hydraulic Research, 14, 127-144. http://dx.doi.org/10.1080/00221687609499677
- Ikeda, S. (1982) Incipient Motion of Sand Particles on Side Slopes. Journal of the Hydraulics Division, 108, 95-114.
- Wilcock, P.R. (1987) Bed-Load Transport of Mixed-Size Sediment. Dissertation/Thesis, ProQuest, UMI Dissertations Publishing, Intuition of Technology, Cambridge, 205 p.
- Wilcock, P.R. and McArdell, B.W. (1993) Surface-Based Fractional Transport Rates: Mobilization Thresholds and Partial Transport of a Sand-Gravel Sediment. Water Resources Research, 29, 1297-1312. http://dx.doi.org/10.1029/92WR02748
NOTES
*Corresponding author.










