Journal of Water Resource and Protection
Vol. 3 No. 4 (2011) , Article ID: 4441 , 7 pages DOI:10.4236/jwarp.2011.34029
Stability of Confidence Levels for Flood Frequencies Using Additional Data
1Department of Mathematical Sciences, United States Military Academy, West Point NY, USA
2University of California, Irvine, Bainbridge Island, WA, USA
3Department of Mathematical Sciences, United States Military Academy, West Point NY, USA
E-mail: ted@phdphdphd.com; rwhitley@math.uci.edu; Mick.Smith@usma.edu
Revised January 21, 2011; revised February 27, 2011; accepted March 28, 2011
Keywords: Runoff, Statistics, Simulation, Storm Water Management
ABSTRACT
A comparison of flood values based on prior data and new additional data at various confidence levels is given for five representative sites in Los Angeles, California. The methodology uses computer simulations to give the confidence level values and flood frequency curves. These calculations show confidence level increases roughly in the range of 5% to 10% using some quarter of a century of additional data.
1. Introduction
The United States Army Corps of Engineers (COE) Los Angeles District Office invested considerable resources in the development of their rainfall-runoff design storm unit hydrograph methodology and calibration for their Los Angeles County Drainage Area study, or “LACDA” study in the early 1980’s. The LACDA study included dozens of stream gages that had been essentially “stable” in urbanization impacts for decades. Therefore, little if any adjustments to those stream gage records were needed in order to compensate for the effects of urbanization across the gage record. Furthermore, many of these LACDA gages not only had long periods of time where little if any increase in urbanization occurred, but also the storm drain systems had been fully implemented across the entire period of record. Dozens of rain gages with lengthy time periods of record were also available in this LACDA calibration effort. Consequently, there were considerable rainfall-runoff data to undertake a comprehensive calibration effort of the COE adopted design storm unit hydrograph approach. The calibration effort was concluded by the COE and validation tests conducted of their rainfall-runoff model. The LACDA summary report was eventually published in 1991 [1].
During the LACDA regional study, local county flood control agencies utilized the LACDA data and results to create their own county flood control hydrology design criteria and documented their procedures in Hydrology Manuals, which are then used for the design and planning of all flood control facilities in that county. During the course of the LACDA effort, the County of San Bernardino, California, which is located nearby the LACDA study area, published their Hydrology Manual in 1983 [2]. That Hydrology Manual used a design storm unit hydrograph approach that is consistent with the modeling approach used in the COE LACDA effort, but utilized rainfall data and hydrologic parameters appropriate for the County of San Bernardino area. As part of their Hydrology Manual calibration effort, the County of San Bernardino further examined uncertainty in stream gage runoff data flood frequency estimates such as due to sampling effects and introduced the upper 85-percent confidence level estimate of the flood frequency curve for design and planning purposes. Later, the County of San Bernardino examined arid condition rainfall and runoff data and extended their Manual to include desert hydrology methods in 1986.
In a concurrent effort, the County of Orange, California, which is located adjacent to the LACDA study area with similar coastal exposure, examined in detail the variety of rainfall-runoff models in the development of their Hydrology Manual and related hydrologic modeling approach. As part of their investigation, five Technical Committees reviewed in detail the development and calibration of the proposed hydrologic approach for the County of Orange, each committee composed of well-known hydrology experts, several of whom were authors and developers of hydrologic computer models available through private vendors or in the public domain. After several years of examination, the same design storm unit hydrograph procedure used in the LACDA study and also adopted by the County of San Bernardino was recommended and subsequently adopted by the County of Orange. Furthermore, the 85-percent upper confidence level estimate for peak flow rates that was used by the County of San Bernardino’s Hydrology Manual (1986) was reviewed by the County of Orange and then adopted by a resolution of the County Board of Supervisors. This use of a higher confidence level in flood risk reduction design and planning may be the first application and formal administrative adoption of such a flood risk reduction approach. The resulting summary report for the County of Orange calibration effort [3] was later reviewed and adopted by the COE and then re-published as a COE report [4]. In 1989, the County of Orange extended their calibration effort by examining lower confidence levels, such as the upper 50-percent confidence level (Williamson and Schmidt).
Subsequent to the publication of the LACDA report as well as the Hydrology Manual for the Counties of San Bernardino (1983) and Orange (1986), other county level flood control agencies developed their respective Hydrology Manuals and also elected to use the 85-percent upper confidence level estimate for their design and planning purposes e.g., the County of San Joaquin (1997) and the County of Kern (1991). Consequently, one of the largest economic areas of the United States is subject to flood risk reduction design and planning based upon similar hydrologic approaches and use of risk reduction based upon an 85-percent upper confidence level of flood frequency curve estimates.
2. Methods
The stream gage data originally used in the LACDA regional calibration included data through the year 1982. With additional data available, a comparison of new flood frequency curves and confidence levels is appropriate in order to determine to what extent the additional data changes the original results.
The re-analysis of the LACDA flood frequency curves was accomplished by including nearly a quarter century of additional stream gage data that post-dated the LACDA study itself. Five stream gages (Alhambra Wash, Compton Creek, Eaton Wash, Rubio Wash and Arcadia Wash) were the focus of this re-analysis; complete tables of the relevant discharge data are given in the reports for County of San Bernadino and the County of Orange. These watersheds were selected based on several factors including different topographies, watershed shapes, main watercourse slopes, sizes, stream gage record homogeneity and record length, and hydrometeorological similarities to watersheds in the subject County of Orange area.
As part of the analysis, an “adopted” skew value is assumed to give the “correct” skew value, i.e. the uncertainty stemming from the estimation of the skew is ignored. (The adopted skew value used in the re-analysis is the value used in the original calibration report; an examination of statistical results from this re-analysis shows that due to the slight variation in statistical estimates, it is logical that the skew would also vary only slightly if at all) These adopted skew values, as well as the statistical estimators for the mean, standard deviation and skew, for both the old and the extended data sets, are given in Table 1.
The approach, consistent with what had been done previously, was to follow the general procedure of the Water Resource Council’s Bulletin 17B [5], see also [6] and [7], supplemented by a more accurate determination of confidence levels produced by means of computer simulations for the case where the underlying log-Pearson 3 distribution has an estimated mean and estimated standard deviation but the skew is taken to be known. The adopted skew value used in the re-analysis was taken to be the same value used in the original calibration report.
There has been an extended discussion of possible improvements in the methodology of Bulletin 17B, see [7-12]. The issue here, however, is in the possible changes due to additional data when applying the methodology used in analyzing the original data.
A flood frequency curve for the discharge Q is obtained from the basis Equation (1) of [5]
 (1)
(1)
 and
and  the usual estimators for the mean and standard deviation of the logarithms of the maximal annual discharges. In [5], K is read from a table given in terms of exceedance probability and skew (which implicitly implies a skew value which is known exactly). The plot of the values of Equation (1) for values of K corresponding to various exceedence probabilities gives the flood-frequency curves. Even though this procedure is known to be inaccurate in some ways, it supplies a unified way of computing flood-frequency curves depending only on the simple calculations of
the usual estimators for the mean and standard deviation of the logarithms of the maximal annual discharges. In [5], K is read from a table given in terms of exceedance probability and skew (which implicitly implies a skew value which is known exactly). The plot of the values of Equation (1) for values of K corresponding to various exceedence probabilities gives the flood-frequency curves. Even though this procedure is known to be inaccurate in some ways, it supplies a unified way of computing flood-frequency curves depending only on the simple calculations of 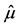 and
and . In applications, the K-values for various confidence levels can be more accurately obtained by means of computer simulations [14], which were done in the development of the Hydrology Manuals discussed here.
. In applications, the K-values for various confidence levels can be more accurately obtained by means of computer simulations [14], which were done in the development of the Hydrology Manuals discussed here.
The simulation program of [14], used in the earlier study, was completely rewritten to take advantage of the great increase in the speed of the personal computers and software improvement in the last twenty years. This new program is described below and can accessed at www.
MathLogix.com for research use. This is the required methodology for the hydrology manuals discussed.
Basic to the procedures of [5] and [7] is the assumption that the logarithms of yearly maximal discharges have a Pearson III distributions; the mathematics of such distributions are discussed in [15] and in [9-11].
The density of a Pearson III distribution is given by
 (2)
(2)
where  is the gamma function and
is the gamma function and 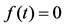 for
for
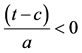 The parameter b is related to the skew γ, denoted by G in [5], by
The parameter b is related to the skew γ, denoted by G in [5], by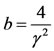 ; the parameter a has the same sign as the skew. For the important case of zero skew, the distribution can, by a limiting argument, be shown to have a normal distribution.
; the parameter a has the same sign as the skew. For the important case of zero skew, the distribution can, by a limiting argument, be shown to have a normal distribution.
The problem considered is calculating confidence level estimates for the value of the T-year flood xp, where
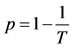 .
.
Let X have the density given in (2) and suppose that the site has m years of yearly maximal discharge data. Let  denote the sample mean of X, i.e. for a sequence of independent random variables X1, X2, …, Xm each with the same distribution as X,
denote the sample mean of X, i.e. for a sequence of independent random variables X1, X2, …, Xm each with the same distribution as X, .
.
Let 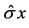 denote the unbiased estimator for the standard deviation,
denote the unbiased estimator for the standard deviation,
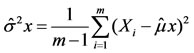
It can be shown (see [14]) that:
 for skew > 0(3)
for skew > 0(3)
and
 for skew < 0(4)
for skew < 0(4)
Here  means that the two sides of the equivalence have the same probability distribution. The random variable Z has a gamma distribution with the density given by:
means that the two sides of the equivalence have the same probability distribution. The random variable Z has a gamma distribution with the density given by:
 (5)
(5)
for t > 0 and zero for t < 0. Corresponding to xp zp is the value satisfying Prob , and
, and  and
and  denote the sample estimates for the mean and standard deviation of Z, based on the same number m of data points. (Note the distributions in (3) and (4) are the same in the case of zero skew, and in this case Z is normally distributed with mean zero and standard deviation one.)
denote the sample estimates for the mean and standard deviation of Z, based on the same number m of data points. (Note the distributions in (3) and (4) are the same in the case of zero skew, and in this case Z is normally distributed with mean zero and standard deviation one.)
Equations (3) and (4), given in [14], are the key to simulating confidence levels for T-year flood values in the case of known skew and were used in the construction of the flood frequency curves for the sites for which additional data were now available.
Confidence levels are a useful way of describing the level of protection obtained from an estimate of a T-year flood. As an example of how this works, consider the probability distribution of the random variable Y given by the right-hand side of (3) for the case where T = 100, a known positive skew γ, and a site with m yearly maximal discharge data values. If the probability density of Y were known in a closed form, it would allow the calculation of a point K0.80 with the property that Prob (Y ≤ K0.80) = 0.80. While this density is not known explicitly, by means of computer simulations the value of K0.80 can be computed to high accuracy. The interpretation of the use of the value K0.80 is as follows: If numerous sites with the same skew γ were sampled each with m points, then the statistic of the left-hand side of (3) would be less than or equal to K0.80 at roughly 80% of the sites. This is to say that at those sites
 (6)
(6)
holds, and so mitigation measures built for the value given by the right-hand side of (6) will for those sites provide protection for the 100-year flood. The remaining 20% of the sites will not receive the desired protection from the 100-year flood. By using a another value of Kp, for p > 0.80, the confidence, as described in terms of the percentage of the sites at which this procedure furnishes the desired protection, can be increased at the expense of constructing mitigation measures based on this larger flood value.
The computer simulations used to calculate values for Kq take as input the number m of site data points, the T of the T-year flood needed, and the value  of the site skew. The program provides values of Kq for:
of the site skew. The program provides values of Kq for:
q = 0.000 1, 0.001, 0.005, 0.01(0.01)0.99, 0.099 5, 0.999, 0.999 9
This simulation involves the simulation of 1 000 000 sites, each site with m data points, generated from the IMSL software library gamma distribution routines and a random number generator. The values of Kq are then obtained by interpolation in a histogram generated by the simulation. This is done eight times, and the final values of Kq are taken to be the average of the eight values obtained.


Table 1. Statistical parameters.
These Kq values are tested by means of random gamma simulations using a different random number generator with a much longer period than the one used to generate the Kq values. The test counts the fraction of the random gamma values for which (3) or (4) is less than each Kq and compares it with the desired value of q for a simulation of one million sites. This was done three times and it was found that the observed proportions differ from the q values at the most in the fourth decimal place.
The LACDA flood frequency estimates were updated by including approximately 20 years of additional stream gage records, as indicated in Table 1. Note that there is very little change in the means and standard deviations of the logarithms to the base 10 of the maximal yearly discharges. The skews computed for each site
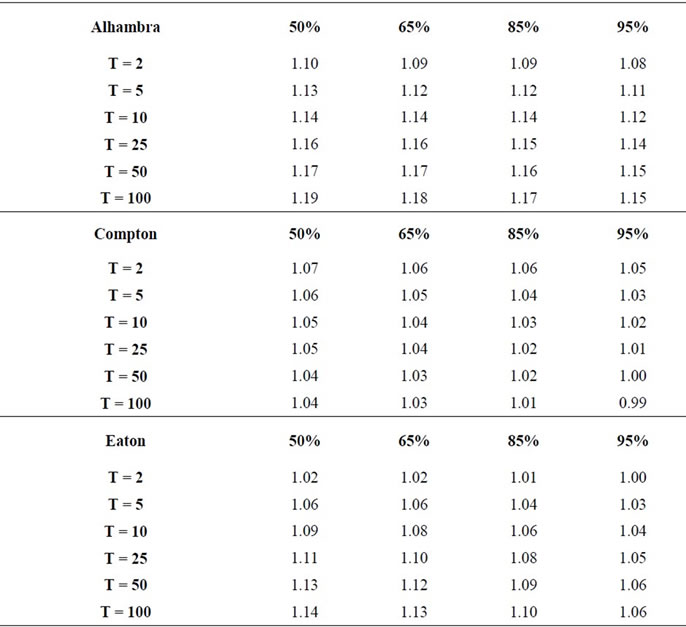

Table 2. Change in confidence level estimates (αx,T,g) due to added years of records.
from the site data are given in the table, but the skews used in the re-analysis are the adopted COE skews that were used in the original calibration report [4] which are also given in the table.
To see how the values in Table 2 were computed, consider sample results. For T = 2 year flood, 50% confidence levels: Alhambra extended record 3 126 cfs, un-extended record 2 854 cfs, from data given in detail in the complete report, for a ratio of extended to un-extended of 1.10; Compton extended record 2 861 cfs, un-extended record 2 682 cfs for a ratio of extended to un-extended of 1.07. For a T = 100 year flood with 95% confidence: Eaton extended record 11 098 cfs, un-extended record 10 436 cfs for a ratio of extended to un-extended of 1.07; Rubio extended record 6 503 cfs, un-extended record 6 169 cfs for a ratio of extended to un-extended of 1.05.
Several comments are appropriate as to the understanding of the simulation results:
Tabulated simulation results show an increase in statistically developed estimates of various upper confidence level return frequency flood peak flow rates. The apparent consistencies in these results do not establish a trend, however. The five selected stream gage sites are but a small subset of the entire LACDA study area and therefore regionalization across many dozens of stream gages has not been accomplished. Furthermore, a closer look at the gage records show that these five gages are not independent records; that is, all five gages show similar impacts from similar storm events over the last 20 years of records.
A severe thunderstorm occurred on March 1, 1983, which impacted these five gage sites and not the entire LACDA study area. This severe storm has been ranked at the 100-year to 500-year return frequency interval. Consequently, the impact of this single severe storm event is localized with respect to the LACDA study area and had regionalization been considered, the effect of that 1983 storm would be reduced. This 1983 storm event was not included in the original calibration effort but was instead used to validate the rainfall-runoff design storm unit hydrograph method under consideration and eventual adoption (the validation test results were found to be good to excellent). However, this 1983 storm event is included in the current subject re-analysis. Therefore, the tabulated results include the impact of including this severe storm in the re-analysis but not in the original analysis of the early 1980’s.
It is extremely unlikely that the addition of an additional 20 years of runoff data to a stream gage (such as considered in the subject study) would result in no change of the flood frequency curve, and it is expected that the confidence levels would change due to the decrease in standard deviation. Therefore, such an exercise will almost always result in either an increase or decrease in flood frequency values. If flood control design is based upon the 50-percent confidence level throughout the entire region, for say the 100-year return frequency event, then 50-percent of the designs will be considered an “over-design” and 50-percent would be considered an “under-design” for the target level of flood risk reduction with, of course, no knowledge provided as to which particular system is in which category of design condition. Now, with additional runoff data and newly developed flood frequency estimates, a flood risk manager may decide to “do nothing”: should the new statistical results indicate a trend of reduction in flood frequency estimates but, in the event the new statistical results indicate an apparent trend in flood frequency increase, the manager may decide to increase design values for flood projects. Under such a scheme, the manager could cause a monotonically increasing level for flood control design as additional data are collected in the future.
Although this paper focuses on the testing of stream gage data to assess changes in flood frequency characteristics due to additional runoff data, the mathematical approach and accompanying simulation program provide improvements in the general application of log-Pearson 3 models which currently are not available anywhere else, except under very limited conditions. A computer program is available at the cited website for downloading for research purposes, and hopefully fills this apparent gap. The use of confidence levels so obtained provide a simple way of explicitly addressing those uncertainties in T-year values which arise from using estimates of the mean and standard deviation in calculations.
3. Conclusions
A comparison of flood values based on prior data and new additional data at various confidence levels is given for five representative sites in Los Angeles, California. The methodology used is the same as that used in the prior studies, and depends upon computer simulations to give the confidence level values and flood frequency curves. The mathematical computer simulation program, which provides these confidence levels for the log-Pearson 3 distribution, is available at a provided web site. These calculations are used to evaluate possible changes in local county Flood Control Agency Hydrology Manuals in order to better estimate flood frequency levels for use in flood control design and planning and flood risk reduction assessment.
REFERENCES
- U.S. Army Corps of Engineers, Los Angeles District, Los Angeles County Drainage Area (LACDA) Review, 1991.
- County of San Bernadino, California, Hydrology Manual, 1983 and 1986.
- T. V. Hromadka II, “Calibrating the Proposed Orange County EMA Hydrograph Procedure (A Study of Basin Factors and Coastal S-Graphs),” published by the Orange County Environmental Management Agency (OCEMA), Santa Ana, California, 1985.
- T. V. Hromadka II, et al., “Derivation of a Rainfall-Runoff Module to Compute N-year Floods for Orange County Watersheds,” publication U.S. Army Corp of Engineers, Los Angeles Division, November 1987.
- Interagency Committee on Water Data, Guidelines for determining flood flow frequency, Bull 17B, p. 28, Hydrol. Subcomm., Washington, D.C., March 1982.
- D. R. Maidment, Ed., Handbook of Hydrology, McGraw-Hill, 1993.
- Committee on Techniques for Estimating Probabilities of Extreme Floods, Water Science and Technology Board, Commission on Physical Sciences, Mathematics, and Resources, Nation Research Council, Estimating Probabilities of Extreme Floods, National Academy Press, Washington, D.C., 1988.
- V. W. Griffis and J. R. Stedinger, “Evolution of Flood Frequency Analysis with Bulletin 17B,” Journal of Hydrologic Engineering, Vol. 12, No. 3, 2007, pp. 283-297. doi:10.1061/(ASCE)1084-0699(2007)12:3(283)
- V. W. Griffis and J. R. Stedinger, “Log-Pearson Type3 Distribution and Its Application in Flood Frequency Analysis I:Distribution Characteristics,” Journal of Hydrologic Engineering, Vol. 12, No. 5, 2007, pp. 482-292. doi:10.1061/(ASCE)1084-0699(2007)12:5(482)
- V. W. Griffis and J. R. Stedinger, “Log-Pearson Type3 Distribution and Its Application in Flood Frequency Analysis II: Parameter Estimation,” Journal of Hydrologic Engineering, Vol. 14, No. 2, 2009, pp. 209-212. doi:10.1061/(ASCE)1084-0699(2009)14:2(209)
- V. W. Griffis and J. R. Stedinger, “Log-Pearson Type3 Distribution and Its Application in Flood Frequency Analysis III: Sample Skew and Weighted Skew Estimators, Parameter Estimation,” Journal of Hydrologic Engineering, Vol. 14, No. 2, 2009, pp. 121-130.doi:10.1061/(ASCE)1084-0699(2009)14:2(121)
- J. R. Stedinger and V. W. Griffis, “Flood Frequency Analysis in the United States, Time to Update,” Journal of Hydrologic Engineering, Vol. 13, No. 4, 2008, pp. 199-204.
- V. W. Griffis and J. R. Stedinger, “Flood Frequency Analysis in the United States,” Applications of Statistical Distributions in Hydrology, ASCE Monograph, 2011.
- R. J. Whitley and T. V. Hromadka II., “Computing Confidence Intervals for Floods I,” Microsoftware for Engineers, Vol. 2, No. 3, 1986, pp.138-150.
- R. J. Whitley, T. V. Hromadka II and M. J. Smith, “The Log-Pearson III Distribution in Hydrology, Chapter 6,” Environmental Sciences & Environmental Computing, Vol. III, P. Zannetti, et al., Editors. EnviroComp Institute, (http://www.envirocomp.org/esec), An Electronic Book, 2007.

