Journal of Software Engineering and Applications
Vol.7 No.8(2014), Article
ID:47998,15
pages
DOI:10.4236/jsea.2014.78060
Fine-Grained Work Element Standardization for Project Effort Estimation
Peraphon Sophatsathit
Department of Mathematics and Computer Science, Faculty of Science, Chulalongkorn University, Bangkok, Thailand
Email: speraphon@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 May 2014; revised 2 June 2014; accepted 1 July 2014
ABSTRACT
Traditional project effort estimation utilizes development models that span the entire project life cycle and thus culminates estimation errors. This exploratory research is the first attempt to break each project activity down to smaller work elements. There are eight work elements, each of which is being defined and symbolized with visually distinct shape. The purpose is to standardize the operations associated with the development process in the form of a visual symbolic flow map. Hence, developers can streamline their work systematically. Project effort estimation can be determined based on these standard work elements that not only help identify essential cost drivers for estimation, but also reduce latency cost to enhance estimation efficiency. Benefits of the proposed work element scheme are project visibility, better control for immediate pay-off and, in long term management, standardization for software process automation.
Keywords:Project Effort Estimation, Work Element, Symbolic Flow Map, Latency Cost, Software Process Automation

1. Introduction
Traditional software project effort and cost estimation rely primarily on life cycle models, namely, waterfall, spiral, water-fountain, etc. The amount of effort expended, which eventually is translated into cost and hereafter may be used interchangeably, must be determined before the project commences. Hence, effort estimation is inevitably carried out in the absence of project work details. Various cost estimation techniques and models have been devised to arrive at an educated guess work. A few popular ones are SLIM model/Putnam model [1] , COnstructiveCOstMOdel (COCOMO 81 [2] and COCOMO II [3] ), Walston-Felix model [4] , Bailey-Basili model [5] , Albrecht-Gaffney model [6] , Kemerer empirical model [7] , and Matson, Barrett and Mellichamp model [8] . These models are supported by extensive researches and well-established metrics to derive practical costing formula for accurate estimation. The underlying metrics that participate in the estimation process are lines of code (LOC), function point (FP) [9] , use case point (UCP) [10] , application point (AP) [3] , and their variants such as source lines of code (SLOC), delivered source instructions (DSI), unadjusted use case point (UUCP), etc. Nevertheless, one of the biggest caveats is the granularity of measurement basis. As project life cycle (LC) spans a considerable period of time, smaller phase-wise breakdown is set up along well-defined development process cut-off points, or technically speaking, project milestones. Seemingly manageable as the phases are, phase-wise estimation is still uncommon and impractical to perform, hence the dominance of LC level measure. All of these classical approaches use project lifecycle span in the estimation process which inevitably incorporate estimation errors, hidden phase overhead, and phase-transition overhead. The latter two cost factors hereafter will be referred to as latency overheads.
The above effort estimation research attempts are just tip of the ice burg. Measurements and their accuracy are still subject to validation that involves numerous techniques, which unfortunately are far from maturity. Many researches are underway to arrive at reliably accurate effort estimation techniques, ranging from parametric modeling, knowledge-based modeling, case-based reasoning, statistical inferences, fuzzy logic, neural networks, and analogies [11] [12] . What follows the underlying method of these models is how well the method performs. This includes errors of measurement, variations in the data sets, and comparative performance statistics with other techniques.
This paper will explore a finer grain of project effort estimation based on a well-established measurement paradigm and emerging research endeavors. The study encompasses various viewpoints that propose a breakdown of project LC in order to perform finer grained estimate at activity level. Standard operational elements will be defined and put to use. The ultimate goal is to streamline work elements so that the amount of time (which subsequently can be converted to equivalent effort) can be systematically and accurately estimated. Nevertheless, whether or not the pros and cons of these novel viewpoints will be applicable to traditional project management, as well as new paradigms of practice such as agile, eXtreme Programming (XP), and Agile Unified Process (AUP), remain to be validated with real project implementation.
This paper is organized as follows. Section 2 recounts some principal building blocks that are applied in many literatures. Section 3 describes traditional project LC estimation, along with Industrial Engineering standard work study, that sets up the proposed fine-grained estimation approach. Section 4 elucidates preliminary comparative analyses of the proposed breakdown. Suggestions for future direction and prospectus will be discussed in Section 5. Some final thoughts are presented in the Conclusion.
2. Related Work
Conventional effort estimation techniques [13] focus on project life cycle data to carry out the project effort and cost involved. Various estimation techniques have been devised to improve estimation accuracy. Table 1 summarizes a brief predominant research work and their findings in this area.
A few emerging research endeavors have been attempted to estimate at a finer level using phase-wise project data. Breaking up in phases may uncover activities that were hidden too subjective to measure and average out by LC approach. Different project dimensions can then be taken into account to arrive at a more accurate estimation. The empirical findings usually are inapplicable for generic use depending on phase distribution [14] . Various user groups such as IFPUG, ISBSG (International Software Benchmarking Standards Group), are examples of domain specific estimation. Project managers (PMs) must decide what data are to be collected to suit the applicable domain. Jodpimai, Sophatsathit, and Lursinsap [15] explored the relationship of different project dimensions to select only a handful of relevant cost drivers as oppose to standard 16 factors in existing approaches, yet yielding similar outcome. The needs for standardizing its deliverables and development process are key factors to software products. Typical acclaimed standards and working groups are:
Ÿ ISO/IEC 14143 [six parts] Information Technology—Software Measurement—Functional Size Measurement
Ÿ ISO/IEC 19761:2011 Software engineering—COSMIC: A Functional Size Measurement Method
Ÿ ISO/IEC 20926:2009 Software and Systems Engineering—Software Measurement—IFPUG Functional Size Measurement Method
Ÿ ISO/IEC 20968:2002 Software engineering—Mk II Function Point Analysis—Counting Practices Manual
Ÿ ISO/IEC 24570:2005 Software Engineering—NESMA Functional Size Measurement Method Version 2.1 —Definitions and Counting Guidelines for the Application of Function Point Analysis
Ÿ 16326 WG—Information Technology-Software Engineering—Software Project Management Working Group (IEEE)
Ÿ ERCIM Working Group Software Evolution
Ÿ Project Management Institute (PMI) and Project Management Body of Knowledge (PMBOK®)
While conventional estimation models take the entire LC activities into estimation consideration, finer grained activity breakdown has not been practiced in real software projects. Frederick W. Taylor [17] introduced principles of scientific management in 1911, and Frank B. Gilbreth [18] set up operational work elements that subsequently became work study standard measurement known as Therblig. This study will exploit the use of work element process chart to create fine-grained project activity elements, thereby effort estimation can be determined more accurately than current LC practice.
Such a fine-grained breakdown entails phase-wise estimation that in turn permits detailed project visibility. In so doing, this work will attempt to adapt UML style to represent project activity element. Consequently, effort estimation can be managed systematically using standard flow diagrams, activity element set up, and visibly traceable operations.
3. Proposed Fine-Grained Operational Estimation Technique
Classical cost estimation employs the mixture of constituent cost factors (aka cost drivers) using COCOMO or COCOMO II to determine project cost. However, the number of parameters has been a formidable obstacle to accurate effort estimation since project inception. Several recent research findings [19] [20] advocate ensemble of multiple estimation methods, taking joint attributes into account. The lack of recognition to process variation and effort distribution pattern over project LC are predominant threats to model validity. Some shortcomings of existing approaches often result from inaccurate estimation, high risks of project failure, and ill-defined project artifacts such as workload, assignment, etc. For instance, project size is unarguably the principal estimator that is used throughout the entire project LC. If the project is broken down into finer grain of measure on phase basis, project size may no longer be the appropriate cost estimator of feasibility study and requirement analysis phases.
Figure 1 depicts an overview of simplified project work flow for a typical Software Project Management course. The prerequisite of this course is Software Engineering, thereby students will be ready to embark on application of software engineering models, techniques, process, and hands-on experience. Documents prescribing

Figure 1. Overview of simplified project work flow.
dotted lines are basically internal information used by developers, while those on solid lines are external information open to customers. As each activity moves from one phase to the next, efforts are spent on constituent tasks to accomplish the activity. Unfortunately, the work load involved are not straightforwardly and procedurally described, measured, and collected to determine a reliable estimation. An exploratory research attempt based on well-established Motion and Time Study by Industrial Engineering has been conducted with the hope of setting up work elements in project effort estimation. Figure 2 shows the 18 standard motion elements in Motion and Time Study.
The prime objective of this undertaking is to create visually standard symbols to represent descriptive and subjective constituent smaller tasks of project activity. In so doing, PM and team members can streamline their development process to arrive at a more objectively manageable work flow. Hence, an analogy of Therbligs has been defined in Figure 3 to establish standard work elements involved in each activity. The first element “O” denotes operation to be performed by the team members. Subsequent elements, namely, “D”, “I”, “M”, “T”, “A”, “S”, “P” denote delay, inspection or review, meeting or discussion, movement or transfer, adjustment, storage, and planning or decision, respectively.
Figure 4 illustrates a symbolic flow map of how the activity is procedurally broken down to work elements. The illustration shows a dialog box activity that is broken down to seven smaller tasks proceeding in the following sequence: O-O-P-M-I-T-T-A-P. This symbolic flow map not only serves as a visual trace of development process work flow, but also a detailed estimation of processing time which can be straightforwardly converted to equivalent effort estimate.
Details on procedural research will be carried out as follows. First and foremost, data are collected from students’ reports using pre-designed forms. Second, missing value and outlier will be screened out to reduce large variations. Third, data are normalized on the same comparable scale. Fourth, feature selection is performed to choose only relevant features for use in the estimation. Finally, performance evaluation will be applied to gauge how the proposed approach stacks up against traditional LC approach. Figure 5 illustrates the proposed process flow which will be elucidated in the sections that follow.

Figure 2. Standard 18 motion elements or Therbligs. Source: Wikipedia (accessed on May 16, 2014).
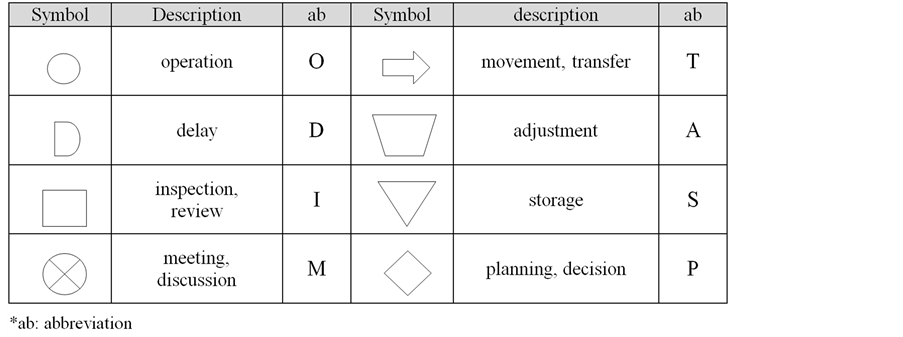
Figure 3. A novel standard work element definition.
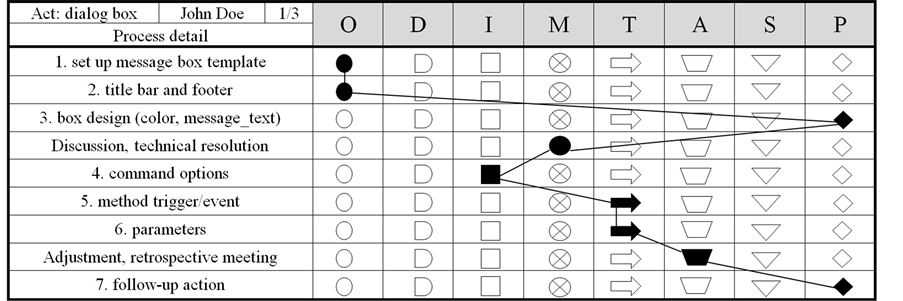
Figure 4. A symbolic flow map of an activity breakdown to work elements.
3.1. Data Collection
The novel approach will utilize conventional waterfall model where each phase is well defined and known by all software developers. As existing standard benchmarking archives such as COCOMO81, NASA93, Desharnais, USP05, MAXWELL1 are available in overall LC figures, this exploratory research will be conducted on a senior elective Software Project Management class to see how this novel scheme can be put to real use.
The process began from collecting data of the uppercase phases, i.e., requirements, specification, and design,
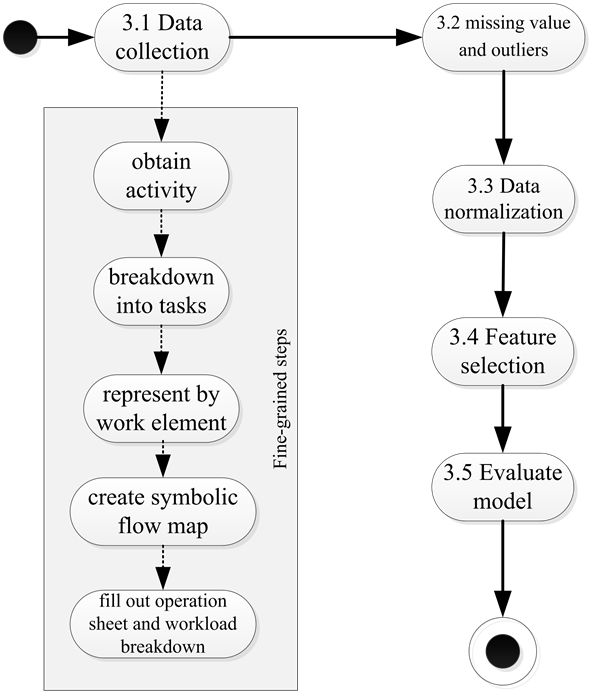
Figure 5. The proposed research process flow.
and the lowercase phases, i.e., coding, testing, and implementation. At phase level, functional size measurement [20] such as FP and LOC are employed as high level effort estimation since effort estimation metrics are conventionally governed by these two major metrics. Moreover, FP metric can be converted to LOC via backfiring [21] . The information can then be used to estimate overall LC effort. The results so obtained would be used to gauge the accuracy of the proposed fine-grained measurement. Table 2 depicts typical series of activities during the project LC.
An operation data sheet is set up as shown in Figure 6 to record data pertinent to the above symbolic flow map, including idle or overhead that may or may not be prime tasks. Project related data are filled up in the header section, namely, activity, activity ID (primary key), programmer (or group leader), group ID, build, document control number, page, start date, activity duration, project name, and authorized personnel.
Measurements are perhaps the heart of this fine-grained approach. The time it takes to perform each task, by the very novel notion, can be taken directly from “standard time” plus “allowance” to arrive at operation time. This is equal to man-time measurement or, in the context of this study equivalent effort (equiv-Effort), i.e., man-hour, man-day, etc. The question is how both standard time and allowance are obtained. Since this is the first attempt ever to introduce such a novel notion, no reference values can be used as oppose to those of the Industrial Engineering. The fact that software development procedure has not been standardized and the nature of the development process varies from task to task, programmer to programmer, makes standardization virtually impossible and impractical to implement with current state-of-the-practice. Notice that each task plays a different role under certain situations. On the one hand, it may play the prime task, so some allowances such as personal, fatigue, administrative, are added to supplement the operation time. On the other hand, it may be idle or overhead that must be taken separately into account as part of inherent “allowance”. For example, discussion and technical resolution in the operation data sheet is a prime task in design, especially among the design team members. Thus, allowance should be incorporated explicitly. However, during unit test, individual spends less
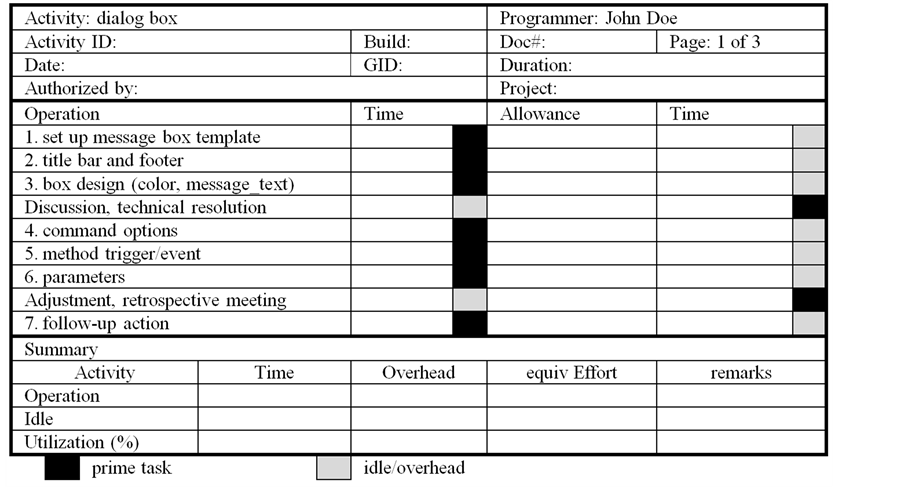
Figure 6. Operation data sheet.
Table 2. Activities and metrics of project tasks.
discussion and technical resolution effort with other members of the team except for occasional consultation with test specialist or PM. In this case, allowance may be accounted for as percentage of the test effort which is not considered a prime task. Consequently, the actual activity operation time can be precisely used to determine the equivalent effort estimation, while idle could attribute to latency overhead. The efficiency of operation is directly obtained from utilization factor.
The above operation data are further broken down by team members to depict work load responsibility of each member (shaded area) as shown in Figure 7. Team members are listed on top which contains cross references to operation data sheet and other related documents. The breakdown permits individual load distribution percentage to be determined accordingly.
A trial collection of work element tallies was taken in order to gauge their distribution based on the governing activity breakdown. These statistics would serve as preliminary effectiveness of fine-grained measures, which in turn could attribute to standardization of activity measurement.
3.2. Missing Value and Outlier
This step deals with two imposing problems in data collection, namely, missing value and outlier detection [22] . Missing value is a common phenomenon in project management where numerous small activities, assignments, and work products are too trivial, hard to identify or account for, or due to human errors. For example, button change, color change of error message display, or unrecorded informal discussion, etc. The efforts spent on such changes are, in many cases, insignificant to be recorded but appeared on request for change or maintenance re-
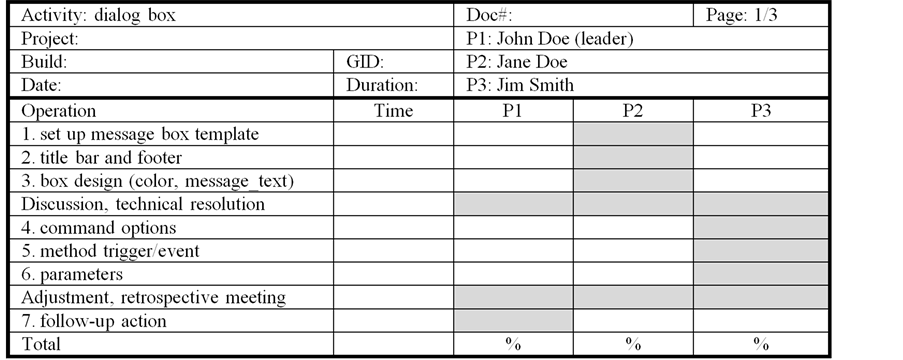
Figure 7. Work load breakdown by team members.
ports. Outlier usually results from freak accidents or exceptional situations where unusually high or low values are recorded. For example, the existence of data singularity in matrix multiplication caused an unusually difficult and extensive test effort to correct, hence the exceptional high effort outlier value.
There are several techniques to handle missing values. One of the most popular and effective techniques is k-nearest neighbor (k-NN) imputation [23] . The technique, as its name implies, uses k data points from the closest proximity of the missing value position to interpolate the most likely value. Such an imputation obviously incurs some errors if the actual values are not missing. A viable error estimation is to acquire other projects having the same “feature” value. The use of same feature value from other projects permits cross validation that fills the estimation of missing value to yield more accurate results.
Measuring errors is actually carried out by determining the Euclidean distant between the project having missing values and the ones without. The smaller the average of N measurements, the more accurate the predicted missing values.
Outlier detection is typically handled by examining the kurtosis and skewness of data distribution. Normality test is set up as the null hypothesis using z-score to determine if there exists a significant possibility that null hypothesis is accepted, i.e., normality holds with less than 0.001. This is written as p-value < 0.001. On the contrary, if the null-hypothesis is rejected, the highest value is treated as the outlier and is discarded. This process is repeated until all outliers are removed.
3.3. Data Normalization
This is a standard technique to linearly scale data of different ranges to the same scale, yet still preserves the relationship with the original values. This is done by Equation (1) as follows:
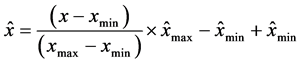 (1)
(1)
where 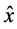 denotes the reference range, while x denotes individual range.
denotes the reference range, while x denotes individual range.
3.4. Feature Selection
This is the most important activity of project cost estimation. Many existing estimation techniques utilize several cost factors as estimation parameters. For example, the COCOMO model [3] uses 17 cost drivers in the estimation process. Jodpimai, Sophatsathit, and Lursinsap [15] found that only a handful of cost drivers were effective factors that could derive as accurate estimation as the comparative models without employing the full-fledge parameter set. Moreover, fewer cost drivers translated into faster computation time. The findings revealed that certain features were vital cost drivers that could yield accurate estimation.
The process of acquiring good selected features is straightforward. In a typical experiment, the data so collected are divided into two non-overlapping sets, that is, a training set and a test set. The former is used in various parameter adjustments during model creation process, whereas the latter is held out for model validation process. The first step is to eliminate independent features that do not contribute or affect project effort estimation. The next step is to reduce all redundant features that are less relevant to project effort estimation. This is done by means of Pearson’s correlation. Features that result in low value will be less relevant and thus eliminated. Finally, only those features that are related to effort estimation in the form of a mathematical function will be retained [15] .
There are a number of models that can be used in the feature selection process, ranging from conventional COCOMO, RUP, statistical, and neural network model. The basis for effort estimation must rest on proper use of these selected features in the estimation process, thereby accurate estimation results can be obtained.
Based on standard 17 cost drivers [3] , a phase-wise breakdown and costing features are set up as shown in Table 3 since the project sizes are relatively small, namely, uppercase and lowercase groups. The first group composes of software complexity, analyst capability, while the second group composes of execution time constraint, main storage constraint, and programmer capability. The features will be applied to their corresponding phases.
3.5. Performance Evaluation
There are many performance evaluation methods and their corresponding metrics for effort estimation. Each method has its own applicability to gauge the model accuracy or the relationship between actual and predicted estimation results, given the set of selected features. Table 4 summarizes some common methods and metrics for performance evaluation purpose.
Model evaluation is usually carried out by comparing the difference between predicted (estimated) effort y'i and actual effort yi. Effort is performed on the phase basis using related factors. For example, factors used in requirements and specification effort estimation involve FP to deal with both functional and non-functional requirements. As project requirements become materialized, size estimation via LOC is used instead since it yields more accurate outcome than that of FP. Some metrics are criticized for penalizing over-estimation (such as MRE), while others are just the opposite (such as BRE and MER). Two commonly used metrics are MMRE and PRED (0.25) since they are independent of units of measure and easy to use. However, they are found to give inconsistent results depending on properties of y'i/yi distribution. In which case, MdMRE is used to solve the outlier problem as MMRE cannot properly handle such inconsistencies. At any rate, this study adopted MMRE and PRED (0.25) accuracy metrics.
A noteworthy shortcoming of this exploratory research endeavor concerns project data. The above procedures have been implemented with industrial projects and extensive public data by the author’s research team, where the resulting outcomes are currently under investigation. The very notion of work element has just been introduced after data collection was completed. It was then put to test with classroom environment as it was deemed too novel to be adopted by real projects for the time being. The inherent shortfall of classroom setting was that
Table 4. Summary of methods/metrics for performance evaluation.
project size was too small to warrant any reliable practice or significance.
4. Preliminary Analyses
This exploratory research sets out to compare the proposed measurement with that of traditional LC. Due to the small number of students enrolled in the class, the samples were not a good representative of any conclusive inferences. Anyhow, the above procedures were followed to ensure that pertinent data were properly collected. Each team consisted of a project manager (PM), a system analyst (SA), a programmer, and a user. Students were asked to estimate phase effort that they would expend. These estimates would be used as the target values to be compared with the fine-grained figures from operation data sheet. They also collected actual LC efforts on class assignment by role and by development phases. Figure 8 depicts work element histogram of individual’s load distribution of the dialog box task based on the breakdown in Figure 7. Figure 9 and Figure 10 show the total project LC effort (y-axis) expended by role and by phase, respectively.
Table 5 summarizes individual’s load distribution based on operation data sheet. In analysis phase, the programmer played very little role in the assignment. Thus, his contribution in this phase was virtually non-existent (0.3%), while SA did most of the work in the first two phases and gradually reduced his role afterwards. The programmer made up for the loss in programming and testing, and the user participated heavily during the inception (analysis) phase and the closing (implementation) phase. Figure 11 shows the resulting plot.
Table 6 and Figure 12 show the value of MMRE and PRED (0.25) and corresponding plot of the class. The predictions from work elements of all parties fluctuated somewhat to the actual value as MMRE was moderate and PRED was not significant enough to yield any close predictions. The deviation was resulted from excessive allowances that were quite difficult to administer. This was a pioneer attempt to undertake something of this nature in Software Engineering which, on the contrary, has been well established with supporting standards in Industrial Engineering.
Table 7 and Figure 13 show the result comparison of total project effort obtained from COCOMO estimation in organic mode with the actual work element count by the proposed method. The reason being organic mode was that students were familiar and experienced with project development process. Work element breakdown was additional clerical tasks that they had to do as part of project documentation. The effort discrepancies were likely precipitated from fine-grained measurements having fewer latency cost.
Perhaps the most fruitful findings came from the presence of visual operation from symbolic flow map. Every
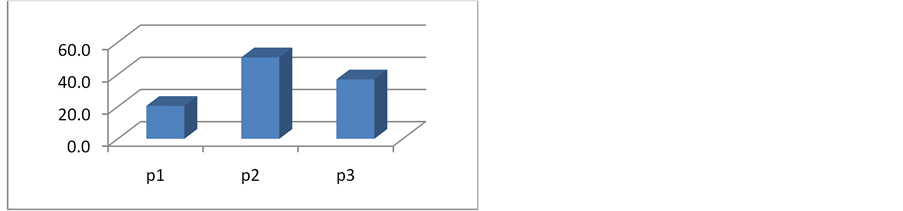
Figure 8. Individual’s work element distribution of the dialog box task.
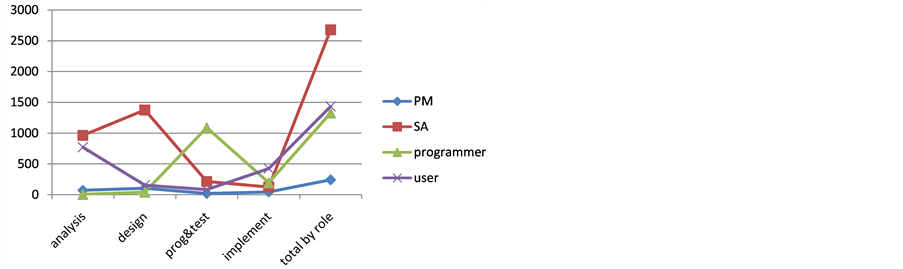
Figure 9. Total project LC effort by role.
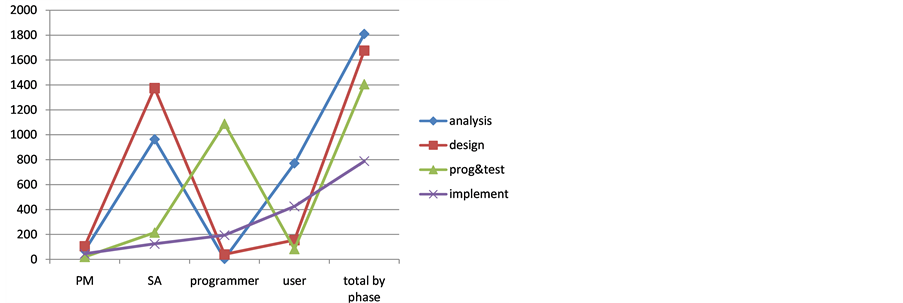
Figure 10. Total project LC effort by phase.
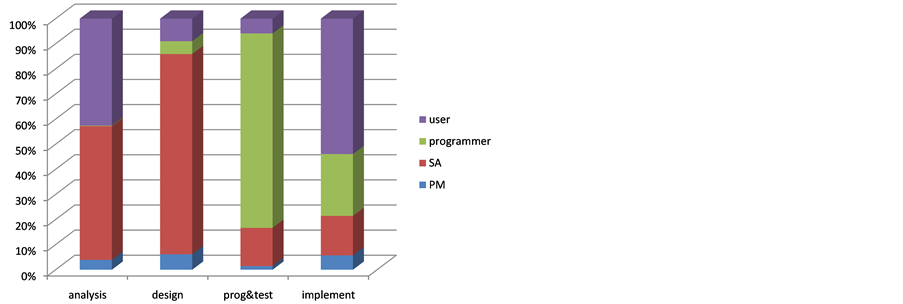
Figure 11. Work load distribution plot.
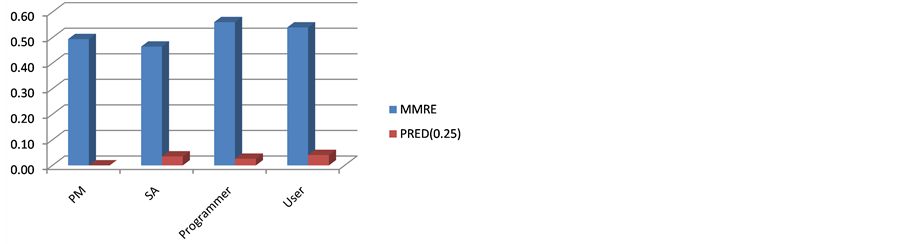
Figure 12. MMRE and PRED (0.25) plots.
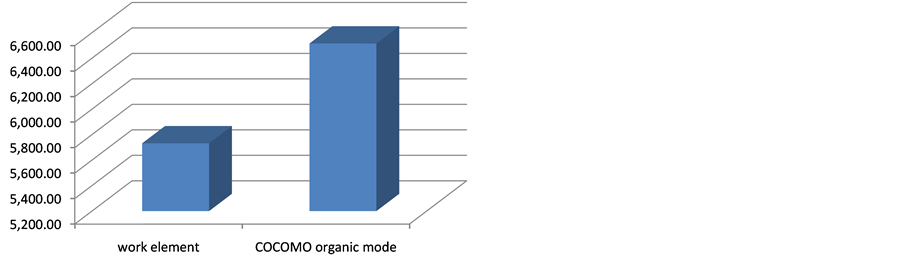
Figure 13. Actual total work element effort VS COCOMO organic mode estimation plot.
Table 5. Work load distribution from operation data sheet.
Table 6. MMRE and PRED (0.25) values.
Table 7. Actual total work element effort VS COCOMO estimation.
member was well aware of his own assignment and the course of action with other team members. The posted symbolic flow map of each activity (which could be posted in the so called “project war room”) proved to be an extremely valuable tracking tool during a “sit down” meeting to discuss the course of action, effort spent, and possibly (which rarely happened) activity reassignment. This attributed to finer grained analysis that portrayed a more visible activity tracking, not to mention more accurate measurements which in turn lessened the estimation errors. From a practical standpoint, the risk of over/under estimation is reduced, thereby improving project estimation and bidding opportunity.
5. Findings and Future Direction
This survey sets out to explore fine-grained project cost estimation, aiming at more accurate result than using traditional LC approach. Admittedly, the novelty of such an undertaking does not offer much provision for overall project management. All experimental data were improvised from classroom assignments. As mentioned earlier, performance could not be measured accurately due to the small sample size and unfamiliarity with work element notion. Fortunately, students were special group of people that possessed exceptional abilities, i.e., fast learning, flexibility, and adaptability. These attributes bring new work disciplines and culture to modern project management know-how. That is why this study embarks on a new realm of fine-grained measurement to cope with such a revolutionary transformation. The findings unveil some noteworthy results that have potential benefits to software project management.
Ÿ modern software products are short-live which cannot fit into traditional LC analysis. The proposed finegrained approach could open a new realm of exploiting development process standard to foster some forms of subjective project task measurements.
Ÿ fine-grained analysis can be adapted to cope with more scrutinized investigation provided that appropriate metrics and analysis techniques are applied.
Benefits from this exploratory estimation proposal can be summarized as follows:
1) Operational work element is an inherent, not accidental characteristic of project management [30] . The nature of software development process irrespective of the underlying model lends itself to collecting data which are readily available. What has not been done is the breakdown of activity structure. In addition, the difficulty of data collection process is seen as disruptive and infeasible as many tasks are operationally intertwined. This makes it hard to succinctly separate.
2) Modern development paradigms are seen to be unfitted to LC estimation. As the term “phase” has been ingrained in software engineering since the inception of waterfall model and has become a stigma of software project management. A closer look into this investigation reveals that if the term is viewed as a milestone of partial work products that can be accurately measured by a well-established standard, the term can be generalized to cover all paradigms of software development. For example, some “standard” work elements in the dialog box task can be reused elsewhere by other tasks in the project, thus reducing the time and effort to set up and measure similar tasks. As work elements become standardized, development process can be streamlined and automatically generated to attain software automation.
3) Various available tools, techniques, and metrics can be tailored to fit work element operation without having to reinvent the wheel. The available software body of knowledge (SWEBOK) can be straightforwardly adapted and exploited by software PM.
4) Training to work with systematic operating procedures and assessments in this fine-grained measurement is required. Proper planning must be carried out to set up the necessary programs for all personnel involved.
5) The advent of smart phone technology offers unlimited avenues for software research and development. As such, newer development paradigms and management techniques are called for. Undoubtedly, the success of such an undertaking can be tailored to support project estimation and streamline the development process.
6. Conclusions
This exploratory research proposes a novel work element standardization to streamline software development process. The ultimate goal is to reach software automation, wherein tasks can be automated succinctly. A number of benefits can be drawn from such an elaborative attempt. They are:
1) increasing operational visibility. This is perhaps the most important aspect of software project management that PM will be able to scrutinize any potential mishaps caused by activities or actions that have gone awry in each phase and transition between phases.
2) applying appropriate individual metrics to properly measure the performance of each designated phase. This will improve the estimation result as oppose to using the “one size fits all” metric to measure all activities of all phases.
3) handling overhead/latency cost effectively. As effort spent in each task depends primarily on standard work elements involved, such handling not only leverages out the latent cost within the activity and between activity transition, but also helps PM see the hidden problems, duplication of efforts, and overhead incurred within and between activity and phase transitions.
Despite numerous incomplete work element analyses due to the lack of essential body of knowledge and experience, the precursory establishment of work element definitions will hopefully serve as the forerunner of development process standardization research endeavors. It is envisioned that more accurate estimation not only can be achieved from the proposed approach, but also can be tailored to suit other development paradigms such as AUP and XP. As such, project manager will be able to efficiently manage and produce better project output that makes up for high quality software products. Future software process automation can be realized as well.
References
- Putnam, L. (1978) A General Empirical Solution to the Macro Software Sizing and Estimating Problem. IEEE Transactions on Software Engineering, SE-4, 345-361. http://dx.doi.org/10.1109/TSE.1978.231521
- Boehm, B. (1981) Software Engineering Economics. Prentice Hall PTR, Upper Saddle River.
- Boehm, B., Abts, C., Brown, A., Chulani, S., Clark, B., Horowitz, E., Madachy, R., Reifer, D. and Steece, B. (2000) Software Cost Estimation with COCOMO II. Prentice Hall PTR, Upper Saddle River.
- Walston, C.E. and Felix, C.P. (1977) A Method of Programming Measurement and Estimation. IBM Systems Journal, 16, 54-73. http://dx.doi.org/10.1147/sj.161.0054
- Bailey, J.W. and Basili, V.R. (1981) A Meta-Model for Software Development Resource Expenditures. Proceedings of the 5th International Conference on Software Engineering, 107-116.
- Albrecht, A.J. and Gaffney Jr., J.E. (1983) Software Function, Source Lines of Code, and Development Effort Prediction. IEEE Transactions on Software Engineering, SE-9, 639-648. http://dx.doi.org/10.1109/TSE.1983.235271
- Kemerer, C.F. (1987) An Empirical Validation of Software Cost Estimation Models. IEEE Transactions on Software Engineering, 30, 416-429.
- Matson, J.E., Barrett, B.E. and Mellichamp, J.M. (1994) Software Development Cost Estimation Using Function Points. IEEE Transactions on Software Engineering, 20, 275-287. http://dx.doi.org/10.1109/32.277575
- Albrecht, A. (1979) Measuring Application Development Productivity. I. B. M. Press, New York, 83-92.
- Karner, G. (1993) Resource Estimation for Objectory Projects. Objective Systems SF AB.
- Shepperd, M. and Schofield, C. (1997) Estimating Software Project Effort Using Analogies. IEEE Transactions on Software Engineering, 23, 736-743. http://dx.doi.org/10.1109/32.637387
- Li, J.Z., Ruhe, G., Al-Emran, A. and Richter, M.M. (2007) A Flexible Method for Software Effort Estimation by Analogy. Empirical Software Engineering, 12, 65-106. http://dx.doi.org/10.1007/s10664-006-7552-4
- Nasir, M. (2006) A Survey of Software Estimation Techniques and Project Planning Practices. Proceedings of the seventh ACIS International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/Distributed Computing (SNPD’06), Las Vegas, 19-20 June 2006, 305-310.
- Yang, Y., He, M., Li, M., Wang, Q. and Boehm, B. (2008) Phase Distribution of Software Development Effort. Proceedings of the Second ACM-IEEE International Symposium on Empirical Software Engineering and Measurement (ESEM’08), Kaiserslautern, 9-10 October 2008, 61-69.
- Jodpimai, P., Sophatsathit, P. and Lursinsap, C. (2010) Estimating Software Effort with Minimum Features using Neural Functional Approximation. Proceedings 2010 International Conference on Computational Science and Its Applications (ICCSA), Fukuoka, 23-26 March 2010, 266-273. http://dx.doi.org/10.1109/ICCSA.2010.63
- Dejaeger, K., Verbeke, W., Martens, D. and Baesens, B. (2012) Data Mining Techniques for Software Effort Estimation: A Comparative Study. IEEE Transactions on Software Engineering, 38, 375-397. http://dx.doi.org/10.1109/TSE.2011.55
- Taylor, F.W. (1911) The Principles of Scientific Management. Harper & Brothers, New York and London, LCCN11010339, OCLC233134.
- Gilbreth, F. and Gilbreth, C.E. (1948) Cheaper by the Dozen.
- Kocaguneli, E., Menzies, T. and Keung, J.W. (2012) On the Value of Ensemble Effort Estimation. IEEE Transactions on Software Engineering, 38, 1403-1416. http://dx.doi.org/10.1109/TSE.2011.111
- Gencel, C. and Demirors, O. (2008) Functional Size Measurement Revisited. ACM Transactions on Software Engineering and Methodology, 17, 15:1-15:36.
- Jones, C. (1995) Backfiring: Converting Lines of Code to Function Points. Computer, 28, 87-88. http://dx.doi.org/10.1109/2.471193
- Tsunoda, M., Kakimoto, T., Monden, A. and Matsumoto, K.-I. (2011) An Empirical Evaluation of Outlier Deletion Methods for Analogy-Based Cost Estimation. Proceedings of the 7th International Conference on Predictive Models in Software Engineering, Banff, 20-21 September 2011, 17:1-17:10.
- Keller, J.M., Gray, M.R. and Givens, J.A. (1985) A Fuzzy K-nearest Neighbor Algorithm. IEEE Transactions on Systems, Man and Cybernetics, SMC-15, 580-585. http://dx.doi.org/10.1109/TSMC.1985.6313426
- Kitchenham, B., Pickard, L., MacDonell, S. and Shepperd, M. (2001) What Accuracy Statistics Really Measure [Software Estimation]. Proceedings IEE—Software, 148, 81-85.
- Foss, T., Stensrud, E., Kitchenham, B. and Myrtveit, I. (2003) A Simulation Study of the Model Evaluation Criterion MMRE. IEEE Transactions on Software Engineering, 29, 985-995. http://dx.doi.org/10.1109/TSE.2003.1245300
- Friedman, M. (1937) The Use of Ranks to Avoid the Assumption of Normality Implicit in the Analysis of Variance. American Statistical Association, 32, 675-701. http://dx.doi.org/10.1080/01621459.1937.10503522
- Abran, A. and Robillard, P. (1996) Function Points Analysis: An Empirical Study of Its Measurement Processes. IEEE Transactions on Software Engineering, 22, 895-910. http://dx.doi.org/10.1109/32.553638
- Redei, G.P. (2008) Encyclopedia of Genetics, Genomics, Proteomics and Informatics. Springer, Heidelberg.
- de Vries, D. and Chandon, Y. (2007) On the False-Positive Rate of Statistical Equipment Comparisons Based on the Kruskal-Wallis HStatistic. IEEE Transactions on Semiconductor Manufacturing, 20, 286-292. http://dx.doi.org/10.1109/TSM.2007.901398
- Brooks, F.P. (1987) No Silver Bullet. Computer, 20, 10-19. http://dx.doi.org/10.1109/MC.1987.1663532
NOTES

1http://promise.site.uottawa.ca/SERepository.


