Journal of Software Engineering and Applications
Vol. 6 No. 9 (2013) , Article ID: 36238 , 12 pages DOI:10.4236/jsea.2013.69057
A Decision Support System for Selection of Solar Power Plant Locations by Applying Fuzzy AHP and TOPSIS: An Empirical Study
![]()
1Advanced Industrial Engineering Management Systems Research Center, King Mongkut’s University of Technology North Bangkok, Bangkok, Thailand; 2Industrial Engineering and Management, Lappeenranta University of Technology, Lappeenranta, Finland.
Email: athakorn@kmutnb.ac.th, nueng_mie@hotmail.com, markku.tuominen@lut.fi
Copyright © 2013 Athakorn Kengpol et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 5th, 2013; revised August 7th, 2013; accepted August 16th, 2013
Keywords: Solar Power Plant; Site Selection; Decision Support System; Fuzzy Analytic Hierarchy Process (FAHP); Technique for Order Preference by Similarity to Ideal Solution (TOPSIS)
ABSTRACT
The objective of this research is to propose a decision support system for avoiding flood on solar power plant site selection. Methodologically, the geographic information system (GIS) is used to determine the optimum site for a solar power plant. It is intended to integrate the qualitative and quantitative variables based upon the adoption of the Fuzzy Analytic Hierarchy Process (Fuzzy AHP) and the Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) model. These methods are employed to unite the environmental aspects and social needs for electrical power systematically. Regarding a case study of the choice of a solar power plant site in Thailand, it demonstrates that the quantitative and qualitative criteria should be realized prior to analysis in the Fuzzy AHP-TOPSIS model. The fuzzy AHP is employed to determine the weights of qualitative and quantitative criteria that can affect the selection process. The adoption of the fuzzy AHP is aimed to model the linguistic unclear, ambiguous, and incomplete knowledge. Additionally, TOPSIS, which is a ranking multi-criteria decision making method, is employed to rank the alternative sites based upon overall efficiency. The contribution of this paper lies in the evolution of a new approach that is flexible and practical to the decision maker, in providing the guidelines for the solar power plant site choices under stakeholder needs: at the same time, the desirable functions are achieved, in avoiding flood, reducing cost, time and causing less environmental impact. The new approach is assessed in the empirical study during major flooding in Thailand during the fourth quarter of 2011 to 2012. The result analysis and sensitivity analysis are also presented.
1. Introduction
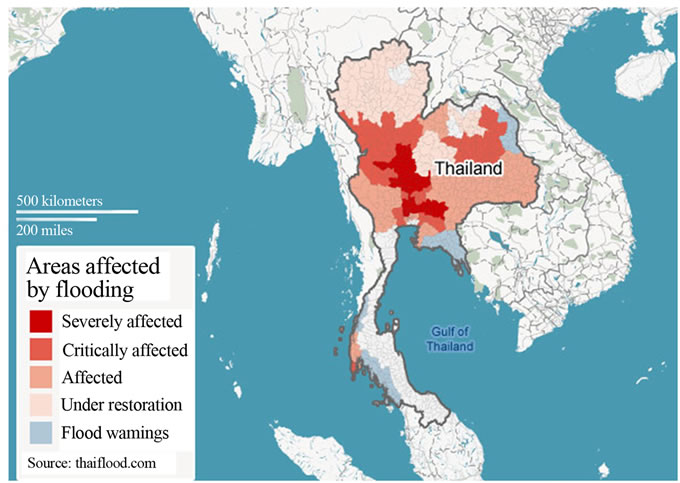
It is known that natural disaster is increasing around the world, for example the tsunami in Southeast Asia, an earthquake in Haiti, a hurricane in USA. For example during 4th Quarter in year 2011-2012, the ASEAN Economics Community (AEC) has encountered major flooding, especially in Thailand, the World Bank has estimated Billion USD 47.5 in economic damage and loss resulting from flooding, as 1st December 2011. Most of this cost is the manufacturing industry, as seven major industrial estates have covered by as much 3 meters during the floods, as illustrated in Figure 1. Thailand has experienced the worst flooding for 50 years over the last few months, leaving more than 360 people dead and causing severe damage across the country, hundreds of thousands of homes have been destroyed or damaged and the floodwaters have severely disrupted manufacturing operations in central regions of the country, as can be seen in Figure 2.
A third of the country remains under water and the floods have forced several industrial parks to close. There is a need to ensure that the area is appropriate and there is minimum risk from natural disaster.
Electric power is a crucial elemental factor to a nation’s economic and social development and it plays an increasing role in the everyday life and society because of the growth of the population, communities, industries, investment, education and tourism. Overall, the examination of the electricity consumption needs in Thailand shows that the electricity consumption has been growing
 (a)
(a) (b)
(b)
Figure 1. Flooding industrial areas and power plant in Thailand of 2011.
 (a)
(a)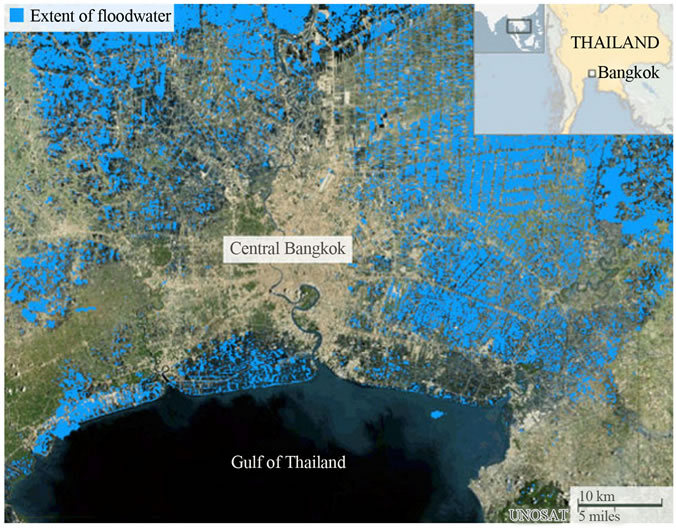 (b)
(b)
Figure 2. Flooding map in Thailand.
rapidly. Figure 3 shows the forecasted figures of Thailand’s growing electricity consumption from 2008 to 2030.
Thus, the other energy sources have been sought to substitute the fossil energy (for example; natural gas and coals) because the fossil fuel for power generation includes gasoline, coal, and natural gas whose emission increases in extent of the global atmosphere and causes an adverse affect environmentally. In addition, fossil fuel price, with its limited quantity, is likely to rise constantly. Following the 1973 energy crisis, there has been more interest in pursuing the research and development relating to the renewable energy as substitution for the fossil fuel. There is a growing awareness of environmental effects as a result of the adverse effects of fossil fuels on the environment, and the uncertain nature of reliance on imported fossil fuel, and the arrival of renewable energy alternatives, has influenced many nations, especially the developed nations on utilization of the renewable energy sources. In Thailand, the demand of electric power consumption has been growing continuously. The Department of Energy has formulated a long term 20 years “Power Development Plan” (Power Development Plan: PDP 2010), primarily aiming to promote the consumption of the renewable energy-based electricity and to reduce the dependence on natural gas, a primary source of electric generation in its country. Solar energy is one of the attractive renewable energies (i.e. wind energy and hydro energy) that are used to produce the electricity. These renewable energies are significant to electric generation. Table 1 exhibits the renewable alternative energies in Thailand.
In addition to renewable energy such as solar energy that Thailand has most potential to make use of in order to produce the electric power (See Table 1), [2] study demonstrates the need for constructing sites for each kind of power plants as shown in Table 2. The nuclear power plant needs for smallest constructing site, however, since the 2011 explosion of the nuclear power plant in Japan and the consequential damages, have a severe impact on human health and assets. The government takes this into account and agrees to decrease the portion set out in the former power production capacity development plan
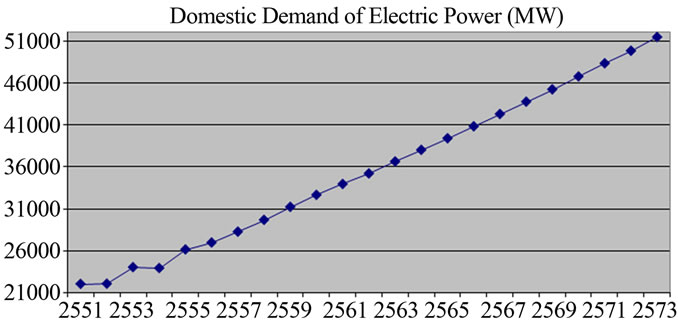
Figure 3. Forecasted figures of Thailand’s growing electricity consumption from 2008 to 2030.

Table 1. Potentiality of renewable energies in Thailand.

Table 2. Comparison of required land and CO2 emission in different energy generation technologies [2].
(PDP 2010) (2nd edition) from 10% to no less than 5% of total production capacity and postpone the nuclear power plant constructing plan for three years (adjourned from the year 2023 to 2026) [3]. This is to prepare safety readiness following a lesson from the explosion of the nuclear power plant in Japan and to induce public acceptance. Therefore, the 2nd appropriate renewable energy needed for the smallest constructing site is solar energy, which in Table 2 shows the solar energy needs of the land use (630 km2/GW/year) and the CO2 emission (600 CO2) is the minimum among all the renewable energy.
According to [4], the examination of electric power generation from solar energy indicates that Thailand has potential to generate the electricity adequately from solar energy. In Figure 4, the northeast and central part of Thailand is irradiated mostly, a total of direct normal irradiation ranges between 1350 - 1400 kWh/m2.
In general, it is reasonable that the solar plant should be set up to respond to the consumers’ growing demand of electricity consumption and to fulfill the government policy on power production capacity development plan (PDP 2012), prescribing that renewable energy-based electric generation is of 4804 MW, or accounting for 6% to strengthen the domestic power production. Thus, selecting the construction site for a power plant is a crucial factor needed to be taken into account in terms of appropriateness of the location.
The purpose of this study, therefore, is to develop the Decision Support System for selecting the solar power plant site based upon the qualitative and quantitative criteria under cost and environmental factors. The FAHP, which is a combination of AHP and fuzzy logic, is proposed for evaluating alternative when qualitative and quantitative observation and preferences are expressed. However, a disadvantage of the FAHP approach is that input data, expressed in linguistic terms, depends upon opinions and experience to determination of makers and thus involves subjectivity. The evaluation of criteria, sub-criteria and alternative sites usually requires specified knowledge, information as well as experience, how-
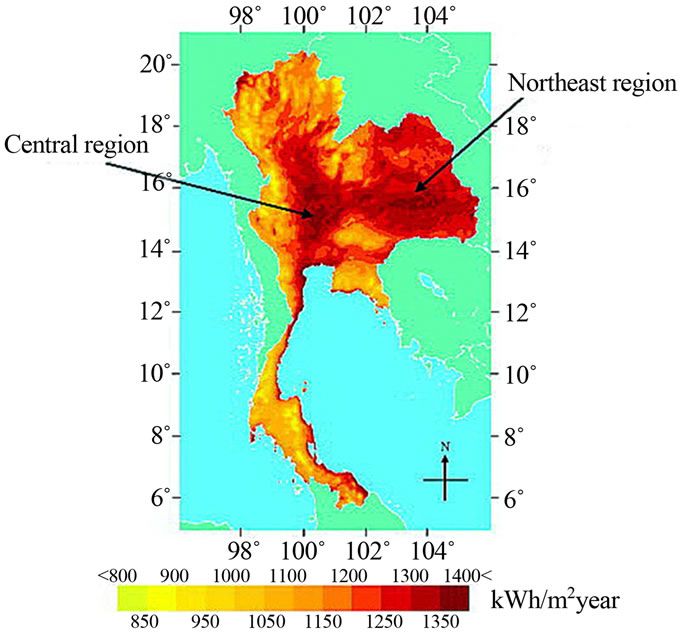
Figure 4. A map of Thailand showing geographical distribution of year, sum of direct normal irradiation [4].
ever, experts may display bias in judgments during providing preference of one criterion over another criterion [5]. This is why the TOPSIS is combined with FAHP. The detail of FAHP and TOPIS can be seen in the next section.
This paper contains the following: Section 2 describes the background of the models used in this study and relevant literature review. Section 3 illustrates more detail of the decision support system. Section 4 summarizes the results and gives recommendations from this research.
2. Literature Review
It is important to study previous researches on solar power plant site selection: for example, [6] propose how to choose the optimal location for a solar power plant through the use of the integrated data envelopment analysis (DEA) and principle component analysis (PCA) approach. [7] examine how to determine the optimal location for a wind observatory at a university campus with the application of the analytic hierarchy process (AHP). [8] employ AHP as a guideline in planning a decision support system for the international power plant location by Japanese producers and its applications in the EC. [9] propose the integrated approach for site selection procedures in which both qualitative and quantitative researches are taken into consideration through the use of AHP-based decision. [10] propose methodology that boosts the decision-maker to evaluate the waste management problem in Beijing and other booming regions in the developing countries through the use of the integrated AHP and geographical information system (GIS). [11] propose the geographic information system (GIS) algorithms and the computer-based techniques in selecting the location of warehouses. Likewise, [12] propose the GIS algorithms to select the shopping malls. [13] propose the geographic information system (GIS) along with the Multiple Criteria Decision Making to select the large-scale wind turbines. [14] apply the GIS to evaluate the location of the municipality’s refuse disposals (Land Fill). [15,16] propose the multiple criteria simulation by using the Integer Goal Programming for troubleshooting for determining the location of the fire station. [17] propose a selecting method for thermal power plant sites by using the ELECTRE II to solve the problems. [18] demonstrate the selection of the restaurant location in Teipei, China through the Analytic Hierarchy Process. [19] propose the Analytic Hierarchy Process algorithm and Data Envelopment Analysis for selecting the railway station sites in Iran. [20] propose the Fuzzy TOPSIS principles to select the distribution centre location.
2.1. Fuzzy Analytical Hierarchy Process
Notwithstanding the accuracy of the AHP, it has some disadvantages. AHP fails to reflect the human’s viewpoint and thinking model adequately and the decisionmaker has a conflict while contemplating, thereby resulted in the errors of the numbers [21]. Thus, the Fuzzy theory has been adopted to support a decision process to cope with the frequently-occurring problems in the criteria analysis process. The Fuzzy Analytic Hierarchy Process (FAHP) adopts the Fuzzy Set Theory together with AHP in the ambiguous context, on which the pairwise comparison method is focused, and fuzzy data set is used instead of the scoring method for assessment only [22]. Since a decision-maker may have faced a conflict during contemplating to prioritize the fixed number, the fuzzy theory can be adopted to support the decision process and to resolve the problems occurring in the criteria analysis process. There are, for example, in [23] the fuzzy AHP and the artificial network which are adopted to develop the decision support system for selecting the location of the convenience store. The weight of factors is evaluated using the questionnaires and interview method, and then evaluated by the retail experts. [21] study the selection of the most satisfactory carriers based upon the factors examined. The sales managers from manufacturing companies in Turkey are interviewed to determine the weight of the factors by using the fuzzy AHP techniques. [24] examine the application of the fuzzy AHP to select the research and to develop project contributors in the multiple criteria decisions, in which the evaluators are experts from educational institutions, industry, and the government sector. In addition, [22] study the application of the fuzzy AHP to evaluate the cargo shipping company by using the formula of [25].
In order to cope with the uncertainty, fuzzy AHP is more favoured in site selection. [26] formulate the multicriteria decision analysis process in which the geographic information system (GIS) analysis with the fuzzy analytical hierarchy process (FAHP) are integrated and employed to determine an optimum site for a new hospital in a Tehran urban area. [27] propose the fuzzy AHP approach for supplier recruitment by Turkey based washing machine company. [28] propose a combined multi-criteria decision making (MCDM) approach for choosing the supermarkets site in Turkey. FAHP is an application combining fuzzy set with AHP to resolve the certain defects of AHP in a human’s opinion. The most widely used method for the solution on fuzzy AHP applications is the extended analysis method proposed by [29]. A simple calculation for Fuzzy AHP is conducted using [25] fuzzy logic as a tool supporting the decisionmaking under the uncertainty of data with permissible flexibility and rationale simulating the human’s thought process. However, the feature of the logic is superior to Boolean logic: its concept with extension of the partial truth, in which real value lies between completely true and completely false. The traditional logic includes only true and false. For calculating the simple fuzzy, [29] proposes as following. The step of Chang’s extent analysis can be given as in the following:
Step 1: The value of fuzzy synthetic extent with respect to ith object is defined as
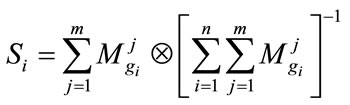 (1)
(1)
where all the 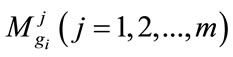 are triangular fuzzy number (TFN), and
are triangular fuzzy number (TFN), and  denotes the extended multiplication of two fuzzy numbers.
denotes the extended multiplication of two fuzzy numbers.
We consider triangular fuzzy number to describe a fuzzy event as denoted as (l, m, u) as shown in Figure 5. The parameters l, m and u denote the smallest possible value, the most promising value and the largest possible value of fuzzy event. To obtain , perform the fuzzy addition operation of m extent analysis values
, perform the fuzzy addition operation of m extent analysis values
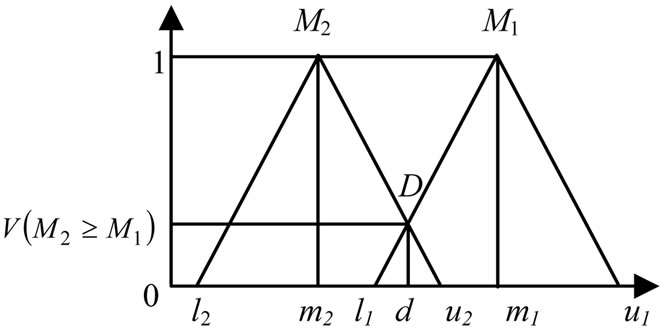
Figure 5. The intersection between M1 and M2.
for a particular matrix such that
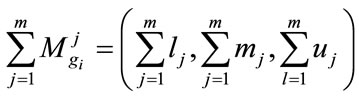 (2)
(2)
and to obtain , perform the fuzzy addition operation of
, perform the fuzzy addition operation of 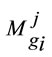 (j = 1,2,…, m) values such that
(j = 1,2,…, m) values such that
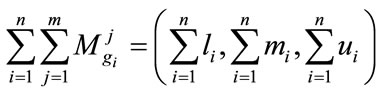 (3)
(3)
and then compute the inverse of the vector in Equation (2), such that
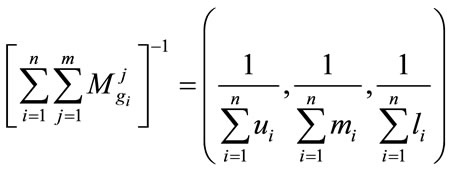 (4)
(4)
Step 2: As 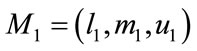 and
and 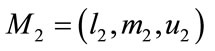 are two triangular fuzzy numbers the degree of possibility of
are two triangular fuzzy numbers the degree of possibility of 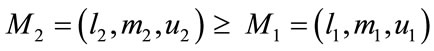 is defined as
is defined as
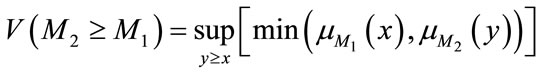 (5)
(5)
where  and
and 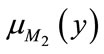 are the membership function of M1 and M2 as shown in Figure 5, and x, y are the values on the axis of membership function of each criterion. This can be equivalently expressed as follow:
are the membership function of M1 and M2 as shown in Figure 5, and x, y are the values on the axis of membership function of each criterion. This can be equivalently expressed as follow:
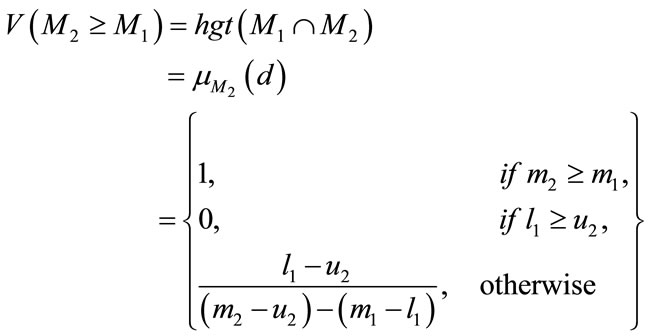 (6)
(6)
where d is the ordinate of the highest intersection point D between 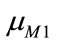 and
and 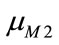 is illustrated in Figure 5. To compare
is illustrated in Figure 5. To compare  and
and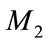 , we need both the value of
, we need both the value of 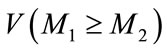 and
and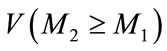 .
.
Step 3: The degree of possibility for a convex fuzzy number to be greater than k convex fuzzy number,  can be defined by
can be defined by
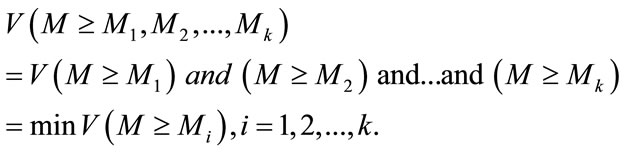 (7)
(7)
Assume that, we calculate the minimum degree possibility 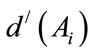 as
as
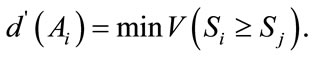 (8)
(8)
For k = 1, 2,..., n;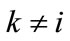 . Then the weight vector
. Then the weight vector 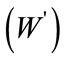 is given by
is given by
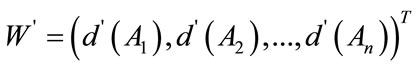 (9)
(9)
where 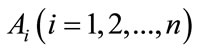 are n elements.
are n elements.
Step 4: Via normalization, the normalized weight vector 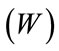 are
are
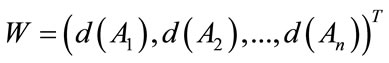 (10)
(10)
where W is a non-fuzzy number that gives priority weights of an attribute or an alternative over another.
2.2. Technique for Order Preference by Similarity to Ideal Solution (TOPSIS)
Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) is developed by [30]: the main concept of TOPSIS is the optimal alternative, that it should not be distanced from the positive ideal solution and negative ideal solution. The description on TOPSIS is demonstrated in [31] the result of analysis shows the index of each alternative, the index of maximum value is the optimal solution for decision-making in the respective situation. TOPSIS assumes that we have m alternatives and n criteria and we have the score of each alternative with respect to each criterion. The method is illustrated below.
Step 1: Calculate the normalized decision matrix, raw values (xij) are transformed to normalized values (nij) using the equation:
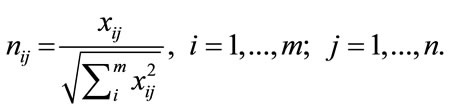 (11)
(11)
Step 2: Calculate the weighted normalized decision matrix, the weight normalized value (vij), using the equation:
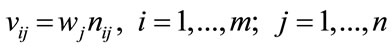 (12)
(12)
where 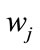 is the weight of the
is the weight of the 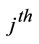 attribute or criterion, and
attribute or criterion, and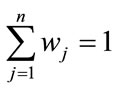 .
.
Step 3: Determine the positive ideal solution (A+) and negative ideal solution (A−), where 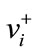 denotes the maximum values of vij and
denotes the maximum values of vij and 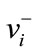 denotes the minimum values of vij.
denotes the minimum values of vij.
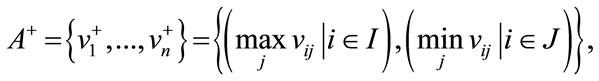 (13)
(13)
 (14)
(14)
where I is associated with benefit criteria, and J is associated with cost criteria.
Step 4: Calculate a distance of the positive ideal solution 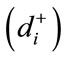 separately by using the displacement differentiation from
separately by using the displacement differentiation from
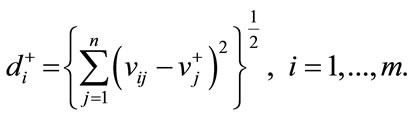 (15)
(15)
Similarly, the separation from the negative ideal solution 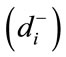 is given as
is given as
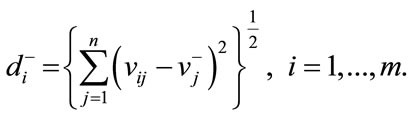 (16)
(16)
Step 5: Calculate the relationship proximal to the problem-solving approaches, proximal relationship from alternative Ai to determine A+
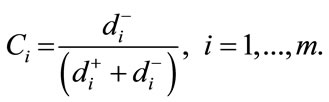 (17)
(17)
where 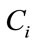 denotes the final performance score in TOPSIS method.
denotes the final performance score in TOPSIS method.
Step 6: Rank the calculated values to determine the best solution, then choose the shortest distance for the positive ideal solution and negative ideal solution, choose the maximum value of Ci.
3. The Decision Support System for Site Selection of Solar Power Plant
A selection process to determine the optimum site for a solar power plant can be contemplated along with many different types of data. In the Decision Support System, it concerns selection of the appropriate site and composite ranking. Thus, it’s needed to consider several indicators, for examples, climate, geographical, transportation, environment and cost. At this stage, the potential sites are provided for consideration using the fuzzy AHP method, and then scores for each area are compared. In this study, [32] criteria are adopted into the hierarchy model. Figure 6 shows the decision support system model.
3.1. Part I: Preliminary Screening Site
As shown in Figure 6, this part is the data preparation of each site for the decision support system. It consists of feasible data for solar power plant site. In the initial process of spatial analysis, the geographic information system (GIS) is used to determine the optimum site for a solar power plant. GIS analysis screens the possible sites while the inappropriate sites are excluded under the geographic characteristics. There are, for example, slope, geographic direction, and height of construction, which are regarded as important variants. Building solar power plants on rough and cragged, mountainous land with shallow valleys is tough and usually inappropriate. Ini-
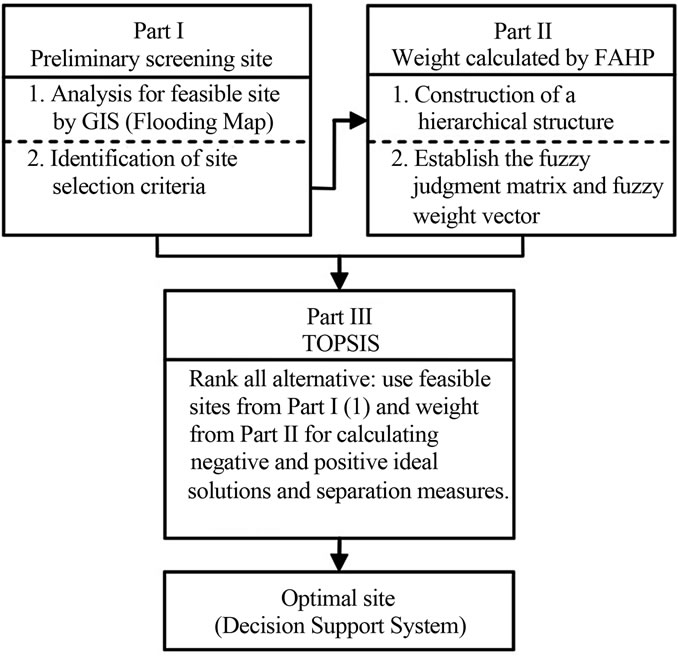
Figure 6. Systems model of decision support system.
tially, GIS screens the potential area for the optimum solar power plant site and selects the possible area under the condition of least slope area, and being remote and far away from a community and river basin where flood is predisposed to occur, neither situated in forestry area nor proximity to historical buildings. Given Thailand’s unpredicted great flood in 2011 to 2012, the flooded area in Figure 7 is excluded because it may affect a selection of solar power plant site.
3.2. Part II: Weight Calculated by Using FAHP
Once sites are geographically screened as mentioned in the first stage, the relevant factors for selection of the construction site are weighted by using fuzzy AHP to determine actual extent of significance for each factor. Each factor’s weight is further analysed below (adopted from [32]. As shown in Table 3, there is a four-level hierarchy model for the solar power plant site selection problem in the northeast part of Thailand. The first level is to find the optimum site for solar power plant among potential candidates. As shown in the second level, the aim of the model is divided into five criteria, namely climate, geographical, transportation, environment and cost. The third level consists of 19 sub-criteria which are related to the main criteria. Also, the three potential sample sites as shown in Figure 7 are given at the final level of the proposed hierarchical model. A hierarchical structure formed after all criteria and alternatives are shown in Table 3.
3.3. Part III: TOPSIS
In part II, obtained results are used as input weights in
Table 3. The hierarchy of the site selection problem [32].
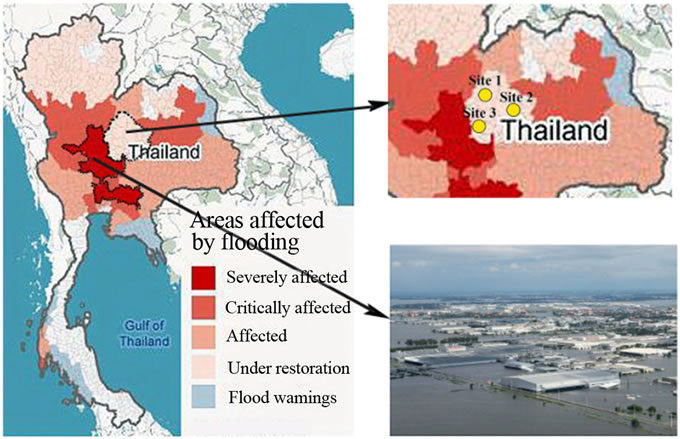
Figure 7. Preliminary screening site for flooding.
TOPSIS. It enables consistent and systematic criteria, which is based upon choosing the best alternative having the shortest distance from the positive ideal solution and the farthest distance from negative ideal solution. TOPSIS, by considering ideal and a non ideal solution, can help the decision maker to evaluate ranking and select the most appropriate.
4. The Decision Support System to Evaluate Site Selection of Solar Power Plant
In this research, the authors have developed a computer program, as illustrated in Figures 8-13, to assist the user in dealing with FAHP and TOPSIS model of decision support system. The five criteria consist of climate (A), geographical (B), transportation (C), environment (D) and cost (E) (as shown in Table 3).
On pair wised comparison among fuzzy parameters, the linguistic variables are defined for varying degrees of
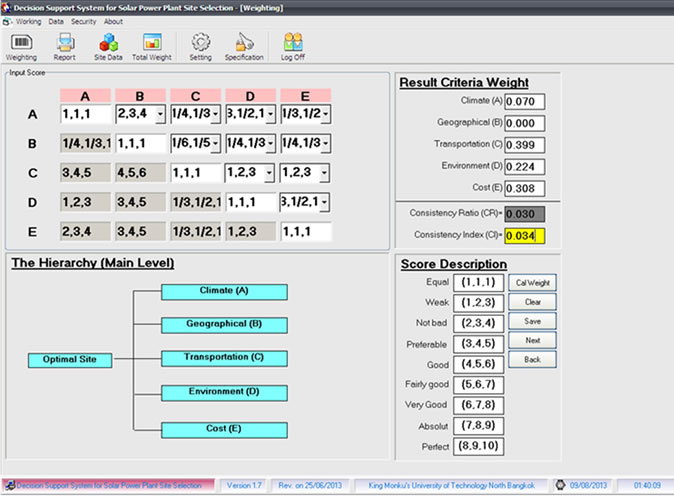
Figure 8. The decision support system for fuzzy comparison matrices at the main criteria (developed by the authors).

Figure 9. The decision support system for fuzzy comparison matrices at the sub criteria (developed by the authors).
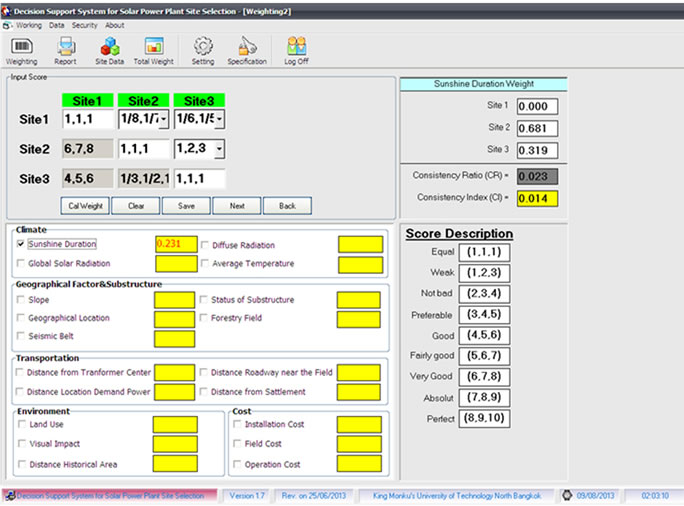
Figure 10. The decision support system for the weights of alternative sites with respect to sub criteria (developed by the authors).
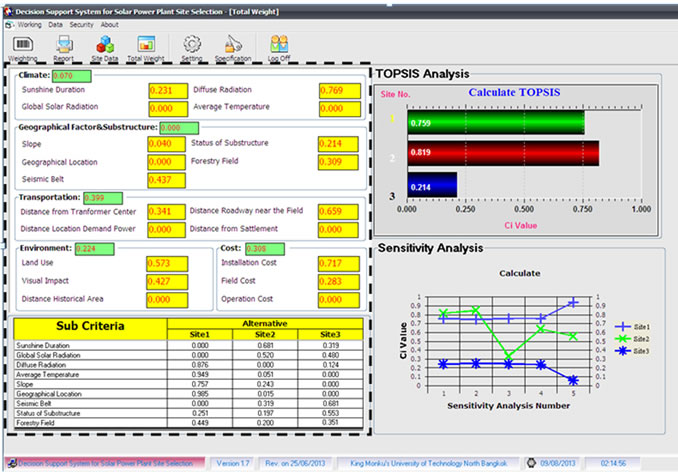
Figure 11. The decision support system for total weights (Dash Line) (developed by the authors).

Figure 12. The result of the decision support system for TOPSIS (Dash Line), developed by the authors.
preference (as shown in Table 4).
From Table 5, the values of fuzzy synthetic extent of five criteria with respect to the goal extract from the

Figure 13. The result from sensitivity analysis (Dash Line), developed by the authors.
judgments of the experts on pairwise comparisons are determined after discussions to ensure the different points of view as a final group decision in a concurrence, as illustrated in Figure 8. The calculation as below by using Equation (2). Therefore, the weight vector is given as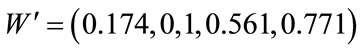 . After the normalization process, the weight vector of the main attributes which are climate attribute, geographical attribute, transportation attribute, environment attribute and cost attribute are found to be
. After the normalization process, the weight vector of the main attributes which are climate attribute, geographical attribute, transportation attribute, environment attribute and cost attribute are found to be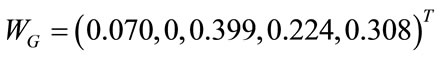 . This affirms that the consistency ratio value (CR) should be less than 0.1 (calculated value is 0.030 < 0.1), which means the outcome of weight gives a user considerable confidence before using it [33]. It can be seen that the significance of a comparative approach of each pair of each alternatives with reliability can be compared for the appropriate alternative. The same calculations are applied to the other pairwise comparison matrices, and the priority weights of each main attribute, sub-attribute and alternative can be found in Tables 6-10, as illustrated in Figure 9.
. This affirms that the consistency ratio value (CR) should be less than 0.1 (calculated value is 0.030 < 0.1), which means the outcome of weight gives a user considerable confidence before using it [33]. It can be seen that the significance of a comparative approach of each pair of each alternatives with reliability can be compared for the appropriate alternative. The same calculations are applied to the other pairwise comparison matrices, and the priority weights of each main attribute, sub-attribute and alternative can be found in Tables 6-10, as illustrated in Figure 9.
The sub-criteria on solar power plant site selection are shown in Tables 6-10 and summarized in Table 11, as illustrated in Figure 11. On the other hand, comparative evaluation of the solar power plant site alternatives with respect to relevant attributes is shown in Table 12, as illustrated in Figure 10.
The weights of alternative sites with respect to the each criterion is determined by adding the weights per site multiplied by weights of the corresponding sub-criteria and are shown in Table 12. From Table 13, for example, computation of the normalized value 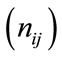 is calculated using Equation (12). From Table 14, determine the positive ideal solution
is calculated using Equation (12). From Table 14, determine the positive ideal solution 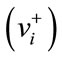 and negative ideal solution
and negative ideal solution 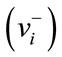 using Equations (13), (14). Next, calculate a distance of the ideal solution separately by using the displacement differentiation from Equations (15), (16).
using Equations (13), (14). Next, calculate a distance of the ideal solution separately by using the displacement differentiation from Equations (15), (16).

Table 4. Triangular fuzzy number of linguistic variables used in this study [26].

Table 5. Fuzzy comparison matrices at the main level.

Table 6. Evaluation of the sub attributes with respect to climate aspects.
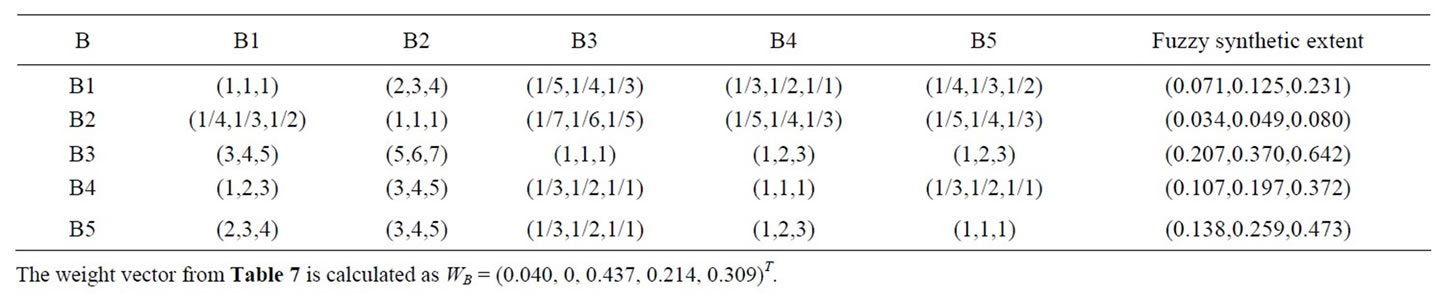
Table 7. Evaluation of the sub attributes with respect to geographical aspects.

Table 8. Evaluation of the sub attributes with respect to transportation aspects.

Table 9. Evaluation of the sub attributes with respect to the environment aspects.

Table 10. Evaluation of the sub attributes with respect to cost aspects.
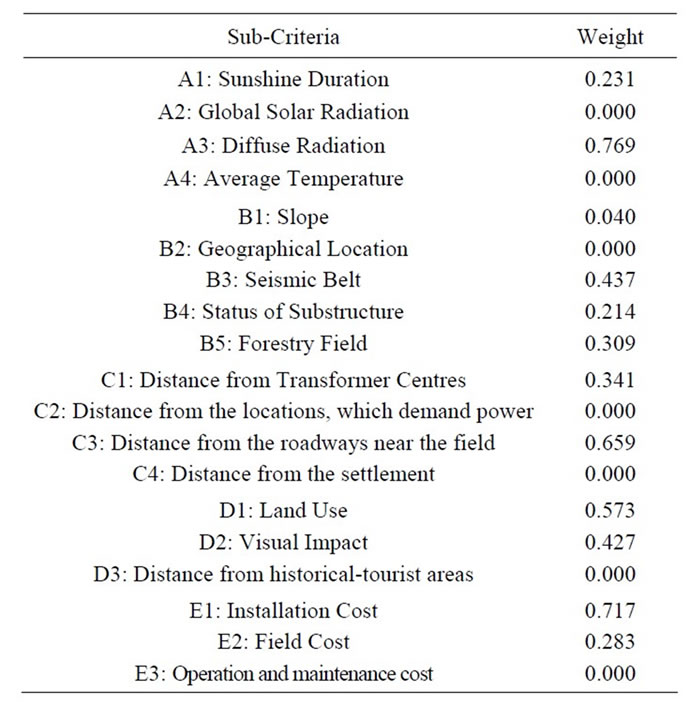
Table 11. The weight summarized of sub criteria.
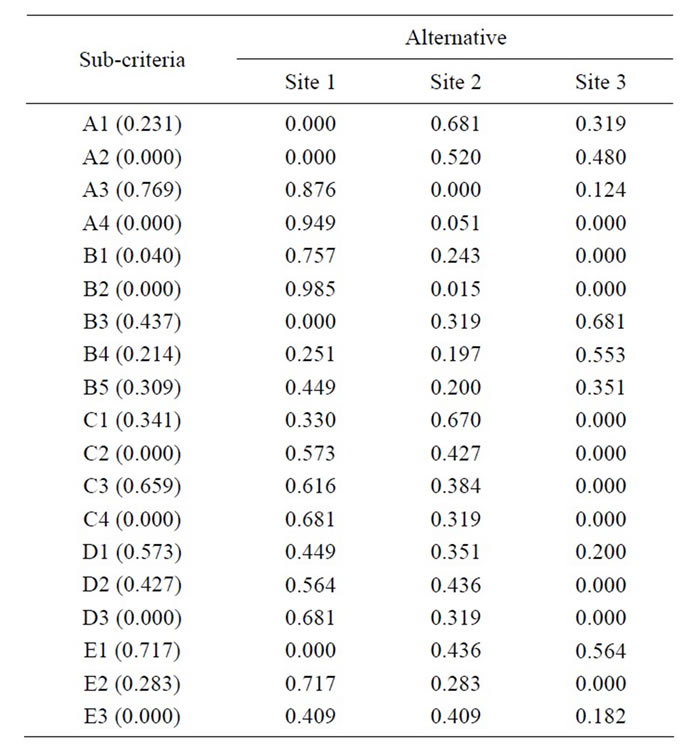
Table 12. The weights of alternative sites with respect to sub criteria.
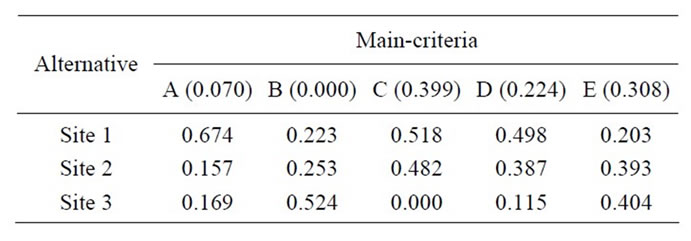
Table 13. Priority weights of alternative sites with respect to main goal.
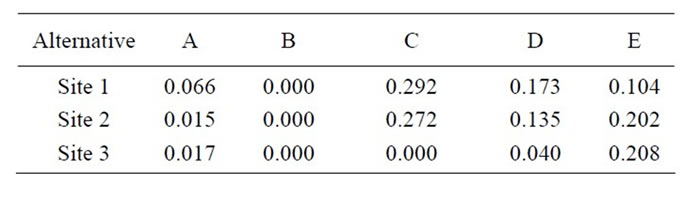
Table 14. The weighted normalized decision matrix.
Finally, calculate the relative closeness to the ideal solution ( ) by Equation (17) is shown in Table 15 as follows.
) by Equation (17) is shown in Table 15 as follows.
4.1. Application of TOPSIS in Ranking of Alternative
Finally, the TOPSIS method is applied to rank the alternative sites. The weighted normalized decision matrix, prepared by using Equation (12), can be seen from Table 14. The priority weights of alternative sites with respect to criteria, calculated by fuzzy AHP (shown in Table 13), can be used in the TOPSIS. By using the TOPSIS method, the ranking of alternative sites are calculated. Table 15 shows the evaluation results and final ranking of alternative sites for a solar power plant.
The result of TOPSIS as the numerical example using fuzzy AHP weights is shown in Table 15. From Table 15, the evaluation of the solar power plant site is selected and the Ci values the ranking of the solar power plants from the most preferable to the least. The highest Ci value (0.819) is selected at the site 2, as illustrated in Figure 12.
4.2. Sensitivity Analysis of Fuzzy-AHP and TOPSIS
There are two types of Fuzzy-AHP and TOPSIS to analyse in the sensitivity study. It gains the weight from fuzzy-AHP which is changed at two alternatives and the others are constant. Meanwhile the weight of the first
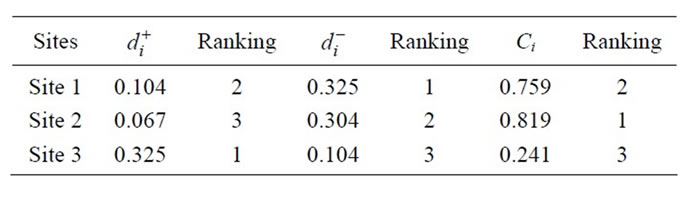
Table 15. The final evaluation and ranking of alternative sites.
main criteria A is changed with B, C, D and E respecttively but the others are constant. The new results are done by TOPSIS, which can be seen from the changes of weight and also the sensitivity analysis, as illustrated in Figure 13.
The results of sensitivity analysis show the weight changing affect the outcome of the site selection of the solar power plant. While the weights are changing mutually, the values of Ci and the rankings are changing, too. If A and C’s priority weights of criteria are exchanged, then the Ci value of site 1 springs from 0.759 to 0.758, and ranking of site 1 are changing from 2 to 1. This also leads to changes in ranking of site 2 from 1 to 2. Except this, site 1 has the largest Ci value when faced with other changes. According to the sensitivity analysis results, site 1 is robust to be the most appropriate alternative. That is because it has the highest Ci value after the weight exchanges carried out here. Sensitivity analysis can be further expanded by exchanging weights in difference manners.
5. Conclusions
The objective of this research is to design a decisive support system for avoiding flood on solar power plant site selection based upon five main criteria including climate, geographical, transportation, environmental and cost criteria. In this research, the first step we define the proper area, then the combination of AHP and fuzzy logic, is applied for evaluating alternatives when qualitative and quantitative observation and preferences are expressed. However, a disadvantage of the FAHP approach is that input data, expressed in linguistic terms, depends upon opinions and experience to determination of decision makers and thus involves subjectivity. The evaluation of criteria, sub-criteria and alternative sites usually requires specified knowledge, information as well as experience, however, experts may display bias in judgments during providing preference of one criterion over another criterion [5]. This is the reason why the TOPSIS is proposed to reaffirm as a systematic method for ranking of alternatives. Additionally, both FAHP and TOPSIS are not too complicated models compared to the other methods in multiple criteria analysis.
The contribution of this paper lies in the evolution of a new approach that is flexible and practicable to the decision maker, in providing the guidelines for solar power plant site selection under stakeholder needs based upon quantitative and qualitative criteria, at the same time, the desirable functions are achieved, in avoiding flood, reducing cost, time and environmental impact. The decision support system is assessed in the empirical study as well.
The future research can be done in the comparison between FAHP with another model, for example, Analytic Network Process, or comparison between TOPSIS and Maximise Agreement Heuristic, as can be seen in [34,35].
REFERENCES
- Renewable Energy Development Plan 15 Years. http://www.eppo.go.th/ccep/download/REDP_15_yrs.pdf
- R. Ramanathan, “Comparative Risk Assessment of Energy Supply Technologies: A Data Envelopment Analysis Approach,” Energy, Vol. 26, No. 2, 2001, pp. 197-203. doi:10.1016/S0360-5442(00)00058-X
- The Power Development Plan of the Country, 2012-2030 (Revision 3). http://www.eppo.go.th/power/ PDP2010-r3/PDP2010-Rev3-Cab19Jun2012-T.pdf
- S. Janjai, J. Laksanaboonsong and T. Seesaard, “Potential Application of Concentrating Solar Power Systems for the Generation of Electricity in Thailand,” Applied Energy, Vol. 88, No. 12, 2011, pp. 4960-4967. doi:10.1016/j.apenergy.2011.06.044
- D. Choudhary and R. Shankar, “An STEEP-Fuzzy AHPTOPSIS Framework for Evaluation and Selection of Thermal Power Plant Location: A Case Study from India,” Energy, Vol. 42, No. 1, 2012, pp. 510-521. doi:10.1016/j.energy.2012.03.010
- A. Azadeh, S. F. Ghaderi and A. Maghsoudi, “Location Optimization of Solar Plants by an Integrated Hierarchical DEA PCA Approach,” Energy Policy, Vol. 36, No. 10, 2008, pp. 3993-4004. doi:10.1016/j.enpol.2008.05.034
- H. Aras, S. Erdogmus and E. Koc, “Multi-Criteria Selection for a Wind Observation Station Location Using Analytic Hierarchy Process,” Renewable Energy, Vol. 29, No. 8, 2004, pp. 1383-1392. doi:10.1016/j.renene.2003.12.020
- S. Yurimoto and T. Masui, “Design of a Decision Support System for Overseas Plant Location in the EC,” International Journal of Production Economics, Vol. 41, No. 1-3, 1995, pp. 411-418. doi:10.1016/0925-5273(95)00017-8
- J. Korpela and M. Tuminen, “A Decision Aid Warehouse Site Selection,” International Journal of Production Economics, Vol. 45, No. 1-3, 1996, pp. 169-180. doi:10.1016/0925-5273(95)00135-2
- W. Guiqin, Q. Li, L. Guoxue and C. Lijun, “Landfill Site Selection Using Spatial Information Technologies and AHP: A Case Study in Beijing, China,” Journal of Environment Management, Vol. 90, No. 8, 2009, pp. 2414- 2421. doi:10.1016/j.jenvman.2008.12.008
- M. Vlachopoulou, G. Silleos and V. Manthou, “Geographic Information Systems in Warehouse Site Selection Decision,” International Journal of Production Economics, Vol. 71, No. 1-3, 2001, pp. 205-212. doi:10.1016/s0925-5273(00)00119-5
- E. W. L. Cheng and H. L. L. Yu, “A GIS Approach to Shopping Mall Location Selection,” Building and Environment, Vol. 42, No. 2, 2007, pp. 884-892. doi:10.1016/j.buildenv.2005.10.010
- A. Bennui, P. Rattanamanee, U. Puetpaiboon, P. Phukpattaranont and K. Chetpattananondh, “Site Selection for Large Wind Turbine Using GIS,” International Conference on Engineering and Environment (ICEE), Songkhla, 10-11 May 2007, 6 Pages.
- M. Zamorano, E. Molero, A. Hurtado, A. Grindlay and A. Ramos, “Evaluation of a Municipal Landfill Site in Southern Spain with GIS-Aided Methodology,” Journal of Hazardous Materials, Vol. 160, No. 2-3, 2008, pp. 473-481. doi:10.1016/j.jhazmat.2008.03.023
- M. A. Badri, A. K. Mortagy and C. A. Alsayed, “A MultiObjective Model for Locating Fire Stations,” European Journal of Operational Research, Vol. 110, No. 2, 1998, pp. 243-260. doi:10.1016/S0377-2217(97)00247-6
- M. A. Badri, “Combining the Analytic Hierarchy Process and Goal Programming for Global Facility Location-Allocation Problem,” International Journal of Production Economics, Vol. 62, No. 3, 1999, pp. 237-248. doi:10.1016/S0925-5273(98)00249-7
- H. O. Barda, J. Dupuis and P. Lencioni, “Multicriteria Location of Thermal Power Plant,” European Journal of Operational Research, Vol. 45, No. 2-3, 1990, pp. 332- 346. doi:10.1016/0377-2217(90)90197-J
- G. H. Tzeng, M. H. Teng, J. J. Chen and S. Opricovic, “Multicriteria Selection for a Restaurant Location in Taipei,” International Journal of Hospitality Management, Vol. 21, No. 2, 2002, pp. 171-187. doi:10.1016/S0278-4319(02)00005-1
- N. Mohajeri and G. R. Amin, “Railway Station Site Selection Using Analytical Hierarchy Process and Data Envelopment Analysis,” Computer and Industrial Engineering, Vol. 59, No. 1, 2010, pp. 107-114. doi:10.1016/j.cie.2010.03.006
- A. Awasthi, S. S. Chauhan and S. K. Goyal, “A MultiCriteria Decision Making Approach for Location Planning for Urban Distribution Centers under Uncertainty,” Mathematical and Computer Modelling, Vol. 53, No. 1-2, 2011, pp. 98-109. doi:10.1016/j.mcm.2010.07.023
- C. Kahraman, U. Cebeci and Z. Ulukan, “Multi-Criteria Supplier Selection Using Fuzzy AHP,” Logistic International Journal Management, Vol. 16, No. 6, 2003, pp. 382-394. doi:10.1108/09576050310503367
- M. Celik, I. D. Er and A. F. Ozok, “Application of Fuzzy Extended AHP Methodology on Shipping Registry Selection: The Case of Turkish Maritime Industry,” Expert Systems with Application, Vol. 36, No. 1, 2009, pp. 190- 198. doi:10.1016/j.eswa.2007.09.004
- R. J. Kuo, S. C. Chi and S. S. Kao, “A Decision Support System for Selecting Convenience Store Location through Integration of Fuzzy AHP and Artificial Neural Network,” Computers in industry, Vol. 47, No. 2, 2002, pp. 199-214. doi:10.1016/S0166-3615(01)00147-6
- C. C. Huang, P. Y. Chu and Y. H. Chiang, “A Fuzzy AHP Application in Government-Sponsored R&D Project Selection,” Omega, Vol. 36, No. 6, 2008, pp. 1038-1052. doi:10.1016/j.omega.2006.05.003
- D. Y. Chang, “Application of the Extent Analysis Method on Fuzzy AHP,” European Journal of Operation Research, Vol. 95, No. 3, 1996, pp. 649-655. doi:10.1016/0377-2217(95)00300-2
- H. M. Vahidnia, A. A. Alesheikh and A. Alimohammadi, “Hospital Site Selection Using Fuzzy AHP and Its Derivatives,” Journal of Environment Management, Vol. 90, No. 10, 2009, pp. 3048-3056. doi:10.1016/j.jenvman.2009.04.010
- O. Kilincci and S. A. Onal, “Fuzzy AHP Approach for Supplier Selection in a Washing Machine Company,” Expert System with Application, Vol. 38, No. 8, 2011, pp. 9656-9664. doi:10.1016/j.eswa.2011.01.159
- S. Onut, T. Efendigil and S. S. Kara, “A Combined Fuzzy MCDM Approach for Selecting Shopping Center Site: An Example from Istanbul, Turkey,” Expert System with Applications, Vol. 37, No. 3, 2010, pp. 1973-1980. doi:10.1016/j.eswa.2009.06.080
- D. Y. Chang, “Extent Analysis and Synthetic Decision,” Optimization Techniques and Applications, Vol. 1, 1992, pp. 352-355.
- C. L. Hwang and K. Yoon, “Multiple Attribute Decision Making: Method and Applications,” Springer-Verlag, New York, 1981.
- G. R. Jahanshahloo, F. H. Lotfi and M. Izadikhah, “Extension of the TOPSIS Method for Decision-Making Problems with Fuzzy Data,” Applied Mathematics and Computation, Vol. 181, No. 2, 2006, pp. 1544-1551. doi:10.1016/j.amc.2006.02.057
- T. Demirel and Z. Vural, “Multi-Criteria Solar Energy Plant Location Selection Using Fuzzy ANP,” Proceedings of the 9th International FLINS Conference, Chengdu, 2-4 August 2010, pp. 465-470. doi:10.1142/9789814324700_0069
- T. L. Saaty, “The Analytic Hierarchy Process,” Mc-Graw Hill, New York, 1980.
- A. Kengpol and P. Boonkanit, “The Decision Support Framework for Developing Ecodesign at Conceptual Phase Based upon ISO/TR 14062,” International Journal of Production Economics, Vol. 131, No. 1, 2011, pp. 4-14. doi.org/10.1016/j.ijpe.2010.10.006
- A. Kengpol and M. Tuominen, “A Framework for Group Decision Support Systems: An Application in the Evaluation of Information Technology for Logistics Firms,” International Journal of Production Economics, Vol. 101, No. 1, 2006, pp. 159-171. doi.org/10.1016/j.ijpe.2005.05.013

