Journal of Software Engineering and Applications
Vol.5 No.5(2012), Article ID:19424,9 pages DOI:10.4236/jsea.2012.55038
Face Recognition in the Presence of Expressions
![]()
1Centre for Visual Computing, University of Bradford, Bradford, UK; 2School of Computing, Mathematics, and Digital Technology, Manchester Metropolitan University (MMU), Manchester, UK; 3School of Computing, Informatics and Media, University of Bradford, Bradford, UK.
Email: *helen198111@hotmail.com
Received February 21st, 2012; revised March 25th, 2012; accepted April 27th, 2012
Keywords: Face Recognition; Feature Distances; Expressions; Regression Analysis
ABSTRACT
The purpose of this study is to enhance the algorithms towards the development of an efficient three dimensional face recognition system in the presence of expressions. The overall aim is to analyse patterns of expressions based on techniques relating to feature distances compare to the benchmarks. To investigate how the use of distances can help the recognition process, a feature set of diagonal distance patterns, were determined and extracted to distinguish face models. The significant finding is that, to solve the problem arising from data with facial expressions, the feature sets of the expression-invariant and expression-variant regions were determined and described by geodesic distances and Euclidean distances. By using regression models, the correlations between expressions and neutral feature sets were identified. The results of the study have indicated that our proposed analysis methods of facial expressions, was capable of undertaking face recognition using a minimum set of features improving efficiency and computation.
1. Introduction
The 3D face recognition techniques have drawn people’s attention. Many researchers have moved towards 3D human face recognition techniques. 3D face recognition is based on 3D images in which either the shape (3D surface) of the human face is used individually or the combination with the texture (2D intensity image) is used for the purpose of recognition. The 3D images are specifically captured and generated by a 3D camera, which produces point clouds, triangle meshes or polygonal meshes and texture information to represent 3D facial images.
In a face recognition system based on either 2D or 3D images, there are several procedures to be carried out. The initial step is the face detection. This involves the extraction of a face image from a large scene or image or video sequences. The following procedure is for face alignment, which involves aligning the face image with a certain coordinate system and aids accurate results. These procedures can be accomplished by several key tasks: Firstly, model and representation of facial surfaces. In an efficient way, it aims to reduce the computational complexity and help to increase the good performance in the recognition part; Secondly, extraction of 3D facial features. Feature extraction is to localise a set of feature points associated with the main facial characteristics, eyes, nose and mouth. At present the most popular methods for facial feature extraction are point clouds, facial profiles and surface curvature-based features etc. [1]. Thirdly, algorithm and methodology used for 2D/3D facial surface data in an efficient way.
Our study aims to cover state-of-the-art 3D face recognition techniques, including the technical background, ideas, methodologies, and concepts. More specifically, there are a few issues we will address in the study: Explore the existing face recognition systems dealing with expressions and relevant researchers as well as the current state-of-the-art in this area; Investigate the challenges in existing face recognition systems; Identify the problems in the 3D face recognition, i.e. recognising faces in the presence of expressions; Propose relevant methods to enhance it in the development of an efficient 3D face recognition dealing with expressions; Investigate the effects of our previous curvature-based method [2] in face recognition under expression variations.
2. Background
Face recognition under expression variations is required in some applications and over last two decades many computer vision researchers have been attracted to focus on the problems of recognising faces under expression variations. Significant progress [3-6] has been made. Many studies of 3D face recognition differentiate in terms of techniques. Lu et al. [7] match 2.5D facial images in the presence of expression variations and pose variations to a stored 3D face model with neutral expression by fitting the two types of deformable models, expression-specific and expression generic, generated from a small number of subjects to a given test image which is formulated as a minimisation of a cost function. Basically, mapping a deformable model to a given test image involves two transformations, rigid and non-rigid transformation. Therefore, the cost function is formed by translation vector and rotation matrix for rigid transformation, and a set of weights α. Kakadiaris et al. [8] address main challenges concerning the 3D face expressions recognition; Accuracy gain: For using 3D facial expression recognition independently or combined with other modalities, a significant accuracy gain of the 3D system with respect to 2D face recognition system must be produced in order to justify the introduction of a 3D system; Efficiency: 3D acquisition captures and creates larger data files per subject which causes significant storage requirements and slow processing. The data preprocessing for efficient data must be addressed. Automation: A system designed for the applications must be able to function fully automatically. Testing database: Larger and widely accepted databases for testing the performance of 3D facial expression recognition system should be produced. Kakadiaris have addressed the majority of the challenges by utilising a deformable model and mapping the 3D geometry information onto a 2D regular grid. The advantage of this is combining the 3D data with the computational efficiency of 2D data. They achieve the recognition rate of 97%. Lee et al. [9] propose an expression-invariant face recognition method. They extract the facial feature vector and obtain the facial expression state by the facial expression recogniser from the input image. The two main strategies for expression transformations are direct and indirect transformations. Direct transformation transforms a facial image with an arbitrary expression into its corresponding neutral face, whereas indirect transformation obtain relative expression parameters, shape difference and appearance ratio by model translation. By transforming them into its corresponding neutral facial expression vector using direct or indirect facial expressions transformation, they compare the recognition rate of each proposed method based on three different distance-based matching methods, nearest neighbor classifier (NN), LDA and generalised discriminant analysis (GDA). They achieve the highest recognition rate 96.67% based on NN, LDA using indirect expression transformation. Al-Osaimi et al. [10] introduce a new definition called the shape residue between the non-neutral and the estimated neutral 3D face models and present a method for decomposing an unseen 3D facial image under facial expressions to neutral face estimates and expression residues based on PCA. The residues are used for expression classification while the neutral face estimates are used for expression robust face recognition. In a result, 6% increase in the recognition performance is achieved when the decomposition method is employed. Li et al. [11-13] use low-level geometric features to create sparse representation models collected and ranked by the feature pooling and ranking scheme in order to achieve satisfactory recognition rate. They intentionally discard the expression-variant features, which are considered as higher-ranked. The recognition rate 94.68% is achieved.
Expressions seem to occur in a real word scenarios as even subtle expression variations can be captured into the 3D acquisition system. It has been claimed that face expressions can affect the accuracy and the performance of face recognition systems since the geometry of the face significantly changes as a result of facial expression. In general, the six significant expressions, happiness, anger, disgust, surprise, sad and fear, which make an adverse effect on face recognition. The adverse influence of face expression on face recognition is listed by Bronstein et al. [14] and needs to be solved no matter what dimensions face representation is being used (2D or 3D). However, its nonlinear nature and a lack of an associated mathematical model make the problem of face expression hard to deal with. There is no doubt that some progress has been made to solve this problem existing in 3D face recognition, but there are still some challenges remaining at this stage. For instance, Bronstein et al. [15,16] assume facial scans are isometric surfaces, which are not stretched by expressions so as to produce an expression invariant facial surface representation for recognising faces. However, there is one constraint in that they only considered frontal face scans and assumed the mouth to be closed in all expressions, which is not considered realistic.
Another issue with expressions is that there are less reliable invariants when faces carry heavy expressions. In addition, another issue is how to optimise the combination of small rigid facial regions for matching in order to reduce the effect of expressions. Using rigid facial regions can improve the performance on a database with expression variations [17,18]. The selection of rigid regions, however, is based on the optimal extraction and combination.
Researchers’ attempts to reduce the computational cost have left another unresolved issue. Achieving less computational cost for real world applications has become a big challenge. Current studies intentionally use additional 2D texture information with an attempt to deal with expressions, which makes impact on computational time. In general, more information trained in 3D face data leads to more computational cost and time. Some algorithms can work on the verification process with a time cost of about 10 seconds on a normal PC [18], whereas efficient face matching with less computational cost is still a problem when dealing with a large gallery with thousands of faces. In addition, modeling relations between expressions and the neutral by expressionvariant features and combining with expression-invariant features still remains a research question.
3. 3D Face Databases
The development of face recognition systems somehow relies on face image databases for the purpose of comparative evaluations of the systems. With the techniques of 3D face capture rapidly developing, currently more and more face databases on 3D have been built and oriented to different experimentation purposes: automatic face recognition, gender classification and facial expressions. In our proposed face recognition methods, two public databases will be utilised and compared in order to compare to benchmarks. From literature review, there are two popular databases among available public databases, GavabDB [12] and BU3D-FE [13]. The GavabDB contains 427 3D facial surface images corresponding to 61 individuals (45 males and 16 females), and there are nine different images per person. The other database BU-3DFE is considered as a facial expression database. In brief, each one of 100 subjects (56 female, 44 male) is instructed to perform seven universal expressions, i.e. neutral, happiness, surprise, fear, sadness, disgust and anger. The facial data contains about 13,000 - 21,000 polygons. In addition, 83 feature points on each facial model are located, refer to [13].
4. Proposed Method
4.1. Extraction of Shape Features
Facial feature extraction is important in many face-related applications [19]. Our 3D feature is a set of expression-invariants and expression-variants representations. This is achieved by analysing the facial region’s sensitiveity to the expressions and representing by a set of geometric descriptors. To eliminate the computational time from the preprocessing step, such as face alignment and normalisation, we introduce a distance-based feature to avoid the preprocessing.
Having considered computational time, we intentionally discard the texture information in our proposed method, in a similar way to the other chapters. Hence, the resulting performance is completely reliant on the features extracted from the shape of the image. The shape feature analysis based on the triangle meshes of faces, reflecting the facial skin wave, represents the intrinsic facial surface structure associated with the specific facial expressions. Motivated by this idea, we propose a set of novel distance-based geometric descriptors based on Euclidean and geodesic distances. Instead of focusing on the entire face we investigate face models by segmenting into two regions: the top face region, as shown in Figure 1(a), including eyes, eyebrows and nose; the low region, as shown in Figure 1(b), including the mouth only. The top region is used because it is comparatively insensitive to expression variations [4]. More specifically, the nose region suffers less from the effect of expression variations. However, the nose region alone is not sufficiently discriminatory for the purpose of face recognition because it represents only a small fraction of the face. Thus, we introduced more information, such as eyebrows and eyes, to be used to perform face recognition under expression variations. Expressionvariant regions are introduced and evaluated in our proposed method, found in the low region. Due to the significant change of the mouth region from laugh to neutral, we consider the low region as being sensitive to expression variations [17].
Based on the analysis of the expression-variant and expression-invariant regions, there are a few concerns about selecting the feature points. Firstly, selecting meaningful and significant positions as feature points, such as eye corners and top of the eyebrows, and the most distinctive position, the nose tip, is one concern. By taking this into consideration, accuracy of the extracted features can be improved. Secondly, for the insensitive region, another concern is that feature points are chosen to ensure minimum variations under change of expressions. For example, compared to the eye regions, the cheek region produces visible variations caused by expressions. Thus, we avoid locating feature points in the cheek region. Thirdly, for the expression-sensitive region, distinct positions along the outer mouth contour are taken into consideration rather than the areas including undesirable feature points, such as the chin regions. Fourthly, due to the missing data in the dark region resulting from scanning, such as the inner contour of mouths when laughing, we exclude those areas when selecting feature points. Fifthly, we determine the number of feature points by analysing the face representation efficiency and computation
 (a)
(a) (b)
(b)
Figure 1. Illustration of expression-sensitive and expression-insensitive regions on a sample subject. (a) The upper face: expression-insensitive region; (b) The lower face: expression-sensitive region.
requirements. More features make face representation more accurate; however, they cause more computational time. Thus, choosing the number of feature points is based on the requirement that fewer features represent faces efficiently.
Taking advantage of 83 feature points on annotated face models in the BU3D-FE database [13], twelve significant positions are selected as a set of feature points. More specifically, they are top of the eyebrow, top of the upper eyelid, lowest point of the lower eyelid, the outer eye corner, the inner eye corner, the nose tip, the left and right edges of nose wings for insensitive regions; and mouth corners, mid-upper and mid-lower lips in expression-variant regions, as shown in Figure 2. The explanation and illustration of the set of distance-based features is shown in Table 1 and Figure 3 respectively.
Not only is this set of features utilised in our method, but also contour shape features are considered, as shown in Figure 3. The contour shape features describe face elements, i.e. contour shape of eyebrows, eyes, nose and mouth. We select a set of control points on annotated face models to form the contours. Specifically, the contour shape features are represented by the vector  where
where  and
and  are coordinates of controlpoints.
are coordinates of controlpoints.
 (a)
(a) (b)
(b)
Figure 2. (a) Localisation of twelve landmarks; (b) Labelled of distance-based features.

Table 1. Seven distance-based features definition.

Figure 3. Illustration of the contour shape features describe face elements, i.e. contour shape of eyebrows, eyes, nose and mouth.
We utilise two intrinsic geometric descriptors, namely geodesic distances and Euclidean distances, to represent the facial models by describing the set of distance-based features and contours. The intrinsic geometric descriptors are independent of the chosen coordinate system.
We can observe that not all the distance vectors are invariant to expression variations. For example, the mouth opening (G) in Figure 2(b) shows a change of a distance vector caused by an open mouth, when the face of the same individual changes from neutral to a laugh expression. However, there are some certain distance vectors that remain stable under expression variations, for example, the eye width (C) in Figure 2(b). Thus, for the distance-based features, as we mentioned, we consider A, B, C and D distances in the top region as expression-invariants since they are insensitive under expression variations, whereas E, F and G are considered as expression-variants. We utilise Euclidean distances as the geometric descriptor to represent the set of distancebased features.
4.2. Geometric Descriptors
4.2.1. Euclidean Distance
In general, the distance between point p and point q in Euclidean n-space is
 (1)
(1)
where n is the dimension of Euclidean space. Specifically in this case, the Euclidean distance between points p and q in three dimensional Euclideanspace is
 (2)
(2)
The face model in the database comprises a triangle mesh, which is discretely defined to be a set of connected point clouds. The geodesic distance computation of triangle meshes is initialised by one or more isolated points on the mesh and the distance is propagated from them. More specifically, the geodesic distance of discrete meshes is considered as a finite set of Euclidean distances between pair-wise involved vertices. Thus, another geometric descriptor, geodesic distance, is utilised in our feature sets. Geodesic distance is capable of representing the contour shape features on the discrete meshes. Similarly, the selected contour features contain expression-invariants and expression-variants. The eye contour and the mouth contour are sensitive to expression variations. However, the eyebrow contour and the nose contour comparatively remain stable during expression variations.
4.2.2. Geodesic Distance
On a triangle mesh, the geodesic distance with respect to a point turns out to be a piecewise function, where in each segment the distance is given by the Euclidean distance function. Thus the geodesic distance computation is initialised by one or more isolated points on the mesh and the distance is propagated from them.
 (3)
(3)
where  is geodesic distance of a contour,
is geodesic distance of a contour,  is the Euclidean distance between two points and n is the number of control points of each contour.
is the Euclidean distance between two points and n is the number of control points of each contour.
Depending on the different facial feature extraction methods, the slight influence of face sizes and different scales of the faces can be eliminated, either by normalisation or by preprocessing before the recognition process. Thus, in addition to the geometric descriptors derived from the face models, we also consider defining two distance-based features to avoid the face alignment process and the normalisation process.
We introduce a distance-based feature for normalising the set of seven distance-based features, which is considered as a stable expression-invariant feature, as shown in Figure 4(a). In order to be consistent with the geometric descriptor used for the features, we utilise Euclidean distance to represent the feature, named N1 Thus seven normalized Euclidean distances are derived by the ratios of seven Euclidean distances to N1. Similarly, since geodesic distances are not scale-invariant, the next step is to normalise each geodesic distance by another distance-based feature [20], the eyes-to-nose distance, as shown in Figure 4(b), i.e. N2, sum of geodesic distances between the nose tip and the two inner eye corners. This guarantees invariance with respect to scaling and facial sizes under expression variations. Thus, for the set of contour shape features, this stable expression-invariant feature, N2 is represented by geodesic distance descriptor to ensure its consistency with the descriptor for the contour shape features. Deriving six normalised geodesic distances is accomplished by the ratios of the six geodesic distances to N2.
Thus, the geometric descriptors for the whole set of features are comprised of two sets of ratios. Meanwhile, the attributes of the ratio-based geometric descriptors that are unique to each face model are investigated and
 (a)
(a) (b)
(b)
Figure 4. Illustration of two distances for normalisation of two feature sets. (a) For distance-based feature set; (b) For the contour shape feature set.
proved before carrying out the next step. Compared to the commonly used descriptors in [14,21], our geometric descriptors benefit from fast computation due to their simplicity. In the next section, we adopt regression models to learn the relationship between pair-wise expressions based on the combination of these thirteen ratio-based geometric descriptors.
4.3. Regression Analysis Models
The regression analysis model is utilised for analysing the variables and modelling the relationship between them. Recently, regression analysis has been imported and applied in the face recognition area [22,23]. In this chapter, we evaluate two types of regression model: partial least square regression and multiple linear regressions. Specifically, we employ them to learn the correlation between pair-wise expressions and predict the 3D face neutral shape information for dealing with the problem of matching faces under expression variations.
4.3.1. Partial Least Square Regression
In this section, we will introduce a commonly used regression model that will be used to train and predict the feature set when the face models are neutral. Owing to the multiple dimensions of the involved variables, i.e. the total number of the ratio-based geometric descriptors, we will use a subspace regression model based on latent variables, named partial least square (PLS) [24].
X refers to a vector with the independent variables (predictors) and Y refers to a related vector of the dependent variables (responses).
 (4)
(4)
X is a matrix of predictors and Y is a matrix of responses. E and F are the error terms. There is a linear relation between T and U given by a set of coefficients B. A number of variants of PLS exist for estimating the T, P and Q.
The goal of PLS is to predict Y from X using a common structure of reduced dimensionality. For this purpose, PLS introduces some latent variables:
 (5)
(5)
T and U preserve the most relevant information of the interaction model between X and Y.
4.3.2. Multi Linear Regression
To compare with the performance of PLS, we utilise the multiple linear analysis regression (MLR) [25] method to model and learn the relationship between neutral and non-neutral facial geometric descriptors and performed recognition rate. A regression model relates Y to a function of X and β.
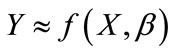 (6)
(6)
Given a data set  of n statistical units, a linear regression model assumes that the relationship between the dependent variable yi and the p-vector of regressors xi is approximately linear. This approximate relationship is modelled through a term εi, an unobserved random variable that adds noise to the linear relationship between the dependent variables and responses. Thus, in detail,the model is of the form:
of n statistical units, a linear regression model assumes that the relationship between the dependent variable yi and the p-vector of regressors xi is approximately linear. This approximate relationship is modelled through a term εi, an unobserved random variable that adds noise to the linear relationship between the dependent variables and responses. Thus, in detail,the model is of the form:
 (7)
(7)
where  denotes the transpose, so that
denotes the transpose, so that  is the inner product between vector xi and β. Commonly these n equations are integrated together and written in vector form as:
is the inner product between vector xi and β. Commonly these n equations are integrated together and written in vector form as:
 (8)
(8)
where:
 (9)
(9)
Multi linear regression is based on linear regression but dealing with multiple X and Y.
5. Results and Analysis
We have established a set of ratio-based geometric descriptors of face models that serves as input to the regression analysis model for simulating the relation between non-neutral and neutral faces. Relying on the ratios-based geometric descriptors, the effects of head rotation, translation and different scales can be eliminated, even without face alignment and normalisation in the preprocessing stage. Our proposed method is carried out on the BU3D-FE database [13]. In order to evaluate the two regression models, we set up a framework allowing for investigating improvement of expression-variants. To enhance the significance of the regression models, a Neural Network (NN) approach is employed for comparison. The comparison results are listed in Table 2.
From Table 2, we can observe that PLS, NN and MLR improve the rates by introducing expression-variants; however, PLS somehow places more emphasis on the expression-invariants in comparison to variants. Another conclusion is that employing variants indeed enhances the significance of expression-invariants. To further investigate the optimised performance of PLS, we set up another experiment allowing for PLS modelling multiple relationships between four intensities of six expressions and neutral, and vice versa. The results are shown in Figures 5 and 6, respectively.
Figure 5 shows the results of modelling intensity 1 angry to other expressions and neutral. The blue bars present the rate of expression-invariants and the red bars present the accuracy rate of the combination of expression-variants and expression-invariants. The improvement varies in four intensities. However, on average the results further confirm the power of the expressionvariants. In Figure 6, the diagram shows the results of modelling neutral to six other random intensity expres-

Table 2. Comparison of multiple regression models.

Figure 5. Illustration of the improvement with additional expression-variants employed under intensity 1 of angry expression.

Figure 6. Illustration of the improvement with additional expression-variants employed under neutral.
sions. The blue bars present the accuracy rate of expression-invariants and the red bars present the accuracy rate of the combination. Thus the results confirm that ratio-based expression-variants can improve the performance. The recognition experiments and results will be carried out and described in the following.
In summary, for the purpose of recognising faces in our experiments, we choose PLS for modelling relationships and use the combination of ratio-based expression-variants and expression-invariants as the feature sets.
In this experiment, we present the experimental results for recognising faces under expression variations. In particular, the experiment is implemented on the BU-3DFE database. In the experiments, we divide these 100 subjects into two sets: the training set with 80 subjects; and the testing set with 20 subjects. The experiments ensure that any subject used for training does not appear in the testing set because random partition is based on the subjects rather than the individual expressions. Four intensities of each expression are ensured to be involved in this experiment. For each iteration, the PLS regression analysis model is reset and retrained from the initial state.
In Table 3, we report the recognition rate of matching six expressions with four intensities to neutral. The promising recognition accuracy is achieved even without the texture information. Happy and surprise expressions achieve the highest accuracy rate of 89%, however, sad, angry, disgust and fear perform less accurately than the other three expressions. This is because happy and surprise expressions are comparatively clean and simple; their measurement allows for simplicity; some noises are produced when other expressions occur. Interestingly, the accentuated intensity of expressions achieves the lowest recognition rate and the recognition rate ascends along with a descending intensity. However, as we can see, the facial expressions have significantly degraded the performance of the face recognition in the absence of expression variations since the neutral face recognition accuracy rate achieves the highest at 90.3%.

Table 3. Neutral face recognition rates (RR) using PLS regression analysis model.
Comparison with Benchmark Algorithms
The final recognition rates of our proposed 3D face recognition method under expressions will be listed and discussed. Some researchers have developed and achieved their results of face recognition under expressions. Despite our results are not the best, we further discuss the feature sets, database, speed and the size of face models of our method in comparison with the current existing 3D face recognition methods, as shown in Table 4. The highest accuracy rate of 97% is generated by Alyuz et al. [4] using the nose, the forehead, the eyes and the central face, which covers the whole face with overlapping. In their work, face registration and face alignment are employed. These techniques cost computational time, although they play important roles in recognition rates. The point sets in the determined regions and the curvature related to the corresponding regions are used for dissimilarity calculation. The accuracy rate of 81.7% is achieved by Gervei et al. [26] using a least feature set with 40 dimensions. Compared to other methods, our proposed method use a minimum feature set to achieve a promising accuracy rate.
To further investigate the effect of the curvature descriptors of the T shape profile [2], incorporating curvature information is analysed, as shown in Table 4.
It has been proved that the proposed method is promising in dealing with expressions. Thus, we combine the distance-based feature sets with the curvature descriptors of the T shape profiles for face recognition under expressions. The results are listed in Table 4. We notice that the recognition rates are slightly higher with the curvature descriptors of the T shape profiles. Based on the

Table 4. Our method of face recognition under expressions in comparison with other existing methods.
results, it is observed that the use of the T shape profiles in the expression-invariant regions makes it possible to improve recognition performance.
The design criteria of the methods are based on the accuracy rate and speed (computational time). Regarding to various circumstances face recognition methods apply, there is no simple answer to the question of which method would fit best. In addition, the value of methods varies significantly with each application requirements and circumstances. Based on the design criteria, in some cases, fast processors are facilitated for face recognition techniques and the recognition rate can be considered as the top priority. The computational time can be sacrificed due to fast processors for high accuracy rate. However, the accuracy rate could be trade-off for the fast computation if the face recognition techniques are installed on a portable or wireless device. Therefore, in some circumstances, accuracy rate and speed can be trade off. In summary, our proposed methods are suitable for the cases essentially requiring fast computation.
6. Conclusions
The fundamental face recognition technique in the presence of expression variations was based on a correlation-learning model which generated a non-neutral model with a neutral model in order to match non-neutral faces to neutral faces. One of the issues pointed out by the researcher was reducing the computational cost. Rather than taking a large number of features into account, we intended to use the limited feature set representing contour information and face structure information. We built a novel framework of learning the correlation between various expressions and neutral with the limited feature set. Thus, there were two main advantages of our proposed method: training the correlations between expressions and neutral provide the flexibility of extending the feature sets; using the minimum feature set extracted from the facial structure information and the contour information explicitly to represent face models. Furthermore, incorporation of our previous T shape method leads to better performance.
There are two main requirements, however, needed to be investigated for improving the recognition rate in the future work. One is employing more geometric descriptors to represent the natural structure of the face model, for example area, curvature and weights allocated to descriptors. By introducing a set of weights to those geometric descriptors, the framework will be able to manipulate the weights and render them reliable for the task. The other one is to define the feature set to each particular expression in order to obtain the corresponding natures of each expression. These possible improvements are considered as the tasks in the future work for the purpose of strengthening the power of the framework.
REFERENCES
- Y. Wang, C. Chua and Y. Ho, “Facial Appearance Detection and Face Recognition from 2D and 3D Images,” Pattern Recognition Letters, Vol. 23, No. 10, 2001, pp. 1191-1202. doi:10.1016/S0167-8655(02)00066-1
- X. Han, H. Ugail and I. Palmer, “Method of Characterising 3D Faces Using Gaussian Curvature,” Chinese Conference on Pattern Recognition, Nanjing, 4-6 November 2009, pp. 528-532.
- B. Amberg, R. Knothe and T. Vetter, “Expression Invariant 3D Face Recognition with a Morphable Model,” IEEE International Conference on Automatic Face and Gesture Recognition, 2008, pp. 1-6. doi:10.1109/AFGR.2008.4813376
- N. Alyuz, B. Gokberk, H. Dibeklioglu and L. Akarun, “Component-Based Registration with Curvature Descriptors for Expression Insensitive 3D Face Recognition,” IEEE International Conference on Automatic Face & Gesture Recognition, Amsterdam, 17-19 September 2008, pp. 1-6.
- D. Smeets, T. Fabry, J. Hermans, D. Vandermeulen and P. Suetens, “Fusion of an Isometric Deformation Modeling Approach Using Spectral Decomposition and a RegionBased Approach Using ICP for Expression-Invariant 3D Face Recognition,” The 20th International Conference on Pattern Recognition, Istanbul, 23-26 August 2010, pp. 1172-1175. doi:10.1109/ICPR.2010.293
- Y. Wang, G. Pan and Z. Wu, “3D Face Recognition in the Presence of Expression: A Guidance-Based Constraint Deformation Approach,” IEEE Conference on Computer Vision and Pattern Recognition, 2007, pp. 1180-1187. doi:10.1109/CVPR.2007.383277
- X. Lu and A. K. Jain, “Deformation Modeling for Robust 3D Face Matching,” IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Vol. 2, 2006, pp. 1377-1383. doi:10.1109/CVPR.2006.96
- I. A. Kakadiaris, G. Passalis, G. Toderici, M. N. Murtuza, Y. Lu, N. Karampatziakis and T. Theoharis, “Three-Dimensional Face Recognition in the Presence of Facial Expressions: An Annotated Deformable Model Approach,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 29, No. 4, 2007, pp. 640-649. doi:10.1109/TPAMI.2007.1017
- H. Lee and D. Kim, “Expression-Invariant Face Recognition by Facial Expression Transformations,” Pattern Recognition Letters, Vol. 29, No. 13, 2008, pp. 1797-1805. doi:10.1016/j.patrec.2008.05.012
- F. R. Al-Osaimi, M. Bennamoun and A. Mian, “On Decomposing an Unseen 3D Face into Neutral Face and Expression Deformations,” Advances in Biometrics, Vol. 5558, 2009, pp. 22-31. doi:10.1007/978-3-642-01793-3_3
- X. Li, T. Jia and H. Zhang, “Expression-Insensitive 3D Face Recognition Using Sparse Representation,” IEEE Conference on Computer Vision and Pattern Recognition, 2009, pp. 2575-2582.
- A. B. Moreno and A. Sanchez, “GavabDB: A 3D Face Database,” Proceedings 2nd COST Workshop on Biometrics on the Internet: Fundamentals, Advances and Applications, Vigo, 25-26 March 2004, pp. 77-82.
- L. J. Yin, X. Z. Wei, Y. Sun, J. Wang and M. J. Rosato, “A 3D Facial Expression Database for Facial Behavior Research,” International Conference on Automatic Face and Gesture Recognition, Southampton, 2-6 April 2006, pp. 211-216. doi:10.1109/FGR.2006.6
- A. M. Bronstein, M. M. Bronstein and R. Kimmel, “Robust Expression-Invariant Face Recognition from Partially Missing Data,” European Conference on Computer Vision, Vol. 3953, 2006, pp. 396-408. doi:10.1007/11744078_31
- A. M. Bronstein, M. M. Bronstein and R. Kimmel, “ThreeDimensional Face Recognition,” International Journal of Computer Vision, Vol. 64, No. 1, 2005, pp. 5-30. doi:10.1007/s11263-005-1085-y
- A. M. Bronstein, M. M. Bronstein and R. Kimmel, “Expression-invariant 3D Face Recognition,” International Conference on Audioand Video-based Biometric Person Authentication, Guildford, 9-11 June 2003, pp. 62-69.
- K. I. Chang, K. W. Bowyer and P. J. Flynn, “Multiple Nose Region Matching for 3D Face Recognition under Varying Facial Expression,” IEEE Transaction on Pattern Analysis and Machine Intelligence, Vol. 28, No. 10, 2006, pp. 1695-1700. doi:10.1109/TPAMI.2006.210
- T. Faltemier, K. W. Bowyer and P. Flynn, “A Region Ensemble for 3D Face Recognition,” IEEE Transactions on Information Forensics and Security, Vol. 3, No. 1, 2008, pp. 62-73. doi:10.1109/TIFS.2007.916287
- K. Fatimah, N. Khalid and A. Lili, “3D Face Recognition Using Multiple Features for Local Depth Information,” International Journal of Computer Science and Network Security, Vol. 9, No. 1, 2009, pp. 27-32.
- S. Berretti, A. Del Bimbo and P. Pala, “3D Face Recognition Using Isogeodesic Stripes,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 32, No. 12, 2010, pp. 2162-2177. doi:10.1109/TPAMI.2010.43
- C. Samir, A. Srivastava and M. Daoudi, “3D Face Recognition Using Shapes of Facial Curves,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 28, No. 11, 2006, pp. 1858-1863. doi:10.1109/TPAMI.2006.235
- X. Chai, S. Shan, X. Chen and W. Gao, “Locally Linear Regression for Pose-Invariant Face Recognition,” IEEE Transactions on Image Processing, Vol. 16, No. 7, 2007, pp. 1716-1725. doi:10.1109/TIP.2007.899195
- I. Naseem, R. Togneri and M. Bennamoun, “Linear Regression for Face Recognition,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 32, No. 11, 2010, pp. 2106-2112. doi:10.1109/TPAMI.2010.128
- R. D. Tobias, “An Introduction to Partial Least Squares Regression,” SUGI Proceedings, Orlando 2-5 April 1995, 1995, pp. 1-8.
- M. Tranmer and M. Elliot, “Multiple Linear Regression,” The Cathie Marsh Centre for Census and Survey Research (CCSR) 2008.
- O. Gervei, A. Ayatollahi and N. Gervei, “3D Face Recognition Using Modified PCA Methods,” World Academy of Science, Engineering and Technology, No. 39, 2010, pp. 264-267.
- X. Li and F. Da, “3D Face Recognition by Deforming the Normal Face,” International Conference on Pattern Recognition, Istanbul, 23-26 August 2010, pp. 3975-3978. doi:10.1109/ICPR.2010.967
- M. H. Mahoor and M. Abdel-Mottaleb, “3D Face Recognition Based on 3D Ridge Lines in Range Data,” IEEE International Conference on Image Processing, Vol. 1, 2007, pp. 137-140. doi:10.1109/ICIP.2007.437891
NOTES
*Corresponding author.

