Journal of Biomedical Science and Engineering
Vol.7 No.4(2014), Article ID:43595,13 pages DOI:10.4236/jbise.2014.74022
Detection of Stiff Nodules Embedded in Soft Tissue Phantoms, Mimicking Cancer Tumours, Using a Tactile Resonance Sensor
Anders P. Åstrand1,2,3, Ville Jalkanen1,2, Britt M. Andersson1,2, Olof A. Lindahl2,4,5
1Department of Applied Physics and Electronics, Umeå University, Umeå, Sweden
2Centre for Biomedical Engineering and Physics, Umeå University, Umeå, Sweden
3Industrial Doctoral School, Umeå University, Umeå, Sweden
4Department of Radiation Sciences, Biomedical Engineering, Umeå University, Umeå, Sweden
5Department of Engineering Sciences and Mathematics, Luleå University of Technology, Luleå, Sweden
Email: anders.astrand@umu.se, ville.jalkanen@umu.se, britt.andersson@umu.se, olof.lindahl@umu.se
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 28 January 2014; revised 1 March 2014; accepted 9 March 2014
ABSTRACT
Background: Prostate cancer (PCa) is the most common form of cancer among males in Europe and in the USA and the most common curative treatment is removal of the prostate, i.e. prostatectomy. After the removal, the prostate is histopathologically analysed. One area of interest is to examine the perifery of the prostate, as tumours on and near the surface can indicate that the PCa has spread to other parts of the body. There are no current methods to examine the surface of the prostate at the time of surgery. Tactile resonance sensors can be used for detecting areas of different stiffness in soft tissue. Human prostate tissue affected by cancer is usually stiffer than healthy tissue, and for this purpose, a tactile resonance sensor was developed. The aim of this study was to investigate the depth at which embedded stiffer volumes could be detected, using soft tissue phantoms. Methods: With the tactile resonance sensor used in this study, the shift of the resonance frequency and the force at contact with tissue can be measured, and combined into a tissue stiffness parameter. The detection sensitivity of the sensor at impression depths, 0.4 and 0.8 mm, was measured for detection of inserted nodules of stiff silicone in softer silicone and in chicken muscle tissue, mimicking prostate tissue with cancer tumours. Results: Measurements on the silicone samples detected the hidden stiffer object at a depth of 1 - 4 mm with a difference in the stiffness parameter of 80 - 900 mN/kHz (p < 0.028, n = 48). At the depth 5 - 6 mm the difference was smaller but still significant < 30 mN/kHz (p < 0.05, n = 24). For the measurements on chicken muscle, the detectable depth was 4 mm (p < 0.05, n = 24). Conclusion: This model study suggests that, with only a small impression depth of ≤1 mm, the resonance sensor system described here can detect stiffness variations located at least 4 mm in silicone and chicken muscle, mimicking tumours in prostate tissue.
Keywords:Tissue Stiffness; Resonance Sensor; Prostate Cancer; Piezoelectric; Depth Sensitivity; Tactile Sensor

1. Introduction
The most common form of cancer in males in Europe and the USA is prostate cancer (PCa). The American Cancer Society estimates that more than 238,000 new cases will be diagnosed in 2013, and that close to 30,000 men will die from PCa [1] . The situation in Sweden is monitored by The National Board of Health and Welfare (Socialstyrelsen), and their latest report [2] shows that 9663 new cases were diagnosed in 2011 and that 2382 men died due to PCa in Sweden during that year. Common diagnostic methods are a blood test for a prostate specific antigen (PSA) and a digital rectal examination (DRE), where the physician palpates the prostate from the rectum [2] . However, the PSA-level can be elevated due to other causes except PCa, like prostatis and other inflammations, and this can lead to over-diagnosis of cancer [3] . After indication of prostate cancer, a transrectal ultrasound (TRUS) guided systematic biopsy is used to finally diagnose PCa [4] . Radical prostatectomy is the most common curative treatment for diagnosed PCa. The excised prostate is analysed and examined by pathologists to assess types and locations of areas with tumours. The surface of the prostate is of special interest as occurrence of tumours at and below the surface can indicate that the PCa has spread to other organs in the body [5] .
In general, when performing a prostatectomy during open surgery, palpation can be used for assessing areas of stiffness or other abnormalities in the tissue. Studies have reported that tumours in soft tissue are usually stiffer than those in the surrounding healthy tissue [6] -[10] . There are also other tissue types in the prostate that can be stiffer than surrounding healthy tissue, for example stroma and stones [9] . However, as digital palpation is subjective, a tactile sensor can give more accurate quantification [11] .
Tactile resonance sensor systems based on the principle of the indentation of an oscillating piezoelectric element into soft tissue have been used to measure the differences in stiffness and elasticity of the skin to detect oedema and lesions [12] [13] , to detect lymph nodes containing metastases [14] , and to measure the stiffness of the liver to indicate liver fibrosis [15] . It has also been used to study stiffness variations related to the heterogeneous prostate tissue histology including malignant tissue [9] [16] .
The tactile resonance sensor system used in this study was presented recently [17] [18] , where measurements were performed on soft tissue phantoms made of silicone. The measured parameters are the change in resonance frequency of the piezoelectric element, Δf, and the applied force, F, when the sensor comes into contact with the tissue. From Δf and F, a stiffness parameter, 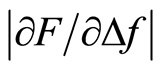 , used as a measurement parameter for tissue stiffness is obtained [19] [20] . In earlier studies on human prostate tissue slices (thickness approx. 10 to 15 mm), using a tactile resonance sensor, the detected cancer tissue was located close to the boundary of a slice, i.e. close to the surface of the whole prostate. The findings were confirmed by morphometric analysis [9] [16] . However, the sensitivity for this type of sensor to detect tumours located beneath the surface of the prostate gland has not yet been evaluated.
, used as a measurement parameter for tissue stiffness is obtained [19] [20] . In earlier studies on human prostate tissue slices (thickness approx. 10 to 15 mm), using a tactile resonance sensor, the detected cancer tissue was located close to the boundary of a slice, i.e. close to the surface of the whole prostate. The findings were confirmed by morphometric analysis [9] [16] . However, the sensitivity for this type of sensor to detect tumours located beneath the surface of the prostate gland has not yet been evaluated.
It is well known that tumours in the prostate may be located on a depth beneath the prostate surface. Therefore, it would be of great clinical interest to know the tactile resonance sensor’s detection sensitivity to stiffness changes and its dependence of impression depth for detecting tumours in the prostate.
The aim of this study was to evaluate the ability of a tactile resonance sensor system to detect stiff nodules embedded in soft tissue models mimicking cancer tumours below a layer of normal tissue in the prostate. This was done through analysing the depth sensitivity of the stiffness parameter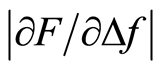 . The soft tissue models consisted of silicone and chicken muscle tissue with inclusions of stiff nodules of silicone.
. The soft tissue models consisted of silicone and chicken muscle tissue with inclusions of stiff nodules of silicone.
2. Materials and Methods
2.1. The Resonance Sensor
The resonance sensor used in this study was based on a piezoelectric element divided into two sections of functionality by a non-conducting section, Figure 1. The driving section of the element oscillated at its first longitu-
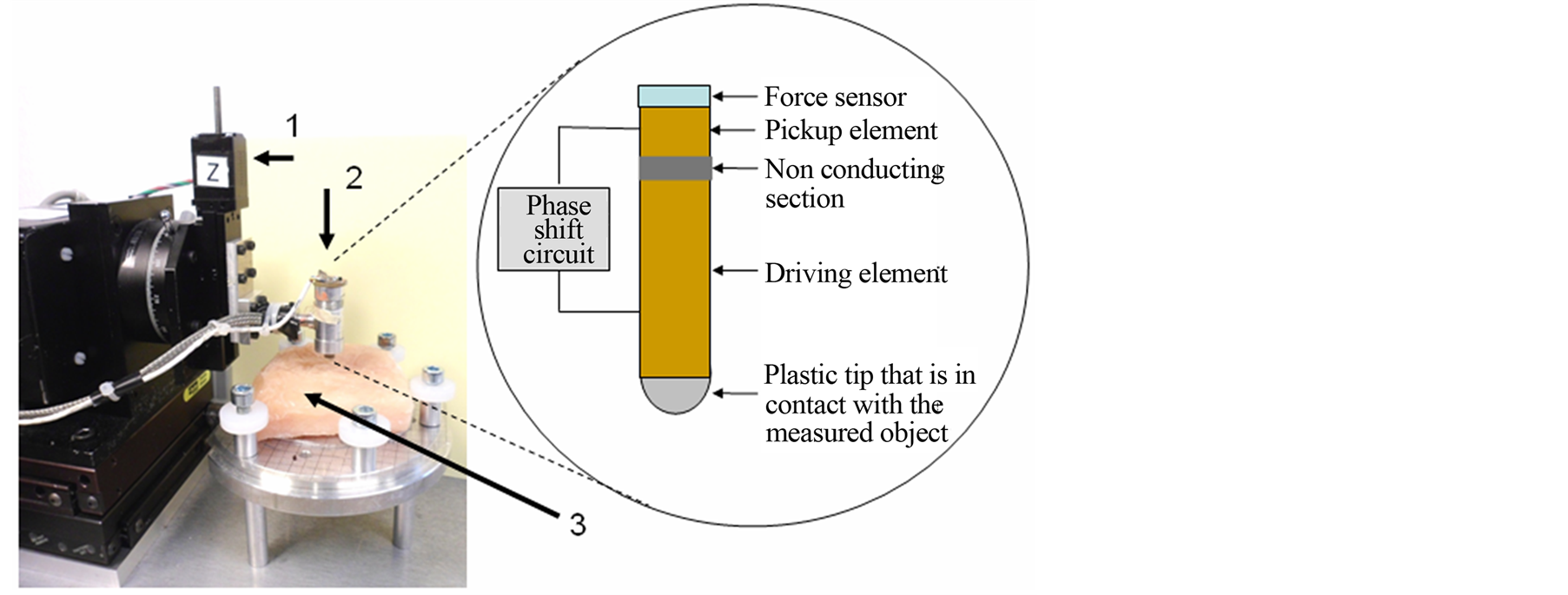
Figure 1. A side view of the measurement system and the sensor. The blowup shows the piezoelectric element and the force sensor inside the aluminium case sensor head. 1) Translation stage and stepper motor for vertical movement; 2) Sensor head; 3) A slice of chicken breast was placed on the platform for illustration only.
dinal resonance mode by an alternating voltage. The other section of the element was used as a pickup element to detect the oscillations. The signal from the pickup section was constantly transferred to a feedback circuit where the phase-shift circuit ensured that a zero phase condition between the pickup and drive signals was maintained. This ensured that the whole sensor would be kept at its resonance frequency [21] .
When the driving section of the element comes into contact with an object there will be a change in the resonance frequency, Δf = f − f0, where f0 is the free (unloaded) resonance frequency of the element and f is the resonance frequency of the element when in contact with an object. A soft material that can be deformed by the sensor results in a negative Δf, whereas a hard object would results in a positive Δf [21] .
The piezoelectric element was cylinder shaped and made of lead zirconate titanate, PZT (Type 7A, Morgan electro mechanics, Bedford, Ohio, USA) as described previously [17] . The cylinder was 15 mm long with the outer diameter of 5 mm and inner diameter of 3 mm. To measure the applied force, F, a preloaded force sensor was used [17] . The piezoelectric element and the force sensor were mounted inside an aluminium casing, which formed the sensor head as shown in Figure 1. The unloaded resonance frequency was f0 = 113.8 kHz. The signals from the force sensor and the piezoelectric sensor were collected to a computer by using a data acquisition card [17] . A sampling rate of 1 kHz was used.
2.2. The Measurement System
The measurement system has two translation stages for movement in horizontal Xand Ydirections. The sensor head was mounted onto a third, vertical translation stage in connection with a rotational stage to keep the contact angle α perpendicular to the surface of the measured object [17] . The movement of the three motorized translation stages (X-, Yand Z-direction), with a resolution of 2.5 µm, was controlled with a Lab View® program. Measurement objects were placed onto a platform, as shown in Figure 1. Petri dishes were fixated by brackets using threaded holes for a secure attachment. Biological tissue was pinned down onto a stiff plate of polystyrene foam that was held in place with the brackets.
2.3. Soft Tissue Phantoms
A two-component silicone (Wacker SilGel 612; Wacker-Chemie GmbH, Germany) [22] was used as soft tissue phantoms. The two components A and B can be mixed in different ratios by weight, according to the manufacturer’s instructions, to create silicone of a desired stiffness [22] . This silicone has been used for soft tissue phantoms in earlier studies [16] [17] [21] [23] [24] . In those studies, the hardness was defined by a cone penetration value measured according to DIN ISO 2137 [25] . In this study the Shore-000 scale according to ASTM D2240 [26] for measuring hardness in soft materials were used. Both the cone penetration value and the corresponding Shore-000, given by the manufacturer, are given in Table 1 for the two specific mixtures used in this study. A previous study on this silicone and prostate tissue, both healthy and with tumours, show that the mixtures used in this study is relevant to the range of stiffness showed by prostate tissue [16] .
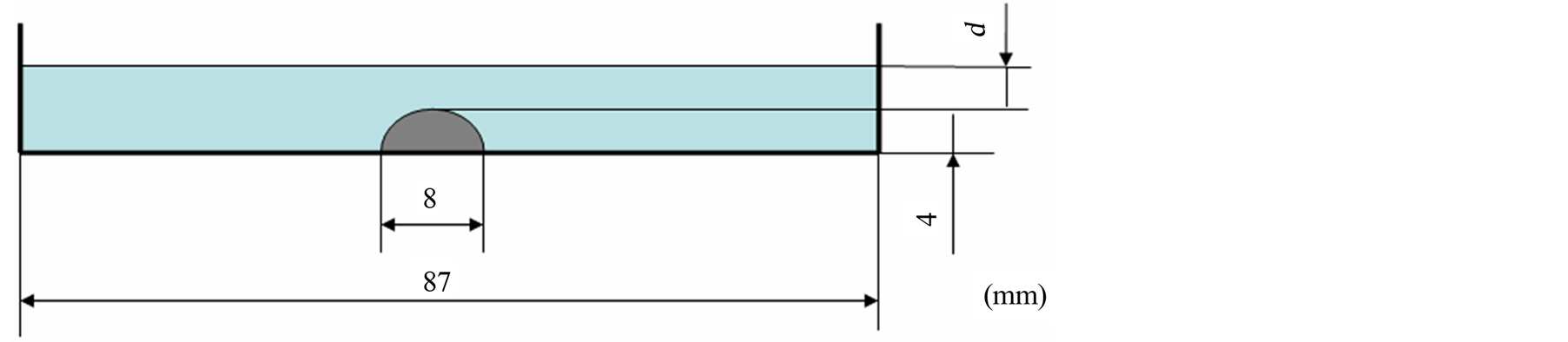
Flat silicone discs were cast in Petri dishes (inside diameter 87 mm and height 13 mm). The bottom of the Petri dish has a 0.7 mm protruding rim that had to be ground off to assure full contact with the measurement platform. The measurements with the resonance sensor were performed on 10 different discs. One disc with a thickness of 5 mm was made of homogeneous stiff silicone, Shore hardness 88 (scale 000), Table 1. The other nine discs all had a nodule shaped as a hemisphere with diameter 8 mm and height 4 mm of the same stiff mixture, Shore hardness 88 (scale 000), fixed at the bottom of the Petri dish, Figure 2(a). For these discs, the hemisphere was embedded in, and covered by, a softer silicone with Shore hardness 33 (scale 000), Table 1, with different total thicknesses ranging from 5 to 13 mm with a step of 1 mm. This corresponded to a varying distance, d, of 1 to 9 mm from the top surface of the silicone disc to the highest point of the embedded hemisphere, Figure 2(a). The silicone discs are labelled by their d value throughout this study.
 (a)
(a)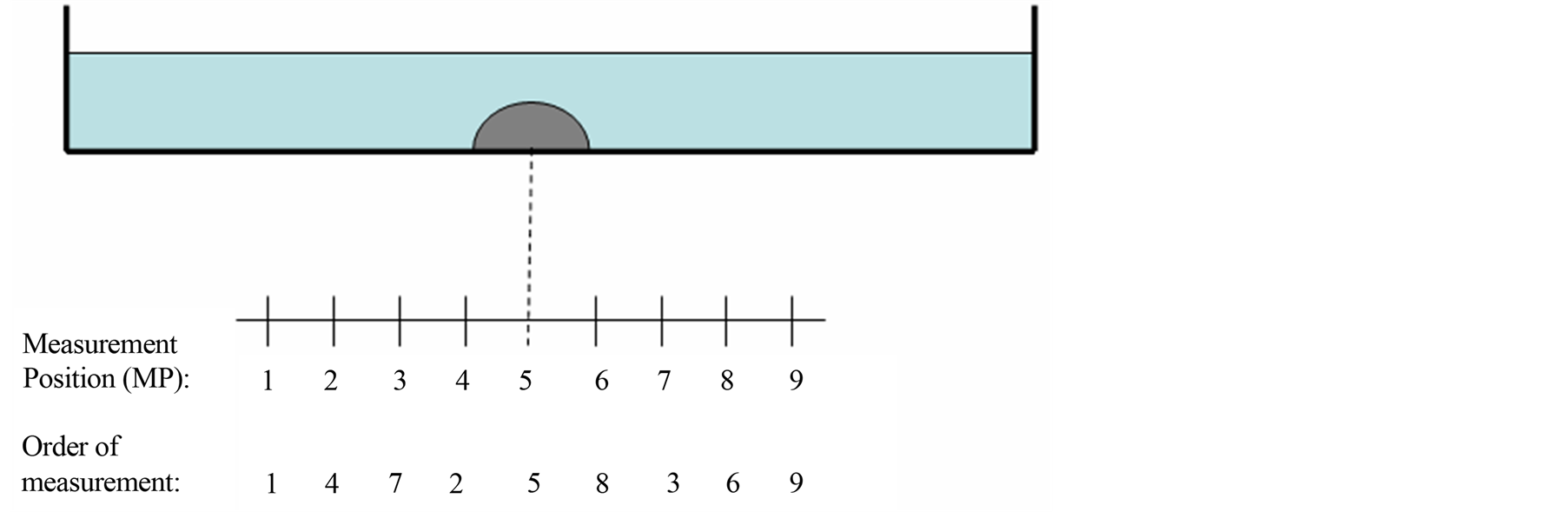 (b)
(b)
Figure 2. An illustration of a soft silicone disc with a stiff silicone inclusion. A side view of the silicone disc in a Petri dish. The distance between adjacent measurement positions is 5 mm. a) The figure illustrates a stiff silicone nodule shaped as a hemisphere fixed at the bottom of a Petri dish, covered by soft silicone with distance, d, to the top surface. b) The measurements were performed in a specific order, but it is the measurement positions (MPs) that will be referred to in the text.
Table 1. Hardness values for two silicone mixtures. The mixing ratio and hardness value for the Wacker silicone used in this study. For comparison, the hardness values are given both as Shore-000 values and cone penetration values according to the manufacturer’s specifications [22] .
2.4. Soft Biological Tissue
Chicken muscle tissue was used as a biological tissue in this study. It was obtained from commercially available chicken (pullum) breast bought at the local grocery store. Slices with different thickness, 5 - 11 mm, were cut from semi defrosted breasts, using an electric slicing machine (Hugin MS-285A, KF, Stockholm, Sweden). Indentation measurements with the resonance sensor were made on completely defrosted slices, at room temperature (21˚C to 23˚C). A silicone nodule shaped as a hemisphere, of the same type as the one used in the silicone discs, Figure 2(a), was attached to the polystyrene foam plate, and the x-y positioning stages were adjusted so that the measurement position (MP) in the centre of the measurement sequence was over the peak of the hemisphere. An incision of the same size as the silicone nodule was made on the bottom of each slice of chicken muscle.
The slices were then placed on the polystyrene foam plate and pinned down so that the silicone nodule filled the incision, Figure 3. The thickness, d, of the tissue above the stiff nodule in analogy with the silicone discs, Figure 2(a), varied therefore from 1 to 7 mm. The hardness of the slices was also measured using a hardness tester using the Shore-000 scale (Bareiss HPE II Shore-000, Heinrich Bareiss Prüfgerätebau GmbH, Oberdischingen, Germany). The instrument for this type of hardness tests has a steel ball with a diameter of 12.7 mm and an impression depth of 2.5 mm at a load of 113 g.
2.5. Measurement Method
The measured parameters, f and F, are dependent on the contact angle, α, according to earlier reports [11] [17] [27] . To ensure that the measurements were made perpendicular to the surface, α = 0˚, of the measurement object, flat objects were used. The indentation velocity was set at νi = 4 mm∙s−1. All measurements were made at room temperature, 21˚C to 23˚C.
Indentation measurements on the silicone discs were made across the disc at nine MPs located 5 mm apart along a straight line covering a distance of 40 mm of the silicone surface, Figure 2(b). MP 5 was aimed directly above the centre of the hemisphere. The order of the performed measurements was chosen so that consecutive measurements would not be adjacent to each other, Figure 2(b). The reason for this was to eliminate the possible effects that two adjacent indentations close in time would have on the measurements. Each silicone disc was subjected to six repeated measurement series with at least 15 minutes in between the measurements at each specific MP.
The indentation measurements on the slices of chicken muscle were made at five MPs along a straight line of 20 mm across the position of the silicone nodule located beneath the MP 3, Figure 3. There was 5 mm between adjacent MPs, similar to the silicone discs. The surface of the slices of chicken muscle was kept moist by spraying water at room temperature with an atomizer before each measurement series.
For each measurement series, 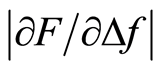 was determined as the line fit of Δf and F at an interval of Iz ± 0.1 mm, Figure 4. The maximum Iz was set to a depth of 1 mm for all measurements, and Δf and F were analysed
was determined as the line fit of Δf and F at an interval of Iz ± 0.1 mm, Figure 4. The maximum Iz was set to a depth of 1 mm for all measurements, and Δf and F were analysed

Figure 3. A cross-section side view of a biological tissue model with a stiff silicone inclusion. A cut out of a 9 mm thick slice of chicken muscle with an insertion of a stiff silicone nodule. The height of the nodule was 4 mm, and the distance between adjacent measurement positions (MPs) is 5 mm. The silicone in the figure was stained for better visibility.
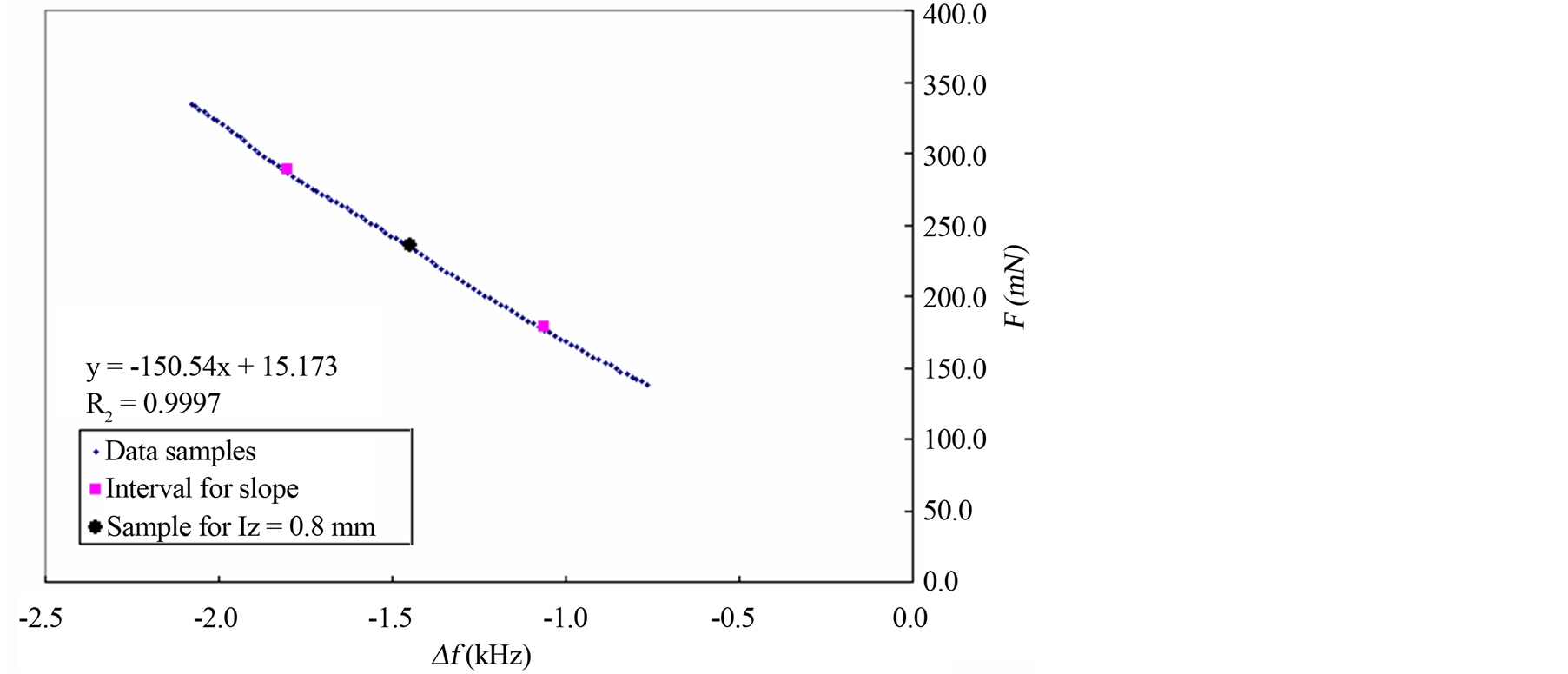
Figure 4. An illustration of how 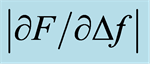 was obtained by linear regression. The
was obtained by linear regression. The 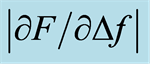 was calculated for each measurement from sampled Δf against F. For easier viewing, only a part of the sampled data is shown in this figure. The interval Iz = 0.8 mm ± 0.1 mm includes a total of 50 samples where Iz = 0.8 mm is in the centre. 25 samples are equal to 0.1 mm at vi, = 4 mm/s and at the sampling rate of 1 kHz. A line fit (not shown in figure) between Δf and F gave the line slope and thus
was calculated for each measurement from sampled Δf against F. For easier viewing, only a part of the sampled data is shown in this figure. The interval Iz = 0.8 mm ± 0.1 mm includes a total of 50 samples where Iz = 0.8 mm is in the centre. 25 samples are equal to 0.1 mm at vi, = 4 mm/s and at the sampling rate of 1 kHz. A line fit (not shown in figure) between Δf and F gave the line slope and thus , here 150.54 mN/kHz.
, here 150.54 mN/kHz.
for Iz = 0.4 mm and Iz = 0.8 mm on both the silicone and the slices of chicken muscle.
2.6. Statistics
The measured values in this paper are presented as mean ± standard deviation (SD). Statistics were calculated with Wilcoxon’s signed rank test for the silicone discs and a nonparametric Kruskal-Wallis followed by multiple comparisons to test for differences for the slices of chicken muscle. The software used was IBM SPSS Statistics 21. Line fitting for obtaining 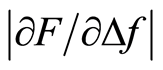 was done by linear regression using Excel. A p-value of ≤0.05 was considered significant for all statistical tests.
was done by linear regression using Excel. A p-value of ≤0.05 was considered significant for all statistical tests.
3. Results
3.1. The Stiffness Parameter, Measurements on Silicone
From the measurements made across the silicone discs,  at Iz = 0.4 mm detected the location of the silicone nodule at MP 5 for the discs with d = 1 to 4 mm, Figure 5. The peak decreased with increasing d. For silicone discs with d = 5 to 9 mm the presence of the stiff nodule at MP 5 was not significantly different from MPs 1 to 4, and MPs 6 to 9. The silicone disc composed entirely of the stiff mixture is shown in comparison to the silicone discs with the stiff inclusions, Figure 5. These results were the basis for further investigation of the depth sensitivity of
at Iz = 0.4 mm detected the location of the silicone nodule at MP 5 for the discs with d = 1 to 4 mm, Figure 5. The peak decreased with increasing d. For silicone discs with d = 5 to 9 mm the presence of the stiff nodule at MP 5 was not significantly different from MPs 1 to 4, and MPs 6 to 9. The silicone disc composed entirely of the stiff mixture is shown in comparison to the silicone discs with the stiff inclusions, Figure 5. These results were the basis for further investigation of the depth sensitivity of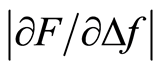 .
.
3.2. Depth Sensitivity, Measurements on Silicone
The depth sensitivity of 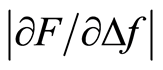 for the sensor was studied by collecting the measurement data from MP 5 i.e. close to the position over the centre of the stiff nodule for all silicone discs. The mean values of
for the sensor was studied by collecting the measurement data from MP 5 i.e. close to the position over the centre of the stiff nodule for all silicone discs. The mean values of  at MP 1, 2, 8 and 9 (the soft silicone background in Figure 2(b)) was subtracted from the value of
at MP 1, 2, 8 and 9 (the soft silicone background in Figure 2(b)) was subtracted from the value of  at MP 5 (close to centre of the stiff nodule) in Figure 5 to get the
at MP 5 (close to centre of the stiff nodule) in Figure 5 to get the 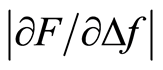 corresponding only to the sensed stiffness variations caused by the embedded silicone nodule, Figure 6. A significant difference between the
corresponding only to the sensed stiffness variations caused by the embedded silicone nodule, Figure 6. A significant difference between the 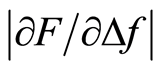 and the zero-level was seen for d ≤ 4 mm, while for d ≥ 5 mm the difference compared with the zero-level averaged to 10.6 mN/kHz. Table 2 summarizes the results from the statistical test of these differences.
and the zero-level was seen for d ≤ 4 mm, while for d ≥ 5 mm the difference compared with the zero-level averaged to 10.6 mN/kHz. Table 2 summarizes the results from the statistical test of these differences.
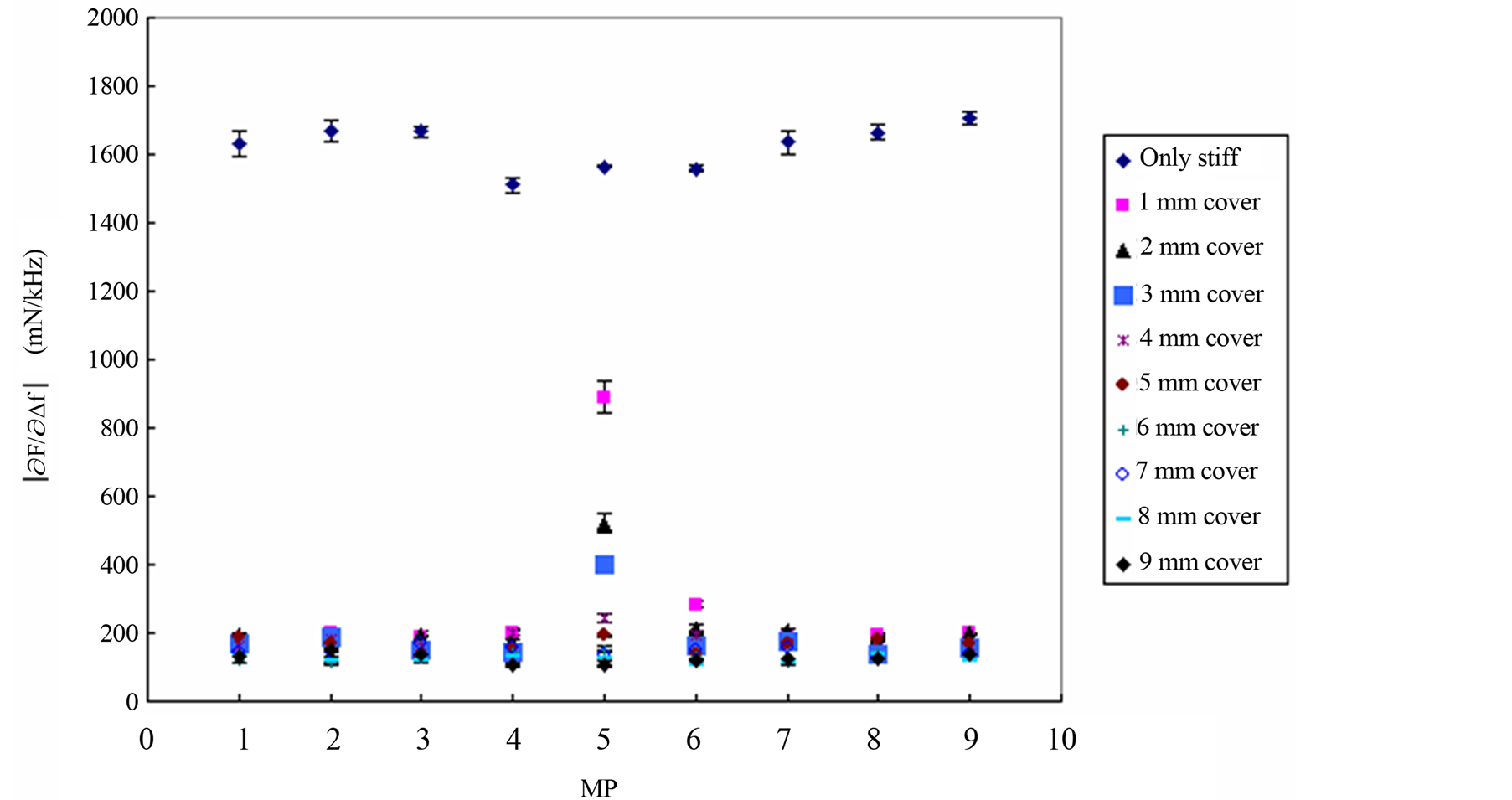
Figure 5. Measurements on silicone discs with stiff inclusions at different d. For each MP, 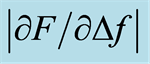 (mean ± SD, n = 6) was calculated for 10 different silicone discs, of which nine were made of soft silicone with a nodule of stiff silicone at MP 5. The soft silicone varies in thickness from d = 1 to 9 mm above the centre of the stiff nodule.
(mean ± SD, n = 6) was calculated for 10 different silicone discs, of which nine were made of soft silicone with a nodule of stiff silicone at MP 5. The soft silicone varies in thickness from d = 1 to 9 mm above the centre of the stiff nodule.
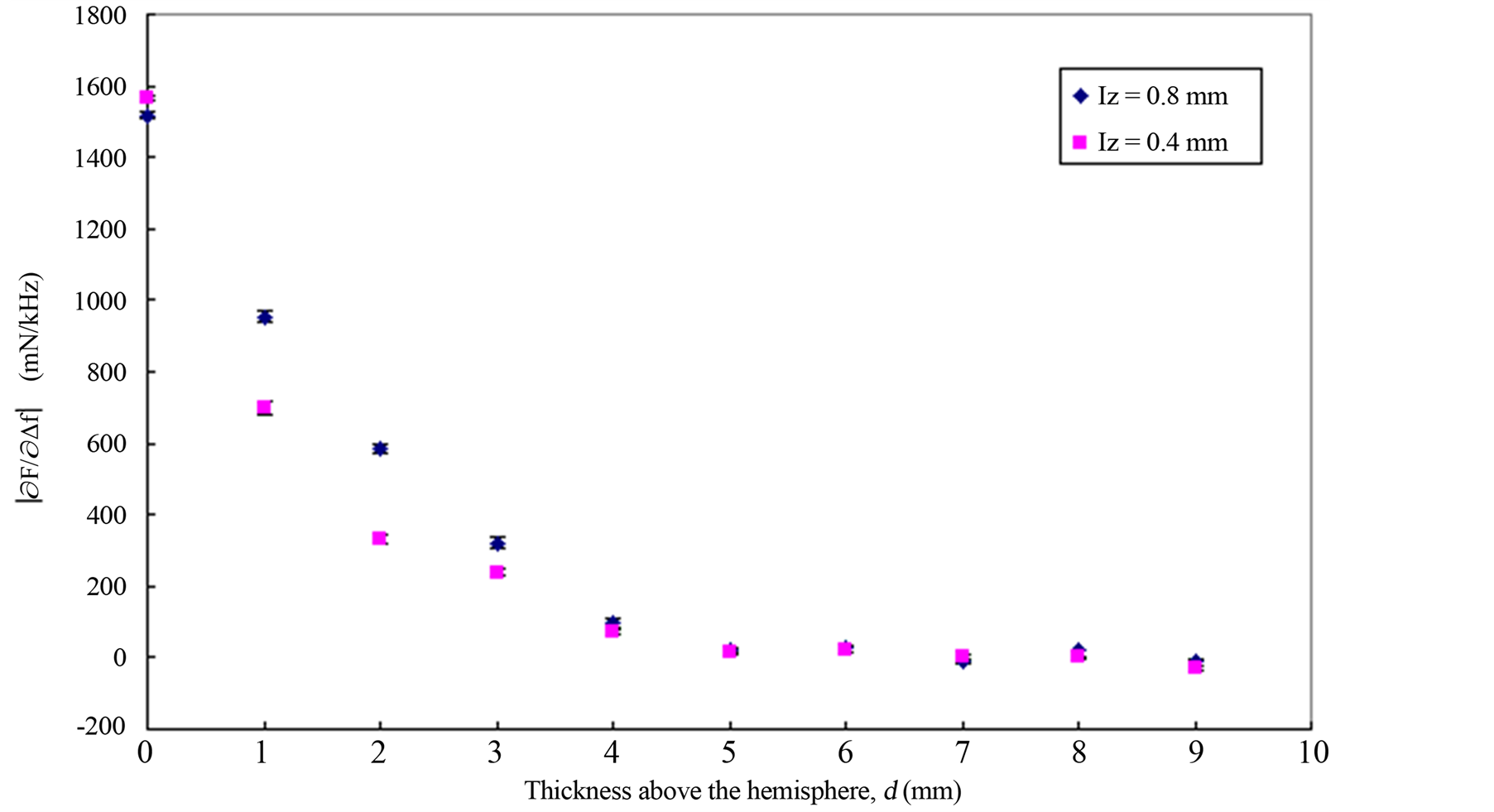
Figure 6. The depth sensitivity of  for the measurements on silicone. The
for the measurements on silicone. The  (mean ± SD, n = 6) at MP 5 for measurements made on 10 different silicone discs, of which nine were made of soft silicone with a nodule of stiff silicone at MP 5. The figure shows
(mean ± SD, n = 6) at MP 5 for measurements made on 10 different silicone discs, of which nine were made of soft silicone with a nodule of stiff silicone at MP 5. The figure shows  as a function of d measured at MP 5, i.e. above the stiff nodule at Iz = 0.4 mm and 0.8 mm.
as a function of d measured at MP 5, i.e. above the stiff nodule at Iz = 0.4 mm and 0.8 mm.
For the statistical tests of significant differences between  for Iz = 0.4 and 0.8 mm at MP 5 and the average
for Iz = 0.4 and 0.8 mm at MP 5 and the average 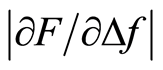 of the surrounding soft silicone (at MP 1, 2, 8 and 9) was tested against a zero-level calculated from the difference between
of the surrounding soft silicone (at MP 1, 2, 8 and 9) was tested against a zero-level calculated from the difference between  at each of the MPs 1, 2, 8 ,9 and their average value.
at each of the MPs 1, 2, 8 ,9 and their average value.
Table 2. Statistics for the depth sensitivity of 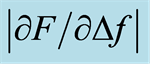 for the measurements on silicone discs. The p-values from Wilcoxon signed rank test for testing differences between
for the measurements on silicone discs. The p-values from Wilcoxon signed rank test for testing differences between 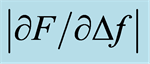 of the embedded stiff silicone nodule at MP 5 for d = 5 mm to 9 mm and the soft silicone background of MP 1, 2, 8 and 9. The asterisk (*) denotes a statistically significant difference p < 0.05.
of the embedded stiff silicone nodule at MP 5 for d = 5 mm to 9 mm and the soft silicone background of MP 1, 2, 8 and 9. The asterisk (*) denotes a statistically significant difference p < 0.05.
3.3. Measurements on Biological Tissue
From the measurements made on chicken muscles,  were calculated and shown in Figure 7. It was only possible to make one measurement in each MP on the chicken muscles, because the tissue was left with a remaining indentation after each impression as it did not reach a full elastic recovery. Measurements were conducted on 18 slices. They were divided into three groups depending on their thickness, resulting in three groups of slices with d = 1.5 ± 0.5 mm, d = 3.5 ± 0.5 mm, and d = 6.5 ± 0.5 mm covering the stiff silicone nodule. The
were calculated and shown in Figure 7. It was only possible to make one measurement in each MP on the chicken muscles, because the tissue was left with a remaining indentation after each impression as it did not reach a full elastic recovery. Measurements were conducted on 18 slices. They were divided into three groups depending on their thickness, resulting in three groups of slices with d = 1.5 ± 0.5 mm, d = 3.5 ± 0.5 mm, and d = 6.5 ± 0.5 mm covering the stiff silicone nodule. The 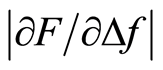 was significantly different at MP 3 compared with either MP 1 or 5 for the thin and medium thick muscle slices. For the thickest muscle slice there was no significant difference found between the different MPs. The contact force for MPs 1 and 5, i.e. tissue furthest from the silicone nodule, was in the range of 50 - 70 mN for the different d. For MP 3, aimed above the silicone nodule, the contact force was in the range of 70 - 350 mN for the different d.
was significantly different at MP 3 compared with either MP 1 or 5 for the thin and medium thick muscle slices. For the thickest muscle slice there was no significant difference found between the different MPs. The contact force for MPs 1 and 5, i.e. tissue furthest from the silicone nodule, was in the range of 50 - 70 mN for the different d. For MP 3, aimed above the silicone nodule, the contact force was in the range of 70 - 350 mN for the different d.
The measurements made with the Shore-000 hardness tester were repeated three times on each muscle slice, before the stiff silicone nodule was embedded which resulted in the following Shore-000 values: thin slices (5 - 6 mm) = 44.8 ± 2.84, medium slices (7 - 8 mm) = 41.3 ± 7.91 and the thick slices (10 - 11 mm) = 34.7 ± 4.02.
4. Discussion
In this study we present results on how deep below the surface a tactile resonance sensor system can distinguish an embedded volume, stiffer than its surrounding, mimicking cancer tumours in prostate cancer. This gives an important indication on the possibility of the tactile resonance sensors to locate cancer tumours at and below the surface of excised prostate glands in the clinical situation. We have explored depth sensitivity for the tactile resonance sensor system using flat silicone discs and biological tissue (slices of chicken breast muscle).
4.1. The Measurements
In an earlier study [17] the νi = 5 mm∙s−1 was used, but it was reported that a lower νi would be more favourable to measure Δf and to reduce errors in Iz, see section 4.4. For this reason νi = 4 mm∙s−1 was used here for both silicone discs and biological tissue. The maximum impression depth used in this study was1 mm, and data from 0.4 and 0.8 mm were analysed. Slower indentation rate or larger impression depths would have increased the influence of the viscous behaviour exhibited by the chicken tissue. It is clear that the 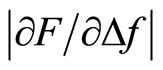 (derived from the measured parameters Δf and F) shown in Figures 5-7 can be used as a parameter to detect hidden stiffer volumes in both the silicone discs and the biological tissue. The use of
(derived from the measured parameters Δf and F) shown in Figures 5-7 can be used as a parameter to detect hidden stiffer volumes in both the silicone discs and the biological tissue. The use of 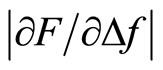 have been found to be suitable for measurements with small impression depths where the parameter will vary proportionally with the stiffness e.g. the Young’s modulus [19] . In a study by Kim et al. [28] , indentation experiments were done to determine the stiffness of prostate tissue. They used the indentation force for contact detection and a 3 mm impression depth showed to detect tumour lesions at depths up to 3.4 mm. Other studies, report the use of a rolling indenter probe in studies on tissue phantoms of silicone and porcine tissue [29] [30] . In those studies, a force sensor was used to measure the indentation force for impression depths up to 6 mm with which they could detect stiffer volumes at depths up to 22 mm. In our study, the stiffness parameter
have been found to be suitable for measurements with small impression depths where the parameter will vary proportionally with the stiffness e.g. the Young’s modulus [19] . In a study by Kim et al. [28] , indentation experiments were done to determine the stiffness of prostate tissue. They used the indentation force for contact detection and a 3 mm impression depth showed to detect tumour lesions at depths up to 3.4 mm. Other studies, report the use of a rolling indenter probe in studies on tissue phantoms of silicone and porcine tissue [29] [30] . In those studies, a force sensor was used to measure the indentation force for impression depths up to 6 mm with which they could detect stiffer volumes at depths up to 22 mm. In our study, the stiffness parameter 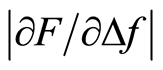 was used and stiff silicone nodules at depth of at least 4 mm could be detected with impression depths <1 mm. However, if the ratio between the impression depth and the detecting depth is considered, the method used by [29] [30] show similar results.
was used and stiff silicone nodules at depth of at least 4 mm could be detected with impression depths <1 mm. However, if the ratio between the impression depth and the detecting depth is considered, the method used by [29] [30] show similar results.
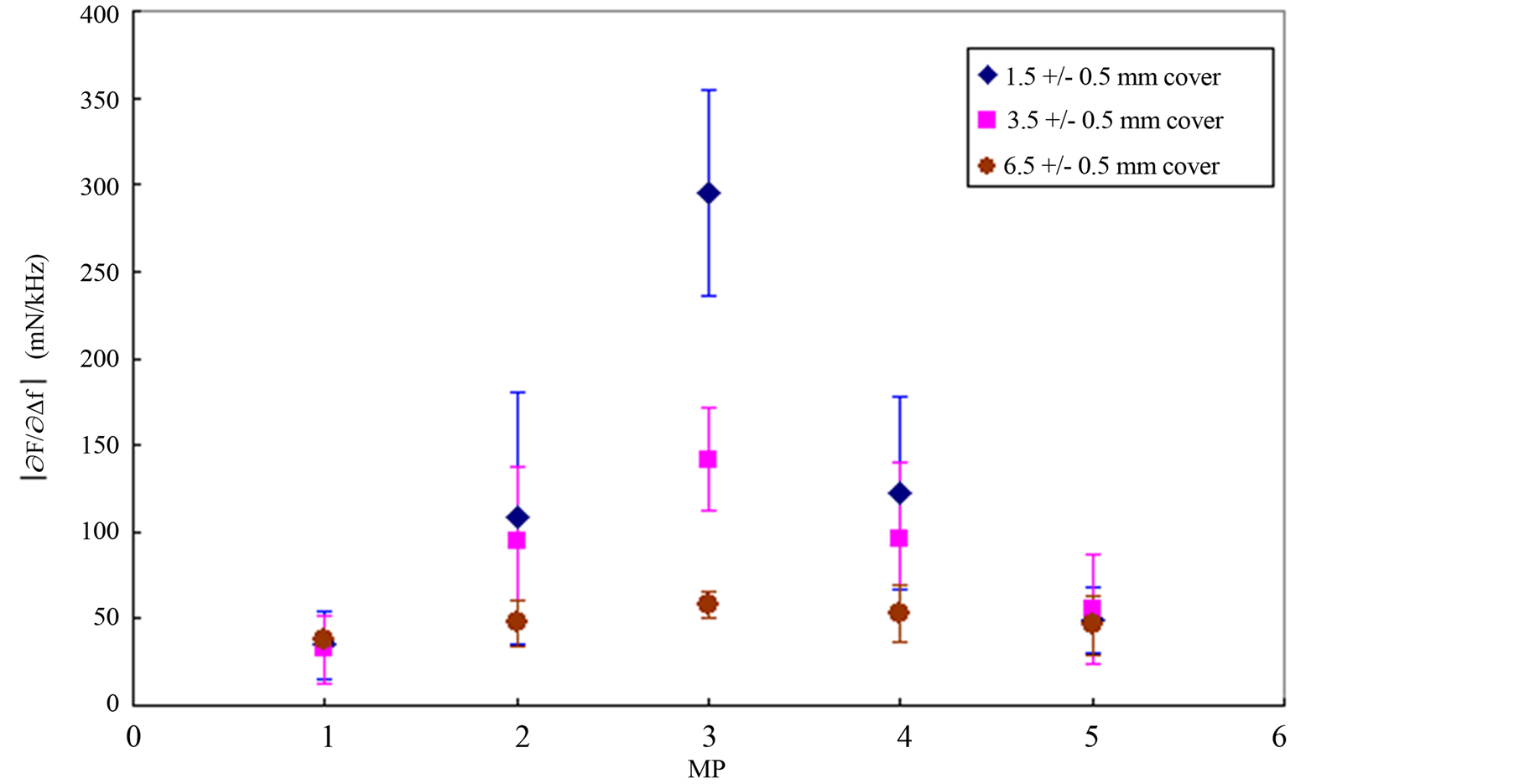
Figure 7. The depth sensitivity of  for measurements on a biological tissue model. The
for measurements on a biological tissue model. The 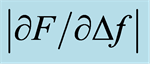 (mean ± SD, n = 6) calculated for the three groups of chicken muscle slices with different d, covering a stiff nodule made of stiff silicone inserted from underneath at MP 3. Measurements shown in the figure are for Iz = 0.8 mm. The values of
(mean ± SD, n = 6) calculated for the three groups of chicken muscle slices with different d, covering a stiff nodule made of stiff silicone inserted from underneath at MP 3. Measurements shown in the figure are for Iz = 0.8 mm. The values of 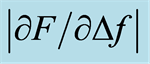 at MPs 1 and 5 are valid for slices without a silicone nodule inclusion.
at MPs 1 and 5 are valid for slices without a silicone nodule inclusion.
4.2. Measurements on Silicone
For evaluation of sensor techniques regarding human soft tissue characterization, silicones have been used as tissue phantoms in previous studies [16] [17] [23] . The reason for this is the similarities to human tissue regarding mechanical properties. Silicone is an elastomer and can be regarded as incompressible and with a mechanical strain-stress relationship that can be described using hyperelastic models [31] [32] . Most biological soft tissues can be modelled as hyperelastic but also exhibit viscoelastic behaviour [32] [33] . However, with small impression depths and fast indentation rates, the viscous component can be minimized, as discussed in Section 4.1. The advantages with silicone are that it is homogeneous and isotropic and can be mixed to a desired hardness. It is also easy to enclose small pieces of harder or softer objects which have been shown here. The silicones are also relatively stable over time as opposed to biological materials that can degrade or dehydrate during the time of measurements.
The silicone discs used as soft tissue phantoms were homogeneous and had even surfaces, which gave measurements with good repeatability. In addition, the order of the performed measurements was chosen, Figure 2(b), to eliminate the possible effects that two adjacent indentations close in time would have on the measurements, thus improving repeatability. From the derived , it was clear that the sensor could detect a stiff silicone nodule beneath a layer of softer silicone. In Figure 5, the values of
, it was clear that the sensor could detect a stiff silicone nodule beneath a layer of softer silicone. In Figure 5, the values of  for the stiff silicone, the same type as the nodule inclusions were made from, show some variability which was not expected from measurements on a solid flat disc of silicone. The repeatability at each MP had a small standard deviation, <2.3% of the measured value. The variability in
for the stiff silicone, the same type as the nodule inclusions were made from, show some variability which was not expected from measurements on a solid flat disc of silicone. The repeatability at each MP had a small standard deviation, <2.3% of the measured value. The variability in 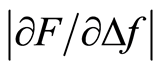 at different MPs may be due to local variations in the homogeneity of the silicone or dust particles or surface impurities that affect Δf. The stiffer silicone used in this study is more stiff than average normal prostate tissue [16] . However, the choice of a relatively stiff silicone for the inclusions was made to obtain a significant contrast between the inclusion and the surrounding softer silicone, while still representing a relevant range of stiffness [16] .
at different MPs may be due to local variations in the homogeneity of the silicone or dust particles or surface impurities that affect Δf. The stiffer silicone used in this study is more stiff than average normal prostate tissue [16] . However, the choice of a relatively stiff silicone for the inclusions was made to obtain a significant contrast between the inclusion and the surrounding softer silicone, while still representing a relevant range of stiffness [16] .
The time between each measurement at the same position was chosen to be at least 15 minutes to ensure that the silicone had regained its original shape. From Figure 6, it was noticed that the stiff inclusion could be detected for d ≤ 4 mm. However, a statistical analysis of the difference in 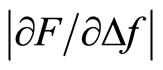 between MP 5 and the soft background showed that the stiffer nodules, with some exception, could be distinguished with a weak significance at depths from 5 to 9 mm. For d = 7 mm there were no significant difference, Table 2, which needs further investigation, but reasons could be the same as for the stiff silicone disc mentioned above. The
between MP 5 and the soft background showed that the stiffer nodules, with some exception, could be distinguished with a weak significance at depths from 5 to 9 mm. For d = 7 mm there were no significant difference, Table 2, which needs further investigation, but reasons could be the same as for the stiff silicone disc mentioned above. The 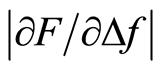 for two different impression depths were studied in this report, and the depth sensitivity for detecting the stiff inclusion was very similar for both Iz = 0.4 and Iz = 0.8 mm. The depth sensitivity for this tactile resonance measurement system agrees with an estimated sensing depth from a previous study [34] . In that study, the sensing depth was extrapolated from the measured stiffness and the histological data of prostate tissue. The results showed an estimated sensing depth of 3.5 to 5.5 mm for an impression depth of 1.0 mm. In the present study the sensing depth was obtained from measurements on silicone samples with a stiff embedded inclusion at variable depths, d = 1 to 9 mm with steps of 1 mm.
for two different impression depths were studied in this report, and the depth sensitivity for detecting the stiff inclusion was very similar for both Iz = 0.4 and Iz = 0.8 mm. The depth sensitivity for this tactile resonance measurement system agrees with an estimated sensing depth from a previous study [34] . In that study, the sensing depth was extrapolated from the measured stiffness and the histological data of prostate tissue. The results showed an estimated sensing depth of 3.5 to 5.5 mm for an impression depth of 1.0 mm. In the present study the sensing depth was obtained from measurements on silicone samples with a stiff embedded inclusion at variable depths, d = 1 to 9 mm with steps of 1 mm.
4.3. Measurements on Biological Tissue
Chicken muscle tissue was chosen as a further step towards mimicking the prostate tissue, and slices were prepared for the experiments. A tissue, as opposed to silicone, has a viscoelastic behaviour and possible wet/moist surface with dehydration effects, besides being less homogeneous. These conditions lead to a measurement situation that differs from that on the silicone, but might resemble measurements on prostate tissue more. The reason for cutting the chicken breasts in a semi defrosted state was to get as even surfaces as possible. However, all measurements were made on thawed slices. After each impression by the sensor the tissue did not reach a full elastic recovery, which made repetitive measurements at the same MP impossible, and this was also the case for the Shore-000 hardness tester. This was expected due to above mentioned characteristics of biological tissue. Therefore different slices were used for each measurement series. As could be expected there were larger standard deviations relative to the mean for the measurements on slices of chicken muscle, Figure 7, than compared to the measurements on silicone, Figure 5. During some measurements on slices with a small d, the sensor penetrated the tissue and therefore came in direct contact with the embedded stiff silicone nodules. These slices and the corresponding data were therefore excluded from the analysis.
The chicken muscles were wet from the commercial treatment, soaking in salt water, when they were placed on the polystyrene. To keep a moist, but not wet surface, the surface of the slices of the chicken muscle was sprayed with water (at room temperature) with an atomizer before the measurement commenced. This ensured constant contact conditions with the resonance sensor throughout the measuring time. It could be argued that spraying saline would have been a better choice to avoid possible osmotic effects. However, since the time span between the first and the last measurement on each slice was only 5 minutes, the advantage of using saline can be disregarded. However, too much water on the surface resulted in faulty measurements, as the resonance sensor will initially measure the water layer before reaching the tissue surface. Such measurements were easily detected as Δf indicated that contact was made, i.e. a relatively high Δf was obtained while F was approximately zero. For that reason, slices with such measurements were excluded from the analysis.
The chicken breasts were sliced when semi defrosted in order to get a smooth surface. However, at the time of measurements, the thickness of the completely defrosted slices varied ±1 mm along the line of MPs, i.e. the slices were not perfectly plane parallel. As the row of measurement points was 20 mm for the chicken muscles, this may have resulted in a deviation from a perpendicular contact of a magnitude of 2 to 3˚. However, according to earlier reports [11] [17] [27] , small variations in the contact angle do not affect the measured values of Δf and F. On the silicone discs, the contact angle was assumed to be 0˚, i.e. the measurements were made perpendicular to the surface since the Petri dishes with silicone were cured on a horizontal surface, and therefore assumed to be flat.
The chicken muscle samples, compared to the silicone, were in addition to the above mentioned differences also more inhomogeneous with more uneven surfaces as well as covered with a thin film of moist. Regardless of these differences, the results show that the tactile sensor could detect the embedded stiffer inclusions consistently with the measurements on silicone samples. The statistical analysis of the measurements at the different MPs, Figure 7, showed that the embedded silicone nodules in chicken muscle could be detected statistically significant on slices with d < 4 mm. This was also achieved, as expected, in silicone samples and then even with slightly higher depth sensitivity, d > 4 mm, Table 2. No differences were found between the MPs for the group of thickest chicken slices (d = 6.5 ± 0.5 mm) used in this study. In our biological model we could detect stiffer nodules at depths of about 4 mm, which indicates that stiffer cancer tumours inside prostate tissue can be detected with the sensor. All this was considered to be valuable information for future measurements on prostate tissue.
4.4. Error Estimates
The error estimates for this measurement system have been reported earlier [17] . However, in this study a lower νi was used to reduce the error, ε, in Iz caused by the uncertainty in finding the correct data sample indicating contact between the sensor and the surface. The relative ε for Iz = 0.4 mm was 4%, and for Iz = 0.8 mm it was 2%. For the measured parameters, Δf, F and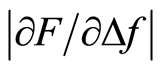 , ε was reported to be <1.5% [18] .
, ε was reported to be <1.5% [18] .
5. Conclusion
It can be concluded that with this experimental set-up, and with an impression depth of 0.4 - 0.8 mm, the tactile sensor could detect stiffness changes at least 4 mm from the surface of a biological specimen. Although this is an indication of the ability of the tactile sensor to detect hardened nodules, like cancer tumours in soft tissue, it has to be considered that the present tissue model has its limitations as all models have. Measurements on human prostate tissue will reveal the full value of the ability of the sensor. A future aim is a method for detecting areas with cancer tumours at and below the surface on excised prostates, and possibly also other types of cancer in soft tissue or organs. Hence the results of this study form a valuable step towards this.
Competing Interests
The authors report no competing or conflicts of interest. The authors alone are responsible for the content and writing of the paper.
Authors’ Contributions
APÅ participated in the conception and design, acquisition of data, analysis and interpretation of data and also drafted the manuscript. VJ participated in the conception and design, analysis and interpretation of data, revising of the manuscript critically for important intellectual content. BMA participated in the conception and design, analysis and interpretation of data, revising the manuscript critically for important intellectual content. OAL participated in the conception and design, analysis and interpretation of data, revising the manuscript critically for important intellectual content.
All authors have given final approval of the final manuscript to be published, agree to be accountable for all aspects of the work.
Acknowledgements
The study was supported by The Industrial Doctoral School at Umeå University and by grants from Objective 2 North Sweden-EU Structural Fund.
References
- American Cancer Society (2013) http://www.cancer.org
- The National Board of Health and Welfare (Socialstyrelsen) (2013) http://www.socialstyrelsen.se
- Schröder, F.H., Hugosson, J., Roobol, M.J., Tammela, T.L.J., Ciatto, S., Nelen, V., Kviatkowski, M., Lujan, M., Lilja, H., Zappa, M., Denis, L.J., Recker, F., Berenguer, A., Määttänen, L., Bangma, C.H., Aus, G., Villers, A., Rebillard, X., van der Kwast, T., Blijenberg, B.G., Moss, S.M., de Koning, H.J., Auvinen, A. and E.R.S.P.C Investigators (2009) Screening and Prostate-Cancer Mortality in Randomized European Study. New England Journal of Medicine, 360, 1320-1328. http://dx.doi.org/10.1056/NEJMoa0810084
- Candefjord, S., Ramser, K. and Lindahl, O.A. (2009) Technologies for Localization and Diagnosis of Prostate Cancer. Journal of Medical Engineering & Technology, 33, 585-683.
- Wang, J., Wang, J., Sun, X., Song, W., Nor, J.E., Wang, C.Y. and Taichman, R. (2005) Diverse Signalling Pathways through the SDF-1/CXCR4 Chemokine Axix in Prostate Cancer Cell Lines Leads to Altered Patterns of Cytokine Secretion and Angiogenesis. Cellular Signalling, 17, 1578-1592. http://dx.doi.org/10.1016/j.cellsig.2005.03.022
- Lindahl, O.A., Constantinou, C.E., Eklund, A., Murayama, Y., Hallberg, P. and Omata, S. (2009) Tactile Resonance Sensors in Medicine. Journal of Medical Engineering & Technology, 33, 263-273. http://dx.doi.org/10.1080/03091900802491188
- Gwilliam, J.C., Pezzementi, Z., Jantho, E., Okamura, A.M. and Hsiao, S. (2010) Human vs. Robotic Tactile Sensing: Detecting Lumps in Soft Tissue. IEEE Haptics Symposium 2010, Waltham, 21-28.
- Tiwana, M.I., Redmond, S.J. and Lovell, N.H. (2012) A Review of Tactile Sensing Technologies with Applications in Biomedical Engineering. Sensors and Actuators, A179, 17-31. http://dx.doi.org/10.1016/j.sna.2012.02.051
- Jalkanen, V., Andersson, B.M., Bergh, A., Ljungberg, B. and Lindahl, O.A. (2006) Resonance Sensor Measurements of Stiffness Variations in Prostate Tissue in Vitro—A Weighted Tissue Proportion Model. Physiological Measurement, 27, 1373-1386. http://dx.doi.org/10.1088/0967-3334/27/12/009
- Krouskop, T.A., Wheeler, T.M., Kallel, F., Garra, B.S. and Hall, T. (1998) Elastic Moduli of Breast and Prostate Tissues under Compression. Ultrason Imaging, 20, 260-274. http://dx.doi.org/10.1177/016173469802000403
- Sakai, N., Tatsuta, M., Yano, H., Iishi, H. and Ishiguro, S. (2000) Diagnosis of the Extent of Gastric Cancers by a New Endoscopic Ultrasonic Tactile Sensor. Gastrointest Endosc, 51, 69-73. http://dx.doi.org/10.1016/S0016-5107(00)70390-7
- Lindahl, O.A., Ängquist, K.-A. and Ödman, S. (1991) Impression Technique for the Assessment of Oedema—Technical Improvement and Methodological Evaluation of a New Technique. Medical & Biological Engineering & Computing, 29, 591-597. http://dx.doi.org/10.1007/BF02446090
- Sasai, S., Zhen, Y.-X., Suetake, T., Tanita, Y., Omata, S. and Tagami, H. (1999) Palpation of the Skin with a Robot Finger: An Attempt to Measure Skin Stiffness with a Probe Loaded with a Newly Developed Tactile Vibration Sensor and Displacement Sensor. Skin Research Technology, 5, 237-246. http://dx.doi.org/10.1111/j.1600-0846.1999.tb00136.x
- Miyaji, K., Furuse, A., Nakajima, J., Kohno, T., Ohtsuka, T., Yagyu, K., Oka, T. and Omata, S. (1997) The Stiffness of Lymph Nodes Containing Lung Carcinoma Metastases—A New Diagnostic Parameter Measured by a Tactile Sensor. Cancer, 80, 1920-1925. http://dx.doi.org/10.1002/(SICI)1097-0142(19971115)80:10<1920::AID-CNCR8>3.0.CO;2-R
- Kusaka, K., Harihara, Y., Torzilli, G., Kubota, K., Takayama, T., Makuuchi, M., Mori, M. and Omata, S. (2000) Objective Evaluation of Liver Consistency to Estimate Hepatic Fibrosis and Functional Reserve for Hepatectomy. Journal of the American College of Surgeons, 191, 47-53. http://dx.doi.org/10.1016/S1072-7515(00)00309-4
- Jalkanen, V., Andersson, B.M., Bergh, A., Ljungberg, B. and Lindahl, O.A. (2006) Prostate Tissue Stiffness as Measured with a Resonance Sensor System: A Study on Silicone and Human Prostate Tissue in Vitro. Medical & Biological Engineering & Computing, 44, 593-603. http://dx.doi.org/10.1007/s11517-006-0069-6
- Åstrand, A.P., Jalkanen, V., Andersson, B.M. and Lindahl, O.A. (2013) Contact Angle and Indentation Velocity Dependency for a Resonance Sensor—Evaluation on Soft Tissue Silicone Models. Journal of Medical Engineering & Technology, 37, 185-196. http://dx.doi.org/10.3109/03091902.2013.773097
- Åstrand, A.P. (2012) A Flexible Resonance Sensor System for Detection of Cancer Tissue—Evaluation on Silicone. Lic. Thesis, Chapter 4, 5-8. Umeå University, Umeå.
- Jalkanen, V., Andersson, B.M., Bergh, A., Ljungberg, B. and Lindahl, O.A. (2008) Explanatory Models for a Tactile Resonance Sensor System—Elastic and Density-Related Variations of Prostate Tissue in Vitro. Physiological Measurement, 29, 729-745. http://dx.doi.org/10.1088/0967-3334/29/7/003
- Jalkanen, V., Andersson, B.M. and Lindahl, O.A. (2010) Stiffness of a Small Tissue Phantom Measured by a Tactile Resonance Sensor. Proceedings of XII Mediterranean Conference on Medical and Biological Engineering and Computing (Chalkidiki) IFMBE Proceedings, 29, 395-398.
- Omata, S. and Terunuma, Y. (1992) New Tactile Sensor like the Human Hand and Its Applications. Sensors and Actuators, 35, 9-15. http://dx.doi.org/10.1016/0924-4247(92)87002-X
- Wacker-Chemie GmbH (2011) http://www.wacker.com
- Eklund, A., Bergh, A. and Lindahl, O.A. (1999) A Catheter Tactile Sensor for Measuring Hardness of Soft Tissue: Measurement in a Silicone Model and in an in Vitro Human Prostate Model. Medical & Biological Engineering & Computing, 37, 618-624. http://dx.doi.org/10.1007/BF02513357
- Lindahl, O.A. and Omata, S. (1995) Impression Technique for the Assessment of Oedema: Comparison with a New Tactile Sensor That Measures Physical Properties of Tissue. Medical & Biological Engineering & Computing, 33, 27- 32. http://dx.doi.org/10.1007/BF02522941
- Beuth Verlag GmbH (2013) http://www.beuth.de
- American Society for Testing and Materials, ASTM (2013) http://www.astm.org/Standards/D2240.htm
- Murayama, Y. (2005) Development of a Micro Tactile Sensor and Its Biomedical Applications. PhD Thesis, Chapter 5. Nihon University, Nihon.
- Kim, Y., Ahn, B., Lee, J.W., Rha, K.H. and Kim, J. (2013) Local Property Characterization of Prostate Glands Using Inhomogeneous Modelling Based on Tumor Volume and Location Analysis. Medical & Biological Engineering & Computing, 51, 197-205. http://dx.doi.org/10.1007/s11517-012-0984-7
- Sangpradit, K., Liu, H., Dasgupta, P., Althoefer, K. and Seneviratne, L.D. (2011) Finite-Element Modelling of Soft Tissue Rolling Indentation. IEEE Transactions on Biomedical Engineering, 58, 3319-3327. http://dx.doi.org/10.1109/TBME.2011.2106783
- Liu, H., Sangpradit, K., Li, M., Dasgupta, P., Althoefer, K. and Seneviratne, L.D. (2014) Inverse Finite-Element Modeling for Tissue Parameter Identification Using a Rolling Indentation Probe. Medical & Biological Engineering & Computing, 52, 17-28. http://dx.doi.org/10.1007/s11517-013-1118-6
- Bergström, J.S. and Boyce, M.C. (1998) Constitutive Modelling of the Large Strain Time-Dependent Behaviour of Elastomers. Journal of the Mechanics and Physics of Solids, 46, 931-954. http://dx.doi.org/10.1016/S0022-5096(97)00075-6
- Martins, P.A.L.S., Natal, J.R.M. and Ferreira, A.J.M. (2006) A Comparative Study of Several Material Models for Prediction of Hyperelastic Properties: Application to Silicone-Rubber and Soft Tissue. Strain, 42, 135-147. http://dx.doi.org/10.1111/j.1475-1305.2006.00257.x
- Fung, Y.C. (1993) Bioviscoelastic Solids. In Biomechanics-Mechanical Properties of Living Tissues. 2nd Edition, Springer-Verlag Inc., New York, 242-311.
- Jalkanen, V., Andersson, B.M., Bergh, A., Ljungberg, B. and Lindahl, O.A. (2007) Spatial Variations in Prostate Tissue Histology Measured by a Tactile Resonance Sensor. Physiological Measurement, 228, 1267-1281. http://dx.doi.org/10.1088/0967-3334/28/10/011
Abbreviations
DRE—Digital rectal examination
PCa—Prostate cancer
MP—Measurement position
PLL—Phase-locked loop
PSA—prostate specific antigen
SD—Standard deviation
TRUS—Trans rectal ultrasound
α—Contact angle
d—Thickness above centre of stiff hemisphere (nodule) inclusion
ε—Error
Δf—Frequency shift
f—Loaded resonance frequency
f0—Free (unloaded) resonance frequency
F—Contact force
IZ—Impression depth of interest, vertical direction
n—Number of measurements
vi—Indentation velocity
F Δf —Stiffness parameter
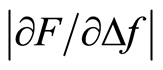 —Stiffness parameter
—Stiffness parameter


