Journal of Biomedical Science and Engineering
Vol.6 No.8(2013), Article ID:35581,9 pages DOI:10.4236/jbise.2013.68097
Acoustic measures of the cry characteristics of healthy newborns and newborns with pathologies
![]()
Department of Electrical Engineering, École de Technologie Supérieure, Montreal, Canada
Email: Yasmina.kheddache.1@ens.etsmtl.ca, chakib.tadj@etsmtl.ca
Copyright © 2013 Yasmina Kheddache, Chakib Tadj. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 21 June 2013; revised 19 July 2013; accepted 29 July 2013
Keywords: Newborn Cry; Dysphonic Cry; Noise Estimation
ABSTRACT
Several hypotheses have been formulated as a result of observing spectrograms of the audio signals of the newborn infant cry in numerous studies. Our study is based on a few of these hypotheses. The purpose of this article is to differentiate pathological crying from healthy crying through acoustic cry analysis based on neurophysiological parameters of newborns. The automatic estimation of the characteristics of relevant cry signals, such as phonation, hyperphonation, and dysphonation, expressed as percentages, as well as unvoiced sound and mode change percentages, have enabled us to distinguish among the pathologies selected for this study. The results obtained have helped us to make quantitative associations between cry characteristics and pathological conditions affecting newborns.
1. INTRODUCTION
Crying provides information on the level of functioning of the central nervous system (CNS), because the cry signal is the result of coordination among several brain regions that control respiration and the vocal fold vibration from which the cry sounds are produced [1-3]. Deficits in brain functioning may affect the vagal control of the cry [2].
Newborn crying is characterized by voiced/unvoiced sounds and a higher fundamental frequency, F0, than those of adults, and by abrupt changes in frequency that do not occur in adults. Unvoiced sounds, or turbulences, are produced by forcing air through a constriction in the vocal tract, and voiced sounds are generated by forcing air through the glottis [1,4].
We can distinguish three cry modes of vocal fold vibration [1]: phonation, hyperphonation, and dysphonation, as defined in Section 4. By observing spectrograms and spectra of audio signals of cries, associations have been made with pathological conditions [1,5].
Our main goal in this study is to use cry characteristics to improve infant monitoring in the first days of life. Automatic measurement of these characteristics allows us to associate the most relevant characteristics with pathologies of interest, and also to extend the measurement to other pathologies.
In this paper, we concentrate on the measurement of certain acoustic parameters of pathological and healthy newborn cries, particularly the percentage of dysphonic cries characteristic of the pathologies studied. The percentages of other cry characteristics, such as phonated and hyperphonated cries, which were investigated in [6], and also of unvoiced sounds and mode changes, are estimated. The principal objective of this work is to determine the relationship between this acoustic parameter and the various pathologies studied.
In order to evaluate dysphonia in healthy and pathological cries, the noise component in newborn cry signals must be estimated.
Several approaches have been proposed for the estimation of noise power levels. In the context of degraded speech due to additive noise, the MMSE (minimum mean-squared error)-based noise estimator and the ACF (adaptive comb filtering) method have been used [7-9]. However, only the ACF method has been used with NNE (normalized noise energy) measurement for determining the noise component of pathological voice signals [4,10].
In the case of the newborn, determination of the noise component in dysphonic cries using these two methods can produce an over estimation of noise. In the case of MMSE-based noise estimation, an initialization of 0.5 s with noise only is used. However, in the case of ACF, the overload problem caused by rapid change in fundamental frequency produces undesirable results [11].
In this paper, we present the performance of a new proposal based on the use of the MMSE and ACF methods to estimate the amount of noise present in the cries of newborns, and also to determine the percentage of dysphonia in healthy and pathological cries. We used the MMSE-based noise estimator combined with the ACF method to initialize noise estimation.
This paper is organised as follows. We first present a broad definition of dysphonation in the newborn cry in Section 2, and the database used in this work in Section 3. We then explain our methodology for the automatic estimation of the percentage of dysphonation in healthy and pathological cries of newborns, and that for other relevant characteristics in Section 4. In Section 5, we address dysphonation estimation in newborn cries. We review NNE acoustic measurement in Section 5, and discuss the implementation of MMSE-based noise estimation adapted to newborn cries using the ACF-based noise estimator for initialization of the estimation. An analysis of our results is presented in Section 6, and our conclusions are provided in Section 7.
2. DYSPHONIC CRY
In the literature, dysphonia is considered a functional voice disorder affecting the respiratory, cervical, costal, and abdominal muscles [12]. The level of dysphonia is measured by the amount of turbulent noise present, or by parameters (timbre, intensity, and pitch) that deviate from the normal [13].
The dysphonic cry is the product of a portion of the expiratory phase of the respiratory tract. It is characterized by harmonics that are undefined and non equidistant [14], and caused by noisy or non harmonic vibration of the vocal folds due to unstable respiratory control [1,15]. Dysphonation is a cry characteristic that yields negative cry ratings, such as increased variability of F0 and increased hyperphonation [14]. According to [1], dysphonation and frequent mode changes between phonation and dysphonation are associated with prenatal insult and perinatal risk. The presence of one of these markers indicates poor control of the respiratory system. The authors of [14] show that the percentage of dysphonic crying is more important than the presence or absence of that characteristic.
According to [5], noise concentration is extremely rare in normal infant crying. Without any alteration of the voice organs, a healthy infant can temporarily produce noisy vocalization. However, a healthy infant’s cry is generally noiseless, compared to that of an infant with a pathological condition [13]. A dysphonic cry can also be a result of the immature innervation of the larynx. In this case, the cry spontaneously disappears [12,13]. The infant that cannot produce a regular cry at all is certainly sick [13]. A higher noise concentration has been found in both the voiced and voiceless signals of the cries of infants with herpes simplex virus encephalitis [2,5] and laryngitis, and in infants exposed to parental cocaine, marijuana, or alcohol use [1,2]. The dysphonic cries are associated with higher scores for anguish, anger, and urgency [14].
3. CRY DATABASE
The database we used is the same as the one used in [6]. It contains 3396 cry samples of 1 s duration from 68 newborn babies aged 1 day to 4 weeks. Thirty-one healthy newborns produced 1774 of the samples (764 of the babies were premature) and thirty-seven newborns with a pathological condition produced 1622 of the samples (1079 of the babies were premature). Table 1 shows the pathologies studied according to the gestational age of the newborns (Premature infant with less than 37 weeks gestation and full-term infant between 37 and 42 weeks). These cries were collected with the aid of medical staff in the Neonatology department at Saint-Justine Hospital in Montreal. The conditions in which the cries were registered are: hunger, blood sampling, and diaper changing. The cries were registered using a small recording device placed 10 cm from the baby’s mouth, at a sampling rate of 44.1 kHz. For each baby, three recordings of 2 to 3 minutes’ duration were made, with at least a one hour interval after each recording session (over a period of 10 days at most). The time and date of the session; the gender and date of birth of the baby; the pathology of the baby; and the reason for the crying were noted for each

Table 1. The pathologies studied.
crying episode.
The spectrograms of different cry modes are shown in Figure 1. The phonated cry was extracted from a healthy, full-term newborn. The hyperphonated cry was extracted from a premature newborn suffering from IUGR—microcephaly, and the dysphonated cry was extracted from a full-term newborn suffering from asphyxia.
4. METHODOLOGY
The methodology adopted for automatic estimation of dysphonation and for the other characteristics presented in Table 2 for pathological and healthy newborn cries using Matlab is as follows:
• Distribution of the cry samples by pathology and by gestational age;
• Noise filtering and segmentation of the recordings into useful and non useful portions using Praat;
• Division of the signals into overlapping frames of 1024 samples with 512 recovering, and multiplication of each frame by the Hanning window;
• Estimation of F0 using the SIFT algorithm (simple inverse filtering tracking) [16,17];
• Estimation of spectral noise power using the MMSE-based noise estimator and the ACF method for initializing noise estimation;
• Calculation of NNE (normalized noise energy);
• Identification of phonic, dysphonic, and hyperphonic segments, as well as unvoiced segments;
• Calculation of the average percentage of phonic (APph), hyperphonic (APhyp), and dysphonic (APdys) segments, and the number of changes in cry mode (APch.mo) and the number of unvoiced segments (APunv).

Figure 1. Spectrograms of different cry modes. (a) Phonation; (b) Hyperphonation; (c) Dysphonation.
We followed this methodology, by pathology and by gestational age, using these formulas:
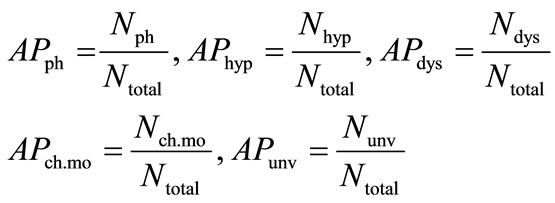
where Ntotal, Nph, Nhyp, Ndys, Nunv and Nch.mo are the total number of segments, the total number of phonic segments, the total number of hyperphonic segments, the total number of dysphonic segments, the total number of unvoiced segments, and the total number of changes in cry mode respectively.
• Application of ANOVA variance analysis for healthy and pathological cries to analyze the estimated characteristics by gestational age (full-term, preterm).
The first three characteristics presented in Table 2 were investigated in [6].
5. DYSPHONATION ESTIMATION IN NEWBORN CRIES
Many approaches have been proposed for evaluating the noise components of pathological voice signals, such as the harmonic-to-noise ratio (HNR) and FFT spectra methods, both of which are considered to be unhelpful for distinguishing a pathological voice from a normal voice [18]. In [10,18], the authors indicate that NNE measurement is an effective method for doing so. If an NNE value is under a threshold (−10 dB), the voice is regarded as normal, and if it is over the threshold, or equal to it, the voice is regarded as pathological.
Our study is based on the hypothesis that a newborn’s cries are considered to be dysphonic if the NNE value is larger than or equal to −10 dB [19].
Two methods have been studied to estimate the noise component of healthy and pathological cry signals: 1) the ACF-based noise estimator; and 2) the MMSE-based noise estimator. However, both these methods either

Table 2. Measured characteristics of cries.
produce undesirable results, or over estimate noise in the case of newborn cries.
In the first method, according to [7,11,20], overload problems due to rapid changes in F0 create segments on the cry waveform that are much shorter than neighboring segments. This is an issue because the filter coefficients are not in the same relative positions in their respective segments. The authors suggest turning off the coefficients involved in the short segments, but this proposal is at variance with the principle of the adaptive filtering method [11].
In the second method, over estimation of the noise in the cry signals is caused by initialization of noise estimation in which noise is only considered in the initial 0.5 s of the signal, according to [21].
To avoid this over estimation and improve noise tracking in the cry signal, we are using a new approach, based on combining the two methods: the MMSE-based noise estimator with an initial estimation of noise using the ACF-based noise estimator. This implementation is illustrated in the simplified block diagram in Figure 2.
5.1. Normalized Noise Energy Estimation (NNE)
The number of dysphonic components estimated in cry signals is quantified by means of NNE acoustic measurement, which, in this context, is defined as the ratio of the estimated noise component energy to the total cry energy [18].
The cry signal yk(n) in the kth frame is assumed to consist of periodic component xk(n) and the additive noise component wk(n), and is represented as follows:
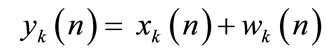
Let Y(l), X(l), and W(l) be the l-point discrete Fourier transform (DFT) of y(n), x(n), and w(n) respectively.
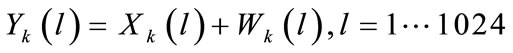
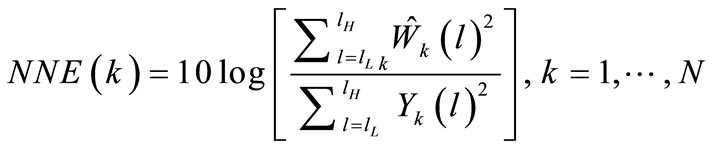
where: N is the number of frames over the whole analysis interval of the cry.
lH and lL are lowest and highest points of the frequency band where the noise energy is evaluated; and 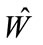 is the estimate of W.
is the estimate of W.
5.2. ACF-Based Noise Estimator
A time variant digital ACF method was proposed by Frazier in 1975 for enhancing the intelligibility of speech signals degraded by the addition of competing speech signals or background noise [7]. This method is based on the observation that the waveforms of voiced sounds are
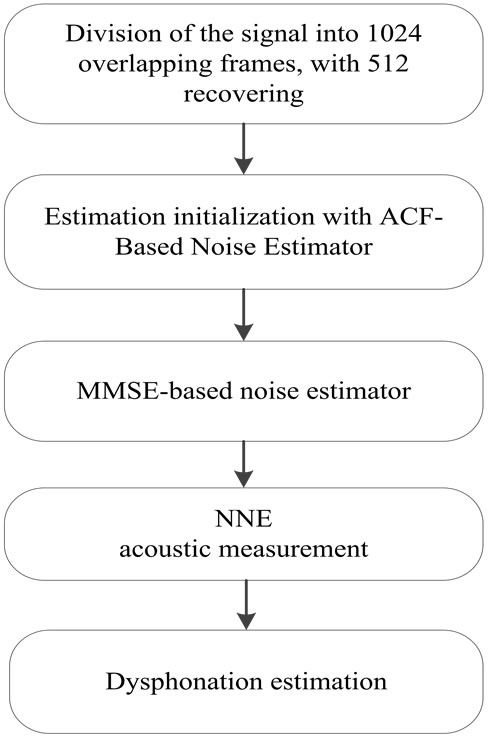
Figure 2. Dysphonation estimation in newborn cries.
periodic, with a period that corresponds to the fundamental frequency F0. We have adapted this method and applied it to estimating the noise components of a cry signal. The frequency spacing of the adaptive comb filter varies with the estimated F0 from a cry signal, and the spacing of the filter coefficients is adjusted to the individual pitch periods [10].
The estimation of F0 is achieved by means of the SIFT method, because it is so robust [6].
The ACF implementation is as follows:
The unit sample response of an adaptive comb filter h(n) over one pitch period is:
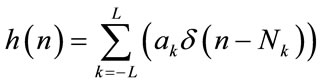
where δ(n) is a unit sample function.
According to [20], for a given SNR (speech-to-noise ratio), ACF decreases in intelligibility as the filter length increases, but with a length of 3 pitch periods, the intelligibility score does not decrease. For this purpose, the length of the filter (2L + 1 pitch periods) is on the order of three times the length of one pitch period, which is equivalent to 3072 samples, or 0.069 s.
ak: the filter coefficients that satisfy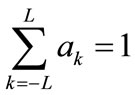 obtained from the Hamming windows shape [8]:
obtained from the Hamming windows shape [8]:
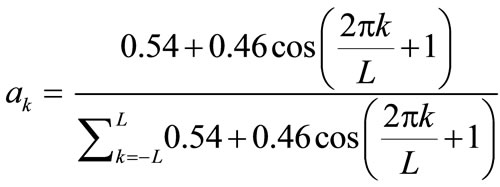
Nk: updated once in every pitch period.
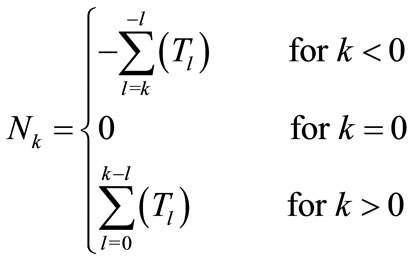
Tl: the pitch period that contains the points of the cry waveform that are multiplied by the filter coefficients ak.
The output of the filter is given by x(n):
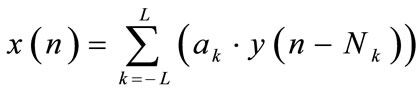
then, an estimated noise component is given by:
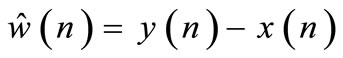
5.3. MMSE-Based Noise Estimator
The algorithm used to estimate the spectral density of the noise power is based on the minimum mean-squared error. The MMSE-based approaches have mainly been used in speech enhancement applications for reducing the additive non stationary noise without decreasing speech intelligibility [8]. According to [8], the MMSEbased spectral noise power estimator is much less demanding and at the same time robust to increasing noise levels. The authors state that it has been improved by using a soft speech probability presence (SPP) with fixed priors, instead of a voice activity detector (VAD). They show that the SPP approach results in less overestimation of the spectral noise power, and even less computational complexity.
The application of the MMSE-based noise estimator in cry signals is based on the assumption that the noise component of cries is more stationary than the periodic component signal, so the spectral noise power estimate of the previous frame is used for noise power ( ) estimation. In [21], a period of 0.5 s with noise only is used for initialization. To prevent initialization from being excluded from performance measurements, we use an ACF measure for initialization of the estimated noise in a period of 0.069 s, which corresponds to 3072 samples.
) estimation. In [21], a period of 0.5 s with noise only is used for initialization. To prevent initialization from being excluded from performance measurements, we use an ACF measure for initialization of the estimated noise in a period of 0.069 s, which corresponds to 3072 samples.
In our study, we replace the SPP with a periodic component probability presence (PCPP).
The MMSE implementation using the PCPP is as follows:
The power spectrum of the noisy signal is estimated on a frame-by-frame basis and observed over a time span of about 1 s. This is assuming that the periodic component xk (n) and the additive noise component wk(n) have zero mean and are independent.
 : cry signal,
: cry signal,
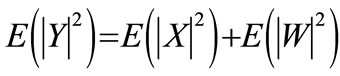
E(.): statistical expectation operator.
The spectral periodic component and noise power are defined respectively by:
 Then, the a posteriori SNR is
Then, the a posteriori SNR is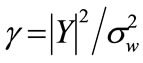 and the a priori SNR is
and the a priori SNR is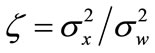 .
.
Assuming that both the periodic component and the noise DFT coefficients have a complex Gaussian distribution [21], the PCPP is obtained with Bayes’ theorem, assuming uniform priors 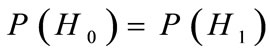 [9].
[9].
H0: absence of the periodic component; H1: presence of the periodic component.
The processing steps of the MMSE-based noise estimator are as follows:
• Estimate the PCPP:

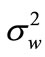 : Previous noise power estimate
: Previous noise power estimate
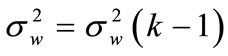
 , optimal noise level fixed a priori.
, optimal noise level fixed a priori.
Avoid the stagnation of the noise power update due to an underestimated noise power:
Recursive smoothing of the a posteriori PCPP:
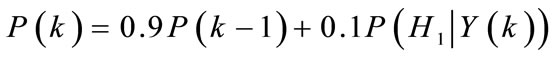
forcing the a posteriori PCPP estimate to be lower than 0.99:
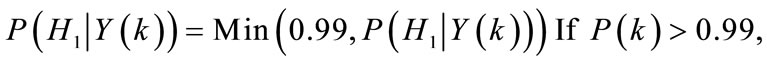 else
else
• 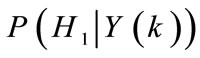
• Estimate the noise periodgram:
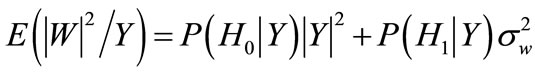
• 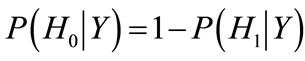
• Obtain the noise power spectral density via recursive smoothing with  [8]:
[8]:
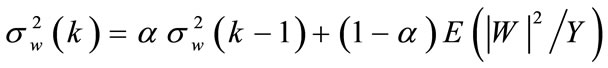
6. RESULTS AND ANALYSIS
Cry signals were classified and analyzed according to the type of disease afflicting the newborn and the gestational age of the newborn (full term, preterm).
Figure 3 shows that there is a large difference in the amount of noise estimated in cry signals using the two methods studied when used separately. These results confirm that these methods (the MMSE-based noise estimator and the ACF-based noise estimator) produce an over estimation of noise for both healthy and pathological cries. We also deduce from these results that noise estimation in cry signals using the MMSE-based noise estimator with ACF estimation initialization provides useful results for distinguishing between healthy and pathological cries. Consequently, we use this method for dysphonation estimation in healthy and pathologic cry signals.
The complete set of characteristics given in Table 2 was estimated for the entire database presented in Table 1, as explained in Section 4. The average percentage of dysphonic segments and unvoiced segments, and the percentage of mode changes by pathology are presented in Figure 4, and the average percentage of cry modes (dysphonia, hyperphonation, and phonation) by pathology and gestational age are presented in Figure 5.
Figure 4 shows that the estimated average percentages of dysphonic segments and unvoiced segments readily allow a distinction to be made between a healthy newborn and a sick newborn, especially for a full-term baby. These percentages are (17.2%, 1.84%) for meningitis, (25.6%, 5.13%) for vena cava thrombosis, (28.4%, 6.9%) for peritonitis, (36.3%, 3.1%) for lingual frenum, and (41.9%, 8.6%) for asphyxia respectively, compared to (16%, 1.3 %) for healthy cry samples.
The results shown in Figure 4 also indicate that the average percentages of dysphonic segments and unvoiced segments in the cry samples of healthy preterm newborns (19%, 2.8%) respectively are higher than those of healthy full-term newborns. This difference may be a result of the immature innervation of the larynx in preterm newborns. In this category of newborns, the average percentages of dysphonic and unvoiced segments contained in some pathological cry samples are a little higher, and are lower for other pathologies than those for healthy preterm newborns. These percentages are (23.5%,
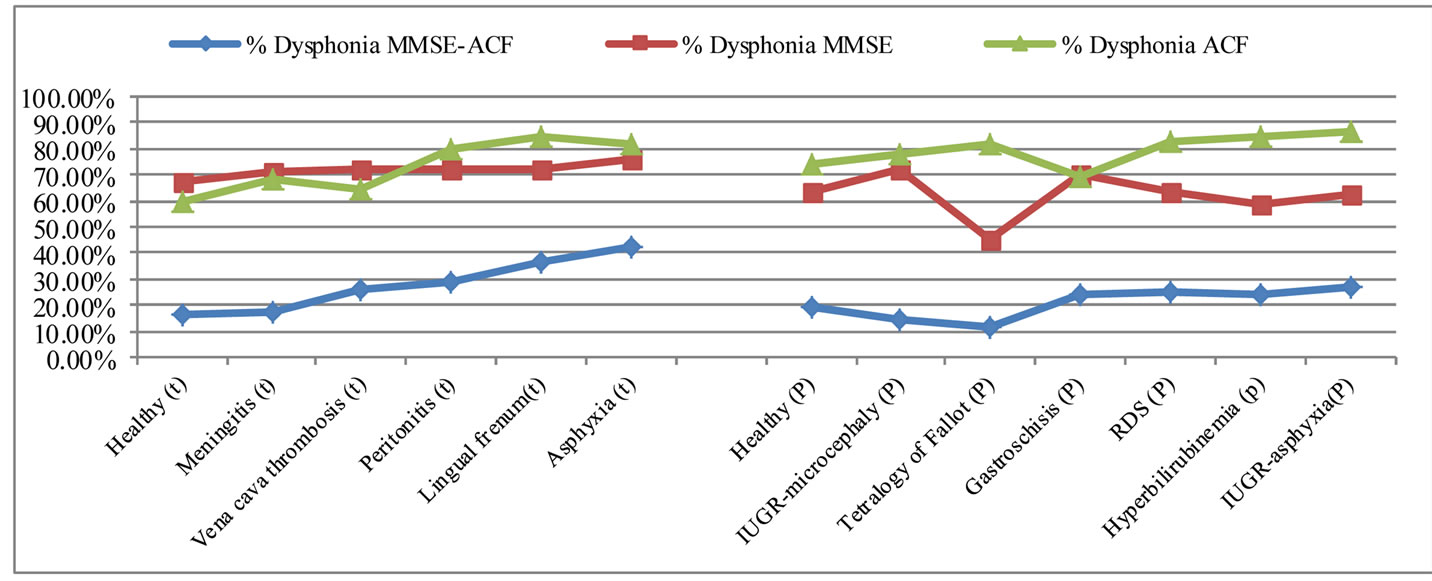
Figure 3. The average percentage of dysphonic segments by pathology and by measurement method.
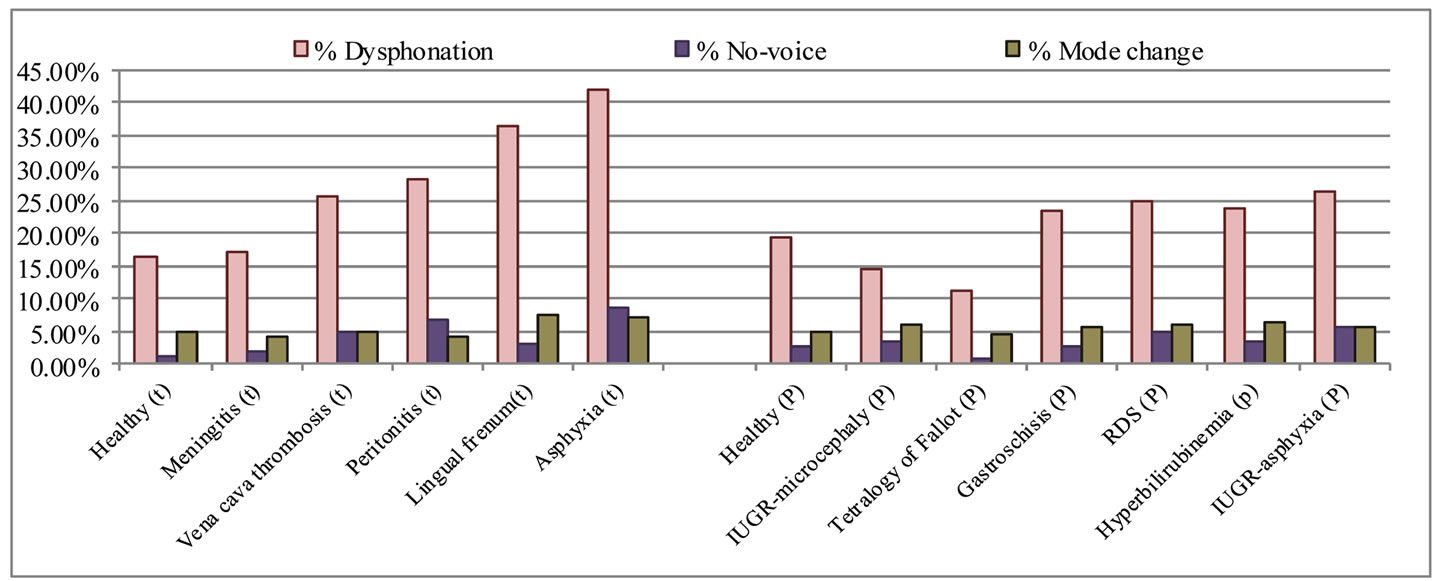
Figure 4. The average percentage of dysphonic and no-voice segments and the percentage of mode changes by pathology.
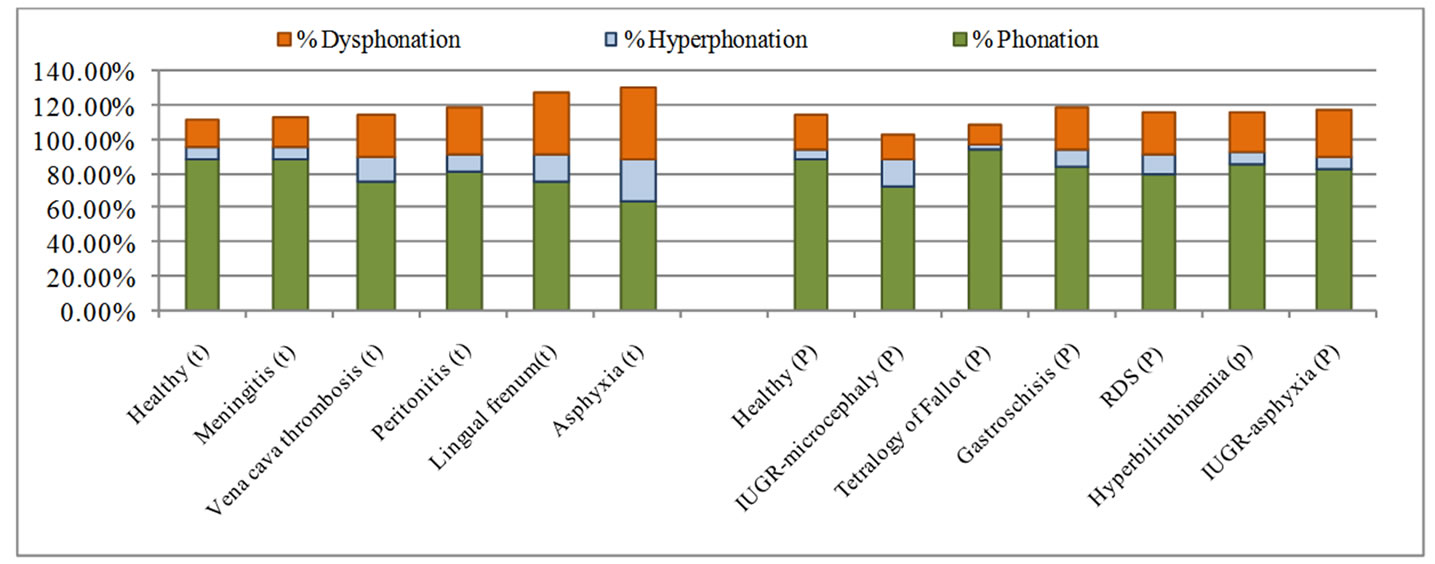
Figure 5. Distribution of cry modes (dysphonia, hyperphonation, phonation) by pathology.
2.6%) for gastroschisis, (25.1%, 4.9%) for RDS (respiratory distress syndrome), (23.9%, 3.5%) for hyperbilirubinemia, (26.5%, 5.7%) for IUGR—asphyxia, (11.4%, 0.9%) for the tetralogy of Fallot, and (14.5%, 3.6%) for IUGR—microcephaly respectively.
Concerning the mode-change characteristic, Figure 4 shows that this characteristic varies from one pathological condition to another, and are dependent on gestational age. The percentages we found for full-term newborn cries are (4.1%) in meningitis, (4.9%) in vena cava thrombosis, (4%) in peritonitis, (7.7%) in lingual frenum, and (7.3%) in asphyxia, while it was (4.9%) for healthy cry samples. For preterm newborns, the average mode change percentages were as follows: (5.7%) for gastroschisis, (6%) for RDS, (6.3%) for hyperbilirubinemia, (5.5%) for IUGR—asphyxia, (4.7%) for the tetralogy of Fallot, and (6%) for IUGR—microcephaly, while it was (4.8%) for healthy cry samples.
We performed ANOVA variance analysis for healthy and pathological cries to compare the behavior of the estimated characteristics (percentage of dysphonic and novoice segments, and of mode changes of cries) with respect to gestational age (full-term, preterm). We note from the results in Table 3 that there is significant statistical difference (F = 9.710, p < 0.05) between the average percentage of no-voice segments of healthy premature cries and that of full-term healthy cries, and also between the average percentage of mode changes in healthy premature cries and that of full-term healthy cries (F = 31.300, p < 0.05). For all other cases, no significant difference was found by gestational age. We can conclude that the percentage of no-voice segments and mode changes is dependent on gestational age for healthy cries, and that these characteristics are not dependent on gestational age, but on the pathology itself for pathological cries. The percentage of dysphonia is not dependent on gestational age in either healthy or pathological cries.
The distribution of cry modes (dysphonation, hyperphonation, and phonation) by pathology and by gestational age that we show in Figure 5 is designed to provide a better characterization of pathological and healthy cries. The results of this study show (Figures 4 and 5) that the cries of healthy full-term infants are phonic cries. Those of an infant with meningitis are slightly more hyperphonic and dysphonic. Those of an infant with vena cava thrombosis or peritonitis contain more hyperphonation, dysphonation, and no-voice segments than the cries of a healthy infant. Those of an infant with lingual frenum present with more hyperphonation and dysphonation, and more mode changes. The highest average percentages of all the estimated characteristics are found in the cries of an infant with asphyxia. In the preterm newborn category, we found that the cries of an infant with IUGR—microcephaly are characterized by more hyperphonic and fewer dysphonic segments than those of a healthy preterm newborn. The cries of an infant with gastroschisis are more hyperphonic and dysphonic, and have more mode changes than the cries of a healthy infant. We also found that the percentages of all the estimated characteristics are higher in cry signals related to the following pathologies: RDS, hyperbilirubinemia, IUGR—asphyxia compared to healthy preterm cries. In contrast, the percentages of all the estimated characteristics are lower in the cries of an infant with the tetralogy of Fallot.
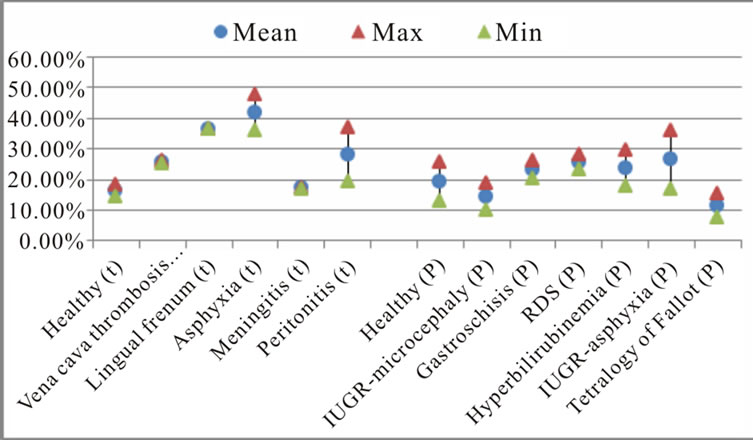
The calculation of the standard deviation for estimated characteristics by pathologies is shown in Figure 6. The results indicate a large dispersion for measured dysphonic segments in healthy preterm newborn, hyperbilirubinemia, asphyxia, Peritonitis, IUGR—asphyxia diseases. The best estimation of dysphonic segments is found in the case of healthy full-term, Vena cava thrombosis, Lingual frenum and meningitis diseases. For novoice segments estimation, the large dispersion is found in the case of asphyxia, Peritonitis, IUGR—asphyxia, IUGR—microcephaly and RDS. The best estimation of
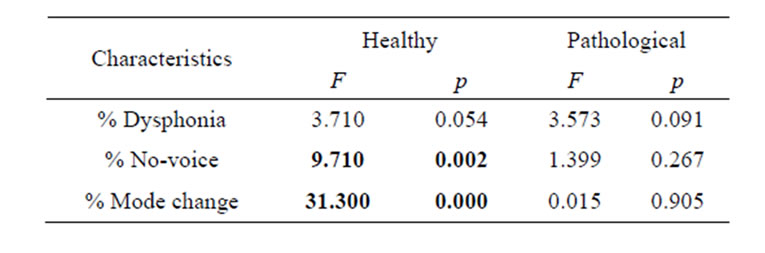
Table 3. Analysis of variance (ANOVA) according to gestational age.
 (a)
(a)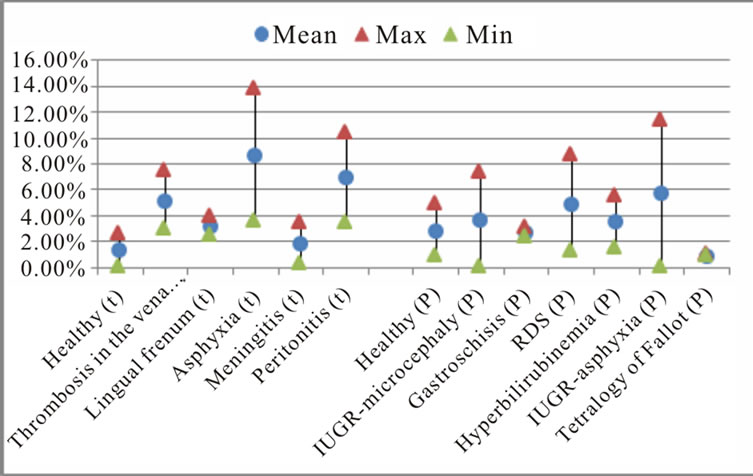 (b)
(b)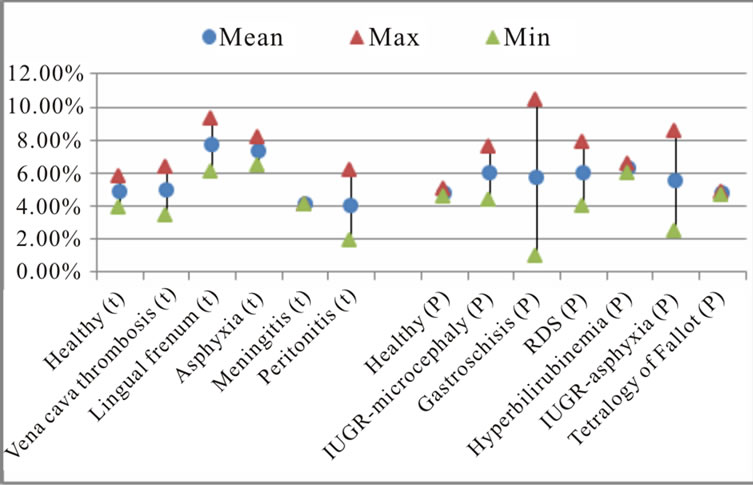 (c)
(c)
Figure 6. The mean percentage and standard deviation of (a) dysphonic segments; (b) no-voice and (c) mode change by pathologies.
no-voice segments is found in the case of Gastroschisis, tetralogy of Fallot and Lingual frenum diseases. For mode change segments estimation the large dispersion is found in the case of Gastroschisis and IUGR—asphyxia. The best estimation for this characteristic is found in healthy preterm newborn, meningitis, tetralogy of Fallot and hyperbilirubinemia diseases.
7. CONCLUSIONS
In this paper, we have presented one of the most important steps of our research project, which is the quantitative characterization of cry signals. We have performed an automatic estimation of the most promising characteristics associated with pathological conditions that have been reported in the literature. As a result, we have established quantitative relationships between the pathologies studied and the characteristics of the cries of newborns. We have also proved that some of the characteristics of healthy cries depend on gestational age, and other characteristics depend on the pathology itself.
The conclusion from the results we obtained is that there are clear differences between the characteristics of healthy cries and those of pathological cries in some pathologies, like asphyxia, gastroschisis, and vena cava thrombosis, RDS, hyperbilirubinemia, and IUGR—microcephaly. For each pathology studied, we have identified the most relevant characteristics for differentiating pathological cries from healthy cries. That differentiation can be used in diagnosing pediatric pathology.
However, it should be noted that validation of these results will require extension of the tests to a larger database containing a greater variety of pathologies and more subjects for each pathology.
8. ACKNOWLEDGEMENTS
We thank Dr. Barrington and members of the Neonatology group at Saint-Justine Hospital in Montreal (QC) for helping us to collect the Infant Cry database. This research has been funded by a grant from the Bill & Melinda Gates Foundation through the Grand Challenges Explorations Initiative.
REFERENCES
- LaGasse, L.L., Neal, A.R. and Lester, B.M. (2005) Assessment of infant cry: Acoustic cry analysis and parental perception. Mental Retardation and Developmental Disabilities, 83-93.
- Michelson, K., Todd de Barra, H. and Michelson, O. (2007) Sound spectrographic cry analysis and mothers perception of their infant’s crying. Nova Science Publishers, New York, 31-64.
- Singer, L.T. and Zeskind, P.S. (2001) Biobehavioral assessment of the infant. In: Zeskind, P.S. and Lester, B.M., Eds., Analysis of Infant Crying. The Guilford Press, New York, 149-166.
- Manfredi, C., D’Aniello, M. and Bruscaglioni, P. (1998) Acoustic measure of noise energy in patients having undergone a vocal fold operation. Proceedings of 9th European Signal Processing Conference, EUSIPCO 98, 2, 1141-1144,.
- Wasz-Hockert, O., Michelsson, K. and Lind, J. (1985) Twenty-five years of Scandinavian cry research in infant crying: Theoretical and research perspectives. Lester, B.M. and Boukydis, C.F.Z., Eds., Plenum Press, New York, 83-104.
- Kheddache, Y. and Tadj, C. (2013) Frequential characterization of healthy and pathological newborn cries. Submitted.
- Frazier, R.H., Siamaksamsam, L., Braida, D. and Oppenheim, A.V. (1978) Enhancement of speech by adaptive filtering. Signal Processing, 4, 354.
- Gerkmann, T. and Hendrik, R.C. (2012) Unbiased MMSEbased noise power estimation with low complexity and low tracking delay. IEEE Transactions on Audio, Speech, and Language Processing, 20, 1383-1393. doi:10.1109/TASL.2011.2180896
- Gerkmann, T. and Hendriks, R.C. (2011) Noise power estimation based on the probability of speech presence. IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, 16-19 October 2011, 145-148.
- Kasuya, H., Ogawa, S. and Kikuchi, Y. (1986) An adaptive comb filtering method as applied to acoustic analyses of pathological voice. ICASSP, Tokyo, 669-672.
- Frazier, R.H. (1975) An adaptive filtering approach to speech enhancement. Massachusetts Institute of Technology. http://hdl.handle.net/10945/20716
- Hirschberg, J., Dejonckereb, P.H., Hiranoc, M., Moric, K., Schultz-Coulon, H.J. and Vrtickae, K. (1995) Voice disorders in children. International Journal of Pediatric Otorhinolaryngology, 32, 109-125. doi:10.1016/0165-5876(94)01149-R
- Hirschberg, J. (1999) Dysphonia in infants. Elsevier Science, Ireland, 293-296.
- Cecchini, M., Lai, C. and Langher, V. (2010) Dysphonic newborn cries allow prediction of their perceived meaning. Infant Behavior & Development, 33, 314-320. doi:10.1016/j.infbeh.2010.03.006
- Lester, B.M. and LaGasse, L.L. (2008) Crying. Elsevier, Amsterdam, 80-90.
- Markel, J.D. (1972) The SIFT algorithm for fundamental frequency estimation. IEEE Transactions on Audio Electroacoustic, Au-20, 367-377.
- Lederman, D. (2010) Estimation of infants’ cry fundamental frequency using a modified SIFT algorithm. arXiv:1009.2796.
- Kasuya, H., Ogawa, S., Mashima, K. and Ebihara, S. (1986) Normalised noise measure to evaluate the pathological voice. Journal of the Acoustical Society of America, 1329- 1334. doi:10.1121/1.394384
- Manfredi, C., Tocchioni, V. and Bocchi, L. (2006) A robust tool for newborn infant cry analysis. Proceedings of the 28th IEEE, 509-512.
- Lim, J., Oppenhem, A.V. and Barida, L.D. (1978) Evaluation of an adaptive comb filtering method for enhancing speech degraded by white noise addition. IEEE ASSP, 26, 354-358.
- Hendriks, R.C., Heusdens, R. and Jensen, J. (2010) MMSEbased noise PSD tracking with low complexity. ICASSP, 4266-4269.

