Journal of Biomedical Science and Engineering
Vol. 5 No. 9 (2012) , Article ID: 22422 , 9 pages DOI:10.4236/jbise.2012.59064
Analysis of the variability of auditory brainstem response components through linear regression
![]()
1Laboratory of Biomedical Engineering, Faculty of Electrical Engineering, Federal University of Uberlândia, Uberlândia, Brazil
2Cybernetic Intelligence Research Group, School of Systems Engineering, University of Reading, Reading, UK
3Catholic University of São Paulo, São Paulo, Brazil
Email: *khelinenaves@yahoo.com.br
Received 8 June 2012; revised 5 July 2012; accepted 18 July 2012
Keywords: Auditory Brainstem Response; Hearing Loss; Linear Regression
ABSTRACT
The analysis of the Auditory Brainstem Response (ABR) is of fundamental importance to the investigation of the auditory system behavior, though its interpretation has a subjective nature because of the manual process employed in its study and the clinical experience required for its analysis. When analyzing the ABR, clinicians are often interested in the identification of ABR signal components referred to as Jewett waves. In particular, the detection and study of the time when these waves occur (i.e., the wave latency) is a practical tool for the diagnosis of disorders affecting the auditory system. In this context, the aim of this research is to compare ABR manual/visual analysis provided by different examiners. Methods: The ABR data were collected from 10 normal-hearing subjects (5 men and 5 women, from 20 to 52 years). A total of 160 data samples were analyzed and a pairwise comparison between four distinct examiners was executed. We carried out a statistical study aiming to identify significant differences between assessments provided by the examiners. For this, we used Linear Regression in conjunction with Bootstrap, as a method for evaluating the relation between the responses given by the examiners. Results: The analysis suggests agreement among examiners however reveals differences between assessments of the variability of the waves. We quantified the magnitude of the obtained wave latency differences and 18% of the investigated waves presented substantial differences (large and moderate) and of these 3.79% were considered not acceptable for the clinical practice. Conclusions: Our results characterize the variability of the manual analysis of ABR data and the necessity of establishing unified standards and protocols for the analysis of these data. These results may also contribute to the validation and development of automatic systems that are employed in the early diagnosis of hearing loss.
1. INTRODUCTION
The study of the Auditory Brainstem Response (ABR) is an important tool for the evaluation of the auditory capacity and plasticity, as well as for the investigation of the integrity of the structures involved in the transmission of electrical impulses through the auditory system [1-3]. The classical process of analysis of the ABR consists in the identification of relevant temporal and morphological features of the Jewett waves. The waves I, III and V are characterized by presenting the most evident positive peaks in the whole signal, and they are usually employed for the evaluation of the integrity of the auditory pathway [4-6]. When the objective of the ABR exam is the investigation of electro-physiological thresholds, the wave V is the most relevant, as it remains more evident in the signal even under low power intensity (e.g., 20 dB) [1]. Currently, ABR analysis can be employed in distinct contexts. For instance, it can be used for the determination of electrophysiological thresholds in children, diagnosis of neural dysfunctions [2,7], intra-operative monitoring [8], and cardiac surgery, staging of coma, detection of degenerative diseases that produce hearing impairment, and in the diagnosis of disorders that cannot be identified by tonal audiometry (e.g., in some motor deficiencies) [9]. The most common use of ABR analysis in clinical practice is the diagnosis of early hearing loss, particularly in newborns and children. According to the World Health Organization (WHO), 1.4 million of children worldwide suffer from hearing problems. Olusanya and et al. [10] recently estimate that 855 babies are born every day in developing countries with hearing loss with little expectation of being diagnosed. A late diagnosis may hamper the cognitive development of patients, language skills, consequently resulting in delay of the learning and emotional processes [11,12]. Another relevant application of ABR analysis is in the identification of diseases in the auditory nerve, such as tumor (schwannoma), neuropathy, dys-synchrony and degenerative diseases affecting the brainstem.
In most clinical situations, the ABR waves are identified through a manual/visual assessment. The process of identification of the ABR components is dependent upon many variables, such as the employed experimental protocol, the clinical conditions of the subject and more importantly, on the previous experience of the examiner. The visual analysis of the ABR yields inconsistency in the results obtained by distinct examiners [13-15]. This makes the process of identification of the Jewett waves prone to error and can contribute to the erroneous diagnosis of some diseases. The consequences of a non-precise diagnosis are numerous, for instance, leading to inadequate treatment, or even delaying discovery of a serious illness. In this context, given the importance of the ABR analysis and the subjective nature of its interpretation, the main objective of this study is to compare the results of the visual analysis of the ABR obtained by distinct examiners. The examiners focused their analysis on classical features (i.e., temporal and morphological) manually extracted from the signal, as it is practiced in the clinical routine. The results of this study quantify the variability found in the responses given by the examiners. Such results can be useful for highlighting the necessity of continuing training and standardization of procedures used for the interpretation of the ABR in the clinical practice. In the future, they can also be employed in the development of more accurate intelligent algorithms used for the automatic detection of the ABR waves.
2. METHODS
In total, ten subjects (five men and five women), with mean age of 36 years (minimum = 20 and maximum = 52), participated in the experiments. Subjects were selected based on their performance in standard exams that verify the integrity of the auditory system. The following exams were applied: otoscopy, pure tone audiometry and speech audiometry (WRS—Word Recognition Score and SRTSpeech Recognition Threshold) for the confirmation of the hearing thresholds. The audiometer model AC40 (Interacoustics, USA), duly calibrated according to recent international technical norms was employed. Pure tone thresholds were considered as normal from 0 to 25 dB HL (Hearing Level), in the frequencies of 250 Hz, 500 Hz, 1 kHz, 2 kHz, 3 kHz, 4 kHz, 6 kHz and 8 kHz. Prior to data collection, the subjects signed a Consent Form approved by the Ethical Committee of the Federal University of Uberlândia (Project number: 160/06). Four examiners (E1, E2, E3 and E4) with experience in audiology participated in this study. All of them have theoretical and practical experience in the detection and analysis of ABR as shown in Table 1.
2.1. Data Collection
ABR data were collected by means of the commercial amplifier Bio-logic’s Evoked Potential System (EP), from Bio-Logic, USA. Prior to the positioning of electrodes on the scalp of the subject, the skin was properly cleansed and abraded. The electrodes were positioned according to the International 10 - 20 System proposed by Jasper in 1958 [16]. Four electrodes were placed, M1 (mastoid right) and M2 (mastoid left), Cz (active) and Fz (ground) [28]. And two channels of information were recorded. Channel 1(M1-Cz), representing information detected from the right ear and Channel 2 (M2-Cz) from the left ear. The signals were collected at a sample rate of 37,101 Hz, meaning that the time interval between two consecutive samples was of 0.027 ms. Each signal, resulting from an auditory stimulus, lasted 13.824 ms (or 512 samples). In this study we work with the averaged ABR, which is obtained by averaging 2000 ABR samples. This process can be seen as a filter that reduces background activity and highlights the signal of interest. The auditory stimuli (clicks) were used for the 80, 60, 40 and 20 dBHL power intensities for each ear. The stimulus rate was set to 21 cycles/s, as commonly use in clinical practice. The data were analyzed later in MatLab (Mathworks). The examiners evaluated a total of 160 ABR samples. The data were collected from 10 subjects. For each subject we collected ABR samples by stimulating both the left and right ears with auditory stimuli of 80, 60, 40 and 20 dBHL (hearing level). This procedure was repeated twice for each ear. The examiners following their individual criteria and professional experience, and the analysis consisted in the visual identification of the waves I, II, III, IV and V. All pairs of the results obtained by distinct examiners were statistically compared.
2.2. Data Analysis
2.2.1. Descriptive Statistics
With the aim of understanding the obtained differences between responses of the examiners, we analyzed the discrepancies found for the latency of each Jewett wave (I, II,
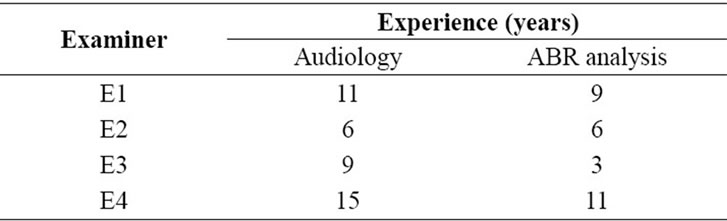
Table 1. Experience in years for each examiner.
III, IV and V). The discrepancies were categorized into four groups: null (no difference at all), small (<0.1 ms), moderate (between 0.1 ms and 0.2 ms) and large (>0.2 ms). The frequency (number of occurrences) was estimated for each category.
2.2.2. Model-Based Analysis
When studying the relationship between results of pair of examiners, it is expected that a linear regression provide a good fit if there is complete agreement in the analyses, as showed in the Figure 1 that depicts the relation between examiners E2E3. With this hypothesis in mind we studied the variability of the parameters of a linear model (y = ß0+ ß1·x) using Bootstrap [17,18]. The dependent variable y represents the data obtained from an examiner for a particular Jewett wave and the independent variable x represents the data from another examiner for the same wave. Ideally, if the examiners fully agree in their responses then ß0 = 0 and ß1 = 1. In practice both ß0 and ß1 varies, and one of the aims of this research was to estimate this variability and its implications for the practical interpretation of ABR. In order to estimate the coefficients ß0 and ß1 of a relationship between examiners, linear regression was employed.
The following sequence of steps was employed for the estimate of the variability of the coefficients ß0 and ß1:
1) The residuals (R) of the model fitted to the data were obtained as R = Y – Z where Y is the data and Z the value estimated by the regression. Note that the data here is a set of bi-dimensional data points of the form (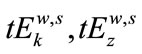 ), where
), where  (
(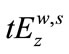 ) is the manually detected occurrence time in milliseconds by examiner k(z), for wave w and stimulus intensity s. In this study w = 1, …, V; k = z = 1, …, 4; s = 80, 60, 40, 20 dBHL. Figure 1(a) illustrates the data points (Y) for the results of wave V when comparing the detection time of examiners 2 and 3, for all stimulus intensity and all subjects that participated in the research. The estimated linear model (Z) for these data is shown in Figure 1(b), whereas the residue R is shown in Figure 1(c).
) is the manually detected occurrence time in milliseconds by examiner k(z), for wave w and stimulus intensity s. In this study w = 1, …, V; k = z = 1, …, 4; s = 80, 60, 40, 20 dBHL. Figure 1(a) illustrates the data points (Y) for the results of wave V when comparing the detection time of examiners 2 and 3, for all stimulus intensity and all subjects that participated in the research. The estimated linear model (Z) for these data is shown in Figure 1(b), whereas the residue R is shown in Figure 1(c).
2) At this stage, the residuals R (see example in Figure 1(c)) are re-sampled, with replacement, by means of Bootstrap. A total of N = 800 new samples of R, so-called, 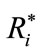 , i = 1, …, N, are generated. Each
, i = 1, …, N, are generated. Each  is then added to Z generating therefore new samples
is then added to Z generating therefore new samples  from which it is possible, through linear regression (
from which it is possible, through linear regression (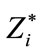 ), to estimate the coefficients
), to estimate the coefficients  and
and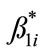 . The histogram of each of the set of parameters represents the empirical probability distribution function of ß0 and ß1. From it, it is possible to obtain information about the variability (e.g., standard deviation) of the parameters of the linear model.
. The histogram of each of the set of parameters represents the empirical probability distribution function of ß0 and ß1. From it, it is possible to obtain information about the variability (e.g., standard deviation) of the parameters of the linear model.
The application of the algorithm, based on the Bootstrap, to calculate the confidence interval for the mean is given in the following example [19]:
1) Experiment: Conduct the experiment. Assuming that the sample is X = (–2.41, 4.86, 6.06, 9.11, 10.20, 12.81,

Figure 1. Linear Regression for examiners E2E3 for the wave V. (a) is the mark of the wave for the following intensity: “○” is the mark for 80 dBHL, “+” for 60 dBHL, “¯” for 40 dBHL and “*” for the 20 dBHL; (b) is the linear model; and (c) is the residuals.
13.17, 14.10, 15.77, 15.79) of size 10, with mean µ = 9.946.
2) Re-sampling: Using a pseudo-random number generator, select a sample, with replacement, from the 10 values of X. Thus we estimate the bootstrap sample X* = (9.11, 9.11, 6.06, 13.17, 10.20, –2.41, 4.86, 12.81, –2.41, 4.86). Note that some of the original sample values appear more than once, while others do not appear at all.
3) Estimate the average of X*: the mean for all 10 values of X* is calculated (µ* = 6.54).
4) Repetition: Repeat step 2, N times, to obtain the total of N means, µ1*, ..., µN*. For example, N = 1000.
5) Estimate the approximate distribution of µ*: Sort, in ascending order, them mean values estimated in step 4 to obtain: µ(1)* ≤ µ(2)* ≤ ... ≤ µ(1000)*, where µ(k) is the k-th smallest value of µ1*, ..., µN*.
6) Confidence Interval: the confidence interval desired, (1 – α) 100%, is given by: [µ(q1)*, µ(q2)*], where q1 is the integer part of (Nα/2) and q2 = N – q1 + 1. For α = 0.05 and N = 1000, q1 = 25 and q2 = 976.
3. RESULTS
3.1. Data Consistency Analysis
The first step in signal analysis is the visual inspection of the collected data. This can help the detection of outliers, patterns and possible inconsistencies in the data set. Figure 2 shows a graph of the intensity (in dBHL) versus the latency (in ms) provided by the four examiners, for all subjects, and for waves I, II, III, IV and V. The results include the analysis of 160 ABR samples. In the graph the shaded areas represent the area limited by the minimum and maximum latency values obtained for the analysis of each wave and each intensity. In addition, the standard deviation of the samples is presented together with a central tendency (i.e., the mean) and its confidence interval estimated through the Bootstrap [17]. The visual inspection of the graph reveals that the latency increases as the intensity decreases. This behavior is in accordance with findings reported in the literature, discussing the differences in the ABR patterns as function of the intensity [2,20-22]. Another relevant observation is that at the 80 dBHL intensity, the ABR signal has a relatively high signal-to-noise ratio, which allows for a more precise evaluation of the waves, as they are more evident. For this reason, at the high intensity the latency is an important discriminatory feature of the Jewett waves. Note in the graph that at this intensity there is no overlap between the shaded areas and the central tendencies of the waves. However, as we decrease the intensity, the visual detection of some waves is impaired. For instance, the examiners could not visually detect the presence of the waves I and II at the 20 dBHL intensity. The wave III is more evident in the intensities of 80, 60 and 40 dBHL. In the 20 dBHL intensity the number of detections was significantly smaller. The waves IV and V remain evident for all intensities, but they tend to overlap at the 20 dBHL, as the detection of the waves IV and V gets more complex (be-

Figure 2. Latency values obtained for each Jewett wave as function of the intensity (dB HL). The shaded areas are bounded by the minimum and maximum values of latency found for each wave. The standard deviation, the central tendency and its confidence interval are also presented.
cause the signal amplitude for this intensity tends to decrease). The number of detections is significantly lower at low intensity. This happens because of the way the neurons are activated by low intensity. In general waves I, II and III are less evident at lower intensity, different from waves IV and V, which are evident even at low intensity, being therefore employed in auditory threshold detection studies. As a consequence of this we have less manual detections, mainly for waves I, II and III and this could interfere on the confidence intervals estimated for the parameter of the linear model.
The experimental results illustrated in Figure 2 are in accordance with those found in the literature [2,21,23,24], showing, therefore, the consistency of our data set and the visual detection of the Jewett waves executed by the examiners.
3.2. Descriptive Statistics
Following the consistency verification of the data provided by the examiners we carried out a data discrepancy analysis in order to verify, by means of descriptive statistics, the discrepancies in the visual detection of the Jewett waves. The main difficulty in this analysis was to set thresholds for the latency, which would allow for the data categorization into distinct groups (i.e. null, small, moderate and large). For this, we employed the patterns of reproducibility of ABR data suggested by Hood [1,2], Vannier [24] and Burkard and Don [25]. These authors consider variations in the latency values between 0.1 and 0.2 ms as acceptable for subjects with normal hearing and without neurological impairment. Based on this we categorized the data as described in Table 2 shows the frequency found for each category. This analysis revealed that, if we consider the null and small categories as an acceptable standard for ABR analysis we have 81.62% of agreement between the examiners. This number can increase to 96.21% if we also consider the moderate category. Differences larger than 0.2 ms, which are not acceptable at all, represent 3.79% of the total samples.
3.3. Data Variability Analysis
In order to assess the variability of the visual analysis of examiners we applied the model-based approach described in Section 2.2.2. Table 3 and Figure 3 depict the obtained results. In the linear model, the parameter ß0 is the intercept and has the same unit as the input signal (ms). The dimensionless parameter ß1, the slope, is responsible for modulating the independent variable of the model. If ß0 = 0 and ß1 = 1 then there is complete agreement between the analysis of pair of examiners. Small values for ß1 could indicate a disagreement between the classifications of a particular wave. For instance, E1 could classify a given wave as I whereas E2 could classify it as II. Large

Table 2. Analysis of the categorized discrepancy between results provided by examiners. The number of occurrences is presented for each category. The discrepancies were categorized into four groups and the number of occurrences (frequency) estimated for each category: null (no difference at all), small (<0.1 ms), moderate (between 0.1 ms and 0.2 ms), large (>0.2 ms).
values of ß0 (e.g., >0.2 ms) represent significant systematic discrepancies in the analysis of a particular wave. The results shown in Table 3 suggest that there was no disagreement between wave classifications for all cases, because the values of ß1 are close to 1.0 with a small standard deviation, indicating little variability of this parameter. Based on the analysis of the mean and standard deviation of our data we found the worst results for the wave IV (ß1 = 0.94 ± 0.088) and the best for the wave V (ß1 = 0.99 ± 0.013). In contrast, some large values and variability were found for the parameter ß0 in the analysis of waves I, III and IV. For the cases of waves I and III, there were significant differences between a pair of examiners, whereas for the wave IV there was a general disagreement, showing therefore the difficulty in the visual detection of this wave. The probability distributions for ß0 and of ß1 highlights the discrepancies found for wave IV. As expected, ß0 and ß1 are closer to the ideal values in the analysis of wave V, which is the less affected by the changes in the intensity.
4. DISCUSSION AND CONCLUSION
The main objective of this study was to verify whether there were discrepancies in the visual analysis of ABR, provided by four seasoned examiners, and how they could be quantified by means of descriptive statistics and model analysis. The motivation of this research comes from our own clinical experience that have shown that subjectivity and lack of standards in the interpretation of ABR is common and can lead to erroneous and/or inaccurate diagnosis of disorders that affect the auditory system. This subjectivity is also reported in many published research works [15,26].

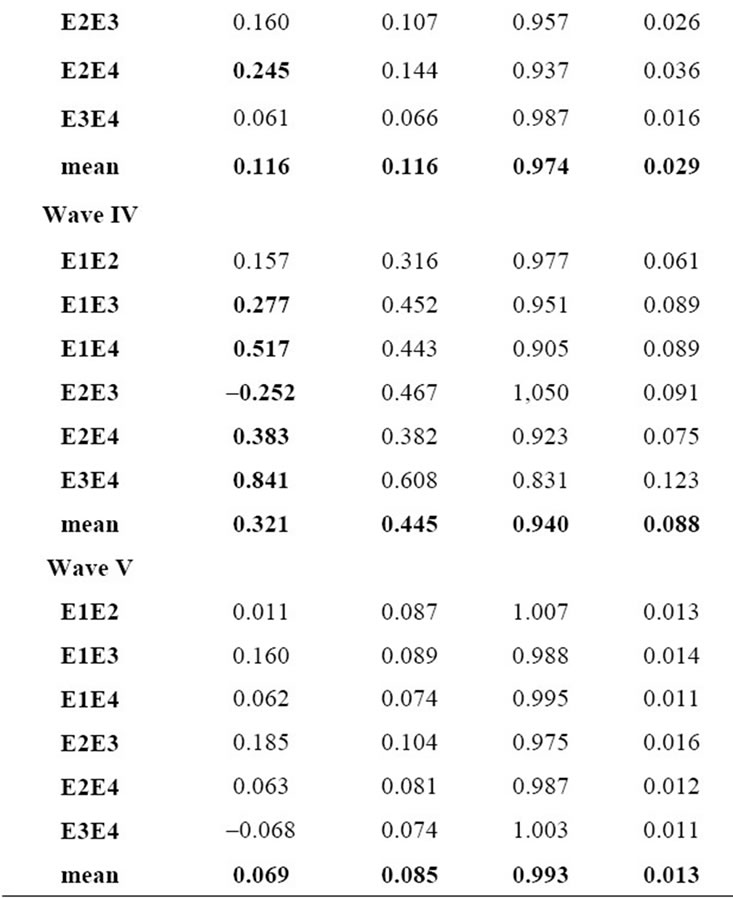
Table 3. Mean and standard deviation of the coefficients of the linear model.
The first stage of our analysis was to verify whether the latency values obtained by the examiners were compatible with those reported in the literature. The results presented in Figure 2 depict all information provided by the examiners. They are consistent with patterns described in other studies. For the intensity of 80 dBHL we obtained the following mean values for the Jewett waves: 1.56 ms (wave I), 3.77 ms (wave III) and 5.53 ms (wave V). Antonelli [23] reported that the normal average values of latency in the 100 dB SPL (Sound Pressure level) intensity for the waves I, III and V, are respectively equal to 1.54 ms, 3.73 ms and 5.52 ms. Hernandez [21] evaluated the behavior of waves generated at different power intensities. In the intensities of 90, 70, 50, 30, 10 dBHL the wave V was always found, and the average latency values were 1.49 ms, 3.73 ms and 5.53 ms, for the waves I, III and V, respectively. These results indicate the coherence in the visual analysis provided by the examiners in this research. Another problem we had to face in our analysis was in the establishment of acceptable threshold levels for the variation of the latency of Jewett waves. There is some disagreement in the literature, as some authors report a variation of 0.1 ms as acceptable, whereas others report 0.2 ms [2,5,15,24,26]. In addition, some studies concerning the development of automatic systems for the detection of Jewett waves have considered values of latency between 0.1 ms and 0.2 ms as acceptable for the validation of these systems [27-30]. Therefore, we employed simple descriptive statistics for categorization of the discrepancies between results provided by the examiners. The discrepancies were categorized into four groups and the number of occurrences (frequency) estimated for each category: null (no difference at all), small (<0.1 ms), moderate (between 0.1 ms and 0.2 ms), large (>0.2 ms). This analysis showed that discrepancies larger than 0.2 ms, which are not acceptable, accounted for 3.79% of the total samples. Moderate differences accounted for 14.6%, which means that more than 18% of the investigated samples presented variations larger than 0.1 ms. The figures highlight the necessity of standardization in the process of analysis of ABR, as in some cases moderate and large discrepancies can interfere with the accurate diagnosis of some neurological disorders.
In the study proposed here we used Regression Analysis as a tool for characterizing the relationship between results obtained from distinct examiners. The classical process of identification of Jewett waves is obtained by means of the visual inspection of peaks and their occurrence time in the Auditory Brainstem Evoked Potential waveform. Therefore, discrepancies between examiners may happen. Thus, Regression Analysis, together with the use of the Bootstrap for the assessment of the variability of the parameters of the liner model, is a suitable tool for detecting such discrepancies and their variability. From
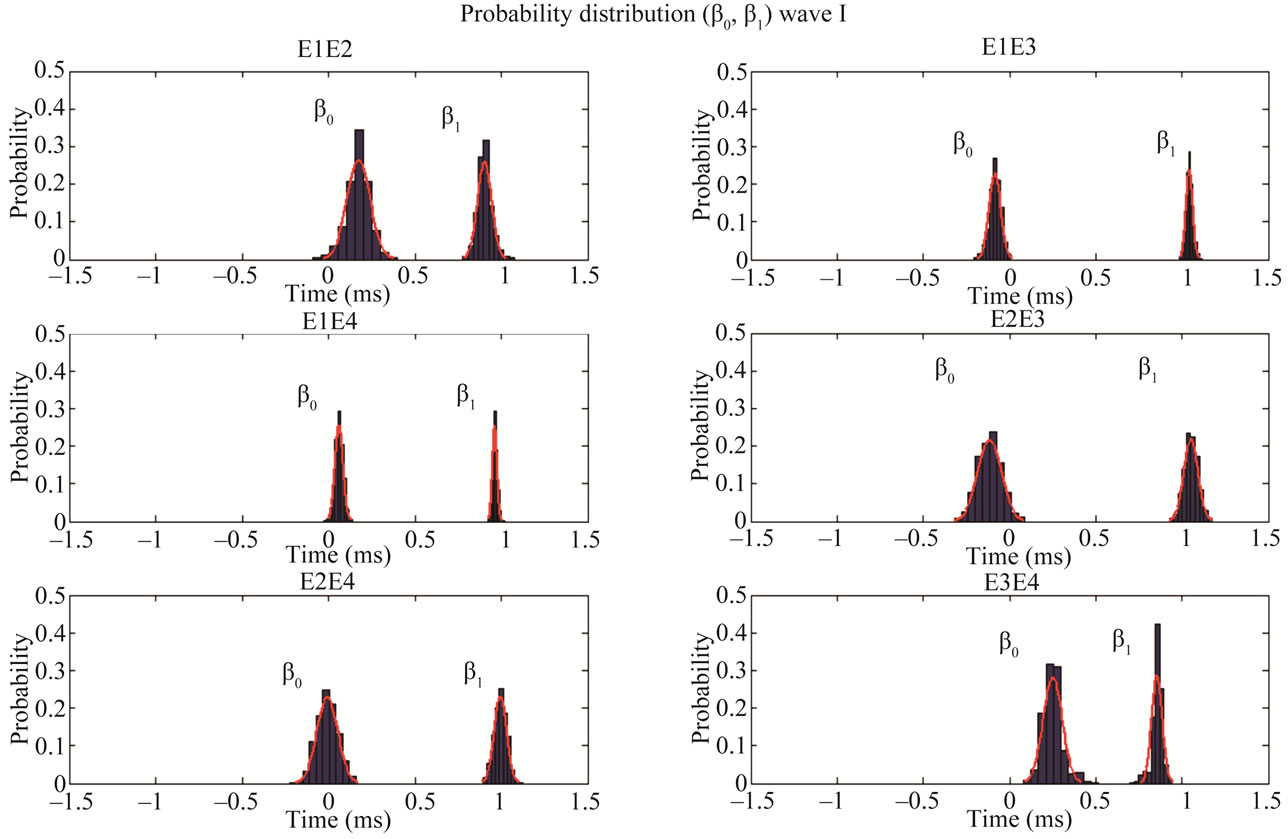
Figure 3. Probability distribution of the parameters ß0 (left) and ß1 (right) for the wave I for distinct pair of examiners. The parameter ß1 suggests that all examiners are in agreement regarding the analysis of the wave I, and the parameter ß0 indicates that the discrepancy is less than 0.112 ms (mean value) for all pairs. Note that only the pair E3E4 shows a significant discrepancy 0.254 ms.
the best of our knowledge, this type of analysis has not been employed for the characterization of the relationship between results obtained from distinct examiners and for different Jewett waves (I, II, III, IV and V).
An important and innovative aspect of this research was the investigation of the variability of the discrepancies of the analyses of the examiners through the parameters (ß0 and ß1) of a linear model using Bootstrap. We concluded that the parameter ß1 can be employed for checking the agreement between classifications of a particular Jewett wave. If the value of ß1 is either small or large it can indicate that two examiners classified the wave differently. The parameter ß0 can be interpreted as the accuracy of the latency value. Ideally, it should be null, however in this study it should take into account the acceptable limits of variation found for the latency of each wave with its standard deviations. This study shows that the variability of results obtained among the examiners is not the same for all waves. For instance, for the waves I, II and III the mean difference was 0.11 ms, for the wave V of 0.08 ms, and for the wave IV of 0.40 ms. The number of examiners that participated in this study is small, although it is in accordance to other similar investigations (e.g. Hunt 1986, [31]) the authors recruited three examiners for participation in practical experiments. This may affect our results, for instance the Regression to the mean effect can interfere with the estimated values for ß0 and ß1.
A simple way to avoid such a problem would be to significantly increase the number of examiners involved in the research. Although pairwise analysis such as the one employed in this study is often found in literature, it has some limitations: the order of the comparison my influence upon the final results; there is an assumption that each paired comparison is independent; generally, different pairs may have different total number of comparesons. The probability distribution functions (PDFs) shown in Figure 3 were obtained from data analyzed by only four examiners. Possibly the increase of the number of examiners would result in more accurate PDFs that could better represent the data. This is an important limitation of our study that should be addressed in future investigations.
The results can be seen as practical scales that can be used in the assessment of automatic systems that detect Jewett waves, and also as practical tools to ease the interpretation and visual analysis provided by examiners. Another important aspect of our results is that they account for the ABR data collected from stimulus signals with intensities ranging from 20 dB HL to 80 dB HL and for all waves that could be detected at these intensities. The contribution of this study in the Evoked Potentials Analysis is supported by our strategy for data analysis that can:
1) Provide an interpretation for the parameters (ß0 and ß1) of the linear model. These two parameters can give us complementary information. In our study ß0 gives us an estimate of the accuracy of the agreement between examiners, whereas the analysis of its variability, estimated by means of the Bootstrap, is a measure of the precision of such agreement. The closer ß0 is to zero the smaller are the differences between examiners when visually detecting the time when the Jewett waves occurs. ß1, the angular coefficient, gives us information on the agreement of the type of Jewett wave (I, II, III, IV and V) labeled by examiners. A value of ß1 close to one is an indicative that the examiners agreed in the labeling of a specific Jewett wave.
2) Provide a model representing the relationship between the agreements of distinct examiners. The model parameters together with their variability can be used in generative models, for generating new data sets which takes into account the underlying differences between examiners. Such differences may be due to subjective variables such as the effect of the duration of the data analysis on the concentration of the examiner, clinical experience, the visual detection method selected by the examiner. Variables which are inherent to the process of data collection, such as noise, may also contribute to increasing the differences of results obtained by examiners.
Generative models like this can be used for generating known data, with different features controlled by the variability of the original data set, which can be employed for assessing systems developed for the automatic detection of Jewett waves. Descriptive statistics methods could have been used in the data analysis. However, these methods might not highlight any potentially interesting structure in the data to the extent that the linear regression could if the regression reveals that the linear dependence is only an approximation. In other words, if the data (or residuals) follow the Gaussian distribution then most likely the descriptive statistics such as Intraclass Correlation Coefficients (ICC) and Bland-Altman plots would convey the same information as the regression. However, if the linear regression assumptions are violated the regression plots can reveal it, the descriptive stats may not. In this study we don’t know the pattern of the response expected since it is not described in literature and the linear model was adequate.
5. ACKNOWLEDGEMENTS
The authors would like to thank the Brazilian government, which through the Foundation for Research Support of the Minas Gerais State (FAPEMIG), has provided financial support for this research (Project FAPEMIG—TEC APQ-2481-6.01/07). Text for this section.
![]()
![]()
REFERENCES
- Eggermont, J.J. (2007) Electric and magnetic fields of synchronous neural activity. In: Burkard, R.F., Eggermont, J.J. and Don, M., Eds., Auditory evoked potentials: Basic principles and clinical application. Lippincott Williams & Wilkins, Baltimore, 2-21.
- Hood, L.J. (1998) Clinical applications of the auditory brainstem response. Singular Publishing Group Inc., San Diego.
- Nodarse, E.M., Abalo, M.C.P. and López, G.S. (2006) Métodos de pesquisaje de las pérdidas auditivas a edades tempranas. Revista Electrónica de Audiologia, 3, 9-18.
- Hall, J.W. (2006) New handbook of auditory evoked responses. Pearson Edication Inc., Boston.
- Misulis, K.E. (2003) Potencial evocado de spehlmann. 2nd Edition, Revinter Ltda, Rio de Janeiro.
- Schwanke, D. (2000) Exame de potenciais evocados auditivos utilizando processador digital de sinais—DSPEA. Dissertação de Mestrado, Instituto de Informática, Universidade Federal do Rio Grande do Sul, Rio Grande do Sul.
- Sininger, Y.S. (2007) Source analysis of auditory evoked potentials and fields. In: Burkard, R.F., Eggermont, J.J. and Don, M., Eds., The use of auditory brainstem response in screening for hearing loss and audiometric threshold prediction. Lippincott Williams & Wilkins, Baltimore, 254- 274.
- Martin, W.H. and Shi, B.Y.B. (2007) Intraoperative monitoring. In: Burkard, R.F., Eggermont, J.J. and Don, M., Eds., Auditory evoked potentials: Basic principles and clinical application. Lippincott Williams & Wilkins, Philadelphia, 355-384.
- Katz, J. (1989) Audiologia clínica. 3rd Edition, Manole, New York.
- de Garcia, B.G., Gaffney, C., Chacon, S., et al. (2011) Overview of newborn hearing screening activities in Latin America. Revista Panamericana de Salud Pública, 29, 145-152.
- Chomsky, N. (2005) Three factors in language design. Linguistic Inquiry, 36, 1-22. doi:10.1162/0024389052993655
- Fitcha, W.T., Hauserb, M.D. and Chomsky, N. (2005) The evolution of the language faculty: Clarifications and implications. Cognition, 97, 179-210.
- Junqueira, C.A.O. and Colafêmina, J.F. (2002) Investiga- ção da estabilidade inter e intra-examinador na identifycação do P300 auditivo: Análise de erros. Revista Brasileira de Otorrinolaringologia, 68, 468-478.
- Pediatrics, A.A.O. (1999) Newborn and infant hearing loss: Detection and Intervention. Pediatricis, 103, 527-530. doi:10.1542/peds.103.2.527
- Vidler, M. and Parker, D. (2004) Auditory brainstem response threshold estimation: Subjective threshold estimation by experienced clinicians in a computer simulation of the clinical test. International Journal of Audiology, 43, 417-429. doi:10.1080/14992020400050053
- Böcker, K.B.E., van Avermaete, J.A.G. and Van den BergLenssen, M.M.C. (2005) The international 10-20 system revisited: Cartesian and spherical co-ordinates. Brain Topography, 6, 231-235.
- Efron, B. and Tibshirani, R.J. (1998) An introduction to the bootstrap, Chapman & Hall/CRC, Boca Raton.
- Johnson, R.W. (2001) An introduction to the bootstrap. Journal of Royal Statistical Society: Series D, 23, 49-54.
- Andrade, A.O. (2005) Decomposition and analysis of electromyographic signals. Ph.D Thesis, School of Systems Engineering, Department of Cybernetics, The University of Reading, Reading.
- Don, M., Ponton, C.W., Eggermont, J.J., et al. (1998) The effects of sensory hearing loss on cochlear filter times estimated from auditory brainstem response latencies. Acoustical Society of America, 104, 2280-2289. doi:10.1121/1.423741
- Hernández, J.D., Castro, F.Z. and Prat, J.J.B. (2003) Normalización de los potenciales evocados auditivos del tronco cerebral I: Resultados en una muestra de adultos normoyentes. Revista Electrónica de Audiologia, 2, 13-18.
- De Montes, C., Manjón, M., vinuales, M. et al. (2002) Estúdio morfológico de los potenciales evocados auditivos de tronco del encéfalo. Influência de la posición del eletrodo de referência. Revista de Neurologia, 34, 84-88.
- Antonelli, A.R., Bellotto, R. and Grandori, F. (1987) Audiologic diagnosis of central versus eighth nerve and cochlear auditory impairment. Audiology, 4, 209-226. doi:10.3109/00206098709081550
- Vannier, E., Adam, O. and Motsch, J.-F. (2002) Objective detection of brainstem auditory evoked potentials with a priori information from higher presentation levels. Artificial Intelligence in Medicine, 25, 283-301. doi:10.1016/S0933-3657(02)00029-5
- Burkard, R.F. and Don, M. (2007) The auditory brainstem response.In: Burkard, R.F. Don, M. and Eggermont, J.J., Eds., Auditory evoked potencials: Basic principles and clinical applications. Lippincott Williams & Wilkins, Baltimore, 229-253.
- Don, M. (1989) Quantitative approaches for defining the quality and threshold of auditory brainstem responses. IEEE Engineering in Medicine & Biology Society, 2, 761- 762.
- Acyra, N., Ozdamarb, O. and Guzelis, C. (2006) Automatic classification of auditory brainstem responses using SVM-based feature selection algorithm for threshold detection. Engineering Applications of Artificial Intelligence, 19, 209-218.
- Boston, J.R. (1989) Automated Interpretation of brainstem auditory evoked potentials: A prototype system. IEEE Transactions on Biomedical Engineering, 36, 528- 532. doi:10.1109/10.24254
- Bradley, A.P. and Wilson, W.J. (2004) On wavelet analysis of auditory evoked potentials. Clinical Neurophysiology, 115, 1114-1128. doi:10.1016/j.clinph.2003.11.016
- Jacquin, A., Causevic, E., John, E.R., et al. (2006) Optimal denoising of brainstem auditory evoked response (BAER) for Automatic peak identification and brainstem assessment. Proceedings of the 28th IEEE EMBS Annual International Conference, New York, 30 August-3 September 2006, 1723-1726.
- Hunt, R.J. (1986) Percent agreement, Pearson’s correlation, and kappa as measures of inter-examiner reliability. Journal of Dental Research, 65, 128-130.
NOTES
*Corresponding author.
#In memoriam.

