Intelligent Information Management
Vol. 4 No. 4 (2012) , Article ID: 21407 , 8 pages DOI:10.4236/iim.2012.44018
A State Estimation Method for Sound Environment System with Unknown Observation Mechanism by Introducing Fuzzy Inference
Department of Management Information Systems, Prefectural University of Hiroshima, Hiroshima, Japan
Email: {orimoto, ikuta}@pu-hiroshima.ac.jp
Received January 21, 2012; revised April 23, 2012; accepted June 14, 2012
Keywords: State Estimation; Sound Environment System; Unknown Observation Mechanism; Fuzzy Inference
ABSTRACT
The observed phenomena in real sound environment system often contain uncertainty such as the additional external noise with unknown statistics. Furthermore, there is complex nonlinear relationship between the specific signal and the observations, and it cannot be exactly expressed in any definite functional form. In these situations, it is one of reasonable analysis methods to treat the objective sound environment system as a fuzzy system. In this study, a state estimation method for a specific signal under the existence of an unknown observation mechanism and external noise of unknown statistics is proposed by introducing fuzzy inference. The effectiveness of the proposed theoretical method is experimentally confirmed by applying it to the actually observed data in the sound environment.
1. Introduction
The observation data in actual sound environment system exhibit various types of fluctuation characteristics, and these often contain uncertainty. For example, the observed signal is inevitably contaminated by the concurrent external noise (i.e., background noise) of arbitrary distribution type of unknown statistics. In this situation, in order to evaluate the specific signal based on the observed noisy data, it is indispensable to introduce some unified state estimation methods adaptable to various uncertainty caused by complexity, diversity and unknown property existing in the actual sound environment systems.
Though several state estimation methods have been proposed up to now, these state estimation algorithms have been realized by introducing the additive model of the specific signal and the external noise under an assumption of known statistics of the external noise [1-8]. On the other hand, it is necessary to pay our attention on the fact that the observation data in the sound environment system are often contain uncertainty due to several causes. For example, the observation in sound environment system can be generally expressed in an additive model of the specific signal and the background noise on energy scale by using the additive property of acoustic energy. However, for an assessment and a countermeasure of the sound environment, several evaluation quantities such as  (averaged energy on a decibel scale),
(averaged energy on a decibel scale),  ((100 – x) percentile level, x = 5, 10, 50, 90, 95) and
((100 – x) percentile level, x = 5, 10, 50, 90, 95) and  (maximum level), etc. for the specific signal, have to be considered. There are complex nonlinear and uncertain relations between the noise evaluation quantities of the specific signal and the background noise, and it is difficult in general to find the functional relationship between them. Furthermore, it is actually difficult to know in advance statistical properties of the background noise. Therefore, in order to remove effects of the background noise from the observed evaluation quantities under existence of the background noise, standard state estimation method based on an additive model of the specific signal and the background noise of known statistics cannot be applied. In this situation, the relationship between the observed evaluation quantities and the background noise has to be generally considered as a system model with unknown observation mechanism. In our previous study, a method for estimating the specific signal for the sound environment system with uncertainty has been proposed by adopting the conditional probability distribution reflecting the correlation information between the specific signal and observation as the system characteristics [9]. Though the method proposed previously can be applied effectively to actual complex sound environmental system with uncertainty, it needs a lot of priori information on the statistics of the specific signal and observations.
(maximum level), etc. for the specific signal, have to be considered. There are complex nonlinear and uncertain relations between the noise evaluation quantities of the specific signal and the background noise, and it is difficult in general to find the functional relationship between them. Furthermore, it is actually difficult to know in advance statistical properties of the background noise. Therefore, in order to remove effects of the background noise from the observed evaluation quantities under existence of the background noise, standard state estimation method based on an additive model of the specific signal and the background noise of known statistics cannot be applied. In this situation, the relationship between the observed evaluation quantities and the background noise has to be generally considered as a system model with unknown observation mechanism. In our previous study, a method for estimating the specific signal for the sound environment system with uncertainty has been proposed by adopting the conditional probability distribution reflecting the correlation information between the specific signal and observation as the system characteristics [9]. Though the method proposed previously can be applied effectively to actual complex sound environmental system with uncertainty, it needs a lot of priori information on the statistics of the specific signal and observations.
In this study, a practical state estimation method for sound environment systems with unknown observation mechanism of contamination by the background noise of unknown statistics is proposed by introducing the fuzzy inference in a different form the previous methods. More specifically, a membership function is first introduced for the unknown mechanism of a sound environment system. Next, by applying a fuzzy inference for the relationship between the observed data (i.e., evaluation quantities observed under the existence of a background noise) and the state variable (i.e., evaluation quantities of the specific signal), a state estimation algorithm is derived, based on Bayes’ theorem as the fundamental principle of the estimation in the similar manner to the previously reported estimation method [4,5]. The effectiveness of the proposed method is experimentally confirmed by applying it to the estimation of evaluation quantities for road traffic noise under existence of a background noise.
2. State Estimation for Sound Environment System with Unknown Observation Mechanism
2.1. Formulation of Sound Environment System by Introducing Fuzzy Inference
Let 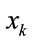 and
and 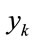 be state variable and observation at a discrete time k for sound environment systems. It is assumed that the mutual relationship between
be state variable and observation at a discrete time k for sound environment systems. It is assumed that the mutual relationship between  and
and  is unknown. For example, the observations in sound environment are inevitably contaminated by the external noise (i.e., background noise) of arbitrary distribution type. In general, by using the additive property of acoustic energy, the observation energy under the existence of external noise can be expressed in an additive model of the specific signal and the background noises in energy scale. However, for the stochastic evaluation quantities:
is unknown. For example, the observations in sound environment are inevitably contaminated by the external noise (i.e., background noise) of arbitrary distribution type. In general, by using the additive property of acoustic energy, the observation energy under the existence of external noise can be expressed in an additive model of the specific signal and the background noises in energy scale. However, for the stochastic evaluation quantities:  and
and  which are used in the evaluation of actual sound environment, there are complex nonlinear relations between the evaluation quantities of the specific signal and the observed evaluation quantities. For an assessment of sound environment, it is often necessary to investigate the fluctuation of evaluation quantities for the specific signal. Therefore, the evaluation quantities of the specific signal at the k-th short time interval and the observed evaluation quantities at the k-th time interval have to be regarded as the unknown state variable
which are used in the evaluation of actual sound environment, there are complex nonlinear relations between the evaluation quantities of the specific signal and the observed evaluation quantities. For an assessment of sound environment, it is often necessary to investigate the fluctuation of evaluation quantities for the specific signal. Therefore, the evaluation quantities of the specific signal at the k-th short time interval and the observed evaluation quantities at the k-th time interval have to be regarded as the unknown state variable 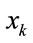 and the observation
and the observation  respectively. Since it is difficult in general to find functional relationship between the state variable
respectively. Since it is difficult in general to find functional relationship between the state variable  and the observation
and the observation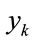 , the relationship between
, the relationship between 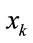 and
and  has to be considered as a sound environment system with unknown observation mechanism. In this study, the following IF-THEN rule is introduced for the unknown mechanism of the sound environment system:
has to be considered as a sound environment system with unknown observation mechanism. In this study, the following IF-THEN rule is introduced for the unknown mechanism of the sound environment system:
Rule 1: IF  is
is  THEN
THEN 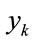 is
is 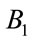
Rule 2: IF  is
is  THEN
THEN 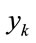 is
is 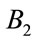
…
Rule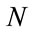 : IF
: IF  is
is  THEN
THEN  is
is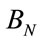 , (1)
, (1)
where 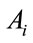 and
and 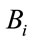 (i = 1, 2,
(i = 1, 2,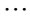 ,
,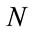 ) denote fuzzy sets corresponding to the several local state spaces of
) denote fuzzy sets corresponding to the several local state spaces of  and
and , and have membership functions
, and have membership functions 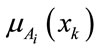 and
and 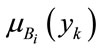 (i = 1, 2,
(i = 1, 2, , N). For example,
, N). For example,  ,
,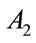 ,
, ,
, are fuzzy sets describing the local
are fuzzy sets describing the local 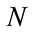 regions with vague borders such as “very low level”, “low level”, …, “very high level”, for the fluctuation range of the sound level
regions with vague borders such as “very low level”, “low level”, …, “very high level”, for the fluctuation range of the sound level . Applying fuzzy inference to (1),
. Applying fuzzy inference to (1), 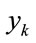 is given by [10]
is given by [10]
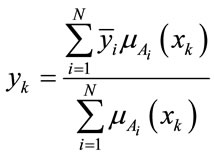 (2)
(2)
where  is the value at which the membership function
is the value at which the membership function  achieved its maximum value. Furthermore, as the membership function
achieved its maximum value. Furthermore, as the membership function , the Gaussian type, defined by [10]
, the Gaussian type, defined by [10]
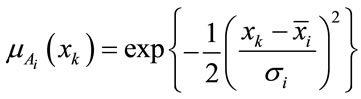 (3)
(3)
where  and
and  are parameters, is adopted.
are parameters, is adopted.
In the next section, an estimation method for the state variable  of the specific signal based on the recursive observation
of the specific signal based on the recursive observation 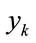 is derived. Though the parameter
is derived. Though the parameter  in (3) can be generally given based on the prior information (or, through trial and error), it can be regarded as unknown constant parameter
in (3) can be generally given based on the prior information (or, through trial and error), it can be regarded as unknown constant parameter  (=
(= for every i) and estimated simultaneously with the state variable
for every i) and estimated simultaneously with the state variable  by introducing the following simple dynamic model:
by introducing the following simple dynamic model:
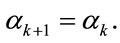 (4)
(4)
2.2. Estimation Algorithm by Introducing Bayes’ Theorem
In order to derive an estimation algorithm for a state variable , with an arbitrary distribution, we focus our attention on Bayes’ theorem for the conditional probability density function (abbr. pdf). Since the parameter
, with an arbitrary distribution, we focus our attention on Bayes’ theorem for the conditional probability density function (abbr. pdf). Since the parameter  is also unknown, the conditional pdf of
is also unknown, the conditional pdf of  and
and 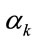 must be considered.
must be considered.
 (5)
(5)
where  is a set of observation data up to k-th time. The conditional joint pdf of the state variable
is a set of observation data up to k-th time. The conditional joint pdf of the state variable , the parameter
, the parameter  and the observation
and the observation  in (5) can be generally expanded in a statistical orthogonal expansion series [4,5]:
in (5) can be generally expanded in a statistical orthogonal expansion series [4,5]:
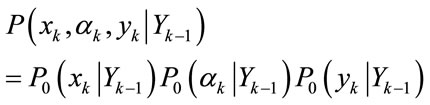
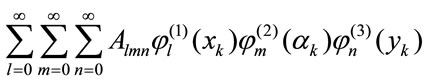 (6)
(6)
After substituting (6) into (5), taking the conditional expectation of the function 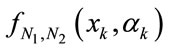 and using the orthonormal condition for the function
and using the orthonormal condition for the function  and
and , through a similar calculation process to that used in a previously reported estimation method [4,5], the estimate of an arbitrary polynomial function
, through a similar calculation process to that used in a previously reported estimation method [4,5], the estimate of an arbitrary polynomial function 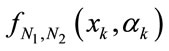 of
of 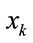 and
and 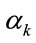 of
of 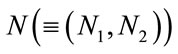 -th order can be derived in an infinite series expression, as follows:
-th order can be derived in an infinite series expression, as follows:
 (7)
(7)
with
 (8)
(8)
The three functions ,
, 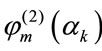 and
and 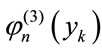 are the orthonormal polynomials of degrees l, m and n, with weighting functions
are the orthonormal polynomials of degrees l, m and n, with weighting functions  and
and , which can be artificially chosen as the pdfs describing the above dominant parts of the actual fluctuation, or as well-known standard pdfs such as Gaussian or Gamma distribution functions. All the coefficients
, which can be artificially chosen as the pdfs describing the above dominant parts of the actual fluctuation, or as well-known standard pdfs such as Gaussian or Gamma distribution functions. All the coefficients  are appropriate constants in the case when the function
are appropriate constants in the case when the function 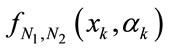 is expressed in a series expansion form using
is expressed in a series expansion form using  and
and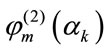 :
:
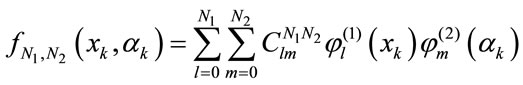 (9)
(9)
As a concrete example of a standard pdf, the wellknown Gaussian distribution is adopted:
 (10)
(10)
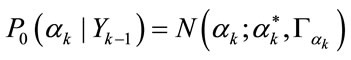 (11)
(11)
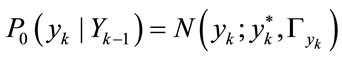 (12)
(12)
with
 ,
,


 . (13)
. (13)
Then, the orthonormal polynomials with three weighting pdfs in (10)-(12) can be given in terms of the wellknown Hermite polynomials [11].
 (14)
(14)
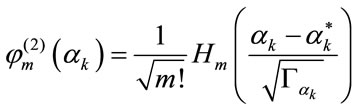 (15)
(15)
 (16)
(16)
Using (2) and (3), the two variables 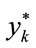 and
and 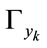 in (13) can be expressed as:
in (13) can be expressed as:
 (17)
(17)
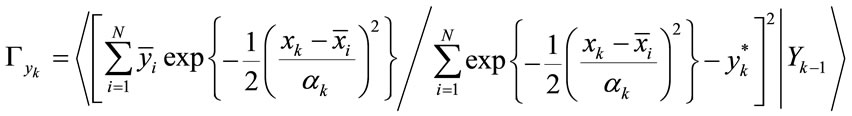 (18)
(18)
Furthermore, each expansion coefficient 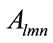 defined by (8) can be expressed as
defined by (8) can be expressed as
 (19)
(19)
The variables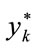 ,
,  and the expansion coefficient
and the expansion coefficient  in (17), (18) and (19) are given by the predictions of
in (17), (18) and (19) are given by the predictions of 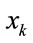 and
and  at a discrete time
at a discrete time  (i.e., the expectation value of arbitrary functions of
(i.e., the expectation value of arbitrary functions of 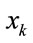 and
and 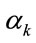 conditioned by
conditioned by ). Consequently, the unified algorithm for estimating the state variable can be obtained. In two special cases when
). Consequently, the unified algorithm for estimating the state variable can be obtained. In two special cases when 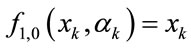 and
and , estimates related to mean and variance of the state variable are expressed as follows:
, estimates related to mean and variance of the state variable are expressed as follows:
 (20)
(20)
 (21)
(21)
with
 (22)
(22)
Furthermore, by focusing on a polynomial function:
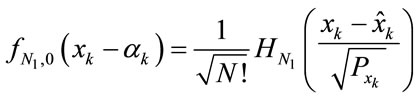 (23)
(23)
the estimate for the expansion coefficient reflecting the non-Gaussian property of the state variable is given by Equation (24), where 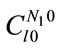
 are coefficients satisfying the following relationship:
are coefficients satisfying the following relationship:
 (25)
(25)
Finally, in order to derive the prediction step necessary to perform the recurrence estimation, the fuzzy inference is introduced again. More specifically, after dividing the fluctuation range of  into
into  fuzzy regions
fuzzy regions 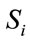 (i =1, 2,
(i =1, 2, , M) with membership functions
, M) with membership functions 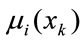 (i = 1, 2,
(i = 1, 2,  , M), by creating fuzzy rules from given data sets, the following IF-THEN rules are obtained.
, M), by creating fuzzy rules from given data sets, the following IF-THEN rules are obtained.
Rule 1: IF  is
is 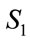 THEN
THEN 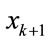 is
is 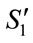
Rule 2: IF  is
is 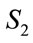 THEN
THEN  is
is 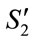
………………………………………..
Rule M: IF  is
is  THEN
THEN 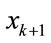 is
is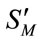 , (26)
, (26)
where  is one of M fuzzy sets
is one of M fuzzy sets  (i = 1, 2,
(i = 1, 2, , M), and is decided adequately based on the prior information or measured data. For example, after evaluating two degrees for conformity of data pair
, M), and is decided adequately based on the prior information or measured data. For example, after evaluating two degrees for conformity of data pair 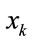 and
and  to
to 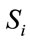 and
and , by selecting
, by selecting  so as to maximize the synthesized degree of these two degrees, each rule of (26) can be assigned. By applying the center average defuzzification formula [12] to (26), a state transition model can be determined as
so as to maximize the synthesized degree of these two degrees, each rule of (26) can be assigned. By applying the center average defuzzification formula [12] to (26), a state transition model can be determined as
 (27)
(27)
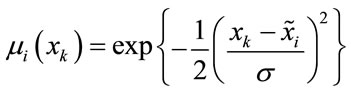 , (28)
, (28)
where 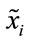 is the value at which the membership function
is the value at which the membership function 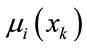 achieved its maximum value, and
achieved its maximum value, and  is a constant parameter. By considering (4) and (27), the prediction algorithm can be given for an arbitrary polynomial function
is a constant parameter. By considering (4) and (27), the prediction algorithm can be given for an arbitrary polynomial function  of
of  and
and  of
of  -th order, as follows:
-th order, as follows:
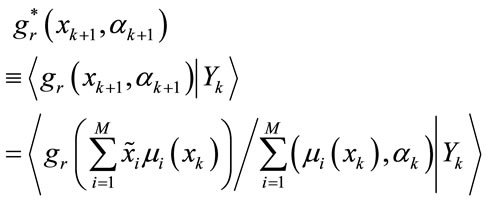 (29)
(29)
The above prediction can be evaluated by the estimates at a discrete time k. Therefore, by combining (7) with (29), the recurrence estimation of  and
and  can be achieved.
can be achieved.
3. Application to Evaluation Quantities of Road Traffic Noise
Finally, complete content and organizational editing be-
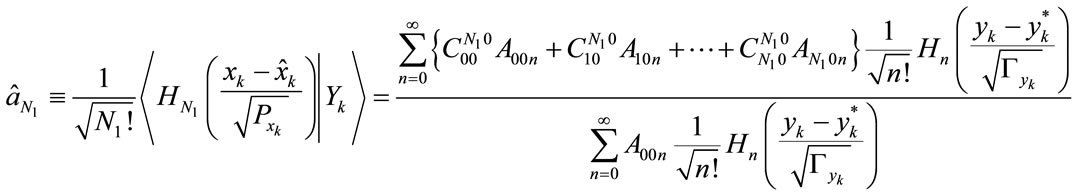 (24)
(24)
fore formatting. Please take note of the following items when proofreading spelling and grammar:
In order to confirm experimentally the validity of the proposed method, it is applied to the actually observed data in the sound environment. As the specific signal, the road traffic noise becoming one of the aggravating environmental noise pollution is adopted. By regarding the observations on several evaluation quantities: 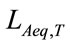 and
and , measured by use of sound level meter with the frequency characteristic of A weight and the time interval
, measured by use of sound level meter with the frequency characteristic of A weight and the time interval  min. under existence of a background noise, as observations
min. under existence of a background noise, as observations , and regarding the evaluation quantities:
, and regarding the evaluation quantities: 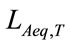 and
and 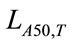 (
( min) for only the specific signal as the state variables
min) for only the specific signal as the state variables , the fluctuation of
, the fluctuation of  is estimated on the basis of
is estimated on the basis of .
.
By dividing the fluctuation ranges of 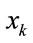 and
and  into 3 fuzzy regions,
into 3 fuzzy regions, : “low level”,
: “low level”,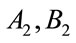 : “middle level”, and:
: “middle level”, and: 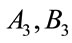 “high level”, (1) is expressed as follows:
“high level”, (1) is expressed as follows:
Rule 1: IF  is
is 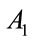 THEN
THEN 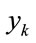 is
is 
Rule 2: IF 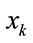 is
is 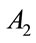 THEN
THEN 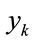 is
is 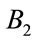
Rule 3: IF  is
is 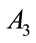 THEN
THEN  is
is . (30)
. (30)
Furthermore, (2) is expressed as follows:
 . (31)
. (31)
In the above formula, the three parameters are decided as:
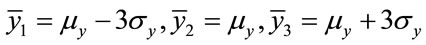 (32)
(32)
where  and
and  are mean and standard deviation of
are mean and standard deviation of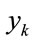 . Furthermore, by determining the parameters of (28) so as to express the whole distribution of actual measured data of
. Furthermore, by determining the parameters of (28) so as to express the whole distribution of actual measured data of 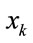 as precisely as possible, the membership functions in Figures 1 and 2 are obtained for
as precisely as possible, the membership functions in Figures 1 and 2 are obtained for 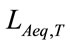 and
and .
.
For comparison, the previously reported method [4,5] without considering fuzzy theory is also applied to the observed data after introducing a linear system model:
 , (33)
, (33)
 (34)
(34)
In (33) and (34), 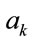 and
and  are unknown parameters to be estimated simultaneously with the state variable
are unknown parameters to be estimated simultaneously with the state variable . Furthermore,
. Furthermore,  and
and  are random noises with mean 0 and variance 1. Tow parameters F and G are estimated by use of auto-correlation technique [4]. The estimation results for
are random noises with mean 0 and variance 1. Tow parameters F and G are estimated by use of auto-correlation technique [4]. The estimation results for  and
and 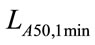 of the road traffic noise by observing
of the road traffic noise by observing 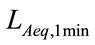 and
and  under existence of a background noise are shown in Figures 3 and 4. The proposed method estimates precisely the fluctuation of the state variables. On the other hand, there are great
under existence of a background noise are shown in Figures 3 and 4. The proposed method estimates precisely the fluctuation of the state variables. On the other hand, there are great
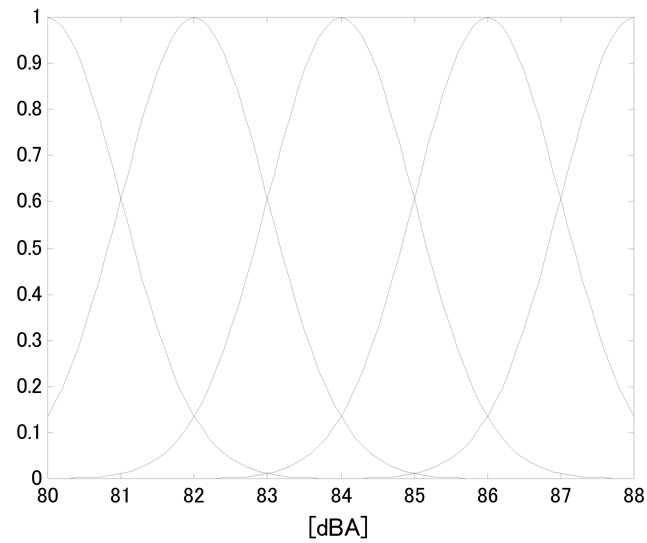
Figure 1. Membership function for LAeq,1min.

Figure 2. Membership function for LA50,1min.

Figure 3. A comparison between the proposed method and the previous method for state estimation results of LAeq,1min for the road traffic noise based on the observation of LAeq,1min under existence of a background noise.

Figure 4. A comparison between the proposed method and the previous method for of state estimation results of LA50,1min for the road traffic noise based on the observation of LA50,1min under existence of a background noise.
discrepancies between the true values and the estimates based on the linear system of (33) and (34). The squared sum of the estimation error is shown in Table 1. It is obvious that the proposed method based on the introduction of fuzzy theory shows more accurate estimation than the results based on the usual linear system model like (33) and (34).
Next, as one of reasonable methods for determining the three parameters in (31), by introducing an unknown parameter  in (32) as:
in (32) as:
 (35)
(35)
and focusing our attention on the Bayes’ theorem for the conditional pdf of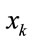 ,
, 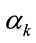 and
and :
:
 , (36)
, (36)
after introducing a dynamical model for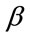 :
:
 (37)
(37)
an estimation algorithm for the state variable can be derived through the same calculation process as (7). The estimation results by the proposed method with introduction of the unknown parameter 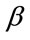 are shown in Figures 5 and 6. In general, the results by the proposed method using (35) estimate precisely the peak values of fluctuation than the results by the method using (32). A comparison between the squared sum of the estimation error in two cases is also shown in Table 1. The estimated results by the algorithm with unknown parameter
are shown in Figures 5 and 6. In general, the results by the proposed method using (35) estimate precisely the peak values of fluctuation than the results by the method using (32). A comparison between the squared sum of the estimation error in two cases is also shown in Table 1. The estimated results by the algorithm with unknown parameter  show more accurate estimation than the results based on the method with the fixed value of
show more accurate estimation than the results based on the method with the fixed value of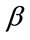 .
.
Furthermore, the proposed method with flexibility is applied to estimate 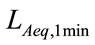 of the road traffic noise based on the observation of
of the road traffic noise based on the observation of  under existence of
under existence of
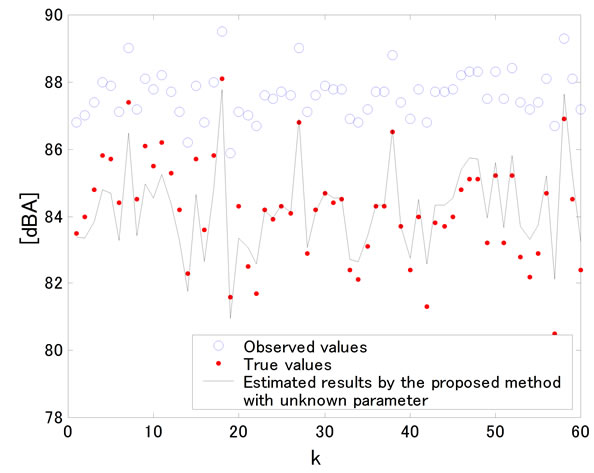
Figure 5. A state estimation result of LAeq,1min for the road traffic noise based on the observation of LAeq,1min by the proposed method with unknown parameter.
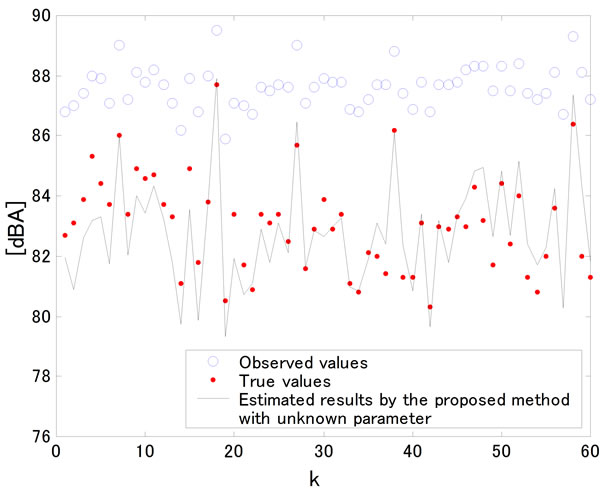
Figure 6. A state estimation result of LA50,1min for the road traffic noise based on the observation of LA50,1min by the proposed method with unknown parameter.
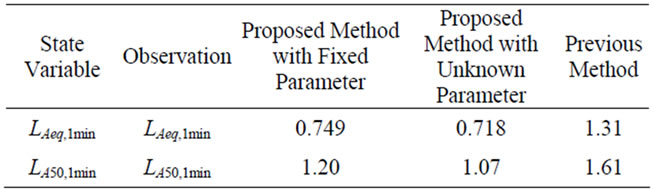
Table 1. Root-mean squared error of the estimation (in dBA).
the background noise as a trial. It must be noticed that the observation and the specific signal to be estimated are different evaluation quantities in this case. Figure 7 shows a comparison between the proposed method and the previous method, and the estimated result by use of the proposed method with unknown parameter is shown in Figure 8. The root mean squared error of the estimation is shown in Table 2. From these results, the effectiveness of the proposed method has been confirmed even
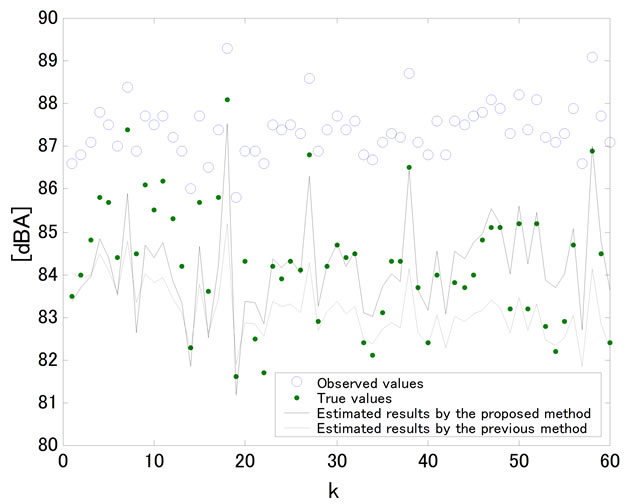
Figure 7. A comparison between the proposed method and the previous method for state estimation results of LAeq,1min for the road traffic noise based on the observation of LA50,1min under existence of a background noise.

Figure 8. A state estimation result of LAeq,1min for the road traffic noise based on the observation of LA50,1min by the proposed method with unknown parameter.

Table 2. Root-mean squared error of the estimation in Figures 7 and 8 (in dBA).
in the case of observation of different evaluation quantity.
4. Conclusions
In this study, a practical state estimation method for the sound environment system with uncertainty has been theoretically proposed by introducing the fuzzy inference. More specifically, after regarding the relationship between the state variable and observed evaluation quantities under existence of a background noise as a sound environment system with unknown observation mechanism, a recursive estimation algorithm for evaluation quantities of the specific signal has been derived. Furthermore, by applying the proposed method to the actually observed data of road traffic noise in the sound environment, the effectiveness of the theory has been confirmed experimentally too.
There are two points to be considered for obtaining improved estimations, as compared with the previous method. The first point is that our proposed method introduces fuzzy theory on the basis of fundamental principles of probability theory. More specifically, based on the Bayes’ theorem which is a normative axiom of probability theory, by introducing fuzzy inference for the uncertainty of the objective system, the generalization ability can be enhanced. The second point is that we can express the fuzziness of phenomena in a form reflecting the vague fluctuation around a true value. That is, by estimating simultaneously the parameter of the membership function with the state variable based on the observation data, the new state estimation algorithm has been derived.
The proposed approach is quite different from the traditional standard approach. Thus, it is still at an early stage of study, and there are left a number of practical problems to be continued in the future, starting from the result of the basic study in this paper. Some of the problems are the following.
1) The proposed method should be applied to the other actual data of sound environment, and its practical usefulness should be verified in each actual situation. For example, the proposed estimation method can be applied to the actual sound insulation systems with complex structure. By applying the proposed method to the input and output data of sound insulation systems, the system parameters reflecting the sound insulation properties can be estimated.
2) The proposed theory should be further extended into more complicated situation with multi-signal sources. In the acoustical engineering field, it is very important to separate only the objective specific signal from many other signals based on the compound observation in the actual situation in the presence of external noise. A future challenge is the development of an estimation method under the multi-signal sources, on the basis of the proposed method.
3) The theory should be developed to find more precise estimation methods for the state variables by introducing a hybrid method of fuzzy theory and statistical methods. More specifically, by taking the higher order correlation information between the state variables and the observation into consideration in the fuzzy theory, a new type of state estimation method can be proposed.
REFERENCES
- R. E. Kalman and R. S. Bucy, “New Results in Linear Filtering and Prediction Theory,” Transactions of ASME, Series D, Journal of Basic Engineering, Vol. 83, No. 1, 1961, pp. 95-108. doi:10.1115/1.3658902
- R. E. Kalman, “A New Approach to Linear Filtering and Prediction Problems,” Transactions of ASME, Series D, Journal of Basic Engineering, Vol. 82, No. 1, 1960, pp. 35-45. doi:10.1115/1.3662552
- H. J. Kushner, “Approximations to Optimal Nonlinear Filter,” IEEE Transactions on Automatic Control, Vol. 12, No. 5, 1967, pp. 546-556. doi:10.1109/TAC.1967.1098671
- M. Ohta and H. Yamada, “New Methodological Trials of Dynamical State Estimation for the Noise and Vibration Environmental System,” Acustica, Vol. 55, No. 4, 1984, pp. 199-212.
- A. Ikuta and M. Ohta, “A State Estimation Method of Impulsive Signal Using Digital Filter under the Existence of External Noise and Its Application to Room Acoustics,” IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, Vol. E75-A, No. 8, 1992, pp. 988-995.
- A. Ikuta and M. Ohta, “A Cancellation Method for Background Noise in Sound and Electromagnetic Environments by Using a Digital Filter for Power State Variables,” International Journal of Acoustics and Vibration, Vol. 8, No. 2, 2003, pp. 104-110.
- S. Julier and J. Uhlmann, “Unscented Filtering and Nonlinear Estimation,” Proceedings of the IEEE, Vol. 92, No. 3, 2004, pp. 401-421. doi:10.1109/JPROC.2003.823141
- G. Kitagawa, “Monte Carlo Filter and Smoother for NonGaussian Nonlinear State Space Models,” Journal of Computational and Graphical Statistics, Vol. 5, No. 1, 1996, pp. 1-25.
- H. Orimoto and A. Ikuta, “Adaptive Method for State Estimation of Sound Environment System with Uncertainty and Its Application to Psychological Evaluation,” Intelligent Information Management, Vol. 2, No. 3, 2010, pp. 212-219. doi:10.4236/iim.2012.23025
- L. X. Wang and J. M. Mendel, “Fuzzy Basic Functions, Universal Approximation, and Orthogonal Least-Squares Learning,” IEEE Transactions on Neural Networks, Vol. 3, No. 5, 1992, pp. 807-814. doi:10.1109/72.159070
- M. Ohta and T. Koizumi, “General Statistical Treatment of the Response of a Non-Linear Rectifying Device to a Stationary Random Input,” IEEE Transactions on Information Theory, Vol. 14, No. 4, 1968, pp. 595-598. doi:10.1109/TIT.1968.1054178
- L. X. Wang, “Fuzzy Systems and Control: Design and Stability Analysis,” PTR Prentice Hall, New York, 1994.

