Intelligent Information Management
Vol.4 No.3(2012), Article ID:19355,9 pages DOI:10.4236/iim.2012.43010
A Survey on the Vehicle Routing Problem and Its Variants
1Education Department, CII Institute of Logistics, Chennai, India
2Department of Management Studies, Pondicherry University, Pondicherry, India
Email: suresh.nandakumar@cii.in, panneer_dms@yahoo.co.in
Received January 18, 2012; revised March 4, 2012; accepted March 12, 2012
Keywords: Vehicle Routing Problem; Exact Methods; Heuristics; Meta-heuristics; VRPTW; Optimization; Ant Colony Optimization; Genetic Algorithms
ABSTRACT
In this paper, we have conducted a literature review on the recent developments and publications involving the vehicle routing problem and its variants, namely vehicle routing problem with time windows (VRPTW) and the capacitated vehicle routing problem (CVRP) and also their variants. The VRP is classified as an NP-hard problem. Hence, the use of exact optimization methods may be difficult to solve these problems in acceptable CPU times, when the problem involves real-world data sets that are very large. The vehicle routing problem comes under combinatorial problem. Hence, to get solutions in determining routes which are realistic and very close to the optimal solution, we use heuristics and meta-heuristics. In this paper we discuss the various exact methods and the heuristics and meta-heuristics used to solve the VRP and its variants.
1. Introduction
The Vehicle Routing Problem (VRP) is used to design an optimal route for a fleet of vehicles to service a set of customers, given a set of constraints. The VRP is used in supply chain management in the physical delivery of goods and services. There are several variants to the VRP. These are formulated based on the nature of the transported goods, the quality of service required and the characteristics of the customers and the vehicles. The VRP is of the NP-hard type.
The vehicle routing problem (VRP) has been very extensively studied in the optimization literature. It started with the seminal papers of [1,2]. Now, VRP offers a wealth of heuristic and metaheuristic approaches, which are surveyed in the papers of [3-5]. The VRP is so widely studied because of its wide applicability and its importance in determining efficient strategies for reducing operational costs in distribution networks. Today, exact VRP methods have a size limit of 50 - 100 orders depending on the VRP variant and the time–response requirements. Consequently, current research concentrates on approximate algorithms that are capable of finding high quality solutions in limited time, in order to be applicable to reallife problem instances that are characterized by large vehicle fleets and affect significantly logistics and distribution strategies.
The VRP was first stated by [1] that was about the routing of a fleet of gasoline delivery trucks between a bulk terminal and a number of service stations supplied by the terminal. The distance between any two locations is given and a demand for a given product is specified for the service stations.
The VRP can be defined as the problem of designing least cost delivery routes from a depot to a set of geographically dispersed locations (customers) subject to a set of constraints.
Dynamic Vehicle Routing Problems (DVRP), sometimes referred to as On-line Vehicle Routing Problems, have recently arisen due to the advances in information and communication technologies that enable information to be obtained and processed in real-time. In DVRP, some of the orders are known in advance before the start of the working day, but as the day progresses, new orders arrive and the system has to incorporate them into an evolving schedule. The existence of a communication system between the dispatcher (where the tours are calculated, e.g. headquarter of the company) and the drivers is assumed. The dispatcher can periodically communicate to the drivers about the new visits assigned to them. In this way, during the day, each driver always has knowledge about the next customers assigned to him/her
The classical VRP is defined as follows: Let G = (V, A) be a directed graph where V = {0,…,n} is the vertex set and A = {(i, j) : i, j Î V, i ≠ j} is the arc set. Vertex 0 represents the depot whereas the remaining vertices correspond to customers. A fleet of m identical vehicles of capacity Q is based at the depot. The fleet size is given a priori or is a decision variable. Each customer i has a non-negative demand qi.
The heuristic methods for the VRP can be divided into construction heuristics, improvement heuristics and metaheuristics
2. VRP Variations
There are different classes or variations of VRP like the capacitated VRP (CVRP), VRP with Time Windows (VRPTW). In the CVRP, a fleet of identical vehicles located at a central depot has to be optimally routed to supply a set of customers with known demands.
The capacitated VRP (CVRP) is described as the graph theoretic problem: Let G = (V, E) be a complete and undirected graph where V = {0,…,n} is the vertex set and E is the edge set. Vertex set Vc = {1, … , n} corresponds to n customers, whereas vertex 0 corresponds to the depot.
The objective of the VRPTW is to serve a number of customers within predefined time windows at minimum cost (in terms of distance travelled), without violating the capacity and total trip time constraints for each vehicle. Combinatorial optimisation problems of this kind are non-polynomial-hard (NP-hard) and are hence best solved by using heuristics. The most important metaheuristics used to solve the VRPTW are Tabu search (TS), genetic algorithm (GA), evolutionary algorithms (EA) and ant colony optimisation algorithm (ACO).
The constraints of the Vehicle Routing Problem with Time Windows (VRPTW) consist of a set of identical vehicles, a central depot node, a set of customer nodes and a network connecting the depot and customers. There are N + 1 customers and K vehicles. The depot node is denoted as customer 0. Each arc in the network represents a connection between two nodes and also indicates the direction it travels. Each route starts from the depot. The number of routes in the network is equal to the number of vehicles used. One vehicle is dedicated to one route. A cost cij and a travel time tij are associated with each arc of the network.
In Solomon’s 56 VRPTW 100-customer instances [6], all distances are represented by Euclidean distance, and the speed of all vehicles is assumed to be unity. That is, it takes one unit of time to travel one unit of distance. This assumption makes the problem simpler, because numerically the travel cost cij, the travel time tij and the Euclidean distance between the customer nodes equal each other.
Each customer in the node can be visited only once by one of the vehicles. Every vehicle has the same capacity qk and every customer has a varying demand mi. qk must be greater than or equal to the sum of all demands on the route travelled by the vehicle k., which means that no vehicle can be overloaded. The time window constraint is denoted by a predefined time interval, given an earliest arrival time and latest arrival time. The vehicles must arrive at the customers not later than the latest arrival time. If vehicles arrive earlier than the earliest arrival time, waiting occurs. Each customer also imposes a service time to the route, taking into consideration the loading/unloading time of goods. In Solomon’s instances, the service time is assumed to be unique regardless of the load quantity needed to be handled. Vehicles are also supposed to complete their individual routes within a total route time, which is essentially the time window of the depot.
There are three types of principal decision variables in VRPTW. The principal decision variable xijk (i, j Î {0, 1, 2,…, N}; k Î {1, 2,…, K}; i ≠ j) is 1 if vehicle k travels from customer i to customer j, and 0 otherwise. The decision variable Ti denotes the time when a vehicle arrives at the customer, and wi denotes the waiting time at node i. The objective is to design a network that satisfies all constraints, at the same time minimizing the total travel cost. The model is mathematically formulated below:
Principal Decision Variables
Ti arrival time at node i wi wait time at node i xijk Î {0,1}, 0 if there is no arc from node i to node j, and 1 otherwise,

Parameters:
K total number of vehicles N total number of customers cij cost incurred on arc from node i to j tij travel time between node i and j mi demand at node i qk capacity of vehicle k ei earliest arrival time at node i li latest arrival time at node i fi service time at node i rk maximum route time allowed for vehicle k Minimize 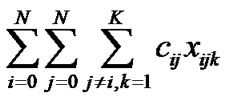
subject to:
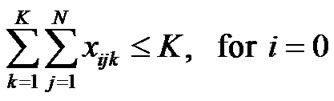 (1)
(1)
 (2)
(2)
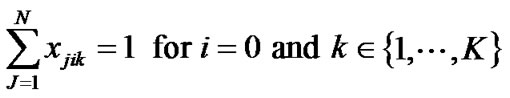 (3)
(3)
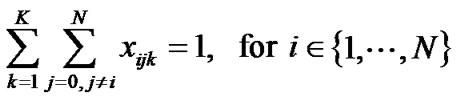 (4)
(4)
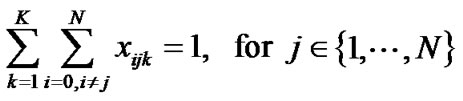 (5)
(5)
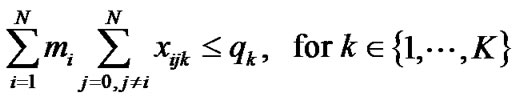 (6)
(6)
 (7)
(7)
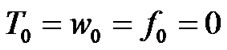 (8)
(8)
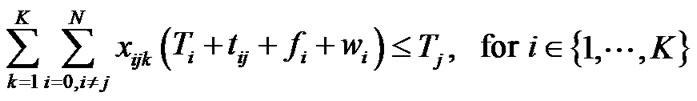 (9)
(9)
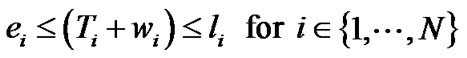 (10)
(10)
The objective function minimizes the total cost of travel of all the vehicles in completing their tours. Constraint set 1 guarantees that the number of tours is K by selecting at most K outgoing arcs from the depot (I = 0).
The constraint set 2 ensures that for each vehicle, there is exactly one outgoing arc from the depot is selected. Similarly, the constraint set 3 ensures that for each vehicle, there is exactly one arc entering into the node with respect to depot (i = 0). These two constraint sets (Constraint set 2 and constraint set 3) jointly ensure that a complete tour for each vehicle is ensured.
The constraint set 4 makes sure that from each node i only one arc for each vehicle emanates from it. The constraint set 5 ensures that for each node j, only one arc for each vehicle enters into it. These two constrains (Constraint set 4 and Constraint set 5) make sure that each vehicle visits each node only once.
The constraint set 6 sees that for each vehicle, the total demand (load) allocated to it is less than or equal to its capacity.
The constraint set 7 ensures that the total time of travel of the route of each vehicle is less than or equal to the maximum route time allocation to that vehicle.
The constraint set 8 sets the arrival time, waiting time and service time of each vehicle at the depot to zero. The constraint set 9 guarantees that the arrival time of each vehicle at the node j is less than the specified arrival time at that node. The constraint set 10 guarantees that the sum of the arrival time and the waiting time of each vehicle at each node i is more than equal to the earliest arrival time at that node and less than or equal to the latest arrival time at that node i, i = 1, 2, 3, …, N. Constraint sets (8) - (10) define the time windows. These formulation completely specify the feasible solutions for the VRPTW.
A constraint is called hard if it must be satisfied, while it is called soft if it can be violated. The violation of soft constraints is usually penalized and added to the objective function. The VRP with hard (resp., soft) time window constraints is abbreviated as VRPHTW (resp., VRPSTW).
An iterative route construction and improvement algorithm for the vehicle routing problem with soft time windows was proposed [7].
There are several heuristics proposed to solve the CVRP and its variants in the literature. Authors [8] have done detailed survey on CVRP in their book “The Vehicle Routing Problem” that describes both exact and heuristic methods for VRPs up to 2002. [9] proposed a twocommodity flow formulation of the CVRP.
The VRPTW belongs to the class of the NP-hard combinatorial optimization problems [10] Lenstra and Rinnooy Kan (1981). Hence, primarily heuristic procedures are generally used for larger instances of the VRPTW. In the recent past, quite good results have been achieved for the VRPTW with meta-heuristics.
Two groups of meta-heuristics have been used for solving the VRPTW Homberger and Gehring (2005) [11].
(1) Meta-heuristics controlling local search processes, such as tabu search [12,13], simulated annealing [14] genetic algorithms [15,16], evolution strategies [17], large neighbourhood search [18], and guided local search [19], also a software framework for a hybridized algorithm of two metaheuristics - Particle Swarm Optimization (PSO) and Genetic Algorithm (GA). The hybrid algorithm is used to optimize the best route for the vehicles that also incorporates a mechanism to trigger swarm condition for PSO algorithm [20]; and (2) Meta-heuristics controlling a subordinate construction heuristic, such as the greedy randomized search procedure (GRASP) proposed by [21], the RNET metaheuristic [22] and multiple ant colony systems as proposed by [23].
Author [18] used a local search method called Large Neighbourhood Search (LNS) for solving vehicle routing problems. LNS is similar to the constraint programming technology and is analogous to the shuffling technique of job-shop scheduling. The technique explores a large neighbourhood of the current solution by selecting a number of customer visits to remove from the routing plan, and re-inserting these visits using a constraint-based tree search.
Both exact algorithms and heuristics have been used to solve the different classes of VRPs. We discuss some of these below.
3. Exact Methods
Exact algorithms to solve VRP especially the capacitated VRP (CVRP) include the branch-and-bound, the branchand-cut and the branch-and-price algorithms, which are briefly described below.
A branch-cut-and-price exact algorithm was suggested by [24] for the Capacitated Vehicle Routing Problem with Two-Dimensional Loading Constraints.
Authors [25] proposed an exact algorithm for the multiple vehicle routing problem with time windows (VRPTW). They proposed an exact branch-and-price algorithm for solving the multiple vehicle routing problem with time windows.
Column generation or Dantzig-Wolfe decomposition provides a flexible framework that can accommodate complex constraints and time-dependent costs.
An exact solution approach was developed by [26] for vehicle routing and scheduling problem with soft time windows (VRPSTW). They proposed a new column generation-based exact optimization approach for the vehicle routing problem with semi soft time windows (VRPSSTW). Elementary shortest path problem with resource constraints and late arrival penalties is solved as a sub-problem. This uses the Dantzig-Wolfe decomposition method.
The authors [27] give an exact solution approach for vehicle routing and scheduling problem with soft time windows (VRPSTW). They proposed a new column generation-based exact optimization approach for the vehicle routing problem with semi soft time windows (VRPSSTW). Elementary shortest path problem with resource constraints and late arrival penalties is solved as a sub-problem. This uses the Dantzig-Wolfe decomposition method.
Algorithms Based on the Set Partitioning Formulation
The Set Partitioning (SP) formulation of the CVRP was originally proposed by [28]. A binary variable is used to represent a feasible route. The Ballinski and Quandt formulation is the following:
Let R denote a set of routes in which r denotes a specific route. Let air be a binary coefficient equal to 1 if and only if vertex i Î V\{0} belongs to route r, let 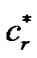 be the optimal cost of the route r, and let yk be a binary variable equal to 1 if and only if route r is used in the optimal solution. The problem is then as given below.
be the optimal cost of the route r, and let yk be a binary variable equal to 1 if and only if route r is used in the optimal solution. The problem is then as given below.
(SP) minimize
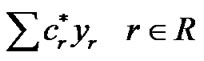 (11)
(11)
subject to
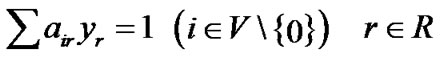 (12)
(12)
 (13)
(13)
A full column generation algorithm was developed by [29] who solved instances (n) in the range 15 to 25.
According [30], it is impractical for a direct application of this formulation, because of the large number of potential routes encountered in most non-trivial instances and of the difficulty of computing the 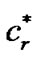 coefficients since it requires solving an exponential number of instances of an NP-hard problem.
coefficients since it requires solving an exponential number of instances of an NP-hard problem.
Authors [31] suggest a genetic and set partitioning two-phase approach for the VRPTW. The VRPTW is formulated as a set partitioning problem (SP). The GA is based on natural reproduction, selection and evolution of Darwin’s theory. Ever since, GA has been popular because it can contribute to find good solutions for complex mathematical problems, like the VRP and other NP-hard problems, in a reasonable amount of time.
The authors [1] described how the VRP may be considered as a generalization of the travelling salesman problem (TSP). They described the generalization of the TSP with multiple salesmen and called this problem the ‘clover problem.’
We consider the problem of routing vehicles stationed at a central facility (depot) to supply customers with known demands, in such a way as to minimize the total distance travelled. The problem is referred to as the vehicle routing problem (VRP) and is a generalization of the multiple travelling salesman problem that has many practical applications.
In [32] the authors present tree search algorithms for the exact solution of the VRP incorporating lower bounds computed from (i) shortest spanning k-degree centre tree (k-DCT), and (ii) q-routes. The final algorithms also include problem reduction and dominance tests. They present computational results for a number of problems derived from the literature. The results of these authors show that the bounds derived from the q-routes are superior to those from k-DCT and that VRPs of up to about 25 customers can be solved exactly.
In [33], the authors have developed a branch-and-cut procedure for the VRPTW. They addressed the problem of finding the minimum number of vehicles required to visit a set of nodes subject to time window and capacity constraints. The fleet is homogeneous and is located at a common depot. Each node requires the same type of service. An exact method is introduced based on branch and cut. In their computations, they obtain ever increasing lower bounds on the optimal solution. This is done by solving a series of relaxed problems that incorporate newly found valid inequalities. They obtain feasible solutions or upper bounds using greedy randomized adaptive search procedure (GRASP). They also introduce a wide variety of cuts to tighten the linear programming (LP) relaxation of the original mixed-integer program. To find violated cuts, it is necessary to solve a separation problem.
4. Heuristic Approaches
The cluster-first, route-second heuristic [34] first locates m seeds and constructs a cluster for each seed so as to minimize the sum of customers to seed distances, while satisfying the capacity constraint. This is achieved by solving a Generalized Assignment Problem (GAP). A route is then determined on each cluster by solving a TSP. Some procedures for selecting the seeds are described in [35]. Exact comparisons with other algorithms are difficult to make because the distance rounding convention used in the experiments is not specified. It is also interesting from a methodological point of view because if can benefit from algorithmic improvements for the Generalized Assignment Problem (GAP) or for the TSP.
In [36] they proposed a neighborhood search heuristics to optimize the planned routes of vehicles in a context where new requests, with a pick-up and a delivery location, occur in real-time. This is a dynamic vehicle routing problem (DVRP). Within this framework, new solutions are explored through a neighborhood structure based on ejection chains. Numerical results show the benefits of these procedures in a real-time context. The impact of a master–slave parallelization scheme, using an increasing number of processors is also investigated.
The authors [37] propose a real-time time-dependent vehicle routing problem with time windows. This problem is formulated as a series of mixed integer programming models that account for real-time and time-dependent travel times, as well as for real-time demands in a unified framework. Vehicle routes and the departure times are treated as decision variables, with delayed departure permitted at each node serviced. A route construction and a route improvement heuristics are proposed by the authors.
An efficient route minimization heuristic for the vehicle routing problem with time windows was suggested by [38]. The heuristic proposed by them is based on the ejection pool, powerful insertion and guided local search strategies.
In [39], a route construction heuristic with an adaptive parallel scheme is presented. The results from extensive computational experiments show the proposed parallel route construction heuristic is efficient and effective for routes construction, which is particularly useful for generation of the initial solutions for many meta-heuristic approaches with improved solution quality and convergence of the solution process.
Authors [40] proposed heuristics and a scatter search (SS) algorithms to solve real-life heterogeneous fleet vehicle routing problem with time windows and split deliveries (HFVRPTWSD). They proposed two constructive heuristics to generate the initial solutions of SS. First is the adaptation of the sequential insertion heuristic and the sequential insertion heuristic.
5. Meta-Heuristics
Many of the most successful meta-heuristics for the large VRPTW instances are based on some form of parallel computation. In [41], they were the first to apply a genetic algorithm to VRPTW. They hybridized a genetic algorithm with a greedy heuristic. Under this scheme, the genetic algorithm searches for a good ordering of customers, while the construction of the feasible solution is handled by the greedy heuristic. During the past few years, numerous papers have been written on generating good solutions for VRPTW with GAs. Almost all these papers present hybridizations of a GA with different construction heuristics [41,42] a, local searches [43,16] and other meta-heuristics such as tabu search [44] and ant colony system [45].
The authors [46] have considered a variant of VRPTW constrained by a limited vehicle fleet, which is a more realistic problem in logistics. A limited number of vehicles is given (m-VRPTW). Under this scenario, a feasible solution is one that may contain either un-served customers and/or relaxed time windows. They present an analytical upper bound for that formulation, and show that their tabu search approach came fairly close to the upper bound. This algorithm is also good from the stability point of view. They also show that the same algorithm could be used to give reasonably good results for the standard VRPTW problem.
In their article, [47] propose an ant colony system (ACS) meta heuristic procedure to solve the DVRP. It is based on the partition of the working day into time slices. A sequence of static vehicle routing problems is then generated. They then used an Ant Colony System algorithm to solve these problems. The properties of ACS have been also exploited to transfer information about good solutions from a time slice to the following one. They define new public domain benchmark problems and they test the algorithms that they proposed on those benchmark instances. A computational study on a newly defined set of benchmarks, finally showed that the method they proposed was able to achieve good results both on artificial and real problems.
In their paper, [48] present a meta-heuristic, which is based on the Threshold Accepting combined with modified Nearest Neighbour and Exchange procedures, to solve the Vehicle Routing Problem with Backhauls and Time Windows (VRPBTW). The VRPBTW assumes that trucks initially start from the depot, deliver goods to the line-haul customers, successively pickup goods from the backhaul consumers, and finally return to depot.
The authors [49] propose a cellular Genetic Algorithm (cGA) which is a kind of decentralized population based heuristic, which is used for solving CVRP, improving several of the best existing results so far in the literature. Their study shows a high performance in terms of the quality of the solutions found and the number of function evaluations (effort).
According to [50] they propose a cooperative parallel meta-heuristic for the VRPTW, based on the solution warehouse strategy. Here several search threads cooperate asynchronously, exchanging information on the best solutions identified. The exchanges are performed through a mechanism called solution warehouse, which holds and manages a pool of solutions.
The authors [11] proposed a two-phase hybrid metaheuristic for the VRPTW. The objective function of the VRPTW considered here combines the minimization of the number of vehicles (primary criterion) and the total travel distance (secondary criterion). The aim of the first phase is the minimization of the number of vehicles by means of a (l; k)-evolution strategy, whereas in the second phase the total distance is minimized using a tabu search algorithm.
In their article, [51] present a novel hybrid ant colony optimization approach called SS_ACO algorithm to solve the vehicle routing problem. The main feature of the hybrid algorithm is to hybridize the solution construction mechanism of the ant colony optimization (ACO) with scatter search (SS). In our hybrid algorithm, we use ACO algorithm and greedy heuristic to generate the initial solutions which are then formed the reference set. Within the scatter search framework, after two-solution combination method for the reference set has been applied, we employ ACO method to generate new solutions through updating the common arc pheromone mechanism. Moreover, during implementing the hybrid algorithm, cyclic transfers, a new class of neighborhood search algorithm can also be embedded into the scatter search framework as neighborhood search to improve solutions. Despite the size of the cyclic transfer neighborhood is very large, a restricted subset of the cyclic transfer neighborhood is adopted to reduce the computational requirements to reasonable levels.
A new and effective meta-heuristic algorithm, active guided evolution strategies, for the VRPTW is presented by [52]. The algorithm combines the strengths of the guided local search and evolution strategies belonging to meta-heuristics into an iterative two-stage procedure. Guided local search is used to regulate a composite local search in the first stage and the neighbourhood of the evolution strategies algorithm in the second stage.
The authors [53] have used a scatter search meta-heuristics to solve the VRPTW. Both a common arc method and an optimization-based set covering model are used to combine vehicle routing solutions. A reactive tabu search meta-heuristic and a tabu search with an advanced recovery feature, together with a set covering procedure are used for solution improvement.
In their article, [54] proposed a multi-depot vehicle routing problem with inter-depot routes, which addresses an extension of the multi-depot vehicle routing problem in which vehicles may be replenished at intermediate depots along their route. They proposed a heuristic combining the adaptive memory principle, a tabu search method for the solution of sub-problems, and integer programming.
A multi-objective evolutionary algorithm (EA) for solving the VRPTW was suggested by [55]. For multiobjective problems, heuristics generally have two aims (1) To minimize the distance of the generated solutionscalled the Pareto approximation, from the true Pareto front, and second to maximize the diversity of them.
Evolutionary algorithms (EAs) are optimizers based on Darwin’s theory of evolution, where only the fittest individuals survive and produce offspring to populate the next generation.
In his article, [56] proposed a hybrid ACO algorithm for solving vehicle routing problem (VRP) heuristically in combination with an exact algorithm. In the basic VRP, geographically scattered customers of known demand are supplied from a single depot by a fleet of identically capacitated vehicles. The intuition of the proposed algorithm is that nodes which are near to each other will probably belong to the same branch of the minimum spanning tree of the problem graph and thus will probably belong to the same route in VRP. Given a clustering of client nodes, the solution is to find a route in these clusters by using ACO with a modified version of transition rule of the ants. At the end of each iteration, ACO tries to improve the quality of solutions by using a local search algorithm, and update the associated weights of the graph arcs.
Authors [57] have formulated an improved ant colony optimization (IACO) algorithm to solve the period vehicle routing problem with time windows (PVRPTW). In PVRPTW, the planning period is extended to several days and each customer must be served within a specified time window. Multi-dimension pheromone matrix is used to accumulate heuristic information on different days. Two cross-over operations are introduced to improve the performance of the algorithm.
In their article, [58] suggested an Ant Colony algorithm hybridized with insertion heuristics for the Time Dependent Vehicle Routing Problem with Time Windows (TDVRPTW). In the TDVRPTW, a fleet of vehicles must deliver goods to a set of customers, time window constraints of the customers must be respected and the fact that the travel time between two points depends on the time of departure, has to be taken into account.
6. Hybrid Methods
Hybrid methods use a combination of exact, heuristic procedure or meta-heuristics to solve the VRP.
The authors [59] have proposed a hybrid method using constraint programming and meta-heuristics. Constraint Programming typically uses the technique of depth-first branch and bound as the method of solving optimization problems. Although this method can give the optimal solution for large problems, the time needed to find the optimal will be prohibitive. This paper introduces a method for using iterative improvement techniques within a Constraint programming framework and applies this technique to vehicle routing problems. They introduced a constraint programming model for vehicle routing, after which they describe a system for integrating constraint programming and iterative improvement techniques. They then described how the method can be greatly accelerated by handling core constraints using fast local checks, while other more complex constraints are left to the constraint propagation system. They have coupled their iterative improvement technique with a meta-heuristic to avoid the search being trapped in local minima. They use two meta-heuristics: a simple Tabu Search procedure and Guided Local Search. They have conducted an empirical study over benchmark problems and it shows the relative merits of these two techniques.
7. Conclusion
Vehicle routing problem forms an integral part of supply chain management, which plays a significant role for productivity improvement in organizations through efficient and effective delivery of goods/ services to customers. In this paper, an attempt has been made to survey the recent developments in the vehicle routing problem (VRP) and its variants. The literature is classified into exact methods, heuristics approaches, meta-heuristics, and hybrid methods. At the beginning, a complete working mathematical model for the vehicle routing problem with time windows (VRPTW) is given. Under exact methods, a descriptive set partitioning formulation for the vehicle routing problem with time windows has been presented. Further, the contributions of different researchers under this category have been discussed.
Since, the VRPTW is a combinatorial problem, development of efficient heuristic is inevitable to find near/ global optimal solution. So, in this paper, in the next three sections, the contributions of researchers in three categories, viz. heuristics, meta-heuristics and hybrid methods, respectively, have been presented.
Under meta-heuristic, the contributions of the researchers on simulated annealing algorithms, tabu search, genetic algorithm, ant-colony optimization and GRASP applied to vehicle routing problems are presented.
Under hybrid methods, a limited number of researches which combine the meta-heuristics with exact methods are presented.
From the literature, it is clear that very few researches have been carried under hybrid methods applied to vehicle routing problem. Hence, future researchers may focus on developing efficient hybrid approaches by combining two or more of the exact methods, heuristics and metaheuristics.
REFERENCES
- G. Dantzig and J. Ramser, “The Truck Dispatching Problem,” Management Science, Vol. 6, No. 1, 1959, pp. 80-91. doi:10.1287/mnsc.6.1.80
- G. Clarke and J. R. Wright, “Scheduling of Vehicle Routing Problem from a Central Depot to a Number of Delivery Points,” Operations Research, Vol. 12, No. 4, 1964, pp. 568- 581. doi:10.1287/opre.12.4.568
- G. Laporte, “The Vehicle Routing Problem: An Overview of Exact and Approximate Algorithms,” European Journal of Operational Research, Vol. 59, No. 3, 1992, pp. 345-358. doi:10.1016/0377-2217(92)90192-C
- M. Gendreau, G. Laporte and J.-Y. Potvin, “Metaheuristics for the VRP,” In: P. Toth and D. Vigo, Eds., The Vehicle Routing Problem, SIAM Monographs on Discrete Mathematics and Applications, Philadelphia, 2002, pp. 129-154. doi:10.1137/1.9780898718515.ch6
- J.-F. Cordeau, M. Gendreau, A. Hertz, G. Laporte and J. S. Sormany, “New Heuristics for the Vehicle Routing Problem,” In: A. Langevi and D. Riopel, Eds., Logistics Systems: Design and Optimization, Springer, New York, 2005, pp. 279-297. doi:10.1007/0-387-24977-X_9
- M. Solomon, “Algorithms for the Vehicle Routing and Scheduling Problem with Time Window Constraints,” Operations Research, Vol. 35, No. 2, 1987, pp. 254-265. doi:10.1287/opre.35.2.254
- F. M. Andres, “An Iterative Route Construction and Improvement Algorithm for the Vehicle Routing Problem with Soft Time Windows,” Transportation Research Part B, Vol. 43, No. 4, 2010, pp.438-447.
- P. Toth and D. Vigo, “An Overview of Vehicle Routing Problems,” SIAM Monographs on Discrete Mathematics and Applications, 2002, pp.1-26. doi:10.1137/1.9780898718515.ch1
- R. Baldacci, E. Hadjiconstantinou and A. Mingozzi, “An Exact Algorithm for the Capacitated Vehicle Routing Problem Based on a Two-Commodity Network Flow Formulation,” Operations Research, Vol. 52, No. 5, 2004, pp. 723- 738. doi:10.1287/opre.1040.0111
- J. K. Lenstra and A. H. G. Rinnooy Kan, “Complexity of Vehicle and Scheduling Problems,” Networks, Vol. 11, No. 2, 1981, pp. 221-227. doi:10.1002/net.3230110211
- J. Homberger and H. Gehring, “A Two-Phase Hybrid Meta-Heuristic for the Vehicle Routing Problem with Time Windows,” European Journal of Operational Research, 2005, Vol. 162, No. 1, pp. 220-238. doi:10.1016/j.ejor.2004.01.027
- J.-Y. Potvin, T. Kervahut, B.-L. Garcia and J.-M. Rousseau, “The Vehicle Routing Problem with Time Windows Part I: Tabu Search,” INFORMS Journal on Computing, Vol. 8, No. 2, pp. 158- 164. doi:10.1287/ijoc.8.2.158
- E. Taillard, P. Badeau, M. Gendreau, F. Guertin and J.-Y. Potvin, “A Tabu Search Heuristic for the Vehicle Routing Problem with Soft Time Windows,” Transportation Science, Vol. 31, No. 2, 1997, pp. 170-186. doi:10.1287/trsc.31.2.170
- W. C. Chiang and R. Russell, “Simulated Annealing Meta-Heuristics for the Vehicle Routing Problem with Time Windows,” Annals of Operations Research, Vol. 93, No. 1, 1996, pp. 3-27. doi:10.1007/BF02601637
- S. R. Thangiah, K. E. Nygard and P. L. Juell, “GIDEON: A Genetic Algorithm System for Vehicle Routing with Time Windows,” Proceedings of the Seventh IEEE Conference on Artificial Intelligence Applications, Miami Beach, 24-28 February 1991, pp. 322-328. doi:10.1109/CAIA.1991.120888
- J.-Y. Potvin and S. Bengio, “The Vehicle Routing Problem with Time Windows Part II: Genetic Search,” INFORMS Journal on Computing, Vol. 8, No. 2, 1996, pp. 165-172. doi:10.1287/ijoc.8.2.165
- J. Homberger and H. Gehring, “Two Evolutionary Meta-Heuristics for the Vehicle Routing Problem with Time Windows: Meta-Heuristics for Location and Routing Problems,” Information Systems and Operational Research (Special issue), Vol. 37, 1999, pp. 297-318.
- P. Shaw, “Using Constraint Programming and Local Search Methods to Solve Vehicle Routing Problems,” Principles and Practice of Constraint Programming—CP98, Lecture Notes in Computer Science, Springer-Verlag, New York, 1998, pp. 417-431.
- P. Kilby, P. Prosser and P. Shaw, “Guided Local Search for the Vehicle Routing Problems with Time Windows: Meta-heuristics: Advances and Trends in Local Search for Optimization,” Academic Publishers, Boston, 1999, pp. 473-486.
- S. Masrom, A. M. Nasir, Siti. Z. Z. Abidin and A. S. A. Rahman, “Software Framework for Vehicle Routing Problem with Hybrid Metaheuristic Algorithms,” Proceedings of the Applied Computing Conference, Angers, 17-19 November 2011, pp. 55-61.
- G. Kontoravdis and J. Bard, “A GRASP for the Vehicle Routing Problem with Time Windows,” INFORMS Journal of Computing, Vol. 7, No. 1, 1995, pp. 10-23. doi:10.1287/ijoc.7.1.10
- F.-H. Liu and S.-Y. Shen, “The Fleet Size and Mix Vehicle Routing Problem with Time Windows,” Journal of the Operational Research Society, Vol. 50, No. 7, 1999, pp. 721- 732.
- L. M. Gambardella, E. Taillard and G. Agazzi, “MACSVRPTW: A Multiple Ant Colony System for Vehicle Routing Problems with Time Windows New: Ideas in Optimization,” McGraw-Hill, London, 1999.
- S. Ropke, J.-F. Cordeau, M. Iori and D. Vigo, “Branch-and-Cut-and-Price for the Capacitated Vehicle Routing Problem with Two-Dimensional Loading Constraints,” Proceedings of ROUTE, Jekyll Island, 13 May 2007.
- G. Gutiérrez-Jarpa, G. Desaulniers, G. Laporte and V. Marianov, “A Branch-and-Price Algorithm for the Vehicle Routing Problem with Deliveries, Selective Pickups and Time Windows,” European Journal of Operational Research, Vol. 206, No. 12, 2010, pp. 341-349. doi:10.1016/j.ejor.2010.02.037
- N. Azi, M. Gendreau and J.-Y. Potvin, “An Exact Algorithm for a Vehicle Routing Problem with Time Windows and Multiple Use of Vehicles,” European Journal of Operational Research, Vol. 202, No. 3, 2010, pp. 756-763. doi:10.1016/j.ejor.2009.06.034
- A. G. Qureshi, E. Taniguchi and T. Yamada, “An Exact Solution Approach for Vehicle Routing and Scheduling Problems with Soft Time Windows,” Transportation Research Part E: Logistics and Transportation Review, Vol. 45, No. 6, 2009, pp. 960-977. doi:10.1016/j.tre.2009.04.007
- M. L. Ballinski and R. E. Quandt, “On Integer Program for a Delivery Problem,” Operations Research, Vol. 12, No. 2, 1964, pp. 300-304. doi:10.1287/opre.12.2.300
- Y. Agarwal, K. Mathur and H. M. Salkin, “A set-partitioning-based algorithm for the vehicle routing problem,” Networks, Vol. 19, No. 7, 1989, pp. 731-749. doi:10.1002/net.3230190702
- G. Laporte, “Fifty Years of Vehicle Routing,” Transportation Science, Vol. 43, No. 4, 2009, pp. 408-416.
- G. B. Alvarenga, G. R. Mateus and G. de Tomi, “A Genetic and Set Partitioning Two-Phase Approach for the Vehicle Routing Problem with Time Windows,” Computers and Operations Research, Vol. 34, No. 6, 2007, pp. 1561-1584. doi:10.1016/j.cor.2005.07.025
- N. Christofides, A. Mingozzi and P. Toth, “Exact algorithm for the Vehicle Routing Problem Based on Spanning Tree and Shortest Paths Relaxations,” Mathematical Programming, Vol. 20, No. 1, 1981, pp. 255-282. doi:10.1007/BF01589353
- F. J. Bard, G. Kontoravdis and G. Yu, “A Branch-and-Cut Procedure for the Vehicle Routing Problem with Time Windows,” Transportation Science, Vol. 36, No. 2, 2002, pp. 250-269. doi:10.1287/trsc.36.2.250.565
- M. Fisher and R. Jaikumar, “A Generalized Assignment Heuristic for Vehicle Routing,” Networks, Vol. 11, No. 2, 1981, pp. 109-124. doi:10.1002/net.3230110205
- B. M. Baker and J. Sheasby, “Extensions to the Generalised Assignment Heuristic for Vehicle Routing,” European Journal of Operational Research, Vol. 119, No. 1, 1999, pp. 147-157. doi:10.1016/S0377-2217(98)00348-8
- M. Gandreau, F. Guertin, J.-Y. Potvin and R. Seguin, “Neighborhood Search Heuristics for a Dynamic Vehicle Dispatching Problem with Pick-Ups and Deliveries,” Transportation Research Part E: Logistics and Transportation Review, Vol. 14, No. 3, 2006, pp. 157-174.
- X. Chen, W. S. Wan and X. H. Xu, “The Real-Time Time-Dependent Vehicle Routing Problem,” Transportation Research Part E: Logistics and Transportation Review, Vol. 42, No. 5, 2006, pp. 383-408. doi:10.1016/j.tre.2005.01.003
- N. Yuichi and B. Olli, “A Powerful Route Minimization Heuristic for the Vehicle Routing Problem with Time Windows,” Operations Research Letters, Vol. 37, No. 5, 2009, pp. 333-338. doi:10.1016/j.orl.2009.04.006
- K.-W. Peng, “An Adaptive Parallel Route Construction Heuristic for the Vehicle Routing Problem with Time Windows Constraints,” Expert Systems with Applications, Vol. 38, No. 9, 2011, pp. 11939-11946.
- B. Patrıcia, T. Hugo and Y. Yoshida, “Scatter Search for a Real-Life Heterogeneous Fleet Vehicle Routing Problem with Time Windows and Split Deliveries in Brazil,” European Journal of Operational Research, Vol. 199, 2009, pp. 750-758. doi:10.1016/j.ejor.2008.08.003
- J. L. Blanton and R. L. Wainwright, “Multiple Vehicle Routing with Time and Capacity Constraints Using Genetic Algorithms,” Proceedings of the Fifth International Conference on Genetic Algorithms, San Francisco, 17 July 1993, pp. 452-459.
- J. Berger, M. Salois and R. A. Begin, “Hybrid Genetic Algorithm for the Vehicle Routing Problem with Time Windows,” Lecture Notes in Artificial Intelligence 1418, Springer, Berlin, 1998, pp. 114-127.
- S. R. Thangiah, I. H. Osman and T. Sun, “Hybrid Genetic Algorithms, Simulated Annealing and Tabu Search Methods for Vehicle Routing Problems with Time Windows,” Technical Report UKC/OR94/4, Institute of Mathematics and Statistics, University of Kent, Canterbury, 1995.
- H. Wee Kit, J. Chin and A. Lim, “A Hybrid Search Algorithm for the Vehicle Routing Problem with Time Windows,” International Journal on Artificial Intelligence Tools, Vol. 10, No. 3, 2001, pp. 431-449. doi:10.1142/S021821300100060X
- J. Berger, Barkaoui, M. and Bräysy, O. A, “Route-directed Hybrid Genetic Approach for the Vehicle Routing Problem with Time Windows,” INFOR, Vol. 41, No. 2, 2003, pp. 179-194.
- C. L. Hoong, M. Sim and K. M. Teo, “Vehicle Routing Problem with Time-Windows and a Limited Number of Vehicles,” European Journal of Operational Research, Vol. 148, No. 3, 2003, pp. 559-569. doi:10.1016/S0377-2217(02)00363-6
- R. Montemanni, L. M. Gambardella, A. E. Rizzoli and A. V. Donati, “Ant Colony System for a Dynamic Vehicle Routing Problem,” Journal of Combinatorial Optimization, Vol. 10, No. 4, 2005, pp. 327-343. doi:10.1007/s10878-005-4922-6
- Y.-J. Cho and S.-D. Wang, “A Threshold Accepting MetaHeuristic for the Vehicle Routing Problem with Backhauls and Time Windows,” Journal of the Eastern Asia Society for Transportation Studies, Vol. 6, 2005, pp. 3022- 3037. http://www.easts.info/on-line/journal_06.htm
- E. Alba and B. Dorronsoro, “The Exploration/Exploitation Tradeoff in Dynamic Cellular Genetic Algorithms,” IEEE Transactions on Evolutionary Computation, Vol. 9, No. 2, 2005, pp. 126-142. doi:10.1109/TEVC.2005.843751
- A. Le Bouthillier and T. G. Crainic, “A Cooperative Parallel Meta-Heuristic for the Vehicle Routing Problem with Time Windows,” Computers & Operations Research, Vol. 32, No. 7, 2005, pp. 1685-1708. doi:10.1016/j.cor.2003.11.023
- X. Zhang and L. Tang, “A New Hybrid Ant Colony Optimization Algorithm for the Vehicle Routing Problem,” Pattern Recognition Letters, Vol. 30, No. 9, 2009, pp. 848- 855.
- M. David and O. Bräysy, “Active Guided Evolution Strategies for Large-Scale Vehicle Routing Problems with Time Windows,” Computers & Operations Research, Vol. 32, No. 6, 2005, pp. 1593-1614. doi:10.1016/j.cor.2003.11.017
- R. A. Russell and W.-C. Chiang, “Scatter Search for the Vehicle Routing Problem with Time Windows,” European Journal of Operational Research, Vol. 169, No. 2, 2006, pp. 606-622. doi:10.1016/j.ejor.2004.08.018
- C. Benoit., J.-F. Cordeau and G. Laporte, “The Multi-Depot Vehicle Routing Problem with Inter-Depot Routes,” European Journal of Operational Research, Vol. 176, No. 2, 2007, pp. 756-773. doi:10.1016/j.ejor.2005.08.015
- G.-N. Abel and Bullinaria John A, “An Improved Multi-Objective Evolutionary Algorithm for the Vehicle Routing Problem with Time Windows,” Computers & Operations Research, Vol. 38, No. 1, 2011, pp. 287-300. doi:10.1016/j.cor.2010.05.004
- E. Aziz, “An Algorithm for the Vehicle Problem () International Journal of Advanced Robotic Systems,” Vol. 7, No. 2, 2010, pp.125-132.
- Yu Bin, Yang Zhong Zhen, “An ant colony optimization model: The period vehicle routing problem with time windows,” Transportation Research Part E, Vol. 47, 2011, pp.166–181. doi:10.1016/j.tre.2010.09.010
- Balseiro, S.R., Loiseau. I. and Ramone. J, “An Ant Colony algorithm hybridized with insertion heuristics for the Time Dependent Vehicle Routing Problem with Time Windows,” Computers & Operations Research, Vol. 38, 2011, pp. 954-966. doi:10.1016/j.cor.2010.10.011
- De Backer, B. and Furnon, V, “Meta-heuristics in Constraint Programming Experiments with Tabu Search on the Vehicle Routing Problem,” Proceedings of the Second International Conference on Meta-heuristics (MIC’97), Sophia Antipolis, France, 1997.

