Abstract

In this paper, according to economics of real estate and macro-control theory, combine with the characteristics of the real estate market, macro-control of the real estate market is studied. After giving the dynamic model of three-dimensional nonlinear differential equations based on the total number of houses on the real estate business, the government’s averages housing investment funds and the standard price, systematically established the stability conditions of equilibrium point for this model. What’s more, through the use of extreme value analysis model, government funds have been invested in real estate business building devotion principles and the construction base of the real estate businessmen has also been estimated successfully. This provides the corresponding theoretical basis for government macro control policy-making.

1. Introduction

Having a high correlation and a strong driving force, the real estate industry has become one of the pillar industries of the national economy. As the basic industry of society, the development of the real estate industry is not only directly related to the virtual economy and the bubble economy, but also closely related to the financial crisis. As a result of the failure of the real estate market, the real estate market itself isn’t able to guarantee the efficient allocation of resources. In order to achieve the needs of effective function of the economy, the government must carry out macroeconomic regulation to control the real estate market.

The so-called macro-control is that the government takes a series of economic measures including regulating and controlling the process of the Macroeconomic mainly through fiscal and monetary policy basing on the overall interests of the national economy, in order to achieve the macroeconomic objectives of the basic balance between the social demand and supply in total and so on.

A survey carried out by Sirmans and Worzala [1] underlines the emphasis given to the asset treatment of the housing investment. In the broader context of diversification of mixed asset portfolios, investment in real estate would try to offset the negative consequences of excessive concentration in equities, especially considering the relative correlation of equities’ prices in international financial markets. Modigliani [2] pointed out that although the credit merit plays an indirect role on the construction of the real estate in the mortgage market, but the conduction of monetary policy is mainly through the consumption of capital investment. Kling and McCue [3] studied on the seasonal impact of macroscopically economic to office buildings and industrial constructions, and founded out that the output; the nominal interest rate and money supply shocks have a strong impact on the office buildings. Aoki et al. [4] founded that housing provides housing services to consumers and at the same time it also plays an indirect role in reducing the cost of borrowing, which magnifies the effect of impact on monetary policy of housing investment and housing prices via the research of the real estate market in the United Kingdom. As a result, it has a theoretical basis when studying how the monetary policy responding to the real estate price bubble basing on the conductive effect. Matteo [5] pointed out that the reverse of the currency has obvious negative effects on housing prices, what’s more, monetary policy and the impact on the demand of housing has played a significant role in bringing on the shortterm fluctuations in housing prices.

At present, China’s real estate market has long-term and stable relations [6], to the money supply, and monetary policy can affect real estate investment and real estate prices. Thus we can carry out macroeconomic regulation and control [7] by the means of the implementation of monetary policy to affect the real estate market. However, some academicians have put forward a different view, pointing out that the long-term money supply amount has limited ability to regulate and control [8] the real estate market. In this paper, according to economics of real estate and macro-control theory, combine with the characteristics of the real estate market and [9], macrocontrol of the real estate market is studied. Systematically established the model which is given by dynamic model of three-dimensional non-linear differential equations based on the total number of houses on the real estate business, the government's average housing investment funds and the standard price, which providing the corresponding theoretical basis for government macrocontrol policy-making.

2. Three-Dimensional Nonlinear Dynamic Model

The total number of real estate business building N(t) is a function of time t. D, T, C > 0 are respectively representing the average housing funds for the government’s investment, the standard of consumer prices and construction costs of the average housing of real estate businessmen; γ > 0 is the purchase value-added cost coefficient of customers, which is inversely proportional to value-added rate.

Assumptions:

1) Rate of the change of time of the N(t) has a positive linear relationship with government have invested funds and consumers purchase expenditures, while has a negative linear correlation with the real estate business costs.

2) If the total building number of real estate is more (or less), then the housing price standard should be lowered (or increased).

3) If the price standard is higher (or lower), then the government needs to fully consider the afford ability of housing consumers. At the same time, government should increase (or decrease) funds for housing construction to carry out reasonable regulation and control.

Government set a housing base N_m of the real estate business and also recent prices have a standard T_M, with the foregoing assumptions, we have the following three dimensional dynamic models of coupled nonlinear differential equations about the total number of houses on the real estate business, the government’s average housing investment funds and the standard price.

(1)

where, δ, k > 0 are the proportional coefficient.

To model (1), through the application of Routh-Hurwitz criterion, the stability criteria [10], as well as value analysis, we can wait until the following conclusions occur.

Theorem 1: When N_m > k/γ, the three-dimensional dynamic model of coupled differential equation (1) has a stable equilibrium point

(2)

Fatherly, the government gives the building base which is the number of building of recent price standard to achieve maximum value (the largest consumer affordability) to the real estate businessmen. And also the expanding number of housing can be estimated as follows:

(3)

where, D_m > D^* is the consumption level of moment t_m.

Prove: due to the right side of equation (1) equals to zero, easy to get the equilibrium point of equation (1) as follows:

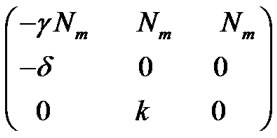(4)

whose characteristic equation:

(5)

Due to γN_m > 0, δkN_m > 0, therefore, when N_m > k/γ, coefficients of equation (5) need to be satisfied as follows:

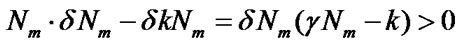(6)

Thus, according to Routh-Hurwitz criterion [10], all the characteristic roots of equation (5) have a negative real part; then basing on the stability decision theory of differential equations’ equilibrium point [10], from which we get to know that the equilibrium point (5) is stable .

To prove the second conclusion, we use extreme discrimination of functions. Diction of the real estate businessmen to expand the housing scale is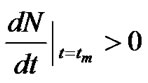, thus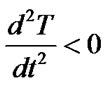. Therefore, housing price standard in the base that the government gives is the number of housing when reaching the maximum number of standard input price. Finally, by the first equation of the model (3) we can know:

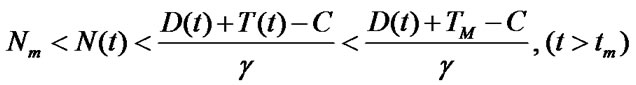(7)

Also by 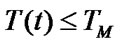we can know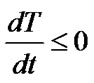, therefore 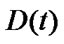is monotonous reduced function. So we get 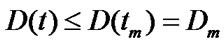(when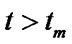), put it into equation (7) we will get the estimate total number of real estate after expanding housing, that is equation (3).

Finally, due to the stability of the results, check on the limits of, then we obtain the results that

According to Theorem 1, the principle of government regulation and control of the building base of real estate is as follows: As long as the government determine the building base of real estate businessmen by reference to the great value of recent price standard (the maximum tolerance of consumers), then the size of buildings of the real estate businessmen will be stabilized at the base to expand the buildings, it is necessary to consider all aspects about the government's housing investment, consumers’ housing afford ability and the price situation in the value-added.

If the tuition fee is higher (or lower), the government carry out macro-control by reducing (or increasing) in the construction funds of average, then the third equation of model1 should be altered as follows:

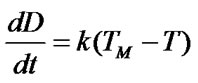(8)

Then, we get the corresponding three-dimensional dynamic model equations as follows:

(9)

According to reference [10] which gives all the necessary conditions that the roots of all the algebraic equations have negative real part, we can prove that:

Theorem 2: The equilibrium point of model (9) is unstable.

According to Theorem 2, our evaluations of the actions of the government are as follows: in reality, there are some local government’s implementations of policies [11] that raising prices to replace part of the government’s investment in real estate investment funds because of lacking real estate investment funds. This is precisely the assumption conditions (7) of model (9). Therefore, under such conditions, the number of the building houses of real estate is bound to be unstable. It will lead to bad housing order of real estate business, which is not conducive to the stability of the coordinated development of the real estate industry. Obviously it is undesirable.

3. Model Improvement

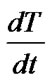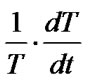In order to avoid the uncertainty of the equilibrium point of model (5), we alter the absolute rate of change and with the relative rate of change and 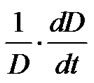in the second and third equation of model (1). Then, we can obtain the improved three-dimensional dynamic model of differential equations among the establishment of the total number of houses on the real estate businessmen, the government's invested housing funds, and the housing standard as follows:

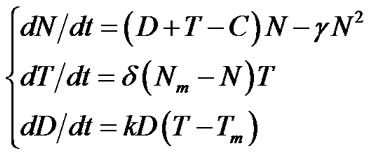(10)

where, δ, k > 0 are the proportion coefficients. Through the application of Routh-Hurwitz criterion, the stability criteria [10], as well as value analysis, we can wait until the following conclusions occur.

Theorem 3: Three-dimensional dynamic model of coupled differential equations (10) has the equilibrium point:

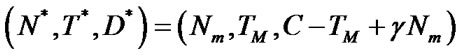(11)

A necessary condition for the equilibrium point for equation (10) stability is:

(12)

Fatherly, GDP to be expanded is estimated:

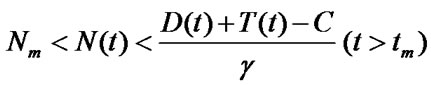(13)

Prove: Because of the right side of equation (11) is zero, we can obtain results easily that equation (13) is the equilibrium point of equation (12). The matrix for liberalized system of model (12) in equation (13) is as follow:

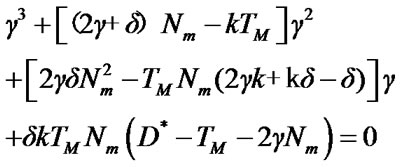(14)

According to [10], it gives a necessary condition that the roots of all the algebraic equations have a negative real part, thus a necessary condition for that the roots of all negative real part of algebraic equation (13) is that all the coefficients of equation (13) need to be positive, that is,

(15)

From the above we can get conditions equation (11), and then basing on the stability equilibrium of equilibrium point [10]. We get to know that the equation (11) to be set up is a necessary condition for equilibrium point equation (8) to be stable. We can get estimates of GDP for the expansion of equation (10) via the use of extreme value analysis of model function (5). End of proof.

Theorem 3 is of great significance in guiding the government macro-control. In fact, to achieve the scale of housing buildings of the real estate businessmen’s demand, house price standard and the stable equilibrium of government funds for each house, which must be requested that the government’s funding for each house is more than the house price standard (D^* > T_M); Moreover, when the increase in the cost of the purchase price is low (γ→∞. High rate of value-added), Real estate required by the Government to build the base can be controlled within the framework of a larger range (It corresponds to the second condition of estimation equation (13)).

Finally, we would also like to point out that, by Routh-Hurwitz criteria we can also obtain all the sufficient conditions for the department of negative real roots of equation (14), but the conditions are very complicated and it’s inconvenient to take practical application of. Therefore, we will no longer to discuss it in detail in this paper. In addition, estimation equation (13) is weaker than equation (3).

4. Conclusions

In this paper, the main results are as follows:

1) The three-dimensional dynamic model of differential equations among the establishment of the total number of houses on the real estate business, the government’s housing funds are invested, the housing standard.

2) The stabilities of equilibrium conditions of each model are given.

3) Government determines the building base of real estate principles and the estimation of real estate businessmen’s building size.

4) These conclusions were used to analyze the government’s macro-control, which can provide references for the government departments of management decision-making.

For future research, we will take some numeric simulations to proof our theory.

5. Acknowledgements

This research was supported by the NUIEPC (Grant 081029018). The first author would like to thank the guidance of the second author Professor Shengwu Zhou at China University of Mining & Technology.

6. References

[1] C. F. Sirmans and E. Worzala, “International Direct Real Estate Investment: A Review of the Literature,” Urban Studies, vol. 40, No. 5-6, 2003, pp. 1081-1114.

[2] F. Modigliani, “The Channels of Monetary Policy in the Federal Reserve—MIT University of Pennsylvania Econometric model of the United States,” In: G. A. Renton, Ed., Modeling the Economy, Heinemann Educational Books, London, 1995, pp. 240-267.

[3] J. L. Kling and T. E. McCue, “Stylized Facts about Industrial Property Construction,” Journal of Real Estate Research, vol. 6, No. 3, 1991, pp. 293-304.

[4] K. Aoki, J. Proudman and G. Vlieghe, “House Prices, Consumption, and Monetary Policy: A Financial Accelerator Approach,” Journal of Financial Intermediation, vol.13, No. 4, October 2004, pp. 414-435.

[5] M. M. Iacoviello, “House Prices and the Macro Economy in Europe: Results from a Structural VAR Analysis,” European Central Bank Working Paper No. 18, April 2000.

[6] J. Xu and X. Xiao, “Game Analysis on the Government and Developer Behaviors in the Process of Macro Control of Real Estate,” Journal of Chongqing Institute of Technology, Vol. 21, No. 8, 2007, pp. 34-36.

[7] X. F. Nie and C. Z. Liu. “A Practical Analysis on the Impact of Monetary Policy upon Real Estate,” Journal of Henan Institute of Financial Management, vol. 23, No. 4, 2005, pp. 63-65.

[8] Y. J. Li and Y. Yang, “The Effect of Interest Rate and Money Supply Impose on Real Estate Investment: In China an Empirical Analysis,” Journal of Xi’an Institute of Finance and Economics, vol. 18, No. 5, 2005, pp. 47-51.

[9] C. Hua, “Three Dimensional Dynamical Models for the Scale of Recruiting Students of universities, Government’s Devotion of Outlays and Standard of Tuitions with Applications to Government’s Macroscopically Controls,” Journal of Chengdu University of Technology (Science & Technology Edition), Vol. 34, No. 6, 2007, pp. 657-660.

[10] Q. Lu, “Qualitative Methods and Bifurcation of Ordinary Differential Equations,” Beijing University of Aeronautics and Astronautics Press, Beijing, 1989.

[11] C. Hua, “Mathematical Models of Dynamical Prices for Sale of Commodity when the Prices Wave: Stability of Prices with Analysis of Macroscopic Adjustment and Control,” Chinese Journal of Engineering Mathematics, Vol. 24, No. 3, 2007, pp. 446-450.