Intelligent Information Management
Vol.2 No.3(2010), Article ID:1483,11 pages DOI:10.4236/iim.2012.23022
Efficient Heuristic to Minimize Makespan in Single Machine Scheduling Problem with Unrelated Parallel Machines
1Department of Mechanical Engineering, Thiagarajar College of Engineering, Madura, India
2Department of Management Studies, School of Management, Pondicherry University, Pondicherry, India
E-mail: sivasankaran.panneerselvam@yahoo.com, sornakumar2000@yahoo.com, panneer_dms@yahoo.co.in
Received November 23, 2009; revised December 30, 2009; accepted February 2, 2010
Keywords: Makespan, Heuristic, Unrelated Parallel Machines, Mathematical Model, ANOVA
Abstract
This paper discusses an efficient heuristic to minimize the makespan of scheduling n independent jobs on m unrelated parallel machines. The problem of scheduling the jobs on the unrelated parallel machines is combinatorial in nature. Hence, the heuristic approach is inevitable for quicker solution. In this paper, a simple and efficient heuristic is designed to minimize the makespan of scheduling n independent jobs on m unrelated parallel machines. A mathematical model is also presented for this problem. A factorial experiment is used to compare the results of the proposed heuristic with that of a mathematical model by taking “Method” (Heuristic and Model) as the first factor and “Problem Size” (No. of machines X No. of Jobs: 2X5, 2X6, ……, 2X9, 3X5, 3X6, ……, 3X9, ……., 5X5, 5X6, …5X9) as the second factor. It is found that there is no significant difference between the results of the proposed heuristic and that of the mathematical model. Further, the mean percent error of the results obtained by the heuristic from the optimal results obtained by the model is 2.336 %. The heuristic gives optimal solution for 76.67 % of the problems.
1. Introduction
The production scheduling problem is classified into single machine scheduling problem, flow shop scheduling problem, job shop scheduling problem, open shop scheduling problem and batch scheduling problem. In this paper, the single machine scheduling problem is considered. The single machine scheduling problem is further classified into single machine scheduling problem with single machine (processor) and single machine scheduling problem with parallel machines (processors). The single machine scheduling problem with parallel machines is again classified into single machine scheduling problem with identical parallel machines, single machine scheduling with uniform parallel machines and single machine scheduling with unrelated parallel machines, which are as explained below.
Let, tij be the processing time of the job j on the machine i, for i = 1, 2, 3, …., m and j = 1 2, 3, …, n.
The three types of parallel machines scheduling problem are defined as follows.
1) If tij = t1j for all i and j, then the problem is called as identical parallel machines scheduling problem.
This means that all the parallel machines are identical in terms of their speed. Each and every job will take the same amount of processing time on each of the parallel machines.
2) If tij = t1j/si for all i and j, then the problem is termed as uniform (proportional) parallel machines scheduling problem.
Here, si is the speed of the machine i and t1j is the processing time of the job j on the machine 1. This means that the parallel machines will have different speeds. The relationship among the speeds of the machines is s1 < s2 < s3 < …. < sm. That is the machine 1 is the slowest machine and the machine m is the fastest machine. So, the relationship among the processing times of a job on the parallel machines is 1/s1 > 1/s2 > 1/s3 > …. > 1/sm.
3) If tij is arbitrary for all i and j, then the problem is known as unrelated parallel machines scheduling problem.
In this type of scheduling, there will not be any relationship among the processing times of a job on the parallel machines. This may be due to technological differences among the machines, different features of the jobs, etc.
In this paper, the single machine scheduling problem with unrelated parallel machines is considered. The essential characteristics of the single machine scheduling problem with unrelated parallel machines are listed as follows.
1) It has n independent single operation jobs.
2) It has m parallel machines.
3) m machines are continuously available and they are never kept idle while a work is waiting.
4) tij is the processing time of the job j on the machine i, for i = 1, 2, 3, .., m and j = 1, 2, 3, …, n.
5) tij is arbitrary for different combinations of i and j, for i = 1, 2, 3, .., m and j = 1, 2, 3, …, n.
Environment of Unrelated Parallel Machines Scheduling Problem
Consider a situation in which we have m different parallel machines and n independent single operation jobs. Each of the jobs can be processed on each of the unrelated parallel machines. In this process, the processing times of each job on different machines are arbitrary. Like in the uniform parallel machines scheduling (tij = t1j/si for all i and j) or in the identical parallel machines scheduling (tij = t1j for all i and j), there will not be any relationship among the processing times of a job on the parallel machines of the unrelated parallel machines scheduling.
In a shaft, if a hole is to be made at one of its ends, it can be done either in a lathe or in a drilling machine. The time taken to make the end-hole in these machines will differ, because the type of setting and the processing technology are altogether different in these machines. Hence, in the single machine scheduling problem with unrelated parallel machines, the processing times of each job on different machines are arbitrary. Like this example, in industries, one can encounter many situations. Hence, the machines which have similar processing capabilities will be grouped together and a batch of single operation jobs will be scheduled on these machines to optimize a desired measure of performance.
There are many measures of performance in the single machine scheduling problem [1]. In this paper, the minimization of the makespan of scheduling n independent single operation jobs on m unrelated parallel machines is considered, because it is considered to be a dominant measure of performance, which represents the earliest completion time of the given batch of jobs.
2. Literature Review
This section presents review of literature of scheduling n independent single operation jobs on m unrelated parallel machines to minimize the makespan. Since, this problem is NP-hard, any attempt to obtain the optimal solution through exact algorithm may end with failure for most of the instances. This is because of exponential computational time to solve such problem. Hence, researchers are focusing on the development of heuristics, which will give near optimal solution. Van De Velde [2] considered the single machine scheduling problem with unrelated parallel machines. The author aimed to minimize the maximum job completion time which means the minimization of makespan. He presented an optimization algorithm and an approximation algorithm that are based on surrogate relaxation and duality to solve this NP hard problem. The idea behind the surrogate relaxation is to replace a set of nasty (complex) constraints with a single constraint that is a weighted aggregate of these constraints.
Glass, Potts and Shade [3] have applied meta-heuristics to the problem of scheduling jobs on the unrelated parallel machines to minimize the makespan and reported that genetic algorithm gives poor results. Also, they reported that a hybrid method in which a descent is incorporated into the genetic algorithm is comparable in performance with the simulated annealing. Francis Sourd [4] has developed two approximation algorithms for minimizing the makespan of independent tasks assigned on the unrelated parallel machines. The first one is based on a partial and heuristic exploration of a search tree. In the second algorithm, a new large neighbourhood improvement procedure is implemented in an already existing algorithm. He reported that the computational efficiencies of these algorithms are equivalent to the best local search heuristic.
Mokotoff and Chretienne [5] have developed a cutting plane algorithm for the unrelated parallel machine scheduling problem, which minimizes the makespan. Their algorithm deals with the polyhedral structure of this scheduling problem. In their work, strong inequalities are identified for fixed values of the maximum completion time and they are used to build a cutting plane scheme from which an exact algorithm and an approximation algorithm are developed. Mokotoff and Jimeno [6] developed heuristics based on partial enumeration for the unrelated parallel machines scheduling problem. For a given mixed integer linear model with binary decision variables, they presented heuristics based on the partial enumeration. Computational experiments are reported for a collection of test problems, showing that some of the proposed algorithms achieve better solutions than other relevant existing approximation algorithms.
Hariri and Potts [7] developed a heuristic, which consists of two phases to minimize the makespan of scheduling n independent jobs on m unrelated parallel machines. In the first phase, a linear programming model is used to schedule some of the jobs and then a heuristic is used in the second phase to schedule the remaining jobs. They have stated that some improvement procedure is necessary to have good solutions. Piersma and Van Dijk [8] have proposed a set of local search algorithms to minimize the makespan of scheduling jobs on the unrelated parallel machines. In these algorithms, the neighbourhood search of a solution uses the efficiency of the machines for each job. They claimed that this approach gives better results when compared to general local search algorithms.
Ghirardi and Potts [9] have considered the problem of scheduling jobs on the unrelated parallel machines to minimize the makespan. They developed a method known as recovering beam search method to minimize the makespan in the unrelated parallel machines. The traditional beam search method is a truncated version of branch and bound method. The recovering beam search allows the possibility of correcting wrong decisions by replacing partial solutions with others. It has a polynomial time complexity function for the NP hard problem of this research. Also, they reported the computational results of this method.
Monien and Woclaw [10] have presented an experimental study on the unspittable-Truemper algorithm to minimize the makespan of scheduling jobs on the unrelated parallel machines. This computes 2-approximate solutions in the best worst-case running time known so far. The goal of their simulation was to prove its efficiency in practice. They compared their technique with the algorithms and heuristics in practice, especially with those based on two-step approach. Gairing, Monien and Woclaw [11] presented a combinatorial approximation algorithm that matches an integral 2-approximation quality. It is a generic minimum cost flow algorithm, without any complex enhancements, tailored to handle unsplittable flow. In their approach, they replaced the classical technique of solving LP-relaxation and rounding afterwards by a completely integral approach.
From these literatures, it is clear that the development of heuristic to minimize the makepsan of scheduling n independent jobs on m unrelated parallel machines is a challenging task. Various authors have proposed different methodologies. The range of heuristics varies from simple search procedure to meta-heuristic. In this paper, an attempt has been made to develop an efficient heuristic to minimize the makepsan of scheduling jobs on the unrelated parallel machines and compare its solution with that of a mathematical model, which gives optimal solution. If the solution of the proposed heuristic does not differ significantly from that of the model, for a given set of randomly generated problems, then one can conclude that the proposed heuristic is an efficient one.
For a given solution methodology, say the heuristic development, if a heuristic performs better, it is considered to be an efficient heuristic. Further, among different solution methodologies, viz., simple heuristics, meta heuristics, model, etc., if a simple heuristic proves to be performing better, then that simple heuristic can be termed as an effective heuristic. In this paper, the authors propose an efficient heuristic which in turn proves to be effective, based on a comparison of the results of this heuristic with that of a mathematical model.
3. Mathematical Model to Minimize Makespan of Scheduling Jobs on Unrelated Parallel Machines
The optimal makespan of scheduling n independent single operation jobs on m unrelated parallel machines can be obtained using a mathematical model. In this section, a mathematical model is presented for this problem.
Let, n be the number of independent jobs with single operation.
m be the number of unrelated parallel machines.
tij be the processing time of the job j on the machine i and it is arbitrary for different combinations of i and j.
A generalized data format of this problem is shown in Table 1. The objective is to schedule n jobs on m unrelated parallel machines such that the makespan is minimized.
The expression for the makespan, M is given as follows.
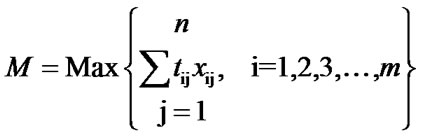
where, xij = 1, if the job j is assigned to the machine i = 0, otherwise, for i = 1, 2, 3, ….., m and j = 1, 2, 3, ….., n.
A descriptive mathematical model to minimize the makespan is as follows:
Minimize 
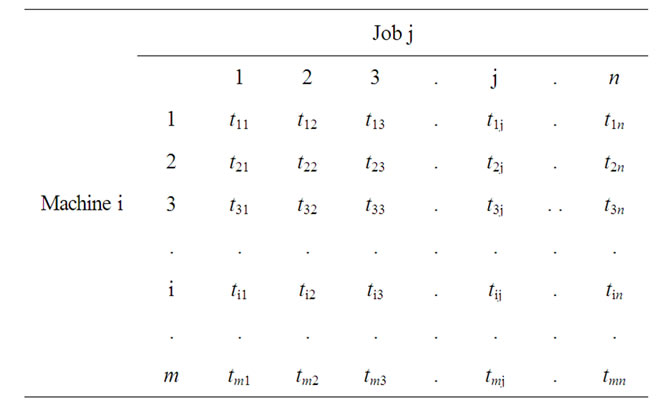
Table 1. Generalized format of processing times.
subject to
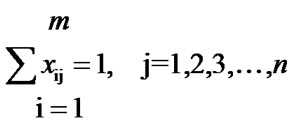
where, xij = 1, if the job j is assigned to the machine i = 0, otherwise, for i = 1, 2, 3, ….., m and j = 1, 2, 3, ….., n The number of variables in this model is mn and the total number of constraints is n. In this model, the objective function is not in workable form. So, an alternate form of this model as follows contains a linear objective function, which is in workable form.
Minimize Z1 = M
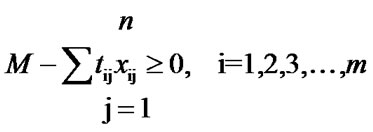
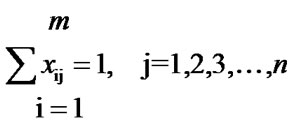
where, xij = 1, if the job j is assigned to the machine i = 0, otherwise, for i = 1, 2, 3, …., m and j = 1, 2, 3, …, n M ≥ 0 and it is the makespan of the schedule.
In this model, the number of variables is mn+1 and the total number of constraints is m+n. This problem comes under combinatorial category. Hence, the development of an efficient heuristic for this problem is highly essential.
4. Heuristic to Minimize Makespan of Scheduling Jobs on Unrelated Parallel Machines
As stated earlier, the problem of scheduling n independent single operation jobs on m unrelated parallel machines to minimize the makespan is a combinatorial problem. Hence, the time taken to obtain the optimal solution using either a mathematical model or a complete enumeration technique or a branch and bound technique will grow exponentially with respect to the increase in the problem size. Hence, the usage of a heuristic to overcome this situation is highly inevitable. In this section, the authors present an efficient heuristic to schedule n independent jobs on m unrelated parallel machines such that the makespan is minimized.
4.1. Rationale of the Heuristic
The proposed heuristic consists of two phases, which are listed as follows.
1) Initial assignment of jobs to the machines.
2) Shifting of jobs from one machine to another.
Phase 1
In this phase, each and every job is assigned to the machine on which it takes the least processing time.
Let the maximum of the completion times of the last jobs on all the machines be M, which is known as the initial makespan of the schedule.
M = Max {Ci }, where Ci is the completion time of the last job on the machine iwhere i = 1, 2, 3, …,m.
Phase 2
After having assigned the jobs to the machines as explained in the phase 1, in this phase, an attempt is made to minimize the makespan by the shifting jobs from one machine to other machines.
Consider the generalized data with three machines and 7 jobs as shown in Table 2.
Let the initial assignment of the jobs on the three machines be as shown in Figure 1.
From the Figure 1, it is clear that the makespan (M) is C3, which is the maximum of C1, C2 and C3. This maximum occurs on the machine 3. If the current makespan is to be reduced, then each of the jobs on the machine 3 is to be shifted to some other machine, provided such shifting of the job is economical in terms of reduction in makespan.
If the job 1 on the machine 3 is considered for shifting to machine 1, then the necessary calculations are as shown below.
The completion time of the last job on the machine 1 after the shift = C1 + t11.
The completion time of the last job on the machine 3 after the shift = C3 – t31.

Table 2. Generalized format of processing times for 3 machines and 7 jobs.
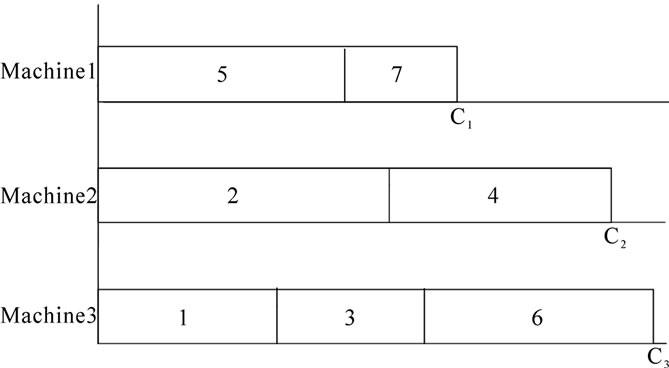
Figure 1. Gantt chart for initial assignment of jobs.
After this shift, let the maximum of the completion times of the last jobs on all the machines be S. If S < M, then the shifting of the job 1 to the machine 1 is to be effected; otherwise, the shifting of the job 1 to the machine 1 is to be avoided. Such shifting of jobs is to be carried out until there is no further reduction in the makespan.
4.2. Steps of the Heuristic
The steps of the proposed heuristic are presented in this section.
Step 1: Input the data:
Number of independent jobs, n Number of unrelated parallel machines, m Processing time T(I,J), I = 1 to m and J = 1 to n.
Set Number of Jobs on Machine I, NJ(I) = 0, I = 1 to m Set Machine Completion Time, MCT(I) = 0, I = 1 to m
Step 2: Assign the jobs to the machines.
Step 2.1: Set the Job Index J = 1
Step 2.2: Find the machine which takes the least processing time for the job J.
Let that machine be K.
Step 2.3: Do the following:
1) Increment the number of jobs on the machine K by 1 NJ(K) = NJ(K) + 1 2) Add the job J to the job sequence JS[ ] of the machine K at NJ(K)th position.
JS[K, NJ(K)] = J 3) Add the processing of the job J to the machine completion time of the machine K.
MCT(K) = MCT(K) + T(K,J)
Step 2.4: J = J + 1 Step 2.5: If J ≤ n then go to Step 2.2; else go to Step 3.
Step 3: Set Job Status Index, JSI to n+1
Step 4: Find the machine whose last job completion time is the maximum (makespan)
Step 4.1: CMAX = 0
Step 4.2: I = 1
Step 4.3: If MCT(I ) > CMAX then update the maximum completion timeCMAX = MCT(I )
Set machine with maximum completion time, MCMAX = I
Step 4.4: I = I + 1
Step 4.5: If I ≤ m then go to Step 4.3; else go to Step 4.6.
Step 4.6: Set the best makespan, BMS = CMAX.
Step 5: Shift the jobs on the machine with BMS to some other machines which give maximum reduction in makespan
Step 5.1: Initialize the job position on the machine MCMAX to 1 [X = 1 ]
Step 5.2: Store the job at position X on the Machine MCMAX in Q.
Q = JS(MCMAX,X)
Step 5.3: Find the machine BMC1, other than MCMAX on which the job Q requires the least time
Step 5.4: Find the completion time on the identified machine to which the job Q is to be transferredBMCCT = MCT(BMC1) + T(BMC1,Q)
Find completion time on the machine MCMAX from which, the job Q is to be transferredMAXCT1 = MCT(MCMAX) – T(MCMAX,Q)
Step 5.5: Find the maximum of the completion times of the last jobs on all the machines.
Let it be MAXMCT.
Step 5.6: If MAXMCT ≥ CMAX then set Least Makespan, LMS1 = 10000 and then go to Step 5.7;
Else, set Least Makespan, LMS1 = MAXMCT and then go to Step 5.7.
Step 5.7: Find the machine BMC2, other than the machine MCMAX, with the least completion time for the last job.
Step 5.8: Find the completion time on the identified machine to which the job Q is to be transferred,
BMCCT = MCT(BMC2) + T(BMC2,Q)
Find completion time on the machine MCMAX from which the job Q is to be transferredMAXCT2 = MCT(MCMAX) – T(MCMAX,Q)
Step 5.9: Find the maximum of the completion times of the last jobs on all the machines. Let it be MAXMCT.
Step 5.10: If MAXMCT ≥ CMAX then set Least Makespan, LMS2 = 10000 and then go to Step 5.11;
Else, set Least Makespan, LMS2 = MAXMCT and then go to Step 5.11.
Step 5.11: If LMS1 > LMS2 then
{Least of Least Makespans, LMS = LMS2 INDEX = 2 Best Machine, BBMC2 = BMC2
}
Else
{Least of Least Makespans, LMS = LMS1 INDEX = 1 Best Machine, BBMC1=BMC1
}
Step 5.12: If LMS = 10000 then go to Step 5.19
Step 5.13: If LMS ≥ BMS then go to Step 5.19
Step 5.14: Update the Best Makespan, BMS = LMS Update Job Status Index, JSI = Q
Step 5.15: Update the results w.r.t. BMS on the machine MCMAX as the best solution.
Transfer current machine completion timesMCT(I ) to BMCT(I ) for all machines (I =1, 2, 3, …, m)
Transfer current number of jobs on each machineNJ(I ) to BNJ(I ) for all machines (I = 1, 2, 3, …, m)
Transfer current job sequences on machinesJS(I,J) to BJS(I,J) for all I = 1, 2, 3, …, m and J = 1, 2, 3, …, NJ(I )
Step 5.16: If INDEX = 1 then go to Step 5.17; else go to Step 5.18.
Step 5.17: Update makespan and other results based on the allocation of the job Q to the machine other than the machine MCMAX, which requires least processing time.
BMCT(BBMC1) = BMCT(BBMC1) + T(BBMC1,Q)
BMCT(MCMAX) = BMCT(MCMAX) – T(MCMAX,Q)
BNJ(BBMC1) = BNJ(BBMC1) + 1 BJS(BBMC1, BNJ(BBMC1)) = Q Removing the job Q from the machine MCMAX ZZ = 0 FOR Z = 1 to BNJ(MCMAX)
If BJS(MCMAX, Z)= Q then go to Step 5.17.1 ZZ = ZZ + 1 BJS(MCMAX,ZZ) = BJS(MCMAX,Z)
Step 5.17.1 NEXT Z BNJ(MCMAX) = BNJ(MCMAX) – 1 Go to Step 5.19
Step 5.18: Update makespan and other results based on the allocation of the job Q to the machine other than the machine MCMAX, which has least completion time.
BMCT(BBMC2) = BMCT(BBMC2) + T(BBMC2,Q)
BMCT(MCMAX) = BMCT(MCMAX) – T(MCMAX,Q)
BNJ(BBMC2) = BNJ(BBMC2) + 1 BJS[BBMC2, BNJ(BBMC2)] = Q Removing the job Q from the machine MCMAX ZZ = 0 FOR Z = 1 to NJ(MCMAX)
If BJS(MCMAX, Z) = Q then go to Step 5.18.1 ZZ = ZZ + 1 BJS(MCMAX,ZZ) = BJS(MCMAX,Z)
Step 5.18.1 NEXT Z BNJ(MCMAX) = BNJ(MCMAX) – 1
Step 5.19: X = X + 1
Step 5.20: If X ≤ NJ(MCMAX) then go to Step 5.2; else go to Step 6.
Step 6: If JSI = n+1 (If JSI is unchanged) then go to Step 8; else go to Step 7.
Step 7: Update the results w.r.t. BMS as the best solution.
Transfer current machine completion timesBMCT(I ) to MCT(I ) for all machines (I =1, 2, 3, …, m)
Transfer current number of jobs on each machineBNJ((I ) to NJ(I ) for all machines (I = 1, 2, 3, …, m)
Transfer current job sequences on machinesBJS(I,J) to JS(I,J) for all I = 1, 2, 3, …, m and J = 1, 2, 3, …, BNJ(I )
Go to Step 3
Step 8: Print the results.
Machine Completion Time, MCT(I ), I = 1, 2, 3,…., m.
Job assignments on the machines, JS(I,J), I = 1, 2,, m & J = 1, 2, …., NJ(I )
Minimized makespan, CMAX.
Step 9: Stop.
5. Comparison of Heuristic and Model
In this section, the solutions obtained through the proposed heuristic are compared with that obtained through the mathematical model using a complete factorial experiment. In the factorial experiment, two factors are assumed, viz., “Method (M)” and “Problem Size (P)”. The number of levels for the method is 2, viz. Heuristic and Model. The number of levels for the Problem Size is 20 which are 2X5, 2X6, 2X7, 2X8, 2X9, 3X5, 3X6, 3X7, 3X8, 3X9, 4X5, 4X6, 4X7, 4X8, 4X9, 5X5, 5X6, 5X7, 5X8 and 5X9. For each of the 40 experimental combinations, the data for three replications have been randomly generated. The process times (minutes) of the problems for the Replication 1, Replication 2 and Replication 3 are given in Table 3, Table 4 and Table 5, respectively. STORM software is used to solve the model. The values of the makespan of the problems using the heuristic and the model are presented in Table 6. The formula to compute the percent deviation of the makespan of a problem given by the heuristic from that given by the model is as follows.
Percentage deviation of makespan 
The respective ANOVA model is as follows.
yijk = μ + Mi + Pj + MPij + eijk
where, μ is the overall mean of the makespan yijk is the response in terms of the makespan for the kth replication of the ith level of the factor M and the jth level of the factor P.
Mi is the effect of the ith level of the factor M on the response yijk
Pj is the effect of the jth level of the factor P on the response yijk
MPij is the effect of the ith level of the factor M and the jth level of the factor P on the response yijk
eijk is the error in the kth replication for the ith level of the factor M and the jth level of factor P.
The results of the corresponding ANOVA model are shown in Table 7. The hypotheses of this ANOVA model are listed as follows.
Factor “Method (M)”:
H0: There is no significant difference between the methods (Model and Heuristic) in terms of the make span.
H1: There is significant difference between the methods (Model and Heuristic) in terms of the makespan.
In the Table 7, the calculated F ratio for the factor “Method (M)” is 0.09183275, which is less than the corresponding table F value (3.97) for (1,80) degrees of freedom at a significance level of 0.05. Hence, the null hypothesis is to be accepted. This means that there is no significant difference between the methods (Heuristic and Model) in terms of the makespan. So, the heuristic performs better for the assumed problems in terms of
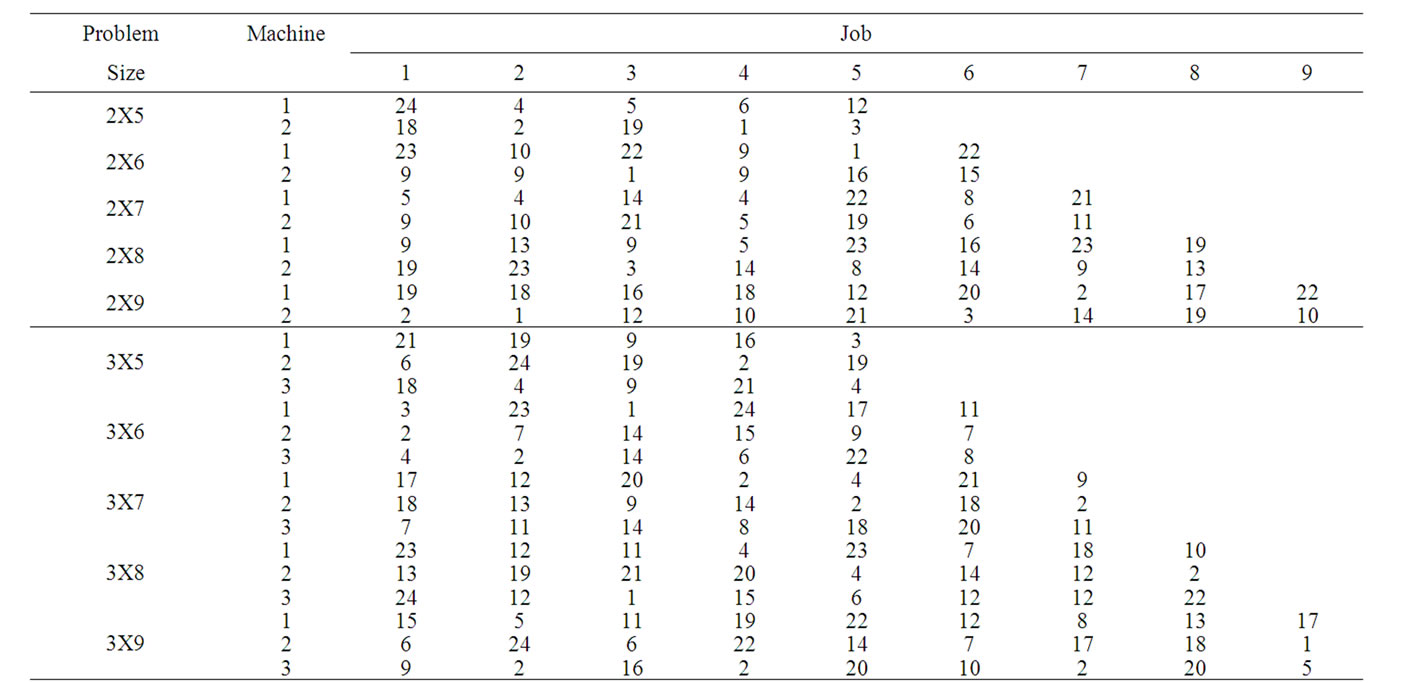
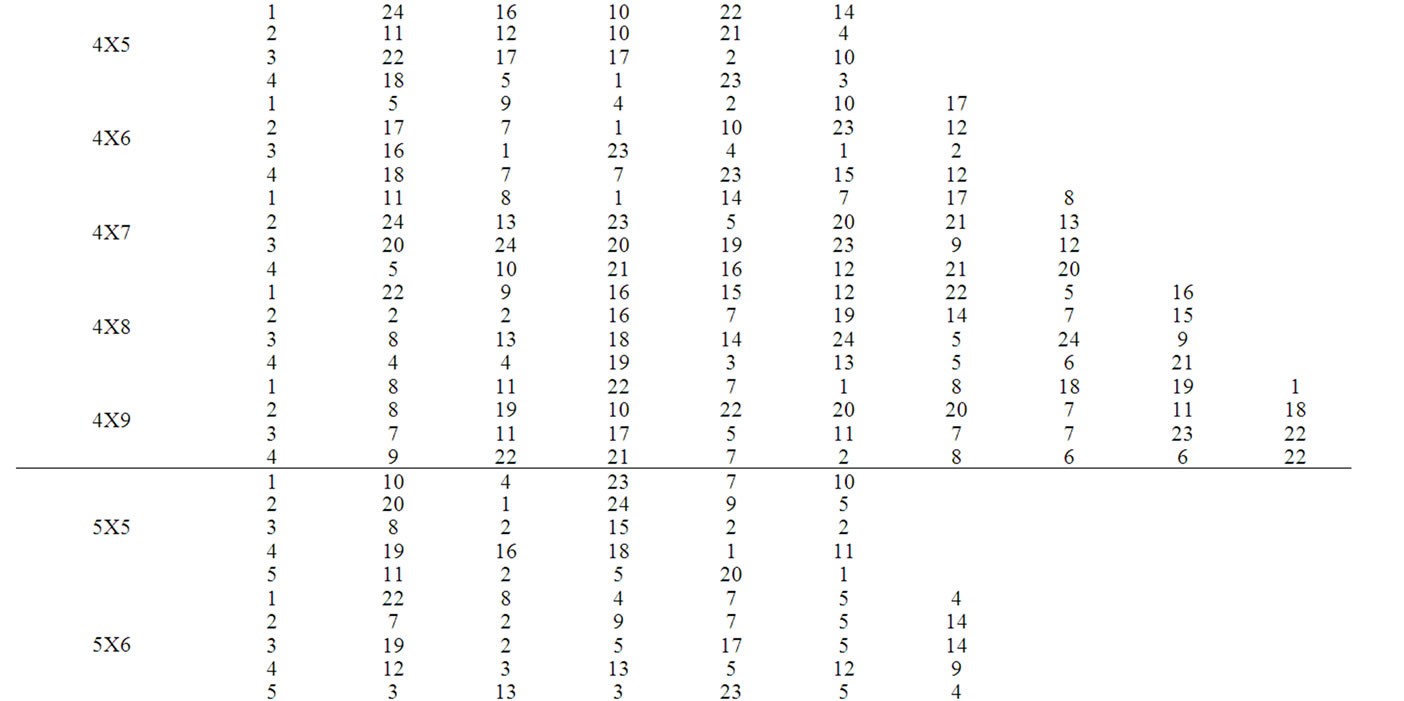

Table 3. Process times of replication 1.
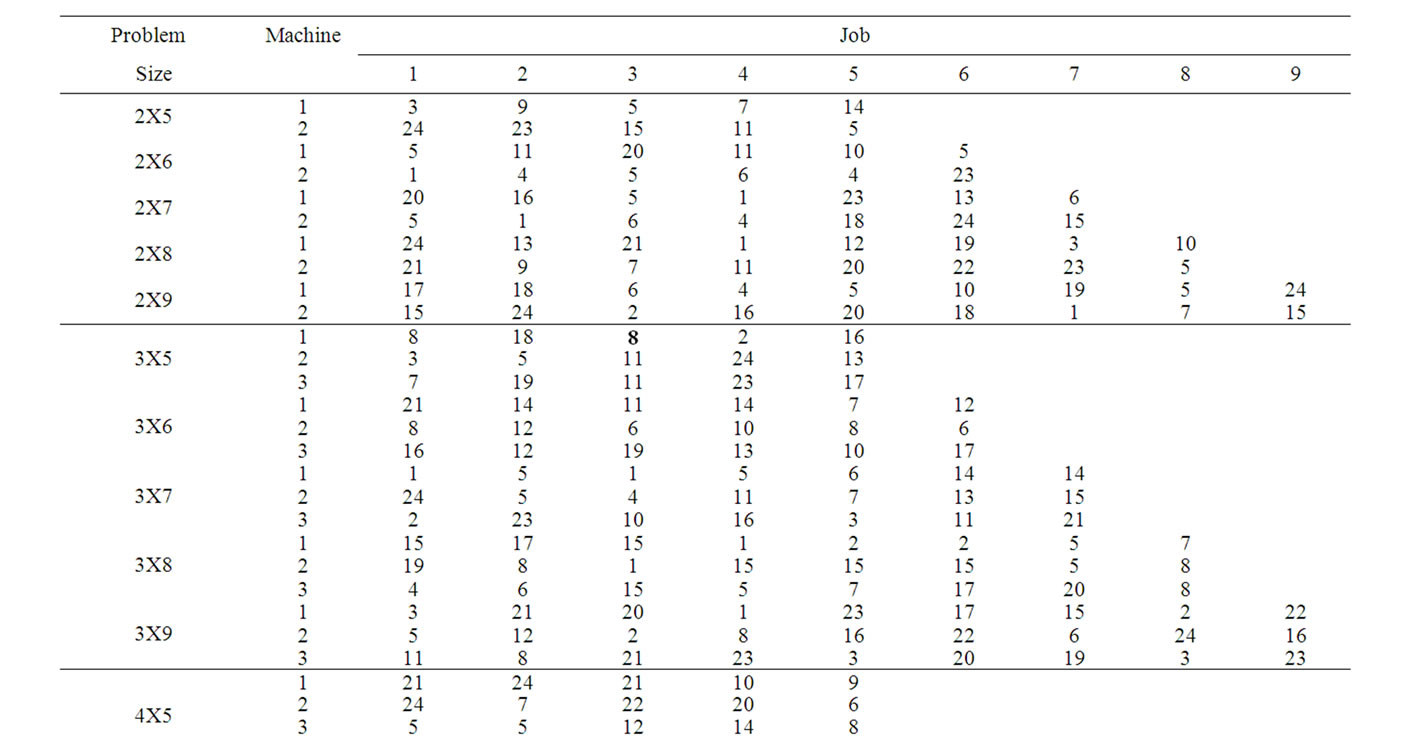

Table 4. Process times of replication 2.
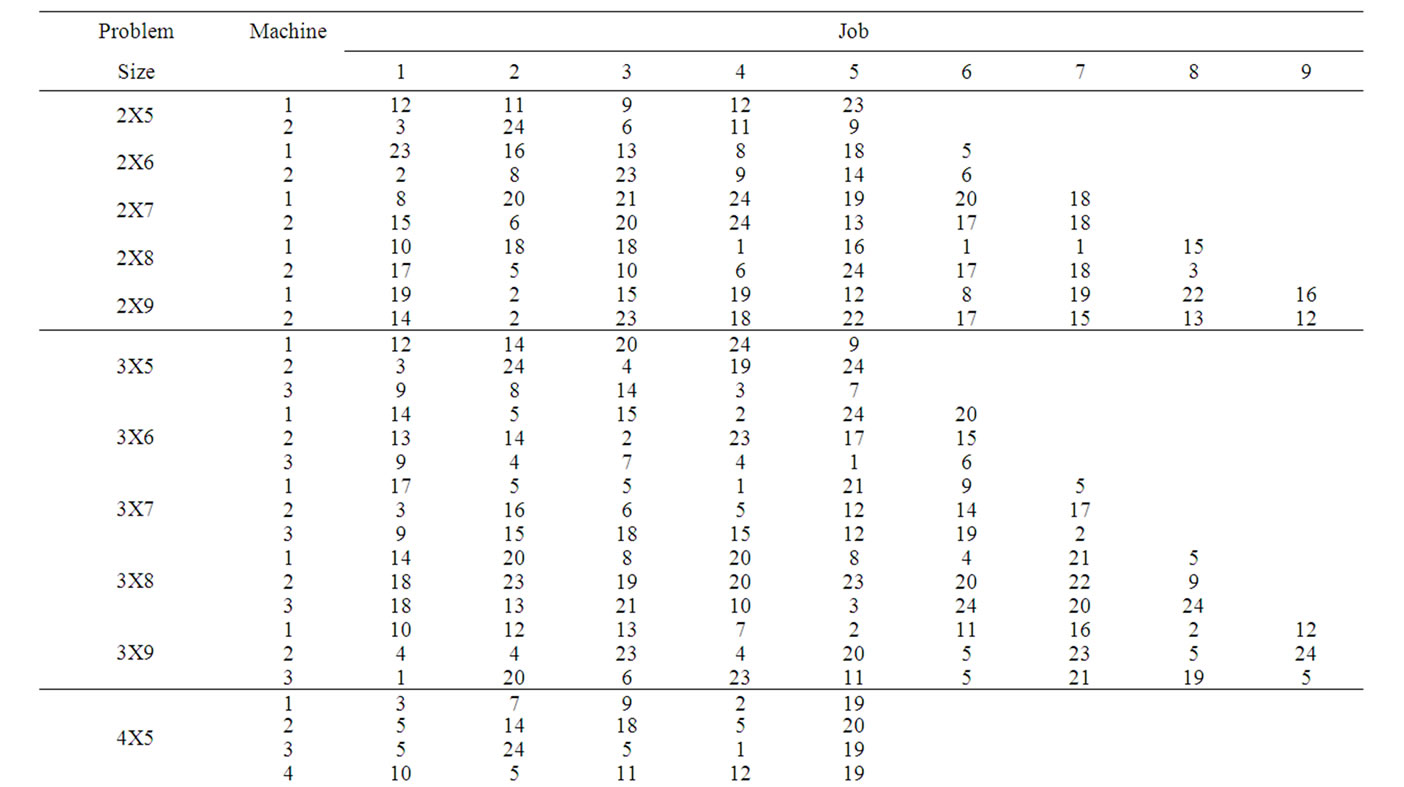
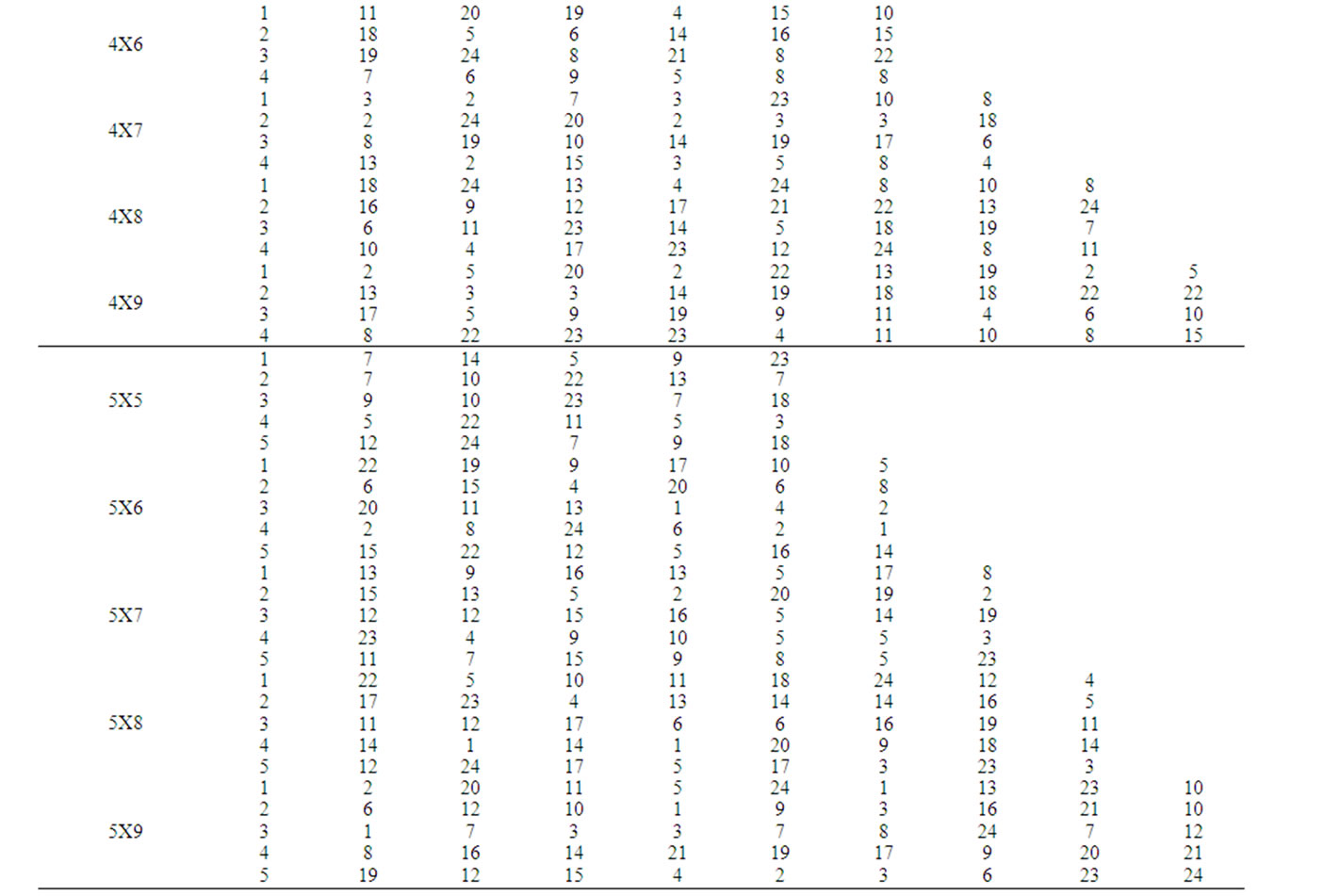
Table 5. Process times of replication 3.



Table 6. Makespan results of the problems.
providing near optimal solution.
Factor “Problem Size” (P):
H0: There is no significant difference between the problems in terms of the makespan [Problem size (P)].
H1: There is significant difference between the problems in terms of the makespan [Problem size (P)].
In the Table 7, the calculated F ratio for the factor, “Problem Size (P)” is 17.60259, which is more than the table F value (1.72) for (19, 80) degrees of freedom at a significance level of 0.05. Hence, the corresponding null hypothesis is to be rejected. This means that there is significant difference between the problems in terms of the makespan.
Interaction “MethodXProblem Size” (MXP):
H0: There is no significant difference between the interaction terms: M1P1, M1P2, ……, M1P20, M2P1, M2P2, ……., M2P20, in terms of the makespan.
H1: There is significant difference between at least one pair of the interaction terms: M1P1, M1P2, ……,M1P20, M2P1, M2P2,…….,M2P20, in terms of the makespan.
In the Table 7, the calculated F ratio for the interaction “Method x Problem Size” is 0.006703162, which is less than the table F value (1.72) for (19,80) degrees of freedom at a significance level of 0.05. Hence, the corresponding null hypothesis is to be accepted. This means that there is no significant difference between the interaction terms, M1P1, M1P2, …………, M1P20, M2P1, M2P2,…….,M2P20, in terms of the makespan.
The mean percentage deviation of the makespan of the problems given by the heuristic from that given by the mathematical model is 2.336 %. As per the ANOVA experiment, there is significant difference between the problems in terms of the makespan and there is no significant difference between the proposed heuristic and the mathematical model as well as between the interaction terms (Method and Problem Size) in terms of the makespan. The proposed heuristic gives optimal makespan for 76.67 percent of the problems. These clearly indicate that the heuristic presented in this paper is an efficient heuristic in terms of providing very near optimal makespan.
6. Conclusions
Production scheduling is the key for the early completion of the components/ products. This paper considered the problem of scheduling n independent single operation jobs on m unrelated parallel machines such that the makespan is minimized. Since, the objective of minimizing the makespan of this problem comes under combinatorial category, obtaining the optimal solution using any of the exact procedures, viz., mathematical model, complete enumeration method, dynamic programming method, branch and bound method, etc., would lead to infeasible alternative for large size problems. Hence, in
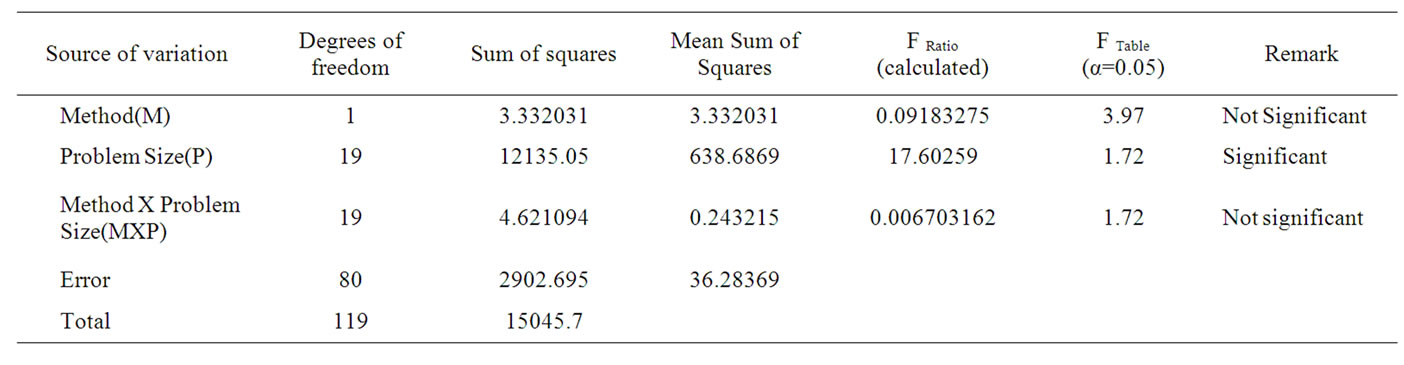
Table 7. ANOVA results.
this paper, an efficient heuristic for this problem is presented to obtain near optimal solution. The acceptability of any heuristic depends on its ability to provide the solution with better accuracy when compared to the optimal solution provided by a suitable mathematical model for a given problem. Hence, a model is also presented for this case. The accuracy can be tested only through a detailed experimentation. Hence, in this paper, a complete factorial experiment has been conducted with two factors, viz. Method (Proposed Heuristic and Model) and Problem Size (No. of Machines X No. of Jobs: 2X5, 2X6, ….,2X9, 3X5, 3X6, ….., 3X9, ..……., 5X5, 5X6, …5X9) with three replications for each experimental combination. From the ANOVA experiment, it is found that there is no significant difference between the methods, viz., “Proposed Heuristic” and “Model” in terms of providing the makespan for scheduling n independent jobs on m unrelated parallel machines. There is significant difference between different problems (2X5, 2X6, …., 2X9, ……., 5X5, 5X6, …5X9) in terms of providing the makepsan. There is no significant difference between interaction terms of “Method” and “Problem Size” in terms of providing the makespan. The mean percent deviation of the makespan obtained by the heuristic from that obtained by the mathematical model is 2.336 %. The percentage of the number of problems for which the optimality has been achieved is 76.67 %. From these results, is clear that the heuristic presented in paper is an efficient one in terms of providing optimal/near optimal makespan for scheduling n independent single operation jobs on m unrelated parallel machines, which is a significant contribution. Since, the proposed heuristic gives results on par with that of the mathematical model, with no statistical significance for the difference between the results, the proposed heuristic is an effective heuristic. The problems of the data set presented can serve as benchmark problems for future researches.
7. Acknowledgment
We thank the anonymous referees for their constructive suggestions, which helped us to improve the paper.
8. References
[1] R. Panneerselvam, “Production and operations management (Second Edition),” PHI Learning Private Limited, New Delhi, 2005.
[2] S. L. Van De Velde, “Duality-based algorithms for scheduling unrelated parallel machines,” ORSA Journal of Computing, Vol. 5, pp. 182–205, 1993.
[3] C. A. Glass, C. N. Potts, and P. Shade, “Unrelated parallel machine scheduling using local search,” Mathematical and Computer Modelling, Vol. 20, pp. 41–52, 1994.
[4] Francis Sourd “Scheduling tasks on unrelated machines: Large neighbourhood improvement procedures,” Journal of Heuristics, Vol. 7, pp. 519–531, 2001.
[5] E. Mokotoff and P. Chretienne, “A cutting plane algorithm for the unrelated parallel machine scheduling problem,” European Journal of Operational Research, Vol. 141, pp. 515–525, 2002.
[6] E. Mokotoff and J. L. Jimeno, “Heuristics based on partial enumeration for the unrelated parallel processor scheduling problem,” Annals of Operations Research, Vol. 117, pp. 133–150, 2002.
[7] A. M. A. Hariri and C. N. Potts, “Heuristics for scheduling unrelated parallel machines,” Computers and Operations Research, Vol. 18, pp. 323–331, 1991.
[8] N. Piersman and W. Van Dijk, “A local search heuristic for unrelated parallel machine scheduling with efficient neighbourhood search,” Mathematical and Computer Modelling, Vol. 24, pp. 11–19, 1996.
[9] M. Ghirardi and C. N. Potts, “Makespan minimization for scheduling unrelated parallel machines: A recovering beam search approach,” European Journal of Operational Research, Vol. 165, pp. 457–467, 2005.
[10] B.Monien and A. Woclaw “Scheduling unrelated parallel machines computational results,” Experimental Algorithms, Springer, Berlin/Heidelberg, Vol. 4007, pp. 195– 206, 2006.
[11] M. Gairing, B. Monien, and A. Woclaw, “A faster combinatorial approximation algorithm for scheduling unrelated machines,” Theoretical Computer Science, Vol. 380, pp. 87–99, 2007.

