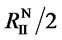iBusiness
Vol.4 No.1(2012), Article ID:18367,5 pages DOI:10.4236/ib.2012.41004
Games in the Bi-Oligopoly Market of High-Technology Equipments
![]()
1Municipal Government, Chaoyang, China; 2Division of Economics, Nanyang Technological University, Singapore City, Singapore; 3School of Science, Shenyang University of Technology, Shenyang, China.
Email: astyao@ntu.edu.sg
Received October 28th, 2011; revised December 13th, 2011; accepted December 28th, 2011
Keywords: Bi-Oligopoly Markets; Nash Equilibrium; Asymmetric Information; Core; Nash Bargaining Solution
ABSTRACT
In this paper we consider the high-tech equipment import market in a developing country. We discuss the behaviors of the foreign supplier, the domestic user, the new domestic supplier, and the role that the government can play in such a bi-oligopoly market. We apply both non-cooperative and cooperative game theory to analyze the market, and conduct comparative static and dynamic analysis on the equilibrium outcomes. We point out that government’s intervention may accelerate the market structure evolution and may improve the welfare outcome.
1. Introduction
In this paper we consider the markets of imported hightechnology equipments in developing countries. We examine a market in which there are a few foreign suppliers and several domestic users. One important feature of this market is characterized by the asymmetric information on the quality of the equipments: before the equipments are used, the users are not certain on their technical performance. In these markets, choosing the equipment produced by one of several suppliers is just like fetching an object from a dark box which contains several objects with similar appearance. In practice the domestic users usually choose their foreign suppliers according to the experience. As a result the barriers against the entry of new suppliers are extremely high, and the old suppliers in the market usually have large monopoly powers.
Another important feature of the high-tech equipments market is that there are only a few individual buyers. We cannot model such a market as an oligopoly market in which a large number of buyers’ decisions are aggregated as a smooth demand curve. In this market the behavior of a single buyer may substantially affect the market equilibrium outcome. We will refer to this type of markets as bioligopoly markets, in which there are one or a few sellers and one or a few buyers. While we can find some articles discussing high-tech equipment imports or exports (refer to [1,2]), we cannot find, however, any theoretical studies on this type bi-oligopoly markets from the IO literature. We believe that non-cooperative game theory and cooperative game theory are powerful tools for dealing with bi-oligopoly. In our study, we came across a large volume of game theory texts and theoretical papers; here we only list a few of them. For example, [3-8] and many other texts and publications provide useful ideas to deal with bi-oligopoly markets. Armed with the game theoretical weapons, as will be seen in the following sections, we are able to conduct a good analysis on our models and derive some interesting and important conclusions. Our presentation is organized as follows.
In Section 2 we give a short discussion on the general characteristics of bi-oligopoly markets. In Section 3 we discuss the non-cooperative game between a user and a new equipment supplier. We consider government interventions in Section 4, modeling the multi-person decisionmaking process of an old supplier, a new supplier, and an equipment user as a cooperative game. We conclude our paper in Section 5.
2. Monopoly Power and Welfare Effects in a Bi-Oligopoly Market
In a bi-oligopoly market, as mentioned above, there are just a few individual sellers and a few individual buyers. The products they want to purchase usually have individually required characteristics. Very often, a particularly designed product has but a single buyer. Because of the existence of uncertainty on the product quality, when choosing a product, the buyer puts priority not on prices but on quality reliance. Usually the buyer chooses suppliers based on his experiences with the products. This leads to high barriers against new suppliers, and against new domestic suppliers in particular.
The monopoly power of the old foreign supplier in the market leads to high equilibrium price, low quantity demanded and a substantial welfare loss of the domestic users in the short-run, and it leads to the supplier’s lack of technical innovation incentives in the long run. These problems have long been observed. It is not uncommon that the governments of the developing countries want to step in these markets to intervene. In some countries, the governments have introduced regulations to encourage domestic investments in high-tech industries, to encourage the foreign firms to cooperate with the new domestic suppliers, and at the same time to subsidize the new domestic suppliers and the domestic users.
The government intervention provides great assistance to the entry of the domestic high-tech equipment suppliers. With subsidies from the government, the domestic suppliers have obvious cost advantage over their foreign counterparts, able to break their “alliance” with the domestic users. Under the pressure of the government intervention, some foreign suppliers are forced to change their strategies, seeking cooperation with the new domestic suppliers, triggering a new coalitional game.
The intervention of government in the bi-oligopoly markets eventually leads to the structural change of the markets. In this subsection we provide a slightly more general account on the dynamics of the market structural change and its performance.
In view of dynamics, any market of high-tech equipments in a developing country experiences three periods of structural evolution along the time horizon: introduction period, development period, and matured period, although there do not exist clear-cut time instants between any two of the consecutive periods.
In the first period, when a new product is introduced triggered by domestic demand, the market is usually controlled by a foreign monopoly supplier. In the second period, attracting by high profit margins and domestic government policies, a few of new foreign or domestic suppliers enter into the market, and the monopoly is replaced by oligopoly, but each supplier still enjoys some supernormal profit because of competitions are more based on brand names (reputations) than on prices. Eventually when the core technology is gradually exposed to the public, the competition between suppliers becomes more and more price-oriented. The equilibrium outcome in the last period is similar to that under perfect competition, each supplier only earning a normal profit (refer to Figure 1). No doubt, during the evolution process, the social welfare

Figure 1. Market structural evolution.
in the domestic country increases step by step. Please do not forget that the domestic government can play an important role to accelerate the structural evolution.
Example 1. Consider the case of a developing country in which the demand for high-tech equipments is as shown in Figure 2. The quantity demanded is in integers, and the maximum number demanded is 4.
In period 1, given the demand curve and the monopoly foreign supplier’s average cost curve (AC = 3.2), the quantity supplied buy the foreign supplier is 1, and the price is 5.
In period 2, soon after a domestic supplier enters, because of not familiar with the new technology and lack of management experience, though it may have cheaper labor cost advantage, its average cost can be as high as the foreign supplier. Here we assume it has the same AC = 3.2. With reputation advantage, the foreign supplier can still charge the profit-maximizing price of 5, selling 1 unit; and the domestic supplier can change a price of 3.4, selling 1 unit. The total number of high-tech equipments sold is 2.
In period 3, the foreign supplier cooperates to some extent with the domestic supplier, transferring some lowerlevel technology to the domestic supplier and outsourcing part of the production activities to the domestic counter-part, each reducing the average cost to AC’ = 2.8. After a period of time, as the technology becomes wellknown to the public, both firms are under the pressure of potential entrants in an international environment of price competition. Eventually each can only charge a price equal to the reduced average cost 2.8. The total demand in this domestic country increases to 4.
Please note that the government of the developing country can play an important role in period 2 through period 3, which will be discussed in more detail in the next two sections.
3. Non-Cooperative Game between the New Supplier and the Equipment User
In the following two sections, our discussions will focus
Figure 2. Supply and demand in a high-tec equipment market.
on the details of the behaviors of the players in the bioligopoly market.
Consider a high-tech equipment market where originally there are a foreign incumbent supplier and a domestic user. Suppose a new domestic supplier (NEW) is considering whether or not to enter. In the first stage of the game, this new supplier chooses between “don’t enter” (DE) and “enter” (E). In the first case the game ends and the market is not changed. In the second case the production of the new supplier could be successful or unsuccessful, determining by Nature with probabilities δ and 1-δ assigned to each of the states. In the second stage, the client chooses between “don’t use” (DU) and “use” (U) the product of the new supplier’s. This game is depicted by the following game tree in Figure 3.
New supplier is successful. If the product is not immediately used by the user, the new supplier can register the product to get some reward r in reputation. Let s be the entry costs. Then in this case the payoff to the new supplier is r – s. On the other hand, if the product is immediately used by the client, a stream of profits earned from the user will be generated. Let p be the present value of this profit stream. Then the total payoff to the new supplier is r – s + p > 0. Now consider the case when the production is not successful. If the user does not use it, the payoff to the new supplier is –s. If, however, the user uses the product for once, the payoff to the supplier is –s + ε, where ε is one-period profit earned from the user.
As for the payoffs to the user, if she does not use the new supplier’s equipment, the payoff to her is normalized to 0; if she uses the unsuccessful product of the new supplier, the payoff to her is –ε, and if she uses the successful product of the new supplier, the payoff to her is y – p > 0.
The normal form of the game looks like:
| New/User | Don’t use | Use |
| Don’t enter | 0, 0 | 0, 0 |
| Enter | δr – s, 0 | δ (r + p) – s + (1– δ) e, δ (y – p) – (1 – δ) ε |
Which strategy profile comes up as Nash equilibrium depends on the values of the parameters. In particular, if
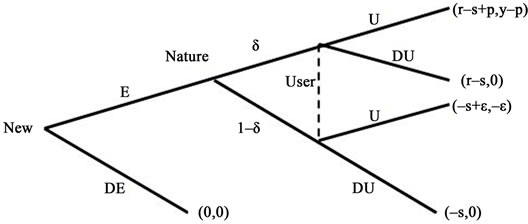
Figure 3. Non-cooperative game between the new supplier and the user.
δ is small such that δ (y – p) – (1 – δ) ε < 0, the new supplier can deduce that the user will not use its product even if it is produced. As a result he will not enter the market (δr – s < 0). In this case the only NE is
Consider now the case with r – s > 0 and with δ sufficiently large so that δr – s > 0. For the new supplier, entry is the dominant strategy. In order that
To sum up we have:
Proposition 1. Whether or not the entry of a domestic supplier is successful depends on the probability δ of its product being successful and the estimate of the client on the δ-value. When δ is sufficiently small, no domestic supplier intends to enter and the foreign supplier’s monopoly sustains. Even δ is sufficiently large; it may require government’s assistance in order that the user is able to recognize the product quality.
4. Government’s Intervention and the Cooperative Game among User, Domestic Supplier and Foreign Suppliers
As is mentioned above, in a bi-oligopoly market, government’s assistance to the entry of the new domestic supplier is a potential threat to the foreign supplier. It creates an incentive for the foreign supplier seeking cooperation with the potential domestic supplier. This cooperation between the domestic supplier and the foreign supplier could be also beneficial to the domestic side when the core technology in the production has not been completely mastered by the domestic suppliers.
Let us consider a market with two foreign suppliers I and II which form a coalition to maintain the monopoly in the market. Assume that, with the assistance from the government, a new domestic supplier N enters. Facing with N’s entry, each of I and II can choose between “Staying in {I, II}-coalition” (S) and “Collude with N” (C). To introduce some asymmetry, we assume that foreign supplier I is stronger and he has business with a few different countries. That he is forced to cooperate with a domestic supplier in a country will set an example for all the other countries. On the other hand, we assume that foreign supplier II is weaker and he has business in this country only. The following bimatrix depicts the game between I and II to choose between S and C:
| I/II | S | C |
| S |
| R’I, |
| C |
|
|
We will assume that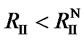 , which means that when the weaker foreign supplier takes away all this country’s business due to her cooperation with the domestic supplier, she makes an improvement. It is easy to see that “C” is a dominant strategy for the weaker foreign supplier, and is thus always played by her. The decision of the stronger foreign supplier, however, is slightly more complicated. There are two cases: 1) when R’I >
, which means that when the weaker foreign supplier takes away all this country’s business due to her cooperation with the domestic supplier, she makes an improvement. It is easy to see that “C” is a dominant strategy for the weaker foreign supplier, and is thus always played by her. The decision of the stronger foreign supplier, however, is slightly more complicated. There are two cases: 1) when R’I >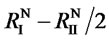 , the NE is
, the NE is 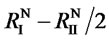 , the NE is
, the NE is
Proposition 2. If the weaker foreign supplier has its major business in China such that cooperation with the domestic entrant becomes her dominant strategy, then the domestic supplier will be successful. On the other hand, the stronger foreign supplier may or may not choose to cooperate, dependent how seriously his businesses with the other countries are affected.
We will now ignore government’s intervention in the following discussion. Let us consider the coalitional game among the domestic user (Y), the foreign supplier (W) and the new domestic supplier (N). Ignoring the empty coalition and those coalitions not containing Y, there are three coalitions should be examined in details: {Y, W}, {Y, N}, and {Y, W, N}. We will denote the coalition values as follows:
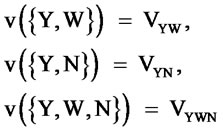 (1)
(1)
Here we assume that 0 < VYN < VYW < VYWN. The main reason that the grand coalition {Y, W, N} has the biggest value is because it combines both of the more advanced technology advantage of the foreign supplier and the cost advantage of the domestic supplier. And for all other coalitions S we define v (S) = 0.
We will consider the existence of a core solution. We are looking for (xY, xW, xN) ≥ (0, 0, 0) such that
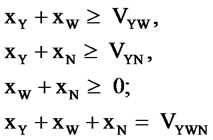 (2)
(2)
Proposition 3. Under our assumption 0 < VYN < VYW < VYWN, the core is always nonempty.
Proof. In fact for any ε > 0 sufficiently small, define xY = VYW – ε, xW = ε, xN = VYWN – VYW. Then it is easy to verify: xY + xW = VYW, xY + xN = VYWN – ε > VYN (for ε > 0 small), xY + xW + xN = VYWN.
Q.E.D.
In view of Proposition 3, the core in general contains infinitely many outcomes, and which outcome in the core will be realized as the solution of the cooperative game actually depends on the bargaining power of the foreign supplier as one side and {Y, N}-coalition as the other side.
At the beginning when the domestic supplier is completely ignorant to the technology, i.e. VYN = 0, the foreign supplier may regard (M, 0) as the status quo, where M is its monopoly profit. As a result the solution looks like
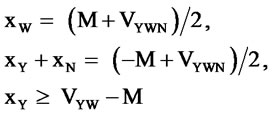 (3)
(3)
In a dynamic process, VYN and VYWN may increase together with time. At each instant τ, the foreign supplier may regard (M, VYN (τ)) as the status quo, and only accept a solution as least as good as
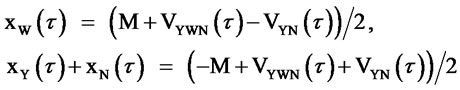 (4)
(4)
In particular, in case the foreign supplier is able to control the technology leakage, it will try to keep its core technology secret in order to make sure that VYN (τ) is never so big, maintaining
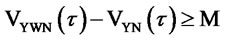 (5)
(5)
Summing up briefly we have Proposition 4. In the dynamic process of the cooperation of the foreign supplier, the domestic supplier and the domestic user, while the domestic supplier can acquire some of the advanced production technology to strengthen its bargaining position, the foreign supplier will try to keep the core technology under private control so that its net profit will not be reduced in the long-run.
Now we consider the role of the government. It could introduce policies encouraging technology transfer from foreign suppliers to domestic suppliers. For example it could give priorities of entering the domestic market to those foreign suppliers who agree to transfer technology to and cooperate with their domestic counter-parts.
Based on the idea in Proposition 4, in the cooperation with the domestic supplier, the foreign supplier has a tradeoff in technology transferring. On the one hand, more advanced technology is transferred to the domestic supplier means larger part of the production task will be
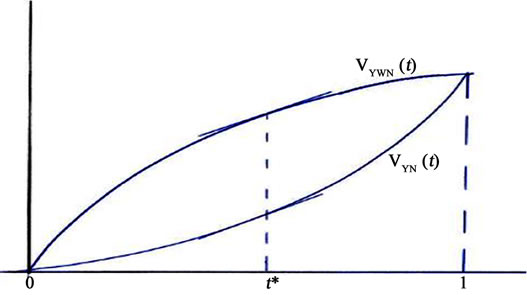
Figure 4. Maximum level of technology transfer.
given to the domestic supplier, lowering the production costs and increasing the “size of the pie” VYWN shared by the three parties involved. In this sense, if we use t to represent the percentage of technology transferred, VYWN(t) could be regarded as an increasing function in t. On the other hand, the higher level of advanced technology has been transferred to the domestic supplier, the stronger bargaining position for the coalition {Y, N}, which implies that VYN (t) is also increasing in t. We may assume that VYWN(t) and VYN(t) are continuous functions defined on the interval [0, 1]. When government encourages the cooperation between the domestic supplier and the foreign suppliers, it at the same time triggers the competition among the potential foreign suppliers in entering this market. A foreign supplier who completely refuses technology transfer will be unlikely accepted as a cooperator. This implies both of M = 0 and VYWN(0) = 0.
As t increases, it is reasonable to assume that VYWN(t) increases in a decreasing speed, i.e. VYWN(t) being a concave function. On the other hand, for the increasing function VYN (t), obviously we have VYN (0) = 0; and if technology were completely transferred to the domestic supplier, then the participation of the foreign supplier is no longer significant, which implies VYN(1) = VYWN(1).
From the result in the last subsection, we now have:
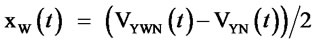 (6)
(6)
Note that xW(t) is continuous on [0, 1], there must exists a t* at which xW is maximized. It is reasonable to assume that the process of technology is from less advanced level to more advanced level. Our above argument leads to:
Proposition 5. Under the intervention of the government, the foreign supplier will eventually agree to cooperate with the domestic supplier, agreeing to transfer the production technology up to a level of t*.
The result of Proposition 5 can be interpreted by Figure 4.
5. Conclusions
We have studied the bi-oligopoly markets of high-tech equipments in developing countries. The most important result is probably that the government can play a very important role in these markets to accelerate the structure evolution and improve the welfare outcomes.
While we present Proposition 5 in the last section, it is just a conclusion in the not-very-long long run. In a bigger time scale, every type of technologies will eventually become out-of-date unless it is being improved by R & D. Any developing country, while on the one hand should introduce open-door policy, encouraging technology transfer from the developed countries, on the other hand, must also invest in R & D, trying to catch up with the developed countries in every field.
REFERENCES
- D. Archibugi and C. Piietrobelli, “The Globalsation of Technology and Its Implication for Developing Countries, Windows of Opportunity or Further Burden?” Technological Forecasting & Social Change, Vol. 70, No. 9, 2003, pp. 861-883. doi:10.1016/S0040-1625(02)00409-2
- A. H. Amsden, “Import Substitution in High-Tech Industries: Prebisch Lives in Asia!” Cepal Review, Vol. 82, 2004, pp. 75-89.
- D. Fudenberg and J. Tirole, “Game Theory,” MIT Press, Cambridge, 1991.
- L. S. Shapley, “A Value for n-Person Games,” in: H. W. Kuhn and A. W. Tucker, eds., Contributions to the Theory of Games, Vol. II, Princeton University Press, Princeton, 1953, pp. 307-317.
- L. S. Shapley and M. Shubik, “Competitive Outcomes in the Cores of Market Games,” International Journal of Game Theory, Vol. 4, No. 4, 1975, pp. 229-237. doi:10.1007/BF01769270
- K. Binmore, A. Rubinstein and A. Wolinsky, “The Nash Bargaining Solution in Economic Modeling,” Rand Journal of Economics, Vol. 17, No. 2, 1986, pp. 176-188.
- R. Amir, S. Sahi, M. Shubik and S. Yao, “A Strategic Market Game with Complete Markets,” Journal of Economic Theory, Vol. 51, No. 1, 1990, pp. 126-143. doi:10.1016/0022-0531(90)90054-N
- S. Houseman, “Outsourcing, Offshoring and Productivity Measurement in United States Manufacturing,” International Labor Review, Vol. 146, No. 1-2, 2007, pp. 61-80. doi:10.1111/j.1564-913X.2007.00005.x


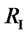 ,
, 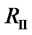
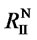
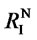 , 0
, 0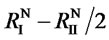 ,
,