ABSTRACT

The problems of e-commerce investment have been a chronic painful agony, due to its large investment, low profits and long payback periods, etc. In this work, we deeply study e-commerce profits, analyze the investment patterns and establish investment recovery matrices. We also propose the great product matrix concept for solving continues investment, in an attempt to find an optimal solution to maximize the investment profits.

1. Introduction

The rapid development of e-commerce not only created business miracle, but also consumed large amount of idle investing capital at the same time. If the idle investment cannot be utilized efficiently, it will cause a waste of money and, consequently, affect the entire e-commerce market development.

Although the development of e-commerce market in China is still in its early stage, it evolved rapidly with emergence of various e-commerce websites and trading websites one after another. Starting from 2006, the ecommerce experienced a period of sustaining growth and came to an outburst in the investment from 2008 to 2010. This is the second climax of e-commence investment in China [1]. Nevertheless, China had a quite rough time developing e-commerce, due to the turmoil in the world economical network. China has faced a fierce competition in the ecommerce market, as misled by the idea: “non-profitable”, and the ignorance of its internal operations. In addition, there are quite a few of websites that are blindly in the pursuit of “national first”, “China’s largest”. As a result, many websites are making zero incomes and forced to shut down [2].

Given such history, many experts conducted extensive researches, trying to find a perfect investment strategy and discover its regular behaviors. Yingzi Xiong, from Xiamen University, proposed a pioneer strategy and found that investors seizing the opportunity beforehand with the help of strong positive feedback from network economy have become a powerful tool in winning competitions [2]. Ouyang et al., from Wuhan University, took advantage from payback period, discounted cash flow method, and measured return on investment (ROI) on e-commerce system’s sustainability [3]. Many researchers such as Fuhai Yan have considered the real option approach and its applications in investment decision making [4]. Wang and Li et al., put the idea into practice [5]. They treat project investment as execution of real option approach, and use it as a competition measurement. This solved the calculation of net present value investments, hence predicted the best opportunity to enhance postapplication e-commerce system so as to strengthen the degree of competitiveness of enterprisers and other concerns.

All the evidences that we mentioned above indicates that more and more people have turned their attentions on the field of e-commerce. Various business models are emerging endlessly, and the prosperous e-commerce market also broadened the investment opportunity. Based on this, this paper studied e-commerce investment recovery with respect of its investment patterns, used ROI to establish matrices, and proposed matrix great product concept. We also solved the problem of continuous investment by matrix multiplication, which is applied to the e-commerce investment model, in order for enterprisers to make highest profit possible. We finally conclude that e-commerce continuous investment models are better than the discrete investment patterns.

2. Some Raised Issues

Enterprises in a planning period will be free to cast the idle funds, recover, and then collect back the principals and interests. This process is the so-called continuous investment and repeats itself over and over again until all the principals and interests are recovered at the end of planning periods. Among rival enterprises, pay back from the investment on a single product often does not look very promising. In order to achieve the aim of sustainable development and increase profits, enterprises always use continuous investment and updated products. With the presence of the hot e-commerce market, how to effectively increase the investments is an inevitable problem at front. There are two criterions for gauging the effectiveness of e-commerce market investment, namely, investment returns and investment recovery respectively [6]. We will focus on investment recovery and use the concept of matrix great product to study the enhancement of the effectiveness of the e-commerce investment model.

Having shown those backgrounds discussed above, we propose to use matrix great product method to optimize ecommerce investment model. We illustrate it via the following example:

In e-commerce market, we are considering to invest to a project in different models in five years [7]:

• Model 1: Invest money throughout the first four years and recover 115% of the invested money

• Model 2: Invest at the beginning of the third year and recover 125% of the invested money at the end of the last year

• Model 3: Invest at the beginning of the second year and recover 140% of the invested money at the end of the last year

• Model 4: Invest at the beginning of each year and recover 106% of the invested money at the end of each year Clearly, this is a continuous investment problem, the common solutions are the followings:

1) Linear Programming Approach: let 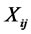be the invested money in the i^th year using j^th model, then it follows that:

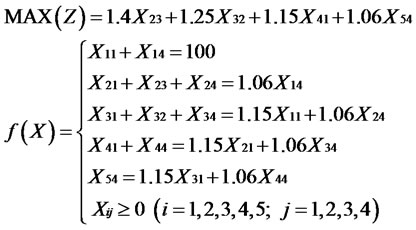
We then can simplify 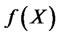to a standard form to obtain the optimal solution.

2) Dynamic Programming Approach: in this method, we consider the five years as five stages. We further denote that 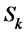be the sum of the profit over all four investment models in the k^th year, be investment for j^th at j^th year, 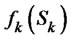be the optimal value function. 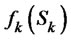stands for the recoverable maximum principal and interest, ranging from the beginning of the year K to the end of the fifth year by using the optimal investment strategy on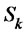. The final step is to list the recurrence relations and boundary conditions for recursion solution [8].

Those two methods mentioned above are difficult to execute due to excessive number of unknown variables. This paper explored the use of investment recovery to establish investment-income matrix. In the next section, we discuss some the observations and principles that we discovered in our work.

3. Principles

We assume without lost of generality that invested money can only be recovered after i period. It is not possible to recover the invested money before i period, hence, , when i > j. Therefore, 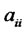can be considered as the money that had not been used during the period i. Since its recovered money equals its invested money,.

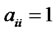• Lemma: investment-income matrix is an n × n upper triangular matrix, and its diagonal elements are all 1.

Using induction method, and a series of proofs and analysis, we can easily get Theorem 1.

• Theorem 1: assume that is an n × n investmentincome matrix, then we get the following properties:

1): All the investment-income matrices 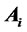are upper triangular matrix with diagonal 1 2):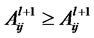

Following the same reasoning, we get the following corollary:

Corollary: if A is an n × n investment-income matrix, for.

Then, we divide the whole planning period into n – 1 individual sub-periods, and denote the be the recoverable funds from period i to j, there is no recovery during the whole periods. Then 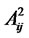stands for the largest recoverable funds from the period i to j, and there is at most once invest and recover among the durations. Similarly, the stands for the largest recoverable funds from the period i to j, and there is at most l – 1 invests and recovers among the durations. As the result, the investment-income matrix A by n × n denotes the investment recovery of all the invest models from period 1^st to n − 1. 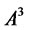Due to the reasoning that there is at least once, twice, ···, n − 2 invests and recovers, so by, we can easily get, , ···, and at most, so do the optimal investment strategy and the largest investment recovery, and, then we get the Theorem 2:

• Theorem 2: assume that is an n × n investmentincome matrix, and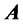, , 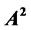, ··· are all convergent, then each limit power law 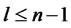[8].

4. Algorithm Summary

On the basis of all the above theorems and proofs, by taking advantage of investment recovery, we can draw the methods and algorithms to establish investment-income matrix:

1) Make certain an investment-income matrix according to the recovery and shortest recovery period of the planning period and the optional investment.

a) The matrix order n is determined by the planning period n₁ and shortest recovery period n₂, that is

.

b) The matrix row sequence i is correspondent with the serial number of cast funds, column j is corresponding to the recovery period number.

c) Determine the matrix elements 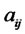by using the investment recovery of alternative projects.

2) By using the matrix great production, we can calculate from, and.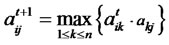

3) Check, if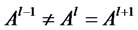, go to step 4), or make t = l + 1, and back to step 2).

4) Investigate the calculation o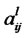f, if

, we define another matrix

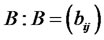, , which is the near cast period before j.

5) Using the optimal cast-recover strategy, according to, we can get the largest recovery rate by investing at the period i and recovering at period j. The recovery rate multiplies the cast funds at the period i, we can calculate the largest recoverable capital and profit of period j. Finally, by the matrix B, we can trace back and find the correspondent optimal cast-recover strategy, and in the next part, we are going to explain it to you in details.

• 5. Example

• Example 1: we use the matrix method to solve the investment problem given in this first part.

• Solutions:

1) Establish the investment-income matrix A:

2) Calculate according to the formula

3) According to 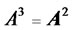m, m denotes that is the great production of 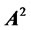and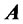. We can get,

4) Thus, by calculating the elements of the matrix, we can finally get the corresponding element 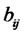of matrix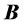, which is as follows:

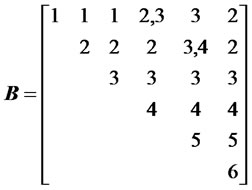
5) For, so the largest recovery rate of this investment is 1.484. From, we trace the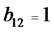, hence, the optimal investment strategy track is 1→2→6.

Therefore, the best investment strategy of this investment is: in the first year, cast 1 million RMB to the model IV, and you can get 1.06 million RMB recoverable capital and interest at the end of this year, then in the second year, cast the 1.06 million RMB to the model III, and recover the total capital and interest until the fifth year, which is the largest capital and interest we can get. The number is 100 × 1.484 = 148.4 (million RMB).

• Example 2: if this department has raised another 200,000 RMB in the second year, and this funds are required to be recovered at the end of the forth year, how to distribute the 20 million under the four modes to maximum the total amount of capital and interest at the end of the forth year?

• Solutions: we can use the results of the Example 1. Because the funds is invested in the second year, so we need to check the second row of matrix 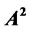and. For, , and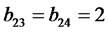, so the best investment strategy of this fund are:

1) Cast the 200,000 RMB to model IV in the second year, and recover at the end of this year, then cast the capital and interest 212,000 RMB (200,000 × 1.06) to the model I in the third year.

2) Cast the 200,000 RMB to model I in the second year, and recover at the end of the third year, then cast the capital and interest 230,000 RMB (200,000 × 1.15) to the model IV in the fourth year.

These two strategies can both maximum the largest capital and interest at the end of the forth year, that is 243,800 RMB (200,000 × 1.19).

6. Conclusions and Discussion

By the above analysis and derivation, we can see that when we are faced with the fast-changing Internet age and e-commerce market, we can excellently solve continuous investment problems by using investment recovery rate and the concept of matrix great product to establish matrix, which is just the innovation point of this paper. We all have experienced the conveniences of the e-commerce, which now has played an increasingly vital role in the daily life, in terms of this, we should notice the risk of investment and the huge waste of the money. In view of nowadays investment to the e-commerce, a great amount of money is just wasted by false investment models and strategies, although the e-commerce have the enlarging tend of authoring the daily life of the overall people, we still have to inspect it clearly and find a sensible way to deal with our money, in other words, optimal investment strategy.

Many actual truths have certified to us that we cannot obtain the largest recovery unless we use the correct method. Hence, in this paper, we introduce the application of the matrix great production method to enhance the business investment effect and help investors get more profits. Of course, we should also see that the further studies on an extension of the development of matrix multiplication, and the best strategies in case of limited investment, both of which are in progress.

REFERENCES