iBusiness
Vol.2 No.1(2010), Article ID:1438,9 pages DOI:10.4236/ib.2010.21004
A Study of Quantum Strategies for Newcomb’s Paradox
![]()
Department of Information Sciences and Arts, Toyo University, Saitama, Japan.
Email: mihara@toyonet.toyo.ac.jp
Received August 24th, 2009; revised October 11th, 2009; accepted November 23rd, 2009.
Keywords: Game Theory, Newcomb’s Paradox, Quantum Strategy, Meyer’s Strategy
ABSTRACT
Newcomb’s problem is a game between two players, one of who has an ability to predict the future: let Bob have an ability to predict Alice’s will. Now, Bob prepares two boxes, Box1 and Box2, and Alice can select either Box2 or both boxes. Box1 contains $1. Box2 contains $1,000 only if Alice selects only Box2; otherwise Box2 is empty($0). Which is better for Alice? Since Alice cannot decide which one is better in general, this problem is called Newcomb’s paradox. In this paper, we propose quantum strategies for this paradox by Bob having quantum ability. Many other results including quantum strategies put emphasis on finding out equilibrium points. On the other hand, our results put emphasis on whether a player can predict another player’s will. Then, we show some positive solutions for this problem.
1. Introduction
Quantum mechanics has been incorporated into many fields called information. The most famous results are a quantum factoring algorithm by Shor [1] and a quantum database search algorithm by Grover [2]. Moreover, the studies on quantum information have succeeded in such as quantum computation, quantum circuit, quantum cryptography, quantum communication complexity, and so on. Recently, game theory based on quantum mechanics, quantum game theory, has been also proposed and it has been shown that quantum game theory is more powerful than classical one.
Game theory is one of the most famous decision making methods and has been used in many situations both theoretically and practically. There had existed the basic concept with respect to these games since early times but in corporation with Morgenstern, von Neumann [3] firstly constructed the theory systematically. However, the main principle of this theory was based on classical physics although he was familiar with quantum mechanics.
In 1998, for a coin flipping game, Meyer [4] proposed a quantum strategy for the first time and showed that the quantum strategy has an advantage over classical ones. This game is called PQ Penny Flip.
PQ Penny Flip: The starship Enterprise is facing some immanent—and apparently inescapable—calamity when Q appears on the bridge and offers to help, provided Captain Picard can beat him at penny flipping: Picard is to place a penny head up in a box, whereupon they will take turns (Q, then Picard, then Q) flipping the penny (or not), without being able to see it. Q wins if the penny is head up when they open the box.
This game is a two-player zero-sum game and the probability that each player wins is at most 1/2 with classical strategies. Meyer showed a quantum strategy with which Q can always win by using a superposition of quantum states effectively. In this game, Picard is constrained to play classically. The quantum strategy is then executed in the following way. Let 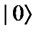 and
and 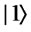 represent the head and tail of the penny, respectively. First, Picard prepares
represent the head and tail of the penny, respectively. First, Picard prepares 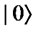 and Q applies a Walsh-Hadamard operation
and Q applies a Walsh-Hadamard operation 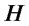 defined in the next section to the state:
defined in the next section to the state:

Next, Picard decides classically whether he flips it or not. However, the state does not change even if Picard flipped it. Finally, Q applies ![]() to the state and always obtains
to the state and always obtains . This means that Q always wins.
. This means that Q always wins.
Moreover, he also showed the importance of a relationship between quantum game theory and quantum algorithms.
Later, other types of quantum strategies have been also proposed. In their strategies, all the players can use quantum operations. For example, Eisert et al. [5] proposed a quantum strategy with entanglement for a famous two-player game called the Prisoner’s Dilemma (also see Du et al. [6,7], Eisert and Wilkens [8], and Iqbal and Toor [9]). In their strategy, entanglement plays an important role. For another famous two-player game called the Battle of the Sexes, Marinatto et al. [10] also proposed a quantum strategy with entanglement. For these games, they showed quantum Nash equilibriums different from classical ones. Furthermore, there are many results being related to games such as the Monty Hall problem by D’Ariano et al. [11], Flitney and Abbott [12], and Li et al. [13], Parrondo’s game by Flitney et al. [14], games in economics by Piotrowski and Sładkowski [15–17], Newcomb’s paradox by Piotrowski and Sładkowski [18], and so on.
In this paper, we study Newcomb’s problem. Newcomb’s problem is a thought experiment between two players, Alice and Bob. Alice is a common human being. On the other hand, Bob may be a wizard having an ability to predict the future, or not. Bob can predict Alice’s will if he is a wizard. Then, the problem is as follows:
Newcomb’s problem: Bob prepares two boxes, Box1 and Box2, and Alice can select either Box2 or both boxes. Box1 contains $1. Box2 contains $1,000 only if Alice selects only Box2; otherwise Box2 is empty($0). Which is better for Alice?
No one knows the answer except Bob. Namely, there exists no best classical strategy. Therefore, this problem is called Newcomb’s paradox. We show some quantum strategies for Newcomb’s paradox by using entanglement.
It is thought that entanglement is essential as the main power of quantum information and many results mentioned above also have used entanglement effectively. First, we show some basic quantum strategies with entanglement. In the other related studies mentioned above, each player operates only each assigned qubit although the states are entangled. On the other hand, our proposed strategies operate not only one qubit but also states between two qubits. Consequently, we show that our quantum strategies with entanglement are more powerful than classical ones.
Finally, we show some quantum strategies for Newcomb’s paradox. Piotrowski and Sładkowski showed a quantum solution for Newcomb’s paradox by using Meyer’s strategy [18]. Newcomb’s paradox is whether a player can predict another player’s will. We also study this problem by applying our strategies. Then, we obtain positive results. That is, in some case, a player can predict another player’s will.
The remainder of this paper has the following organization. In Section 2, first, we define notations and basic operations used in this paper. Moreover, as the tools of our quantum strategies, we show two fundamental lemmas with relation to entanglement. In Section 3, we denote two types of two-player zero-sum games. We then show that in these games, each player cannot win with certainty with classical strategies but one side player can win with certainty with quantum ones. In Section 4, we study Newcomb’s paradox. We modify this problem and show some quantum strategies to it by using the results in Section 3. Finally, in Section 5, we provide some concluding remarks.
2. Preliminaries
In this section, first, we define some notations used in this paper. Let  be a bitwise exclusive-or operator, i.e.,
be a bitwise exclusive-or operator, i.e.,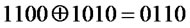 . Let
. Let ![]() be the negation of a bit
be the negation of a bit ![]() for
for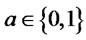 , i.e.,
, i.e., . Moreover, let
. Moreover, let ![]() be the inner product of
be the inner product of  and
and![]() , where
, where  and
and  for
for  (
(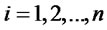 ).
).
Next, we define some basic operations. Let 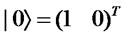 and
and , where
, where  is Dirac notation and
is Dirac notation and  is the transposed matrix of a matrix
is the transposed matrix of a matrix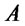 . Let
. Let 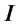 be the
be the  identity matrix. This operation means no operation. A Walsh-Hadamard operation
identity matrix. This operation means no operation. A Walsh-Hadamard operation 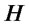 is
is
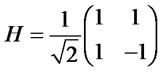
(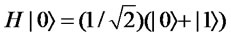 and
and ). Note that
). Note that . This operation is used when we make a superposition of states. As an operation used when they flip a coin classically, players use an operation
. This operation is used when we make a superposition of states. As an operation used when they flip a coin classically, players use an operation ,
,
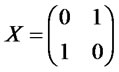
( and
and ). We also define a phase-shift operation
). We also define a phase-shift operation  by
by

( and
and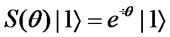 ), where
), where .
.
Moreover, we define an operation between two qubits. Here, we denote an ![]() -qubit state by
-qubit state by , where
, where  is a tensor product. Then, let
is a tensor product. Then, let  be a Controlled Not gate,
be a Controlled Not gate,
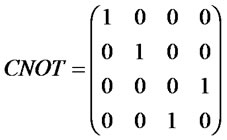
( , where the first bit
, where the first bit  is the controlled bit and the second bit
is the controlled bit and the second bit  is the target bit). We denote the operation by
is the target bit). We denote the operation by  when the
when the 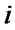 -th bit is the controlled bit and the
-th bit is the controlled bit and the  -th bit is the target bit.
-th bit is the target bit.
Finally, we show two basic results operating entangled states. These results can be used as tools of making a specific state in order that one side player always wins games by using our quantum strategies mentioned in the following sections.
Lemma 2.1 Let
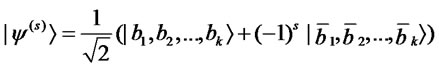
be a  -qubit entangled state, where
-qubit entangled state, where  (
( ) and
) and . Then,
. Then,
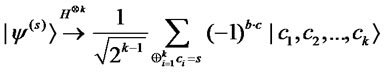
when we apply the Walsh-Hadamard operation  to all the qubits of
to all the qubits of .
.
Proof. When we apply  to all the qubits of
to all the qubits of ,
,
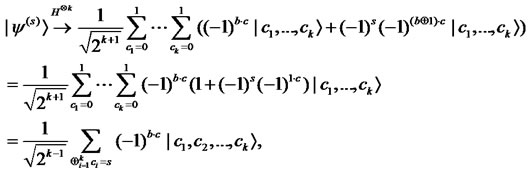
where . Then, the statement of this lemma is then satisfied.
. Then, the statement of this lemma is then satisfied.
This lemma means that a player can obtain a state  satisfying
satisfying 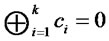 if he makes the state
if he makes the state 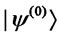 and that he can obtain a state
and that he can obtain a state  satisfying
satisfying  if he makes the state
if he makes the state .
.
Next, we show a result used as a player’s quantum strategy when another player flips coins classically.
Lemma 2.2 Let  be the
be the  -qubit entangled state of Lemma 2.1, and let
-qubit entangled state of Lemma 2.1, and let

Now, let the operation  be applied to some qubits of
be applied to some qubits of , i.e.,
, i.e.,

Figure 1. Two players’ payoff matrix
where . Note that
. Note that  if
if  has been executed. Then,
has been executed. Then,
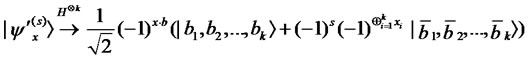
Proof. When we apply  to all the qubits of
to all the qubits of ,
,
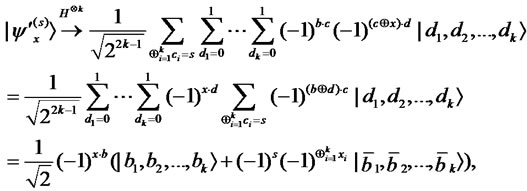
where the last expression is obtained by noting that except for the states corresponding to 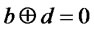 and
and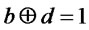 , the states vanish. The statement of this lemma is then satisfied.
, the states vanish. The statement of this lemma is then satisfied.
3. Quantum Strategies Using Entangled States
3.1 Strategic Games
We denote a strategic game ![]() as
as , where
, where
 is the set of players,
is the set of players,
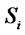 is the set of strategies of player
is the set of strategies of player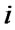 , and
, and
 is the payoff function of player
is the payoff function of player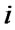 , i.e.,
, i.e., 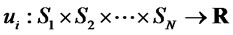 (the set of real numbers).
(the set of real numbers).
The game ![]() can be given also by a matrix shown in Figure 1. For more details, we shall refer the reader to the books by, e.g., references [22,23]. For two players,
can be given also by a matrix shown in Figure 1. For more details, we shall refer the reader to the books by, e.g., references [22,23]. For two players,  ={Alice, Bob}, the set of Alice’s strategies is
={Alice, Bob}, the set of Alice’s strategies is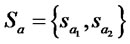 , and the set of Bob’s strategies is
, and the set of Bob’s strategies is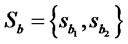 . Then, each value of Alice’s payoff function is
. Then, each value of Alice’s payoff function is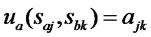 , and each value of Bob’s payoff function is
, and each value of Bob’s payoff function is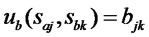 , where
, where . If
. If  for any
for any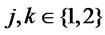 ,
,  can be omitted. In certain circumstances, we represent a value of payoff function not as a real number but as some players’ win or loss, and so on. In addition, quantum strategies are permitted any unitary matrices, i.e., we can make a super
can be omitted. In certain circumstances, we represent a value of payoff function not as a real number but as some players’ win or loss, and so on. In addition, quantum strategies are permitted any unitary matrices, i.e., we can make a super
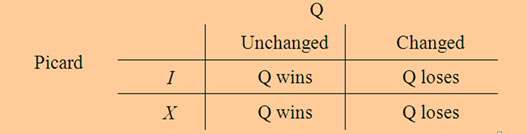
Figure 2. PQ penny Flip

Figure 3. Battle of the sexes
position of some fundamental strategies by quantum strategies.
Now, let us formalize PQ Penny Flip. The set of players is , the set of Piard’s strategies is
, the set of Piard’s strategies is , the set of Q’s strategies is
, the set of Q’s strategies is . Operation
. Operation  means no coin flip, and operation
means no coin flip, and operation  means a coin flip. The payoff matrix is shown in Figure 2. “Unchanged”/”Changed” means that the state of the coin is finally unchanged/changed. Meyer showed a quantum strategy that Q always wins [4].
means a coin flip. The payoff matrix is shown in Figure 2. “Unchanged”/”Changed” means that the state of the coin is finally unchanged/changed. Meyer showed a quantum strategy that Q always wins [4].
Next, we show a simple solution for the Battle of the Sexes using an entangled state. This idea leads to the results of the following subsections. The payoff matrix is shown in Figure 3. Alice prefers movie to soccer, and Bob prefers soccer to movie. However, both prefer having a date.
The strategy is as follows. Alice and Bob share the following entangled state:

where Alice has a first qubit and Bob has a second qubit. In deciding either soccer or movie, both measure the state. Alice/Bob selects soccer when the outcome of the bit is 0, otherwise she/he selects movie. Note that if Alice’s outcome is 0, Bob’s outcome is also 0, and vice versa. Namely, the probability of selecting (Soccer, Soccer)/(Movie,Movie) is 1/2, and the probability of selecting (Soccer,Movie)/(Movie,Soccer) is 0. Therefore, they can have a date with certainty. Moreover, for example, if the payoff of (Soccer,Soccer) is (4,6) instead of (3,5), the probability of selecting (Soccer,Soccer) becomes greater than that of (Movie,Movie) by preparing

as the entangled state, where  is complex numbers satisfying
is complex numbers satisfying  and
and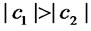 .
.
3.2 ![]() -Coin Even-Odd Games
-Coin Even-Odd Games
First, we denote a zero-sum game using  coins between two players,
coins between two players,  ={Alice, Bob}. Throughout this paper, suppose that Alice is constrained to play classically, i.e.,
={Alice, Bob}. Throughout this paper, suppose that Alice is constrained to play classically, i.e., . Then, we show that neither Alice nor Bob can win the game with certainty.
. Then, we show that neither Alice nor Bob can win the game with certainty.
With only classical strategies but Bob can win it with certainty with our quantum strategy. Here, let H and T
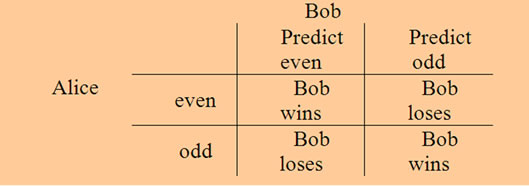
Figure 4. 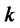 -Coin even-odd check
-Coin even-odd check
represent the head and tail of a coin, respectively.
![]() -Coin Even-Odd Check: First, Alice prepares
-Coin Even-Odd Check: First, Alice prepares 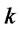 coins and puts them into a box in the state of all the coins being heads, i.e., (H, H,…, H). Suppose that any player cannot see the inside of the box. Next, Bob flips some coins(or not), Alice flips some coins(or not), and Bob flips some coins(or not). Finally, they open the box. Alice wins if the number of H is odd; otherwise Bob wins if the number of H is even.
coins and puts them into a box in the state of all the coins being heads, i.e., (H, H,…, H). Suppose that any player cannot see the inside of the box. Next, Bob flips some coins(or not), Alice flips some coins(or not), and Bob flips some coins(or not). Finally, they open the box. Alice wins if the number of H is odd; otherwise Bob wins if the number of H is even.
Because we can regard this problem as whether Bob can predict Alice’s strategy, the payoff matrix can be also shown as Figure 4. It is obvious that if they use only classical strategies, neither Alice nor Bob can win the game with certainty. However, if Bob uses a quantum strategy, he can win the game with certainty. Now, we show a quantum strategy for this game with which Bob wins with certainty.
Theorem 3.1 For ![]() -Coin Even-Odd Check, there exists a quantum strategy with which Bob wins with certainty.
-Coin Even-Odd Check, there exists a quantum strategy with which Bob wins with certainty.
Proof. We denote H and T by  and
and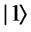 , respectively. This means that Alice prepares
, respectively. This means that Alice prepares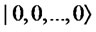 . First, Bob executes the following operation.
. First, Bob executes the following operation.
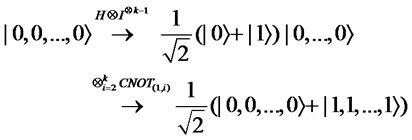
Next, Alice flips the coins using the operations  and
and , because she can only execute classical strategies. Then, the state becomes
, because she can only execute classical strategies. Then, the state becomes
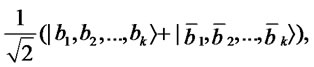
where  (
( ).
).
Finally, by using Lemma 2.1, Bob obtains

Thus, Bob can obtain the bits  satisfying
satisfying . This means that the number of H is even and he can win the game with certainty.
. This means that the number of H is even and he can win the game with certainty.
We can prove the same theorem by using the Meyer’s quantum strategy [4] for  coins:
coins:
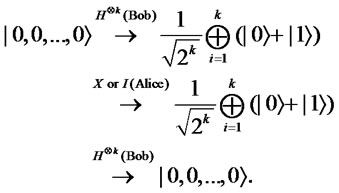
Therefore, we next denote a generalized even-odd game such that Bob cannot win with certainty by using only Meyer’s strategy but can win with certainty with our strategy.
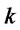 -Coin Even-Odd Check(G): First, Alice prepares
-Coin Even-Odd Check(G): First, Alice prepares ![]() coins and puts them into a box in the state of (H,D
coins and puts them into a box in the state of (H,D ,…, D
,…, D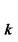 ), where
), where  (
( ). Suppose that any player cannot see the inside of the box and that Bob does not know D
). Suppose that any player cannot see the inside of the box and that Bob does not know D . Next, Bob flips some coins(or not), Alice flips some coins(or not), and Bob flips some coins(or not). Finally, they open the box. Alice wins if the number of H is odd; otherwise Bob wins if the number of H is even.
. Next, Bob flips some coins(or not), Alice flips some coins(or not), and Bob flips some coins(or not). Finally, they open the box. Alice wins if the number of H is odd; otherwise Bob wins if the number of H is even.
The payoff matrix of this problem can be shown as same as Figure 4. Also in this case, it is obvious that if they use classical strategies, neither Alice nor Bob can win the game with certainty. Moreover, because Meyer’s strategy uses the property of:
![]() Bob must know the initial state of all the coins in order to win the game. However, if he uses our quantum strategy, Bob can win the game with certainty. Now, we show a quantum strategy for this game with which Bob wins with certainty.
Bob must know the initial state of all the coins in order to win the game. However, if he uses our quantum strategy, Bob can win the game with certainty. Now, we show a quantum strategy for this game with which Bob wins with certainty.
Theorem 3.2 For ![]() -Coin Even-Odd Check(G), there exists a quantum strategy with which Bob wins with certainty.
-Coin Even-Odd Check(G), there exists a quantum strategy with which Bob wins with certainty.
Proof. Also in this case, we denote H and T by  and
and , respectively. Therefore, Alice prepares
, respectively. Therefore, Alice prepares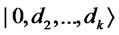 , where
, where 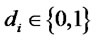 (
(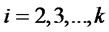 ). First, Bob executes the following operation:
). First, Bob executes the following operation:

Next, Alice flips the coins using the operations 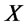 and
and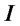 . Then, the state becomes
. Then, the state becomes
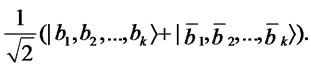
Finally, by using Lemma 2.1, Bob obtains

Thus, Bob can obtain the bits  satisfying
satisfying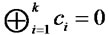 . This means that the number of H is even and he can win the game with certainty.
. This means that the number of H is even and he can win the game with certainty.
3.3 ![]() -Coin Flipping Games
-Coin Flipping Games
Next, we denote zero-sum games between two players modifying the games in the previous subsection and show that neither Alice nor Bob can win the games with certainty with classical strategies but Bob can win them with certainty with our quantum strategy.
![]() -Coin Flip: First, Alice prepares
-Coin Flip: First, Alice prepares ![]() coins and puts them into a box in the state of all the coins being heads, i.e., (H, H,…, H). Suppose that any player cannot see the inside of the box. Next, Bob flips some coins(or not), Alice flips
coins and puts them into a box in the state of all the coins being heads, i.e., (H, H,…, H). Suppose that any player cannot see the inside of the box. Next, Bob flips some coins(or not), Alice flips  coins(
coins(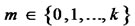 ) under keeping the value of
) under keeping the value of 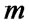 secret from Bob, and Bob flips some coins(or not). Finally, they open the box. Then, Bob wins if all the coins are in the following state: the state of the coins is (H, H,…, H) if
secret from Bob, and Bob flips some coins(or not). Finally, they open the box. Then, Bob wins if all the coins are in the following state: the state of the coins is (H, H,…, H) if  is even, or the state of the coins is (T,H,…, H) if
is even, or the state of the coins is (T,H,…, H) if  is odd. Otherwise Alice wins.
is odd. Otherwise Alice wins.
We show the payoff matrix in Figure 5. We can regard also this problem as whether Bob can predict Alice’s strategy, It is obvious that if they use classical strategies, neither Alice nor Bob can win the game with certainty. Moreover, by the same reason in the previous subsection, Bob cannot also win the game with certainty even if Meyer’s strategy is used. However, if Bob uses our quantum strategy, he can win the game with certainty. Now, we show a quantum strategy for this game with which Bob wins with certainty.
Theorem 3.3 For ![]() -Coin Flip, there exists a quantum strategy with which Bob wins with certainty.
-Coin Flip, there exists a quantum strategy with which Bob wins with certainty.
Proof. Alice prepares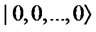 . First, Bob executes the following operation.
. First, Bob executes the following operation.
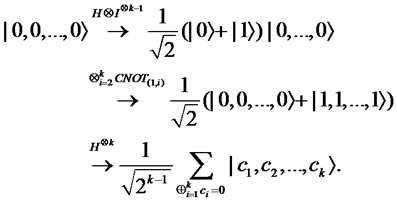

Figure 5.  -Coin Flip
-Coin Flip
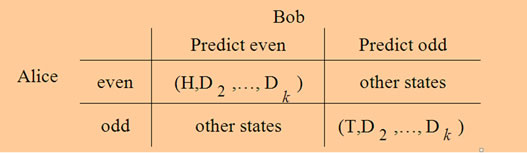
Figure 6.  -Coin Flip(G)
-Coin Flip(G)
Next, Alice flips  coins using the operation
coins using the operation .
.
Then, the state becomes

where  (
( ) and
) and![]() .
.
By using Lemma 2.2, Bob obtains

Moreover, he executes the following operation.
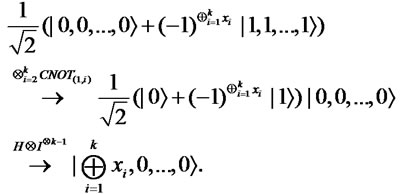
Then, 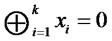 if
if  is even; otherwise
is even; otherwise  if
if  is odd. Therefore, Bob can win the game with certainty.
is odd. Therefore, Bob can win the game with certainty.
Next, we denote a generalized ![]() -coin flipping game.
-coin flipping game.
![]() -Coin Flip(G): First, Alice prepares
-Coin Flip(G): First, Alice prepares ![]() coins and puts them into a box in the state of (H,D
coins and puts them into a box in the state of (H,D ,…, D
,…, D ), where
), where 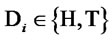 (
(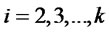 ). Suppose that any player cannot see the inside of the box and that Bob does not know D
). Suppose that any player cannot see the inside of the box and that Bob does not know D . Next, Bob flips some coins(or not), Alice flips
. Next, Bob flips some coins(or not), Alice flips  coins(
coins( ) under keeping the value of
) under keeping the value of 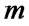 secret from Bob, and Bob flips some coins(or not). Finally, they open the box. Then, Bob wins if all the coins are in the following state: the state of the coins is (H,D
secret from Bob, and Bob flips some coins(or not). Finally, they open the box. Then, Bob wins if all the coins are in the following state: the state of the coins is (H,D ,…, D
,…, D ) if
) if 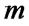 is even, or the state of the coins is (T,D
is even, or the state of the coins is (T,D ,…, D
,…, D ) if
) if  is odd. Otherwise Alice wins.
is odd. Otherwise Alice wins.
We show the payoff matrix in Figure 6. Also in this case, it is obvious that if they use classical strategies, neither Alice nor Bob can win the game with certainty and that Bob cannot win the game with certainty even if Meyer’s strategy is used. However, if Bob can use our quantum strategy, he wins the game with certainty. If Bob wishes to know only whether  is even or odd, we can easily construct the following protocol.
is even or odd, we can easily construct the following protocol.
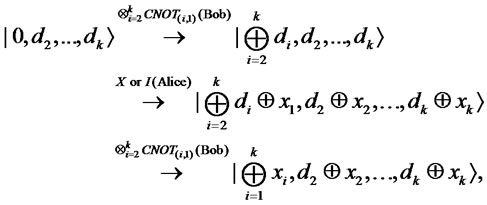
where  (
( ).
).
Now, we show a quantum strategy for this game with which Bob wins with certainty.
Theorem 3.4 For ![]() -Coin Flip(G), there exists a quantum strategy with which Bob wins with certainty.
-Coin Flip(G), there exists a quantum strategy with which Bob wins with certainty.
Proof. Alice prepares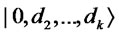 , where
, where 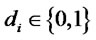 (
(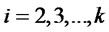 ). First, Bob executes the following operation.
). First, Bob executes the following operation.
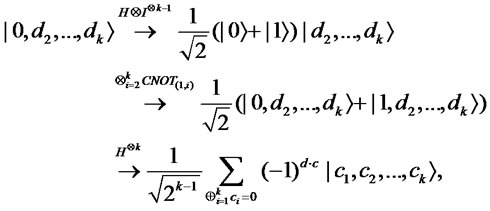
where 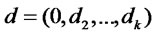 and
and .
.
Next, Alice flips 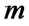 coins using the operation
coins using the operation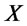 . Then, the state becomes
. Then, the state becomes
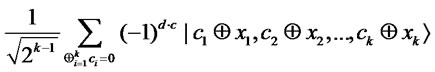
where 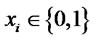 (
( ) and
) and![]() .
.
By using Lemma 2.2, Bob obtains

where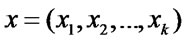 . Moreover, he executes the following operation.
. Moreover, he executes the following operation.
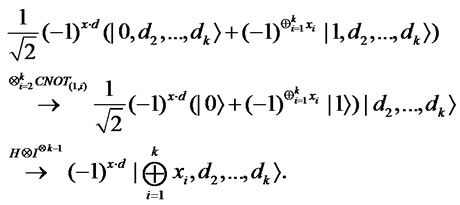
Then, 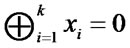 if
if 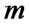 is even; otherwise
is even; otherwise 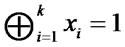 if
if 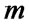 is odd. Therefore, Bob can win the game with certainty.
is odd. Therefore, Bob can win the game with certainty.
Finally, we denote a game combining the Even-Odd game and the Flipping game.

Figure 7. Extended ![]() -Coin Flip
-Coin Flip
Extended ![]() -Coin Flip: First, Alice prepares
-Coin Flip: First, Alice prepares 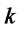 coins and puts them into a box in the state of all the coins being heads, i.e., (H, H,…, H). Suppose that any player cannot see the inside of the box. Next, Bob flips some coins(or not), Alice flips
coins and puts them into a box in the state of all the coins being heads, i.e., (H, H,…, H). Suppose that any player cannot see the inside of the box. Next, Bob flips some coins(or not), Alice flips  coins (
coins (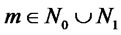 ) under keeping the value of
) under keeping the value of  secret from Bob, and Bob flips some coins(or not), where for some positive even number
secret from Bob, and Bob flips some coins(or not), where for some positive even number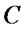 ,
,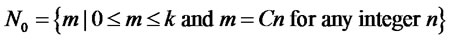 and
and 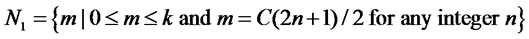 Finally, they open the box. Then, Bob wins if all the coins are in the following state: the number of H is even if
Finally, they open the box. Then, Bob wins if all the coins are in the following state: the number of H is even if  is an element in
is an element in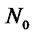 , or the number of H is odd if
, or the number of H is odd if  is an element in
is an element in . Otherwise Alice wins.
. Otherwise Alice wins.
We show the payoff matrix in Figure 7, and construct a quantum strategy such that Bob wins with certainty.
Theorem 3.5 For Extended ![]() -Coin Flip, there exists a quantum strategy with which Bob wins with certainty.
-Coin Flip, there exists a quantum strategy with which Bob wins with certainty.
Proof. Alice prepares . First, Bob executes the following operation:
. First, Bob executes the following operation:

Next, Alice flips 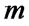 coins using the operation
coins using the operation . Then, the state becomes
. Then, the state becomes

where 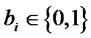 (
( ) and
) and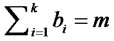 .
.
Bob applies  to the state.
to the state.

Moreover, by using Lemma 2.1, Bob obtains

if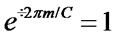 ; otherwise he obtains
; otherwise he obtains

if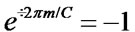 .
.
Thus,  is an element in
is an element in 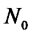 and
and  if
if ; otherwise
; otherwise 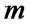 is an element in
is an element in 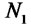 and
and
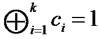 if
if . Therefore, Bob can win the game with certainty.
. Therefore, Bob can win the game with certainty.
When 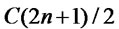 is odd, Bob can always win without operating to
is odd, Bob can always win without operating to ![]() coins. On the other hand, our strategy succeeds even if
coins. On the other hand, our strategy succeeds even if  is even.
is even.
4. Applications to Newcomb’s Paradox
In this section, we study Newcomb’s paradox (Free Will problem) and show some quantum strategies for this problem. A quantum solution of this problem is shown by using Meyer’s quantum strategy by Piotrowski and Sładkowski [18]. We study this problem by using our results in previous section. A problem is as follows:
Newcomb’s problem: Let Bob have the ability to predict Alice’s will. Now, Bob prepares two boxes, Box1 and Box2, and Alice can select either Box2 or both boxes. Box1 contains $1. Box2 contains $1,000 only if Alice selects only Box2; otherwise Box2 is empty($0). Which is better for Alice?
The payoff matrix is shown in Figure 8. The focus of this problem is whether Bob can really predict Alice’s will, or whether Bob can control Alice’s will. Obviously, Alice’s strategy is selecting both boxes if Bob cannot predict Alice’s will. Now, we modify this problem as simplified problems. In addition, we observe only strategies on Box2.
Newcomb1: First, Alice decides whether she selects either Box2 or not, but Bob cannot know her selection. Box2 contains $1,000 only if Alice selects Box2; otherwise Box2 is empty($0). Can Bob let Alice select her first will even if Alice changes her will after the first selection?
Theorem 4.1 For Newcomb1, there exists a quantum strategy that can be positively solved.
Proof. Alice selects a state 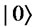 if she selects Box2; otherwise she selects a state
if she selects Box2; otherwise she selects a state . Note that Bob does not know the state. To this state, Bob applies H, Alice applies X if she changes her will, and Bob applies H. Fi
. Note that Bob does not know the state. To this state, Bob applies H, Alice applies X if she changes her will, and Bob applies H. Fi

Figure 8. Newcomb’s problem

Figure 9. Chicken
nally, the state is  if her first selection is Box2; otherwise it is
if her first selection is Box2; otherwise it is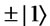 . Then, Bob can let Alice select her first will.
. Then, Bob can let Alice select her first will.
This strategy uses Meyer’s strategy. Moreover, we can also show other proofs by using Theorem 3.3 or Theorem 3.4. For Newcomb1, Bob does not permit Alice’s change. Next, by using 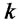 -Coin Flip(G), we modify this problem to problems such that Bob permits Alice’s change.
-Coin Flip(G), we modify this problem to problems such that Bob permits Alice’s change.
Newcomb2: Alice prepares ![]() coins and puts them into a box in the state of (H,D
coins and puts them into a box in the state of (H,D ,…, D
,…, D ), where
), where  (
( ). Next, Bob flips some coins(or not), Alice flips
). Next, Bob flips some coins(or not), Alice flips ![]() coins(
coins( ) under keeping the value of
) under keeping the value of ![]() secret from Bob, and Bob flips some coins(or not), where let Alice do not change her will if
secret from Bob, and Bob flips some coins(or not), where let Alice do not change her will if ![]() is even; otherwise let she change her will. Can Bob know whether
is even; otherwise let she change her will. Can Bob know whether ![]() is even or odd?
is even or odd?
Theorem 4.2 For Newcomb2, there exist a quantum strategy that can be positively solved.
Proof. This result is immediately obtained by Theorem 3.4.
We can regard this problem as Newcomb’s problem when the value of ![]() is her will, i.e., she selects Box2 when
is her will, i.e., she selects Box2 when ![]() is even; otherwise she selects both boxes. Thus, Bob can predict Alice’s will. We can also modify Newcomb’s problem by using
is even; otherwise she selects both boxes. Thus, Bob can predict Alice’s will. We can also modify Newcomb’s problem by using ![]() -Coin Flip and Extended
-Coin Flip and Extended ![]() -Coin Flip.
-Coin Flip.
Next, we denote that we can also modify Alice’s will in Newcomb2 to ![]() -player’s will.
-player’s will.
![]() -Newcomb2: First,
-Newcomb2: First, ![]() players,
players,  , decide whether they selects
, decide whether they selects 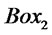 or not. They prepare
or not. They prepare ![]() coins and puts them into a box in the state of (H,D
coins and puts them into a box in the state of (H,D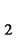 ,…, D
,…, D ), where
), where  (
(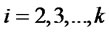 ), and let player
), and let player 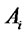 (
(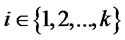 ) deal with the
) deal with the  -th coin. Now, Bob flips some coins(or not). Next, each
-th coin. Now, Bob flips some coins(or not). Next, each 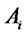 (
(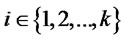 ) flips his/her coin(or not), where let the number of
) flips his/her coin(or not), where let the number of ![]() -player’s flips be
-player’s flips be ![]() (
( ), and let they do not change their will if
), and let they do not change their will if ![]() is even; otherwise let they change their will. Finally, Bob flips some coins(or not). Can Bob know whether
is even; otherwise let they change their will. Finally, Bob flips some coins(or not). Can Bob know whether ![]() is even or odd?
is even or odd?
The quantum strategy for Bob is same as Newcomb2.
Finally, we study the Chicken game. The payoff matrix is shown in Figure 9. In the Chicken game, the Nash equilibrium points are (Swerve, Drive straight) and (Drive straight, Swerve). By classical strategies, the probability that each player selects either Swerve or Drive straight is 1/2. This means that either (Swerve, Swerve) or (Drive straight, Drive straight) may be selected. On the other hand, by our quantum strategies, either (Swerve, Drive straight) and (Drive straight, Swerve) can be selected with certainty because Bob can predict Alice’s will.
5. Conclusions
In this paper, we proposed quantum strategies with entanglement for ![]() -coin flipping games. These games are multi-qubit variations of the quantum strategy by Meyer [4]. One player is constrained to play classically but the other player can use a quantum strategy. We then showed that by using a technique in quantum communication complexity theory, our quantum strategies have an advantage over classical ones. For a player using the quantum strategy, the entanglement is used in order to obtain the information of the enemy and the player can always win the games. Moreover, by rewriting Newcomb’s paradox including multi-player’s will, we also showed that we can use our results as its quantum strategies and that a player can have an ability to predict another player’s will.
-coin flipping games. These games are multi-qubit variations of the quantum strategy by Meyer [4]. One player is constrained to play classically but the other player can use a quantum strategy. We then showed that by using a technique in quantum communication complexity theory, our quantum strategies have an advantage over classical ones. For a player using the quantum strategy, the entanglement is used in order to obtain the information of the enemy and the player can always win the games. Moreover, by rewriting Newcomb’s paradox including multi-player’s will, we also showed that we can use our results as its quantum strategies and that a player can have an ability to predict another player’s will.
Can Bob always win our games even if both players use quantum strategies? This answer is “No”. Meyer also showed that Q cannot always win if Picard can also use a quantum strategy [4]. In the same reason, Bob cannot always win our games if Alice can also use a quantum strategy. Therefore, it is an interesting question whether Bob can always win the games in the case when both players are constrained to only execute some restricted quantum operations.
REFERENCES
- P. W. Shor, “Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer,” SIAM Journal of Computing, Vol. 26, pp. 1484– 1509, 1997.
- L. K. Grover, “A fast quantum mechanical algorithm for database search,” Proceedings of the 28th ACM Symposium on Theory of Computing, pp. 212–219, 1996.
- J. von Neumann and O. Morgenstern, “Theory of games and economic behavior, third edition,” Princeton University Press, Princeton, 1953.
- D. A. Meyer, “Quantum strategies,” Physical Review Letters, Vol. 82, pp. 1052–1055, 1999.
- J. Eisert, M. Wilkens, and M. Lewenstein, “Quantum games and quantum strategies,” Physical Review Letters, Vol. 83, pp. 3077–3080, 1999.
- J. Du, H. Li, X. Xu, M. Shi, J. Wu, X. Zhou, and R. Han, “Experimental realization of quantum games on a quantum computer,” Physical Review Letters, Vol. 88, 137902, 2002.
- J. Du, H. Li, X. Xu, X. Zhou, and R. Han, “Entanglement enhanced multiplayer quantum games,” Physics Letters A, Vol. 302, pp. 229–233, 2002.
- J. Eisert and M. Wilkens, “Quantum games,” Journal of Modern Optics, Vol. 47, pp. 2543–2556, 2000.
- A. Iqbal and A. H. Toor, “Evolutionarily stable strategies in quantum games,” Physics Letters A, Vol. 280, pp. 249–256, 2001.
- L. Marinatto and T. Weber, “A quantum approach to static games of complete information,” Physics Letters A, Vol. 272, pp. 291–303, 2000.
- M. D’Ariano, R. Gill, M. Keyl, R. Werner, B. Kümmerer, and H. Maassen, “The quantum Monty Hall problem,” Quantum Information and Computing, Vol. 2, pp. 355–366, 2002.
- A. P. Flitney and D. Abbott, “Quantum version of the Monty Hall problem,” Physical Review A, Vol. 65, 2002.
- C. F. Li, Y. S. Zhang, Y. F. Huang, and G. C. Guo, “Quantum strategies of quantum measurements,” Physics Letters A, Vol. 280, pp. 257–260, 2001.
- A. P. Flitney, J. Ng, and D. Abbott, “Quantum Parrondo’s games,” Physica A, Vol. 314, pp. 35–42, 2002.
- E. W. Piotrowski and J. Sładkowski, “Quantum-like approach to financial risk: Quantum anthropic principle,” Acta Physica Polonica B, Vol. 32, pp. 3873–3879, 2001.
- E. W. Piotrowski and J. Sładkowski, “Quantum bargaining games,” Physica A, Vol. 308, 391–401, 2002.
- E. W. Piotrowski and J. Sładkowski, “Quantum market games,” Physica A, Vol. 312, pp. 208–216, 2002.
- E. W. Piotrowski and J. Sładkowski, “Quantum solution to the Newcomb’s paradox,” International Journal of Quantum Information, Vol. 1, pp. 395–402, 2003.
- H. Buhrman, R. Cleve, and W. van Dam, “Quantum entanglement and communication complexity,” SIAM Journal of Computing, Vol. 30, pp. 1829–1841, 2000.
- H. Buhrman, W. van Dam, P. Hoyer, and A. Tapp, “Multiparty quantum communication complexity,” Physical Review A, Vol. 60, pp. 2737–2741, 1999.
- R. Cleve and H. Buhrman, “Substituting quantum entanglement for communication,” Physical Review A, Vol. 56, pp. 1201–1204, 1997.
- R. B. Myerson, “Game theory,” Harvard University Press, Cambridge, 1991.
- M. J. Osborne and A. Rubinstein, “A course in game theory,” MIT Press, Cambridge, 1994.

